八年级数学各章知识点(华东师大版)上册
华东师大版八年级数学上册知识点.pdf

华东师大,版,八年级,数学,上册,知识点,八年级上册知识点第11章数的平方11.1平方根与立方根11.2实数2.一个数的绝对值是非负数,即a≥0,因此,在实数范围内,绝对值最小的数是零.两个相反数的绝对值相等.第12章整式的乘除12.1幂的运算12.1.1同底数幂的乘法同底数幂的乘法法则(m、n为正整数)可以逆用,即am+n=am·an(m、n为正整数)。
12.1.2幂的乘方,12.1.3积的乘方1、幂的乘方的意义及运算法则1. 幂的乘方的意义幂的乘方是指几个相同的幂相乘。
如(a3)2是两个a3相乘。
2. 幂的乘方的运算法则(m、n为正整数),即幂的乘方,底数不变,指数相乘。
2、幂的乘方运算法则的逆向运用幂的乘方运算法则可以逆向运用,即amn=(am)n=(an)m(m、n为正整数)。
3、积的乘方的意义及运算法则1. 积的乘方的意义积的乘方指底数是乘积形式的乘方。
2. 积的乘方的运算法则(n为正整数),即积的乘方,把积的每一个因式分别乘方,再把所得的幂相乘。
4、积的乘方运算法则的的逆向运用积的乘方的运算法则可以逆用,即anbn=(ab)n(n为正整数)。
注意:运用积的乘方运算法则进行运算,要注意系数也要乘方;底数是科学计数法的形式时,乘方后的结果往往也需要写成科学计数法的形式。
12.1.4同底数幂的除法1、同底数幂的除法法则一般地,设m,n为正整数,m﹥n,a≠0,有am÷an=am-n这就是说,同底数幂相除,底数不变,指数相减。
注意:只有“同底数”的幂才可应用同底数幂的除法法则,底数互为相反数时可以先化为同底数的幂再进行运算。
()2、逆用同底数幂的除法法则同底数幂的除法法则可以逆用,即am-n=am÷an(m,n都是正整数,且m﹥n,a≠0)12.2整式的乘法12.2.1单项式与单项式相乘12.2.2单项式与多项式相乘1、单项式与单项式相乘单项式与单项式相乘,只要将它们的系数、相同字母的幂分别相乘,对于只在一个单项式中出现的字母,则连同它的指数一起作为积的一个因式。
2024—2025学年华东师大版数学八年级上册第13章《全等三角形》基础复习

第13章基础复习知识点1命题、定理与证明1.一般地,判断某一件事情的语句叫做命题.命题一般由条件和结构两部分组成,可以写成“如果……,那么……”的形式.2.基本事实是在继续学习过程中用来判断其他命题真假的原始依据.3.定理:有些命题可以从基本事实或其他真命题出发,用逻辑推理的方法判断它们是正确的,并且可以作为进一步判断其他命题真假的依据,这样的真命题叫做定理.4.根据条件、定义以及基本事实、定理等,经过演绎推理,来判断一个命题是否正确,这样的推理过程叫做证明.1.下列命题中,是真命题的是()A.无限小数是无理数B.从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离C.平行于同一条直线的两条直线平行D.过一点有且只有一条直线与已知直线垂直2.判断命题“如果n<1,那么W−1<0”是假命题,只需举出一个反例.反例中的n可以为()A.-2u−12 C.0D123.把命题“对顶角相等”改写成“如果⋯⋯,那么⋯⋯”的形式:.4.填写下列证明过程中的推理根据:已知:如图所示,AC、BD相交于点O,DF平分∠CDO与AC相交于点F,BE平分∠ABO与AC相交于点E,∠A=∠C.求证:∠1=∠2.证明:∵∠A=∠C(),∴AB∥CD(),∴∠ABO=∠CDO(),又∵DF平分∠CDO,BE平分∠ABO,∴∠1=12∠Cs∠2=12∠B(),∴∠1=∠2().知识点2三角形全等的判定1.能够完全重合的两个三角形是全等三角形,相互重合的顶点是对应顶点,相互重合的边是对应边,相互重合的角是对应角,全等三角形的对应边相等,对应角相等.2.全等三角形的判定条件:①两边及其夹角分别相等的两个三角形全等.简写为S. A.S.(或边角边).②两角及其夹边分别相等的两个三角形全等.简写为A.S. A.(或角边角).③两角分别相等且其中一组等角的对边相等的两个三角形全等.简写为A. A.S.(或角角边).④三边分别相等的两个三角形全等.简写为S.S.S.(或边边边).⑤斜边和一条直角边分别相等的两个直角三角形全等.简写为H.L.(或“斜边直角边”).5.如图,AB=AD,CB=CD,∠B=32°,∠BAD=72°,则∠ACD的度数是()A.102°B.112°C.114°D.1226.如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是()A.∠A=∠DB.AC=DFC.AB=EDD.BF=EC7.如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,若AB=4,CF=3,则BD的长是()A.0.5B.1C.1.5D.28.图中的小正方形边长都相等,若△MNP≌△MFQ,则点Q可能是图中的()A.点DB.点CC.点BD.点A9.下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC一定全等的是()A.甲和乙B.乙和丙C.甲和丙D.只有丙10.如图所示,在Rt△ACD和Rt△BCE中,若AD=BE,DC=EC,则不正确的结论是()A.Rt△ACD≌Rt△BCEB.OA=OBC.E是AC的中点D.AE=BD11.如图,点D在线段BC上,若BC=DE,AC=DC,AB=EC,且∠ACE=180°-∠ABC-2x°,则下列角中,大小为x°的角是()A.∠EFCB.∠ABCC.∠FDCD.∠DFC12.如图,在等腰△ABC中,AB=AC,AB>BC,点D在边BC上,且C B=14,点E、F在线段AD上,满足∠BED=∠CFD=∠BAC,若△B=20,则.△B+△C=()A.18B.15C.12D.913.如图,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的有()A.1个B.2个C.3个D.4个14.如图,AC=DC,BC=EC,请你添加一个适当的条件:,使得△ABC≌△DEC.15.如图,∠1=∠2,∠3=∠4,,则全等三角形有对.16.如图,已知△ABC中,F是高AD和BE的交点,且AD=BD,CD=4,则线段DF的长度为.17.(南通中考)如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A和B.连结AC并延长到点D,使CD=CA.连结BC并延长到点E,使CE= CB.连结DE,那么量出DE的长就是A、B的距离.为什么?18.如图,在△ABC中,AC=5,中线AD=7,求边AB的取值范围.19.如图,点O是线段AB的中点,OD∥BC且OD=BC.(1)求证:△AOD≌△OBC.(2)若∠ADO=35°,求∠DOC的度数.20.王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合.(1)求证:△ADC≌△CEB.(2)求两堵木墙之间的距离.21.如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.(1)求证:△ABC≌△ADE.(2)求∠FAE的度数.(3)求证:CD=2BF+DE.。
华师大版八年级上册数学知识点

华师大版八年级上册数学知识点
华师大版八年级上册数学知识点如下:
1. 分式与整式
-整式的概念
-分式的概念
-分式的相等性与消去律
-有理数的加法与减法
2. 比例与比
-比例的定义
-比例恒等式与比例方程
-比例的延长与缩短
-平行线分线段成比例
-利用比例解决实际问题
3. 一次函数
-函数的概念
-一次函数的概念
-一次函数的图象与性质
-一次函数的表示与求解
4. 相似与全等
-相似的概念
-全等的概念
-相似三角形的性质
-利用相似解决实际问题
-全等三角形的性质
5. 图形的认识
-点、直线和线段的概念
-角度的概念与计算
-三角形的概念与分类
-四边形的分类与性质
6. 平面直角坐标系
-平面直角坐标系的引入
-平面直角坐标系中的距离
-平面直角坐标系中的中点
-平面直角坐标系中的斜率
-平面直角坐标系中的一次函数方程
以上是华师大版八年级上册数学的一些重要知识点,可能会根据不同版本和教材的差异存在一些差别,建议以教材为准。
华东师大版八年级上册数学知识点集及思维导图
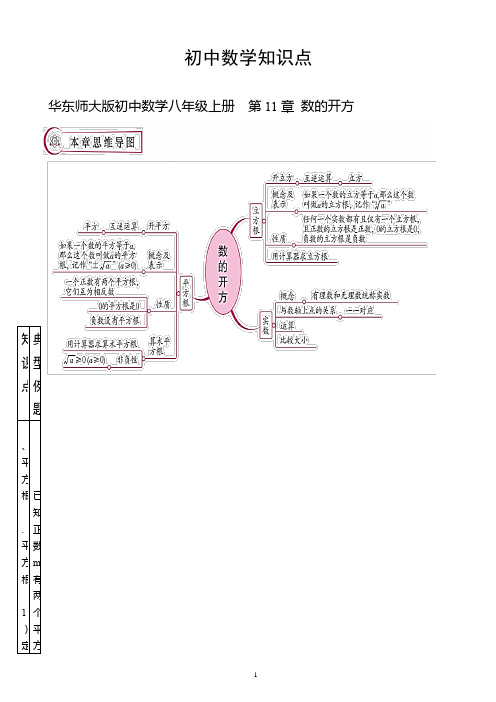
初中数学知识点华东师大版初中数学八年级上册 第11章 数的开方 知识点 典型例题、平方根 .平方根 1)定 已知正数m 有两个平方义:如果一个数的平方等于a ,那么这个数叫做a 的平方根.(2)表示方法:)0(,≥±a a . (3)性质:正数有两个互为相反数的平方根;零的平方根是零;负数没有平方根.2.算术平方根 (1)定义:正数a 的正的平方根,叫做a 的算术平方根.0的算术平方根是0.(2)表示方法:)0(,≥a a .(3)重要性质:双重非负性:)0(,0≥≥a a其他具有非负性的式子:a n a n ,(2为正整数).运算性质:如果几个非负数的和为0,那么每一个非负数都为0. (4)运算性质:一个非负数的算术平方根的平方等于它本身,)0(,)(2≥=a a a . 一个实数的平方的算术平方根等于它的绝对值,a a =2. 3.开平方定义:求一个非负数的平方根的运算,叫做开平方. 二、立方根 1.立方根 (1)定义:如果一个数的立方等于a ,那么这个数叫做a 的立方根.(2)表示方法:3a . (3)性质:正数的立方根是正数,负数的立方根是负数,0的立方根是0.(4)运算性质:a a a ==3333)(. 三、实数 1.无理数定义:无限不循环小数叫做无理数. 2.实数有理数和无理数统称实数. 3.实数的分类 按定义分:⎪⎩⎪⎨⎧⎩⎨⎧无理数分数整数有理数实数按性质分:根,分别是a+3与2a -15,求a 的值,并求这个正数m.已知a a -=-22,求a 的取值范围.若0a 2=++c b ,求a 、b 、c 的值.已知实数a 、b 、c 在数轴上的位置如图所示,化简:222)(c a c b a a ---++一个数的立方根是它本身,则这个数是 .计算:=-33)2( .有下列各数:2π,0,9,32.0 ,2-1,722,⋅⋅⋅3030030003.0,其中无理数有 . 求一个无理数的整数部分和小数部分:已知a 是11的整数部分,b 是11的小数部分,求a 和b 的值.⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负无理数负有理数负实数零正无理数正有理数正实数实数 4.实数与数轴上点的关系 实数与数轴上的点一一对应. 5.实数大小比较常有方法平方法;做差法;倒数法;做商法比较大小:23____32 32____3-5+华东师大版初中数学八年级上册 第12章 整式的乘除 知识点典型例题一、幂的运算 1.同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加.已知32=x ,求32+x 的值.华东师大版初中数学八年级上册第13章全等三角形知识点典型例题一、命题、定理与证明1.命题(1)定义:表示判断的语句叫做命题.(2)组成:命题是由条件和结论两部分组成。
最新华东师大版八年级数学上册知识点总结
例:
的平方和减去它们的积的 2
逆用
倍
定义:把一个多项式化为几
常考点:
个整式的积的形式;叫做多 ①两种因式分解法一起运用
项式的因式分解 (先提公因式;然后再运用公
因式分解的方法:
式法)
因式分解
①提公因式法
例:
②运用乘法公式法
=
=(a+b)(a-b)
②“1”常Байду номын сангаас要变成“”
例:
第十三章:全等三角形
知识点
2 / 16
常运用于股市与气温的统计
15 / 16
综合考查
①扇形统计图与条形统计图一起考;条形统计图的具体数据为 频数;扇形统计图的百分比为频率;从而可以根据公式计算出
总次数 ②根据统计表;会制作条形统计图(单位值;间隔值要相等)
③根据统计表;会制作扇形统计图(计算百分比和百分数) ④扇形圆心角的度数=百分比
幂
幂的乘方
幂的乘方;底数不变;指数 逆用:
的
相乘
例:
运
积的乘方;把积的每一个因 逆用:
算
式分别相乘;再把所得的幂 例=1
积的乘法
相乘
=
=
同底数幂相处;底数不变; 逆用:
同底数幂的除法 指数相减
例:若=2;则的值是?
单项式与单项式相乘;只要
单项式与单项式相 将它们的系数、相同的字母
乘 的幂分别相乘;对于只在一
⑤扇形的面积之比=各部分所占百分数之比=各部分圆心角之比
16 / 16
整
个单项式中出现的字母;连
式
同它的指数一起作为积的一
的
个因式
乘 单项式与多项式相 单项式与多项式相乘;将单
最新华东师大版八年级数学上册知识点总结

最新华东师大版八年级数学(shùxué)上册知识点总结最新华东师大版八年级数学(shùxué)上册知识点总结华师版八年级上册知识点总结第十一章:数的开方知识点平方根内容概念:如果一个数的平方等于a,那么这个数叫做a的平方根算术(suànshù)平方根:正数a的正的平方根记作:a性质:正数有两个平方根,它们互为相反数,0的平方根是0,负数没有平方根概念:如果一个数的立方等于a,那么这个数叫做a的立方根性质:任何实数的立方根只有一个,正数的立方根是正数,负数的立方根是负数,0的立方根是0考点:①〔a的取值范围(fànwéi)a≥〕②(的取值范围≥)③(a的取值范围为任意实数)(≥)④==(多项式与多项式多项式与多项式相乘,先用一个多项式的每一项分别(fēnbié)乘以另一个多项式的每一项,再把所得的积相加例:〔某+2〕〔某3〕=+=例:24÷=〔24÷〕〔÷〕〔÷〕=8整式的除法单项式相除,把系数、同底数幂分别相除作为商的因式,对单项式除于单项式于只在被除式中出现的字母,那么连同它的指数一起作为商的一个因式多项式除于单项式,先用这个多项式除于单项式多项式的每一项除于这个单项式,再把所得的商相加例:(9+)÷(3某)=9÷÷+÷=3+例:(a+b)(a-b)=逆用:=(a+b)(a-b)例:(+)=++逆用++=(+)例:()=+逆用+=()常考点:①两种因式分解法一起运用〔先提公因式,然后再运用公式法〕例:++=++=(+)乘法公式平方差公式两数和与这两数差的积,等于这两数的平方差两数和的平方公式两数和的平方,等于这两数的平方和加上它们的积的2倍两数差的平方公式两数差的平方,等于这两数的平方和减去它们的积的2倍定义:把一个多项式化为几个整式的积的形式,叫做多项式的因式分解因式分解的方法:因式分解①提公因式法②运用乘法公式法=(a+b)(a-b)++=(+)+=()②“1〞常常要变成“12〞例:=()=+〔〕第十三章:全等三角形知识点全等三角形内容性质:全等三角形的对应边和对应角相等三角形全等的判定:1.〔边边边〕S.S.S.:如果两个三角形的三条边都对应地相等,那么这两个三角形全等。
最新华东师大版八年级数学上册知识点总结

华师版八年级上册知识点总结第十一章:数的开方知识点内容备注平方根立方根实数概念:如果一个数的平方等于a,那么这个数叫做 a 的平方根算术平方根:正数 a 的正的平方根记作:性质:正数有两个平方根,它们互为相反数,0 的平方根是0,负数没有平方根概念:如果一个数的立方等于a,那么这个数叫做 a 的立方根性质:任何实数的立方根只有一个,正数的立方根是正数,负数的立方根是负数,0 的立方根是01. 包括有理数和无理数2. 实数与数轴上的点一一对应常见的无理数(无限不循环小数)有:① π②开方开不尽的数,如,等考点:(a 的取值范围 a )②( )③(a 的取值范围为任意实数)④=例:= ()=5⑤=a(a 为任意实数)例:=2, =—2考点:判断下列的数哪些是无理数?有理数:分数和整数的统称如:,, 0 都是有理数知识点内容备注同底数幂相乘,底数不变,同底数幂幂的乘法的指数相加逆用:=运幂的算乘方幂的乘方,底数不变,指逆用:乘法同底数幂的除法单项式与单项式相整乘式==同底数幂相处,底数不变,指数相减单项式与单项式相乘,只要将它们的系数、相同的字母的幂分别相乘,对于只在一个单项式中出现的字母,连同它的指数一起=1逆用:例:若=2,则的值是?例:·=[3 ·(-2)] ·( · x)· (y·)=数相乘例:积的乘方,把积的每一个因式分别相乘,再把所得逆用:例积的的幂相乘例: (- 2 =(- 2+(- 2) =- 6 +10例:( X+2)( X —3) = = 例: 24 =( 24 )()()=8例: (9 )(3x)=9=3平 方 差 乘 公式 法 两 数 和 的 公 平方公式式两 数 差 的平方公式因式分解 两数和与这两数差的积,等于这两数的平方差 两数和的平方,等于这两数的平方和加上它们的积的 2 倍两数差的平方,等于这两数的平方和减去它们的积的 2 倍定义:把一个多项式化为几个整式的积的形式,叫做多项式的因式分解 因式分解的方法:①提公因式法 ②运用乘法公式法=(a+b)(a-b)例: (a+b)(a-b)= 逆用: =(a+b)(a-b)例: 逆用例: 逆用常考点:①两种因式分解法一起运用(先提公因式, 然后再运用公式法)例:=②“ 1”常常要变成“”例:第十三章:全等三角形 知识点内容备注的 作为积的一个因式乘 单 项 式 与 单项式与多项式相乘,将 法多 项 式 相 单项式分别乘以多项式的乘每一项,再将所得的积相 加多项式与多项式相乘,先多 项 式 与 用一个多项式的每一项分多项式别乘以另一个多项式的每一项,再把所得的积相加单项式相除,把系数、同 整 底数幂分别相除作为商的式单 项 式 除 因式,对于只在被除式中的 于单项式 出现的字母,则连同它的 除 指数一起作为商的一个因 法式多项式除于单项式,先用多 项 式 除 这个多项式的每一项除于 于单项式这个单项式,再把所得的商相加性质:全等三角形的对应边和对应角相等三角形全等的判定:常考点:①公共边1. (边边边)S.S.S:.如果两个三角形的三条②公共角全等三角形性质边都对应地相等,那么这两个三角形全等。
华东师大版八年级数学上册知识点总结
式
再将所得的积相加
因式分解
+ + = ( + )
例: + +
= ( + + )=( + )
例:() − = () −
− + = ( − )
= ( + )( − )
第十三章:全等三角形
知识点
内容
备注
全等三角形
性质:全等三角形的对应边和对应角相等
三角形全等的判定:
1. (边边边)S.S.S.:如果两个三角形的三条
边都对应地相等,那么这两个三角形全等。
2.(边、角、边)S.A.S.:如果两个三角形的其
中两条边都对应地相等,且两条边夹着的角都
对应地相等,那么这两个三角形全等。
例:√=2, √( − ) =—2
1. 包括有理数和无理数
考点:
判断下列的数哪些是无
2. 实数与数轴上的点一一对应
理数?
常见的无理数(无限不循环小数) 有理数:分数和整数的统称
有:①π
22
如: ,0. 2̇8̇, 0 都是有理数
7
②开方开不尽的数,如√, √等
第十一章:数的开方
第十二章:整式的乘除
知识点
内容
同底数幂相乘,底数不变,指
同底数幂的乘法
幂
的
运
算
幂的乘方
幂的乘方,底数不变,指数相
积的乘法
同底数幂的除法
单项式与单项式相
乘整式的源自乘数相加 × = +
单项式与多项式相
乘
乘 ( ) =
积的乘方,把积的每一个因式
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十二章:数 的 开 方 (一)1、如果一个数的 等于a ,那么这个数叫做a 的平方根,正数的平方根有 个,它们的关系是 ,0的平方根是 ,负数 。
正数a 的 ,叫做a 的算术平方根。
3、如果一个数的 等于a ,那么这个数就叫做a 的立方根,正数有 的立方根,负数有 的立方根,0的立方根为 。
一、平方根的概念及性质例题分析:1、(1)________的平方等于25,所以25的平方根是________(2)_____的平方等于 ,所以 的平方根是________(3)121的平方根_____,所以它的算术平方根是____(4) 的平方根______,所以它的算术平方根是_______2、下列说法正确的个数是( )①0.25的平方根是0.5;②-2是4的平方根;③只有正数才有平方根;④负数没有平方根 A 、1 B 、2 C 、3 D 、43、下列说法中不正确的是( )A 、9的算术平方根是3B 、16的平方根是2±C 、27的立方根是3±D 、立方根等于-1的实数是-1 4、求下列各数的平方根1)、100 2)、0 3)、 4)、1 5)、 6)、0.095、若2m -4与3m -1是同一个数的平方根,则m 的值是( )A 、-3 B 、1 C 、-3 或1 D 、-16、若一个正数的平方根是2a -1和-a +2,则a =________7、某数的平方根是3+a 和152-a ,那么这个数是多少?二、算术平方根的概念及性质一个正数的平方根有两个,它们互为相反数,而一个正数的算术平方根只能是一个正数 1、16的算术平方根是( )A 、4± B 、4 C 、2± D 、2 2、9的算术平方根是( )A 、-3 B 、3 C 、3± D 、813、下列计算不正确的是( )A 、24±= B 、981)9(2==- C 、4.0064.03= D 、62163-=-4、下列叙述正确的是( )A 、0.4的平方根是±0.2B 、-(-2)3 的立方根不存在C 、±6是36的算术平方根D 、-27的立方根是-3 5、不使用计算器,你能估算出126的算术平方根的大小在哪两个整数之间吗?( )A 、10-11之间B 、11-12之间C 、12-13之间D 、13-14之间6、如果一个数的平方根与立方根相同,那么这个数是( )A 、0 B 、±1 C 、0和1 D 、0或±17、若216a =,则a =________ 1.2=,则a =________ 8、3-2的相反数是________;3-2的绝对值是________ 9、求下列各数的算术平方根1)、0.0025 2)、2)6(- 3)、0 4)(-2)³(-6)三、立方根的概念及性质 9164141259491512、下列说法中错误的是()A、是5的平方根B、-16是256的平方根C、-15是算术平方根D、是的平方根3、下列说法中错误的是()A、负数没有立方根B、1的立方根是1C、38的平方根是2±D、立方根等于它本身的数有3个4、若a是2)3(-的平方根,则3a=()A、-3 B、33C、3333或-D、3和-35、已知x的平方根是2a+3和1-3a ,y的立方根为a ,求x+y的值6、的平方根是______________; 9的立方根是_________________8、计算:(考查平方根、算术平方根、立方根的表示方法)1)、9-2)、38-3)、161456四、能力点:会用若0||2=++zyx,则0,,0===zyx去解决问题例题分析:1、已知x,y是实数,且0)3(432=-++yx,则xy的值是()A、4B、-4C、49D、-492、若054=-++-yxx,则=x________,=y________3、已知0)1(|1|352=-+-+-xyx,求xyz=________4、已知| |+,求的值5、1)0169)12(2=--x;2)01)13(42=-+x;3)24273=-x;4)4)3(213=+x52)15(-72±494 81164-+yx010=+-yx y、x无理数常见的三种形式:1)开方开不尽的数,如2,3 2)特定意义的数,如π 3)有特定结构的数,如0.010010001……1、下列各数:23,-3π,3.1415926,25,191,38-,3.101001000……中无理数有( )2、若无理数a 满足不等式1<a<4,请写出两个符合条件的无理数_______________3、下列各数:722,0,-π,8,364,2-3中无理数有________ __2、下列各数:23,-722,327-,1.414,-3π,3.12122 ,9-中无理数有_______ ____;有理数有______ _________;负数有______ _________;整数有______ _________; 3、设a 是实数,则|a|-a 的值( )A 、可以是负数B 、不可能是负数C 、必是正数D 、可以是正数也可以是负数4、下列实数:191,-2π,8,,39,0中无理数有( )A 、4 B 、3 C 、2 D 、15、下列说法中正确的是( )A 、有限小数是有理数B 、无限小数是无理数C 、数轴上的点与有理数一一对应D 、无理数就是带根号的数6、下列各数中,互为相反数的是( )A 、-3和3 B 、|-3|与- 31C 、|-3|与31D 、|-3|与-3 7、边长为1的正方形的对角线的长是( )A 、整数 B 、分数 C 、有理数 D 、无理数 8、写出一个3和4之间的无理数__________ 9、数轴上表示31-的点到原点的距离是__________10、比较大小:(1)52__________25;(2)35-__________3-11、在下列各数中,0.5,45,3125,-0.03745,31,12.0,1-5,其中无理数的个数为( )A 、2B 、3C 、4D 、512、一个正方形的面积扩大为原来的n 倍,则它的边长扩大为原来的( )A 、n 倍B 、2n 倍C 、n 倍D 、2n倍6.9的平方根是 A. ±3 B.3 C. ±3 D.321、x 为何值时,下列各式有意义:①x +5 ②x -22、解下列方程1) x 2=4 2)x 3-27=0 3)5=x 4)(x-1)2=493、 81的平方根是 ;27的立方根是 。
-27的立方根是 ; 94的平方根是____。
169的算术平方根是 。
4、 下列各数:①3.141、②0.33333……、③75-、④π、⑤252.±、⑥32-、⑦0.3030003000003……(相邻两个3之间0的个数逐次增加2)、其中是有理数的有_______;是无理数的有_______。
(填序号) 5、 的平方是36,所以36的平方根是 。
1、 有五个数:0.125125…,0.1010010001…,-π,4,32其中无理数有 ( )个A 2 B 3 C 4 D 52. 下列各式中无意义的是( ) A 3-B 3±C 23- D ()23-±3、下列各数是无理数的是( ) A 723B 1 C38 D -π4、 把64开平方得( ) A 8 B –8 C ±8 D 325、 下列说法正确的是( )A 4的平方根是2B -16的平方根是±4C 实数a 的平方根是±a D 实数a 的立方根是3a6、有理数中,算术平方根最小的是( ) A 、1 B 、0 C 、0.1 D 、不存在 1. 0.25的平方根是 ;92的算术平方根是 ,16 的平方根是 。
2.=81 ,2516±= ,2)3(-= 。
3. 若某数只有一个平方根,那么这个数等于 。
4. 若-a 有平方根,那么a 一定是 数。
5、若42-x 有意义,则x . 6、 负数 平方根,有 个立方根 7、 要切一块面积为25m 2的正方形钢板,它的边长是 。
8、当0≥a ,(a )2= ,2a= , 9、当x 时,12-x 有意义。
;当x 时, x 2有意义。
10、49+196= ,225= 、25.0144∙=11、(1)2)3(=____;23= ;(2)当0≥a ,(a )2= ,2a= 。
12、(a+2)2+|b -1|+c -3=0,则a +b +c =二.选择题1、a ,b 在数轴上的位置如图所示,则下列各式有意义的是( )A、b a - B 、ab C 、b a + D 、a b -2、如图,以数轴的单位长为边作一个正方形,以数轴的原点为圆心,正方形的对角线长为半径画孤,交数轴于点A ,则点A 表示的数是 ( )A .1 B .1.4 C D a 0 b第十三章 期末考复习 填空 选择 2、下列计算正确的是 ( )A .523a aa =+ B .325⋅=a a a C .923)(a a = D .32-=a a a3、已知22()11,()7a b a b +=-=,则ab 等于 ( )A .—2 B .—1 C .1 D. 24、若2x是有理数,则x 是 ( ).A.有理数 B.整数 C.非负数 D.实数5、我们已经接触了很多代数恒等式,知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式.例如图(3)可以用来解释(a+b )2-(a -b )2=4ab.那么通过图(4)面积的计算,验证了一个恒等式,此等式是( )A . a 2-b 2=(a+b )(a -b ) B .(a -b )(a+2b )=a 2+ab -b 2C .(a -b )2=a 2-2ab +b 2D .(a+b )2=a 2 +2ab +b 27、若a+b=-1,则a 2+b 2+2ab 的值是( )A .-1 B.1 C.3 D.-3 8、(x 2+px+8)(x 2-3x+q)乘积中不含x 2项和x 3项,则p,q 的值 ( ) A.p=0,q=0 B.p=3,q=1 C.p=–3,–9 D.p=–3,q=1 9、9m ·27n 的计算结果是 ( )A.9m+n B.27m+n C.36m+nD.32m +3n二、填空题13、因式分解:3x 2-12 =______________________; 14、当n 是奇数时,(-a 2)n = ;15、有一个三角形的两边长是4和5,要使这个三角形成为直角三角形,则第三边长为 ; 16、 + 49x 2+ y 2 = ( - y)2; 17、4a=2a+3,则(a –4)2003= ;18、若x 2- 3x + k 是一个完全平方式,则k 的值为 ; 19、察下列各式 (x-1)(x+1)=x 2-1(x-1)(x 2 + x + 1)=x 3 -1(x-1)(x 3 + x 2 + x + 1)=x 4 -1根据规律可得(x-1)(x n-1 + …… + x +1)= (其中n 为正整数); 20、请写出三组以整数为边长的直角三角形的三边长:, , ;23、对角线长为2的正方形,边长为多少?第十三章 整式乘除 填空 选择1、m 6·m 6=m a ,则a = ;2、(-x )9÷(-x )6÷(-x )÷x = ;3、若,则m = ; 4、(0.5)2004×(-2)2005= ;5、若a m =2,a n =5,则a m +n 等于 ;6、10·102·103=10x ,则x = ;7、(-x 8)2÷(-x )m=(x 3)4 ,则m = 8、若3×9m×27m=321,则m = ; 9、若B 是一个单项式,且B·(2x 2y -3xy 2)=-6x 3y 2+9x 2y 3,则B = ; 10、当a +b =3,x -y =1时,代数式1997222++-++y x b ab a 的值是 ;二、选择题12、下列计算中,正确的是( ). A 、B 、C 、D 、13、下列计算不正确的是( ).15、计算得( ). A、3 B、-3995 C、3995 D、-400316、下列式子正确的是( ).A、(a+5)(a-5)=a2-5B、(a-b)2=a2-b2C、(x+2)(x-3)=x2-5x-6D、(3m-2n)(-2n-3m)=4n2-9m217、下列运算正确的是( ).A、B、C、D、18、计算(-2x+1)(-3x2)结果正确的是( ).A、6x3+1B、6x3-3C、6x3-3x2D、6x3+x219、若多项式4x2+2kx+25是另外一个多项式的平方,则k的值是( ).A、10B、20C、±10D、±2020、下列多项式相乘,结果为x2-x-6的是( ).A、(x-3)(x+2)B、(x+3)(x-2)C、(x-3)(x-2)D、(x-6)(x+1)21、如果,那么p、q的值是( ).A、5、6B、5、-6C、1、6D、1、-622、(-x-y)2=( ).A、B、C、D、23、计算的结果是( ).A、(a-b)9B、(a-b)18C、(b-a)9D、(b-a)1824、下列计算正确的是( ).A、(1-4a)(1+4a)=1-16a2B、3 31aaaa=∙÷C、(-x)(x2+2x-1)=x3-2x2+1D、25、下列计算结果正确的是( ).A、a4÷a=a4B、(x-y)3÷(x+y)2=x-yC、(a-b)3÷(b-a)2=a-bD、x5÷x3÷x=x226、计算:(x-y)(-y-x)的结果是( ).A、-x2-y2B、-x2+y2C、x2-y2D、x2+y227、如果(x-3)是多项式(x2+4x+m)的一个因式,则m的值是( ).A、21B、-21C、3D、-328、下列运算中正确的是( ).A、(x+2y)(x-2y)=x2-2y2B、(m-3n)(m-3n)=m2-9n2C、(-x-2y)(-x+2y)=x2-4y2D、(a-2b)(-a+2b)=a2-4b229、如果(a-b)2加上一个单项式便等于(a+b)2,则这个单项式是( ).A、2abB、-2abC、4abD、-4ab30、下列各式可以分解因式的是( ) A、B、C、D、31、在下列各式中,计算结果为4xy-x2-4y2的是( ).A、(x-2y)2B、(x-2y)2C、(2y-x)2D、-(x-2y)234、若,,则x -y 等于 ( ). A 、-5 B 、-3 C 、-1 D 、135、如果,,,那么 ( ).A 、a >b >cB 、b >c >aC 、c >a >bD 、c >b >a 36、如果,,则ab 的值是( ).A 、2 B 、1 C 、-2 D 、-137、若多项式可化成一个多项式的平方,则t 2的值为( ).A 、9y2B 、3yC 、±3yD 、±9y238、下列各组多项式,公因式是(x +2)的是( ). A 、 B 、C 、D 、39、若x =1时,代数式的值为5,则x =-1时,代数式的值等于( ). A 、0 B 、-3 C 、-4 D 、-5 40、无论a 、b 为何值,代数式的值总是( ).A 、负数B 、0C 、正数D 、非负数《整式的乘除》 计算题 A 组1、(1)83)2()2(-⨯- =________ (2)42)()(y x y x +⨯+=________(3)543a b a ∙∙=______ (4)53)10(=_______ (5)43)(b =_______2、下列各式的计算中,正确的是( ) A . B .C .D .3、()______;223=⨯a ()______;3=-a ()_______34=-a_____;38=÷a a()()______2247=÷a a4、计算:(1) (2)5、计算:)3()2)(1(32a b a -⋅-)105()104)(2(45⨯⨯⨯6、计算:)35(2)1(22b a ab ab +)21(2)2(22b a b a +-7、计算:)6.0)(1)(1(x x -- ))(2)(2(y x y x -+2))(3(y x -8、(2x 3+6x 2+8x )÷2x=______________ ; (-2y 5)2÷(2y 3)= 。
