东南大学2014学年数学建模与数学实验考试卷(A卷)

合集下载

大学数学建模-东南大学数学建模试卷3A

20XX年复习资料大学复习资料专业：班级：科目老师：日期：东南大学考试卷（ A 卷）课程名称数学建模与数学实验考试学期 20X X X X -20X X X X -3得分适用专业理工各专业考试形式闭卷考试时间长度 20XXXX0分钟可带计算器一．填空题（每空3分，共30分） 1．差分方程是解决实际问题的主要数学工具，请列举3个本课程已介绍的差分方程模型。

2．考虑抢渡长江问题。

假设江两岸是一组平行直线，江面宽为H ，终点在起点下游江对岸的L 处，水流速度及游泳速度分别为常数,v u ，游泳偏角θ（,u v 夹角）保持不变。

则能够成功到达对岸的必要条件为。

如果800,1000,2/,90L m H m v m s θ====，则最小的u 值为。

3．已知11A=13⎡⎤⎢⎥⎣⎦，则1A (mod19)-= 。

4．考虑微分方程0.25(1)(0)0.2dx x x dt x ⎧=-⎪⎨⎪=⎩，该方程的解为。

解曲线变化率最大的时刻为。

5．考虑差分方程组11000.80.250.20.751200,2400n n n n n n x x y y x y x y ++=+⎧⎪=+⎨⎪==⎩，其平衡点为。

6 已知Leslie 矩阵 01 1.80000.40L s ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦。

如果该种群不仅结构稳定，而且总数始终保持不变，则s = ，年学号姓名密封线自觉遵守考场纪律如考试作弊此答卷无效龄结构向量为。

7．已知非线性差分方程21(12)(0)n n n x bx x b +=->的正平衡点是稳定的，则b 的取值范围为。

二。

简述与分析（20XXXX 分）（1）简述无差别曲线的两个主要特征。

（2）考虑如下形式的方程族 1/21/22(,)(34)f x y x y c =+=。

判别其是否满足无差别曲线的特征。

东南大学数学建模试卷10-11-2A做

东南大学考试卷（A 卷）课程名称数学建模与数学实验考试学期 2010-2011-2 得分适用专业各专业考试形式闭卷考试时间长度 120分钟（考试可带计算器）所有数值结果精度要求为保留小数点后两位一．填空题：（每题2分，共10分） 1. 用Matlab 做AHP 数学实验，常用的命令有，等等。

2. 矩阵A 关于模36可逆的充要条件是：。

3. 泛函332230()()2()3J x x t t x t t dt ⎡⎤=++⎣⎦⎰&取极值的必要条件为。

4. 请补充一致矩阵缺失的元素136A ⎛⎫ ⎪= ⎪ ⎪⎝⎭。

5. 请列出本人提交的上机实验内容（标题即可）。

二．选择题：（每题2分，共10分） 1. 在下列Leslie 矩阵中，能保证主特征值唯一的是 ( ) A. 0230.20000.40⎛⎫ ⎪ ⎪ ⎪⎝⎭； B. 0 1.200.10000.30⎛⎫ ⎪ ⎪ ⎪⎝⎭； C. 0070.30000.10⎛⎫ ⎪ ⎪ ⎪⎝⎭； D.以上都对 2. 下列论述正确的是（） A.判断矩阵一定是一致矩阵 B.正互反矩阵一定是判断矩阵 C.能通过一致性检验的矩阵是一致矩阵 D.一致矩阵一定能通过一致性检验 3. n 阶Leslie 矩阵有个零元素。

（）A.不超过2(1)n -；B.不少于2(1)n -；C.恰好2(1)n -；D.恰好21n -4. Matlab 软件内置命令不可以（）A.求矩阵的主特征值B. 做曲线拟合;C. 求解整数线性规划D. 求样条插值函数5. 关于等周问题，下面的描述不正确的有（）A.目标泛函可以表示为最简泛函；B.条件泛函为最简泛函；C.条件泛函取值为常数；D. 函数在区间两个端点处可以取任意值三．判断题（每题2分，共10分）1. 马氏链模型中，矩阵一定有特征值1。

（）2. 插值函数不要求通过样本数据点。

数学建模试卷A参考答案

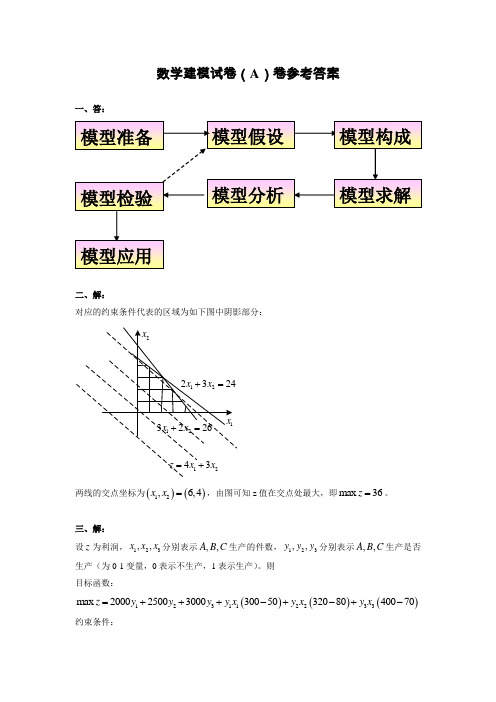
数学建模试卷（A ）卷参考答案一、答：二、解：对应的约束条件代表的区域为如下图中阴影部分：两线的交点坐标为()()12,6,4x x =，由图可知z 值在交点处最大，即max 36z =。

三、解：设z 为利润，123,,x x x 分别表示,,A B C 生产的件数，123,,y y y 分别表示,,A B C 生产是否生产（为0-1变量，0表示不生产，1表示生产）。

则目标函数：()()()123112233max 200025003000300503208040070z y y y y x y x y x =+++-+-+-约束条件：1231231231231232350024000350000,0,0;,0 1;x x x x x x x x x x x x y y or ++≤⎧⎪++≤⎪⎨++≤⎪⎪≥≥≥=⎩四、解：（一）（二）目标层准则层方案层11/2433217551/41/711/21/31/31/52111/31/5311A ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦1(),0,ij n n ij ji ijA a a a a ⨯=>=层次分析法的基本步骤成对比较阵和权向量元素之间两两对比，对比采用相对尺度设要比较各准则C 1,C 2,… , C n 对目标O 的重要性:i j ijC C a ⇒A ~成对比较阵 A 是正互反阵要由A 确定C 1,… , C n 对O 的权向量选择旅游地（三）111122221212n n n n n n w w w w w w w w w w w w A w w w w w w ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎤⎥⎢⎥⎢⎥⎣⎦23a =一致比较允许不一致，但要确定不一致的允许范围考察完全一致的情况12(1),,nW w w w =⇒/ij i ja w w =令12(,,)~T n w w w w =权向量“选择旅游地”中准则层对目标的权向量及一致性检验11/2433217551/41/711/21/31/31/52111/31/5311A ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦准则层对目标的成对比较阵最大特征根λ=5.073权向量(特征向量)w =(0.263,0.475,0.055,0.090,0.110)T 5.07350.01851CI -==-一致性指标随机一致性指标 RI=1.12 (查表) 一致性比率CR =0.018/1.12=0.016<0.1通过一致性检验五、解：()221max ni i i a bx y =+-∑，对,a b 分别求偏导数，可以求解得0.9726,0.0500b a ==。

中国大学MOOC慕课爱课程（4）--层次分析法网课刷课

东南大学考试卷（A 卷）课程名称数学建模与数学实验考试学期2014-2015-3得分适用专业各专业考试形式闭考试时间长度 120分钟（可带计算器）题目一二三四五六七八总分得分批阅人除特殊说明外，所有数据精确到小数点后2位。

1. （15分）层次分析法模型中介绍了成对比较矩阵，假设比较的标度仅取1到9及其倒数。

如果3阶成对比较矩阵， ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=c f e b d x a A 23（1）当x 取何值时，矩阵A 为一致矩阵，此时矩阵A 模最大特征值为多少？（2）若随机一致性指标RI=0.6，且矩阵A 的一致性可以接受，确定x 的可能取值？)41(,9,8,7,6,5,4,3,2.33`)3(,/66/)1(3)1(||)()2(123/12/11/131`)2`6(,3,6,2/1,3/1,1)1(max 3max =<≤=−−−−=−=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=+=======x x x A E f x x A x e f c b a λλλλλλ解2.（15分）考虑如下数组：x 1 2 3 4 5y 400 320 260 200 160(1)借助曲改直方法确定经验公式形式；(2)利用线性最小二乘法确定经验公式参数。

3.(10分）假设人的血液总量为5000毫升。

如果某人瞬间服下100g的固态胶囊，胶囊匀速释放到血液里，并很快均匀。

假设单位时间的排放量为该时刻的血药量的0.001。

（1）做合理假设，建立该问题的数学模型；（2）如果该药在体内的血药浓度低于0.2g/百毫升，药物将不起作用，试确定该药物一次服用后的有效时间。

4.（15分）考虑差分方程组模型：10010.20.4,10000,80000.80.6n n nn n nx x y x y y x y ++=+⎧==⎨=+⎩ （1）求该方程组的平衡点；（2）证明数列{}n x 极限存在。

东南大学数学建模试卷A答案

东南大学考试卷（ A 卷）课程名称数学建模与数学实验考试学期08-09-3得分适用专业考试形式闭卷考试时间长度 120分钟可带计算器一填空题（共32分，每题4分）1．在本课程所介绍的若干模型中，请列举至少4个你最感兴趣的模型。

2．迭代法是求非线性方程近似根的常用方法，已知()y f x =，写出求0x x =附近的近似根的牛顿割线法公式。

3. 已知加密矩阵1113A ⎡⎤=⎢⎥⎣⎦，求1(mod 23)A - 。

4. 已知(,)x y 的三个观察数据(1,1),(2,4),(3,1)-，写出其逐步线性插值的插值函数。

5. 常微分方程'0.02(10.001),(0)100x x x x =-=的解为。

6. 考虑养老保险问题，假如某人30岁起保，每月交保费300元至60岁止，如果所交保费的月利率为r ，写出其第k 的保费本息和k x 所满足的方程。

7．考虑泛函120(')t Jx e x dt -=+⎰，其对应的欧拉方程为。

8. 考虑马氏链1231230.750.050.2((1),(1),(1))((),(),())0.20.60.20.40.20.4x k x k x k x k x k x k ⎡⎤⎢⎥+++=⎢⎥⎢⎥⎣⎦，则其平衡点为（保留小数点后2位）。

二．量纲分析法建模问题（12分）考虑抛体运动。

质量为m 的物体以初速度0v 抛出，证明下落的位移x 与速度v 、时间t 及重力加速度g 满足关系000(/,/)x v t v v gt v ϕ=。

三．层次分析法建模问题（14分）已知成对比较矩阵1311/21/41 A⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦（1）将上述矩阵的元素补齐。

（2）计算上述矩阵模最大特征值（精确到小数点后2位）。

（3）计算上述矩阵的的随机一致性比率（已知随机一致性指标为0.58）。

四．数值分析问题（14分）x y的一组数据已知(,)(1)借助曲改直方法确定经验公式形式。

2014年数学建模A题-省一等奖

关键词：软着陆、SQP算法、轨道优化、景象匹配
1
一
1.1 问题的背景
问题重述
中国是继美国、前苏联之后的第三个能使卫星登上月球实现软着陆的国家。因此，嫦娥三号如何实现软着陆以及能否成功成为外界关注的焦点。北京时间 12 月 10 日晚，嫦娥三号已经成功降轨进入预定的月面着陆准备轨道，这是嫦娥三号“落月”前最后一次轨道调整。在实施软着陆之前，嫦娥三号还将在这条近月点高度约 15 公里、远月点高度约 100 公里的椭圆轨道上继续飞行。嫦娥三号着陆地点选在较为平坦的虹湾区。但由于月球地形的不确定性，最终“落月”地点的选择仍存在一定难度。但嫦娥三号的预定着陆点为 19.51W，44.12N，海拔为 -2641m。在大约距离月球 15 公里时，反推发动机就要点火工作；到离月球 100 米时，卫星将暂时处于悬停状态，此时它已不受地球上工程人员的控制，因卫星上携带的着陆器具有很高智能，它会自动选择一块平整的地方降下去，并在离月球表面 4 米的时候关闭推进器，卫星呈自由落体降落，确保软着陆成功。为了确保探测器能够成功在月球表面实现软着陆，需要认真设计降落过程中探测器的发动机的控制方案，使“嫦娥 3 号” 能够顺利完成科研任务，得到最大化的应用。由于月球上没有大气，嫦娥三号无法依靠降落伞着陆，只能靠变推力发动机，才能完成中途修正、近月制动、动力下降、悬停段等软着陆任务。这将是中国航天器首次在地外天体的软着陆和巡视勘探，同时也是 1976 年后人类探测器首次的落月探测。嫦娥三号在着陆准备轨道上的运行质量为 2.4t，其安装在下部的主减速发动机能够产生 1500N 到 7500N 的可调节推力。在给定主减速发动机的推力方向后，能够自动通过多个发动机的脉冲组合实现各种姿态的调整控制。要保证准确地在月球预定区域内实现软着陆，关键问题是着陆轨道与控制策略的设计。其着陆轨道设计的基本要求：着陆准备轨道为近月点 15km，远月点 100km 的椭圆形轨道；着陆轨道为从近月点至着陆点，其软着陆过程共分为 6 个阶段，要求满足每个阶段在关键点所处的状态；尽量减少软着陆过程的燃料消耗。 1.2 提出问题根据上述的叙述以及基本要求，提出以下三个问题：（1）确定着陆准备轨道近月点和远月点的位置，以及嫦娥三号相应速度的大小与方向。

2014全国大学生数学建模竞赛A题题目及参考答案_

2014全国大学生数学建模竞赛A题题目及参考答案_ 2011高教社杯全国大学生数学建模竞赛题目,请先阅读“全国大学生数学建模竞赛论文格式规范”,A题城市表层土壤重金属污染分析随着城市经济的快速发展和城市人口的不断增加，人类活动对城市环境质量的影响日显突出。

对城市土壤地质环境异常的查证，以及如何应用查证获得的海量数据资料开展城市环境质量评价，研究人类活动影响下城市地质环境的演变模式，日益成为人们关注的焦点。

按照功能划分，城区一般可分为生活区、工业区、山区、主干道路区及公园绿地区等，分别记为1类区、2类区、……、5类区，不同的区域环境受人类活动影响的程度不同。

现对某城市城区土壤地质环境进行调查。

为此，将所考察的城区划分为间距1公里左右的网格子区域，按照每平方公里1个采样点对表层土(0~10 厘米深度)进行取样、编号，并用GPS记录采样点的位置。

应用专门仪器测试分析，获得了每个样本所含的多种化学元素的浓度数据。

另一方面，按照2公里的间距在那些远离人群及工业活动的自然区取样，将其作为该城区表层土壤中元素的背景值。

附件1列出了采样点的位置、海拔高度及其所属功能区等信息，附件2列出了8种主要重金属元素在采样点处的浓度，附件3列出了8种主要重金属元素的背景值。

现要求你们通过数学建模来完成以下任务:(1) 给出8种主要重金属元素在该城区的空间分布，并分析该城区内不同区域重金属的污染程度。

(2) 通过数据分析，说明重金属污染的主要原因。

(3) 分析重金属污染物的传播特征，由此建立模型，确定污染源的位置。

(4) 分析你所建立模型的优缺点，为更好地研究城市地质环境的演变模式，还应收集什么信息,有了这些信息，如何建立模型解决问题,DJHFSJKDHFKDSJKFHSJKDFHJKDSHFDJKSFHJKDSHFJKDSHFJK题目 A题城市表层土壤重金属污染分析摘要,本文研究的是某城区警车配置及巡逻方案的制定问题，建立了求解警车巡逻方案的模型，并在满足D1的条件下给出了巡逻效果最好的方案。

2014数学建模a题

承诺书我们仔细阅读了《全国大学生数学建模竞赛章程》和《全国大学生数学建模竞赛参赛规则》（以下简称为“竞赛章程和参赛规则”，可从全国大学生数学建模竞赛网站下载）。

我们完全明白，在竞赛开始后参赛队员不能以任何方式（包括电话、电子邮件、网上咨询等）与队外的任何人（包括指导教师）研究、讨论与赛题有关的问题。

我们知道，抄袭别人的成果是违反竞赛章程和参赛规则的，如果引用别人的成果或其他公开的资料（包括网上查到的资料），必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。

我们郑重承诺，严格遵守竞赛章程和参赛规则，以保证竞赛的公正、公平性。

如有违反竞赛章程和参赛规则的行为，我们将受到严肃处理。

我们授权全国大学生数学建模竞赛组委会，可将我们的论文以任何形式进行公开展示（包括进行网上公示，在书籍、期刊和其他媒体进行正式或非正式发表等）。

我们参赛选择的题号是（从A/B/C/D中选择一项填写）： A我们的报名参赛队号为（8位数字组成的编号）：所属学校（请填写完整的全名）：山东师范大学参赛队员(打印并签名) ：1. 唐健2. 杨晓梅3. 王娜娜指导教师或指导教师组负责人(打印并签名)：（论文纸质版与电子版中的以上信息必须一致，只是电子版中无需签名。

以上内容请仔细核对，提交后将不再允许做任何修改。

如填写错误，论文可能被取消评奖资格。

）日期： 2014 年 9 月 15 日赛区评阅编号（由赛区组委会评阅前进行编号）：编号专用页赛区评阅编号（由赛区组委会评阅前进行编号）：全国统一编号（由赛区组委会送交全国前编号）：全国评阅编号（由全国组委会评阅前进行编号）：嫦娥三号软着陆轨道设计与控制策略摘要嫦娥三号于2013年12月2日1时30分成功发射，12月6日抵达月球轨道。

嫦娥三号在着陆准备轨道上的运行质量为2.4t，其安装在下部的主减速发动机能够产生1500N到7500N的可调节推力，其比冲（即单位质量的推进剂产生的推力）为2940m/s，可以满足调整速度的控制要求。

东南大学数学建模试题A

东南大学数学建模试题A部门： xxx时间： xxx整理范文，仅供参考，可下载自行编辑东南大学考试卷<）课程名称数学建模与实验考试学期 06-07-2得分适用专业各专业考试形式闭卷考试时间长度 120分钟一．填空题：<每题2分，共10分）1. 无差别曲线形状上具有的两个共性特点是：和。

2. Volterra 模型里，随着捕捞强度的增加，捕食者种群数量，食饵种群数量。

3. 元素属于{}0,1,2,,1n -的方阵A 关于模n 可逆的充要条件是：。

4.非线性方程()0f x =的牛顿迭代公式为。

5. 请补充判断矩阵缺失的元素19_2____3_A ⎛⎫ ⎪= ⎪ ⎪⎝⎭。

二．选择题：<每题2分，共10分）1. 在Leslie 人口模型中，直接反映该地区人口按年龄组分布变化规律的参数是 ( >A. 0λ；B. n *； C. R ； D.以上均可2. 判断矩阵通过一致性检验的标准是 ( >A. 0.1CI <B. 0.01CI <C. 0.1CR <D.0.01CR <3. 模26倒数表中可能出现的数是 ( >A. 13B.2C.26D.54. 最小二乘法得到的函数不可能为<）A.线性函数B. 多项式函数C. 样条函数D. 指数函数5. 在SIR 模型中，若接触数为σ，(0)0,(0)0s i >>，lim ()t s s t ∞→∞=，则<）A.1s σ∞<B.1s σ∞=C.1s σ∞>D.三种情况都有可能三．判断题<每题1分，共5分）1. 数值分析法建模时，可以用函数样本数据的n 阶<1n >）插商值近似代替函数的n 阶导数值<）2. 差分方程模型得到的点列一定能收敛到某个平衡点<）3. 改进的欧拉公式是2阶龙格—库特公式的一个特例。

<）4. 在阻滞增长模型中，当人口达到最大人口容量的时候，人口增长得最快 <）5. 根据Malthus 模型,如果自然增长率为r ，则人口数量加倍所需时间为ln 2r ( >四．应用题<共75分）1.<10分）考虑雇员一天的工作时间t 与工资w ，回答下列问题：<1）假设雇员的满意度曲线形式为()532w t c=+，如果雇主付计时工资，求出雇主与雇员的协议曲线函数表达式。

2014年全国数学建模大赛A题

2014高教社杯全国大学生数学建模竞赛承诺书我们仔细阅读了《全国大学生数学建模竞赛章程》和《全国大学生数学建模竞赛参赛规则》（以下简称为“竞赛章程和参赛规则”，可从全国大学生数学建模竞赛网站下载）。

我们郑重承诺，严格遵守竞赛章程和参赛规则，以保证竞赛的公正、公平性。

如有违反竞赛章程和参赛规则的行为，我们将受到严肃处理。

我们参赛选择的题号是（从A/B/C/D中选择一项填写）： A 我们的报名参赛队号为（8位数字组成的编号）：25001113所属学校（请填写完整的全名）：云南大学参赛队员(打印并签名) ：1. 林博文2. 张竞文3. 方春晖指导教师或指导教师组负责人(打印并签名)：李海燕（论文纸质版与电子版中的以上信息必须一致，只是电子版中无需签名。

以上内容请仔细核对，提交后将不再允许做任何修改。

如填写错误，论文可能被取消评奖资格。

）日期：2014年9月15日赛区评阅编号（由赛区组委会评阅前进行编号）：2014高教社杯全国大学生数学建模竞赛编号专用页赛区评阅编号（由赛区组委会评阅前进行编号）：全国统一编号（由赛区组委会送交全国前编号）：全国评阅编号（由全国组委会评阅前进行编号）：嫦娥三号软着陆轨道设计与控制策略优化摘要嫦娥三号是中国国家航天局嫦娥工程第二阶段的登月探测器，包括着陆器和玉兔号月球车。

嫦娥三号在高速飞行的情况下，要保证准确地在月球预定区域内实现软着陆，关键问题是着陆轨道与控制策略的设计。

2014全国大学生数学建模a题

2014高教社杯全国大学生数学建模竞赛a题摘要2013年嫦娥三号成功发射，标志着我国航天事业上的又一个里程碑，针对嫦娥三号软着陆问题，分别建立着陆前轨道准备模型和软着陆轨道模型，建立动力学方程，以燃料最省为目标进行求解。

问题一：在软着陆前准备轨道上利用开普勒定律、能量守恒定律以及卫星轨道的相关知识，利用牛顿迭代法分别确定了近月点和远月点的速度分别为 1.6925km/s、1.6142km/s，位置分别为（19.91W，20.96N），（160.49E,69.31S）。

问题二：在较为复杂的软着陆阶段，因为相对于月球的半径，嫦娥三号到月球的表面的距离太小，如果以月球中心建立坐标系会造成比较大的误差，因此选择在月球表面建立直角坐标系，在主减速阶段的类平抛面上建立相应的动力学模型，求出关键点的状态和并设计出相应的轨道，接下来通过利用灰度值阀值分割方法和螺旋搜索法对粗避障阶段和精避障阶段的地面地形进行相应的分析，找出安全点，然后调整嫦娥三号的方向以便安全降落，最后在落地时通过姿态发动机调整探测器的姿态，使之可以平稳的落到安全点上，在以上的各个阶段都可以以燃料最省为最优指标，从而建立非线性的最优规划的动力学模型，并基于该动力学模型可以对各个阶段的制导率进行优化设计由此就可以得到各个阶段的最优控制策略，问题三：最后针对所设计的轨道和各个阶段的控制策略进行了误差分析和灵敏度分析。

对系统误差和偶然误差都做了解释；通过灵敏度分析发现，嫦娥三号在近月点的位置对结果的影响最大。

关键字牛顿迭代法，灰度值阀值分割，螺旋搜索法，灵敏度分析一、问题重述嫦娥三号于2013年12月2日1时30分成功发射，12月6日抵达月球轨道。

嫦娥三号在着陆准备轨道上的运行质量为 2.4t，其安装在下部的主减速发动机能够产生1500N到7500N的可调节推力，其比冲（即单位质量的推进剂产生的推力）为2940m/s，可以满足调整速度的控制要求。

在四周安装有姿态调整发动机，在给定主减速发动机的推力方向后，能够自动通过多个发动机的脉冲组合实现各种姿态的调整控制。

数模卷A

共4页第1页东南大学考试卷（A 卷）课程名称数学模型与数学实验考试学期 03-04-3 得分适用专业数学各专业考试形式闭考试时间长度 120分钟一. (15`)在计时工资制体系下,雇主与雇员的付薪方式是按计时工资率付薪.如果雇主要增加雇员的工作时间,他有两种方式:第一种方式是提高计时工资率,在协议线的另一点(22,w t )达成协议,另一种方式是在21t t t <=先达成协议,对工时12t t -付给更高的计时工资.试用图示法分析哪种方式对雇主更有利? 二. (15`) 速度为v 的风吹在迎风面积为s 的风车上，空气密度为ρ，用量纲分析法确定风车获得的功率p 与v ，s ，ρ的关系。

共4页第2页三. (20`)(1) n 个队在同一个场地进行单循环赛,证明最优方案中,两场比赛的间隔场次数的最小值为[23-n ]. (2) 对7=n ,8分别给出一个满足(1)的方案.四.(25`)(1)养老保险是与人们生活密切相关的一种保险类型。

通常保险公司会提供多种方式的养老金计划让投保人选择,在计划中详细列出保险费和养老金的数额。

某保险公司的一份材料指出:在每月交费200元至60岁开始领取养老金的约定下,男子若25岁起投保,届时月养老金2282元;估算所交保险费获得的利率。

(2) 假如保险公司请你帮他们设计一个险种:35岁起保,月利率为0.0046,60岁开始领取养老金,届时投保人养老金为多少为最宜?共4页第3页共4页第4页五.(25`)在传染病的SIR 模型中,用)(),(),(t r t i t s 分别表示健康者、病人和病愈免疫的移出者的比例。

其模型方程为)0,(0)0(,0)0(00>⎪⎪⎪⎩⎪⎪⎪⎨⎧>=>=-=-=μλλμλs s i i si dt ds i si dt di （1）证明 0)(lim =+∞>-t i t （2）证明)(lim t s t +∞>-存在且大于零。

2014年数学建模题目

2014年数学建模题目
2014年全国研究生数学建模竞赛A题是关于小鼠视觉感受区电位信号（LFP）与视觉刺激之间的关系研究。

题目要求探究数十亿个神经元的信息，以期对知觉、行动以及意识等有更进一步的了解，并可能为各种精神疾病研究出新的治疗方法。

具体而言，需要解决的问题包括：
1. 脑电波介绍：脑是支配人和高级动物活动的司令部和信息中心，神经系统承担着感受外界刺激，产生、处理、传导和整合信号，实现各种认知活动（如知觉、学习、记忆、情绪、语言、意思和思维等），以及运动控制等众多功能。

2. 脑电波的应用：脑电波可以用来研究大脑的活动和功能，包括神经元的信息传递和整合。

脑电波的应用范围广泛，包括神经科学、心理学、生理学、医学等领域。

对于这个题目，需要运用数学建模的方法，结合脑电波数据和视觉刺激数据，分析小鼠视觉感受区的电位信号与视觉刺激之间的关系，探究大脑的信息处理机制。

具体而言，需要解决的问题包括：
1. 数据预处理：对脑电波数据进行预处理，包括滤波、去噪、归一化等操作，以提高数据的质量和可靠性。

2. 特征提取：从脑电波数据中提取出与视觉刺激相关的特征，包括时域和频域特征。

3. 模型建立与优化：根据提取的特征，建立数学模型，并不断优化模型参数和结构，以提高预测准确率和稳定性。

4. 结果解释与讨论：对模型的结果进行解释和讨论，探究小鼠视觉感受区的电位信号与视觉刺激之间的关系，以及大脑的信息处理机制。

总之，2014年全国研究生数学建模竞赛A题是一个具有挑战性和重要意义的题目，需要运用数学建模的方法，结合脑电波数据和视觉刺激数据，分析小鼠视觉感受区的电位信号与视觉刺激之间的关系，探究大脑的信息处理机制。

大学数学建模-东南大学数学建模试卷09-10-3A

20XX年复习资料大学复习资料专业：班级：科目老师：日期：东南大学考试卷（A卷）课程名称数学建模与数学实验考试学期20XXXX-20XXXX-3得分适用专业理工各专业考试形式开卷闭卷半开卷考试时间长度20XXXX0分钟（可带计算器）题目一二三四五六七八总分得分批阅人自觉遵守考场纪律如考试作弊此答卷无效密封线学号姓名注：以下各题只需计算到小数点后两位。

一填空与选择（每题3分，共30分）1 已知113,(mod19)02A A -⎡⎤==⎢⎥⎣⎦则。

2 已知一组(1,1),(2,1),(3,2)-观测数据，则其分段线性插值多项式为。

3 根据一组等距节点的观测数据分析知其2阶差分波动最小，则其最合适的拟合多项式阶数是。

4 已知微分方程'()0.005(1/10000)(0)2000x t x x x =-⎧⎨=⎩，则其变化率最大时间为。

5考虑Volterra 模型'0.050.001'0.10.0001x x xyy x xy =-⎧⎨=-+⎩，则,x y 的周期平均值为 x y ⎛⎫ ⎪ ⎪⎝⎭=6 已知非线性差分方程 21(2)n n n x bx x +=-的正平衡点稳定（b>0），则参数b 的取值范围为。

7 记123()((),(),())a k a k a k a k =考虑马氏链0.40.30.3(1)()0.40.40.2(0)(0.3.0.4.0.3)0.30.20.5a k a k a ⎡⎤⎢⎥+==⎢⎥⎢⎥⎣⎦，，其正平衡点为。

8 轮渡船上甲板总面积为A 。

它能运载小轿车，每辆小轿车所占甲板面积为C ，能运载卡车，每辆卡车所占甲板面积为 L 。

每辆小轿车要付渡船费p 元；每辆卡车要付q 元。

调度想知道在渡船上运载多少辆小轿车(x) 和多少辆卡车(y)才能获取最大的利润？下列哪一个选项给出利润函数及需满足的约束条件？（）A. yq xp +，满足 A xL yC ≤+B. yq xp +，满足 A yL xC ≤+C. ))((q p y x ++，满足A yL xC ≤+D. ))((q p y x ++ ，满足A L C y x ≤++))((9 下面哪一个选项最接近小轿车从静止开始起步的的速度变化模型？（）A te--1 B 2)1(t -C 2t t - D 1t e -+20XXXX 模型检验是建模过程中的必要步骤，以下哪一个选项不是常见的模型检验过程。

东南大学数学建模试卷 09-10-2A

共6页第1页东南大学考试卷（A 卷）姓名学号班级课程名称数学建模与实验考试学期得分适用专业各专业考试形式闭卷考试时间长度 120分钟一．填空题：（每题2分，共10分）1. 阻滞增长模型0.5(10.001)(0)100dx x x dtx ⎧=-⎪⎨⎪=⎩的解为。

2. 用Matlab 做常微分方程数学实验，常用的命令有。

3. 整数m 关于模12可逆的充要条件是：。

4. 根据Malthus 模型,如果自然增长率为2%，则人口数量增长为初值3倍所需时间为(假设初值为正)。

5. 请补充判断矩阵缺失的元素13192A ⎛⎫⎪=⎪ ⎪⎝⎭。

二．选择题：（每题2分，共10分）1. 在下列Leslie 矩阵中，不能保证模最大特征值唯一的是 ()A. 0230.20000.40⎛⎫ ⎪ ⎪ ⎪⎝⎭； B. 1.1 1.230.20000.40⎛⎫ ⎪ ⎪ ⎪⎝⎭； C. 0030.20000.40⎛⎫⎪⎪ ⎪⎝⎭； D.以上都不对 2. 判断矩阵能通过一致性检验的标准是（)A. 0.1C R <B. 0.1C I <C.0.1C R >D.0.01C R <3. 模28倒数表中可能出现的数是 () A. 12 B.5 C.14 D.74. 线性最小二乘法得到的函数不可能为（）A.线性函数B. 对数函数C. 样条函数D. 指数函数 5. 关于泛函极值问题，下面的描述正确的有（）A.泛函()J x 在x *处取极值的充要条件是泛函变分()0J x δ*=；B.泛函()J x 在x *处取极值的充分条件是泛函变分()0J x δ*=； C. 泛函()J x 在x *处取极值的必要条件是泛函变分()0J x δ*=；D.A,B,C 均正确学号姓名三．判断题（每题2分，共10分）1. Hill密码体系中，任意一个可逆矩阵都可以作为加密矩阵。

（）2. 拟合函数不要求通过样本数据点。

（）3. Matlab软件内置命令程序可以直接求解一般的整数线性规划问题。