虚拟变量案例
10 虚拟变量回归模型案例分析
0.0011
84.8393
4.8297
0.0000
R2 0.5318 R2 0.4816
F 10.6010 p值 0.0001
解释：美国在1978年至1985年间第四季度 冰箱的销售量均值约在1160000台，第一季 度与第一季度销量没有多大差异，第二季 度销量较第一季度高约308000台，第三季 度销量较第一季度高约410000台
1, 第一季度
D1
0,
其他季度
2, 第二季度
3, 第三季度
D2
0,
其他季度
D3
0,
其他季度
基组：第四季度
数据搜集
1978Q1 1978Q2 1978Q3 1978Q4 1979Q1 1979Q2 1979Q3 1979Q4 1980Q1 1980Q2 1980Q3 1980Q4 1981Q1 1981Q2 1981Q3 1981Q4
Variable Coefficient Std. Error t-Statistic Prob.
C
D1
D2ຫໍສະໝຸດ D31160.000 62.12500 307.5000 409.7500
59.99041 84.83926 84.83926 84.83926
19.33642 0.732267 3.624501 4.829722
1982Q1 1982Q2 1982Q3 1982Q4 1983Q1 1983Q2 1983Q3 1983Q4 1984Q1 1984Q2 1984Q3 1984Q4 1985Q1 1985Q2 1985Q3 1985Q4
第七章虚拟变量
14
1 第一季度 D1 ＝{
0 其他
1 第二季度 D2 ＝{
0 其他 1 第三季度
D3＝{ 0 其他
15
年、季度
1990年1－3月 4－6月 7－9月 10－12月
1991年1－3月 4－6月 7－9月 10－12月
1992年 1－3月 4－6月 7－9月 10－12月
0
7－9月
0
10－12月
0
1992年 1－3月
1
4－6月
0
7－9月
0
10－12月 0
1993年1－3月
1
4－6月
0
7－9月
0
10－12月 0
1994年1－3月
1
D2
D3
0
0
1
0
0
1
0
0
0
0
1
0
0
1
0
0
0
0
1
0
0
1
0
0
0
0
1
0
0
1
0
0
0
0
18
估计结果如下：
Y= 9.0681+0.068301X-2.05875D1-1.8009D2-0.76594D3 所有t值都在1％的水平显著
103
208
1990
105
206
1991
96
203
1992
105
209
1993
78
213
1994
120
220
第七章多元回归分析虚拟变量
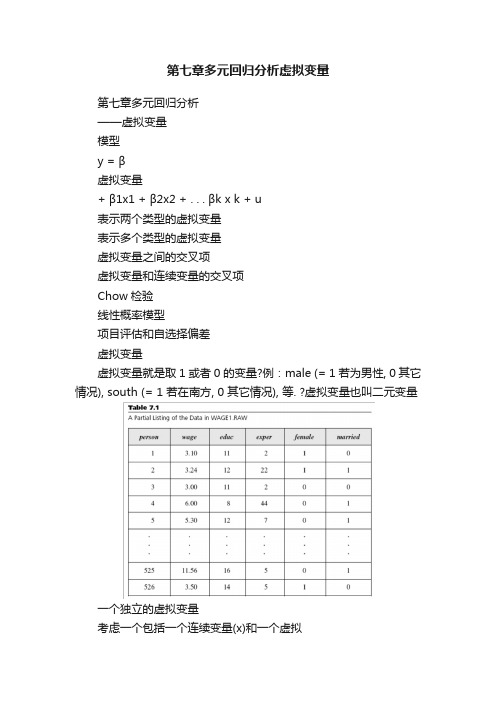
第七章多元回归分析虚拟变量第七章多元回归分析——虚拟变量模型y = β虚拟变量+ β1x1 + β2x2 + . . . βk x k + u表示两个类型的虚拟变量表示多个类型的虚拟变量虚拟变量之间的交叉项虚拟变量和连续变量的交叉项Chow检验线性概率模型项目评估和自选择偏差虚拟变量虚拟变量就是取1 或者0 的变量?例：male (= 1 若为男性, 0 其它情况), south (= 1 若在南方, 0 其它情况), 等. ?虚拟变量也叫二元变量一个独立的虚拟变量考虑一个包括一个连续变量(x)和一个虚拟变量(d)的模型y = β+ δ0d + β1x + u这可以解释成截距项的变化若d = 0, 那么y = β+ β1x + u若d = 1, 那么y = (β+ δ0) + β1x + ud = 0 的样本是参照组δ0 > 0 的例子y y = (β0 + δ0) + β1xd = 1{ δslope = β1d =0 }βy = β0 + β1xx从多个数值的类型变量到虚拟变量?我们可以用虚拟变量来控制有多种类型因素?假设样本中的个人是中学辍学或者仅仅中学毕业或者大学毕业现在要拿仅仅中学毕业和大学毕业的人和中学辍学的人比较定义hsgrad = 1 如果仅仅是中学毕业, 0 其它情况; colgrad = 1 如果大学毕业, 0 其它情况多个数值的类型变量（续）?任何类型变量都可以变成一组虚拟变量?因为参照组由常数项表示了, 那么如果一共有n 个类型，就应该由n –1 虚拟变量如果有太多的类型，通常应该对其进行分组例：前10 , 11 –25, 等虚拟变量之间的交叉项求虚拟变量的交叉项就相当于对样本进行进一步分组例：有男性（male）的虚拟变量和hsgrad（仅仅中学毕业）和colgrad （大学毕业）的虚拟变量加入male*hsgrad 和male*colgrad, 共有五个虚拟变量–> 共有六种类型参照组是女性中学辍学的人此时hsgrad 代表女性仅仅中学毕业者, colgrad 表示女性大学毕业者交叉项表示男性仅仅中学毕业者和男性大学毕业者虚拟变量之间的交叉项（续）?模型可以写成y = β0 + δ1male + δ2hsgrad +δ3colgrad + δ4male*hsgrad + δ5male*colgrad+ β1x + u, 那么:若male = 0 且hsgrad = 0 且colgrad = 0则y = β0 + β1x + u若male = 0 且hsgrad = 1 且colgrad = 0则y = β0 + δ2hsgrad + β1x + u若male = 1且hsgrad = 0且colgrad = 1则y = β0 + δ1male + δ3colgrad + δ5male*colgrad+ βx + u1其它变量与虚拟变量的交叉项?也可以考虑虚拟变量d 和连续变量x 之间的交叉项y = β+ δ1d + β1x + δ2d*x + u若d = 0, 那么y = β+ β1x + u若d = 1, 那么y = (β+ δ1) + (β1+ δ2) x + u这里的两种情况可以看成是斜率的变化δ0 > 0 且δ 1 < 0的例子yy = β+ β1xd = 0d = 1y = (β0 + δ0) + (β 1 + δ1) x。
计量经济学课件虚拟变量
通过引入虚拟变量，可以更准确地刻画经济现象的非线性特征，从而提高计量经济学模型 的精度和预测能力。
拓展应用领域
虚拟变量的引入使得计量经济学模型能够应用于更多的领域，如金融、环境、社会等，进 一步拓展了计量经济学的应用范围。
未来研究方向和趋势
深入研究虚拟变量的理论 和方法
未来研究将进一步深入探讨虚 拟变量的理论和方法，包括虚 拟变量的选择、设定和估计方 法等，以更准确地刻画经济现 象。
https://
未来研究将积极推动虚拟变量 在交叉学科领域的应用，如环 境经济学、金融经济学等，以 促进不同学科之间的交流和合 作。
WENKU DESIGN
WENKU DESIGN
2023-2026
END
THANKS
感谢观看
KEEP VIEW
WENKU DESIGN
WENKU DESIGN
WENKU
REPORTING
要点二
虚拟变量的设置原则
在设置虚拟变量时，需要遵循完备性 和互斥性的原则。完备性要求虚拟变 量的取值能够覆盖所有可能的情况， 而互斥性则要求不同虚拟变量之间不 能存在重叠或交叉的情况。
要点三
虚拟变量的回归系数 解释
在线性回归模型中，虚拟变量的回归 系数表示该定性因素对因变量的影响 程度。当虚拟变量取值为1时，其对 应的回归系数表示该水平与参照水平 相比对因变量的影响；当虚拟变量取 值为0时，则表示该水平对因变量没 有影响。
参数估计与假设检验
参数估计
采用最小二乘法等估计方法，对引入虚拟变量后的模型进行参数估计，得到各 解释变量的系数估计值。
假设检验
根据研究问题和假设，构建相应的原假设和备择假设，通过t检验、F检验等方 法对参数进行假设检验，判断虚拟变量对模型的影响是否显著。
计量经济学第八章关于虚拟变量的回归.
类的截距。
2
2:级差截距系数
教龄X
1
0
薪金与性别：估计结果
1，若是男性 Di 0，若是女性
ˆ 17.969 1.371X 3.334D Y i i i se : (0.192) (0.036) (0.155) t : (93.61) (38.45) (21.455) r 2 0.993
一、虚拟变量的性质
例：教授薪金与性别、教龄的关系
男教授平均薪金和女 教授平均薪金水平相 差2，但平均年薪对 教龄的变化率是一样 的
Yi=1+2Di+Xi+I （1） 1，若是男性 D 其中:Yi=教授的薪金, Xi=教龄, Di=性别 0，若是女性 i 女教授平均薪金：E(Yi | X i , Di 0) 1 X i 被赋予0值的 男教授平均薪金：E(Yi | X i , Di 1) （1 2） X i 类别是基底(基 准),1是基底 男教授
比较英国在第二次大战后重建时期和重建后时期的总 储蓄-收入关系是否发生变化。数据如表。 Yt 1 2 Dt 1 X t 2 ( Dt X t ) t
D=1,重建时期
级差截距:区分两 个时期的截距 级差斜率系数:区分 两个时期的斜率 =0,重建后时期
D=1 D=0
E(Yt | Dt 0, X t ) 1 1 X t E(Yt | Dt 1, X t ) (1 2 ) ( 1 2 ) X t
男教授平均薪金水平比 女教授显著高$3.334K (男：21.3，女：17.969)
1，若是女性 Di 0，若是男性
ˆ 21.303 1.371X 3.334D Y i i i se : (0.182) (0.036) (0.155) t : (117.2) (38.45) (21.455)
虚拟变量 熵权法 -回复
虚拟变量熵权法-回复虚拟变量与熵权法：解析与应用引言在数据分析与决策过程中，虚拟变量与熵权法是两个常用的工具。
虚拟变量是一种用于表征分类变量的方法，熵权法则是一种基于信息熵的多准则决策方法。
本文将分别介绍虚拟变量与熵权法的原理与应用，并探讨它们在实践中的相互关系。
一、虚拟变量概述1. 什么是虚拟变量？虚拟变量（Dummy Variable），也称为指示变量（Indicator Variable），是一种将分类变量转化为数值变量的方法。
它将一个具有有限个取值的分类变量拆分成多个二值变量（通常取0或1）。
虚拟变量的取值为1表示该样本满足该特征，取值为0表示该样本不具备该特征。
2. 虚拟变量的作用及应用场景虚拟变量的主要作用是将分类变量转化为数值变量，使其能够运用于各类数据分析方法。
虚拟变量广泛应用于统计建模、回归分析、人工智能等领域。
例如，在市场调研中，虚拟变量可以用于探究不同人群的购买行为；在医学研究中，虚拟变量可以用于分析不同药物对疾病治疗效果的影响。
二、虚拟变量的构建方法1. 二元虚拟变量对于具有两个类别的分类变量，可以使用二元虚拟变量。
例如，如果我们要研究一个产品的满意度，可以将分类变量“满意”和“不满意”拆分成两个二元虚拟变量，取值为1表示满意，取值为0表示不满意。
2. 多元虚拟变量对于具有多个类别的分类变量，可以使用多元虚拟变量。
例如，如果我们要研究某地区的消费水平，可以将分类变量“低消费”、“中消费”和“高消费”拆分成三个多元虚拟变量，取值为1表示属于该消费水平，取值为0表示不属于该消费水平。
三、熵权法概述1. 什么是熵权法？熵权法是一种使用信息熵原理进行多准则决策的方法。
它利用信息熵来度量各准则的重要性，根据各准则的权重进行综合评价与决策。
通过熵权法，可以解决多准则决策中的权重确定问题，提高决策的客观性与科学性。
2. 熵权法的应用场景熵权法主要应用于风险评估、投资决策、供应商评估、环境影响评价等领域。
第七章虚拟变量
如何刻画我国居民在不同时段的消费行为？
基本思路：采用乘法方式引入虚拟变量的手段。显然， 1979年是一个转折点，可考虑在这个转折点作为虚拟 变量设定的依据。若设X* ＝1979，当 t＜X* 时可引 入虚拟变量。（为什么选择1979作为转折点？）
实质:加法方式引入虚拟变量改变的是截距；乘法方式 引入虚拟变量改变的是斜率。
一、加法类型 （1）一个两种属性定性解释变量而无定量变量的情形
例：按性别划分的教授薪金
(2)包含一个定量变量，一个定性变量模型
, 设有模型，yt = 0 + 1 xt + 2D + ut
其中yt，xt为定量变量；D为定性变量。当D = 0 或1时，上述模型可表达为，
令Y代表年薪， X代表教龄，建立模型：
Yi B0 B1Xi B2D2i B3D3i B4D4i ui
可以看出基准类是本科女教师，B0为刚参加工作的本 科女教师的工资；B1为参加工作时间对工资的影响；B2 是性别差异系数;B3和B4为学历差异系数，B3是硕士学 历与本科学历的收入差异，B4是博士学历与本科学历的 收入差异；通过上述分析，我们可以确定Bi的符号。
问题：如何刻画同时发展油菜籽生产和养蜂生产的交互 作用？
基本思想:在模型中引入相关的两个变量的乘积。
区别之处在于，上页定义中的交互效应是针对数量变量， 而现在是定性变量，又应当如何处理?
（3）分段回归分析
作用: 提高模型的描述精度。
虚拟变量也可以用来代表数量因素的不同阶段。分段线性 回归就是类似情形中常见的一种。
虚拟变量数据的实际例子
虚拟变量数据的实际例子
1. 想象一下，在研究人们对不同品牌的偏好时，虚拟变量数据就能大显身手啦！比如我们给喜欢品牌 A 的人赋值为 1，不喜欢的赋值为 0，这多直观啊！这就像用信号灯来指示喜好，红灯不喜欢，绿灯喜欢，多简单呀！
2. 嘿，你知道吗？在分析一个地区的气候对农作物的影响时，我们可以用虚拟变量来区分不同季节呀！冬天设为 1，其他季节设为 0，这不就清楚地看
到冬季的特殊之处了吗？这就如同给每个季节贴上了独特的标签一样！
3. 来看看性别对消费行为的影响吧！把男性设为 1，女性设为 0，哇哦，一下子就能看出差异了呢！这好像给男女画上了不同的色彩，让我们能轻易辨别。
4. 当研究人们是否拥有汽车这个因素时，虚拟变量就派上用场啦！有车的是1，没车的是 0，这不是很清晰明了吗？这就跟给每个人身上挂个小牌子似的，一眼就能知道有没有车。
5. 再想想看，在分析不同城市居民的生活方式时，我们可以给大城市设为1，小城市设为 0 呀！这多像是给城市分了个类，一下子就能看出不同的特点啦！
6. 还有啊，研究一个人是否吸烟的时候，用虚拟变量来表示，吸烟为 1，不吸烟为 0，是不是很简单直接呀！这就如同把人分成了两类不同的“阵营”呢！
我的观点结论就是：虚拟变量数据在各种实际情况中都超有用，能让我们快速清晰地了解各种现象背后的关键因素。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
虚拟变量（dummy variable）在实际建模过程中，被解释变量不但受定量变量影响，同时还受定性变量影响。
例如需要考虑性别、民族、不同历史时期、季节差异、企业所有制性质不同等因素的影响。
这些因素也应该包括在模型中。
由于定性变量通常表示的是某种特征的有和无，所以量化方法可采用取值为1或0。
这种变量称作虚拟变量，用D表示。
虚拟变量应用于模型中，对其回归系数的估计与检验方法与定量变量相同。
1．截距移动设有模型，y t = 0 + 1 x t + 2D + u t ,其中y t，x t为定量变量；D为定性变量。
当D= 0 或1时，上述模型可表达为，+ 1x t + u t , (D = 0)y t =(0 + 2) + 1x t + u t , (D = 1)D =0D = 1+2图8.1 测量截距不同D= 1或0表示某种特征的有无。
反映在数学上是截距不同的两个函数。
若2显著不为零，说明截距不同；若2为零，说明这种分类无显著性差异。
例：中国成年人体重y（kg）与身高x（cm）的回归关系如下：–105 + x D = 1 (男)y = - 100 + x - 5D =– 100 + x D = 0 (女)注意：①若定性变量含有m个类别，应引入m-1个虚拟变量，否则会导致多重共线性，称作虚拟变量陷阱（dummy variable trap）。
②关于定性变量中的哪个类别取0，哪个类别取1，是任意的，不影响检验结果。
③定性变量中取值为0所对应的类别称作基础类别（base category）。
④对于多于两个类别的定性变量可采用设一个虚拟变量而对不同类别采取赋值不同的方法处理。
如：1 (大学)D =0 (中学)-1 (小学)。
【案例1】中国季节GDP数据的拟合（虚拟变量应用，file：case1及case1-solve）GDP序列图不用虚拟变量的情形若不采用虚拟变量，得回归结果如下，GDP = 1.5427 + 0.0405 T(11.0) (3.5) R2 = 0.3991, DW = 2.6,s.e. = 0.3定义1 （1季度） 1 （2季度） 1 （3季度）D1 = D2 = D3 =0 （2, 3,4季度） 0 （1, 3, 4季度） 0 （1, 2, 4季度）第4季度为基础类别。
GDP = 2.0922 + 0.0315 T – 0.8013 D1 – 0.5137 D2– 0.5014 D3(64.2) (15.9) (-24.9) (-16.1) (-15.8)R2 = 0.9863, DW = 1.96,s.e. = 0.05附数据如下：年GDP t D1D2D31996:11.315611001996:21.660020101996:31.591930011996:42.2209640001997:11.4685651001997:21.8494860101997:31.797270011997:42.362080001998:11.5899491001998:21.88316100101998:31.97044110011998:42.51176120001999:11.6784131001999:21.9405140101999:32.0611150011999:42.5254160002000:11.8173171002000:22.1318180102000:32.2633190012000:42.7280200002．斜率变化以上只考虑定性变量影响截距，未考虑影响斜率，即回归系数的变化。
当需要考虑时，可建立如下模型：y t = 0 + 1 x t + 2 D+ 3 x t D + u t ,其中x t为定量变量；D为定性变量。
当D= 0 或1时，上述模型可表达为，(0 + 2 ) + (1 + 3)x t + u t , (D = 1)y t =+ 1 x t + u t , (D = 0)通过检验3是否为零，可判断模型斜率是否发生变化。
图8.5 情形1（不同类别数据的截距和斜率不同）图8.6 情形2（不同类别数据的截距和斜率不同）例2：用虚拟变量区别不同历史时期（file: case2及case2-solve）中国进出口贸易总额数据（1950-1984）见上表。
试检验改革前后该时间序列的斜率是否发生变化。
定义虚拟变量D如下0 （1950 - 1977）D =1 （1978 - 1984）中国进出口贸易总额数据（1950-1984）（单位：百亿元人民币）年trade T D T *D年trade T D T*D 19500.4151001968 1.0851900 19510.5952001969 1.0692000 19520.6463001970 1.1292100 19530.8094001971 1.2092200 19540.8475001972 1.4692300 1955 1.0986001973 2.2052400 1956 1.0877001974 2.9232500 1957 1.0458001975 2.9042600 1958 1.2879001976 2.6412700 1959 1.49310001977 2.7252800 1960 1.28411001978 3.55029129 19610.90812001979 4.54630130 19620.80913001980 5.6383113119630.857140019817.35332132 19640.975150019827.71333133 1965 1.184160019838.60134134 1966 1.2711700198412.01035135 1967 1.1221800以时间T=time为解释变量，进出口贸易总额用trade表示，估计结果如下：trade = 0.37 + 0.066 time - 33.96D + 1.20 time D(1.86) (5.53) (-10.98) (12.42)0.37 + 0.066 time (D = 0, 1950 - 1977)=- 33.59 + 1.27 time (D = 1, 1978 - 1984)上式说明，改革前后无论截距和斜率都发生了变化。
进出口贸易总额的年平均增长量扩大了18倍。
【案例3】香港季节GDP数据（单位：千亿港元）的拟合（file: case3及case3-solve）1990~1997年香港季度GDP呈线性增长。
1997年由于遭受东南亚金融危机的影响，经济发展处于停滞状态，1998~2002年底GDP总量几乎没有增长（见上图）。
对这样一种先增长后停滞，且含有季节性周期变化的过程简单地用一条直线去拟合显然是不恰当的。
为区别不同季节，和不同时期，定义季节虚拟变量D2、D3、D4和区别不同时期的虚拟变量DT如下（数据见附录）：1 （第2季度）D2 =0 （其他季度）1 （第3季度）D3 =0 （其他季度）1 （第4季度）D4 =0 （其他季度）1 （1998:1~2002:4）DT =0 （1990:1 ~1997:4）得估计结果如下：GDP t = 1.1573 + 0.0668 t + 0.0775 D2 + 0.2098 D3 + 0.2349 D4+ 1.8338 DT - 0.0654 DT t(50.8) (64.6) (3.7) (9.9) (11.0) (19.9) (-28.0)R2= 0.99, DW = 0.9, s.e. = 0.05, F=1198.4, T=52, t0.05 (52-7) = 2.01对于1990:1 ~1997:4GDP t = 1.1573 + 0.0668 t + 0.0775 D2 + 0.2098 D3 + 0.2349 D4对于1998:1~2002:4GDP t = 2.9911 + 0.0014 t + 0.0775 D2 + 0.2098 D3 + 0.2349 D4如果不采用虚拟变量拟合效果将很差：GDP t = 1.6952 + 0.0377 t(20.6) (13.9)R2 = 0.80, DW = 0.3, T=52, t0.05 (52-2) = 2.01【案例4】天津市粮食市场小麦批发价与面粉零售价的关系研究（file: xiezhiyong）首先看天津市粮食市场小麦批发价格的变化情况（图1）。
1995年初，天津市粮食市场的小麦批发价格首先放开。
在经历5个月的上扬之后，进入平稳波动期。
从1996年8月份开始小麦批发价格一路走低。
至2002年12月份，小麦批发价格降至是1160元/吨。
其次看面粉零售价的变化情况。
因为面粉零售价格直接关系到居民的日常生活，所以开始时没有与小麦批发价格一起放开。
当小麦批发价格一路看涨时，1995年1月至1996年6月面粉零售价格一直处于2.14元/千克的水平上。
1996年7月起，面粉零售价格也开始在市场上放开。
受小麦批发价格上涨的影响，一个月内面粉零售价格从2.14元/千克涨到2.74元/千克。
在这个价位上坚持了11个月之后，面粉零售价格开始下降。
与小麦批发价格的下降相一致，在经历了5年零7个月的变化之后，面粉零售价格又恢复到接近开放前2.14元/千克的水平上（2.17元）。
散点图如图2。
按时间分析这些观测点的变化情况（见图3，逆时针方向运动）。
见图4，直接拟合这些数据效果将很差（R2 = 0.027, r = 0.17）。
图1 图2图3 图4利用虚拟变量技术，在模型中加入虚拟变量。
定义D = 0，（1995: 1~1996:6，面粉零售价格放开之前），D = 1，（1996:7~2002:12，面粉零售价格放开之后）。
取对数关系建立模型。
Lnsale的系数没有显著性（对于面粉零售价格放开之前的散点来说回归直线是一条水平线）。
剔出Lnsale变量，得估计结果PRICE = 2.140 + 1.1215 LnsaleD – 7.7458D(131.5) (23.9) (-23.0) R2 = 0.9054,PRICE = 2.140, D=0PRICE = – 5.6058 + 1.1215 Lnsale, D=1一条回归直线的斜率为零，一条回归直线的斜率为1.12。
可决系数从不加虚拟变量模型的0.046增加到0.905（输出结果见下）。
本例也可以建立倒数模型：PRICE = 2.140 + 1.5141D – 1565.9 (1/sale) D (145.9) (32.1) (-27.0) R2 = 0.9231, PRICE = 2.140, D=0PRICE = 3.6541 – 1565.9(1/sale), D=1。