电势 - 理学院主页
合集下载
大学物理6.3 电势PPT
∞
q0
p εp
UP
v E
电势（电势能）零点的选择 电势能） 任意 视分析问题方便而定
通常： 通常： （1）有限带电体： ）有限带电体： （2）无限带电体： ）无限带电体：
U∞ = 0 (a ) U∞ ≠ 0 电场中任选一点
r 际应用中或研究电路问题时： ）实际应用中或研究电路问题时： 取大地、 取大地、仪器外壳等 3、意义： 描述电场能（电场力作功）方面的性质 意义： 描述电场能（电场力作功）
结论：静电场力做功，与路径无关. 结论：静电场力做功，与路径无关. 静电场的这一特性称为静电场的保守性 相应地，静电力是保守力（像重力一样） 7 相应地，静电力是保守力（像重力一样）
1.单个点电荷产生的电场 1.单个点电荷产生的电场 r r r r Q dW = F ⋅ dl = q0 E ⋅ dl
U
o
Q U 外 (r ) = 4 πε 0 r Q U内 ( r ) = 4 πε 0 R
Q 4 π ε0R
Q 4 π ε 0r
o
R
r
例3 解：
计算电量为 Q 的带电球面球心的电势
dq
o
在球面上任取一电荷元dq
Q R
dq 则电荷元在球心的电势为 dU = 4πε 0 R
由电势叠加原理 球面上电荷在球心的总电势 思考： 思考：
W = q0 ∫
Q P
∞
q0
p εp
v E
r r E ⋅ dl
点为无穷远时， 当Q点为无穷远时，电场力所做的功称为q0 点为无穷远时 在电场中的P点的电势能 点的电势能， 在电场中的 点的电势能，即P点电势能为 点电势能为 r ∞ r ε P = q0 ∫ E ⋅ dl
q0
p εp
UP
v E
电势（电势能）零点的选择 电势能） 任意 视分析问题方便而定
通常： 通常： （1）有限带电体： ）有限带电体： （2）无限带电体： ）无限带电体：
U∞ = 0 (a ) U∞ ≠ 0 电场中任选一点
r 际应用中或研究电路问题时： ）实际应用中或研究电路问题时： 取大地、 取大地、仪器外壳等 3、意义： 描述电场能（电场力作功）方面的性质 意义： 描述电场能（电场力作功）
结论：静电场力做功，与路径无关. 结论：静电场力做功，与路径无关. 静电场的这一特性称为静电场的保守性 相应地，静电力是保守力（像重力一样） 7 相应地，静电力是保守力（像重力一样）
1.单个点电荷产生的电场 1.单个点电荷产生的电场 r r r r Q dW = F ⋅ dl = q0 E ⋅ dl
U
o
Q U 外 (r ) = 4 πε 0 r Q U内 ( r ) = 4 πε 0 R
Q 4 π ε0R
Q 4 π ε 0r
o
R
r
例3 解：
计算电量为 Q 的带电球面球心的电势
dq
o
在球面上任取一电荷元dq
Q R
dq 则电荷元在球心的电势为 dU = 4πε 0 R
由电势叠加原理 球面上电荷在球心的总电势 思考： 思考：
W = q0 ∫
Q P
∞
q0
p εp
v E
r r E ⋅ dl
点为无穷远时， 当Q点为无穷远时，电场力所做的功称为q0 点为无穷远时 在电场中的P点的电势能 点的电势能， 在电场中的 点的电势能，即P点电势能为 点电势能为 r ∞ r ε P = q0 ∫ E ⋅ dl
大学物理第23章_电势
。 请与重力做功作一类比
电势与电势差
电势定义为单位电荷具有的电势能，用符号 V 表示
如果一个带电量为 q 的正试验电荷在电场中a点具有电
U V 势能为 （相对零势能点），则该点电势 为
a
a
Va
Ua q
电势的意义：a 点的电势在数值上等于将单 位正电荷从 a 点移到无穷远处（或电势能 为零处）静电场力对它所做的功。
电场力做正功,电势能减少
U Ua Ub 0
Vab
V
Va
Vb
Ua
Ub q
因为q<0，所以电势增大
沿着电场线方向，电势降低。
VP VQ
P dl
Q
VP VQ
P
dl Q
思考（1）把电荷 +q 从P点移动到Q点，电场力 是作正功还是负功？P，Q两点哪点的电势高？
（2）如果移动的是负电荷呢？
A
E
E
x
U 0 U 0 U 0
沿着电场线方向，电势降低
0 0
E
U 0
C
沿着电场线方向，电势降低
电源（比如电池和发电机）的作用就是维持电势差， 其输送能量的多少取决于流过的电荷量和电势差。
例如，一个12.0V的电池为汽车车灯供电，电池提供的能量（转 变为光能和热能）与流过的电荷量（即亮灯时间）成正比——如 果在给定的时间内有5.0C的电量流过车灯，则电池输送的总能量 为(5.0C)(12.0V)= 60 J；而如果车灯亮灯时间加倍，则有10.0C的 电荷流过,电池输送的能量为(10.0C)(12.0Ｖ)= 120 J。
例题23-4 一半径为 r0、总电荷为Q的带电导体球，试确定 距离球心为 r处的电势（a）r > r0，（b）r =r0，(c) r < r0。
电势与电势差
电势定义为单位电荷具有的电势能，用符号 V 表示
如果一个带电量为 q 的正试验电荷在电场中a点具有电
U V 势能为 （相对零势能点），则该点电势 为
a
a
Va
Ua q
电势的意义：a 点的电势在数值上等于将单 位正电荷从 a 点移到无穷远处（或电势能 为零处）静电场力对它所做的功。
电场力做正功,电势能减少
U Ua Ub 0
Vab
V
Va
Vb
Ua
Ub q
因为q<0，所以电势增大
沿着电场线方向，电势降低。
VP VQ
P dl
Q
VP VQ
P
dl Q
思考（1）把电荷 +q 从P点移动到Q点，电场力 是作正功还是负功？P，Q两点哪点的电势高？
（2）如果移动的是负电荷呢？
A
E
E
x
U 0 U 0 U 0
沿着电场线方向，电势降低
0 0
E
U 0
C
沿着电场线方向，电势降低
电源（比如电池和发电机）的作用就是维持电势差， 其输送能量的多少取决于流过的电荷量和电势差。
例如，一个12.0V的电池为汽车车灯供电，电池提供的能量（转 变为光能和热能）与流过的电荷量（即亮灯时间）成正比——如 果在给定的时间内有5.0C的电量流过车灯，则电池输送的总能量 为(5.0C)(12.0V)= 60 J；而如果车灯亮灯时间加倍，则有10.0C的 电荷流过,电池输送的能量为(10.0C)(12.0Ｖ)= 120 J。
例题23-4 一半径为 r0、总电荷为Q的带电导体球，试确定 距离球心为 r处的电势（a）r > r0，（b）r =r0，(c) r < r0。
大学物理-电势
Va E dl a E dl
讨论
a
a
1)电势零点的选择(参考点)
任意 视分析问题方便而定
参考点不同电势不同
10
通常：
理论计算有限带电体电势时选无限远为参考点
实际应用中或研究电路问题时取大地、仪器外 壳等
2)电势的量纲
SI制：单位 V (伏特)
量纲
V
W q
L2 MT
3I
1
3)电势是一个长程物理量
b b
a
f dl q E dl Wa Wb
a
a
b E dl
Wa
Wb
a
q
q 与试验电荷无关
根据静电场 Wa Wb 的环路定理 q q
E dl Va Vb
a
称 a b两点电势差
若选b点的势能为参考零点 则
a点的电势：
势能零点
势能零点
VA VB
11
rB rA
E
dr
Q 4πε0
rB dr rA r 2
()
4πε0 rA rB
（2）r R
VA VB
rB rA
E
dr
0
o A B A dr B
R
drrA r
r
rB
20
（3）r R 令 rB V 0
Q 1 1
VA VB
（4）r R
()
4πε0
rA R
q
x2 R2
x
R，VP
q 4πε0 x
V
dl
q
q
4πε0 R
4πε0 x2 R2
R
r
xo x
Px
o
x
大学物理电势ppt课件
电势定义
$V = frac{kQ}{r}$，其中$k$为静电力常量，$Q$为场源电荷量，$r$为到场源电荷的距离。
点电荷电势公式
点电荷电势计算
对于多个点电荷或连续分布电荷产生的电势，可应用叠加原理进行求解。
叠加原理
对于连续分布电荷，需采用积分方法计算电势，如线积分、面积分或体积分。
积分方法
均匀带电直线、均匀带电平面、均匀带电球体等。
大学物理电势ppt课件
目录
电势基本概念与性质 点电荷与连续分布电荷电势 导体与绝缘体在电场中电势特性 电势能、电势差及等势面 电场力做功与路径无关性讨论 总结回顾与拓展延伸
01
CHAPTER
电势基本概念与性质
电势定义及物理意义
电势定义
描述电场中某点电势能的性质，反映单位正电荷在该点所具有的电势能。
实际应用举例
04
CHAPTER
电势能、电势差及等势面
电荷在电场中具有的势能，与电荷量及所在位置有关。
电势能定义
通过电场力做功来计算，公式为W=qU，其中W为电势能，q为电荷量，U为电势差。
电势能计算
电势能具有相对性，与零电势点的选择有关。
电势能性质
电势能概念及计算
电场中两点间电势的差值，等于单位正电荷从一点移动到另一点时电场力所做的功。
常见连续分布电荷
连续分布电荷电势求解方法
均匀带电直线电势
通过高斯定理和积分方法求解，结果与观察点到直线的垂直距离和线电荷密度有关。
均匀带电平面电势
利用高斯定理和叠加原理，可求得电势与观察点到平面的距离和平面电荷密度之间的关系。
均匀带电球体电势
采用高斯定理和积分方法，可得到球体内外任意一点的电势表达式。
$V = frac{kQ}{r}$，其中$k$为静电力常量，$Q$为场源电荷量，$r$为到场源电荷的距离。
点电荷电势公式
点电荷电势计算
对于多个点电荷或连续分布电荷产生的电势，可应用叠加原理进行求解。
叠加原理
对于连续分布电荷，需采用积分方法计算电势，如线积分、面积分或体积分。
积分方法
均匀带电直线、均匀带电平面、均匀带电球体等。
大学物理电势ppt课件
目录
电势基本概念与性质 点电荷与连续分布电荷电势 导体与绝缘体在电场中电势特性 电势能、电势差及等势面 电场力做功与路径无关性讨论 总结回顾与拓展延伸
01
CHAPTER
电势基本概念与性质
电势定义及物理意义
电势定义
描述电场中某点电势能的性质，反映单位正电荷在该点所具有的电势能。
实际应用举例
04
CHAPTER
电势能、电势差及等势面
电荷在电场中具有的势能，与电荷量及所在位置有关。
电势能定义
通过电场力做功来计算，公式为W=qU，其中W为电势能，q为电荷量，U为电势差。
电势能计算
电势能具有相对性，与零电势点的选择有关。
电势能性质
电势能概念及计算
电场中两点间电势的差值，等于单位正电荷从一点移动到另一点时电场力所做的功。
常见连续分布电荷
连续分布电荷电势求解方法
均匀带电直线电势
通过高斯定理和积分方法求解，结果与观察点到直线的垂直距离和线电荷密度有关。
均匀带电平面电势
利用高斯定理和叠加原理，可求得电势与观察点到平面的距离和平面电荷密度之间的关系。
均匀带电球体电势
采用高斯定理和积分方法，可得到球体内外任意一点的电势表达式。
课件：电势
将单位正电荷从A移到B时电场力作的功
几种常见的电势差（V）
生物电
10-3
普通干电池 1.5
汽车电源 12
家用电器 110或220
高压输电线 已达5.5105
闪电
108109
3
物理学
第五版
5-7 电势
静电场力的功
WAB q AB E dl qUAB q(VA VB )
原子物理中能量单位: 电子伏特eV
o
AB
R
rA
r
oR
r
rB
14
1
物理学
第五版
5-7 电势
电势零点的选取：
有限带电体以无穷远为电势零点，实际
问题中常选择地球电势为零.
VA
E dl
A
物理意义： 把单位正试验电 荷从点A移到无限远 处时静电场力作的功.
q0 A EVpAA
B
EVpBB
E
2
物理学
第五版
5-7 电势
电势差
U AB VA VB
E dl
AB
VA
AB
E dl
VB
已知在积分路径上 E的函数表达式
有限大带电体，选无限远处电势为零.
（2）利用点电荷电势的叠加原理
V
1 4πε0
dq r
8
物理学
第五版
5-7 电势
例1 正电荷q均匀分布在半径为R的细圆
环上. 求环轴线上距环心为x处的点P的电势.
解
dVP
1 4πε0
dq r
1
VP 4πε0r dq
A Ei dli 1Biblioteka nVii 1
VA
n i 1
高中物理选修课件电势与等势面
假设电荷在电场中沿两条不同路径从A点移动到B点，根据电场力做功的定义，两条路径上电场力做的功应该相等 。因此，可以得出电场力做功与路径无关的结论。
保守场和非保守场区别
保守场
保守场是指存在一个标量函数（即势函数），使得场强矢量可以表示为该函数梯度的场。在保守场中 ，电场力做功与路径无关，只与电荷的初末位置有关。
电场强度与电势关系
电场强度与电势梯度关系
电场强度E等于电势φ的负梯度，即E=-∇φ。这表明电场强度 的方向与电势降低最快的方向一致，大小等于单位距离内电 势的降低量。
电场线与等势面关系
电场线总是垂直于等势面，且指向电势降低的方向。等势面 越密集的地方，电场强度越大。
等势面概念及性质
• 等势面定义：电场中电势相等的各个点构成的面叫做等势 面。
等势面概念及性质
等势面性质 等势面一定跟电场线垂直。
在同一等势面上移动电荷时电场力不做功。
等势面概念及性质
电场线总是从电势高 的等势面指向电势低 的等势面。
等差等势面越密的地 方电场强度越大。
任意两个等势面都不 会相交。
02
电场中等势面分布规律
均匀带电球体内部等势面
等势面形状
均匀带电球体内部的等势面是一系列 以球心为中心的同心球面。
电势差
电势差是指电场中两点之间电势的差 值，用符号U表示，单位是伏特（V ）。
等势面
电场中电势相等的各个点构成的面叫 做等势面。
电场线与等势面的关系
电场线总是与等势面垂直，并且从高 电势指向低电势。
解题思路和方法技巧分享
01
判断电势高低的方法
根据电场线的方向判断，沿电场线方向电势逐渐降低；根据电势能的变
电场线与等势面的关系研究
保守场和非保守场区别
保守场
保守场是指存在一个标量函数（即势函数），使得场强矢量可以表示为该函数梯度的场。在保守场中 ，电场力做功与路径无关，只与电荷的初末位置有关。
电场强度与电势关系
电场强度与电势梯度关系
电场强度E等于电势φ的负梯度，即E=-∇φ。这表明电场强度 的方向与电势降低最快的方向一致，大小等于单位距离内电 势的降低量。
电场线与等势面关系
电场线总是垂直于等势面，且指向电势降低的方向。等势面 越密集的地方，电场强度越大。
等势面概念及性质
• 等势面定义：电场中电势相等的各个点构成的面叫做等势 面。
等势面概念及性质
等势面性质 等势面一定跟电场线垂直。
在同一等势面上移动电荷时电场力不做功。
等势面概念及性质
电场线总是从电势高 的等势面指向电势低 的等势面。
等差等势面越密的地 方电场强度越大。
任意两个等势面都不 会相交。
02
电场中等势面分布规律
均匀带电球体内部等势面
等势面形状
均匀带电球体内部的等势面是一系列 以球心为中心的同心球面。
电势差
电势差是指电场中两点之间电势的差 值，用符号U表示，单位是伏特（V ）。
等势面
电场中电势相等的各个点构成的面叫 做等势面。
电场线与等势面的关系
电场线总是与等势面垂直，并且从高 电势指向低电势。
解题思路和方法技巧分享
01
判断电势高低的方法
根据电场线的方向判断，沿电场线方向电势逐渐降低；根据电势能的变
电场线与等势面的关系研究
大学物理 电势
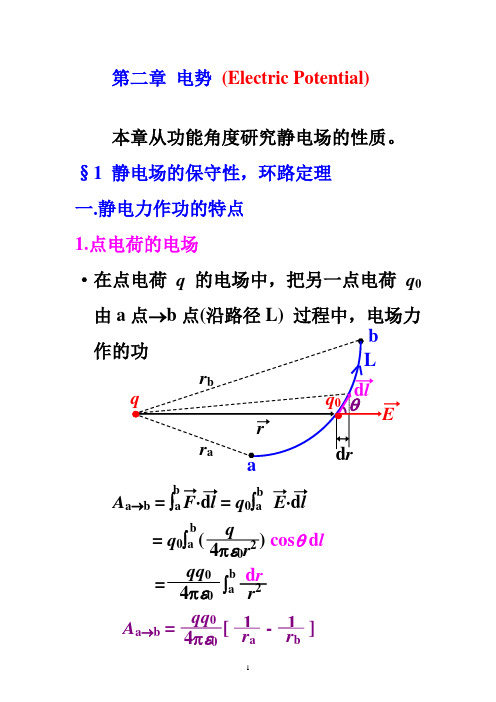
第二章 电势 (Electric Potential)本章从功能角度研究静电场的性质。
§1 静电场的保守性，环路定理 一.静电力作功的特点 1.点电荷的电场·在点电荷q 的电场中，把另一点电荷q 0由a 点→b 点(沿路径L) 过程中，电场力A a →b = ⎰a F ⋅d l = q 0⎰a E ⋅d lb b = q 0⎰a ( ) cos θ d lb4πε0r 2 q = 4πε0qq 0 b ⎰a d r r 24πε0qq 0 A a →b =[ - ] 1 r b 1 r aE可见，电场力作的功只取决于被移动电荷 的起、终点的位置，与移动的路径无关。
2.点电荷系的电场·在点电荷系q 1、q 2、…的电场中，移动 q 0，有其中，每一项均与路径无关， ⇒A a →b 也与路径无关。
·对连续带电体的场强同样可得此结论 静电力作功与路径无关， 静电场是保守力场。
二.环路定理·在静电场中，沿闭合路径 移动q 0，电场力作功b L 2+ q 0⎰a E 2 ⋅ d l+ …A a →b = q 0⎰a E ⋅ d lb= q 0⎰a E 1 ⋅ d lbb静电场的环路定理在静电场中，电场强度沿任意闭合路径的 线积分等于零。
·讨论：(1)环路定理是静电场的另一重要定理，可 用环路定理检验一个电场是不是静电场。
ba= q 0 ⎰ a E ⋅ d l(L 1) + q 0 ⎰ b E ⋅ d l (L 2)= q 0 ⎰ a E ⋅ d lb(L 1)- q 0 ⎰ a E ⋅ d lb(L 2)= 0 A = q 0 ⎰ E ⋅d lE 思考 ：如图电场是静电场吗？ 电场线(2)环路定理要求电场线不能闭合。
静电场是有源、无旋场。
三.电势能 1.电势能的差·静电力是保守力，可引入电势能的概念。
·由保守力作功和势能增量的关系有q 0在电场中a 、b 两点电势能之差等于把 q 0自a 点移至b 点过程中电场力所作的 功。
电势
v v v v q0 ∫ E ⋅ dl = q0 ∫ E ⋅ dl A1 B A2 B v v v v q0 ( ∫ E ⋅ dl + ∫ E ⋅ dl ) = 0
A1B
静电场的环路定理
1
B
2
A
v E
v v E ⋅ dl = 0 ∫
l
B2 A
静电场是保守场
9 - 6 三
电 势
物理学教程 第二版） （第二版）
即电场线是和等势面正交的曲线簇. 即电场线是和等势面正交的曲线簇. 正交的曲线簇
va 在静电场中， 总是与等势面垂直的， 在静电场中，电场强度 E 总是与等势面垂直的，
Wab = ∫
b a
Wab = q0 (U a − U b ) = ∫
b
v v q0 E ⋅ d l = 0
v v q0 ≠ 0 E ≠ 0 dl ≠ 0
+ + +
v oe
v A dr B
r
r
rB
V∞ = 0
Q
Q 1 1 可得U (r ) = Q 由 U A −UB = ( − ) 外 4 πε 0 r 4 πε 0 rA rB ∞ v v = ∞ Q dr = Q 或U 外 ( r ) = E2 ⋅ dr ∫r 2 4 π ε 0r 4 π ε 0r r
UB = 0
o B rB
P
r
r
=0
？
9 - 6 例3
电 势
物理学教程 第二版） （第二版）
均匀带电球壳的电势. 均匀带电球壳的电势.
真空中， 的带电球壳. 真空中，有一带电为 Q ，半径为 R 的带电球壳 ；（2） 试求（1）球壳外两点间的电势差；（ ）球壳内两点 ）球壳外两点间的电势差；（ 间的电势差； 间的电势差； + 解
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
E l El cos Va Vb V 设E在l 上的分量为El E cos
V El l＝ V or El＝ l V V l 0 El＝ lim l 0 l l
l
II
I
V 是电势沿l 方向的方向导数 l V 电势沿等势面切线方向的方向导数 ＝0 l
0
R
3.电势分布
V
1 q 40 R
q 4o r 1
O
rR
rR
r
p
电势的计算例题
结论：均匀带电球面，球内的电势等于球表面的电势，球 外的电势等效于将电荷集中于球心的点电荷的电势。
q 40 R 2
E
r
R
2
场强分布曲线
O
V
r
电势分布曲线
q 40 R
r
R
1
O
r
电势的计算例题
电势沿等势面法线方向的方向导数
V ln
E
V n ln
n为等势面的法向（垂直等势面，指向电势增大的方向）
直角坐标系下，V 是x、y、z方向的函数
V V V E ( i j k ) V ( x, y, z ) x y z
为梯度算符，V 称为电势梯度。
场强与电势的关系
E p＝q0 E dl
r
若选r0处为电势能的零点，则电场中任一点的电势能表为：
E p＝q0 E dl
r
r0
可以看出电势能是场和试验电荷共同性质的体现，即电 势能即与场有关也与试验电荷有关。电势能的单位为焦 耳（J）
电 势
2、 电势及电势叠加原理
为了得到一个只与场有关的物理量，进而用它来描 述电场，我们定义电势，它是电势能EP 与q0之比，它只 取决于电场。电场中某点的电势为
例4 计算电偶极子电场中任一点的电势。 解 ：电偶极子的电场中任一点P的 q q 电势为 VP 4 0 r 4 0 r 式中 r+ 与 r- 分别为 +q 和 -q 到 P 点的距离，由图可知 q re re r r cos r － r＋ cos 2 2
q 1 1 VP re re 4 0 r cos r cos 2 2
q
dr
dl
q0 E dr
W dW q0 a E dl
b
r
ra
q0
E
a
W q0 E dl
a
b
qq0 4
rb
ra
dr qq0 1 1 ( ) 2 r 4 ra rb
b
静电场做功和路径无关。
rb
r dr
dr
dl
q
r
ra
q0
E
a
2、 任意带电体系的电场中 将带电体系分割为许多电荷元，根据电场的叠加性 E E1 E2 En 电场力对试验电荷q0做功为
ra
1 1 q dr ( ) 2 4 0 r 4 0 ra 4 0 ra
q
q
如果是点电荷系在空间的电势分布，选无穷远为电势零 点则有： V E dl
a
a
( E1 E2
a
En ) dl E1 dl
a
En dl
a
Vi
r1
r4 q1
dq V 4 0 r
1
q4
电势的计算例题
电势的计算例题 例1. 均匀带电圆环轴线上的电势 例2. 均匀带电薄圆盘轴线上的电势
例3 均匀带电球面的电势 例4. 电偶极子的电势
例5. 均匀带电线的电势
例1. 均匀带电圆环轴线上的电势（q、a、x）
dq dl
Vp 1 4
q E dS S 0 E dl 0 L
电 势
二、 电势和电势叠加原理
1、 电势能(electric potential energy)
由环路定理知，静电场是保守场。保守场必有相应的势能，对静 电场则为电势能。 以点电荷为例给出静电场的电势能的定义。 静电场力的功： W
在静电场中，电势相等的点所组成的面称为等势面。 1、 典型等势面
点电荷的等势面
等势面
电偶极子的等势面
+
等势面
电平行板电容器电场的等势面
++ ++ + + + + +
等势面
2、 等势面与电场线的关系
q0在等势面上移动，在等势面上移动电场力不作功
dW q0 E dl q0 E cos dl 0
y r r
P
r+ +q x
re cos q 2 4 0 2 re r cos 2
O re/2 re/2
由于r>> re ，所以P点的电势可写为 VP
qre cos Pe r 4 0 r 2 4 0 r 3
§8-5 电场强度与电势的关系 一、 等势面
§8.4 静电场的环路定理 电势
一 静电场力的功 静电场的环路定理 1、 点电荷电场 试验电荷q0从点电荷q的电场中a点经任意路径到 达b点,求此过程中电场力作的功。
在路径上任一点附近取元位移 dl
b
dW F dl q0 E dl
q0 E dl cosθ
rb
r dr
q 2 a
dl
dl
a
O
y
q 1 dl 2 a r
r
x
q 4 r
q
p
x
z
其中r a x
2 2
1 4 (a 2 x 2 )1/ 2
例2.半径为R的均匀带电薄圆盘轴线上的电势分布。
解：以O为圆心，取半径为LL+dL的薄圆 环，带电 dq=ds= •2L •dL
P点电势：
x (1 ) 2 0 R2 x2
p
O
x
R
与用叠加原理得到的结果一致。
讨论： 当R时， E 2 0
即无穷大均匀带电平面的电场。
L
即
L E dl 0
P1 L1
静电场力的功
静电场的环路定理:在静电场中，场强沿任意闭合路 径的线积分（称为场强的环流）恒为零。
L E dl 0
静电场的环路定理说明，静电场是无旋场。 静电场的高斯定理和环路定理是静电场的基本规律，它 们所反映的物理图像是：电荷是电场的源，电场线从正 电荷出发而终止于负电荷，在自由空间中电场线连续通 过；在静电情形下电场没有漩涡状结构。
Va
E pa q0
E dl
ra
r0
电势零点的选取是任意的。一般电势零点可以选在无穷远
Va E dl
a
电势是标量，单位为伏特（V），显然，1V＝1J/1C
由电势的定义，很容易计算真空中点电荷在空间的电势 分布，选无穷远为电势零点则有：
Va E dl
a
q0 0
E 0
dl 0
S
E q0 θ
dl
即
cos 0
E dl
结论：电力线与等势面垂直。
等势面
3、 等势面图示法 等势面画法规定：相邻两等势面之间的电势间隔相 等。
U
U+U
U+2U
U+3U
E
二、电场强度与电势的关系
V V
显然V 0
V
E
a
b
将单位正电荷由a移动到b，电场力做的功为
电势梯度
3、 场强与电势梯度的关系的应用
电势叠加为标量叠加，故可先算出电势，再 应用场强与电势梯度的关系算出场强。 例5 例6 均匀带电圆环轴线上的电场 均匀带电圆盘轴线上的电场
等势面 电场强度与电势梯度的关系
例5.计算均匀带电圆环轴线上的电场。 解：P点电势
1 dq 1 dq V 2 2 1/ 2 4 ( R x ) 4 0 r 0 q 40 ( R 2 x 2 )1/ 2
W F dl q0 L E dl L
p2
p1 q0 p1 E dl q0 p2 E dl
(L1)
p1
(L2)
q0 (
p2
E dl p E dl ) 1
p2
L2
P2
(L1)
(L2)
电场力做功与路径无关，故
W q0 E dl 0
沿着电场线方向，电势降低。
电势的计算
三、电势的计算 1、 点电荷的电势
V + P
i
1 q dr V r E dl r 2 4 0 r
q 4 0 r
1
r
2、点电荷系的电势 V 3、 连续分布带电体的电势
1 qi 4 0 ri
r3 r2 q2 q3
R o r p x E
P点电场
X
qx U E Ex 2 2 3/ 2 x 40 ( R x )
与用叠加原理得到的结果一致。
等势面 电场强度与电势梯度的关系
例6 计算均匀带电圆盘轴线上的电场。
解： V ( R 2 x 2 x) 2 0 U E Ex x
C
r
ra
q0
E
这样静电场力的功可表示为电势能的负增量：
a
Wab Ep (Epb Epa )
电势能的零点选取时任意的，一般可选无穷远处为电势 能的零点，如果这样，电势能中待定的常数C为零。 qq0 C C 0 ra 时Epa＝0 E pa＝ 4 ra 这样，电场中任一点的电势能可表为：