三角函数的图像和性质(1)

合集下载

三角函数的定义和性质

三角函数与复数的关系
三角函数与复数的基本关系：复数可以表示为三角函数的形式，即z=r(cosθ+i sinθ)。
三角函数在复平面上的表示：复平面上，三角函数可以表示为点或向量，其模长和幅角分别对应于实部和虚部。
三角函数与复数在交流电中的应用：交流电的电压和电流可以用三角函数表示，而复数则可以更方便地描述正弦波的幅度和频率。
04
三角函数的扩展知识
反三角函数
添加标题
添加标题
添加标题
添加标题
性质：反三角函数具有连续性、单调性、奇偶性和周期性等性质。
定义：反三角函数是三角函数的反函数，表示为arcsin、arccos和arctan等。
图像：反三角函数的图像与三角函数图像关系密切，可以通过三角函数图像得出反三角函数图像。
应用：反三角函数在数学、物理和工程等领域有广泛应用，例如求解三角形、解决极值问题等。
三角恒等式和不等式
三角恒等式：表示三角函数之间关系的等式，如正弦、余弦、正切等函数之间的相互转化。
三角不等式：表示三角函数值大小关系的不等式，用于比较三角函数值的大小或证明不等关系。
三角恒等变换：通过三角函数的和差、倍角、半角等公式，进行恒等变换，简化表达式或证明等式。
三角不等式的证明方法：利用三角函数的性质和几何意义等方法，证明三角不等式的关系。
三角函数与复数在信号处理中的应用：信号处理中，信号常常被表示为复数形式的三角函数，这使得信号的合成、分析和滤波变得更加方便。
汇报人：XX
感谢观看
周期性：三角函数具有明显的周期性，图像呈现规律性的重复。
奇偶性：三角函数具有奇偶性，可以根据函数值的正负判断其奇偶性。
最大值和最小值：三角函数具有最大值和最小值，可以通过函数的极值点判断其最大值和最小值。

三角函数图像和性质练习题(附答案)

三角函数的图像与性质【1】一、选择题1.已知函数f(x)=2sin ϖx(ϖ>0)在区间[3π-,4π]上的最小值是－2，则ϖ的最小值等于（）A.32 B.23C.2D.3 2.若函数cos()3y x πω=+(0)ω>的图象相邻两条对称轴间距离为2π，则ω等于． A ．12B ．12C ．2D ．43.将函数sin()()6yx x R π=+∈的图象上所有的点向左平行移动4π个单位长度，再把图象上各点的横坐标扩大到原来的2倍（纵坐标不变），则所得到的图象的解析式为A ．5sin(2)()12y x x R π=+∈ B ．5sin()()212x y x R π=+∈ C ．sin()()212x y x R π=-∈ D ．5sin()()224x y x R π=+∈4.函数2)62cos(-+=πx y 的图像F 按向量a 平移到F /，F /的解析式y=f(x),当y=f(x)为奇函数时，向量a 可以等于A.)2,6(-π B.)2,6(π C.)2,6(--π D.)2,6(π-5.将函数sin y x =的图象向左平移(02)ϕϕπ≤≤个单位后，得到函数sin()6yx π=-的图象，则ϕ等于（）A .6πB .76πC .116πD .56π6.函数x x y 2cos 32sin -=)66(ππ≤≤-x 的值域为A.[]2,2- B. []0,2- C. []2,0 D. ]0,3[-7.将函数的图象上所有点的横坐标伸长到原来的倍（纵坐标不变），再将所得的图象向左平移个单位，得到的图象对应的解析式是（）A ．B ．C.D.8.函数f(θ ) =sin θ－1cos θ－2的最大值和最小值分别是()(A) 最大值 43 和最小值0(B)最大值不存在和最小值 34(C) 最大值－43 和最小值0(D) 最大值不存在和最小值－349.ααcos sin +=t且αα33cos sin +＜0，则t 的取值范围是（）A. [)0,2-B. []2,2-C. ()(]2,10,1 -D. ()()+∞-,30,310.把函数)(x f y =的图象沿着直线0=+y x 的方向向右下方平移22个单位，得到函数x y 3sin =的图象，则（）A 、2)23sin(--=x yB 、2)63sin(--=x yC 、2)23sin(++=x yD 、2)63sin(++=x y二、填空题11.设函数).0)(3cos()(πϕϕ<<+=x x f 若)()(x f x f '+是奇函数，则ϕ=. 12.方程2cos()14x π-=在区间(0,)π内的解是．13.函数]),0[)(26sin(2ππ∈-=x x y 为增函数的区间14.已知x R ∈，则函数sin cos ()max sin ,cos ,2x x f x x x +⎧⎫=⎨⎬⎩⎭的最大值与最小值的和等于。

三角函数图像与性质

三角函数图像与性质在数学中，三角函数是研究角与角度关系的一类函数。

其中最重要的三角函数包括正弦函数、余弦函数和正切函数。

这些函数在数学和科学领域中有着广泛的应用，尤其是在研究周期性现象时起到了关键作用。

本文将详细介绍三角函数的图像特征和性质。

正弦函数的图像与性质正弦函数是最基本的三角函数之一，通常用符号$\\sin$表示。

它的图像是一条连续的波浪线，呈现出周期性的特点。

正弦函数的定义域为整个实数集$\\mathbb{R}$，值域为闭区间[−1,1]。

在0度、90度、180度、270度和360度等特殊角度上，正弦函数的取值分别为0、1、0、-1和0。

正弦函数是奇函数，即$\\sin(-x)=-\\sin(x)$，具有对称性。

余弦函数的图像与性质余弦函数是另一个重要的三角函数，通常用符号$\\cos$表示。

它的图像类似于正弦函数，也是一条连续的波浪线，同样呈现周期性。

余弦函数的定义域为整个实数集$\\mathbb{R}$，值域为闭区间[−1,1]。

在0度、90度、180度、270度和360度等特殊角度上，余弦函数的取值分别为1、0、-1、0和1。

余弦函数是偶函数，即$\\cos(-x)=\\cos(x)$，具有对称性。

正切函数的图像与性质正切函数是三角函数中的另一个重要函数，通常用符号$\\tan$表示。

它的图像是一组相互平行的直线，具有间断点。

正切函数的定义域为整个实数集$\\mathbb{R}$，在某些特殊角度上可能不存在定义，例如在90度和270度时。

正切函数的值域为整个实数集$\\mathbb{R}$。

正切函数是奇函数，即$\\tan(-x)=-\\tan(x)$。

三角函数的性质除了上述基本性质外，三角函数还有一些重要的性质：1.周期性：正弦函数和余弦函数的周期为$2\\pi$，即在$[0, 2\\pi]$范围内图像重复；2.奇偶性：正弦函数和正切函数是奇函数，余弦函数是偶函数；3.最值：正弦函数和余弦函数的最大值为1，最小值为-1；正切函数在定义域内取值范围较广；4.单调性：正弦函数、余弦函数和正切函数在各自的定义域上具有不同的单调性特点。

三角函数的图像和性质讲解(定义域,值域,周期,单调性等)

三角函数的图象与性质教学目标：1、掌握正、余弦函数的定义域和值域；2、进一步理解三角函数的周期性和奇偶性的概念，会求它们的周期，会判断它们的奇偶性；3、能正确求出正、余弦函数的单调区间教学重点：正、余弦函数的性质教学难点：正、余弦函数的单调性知识要点：1、定义域：函数sin y x =及cos y x =的定义域都是(),-∞+∞，即实数集R2、值域：函数sin y x =，x R ∈及cos y x =，x R ∈的值域都是[]1,1-理解：（1）在单位圆中，正弦线、余弦线的长都是等于或小于半径的长1的，所以sin 1x ≤，cos 1x ≤，即1sin 1x -≤≤，1cos 1-≤≤。

（2）函数sin y x =在2,()2x k k Z ππ=+∈时，y 取最大值1，当22x k ππ=-，()k Z ∈时，y 取最小值-1；函数cos y x =在2x k π=，()k Z ∈时，y 取最大值1，当2x k ππ=+，()k Z ∈时，y 取最小值-1。

正弦函数s i n y x =，x R ∈和余弦函数cos y x =，x R ∈是周期函数，2k π(0)k Z k ∈≠且都是它们的周期，最小正周期是2π。

4、奇偶性正弦函数sin y x =，x R ∈是奇函数，余弦函数cos y x =，x R ∈是偶函数。

理解：（1）由诱导公式()sin sin x x -=-，cos()cos x x -=可知以上结论成立；（2）反映在图象上，正弦曲线关于原点O 对称，余弦曲线关于y 轴对称。

5、单调性（1）由正弦曲线可以看出：当x 由2π-增大到2π时，曲线逐渐上升，sin x 由-1增大到1；当x 由2π增大到32π时，曲线逐渐下降，sin x 由1减至-1，由正弦函数的周期性知道：①正弦函数sin y x =在每一个闭区间2,222k k ππππ⎡⎤-++⎢⎥⎣⎦()k Z ∈上，都从-1增大到1，是增函数； ②在每一个闭区间32,222k k ππππ⎡⎤++⎢⎥⎣⎦()k Z ∈上，都从1减小到-1，是减函数。

三角函数的图象与性质

-
;
-1
y=cosx
2 3
4 5 4 5
6 x 6 x
五.定义域、值域及取到最值时相应的x的集合:
-6 -5
-4 -3
复习回顾
-2 -
y y=sinx
1 o
-1
2 3
y
si-n6x的对称-5轴：x
k -4
2-,3对称点-：2(k
,0);
-
y cosx的对称轴：x k , 对称点：(k ,0);
1.4.1正弦、余弦函数的图象
复习
回顾三角函数
三角函数线
正弦函数余弦函数正切函数
sin=MP
正弦线MP cos=OM 余弦线OM tan=AT 正切线AT
y PT
-1
O
M A(1,0) x
正弦、余弦函数的图象
问题：如何作出正弦、余弦函数的图象？
途径：利用单位圆中正弦、余弦线来解决。
描图：用光滑曲线
复习回顾
一.正弦余弦函数的作图：几何描点法（利用三角函数线）五点法作简图
二.周期性：
函数y Asin(x )和y Acos(x )，x R的周期T 2 | |
三.奇偶性：
y sin x为奇函数，图像关于原点对称； y cosx为偶函数图像关于y轴对称。
-6 -5
-4 -3
复习回顾 y y=sinx
(0,11)
3
( 2 ,1)
-
(-o12 ,0)
( 2 ,0)
2
( ,-1)
3
线
4
5 6 x
正弦、余弦函数的图象
y
五点画图法
1
(
2
,1)

三角函数的图像及其性质

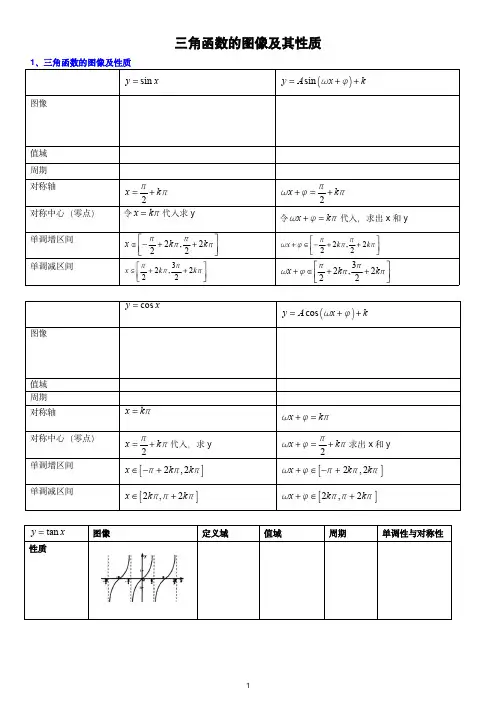
三角函数的图像及其性质1、三角函数的图像及性质sin y xsin y A x k图像值域周期对称轴2x k2x k对称中心（零点）令x k 代入求y令x k 代入，求出x 和y 单调增区间2,222x k k2,222x k k单调减区间32,222x k k32,222x k kcos y xcos y A x k图像值域周期对称轴x kx k 对称中心（零点）2x k代入，求y 2x k求出x 和y 单调增区间 2,2x k k 2,2x k k 单调减区间2,2x k k2,2x k k tan y x图像定义域值域周期单调性与对称性性质【考点分类】考点一：图像变换：1．把函数y ＝sin x 的图象向右平移个单位得到y ＝g （x ）的图象，再把y ＝g （x ）图象上所有点的纵坐标伸长到原来的2倍（横坐标不变），所得到图象的解析式为（）A．B．C．D．2．将函数f （x ）＝sin x 图象上所有点的横坐标变为原来的（ω＞0），纵坐标不变，得到函数g （x ）的图象，若g （x ）的最小正周期为6π，则ω＝（）A．B．6C．D．33．将函数y ＝2sin2x 图象上的所有点向右平移个单位，然后把图象上所有点的横坐标缩短为原来的倍，（纵坐标不变）得到y ＝f （x ）的图象，则f （x ）等于（）A．2sin（x ﹣）B．2sin（x ﹣）C．2sin（4x ﹣）D．2sin（4x ﹣）4．已知曲线C 1：y ＝cos x ，C 2：y ＝sin（2x +），则下面结论正确的是（）A．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再向右平移个单位长度，得到曲线C 2B．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再向左平移个单位长度，得到曲线C 2C．把C 1上各点的横坐标缩短到原来的，纵坐标不变，再向右平移个单位长度，得到曲线C 2D．把C 1上各点的横坐标缩短到原来的，纵坐标不变，再向左平移个单位长度，得到曲线C 25.把函数y ＝cos(3x ＋4)的图象适当变动就可以得到y ＝sin(－3x )的图象，这种变动可以是()A 向右平移4 B 向左平移4 C 向右平移12 D 向左平移126..函数32sin( x y 的图象是由2sin xy 的图象沿x 轴（）得到的。

三角函数的图象和性质

三角函数的图象和性质知识网络三角函数的图象和性质结构简图画龙点晴概念三角函数的图象:(1) 函数x y sin =的图象叫做正弦曲线, 如图1; (2) 函数x y cos =的图象叫做余弦曲线, 如图2; (3) 函数x y tan =的图象叫做正切曲线, 如图3; (4) 函数x y cot =的图象叫做余切曲线, 如图4;周期函数: 对于函数f (x )，如果存在一个非零常数T ，使得当x 取定义域内的每一个值时，都有：f (x +T)=f (x )那么函数f (x )就叫做周期函数，非零常数T 叫做这个函数的周期。

说明：1︒周期函数x ∈定义域M ，则必有x+T ∈M, 且若T>0则定义域无上界；T<0则定义域无下界；2︒“每一个值”只要有一个反例，则f (x )就不为周期函数（如f (x 0+t)≠f (x 0)）; 3︒T 往往是多值的（如y=sinx 2π,4π,…,-2π,-4π,…都是周期）周期T 中最小的正数叫做f (x )的最小正周期（有些周期函数没有最小正周期）. 三角函数的性质: 三角函数的性质如下表:[活用实例][例1] 求下列函数的最值： (1)y=sin(3x+4π)-1 ; (2) y=sin 2x-4sinx+5 ; (3) y=x x cos 3cos 3+- ; (4))3cos(2π-=x y (6π≤x ≤32π).[题解] (1) 当3x+4π=2k π+2π即 x=1232ππ+k (k ∈Z)时y max =0; 当3x+4π=2k π-2π即x=432ππ-k (k ∈Z)时y min =-2. (2) y=(sinx-2)2+1 ∴当x=2k π-2π k ∈Z 时y max =10; 当x=2k π-2πk ∈Z 时y min = 2. (3)y=-1+xcos 31+ 当x=2k π+π k ∈Z 时 y max =2; 当x=2k π k ∈Z 时 y min = 21.(4)∵x ∈[6π,32π] ∴x-3π∈[-6π,3π], ∴当x-3π=0 即x=3π时 y max =2; 当x-3π=3π 即x=32π时 y min =1. [例2] 求下列函数的定义域：(1)y=x x 2cos 21cos 3-- ; (2)y=lg(2sinx+1)+1cos 2-x ; (3)y=)cos(sin x . [题解] (1)∵3cosx-1-2cos 2x ≥0 ∴21≤cosx ≤1 ∴定义域为：[2k π-3π, 2k π+3π] (k ∈Z). (2))(32326726221cos 21sin Z k k x k k x k x x ∈⎪⎩⎪⎨⎧+≤≤-+<<-⇒⎪⎩⎪⎨⎧≥->ππππππππ )(3262Z k k x k ∈+≤<-⇒ππππ ∴定义域为：)](32,62(Z k k k ∈+-ππππ.(3) ∵cos(sinx)≥0 ∴ 2k π-2π≤x ≤2k π+2π(k ∈Z) ∵-1≤sinx ≤1 , ∴x ∈R , 1cos ≤y ≤1.[例3] 已知函数f(x)=2asin 2x-23asinxcosx+b 的定义域为[0，2π]，值域为[-5，4]，求常数a,b 的值。

三角函数的图像和性质

当0<A<1时，图像在y轴方向压缩。
02
周期变换
ω表示周期变换的系数，周期T=2π/|ω|。当ω>1时，周期减小，图像
在x轴方向压缩；当0<ω<1时，周期增大，图像在x轴方向拉伸。
03
相位变换
φ表示相位变换的角度，当φ>0时，图像左移；当φ<0时，图像右移。
正弦型曲线应用举例
振动问题
在物理学中，正弦函数常用来描述简谐振动，如弹簧振子、单摆等。通过正弦函数的振幅、周期和相位等参数，可以描述振动的幅度、频率和初始状态。
三角函数的图像和性质
汇报人：XX 2024-01-28
contents
目录
• 三角函数基本概念 • 正弦函数图像与性质 • 余弦函数图像与性质 • 正切函数图像与性质 • 三角函数复合与变换 • 三角函数在解决实际问题中的应用
01
三角函数基本概念
角度与弧度制
角度制
01
将圆周分为360等份，每份称为1度，用度（°）作为单位来度量
角的大小。
弧度制
02
以弧长等于半径所对应的圆心角为1弧度，用符号rad表示，是
国际通用的角度度量单位。
角度与弧度的换算
03
1° = (π/180)rad，1rad = (180/π)°。
三角函数定义及关系
正弦函数
sinθ = y/r，表示单位圆上任意一点P(x,y)与x轴正方向形成的角θ的正弦值。
光学
在光的反射、折射等现象中，三角函数可以帮助计算入射角、折射角等角度问题。
在工程问题中的应用
1 2
建筑设计
在建筑设计中，三角函数可以帮助计算建筑物的角度、高度、距离等参数，确保设计的准确性和安全性。

专题5.4 三角函数图像与性质(原卷版)

专题5.4三角函数图像与性质1.正弦函数R x x y ∈=,sin 的性质.(1).定义域:R .(2).值域:sin [1,1]x ∈-.(3).周期性:周期函数，周期是)0(,2≠∈k Z k k 且π,最小正周期为π2.(4).奇偶性:奇函数，其图象关于原点对称.(5).单调性:增区间：2,2()22k k k Z ππππ-++∈（）减区间：32,2()22k k k Z ππππ++∈（）(6).对称性:对称轴：)(,2Z k k x ∈+=ππ，对称中心：)(),0,(Z k k ∈π2.余弦函数R x x y ∈=,cos 的性质.(1).定义域:R .(2).值域:]1,1[cos -∈x (3).周期性:周期函数，周期是)0(,2≠∈k Z k k 且π，最小正周期为π2.(4).奇偶性:偶函数，其图象关于y 轴对称.(5).单调性:减区间：)(),2,2(Z k k k ∈+πππ增区间：)(),22,2(Z k k k ∈++ππππ(6).对称性:对称轴：)(,Z k k x ∈=π，对称中心：)(),0,2(Z k k ∈+ππ3.正切函数x y tan =的图象与性质.(1).定义域:},2|{Z k k x R x x ∈+≠∈ππ且.(2).值域:R(3).周期性:周期函数，周期是)0(,≠∈k Z k k 且π，最小正周期为π.(4).奇偶性:奇函数，其图象关于原点对称.(5).单调性:增函数，)2,2(ππππ+-k k 为增区间.(6).对称性:对称中心：)(),0,2(Z k k ∈π4.正弦型函数R x A x A y ∈>+=,0),sin(ϕω的性质.(1).定义域:R .(2).值域:],[A A -(3).周期性:周期函数，周期是||2ωπ=T .(4).奇偶性:当Z k k ∈=,πϕ时为奇函数；当Z k k ∈±=,2ππϕ时为偶函数.(5).单调性:当0>ω时：令Z k k x k ∈+≤+≤+-,2222ππϕωππ，求解增区间.令Z k k x k ∈+≤+≤+,22322ππϕωππ，求解减区间.当0<ω时：注意单调区间的转化.(6).对称性:对称轴：令)(,2Z k k x ∈+=+ππϕω，求解对称轴方程，对称轴处取最值.对称中心：令)(,Z k k x ∈=+πϕω，求解对称中心坐标.5.余弦型函数R x A x A y ∈>+=,0),cos(ϕω的性质.(1).定义域:R .(2).值域:],[A A -(3).周期性:周期函数，周期是||2ωπ=T .(4).奇偶性:当Z k k ∈=,πϕ时为偶函数；当Z k k ∈±=,2ππϕ时为奇函数.(5).单调性:当0>ω时：令Z k k x k ∈+≤+≤,22ππϕωπ，求解减区间.令Z k k x k ∈+≤+≤+,222ππϕωππ，求解增区间.当0<ω时：注意单调区间的转化.(6).对称性:对称轴：令)(,Z k k x ∈=+πϕω，求解对称轴方程，对称轴处取最值.对称中心：令)(,2Z k k x ∈+=+ππϕω，求解对称中心坐标.一、单选题1．已知函数()tan 2f x x =，则（）A ．()f x 的最小正周期为π，对称中心为1,0,2k k Zπ⎛⎫∈ ⎪⎝⎭B ．()f x 的最小正周期为π，对称中心为1,0,4k k Zπ⎛⎫∈ ⎪⎝⎭C ．()f x 的最小正周期为2π，对称中心为1,0,2k k Z π⎛⎫∈ ⎪⎝⎭D ．()f x 的最小正周期为2π，对称中心为1,0,4k k Z π⎛⎫∈ ⎪⎝⎭2．用“五点法”作函数cos 46y x π⎛⎫=- ⎪⎝⎭在一个周期内的图像时，第四个关键点的坐标是A ．5,012π⎛⎫⎪⎝⎭B ．5,112π⎛⎫- ⎪⎝⎭C ．5,112π⎛⎫ ⎪⎝⎭D ．5,012π⎛⎫-⎪⎝⎭3．若函数()sin 3f x x πω⎛⎫=+ ⎪⎝⎭(0)>ω在区间()2ππ，内没有最值，则ω的取值范围是（）A ．][117012612⎛⎤⋃ ⎥⎝⎦，，B ．][1120633⎛⎤⋃ ⎥⎝⎦，，C ．7012⎛⎤⎥⎝⎦，D ．1233⎡⎤⎢⎥⎣⎦，4．已知函数()()sin 06f x x πωω⎛⎫=+> ⎪⎝⎭在区间,2ππ⎡⎤⎢⎥⎣⎦内单调递减，则实数ω的取值范围是（）A ．2,13⎡⎤⎢⎥⎣⎦B ．24,33⎡⎤⎢⎥⎣⎦C ．[)1,2D ．3,22⎡⎫⎪⎢⎣⎭5．已知()()()sin 0,0f x x ωϕωϕπ=+><≤是R 上的奇函数，若()f x 的图象关于直线4x π=对称，且()f x 在区间,2211ππ⎡⎤-⎢⎥⎣⎦内是单调函数，则6f π⎛⎫= ⎪⎝⎭（）A ．B ．12-C ．12D ．26．函数ππ5πtan ,,6612y x x ⎛⎫⎛⎫=-∈- ⎪ ⎪⎝⎭⎝⎭的值域为（）A ．()B ．3⎛⎫- ⎪ ⎪⎝⎭C ．(,(1,)-∞+∞D ．3⎛⎫ ⎪ ⎪⎝⎭7．已知1tan tan αα≥且22,ππα⎛∈-⎫⎪⎝⎭，则α的取值范围为（）A ．,04π⎡⎫-⎪⎢⎣⎭B ．,0,442πππ⎡⎫⎡⎫-⎪⎪⎢⎢⎣⎭⎣⎭C ．0,4π⎛⎤ ⎥⎝⎦D ．,0,244πππ⎛⎤⎛⎤--⋃ ⎥⎥⎝⎦⎝⎦8．已知函数()()sin f x x α=+在,43x ππ⎛⎫∈- ⎪⎝⎭上单调递增，则α的值可以是（）A ．3π-B ．4π-C ．4πD ．3π9．函数()23sin 23f x x π⎛⎫=- ⎪⎝⎭的一个单调递减区间是（）A ．7131212ππ⎡⎤⎢⎥⎣⎦，B ．71212ππ⎡⎤⎢⎥⎣⎦，C ．22ππ⎡⎤-⎢⎥⎣⎦，D ．566ππ⎡⎤-⎢⎥⎣⎦，10．已知函数()()sin 04f x x πωω⎛⎫=+> ⎪⎝⎭在[]0,2π上有且只有4个零点，则ω取值范围是（）A ．1519,44⎡⎫⎪⎢⎣⎭B ．1519,88⎡⎫⎪⎢⎣⎭C ．1721,44⎡⎫⎪⎢⎣⎭D ．1721,88⎡⎫⎪⎢⎣⎭11．函数1tan 24y x π⎛⎫=+ ⎪⎝⎭的定义域是（）A ．4,2xx k k Z ππ⎧⎫≠-+∈⎨⎬⎩⎭∣B ．2,2xx k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭∣C ．32,2xx k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭∣D ．,2xx k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭∣12．函数sin(2)4y x π=-的单调减区间是（）A ．3[,],(Z)88k k k ππππ-+∈B ．3[2,2],(Z)88k k k ππππ-+∈C ．37[22],(Z)88k k k ππππ++∈D ．37[,Z)88k k k ππππ++∈13．已知函数()sin()f x x ϕ=+为偶函数，则ϕ的取值可以为（）A ．π2-B ．πC ．π3D ．014．记函数()sin 4f x x b πω⎛⎫=++ ⎪⎝⎭（0>ω）的最小正周期为T ．若23T ππ<<，且()y f x =的图象关于点3,22π⎛⎫ ⎪⎝⎭中心对称，则10f π⎛⎫= ⎪⎝⎭（）A ．1B ．32C ．52D ．315．已知函数()sin 0,0,2y A x m A πωϕωϕ⎛⎫=++>>< ⎪⎝⎭的最大值为4，最小值为0，且该函数图象的相邻两个对称轴之间的最短距离为2π，直线6x π=是该函数图象的一条对称轴，则该函数的解析式是（）A ．4sin 26y x π⎛⎫=+ ⎪⎝⎭B ．2sin 226y x π⎛⎫=++ ⎪⎝⎭C ．2sin 23y x π⎛⎫=-++ ⎪⎝⎭D ．2sin 23y x π⎛⎫=++ ⎪⎝⎭二、多选题16．已知函数()tan 23f x x π⎛⎫=+ ⎪⎝⎭，则下列说法正确的是（）A ．()f x 在定义域内是增函数B ．6y f x π⎛⎫=- ⎪⎝⎭是奇函数C ．()f x 的最小正周期是πD ．()f x 图像的对称中心是,0,46k k Z ππ⎛⎫-∈⎪⎝⎭17．已知()f x 为R 上的奇函数，且当0x >时，()lg f x x =，记()()sin cos g x x f x x =+⋅，下列结论正确的是（）A ．()g x 为奇函数B ．若()g x 的一个零点为0x ，且00x <，则()00lg tan 0x x --=C ．()g x 在区间,2ππ⎛⎫- ⎪⎝⎭的零点个数为3个D ．若()g x 大于1的零点从小到大依次为12,,x x ⋅⋅⋅，则1273x x π<+<18．已知函数()()tan 0,2f x x πωϕωϕ⎛⎫=+≠< ⎪⎝⎭，点,03π⎛⎫ ⎪⎝⎭和5,06π⎛⎫⎪⎝⎭是其相邻的两个对称中心，且在区间2,33ππ⎛⎫⎪⎝⎭内单调递减，则ϕ=（）A ．3πB ．6πC ．3π-D ．6π-19．设函数()()sin 06f x x πωω⎛⎫=+> ⎪⎝⎭，若()f x 在[]0,π上有且仅有3条对称轴，则（）A ．()f x 在[]0,π上有且仅有2个最大值点B ．()f x 在[]0,π上有且仅有2个零点C ．ω的取值范围是710,33⎡⎫⎪⎢⎣⎭D ．()f x 在0,10π⎛⎫⎪⎝⎭上单调递增20．已知函数()sin (0)4f x x πωω⎛⎫=+> ⎪⎝⎭，则下列命题正确的是（）A ．若()f x 在[0,)π上有10个零点，则3943,44ω⎛⎤∈ ⎥⎝⎦B ．若()f x 在[0,)π上有11条对称轴，则3943,44ω⎛⎤∈ ⎥⎝⎦C ．若()f x ＝22在[0,)π上有12个解，则21,122ω⎛⎤∈ ⎥⎝⎦D ．若()f x 在,32ππ⎛⎫⎪⎝⎭上单调递减，则35,42ω⎡⎤∈⎢⎥⎣⎦21．函数()214f x x π⎛⎫=++ ⎪⎝⎭，对于任意的[)0,1a ∈，方程()()10f x a x m -=≤≤仅有一个实数根，则m 的取值可以为（）A ．8πB ．58πC ．38πD ．34π22．已知函数()tan 3f x x π⎛⎫=+ ⎪⎝⎭，则下列关于()f x 的判断正确的是（）A ．在区间,6ππ⎛⎫⎪⎝⎭上单调递增B ．最小正周期是πC ．图象关于直线6x π=成轴对称D ．图象关于点,06π⎛⎫⎪⎝⎭成中心对称三、解答题23．已知()sin ,()cos f x x g x x==(1)函数()y f x ω=（0>ω）在区间[)0,p 上恰有三条对称轴，求ω的取值范围．(2)函数2()2()()6,h x g x af x a =-++为常数，①当9a =-时，求函数h (x )的零点；②当[,]62x ππ∈-，恒有()0h x >，求实数a 的取值范围．24．已知函数()cos (0)3f x x πωω⎛⎫=+> ⎪⎝⎭，图象上任意两条相邻对称轴间的距离为2π．(1)求函数的单调区间和对称中心．(2)若关于x 的方程22sin cos 40x m x --=在02x π⎛⎫∈ ⎪⎝⎭，上有实数解，求实数m 的取值范围．25．已知函数2π()sin(2)3f x x =+.(1)请用五点法做出()f x 一个周期内的图像；(2)若函数()()g x f x m =-在区间π[0,2上有两个零点，请写出m 的取值范围，无需说明理由.26．已知函数()()3sin 2f x x πϕϕ=+∈-，（，2π）函数关于4x π=对称.(1)求()f x ϕ的值及的解析式；(2)用五点法在下列直角坐标系中画出()f x 在744ππ⎡⎤-⎢⎥⎣⎦，上的图象；(3)写出()f x 的单调增区间及最小值，并写出取最小值时自变量x 的取值集合．27．已知函数()1sin 62f x x π⎛⎫=+- ⎪⎝⎭.(1)求函数()f x 的单调递增区间；(2)求函数()f x 在区间[]0,2π上的所有零点之和.。

三角函数基本性质

三角函数基本性质三角函数是数学中常见的函数类型，它们在解决几何、物理和工程问题中起到了重要的作用。

本文将介绍三角函数的基本性质，包括定义域、值域、周期性等。

1. 正弦函数（sin）的基本性质：正弦函数的定义域为实数集R，值域为闭区间[-1, 1]。

其图像为一条连续的曲线，通过坐标原点，关于y轴对称。

正弦函数是一个周期函数，其周期为2π（或360度）。

在定义域内，正弦函数是奇函数，即满足sin(-x) = -sin(x)。

2. 余弦函数（cos）的基本性质：余弦函数的定义域为实数集R，值域为闭区间[-1, 1]。

其图像为一条连续的曲线，通过坐标原点，关于x轴对称。

余弦函数也是一个周期函数，其周期为2π（或360度）。

在定义域内，余弦函数是偶函数，即满足cos(-x) = cos(x)。

3. 正切函数（tan）的基本性质：正切函数的定义域为实数集R，在其定义域内，正切函数有无穷多个极值点。

其图像没有定义域内的极值点，但在周期性为π的点处有无穷多个间断点。

正切函数的值域为实数集R。

4. 余切函数（cot）的基本性质：余切函数的定义域为实数集R，在其定义域内，余切函数有无穷多个极值点。

其图像没有定义域内的极值点，但在周期性为π的点处有无穷多个间断点。

余切函数的值域为实数集R。

5. 正割函数（sec）的基本性质：正割函数的定义域为实数集R，其在定义域内没有极值点。

其图像在周期性为2π的点处有无穷多个间断点。

注意到正割函数与余弦函数的关系，即sec(x) = 1/cos(x)。

6. 余割函数（csc）的基本性质：余割函数的定义域为实数集R，其在定义域内没有极值点。

其图像在周期性为2π的点处有无穷多个间断点。

注意到余割函数与正弦函数的关系，即csc(x) = 1/sin(x)。

三角函数的基本性质对于解决几何、物理和工程问题至关重要。

在解决角度、周期性、波动等问题时，我们可以利用这些性质计算和推导。

三角函数还与复数、级数等数学概念有着广泛的联系，为更深入的数学研究提供了基础。

专题01 三角函数的图象与性质(解析版)

专题01 三角函数的图象与性质【要点提炼】1.常用的三种函数的图象与性质(下表中k ∈Z ) 函数y ＝sin xy ＝cos xy ＝tan x图象递增区间 ⎣⎢⎡⎦⎥⎤2k π－π2，2k π＋π2 [2k π－π，2k π]⎝ ⎛⎭⎪⎫k π－π2，k π＋π2 递减区间 ⎣⎢⎡⎦⎥⎤2k π＋π2，2k π＋3π2 [2k π，2k π＋π]奇偶性奇函数偶函数奇函数对称中心 (k π，0) ⎝ ⎛⎭⎪⎫k π＋π2，0 ⎝ ⎛⎭⎪⎫k π2，0 对称轴 x ＝k π＋π2 x ＝k π 周期性2π2ππ2.三角函数的常用结论(1)y ＝A sin(ωx ＋φ)，当φ＝k π(k ∈Z )时为奇函数；当φ＝k π＋π2(k ∈Z )时为偶函数；对称轴方程可由ωx ＋φ＝k π＋π2(k ∈Z )求得. (2)y ＝A cos(ωx ＋φ)，当φ＝k π＋π2(k ∈Z )时为奇函数；当φ＝k π(k ∈Z )时为偶函数；对称轴方程可由ωx ＋φ＝k π(k ∈Z )求得. (3)y ＝A tan(ωx ＋φ)，当φ＝k π(k ∈Z )时为奇函数. 3.三角函数的两种常见变换 (1)y ＝sin x ――——————————→向左(φ＞0)或向右(φ＜0)平移|φ|个单位y ＝sin(ωx ＋φ)――——————————→纵坐标变为原来的A 倍横坐标不变y ＝A sin(ωx ＋φ)(A ＞0，ω＞0).y ＝sin ωx ―————————————―→向左(φ＞0)或向右(φ＜0)平移|φω|个单位 y ＝sin(ωx ＋φ)————————————―→纵坐标变为原来的A 倍横坐标不变y ＝A sin(ωx ＋φ)(A ＞0，ω＞0).考点一三角函数的图像与性质考向一三角函数的定义与同角关系式【典例1】 (1)在平面直角坐标系中，AB ︵，CD ︵，EF ︵，GH ︵是圆x 2＋y 2＝1上的四段弧(如图)，点P 在其中一段上，角α以Ox 为始边，OP 为终边.若tan α<cos α<sin α，则P 所在的圆弧是( )A.AB ︵B.CD ︵C.EF ︵D.GH ︵(2)已知角α的顶点为坐标原点，始边与x 轴的非负半轴重合，终边上有两点A (1，a )，B (2，b )，且cos 2α＝23，则|a －b |＝( ) A.15B.55C.255D.1解析 (1)设点P 的坐标为(x ，y )，且tan α＜cos α＜sin α，∴yx ＜x ＜y ，解之得－1＜x ＜0，且0＜y ＜1.故点P (x ，y )所在的圆弧是EF ︵.(2)由题意知cos α>0.因为cos 2α＝2cos 2α－1＝23，所以cos α＝306，sin α＝±66，得|tan α|＝55.由题意知|tan α|＝⎪⎪⎪⎪⎪⎪a －b 1－2，所以|a －b |＝55. 答案 (1)C (2)B探究提高 1.任意角的三角函数值仅与角α的终边位置有关，而与角α终边上点P 的位置无关.若角α已经给出，则无论点P 选择在α终边上的什么位置，角α的三角函数值都是确定的.2.应用诱导公式与同角关系开方运算时，一定要注意三角函数值的符号；利用同角三角函数的关系化简要遵循一定的原则，如切化弦、化异为同、化高为低、化繁为简等.【拓展练习1】 (1)(2020·唐山模拟)若cos θ－2sin θ＝1，则tan θ＝( ) A.43B.34C.0或43D.0或34(2)(2020·济南模拟)已知cos ⎝ ⎛⎭⎪⎫α＋π6－sin α＝435，则sin ⎝ ⎛⎭⎪⎫α＋11π6＝________.解析 (1)由题意可得⎩⎨⎧cos θ－2sin θ＝1，cos 2θ＋sin 2θ＝1，解得⎩⎨⎧sin θ＝0，cos θ＝1或⎩⎪⎨⎪⎧sin θ＝－45，cos θ＝－35，所以tan θ＝0，或tan θ＝43.故选C.(2)∵cos ⎝ ⎛⎭⎪⎫α＋π6－sin α＝32cos α－12sin α－sin α＝32cos α－32sin α＝3sin ⎝ ⎛⎭⎪⎫π6－α＝435，∴sin ⎝⎛⎭⎪⎫α－π6＝－45， ∴sin ⎝ ⎛⎭⎪⎫α＋11π6＝sin ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫α－π6＋2π＝sin ⎝ ⎛⎭⎪⎫α－π6＝－45.答案 (1)C (2)－45考向二三角函数的图象及图象变换【典例2】 (1)(多选题)(2020·新高考山东、海南卷)如图是函数y ＝sin(ωx ＋φ)的部分图象，则sin(ωx ＋φ)＝( )A.sin ⎝ ⎛⎭⎪⎫x ＋π3B.sin ⎝ ⎛⎭⎪⎫π3－2xC.cos ⎝ ⎛⎭⎪⎫2x ＋π6D.cos ⎝ ⎛⎭⎪⎫5π6－2x(2)(2019·天津卷)已知函数f (x )＝A sin(ωx ＋φ)(A >0，ω>0，|φ|<π)是奇函数，将y ＝f (x )的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)，所得图象对应的函数为g (x ).若g (x )的最小正周期为2π，且g ⎝ ⎛⎭⎪⎫π4＝2，则f ⎝ ⎛⎭⎪⎫3π8＝( )A.－2B.－ 2C. 2D.2解析 (1)由图象知T 2＝2π3－π6＝π2，得T ＝π，所以ω＝2πT ＝2.又图象过点⎝ ⎛⎭⎪⎫π6，0，由“五点法”，结合图象可得φ＋π3＝π，即φ＝2π3，所以sin(ωx ＋φ)＝sin ⎝ ⎛⎭⎪⎫2x ＋2π3，故A 错误；由sin ⎝ ⎛⎭⎪⎫2x ＋2π3＝sin ⎣⎢⎡⎦⎥⎤π－⎝ ⎛⎭⎪⎫π3－2x ＝sin ⎝ ⎛⎭⎪⎫π3－2x 知B 正确；由sin ⎝ ⎛⎭⎪⎫2x ＋2π3＝sin ⎝ ⎛⎭⎪⎫2x ＋π2＋π6＝cos ⎝ ⎛⎭⎪⎫2x ＋π6知C 正确；由sin ⎝ ⎛⎭⎪⎫2x ＋2π3＝cos ⎝ ⎛⎭⎪⎫2x ＋π6＝cos ⎣⎢⎡⎦⎥⎤π＋⎝ ⎛⎭⎪⎫2x －5π6＝－cos ⎝ ⎛⎭⎪⎫5π6－2x 知D 错误.综上可知，正确的选项为BC. (2)由f (x )是奇函数可得φ＝k π(k ∈Z )，又|φ|<π，所以φ＝0. 所以g (x )＝A sin ⎝ ⎛⎭⎪⎫12ωx ，且g (x )最小正周期为2π，可得2π12ω＝2π，故ω＝2，所以g (x )＝A sin x ，g ⎝ ⎛⎭⎪⎫π4＝A sin π4＝22A ＝2，所以A ＝2. 所以f (x )＝2sin 2x ，故f ⎝ ⎛⎭⎪⎫3π8＝2sin 3π4＝ 2.答案 (1)BC (2)C探究提高 1.在图象变换过程中务必分清是先相位变换，还是先周期变换.变换只是相对于其中的自变量x 而言的，如果x 的系数不是1，就要把这个系数提取后再确定变换的单位长度和方向.2.已知函数y ＝A sin(ωx ＋φ)(A >0，ω>0)的图象求解析式时，常采用待定系数法，由图中的最高点、最低点或特殊点求A ；由函数的周期确定ω；确定φ常根据“五点法”中的五个点求解，一般把第一个“零点”作为突破口，可以从图象的升降找准第一个“零点”的位置.【拓展练习2】 (1)(多选题)(2020·济南历城区模拟)将函数f (x )＝2sin ⎝ ⎛⎭⎪⎫2x ＋π6的图象向左平移π12个单位长度，再向上平移1个单位长度，得到函数g (x )的图象.若g (x 1)g (x 2)＝9，且x 1，x 2∈[－2π，2π]，则2x 1－x 2的可能取值为( ) A.－59π12B.－35π6C.25π6D.49π12(2)(2020·长沙质检)函数g (x )＝A sin(ωx ＋φ)(A ＞0，ω＞0，0＜φ＜2π)的部分图象如图所示，已知g (0)＝g ⎝ ⎛⎭⎪⎫5π6＝3，函数y ＝f (x )的图象可由y ＝g (x )图象向右平移π3个单位长度而得到，则函数f (x )的解析式为( )A.f (x )＝2sin 2xB.f (x )＝2sin ⎝ ⎛⎭⎪⎫2x ＋π3C.f (x )＝－2sin 2xD.f (x )＝－2sin ⎝ ⎛⎭⎪⎫2x ＋π3 解析 (1)将函数f (x )＝2sin ⎝ ⎛⎭⎪⎫2x ＋π6的图象向左平移π12个单位长度，再向上平移1个单位长度，得到函数g (x )＝2sin ⎝ ⎛⎭⎪⎫2x ＋π3＋1的图象.由g (x 1)g (x 2)＝9，知g (x 1)＝3，g (x 2)＝3，所以2x ＋π3＝π2＋2k π，k ∈Z ，即x ＝π12＋k π，k ∈Z .由x 1，x 2∈[－2π，2π]，得x 1，x 2的取值集合为⎩⎨⎧⎭⎬⎫－23π12，－11π12，π12，13π12.当x 1＝－23π12，x 2＝13π12时，2x 1－x 2＝－59π12；当x 1＝13π12，x 2＝－23π12时，2x 1－x 2＝49π12.故选AD.(2)由函数g (x )的图象及g (0)＝g ⎝ ⎛⎭⎪⎫5π6＝3，知直线x ＝5π12为函数g (x )的图象的一条对称轴，所以T 4＝5π12－π6＝π4，则T ＝π，所以ω＝2πT ＝2，所以g (x )＝A sin(2x ＋φ)，由题图可知⎝ ⎛⎭⎪⎫π6，0为“五点法”作图中的第三点，则2×π6＋φ＝π，解得φ＝2π3，由g (0)＝3，得A sin 2π3＝3，又A ＞0，所以A ＝2，则g (x )＝2sin ⎝ ⎛⎭⎪⎫2x ＋2π3，所以g (x )的图象向右平移π3个单位长度后得到的图象对应的解析式为f (x )＝2sin ⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎪⎫x －π3＋2π3＝2sin 2x ，故选A. 答案 (1)AD (2)A 考向三三角函数的性质【典例3】 (1)若f (x )＝cos x －sin x 在[－a ，a ]上是减函数，则a 的最大值是( ) A.π4B.π2C.3π4D.π(2)(2020·天一大联考)已知f (x )＝cos ⎝ ⎛⎭⎪⎫ωx －π6(ω＞0)，f ⎝ ⎛⎭⎪⎫π6＝f ⎝ ⎛⎭⎪⎫π3，且f (x )在区间⎝ ⎛⎭⎪⎫π6，π3内有最小值，无最大值，则ω＝( ) A.83 B.143 C.8 D.4 (3)已知函数f (x )＝sin ωx ＋cos ωx (ω＞0)，x ∈R .若函数f (x )在区间(－ω，ω)内单调递增，且函数y ＝f (x )的图象关于直线x ＝ω对称，则ω的值为________. 解析 (1)f (x )＝cos x －sin x ＝2cos ⎝ ⎛⎭⎪⎫x ＋π4，且函数y ＝cos x 在区间[0，π]上单调递减，则由0≤x ＋π4≤π，得－π4≤x ≤3π4.因为f (x )在[－a ，a ]上是减函数，所以⎩⎪⎨⎪⎧－a ≥－π4，a ≤3π4，解得a ≤π4.所以0<a ≤π4，所以a 的最大值是π4.(2)由于f ⎝ ⎛⎭⎪⎫π6＝f ⎝ ⎛⎭⎪⎫π3，且f (x )在区间⎝ ⎛⎭⎪⎫π6，π3内有最小值，∴f (x )在x ＝12⎝ ⎛⎭⎪⎫π6＋π3＝π4处取得最小值.因此π4ω－π6＝2k π＋π，即ω＝8k ＋143，k ∈Z .①又函数f (x )在区间⎝ ⎛⎭⎪⎫π6，π3无最大值，且ω＞0，∴T ＝2πω≥π3－π6＝π6，∴0＜ω≤12.②由①②知ω＝143.(3)f (x )＝sin ωx ＋cos ωx ＝2sin ⎝ ⎛⎭⎪⎫ωx ＋π4，因为f (x )在区间(－ω，ω)内单调递增，且函数图象关于直线x ＝ω对称，所以f (ω)必为一个周期上的最大值，所以有ω·ω＋π4＝2k π＋π2，k ∈Z ，所以ω2＝π4＋2k π，k ∈Z .又ω－(－ω)≤2πω2，即ω2≤π2，即ω2＝π4，所以ω＝π2. 答案 (1)A (2)B (3)π2探究提高 1.讨论三角函数的单调性，研究函数的周期性、奇偶性与对称性，都必须首先利用辅助角公式，将函数化成一个角的一种三角函数.2.求函数y ＝A sin(ωx ＋φ)(A >0，ω>0)的单调区间，是将ωx ＋φ作为一个整体代入正弦函数增区间(或减区间)，求出的区间即为y ＝A sin(ωx ＋φ)的增区间(或减区间).【拓展练习3】 (1)(多选题)(2020·济南质检)已知函数f (x )＝2sin(2x ＋φ)(0<φ<π)，若将函数f (x )的图象向右平移π6个单位长度后，得到图象关于y 轴对称，则下列结论中正确的是( ) A.φ＝5π6B.⎝ ⎛⎭⎪⎫π12，0是f (x )的图象的一个对称中心 C.f (φ)＝－2D.x ＝－π6是f (x )图象的一条对称轴(2)(多选题)关于函数f (x )＝|cos x |＋cos|2x |，则下列结论正确的是( ) A.f (x )是偶函数 B.π是f (x )的最小正周期C.f (x )在⎣⎢⎡⎦⎥⎤3π4，5π4上单调递增D.当x ∈⎣⎢⎡⎦⎥⎤34π，54π时，f (x )的最大值为2解析 (1)将函数f (x )的图象向右平移π6个单位长度后，得到y ＝2sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x －π6＋φ＝2sin ⎝ ⎛⎭⎪⎫2x ＋φ－π3的图象，∵其关于y 轴对称，∴φ－π3＝k π＋π2，k ∈Z ，∴φ＝k π＋5π6，k ∈Z .又0<φ<π，∴当k ＝0时，φ＝5π6，故A 正确；f (x )＝2sin ⎝ ⎛⎭⎪⎫2x ＋5π6，f ⎝ ⎛⎭⎪⎫π12＝0，则⎝ ⎛⎭⎪⎫π12，0是f (x )的图象的一个对称中心，故B 正确；因为f (φ)＝f ⎝ ⎛⎭⎪⎫5π6＝2，故C错误；f ⎝ ⎛⎭⎪⎫－π6＝2，则x ＝－π6是f (x )图象的一条对称轴，故D 正确.故选ABD.(2)f (x )＝|cos x |＋cos|2x |＝|cos x |＋cos 2x ＝|cos x |＋2cos 2x －1＝2|cos x |2＋|cos x |－1，由f (－x )＝2|cos(－x )|2＋|cos(－x )|－1＝f (x )，且函数f (x )的定义域为R ，得f (x )为偶函数，故A 正确.由于y ＝|cos x |的最小正周期为π，可得f (x )的最小正周期为π，故B 正确. 令t ＝|cos x |，得函数f (x )可转化为g (t )＝2t 2＋t －1，t ∈[0，1]，易知t ＝|cos x |在⎣⎢⎡⎦⎥⎤3π4，π上单调递增，在⎣⎢⎡⎦⎥⎤π，5π4上单调递减，由t ∈[0，1]，g (t )＝2⎝ ⎛⎭⎪⎫t ＋142－98，可得g (t )在[0，1]上单调递增，所以f (x )在⎣⎢⎡⎦⎥⎤3π4，π上单调递增，在⎣⎢⎡⎦⎥⎤π，5π4上单调递减，故C 错误.根据f (x )在⎣⎢⎡⎦⎥⎤34π，π上递增，在⎣⎢⎡⎦⎥⎤π，54π上递减，∴f (x )在x ＝π时取到最大值f (π)＝2，则D 正确. 答案 (1)ABD (2)ABD考向四三角函数性质与图象的综合应用【典例4】 (2020·临沂一预)在①f (x )的图象关于直线x ＝5π6ω对称，②f (x )＝cos ωx －3sin ωx ，③f (x )≤f (0)恒成立这三个条件中任选一个，补充在下面横线处.若问题中的ω存在，求出ω的值；若ω不存在，请说明理由.设函数f (x )＝2cos(ωx ＋φ)⎝ ⎛⎭⎪⎫ω>0，0≤φ≤π2，_____________________________.是否存在正整数ω，使得函数f (x )在⎣⎢⎡⎦⎥⎤0，π2上是单调的？(注：如果选择多个条件分别解答，按第一个解答计分)解若选①，则存在满足条件的正整数ω.求解过程如下：令ωx ＋φ＝k π，k ∈Z ，代入x ＝5π6ω，解得φ＝k π－5π6，k ∈Z .因为0≤φ≤π2，所以φ＝π6，所以f (x )＝2cos ⎝ ⎛⎭⎪⎫ωx ＋π6.当x ∈⎣⎢⎡⎦⎥⎤0，π2时，ωx ＋π6∈⎣⎢⎡⎦⎥⎤π6，ωπ2＋π6.若函数f (x )在⎣⎢⎡⎦⎥⎤0，π2上单调，则有ωπ2＋π6≤π，解得0<ω≤53.所以存在正整数ω＝1，使得函数f (x )在⎣⎢⎡⎦⎥⎤0，π2上是单调的.若选②，则存在满足条件的正整数ω.求解过程如下： f (x )＝cos ωx －3sin ωx ＝2cos ⎝ ⎛⎭⎪⎫ωx ＋π3＝2cos(ωx ＋φ)，且0≤φ≤π2，所以φ＝π3.当x ∈⎣⎢⎡⎦⎥⎤0，π2时，ωx ＋π3∈⎣⎢⎡⎦⎥⎤π3，ωπ2＋π3. 若函数f (x )在⎣⎢⎡⎦⎥⎤0，π2上单调，则有ωπ2＋π3≤π，解得0<ω≤43.所以存在正整数ω＝1，使得函数f (x )在⎣⎢⎡⎦⎥⎤0，π2上是单调的.若选③，则存在满足条件的正整数ω.求解过程如下：因为f (x )≤f (0)恒成立，即f (x )max ＝f (0)＝2cos φ＝2，所以cos φ＝1.因为0≤φ≤π2，所以φ＝0，所以f (x )＝2cos ωx .当x ∈⎣⎢⎡⎦⎥⎤0，π2时，ωx ∈⎣⎢⎡⎦⎥⎤0，ωπ2. 若函数f (x )在⎣⎢⎡⎦⎥⎤0，π2上单调，则有ωπ2≤π，解得0<ω≤2.所以存在正整数ω＝1或ω＝2，使得函数f (x )在⎣⎢⎡⎦⎥⎤0，π2上是单调的.探究提高 1.研究三角函数的图象与性质，关键是将函数化为y ＝A sin(ωx ＋φ)＋B (或y ＝A cos(ωx ＋φ)＋B )的形式，利用正余弦函数与复合函数的性质求解. 2.函数y ＝A sin(ωx ＋φ)(或y ＝A cos(ωx ＋φ))的最小正周期T ＝2π|ω|.应特别注意y ＝|A sin(ωx ＋φ)|的最小正周期为T ＝π|ω|.【拓展练习4】 (2020·威海三校一联)已知函数f (x )＝2cos 2ω1x ＋sin ω2x . (1)求f (0)的值；(2)从①ω1＝1，ω2＝2，②ω1＝1，ω2＝1这两个条件中任选一个，作为题目的已知条件，求函数f (x )在⎣⎢⎡⎦⎥⎤－π2，π6上的最小值，并直接写出函数f (x )的一个周期.(注：如果选择多个条件分别解答，按第一个解答计分) 解 (1)f (0)＝2cos 20＋sin 0＝2. (2)选择条件①.f (x )的一个周期为π.当ω1＝1，ω2＝2时，f (x )＝2cos 2x ＋sin 2x ＝(cos 2x ＋1)＋sin 2x ＝2⎝ ⎛⎭⎪⎫22sin 2x ＋22cos 2x ＋1＝2sin ⎝ ⎛⎭⎪⎫2x ＋π4＋1.因为x ∈⎣⎢⎡⎦⎥⎤－π2，π6，所以2x ＋π4∈⎣⎢⎡⎦⎥⎤－3π4，7π12.所以－1≤sin ⎝ ⎛⎭⎪⎫2x ＋π4≤1，则1－2≤f (x )≤1＋ 2. 当2x ＋π4＝－π2，即x ＝－3π8时，f (x )在⎣⎢⎡⎦⎥⎤－π2，π6上取得最小值1－ 2.选择条件②.f (x )的一个周期为2π.当ω1＝1，ω2＝1时，f (x )＝2cos 2x ＋sin x ＝2(1－sin 2x )＋sin x ＝－2⎝ ⎛⎭⎪⎫sin x －142＋178.因为x ∈⎣⎢⎡⎦⎥⎤－π2，π6，所以sin x ∈⎣⎢⎡⎦⎥⎤－1，12.所以当sin x ＝－1，即x ＝－π2时，f (x )在⎣⎢⎡⎦⎥⎤－π2，π6上取得最小值－1.【专题拓展练习】一、选择题（1～10题为单项选择题，11～15题为多项选择题） 1．函数2()cos 3f x x π⎛⎫=+⎪⎝⎭的最小正周期为（） A ．4π B ．2πC ．2π D ．π【答案】D 【详解】因为22cos 211213()cos cos 232232x f x x x πππ⎛⎫++ ⎪⎛⎫⎛⎫⎝⎭=+==++ ⎪ ⎪⎝⎭⎝⎭，所以最小正周期为π.2．把函数sin 2y x =的图象向左平移4π个单位长度，再把所得图象所有点的横坐标伸长到原来的2倍（纵坐标不变），所得函数图象的解析式为（） A ．sin y x = B ．cos y x =C ．sin()4y x π=+D ．sin y x =-【答案】B 【详解】把函数sin 2y x =的图象向左平移4π个单位长度，得到sin 2sin(2)cos 242y x x x ππ⎛⎫=+=+= ⎪⎝⎭，再把所得图象所有点的横坐标伸长到原来的2倍（纵坐标不变），所得函数图象的解析式为cos y x =. 3．若16x π=，256x π=是函数()sin()f x x ωϕ=+()0ω>两个相邻的极值点，则ω=（） A ．3 B ．32C ．34D ．12【答案】B 【详解】解：由题意得，52663πππ-=是函数()f x 周期的一半，则243ππω=，得32ω=．故选：B4．将函数()2sin 26f x x π⎛⎫=+⎪⎝⎭的图象向左平移12π个单位长度后得到函数()g x 的图象，则函数()g x 的单调递增区间是（） A ．(),36k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦B ．(),63k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦C ．()44k ,k k Z ππ⎡⎤-+π+π∈⎢⎥⎣⎦D ．()5,1212k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦【答案】D 【详解】将函数()2sin 26f x x π⎛⎫=+ ⎪⎝⎭的图象向左平移12π个单位长度后得到函数()g x 的图象，所以()2sin 22sin 2663g x x x πππ⎛⎫⎛⎫=++=+ ⎪ ⎪⎝⎭⎝⎭，由()222232k x k k Z πππππ-+≤+≤+∈可得()51212k x k k Z ππππ-+≤≤+∈，即函数()g x 的单调递增区间是()5,1212k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦.5．函数()()2sin 06f x x πωω⎛⎫=+> ⎪⎝⎭的图像最近两对称轴之间的距离为2π，若该函数图像关于点()0m ,成中心对称，当0,2m π⎡⎤∈⎢⎥⎣⎦时m 的值为（） A ．6πB ．4π C ．3π D ．512π 【答案】D 【详解】()()2sin 06f x x πωω⎛⎫=+> ⎪⎝⎭的最小正周期2π2ω2T ππ==⨯=,2ω∴=，所以()2sin 26f x x π⎛⎫=+ ⎪⎝⎭，令2,6x k k Z ππ+=∈,则212k x ππ=-, ∴函数f (x )的对称轴心为,0212k ππ⎛⎫-⎪⎝⎭,k Z ∈, 所以212k m ππ=-，当0,2122k m πππ⎡⎤=-∈⎢⎥⎣⎦时,解得：17,66k ⎡⎤∈⎢⎥⎣⎦, 又5π,1,12k Z k m ∈∴=∴=, 6．已知函数()22sin 23sin cos cos f x x x x x =+-，x ∈R ，则（）A ．()f x 的最大值为1B ．()f x 的图象关于直线3x π=对称C ．()f x 的最小正周期为2π D ．()f x 在区间()0,π上只有1个零点【答案】B 【详解】()22sin cos cos f x x x x x =+-2cos 2x x =-2sin 26x π⎛⎫=- ⎪⎝⎭故最大值为2，A 错22sin 2sin 23362f ππππ⎛⎫⎛⎫=-== ⎪ ⎪⎝⎭⎝⎭，故关于3x π=对称，B 对最小正周期为22ππ=，C 错 ()26x k k Z ππ-=∈解得()122k x k Z ππ=+∈，12x π=和712x π=都是零点，故D 错. 7．已知函数()()()3cos 0g x x ωϕω=+>在7,6ππ⎛⎫ ⎪⎝⎭上具有单调性，且满足04g π⎛⎫=⎪⎝⎭，()3g π=，则ω的取值共有（）A ．6个B ．5个C ．4个D ．3个【答案】B 【详解】因为()g x 在7,6ππ⎛⎫ ⎪⎝⎭上具有单调性，04g π⎛⎫= ⎪⎝⎭，()3g π=，所以()()7,62,4422121,442T T n n T n N πππωπππωπππω*⎧-≤=⎪⎪⎪-≥=⎨⎪⎪---==∈⎪⎩得263ω≤≤，423n ω-=，n *∈N ，所以242633n -≤≤，解得15n ≤≤.即1,2,3,4,5n =，可得23ω=，102,3，143，6，经检验均符合题意，所以ω的取值共有5个.8．函数()sin()0,0,||2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示，将函数()f x 的图象向左平移3π个单位长度后得到()y g x =的图象，则下列说法正确的是（）A ．函数()g x 为奇函数B ．函数()g x 的最小正周期为2πC ．函数()g x 的图象的对称轴为直线()6x k k ππ=+∈ZD ．函数()g x 的单调递增区间为5,()1212k k k ππππ⎡⎤-++∈⎢⎥⎣⎦Z【答案】D 【详解】由图象可知3A =，33253441234ππππω⎛⎫=⋅=--= ⎪⎝⎭T ， ∴2ω=，则()3sin(2)f x x ϕ=+.将点5,312π⎛⎫⎪⎝⎭的坐标代入()3sin(2)f x x ϕ=+中，整理得5sin 2112πϕ⎛⎫⨯+= ⎪⎝⎭， ∴522,Z 122k k ππϕπ⨯+=+∈，即2,Z 3k k πϕπ=-∈；||2ϕπ<， ∴3πϕ=-，∴()3sin 23f x x π⎛⎫=-⎪⎝⎭. ∵将函数()f x 的图象向左平移3π个单位长度后得到()y g x =的图象， ∴()3sin 23sin 2,333g x x x x R πππ⎡⎤⎛⎫⎛⎫=+-=+∈ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦. ()()3sin 23sin 233g x x x g x ππ⎛⎫⎛⎫-=-+=--≠- ⎪ ⎪⎝⎭⎝⎭，∴()g x 既不是奇函数也不是偶函数，故A 错误；∴()g x 的最小正周期22T ππ==，故B 不正确. 令2,32πππ+=+∈x k k Z ，解得,122k x k Z ππ=+∈，则函数()g x 图像的对称轴为直线,122k x k Z ππ=+∈. 故C 错误；由222,232k x k k πππππ-++∈Z ，可得5,1212k x k k ππππ-+∈Z ，∴函数()g x 的单调递增区间为5,,1212k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦. 故D 正确；9．设函数()sin 2cos 2f x a x b x =+，其中,,0a b R ab ∈≠，若()6f x f π⎛⎫≤⎪⎝⎭对一切x ∈R 恒成立，则以下结论：①函数()f x 的图象关于11,012π⎛⎫⎪⎝⎭对称；②函数()f x 的单调递增区间是2,()63k k k ππππ⎡⎤++∈⎢⎥⎣⎦Z ；③函数()f x 既不是奇函数也不是偶函数；④函数()f x 的图象关于()26k x k Z ππ=+∈对称．其中正确的说法是（） A ．①②③ B ．②④C ．③④D ．①③④【答案】D 【详解】解：由辅助角公式得：())f x x ϕ=+，由()6f x f π⎛⎫≤⎪⎝⎭恒成立，得22()62k k Z ππϕπ⨯+=+∈，所以2()6k k Z πϕπ=+∈，取6π=ϕ，从而()26f x x π⎛⎫=+ ⎪⎝⎭，由11012f π⎛⎫= ⎪⎝⎭得①正确，由222()262k x k k Z πππππ-≤+≤+∈得()36k x k k Z ππππ-≤≤+∈，所以函数的增区间为,()36k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦，②不正确，根据正弦函数的奇偶性易得③显然正确，由2()62x k k Z πππ+=+∈，得对称轴为()26k x k Z ππ=+∈，④正确， 10．斐波那契螺线又叫黄金螺线，广泛应用于绘画、建筑等，这种螺线可以按下列方法画出：如图，在黄金矩形ABCD （AB BC =）中作正方形ABFE ，以F 为圆心，AB 长为半径作圆弧BE ；然后在矩形CDEF 中作正方形DEHG ，以H 为圆心，DE 长为半径作圆弧EG ；……；如此继续下去，这些圆弧就连成了斐波那契螺线.记圆弧BE ，EG ，GI 的长度分别为,,l m n ，对于以下四个命题：①l m n =+；②2m l n =⋅；③2m l n =+；④211m l n=+.其中正确的是（）A ．①②B ．①④C ．②③D ．③④【答案】A 【详解】不妨设51AB =，则2BC =，所以()512l BE π==⨯，()25135ED =-=所以(352m EG π==⨯，(5135254CG =-=，所以()()254522n GI ππ==⨯=，所以(())3525451222m n l πππ⨯+⨯=⨯==+，故①正确；(2222735354m π-⨯==，))273551522l n ππ-⨯⨯=⋅=，所以2m l n =⋅，故②正确；))35551522l n ππ-⨯++==，((2235352m ππ=⨯⨯-=-，所以2m l n ≠+，故③不正确；11l nl n l n++===⋅(1132mπ==⨯211m l n≠+，故④不正确；所以①②正确，11．已知函数()3sin sin3f x x x=+，则（）A．()f x是奇函数B．()f x是周期函数且最小正周期为2πC．()f x的值域是[4,4]-D．当(0,)xπ∈时()0f x>【答案】ABD【详解】A.()3sin()sin(3)3sin sin3()f x x x x x f x-=-+-=--=-，故()f x是奇函数，故A正确；B.因为siny x=的最小正周期是2π，sin3y x=的最小正周期为23π，二者的“最小公倍数”是2π，故2π是()f x的最小正周期，故B正确；C.分析()f x的最大值，因为3sin3x≤，sin31x≤，所以()4f x≤，等号成立的条件是sin1x=和sin31x=同时成立，而当sin1x=即2()2x k kππ=+∈Z时，336()2x k kππ=+∈Z，sin31x=-故C错误；D.展开整理可得()2()3sin sin cos2cos sin2sin4cos2f x x x x x x x x=++=+，易知当(0,)xπ∈时，()0f x>，故D正确.12．设函数cos2()2sin cosxf xx x=+，则（）A．()()f x f xπ=+B．()f x的最大值为12C．()f x在,04π⎛⎫-⎪⎝⎭单调递增D．()f x在0,4π⎛⎫⎪⎝⎭单调递减【答案】AD【详解】()f x的定义域为R，且cos2()2sin cosxf xx x=+，()()()()cos 22cos 2()2sin cos 2sin cos x xf x f x x x x xππππ++===++++，故A 正确．又2cos 22cos 2()42sin cos 4sin 2x x f x x x x ==++，令2cos 24sin 2xy x=+，则()42cos 2sin 22y x y x x ϕ=-=+，其中cos ϕϕ==1≤即2415y ≤，故y ≤≤当15y =时，有1cos ,sin 44ϕϕ==，此时()cos 21x ϕ+=即2x k ϕπ=-，故max 15y =，故B 错误． ()()()()()22222sin 24sin 22cos 2414sin 2()4sin 24sin 2x x x x f x x x ⎡⎤-+--+⎣⎦'==++，当0,4x π⎛⎫∈ ⎪⎝⎭时，()0f x '<，故()f x 在0,4π⎛⎫⎪⎝⎭为减函数，故D 正确．当,04x π⎛⎫∈-⎪⎝⎭时，1sin 20x -<<，故314sin 21x -<+<，因为2t x =为增函数且2,02x π⎛⎫∈- ⎪⎝⎭，而14sin y t =+在,02π⎛⎫- ⎪⎝⎭为增函数，所以()14sin 2h x x =+在,04π⎛⎫-⎪⎝⎭上为增函数，故14sin 20x +=在,04π⎛⎫- ⎪⎝⎭有唯一解0x ，故当()0,0x x ∈时，()0h x >即()0f x '<，故()f x 在()0,0x 为减函数，故C 不正确． 13．若将函数f (x )=cos(2x +12π)的图象向左平移8π个单位长度，得到函数g (x )的图象，则下列说法正确的是（） A ．g (x )的最小正周期为πB ．g (x )在区间[0，2π]上单调递减C ．x =12π是函数g (x )的对称轴 D ．g (x )在[﹣6π，6π]上的最小值为﹣12【答案】AD 【详解】函数f (x )=cos(2x +12π)的图象向左平移8π个单位长度后得()cos 2812g x x ππ⎡⎤⎛⎫=++ ⎪⎢⎥⎝⎭⎣⎦cos 23x π⎛⎫=+ ⎪⎝⎭，最小正周期为π，A 正确；222()3k x k k Z ππππ≤+≤+∈()63k x k k Z ππππ∴-≤≤+∈为g (x )的所有减区间，其中一个减区间为,63ππ⎡⎤-⎢⎥⎣⎦，故B 错；令23x k ππ+=，得6,2kx k Z ππ=-+∈，故C 错； x ∈[﹣6π，6π]，220,33x ππ⎡⎤∴+∈⎢⎥⎣⎦，1cos(2),132x π⎡⎤∴+∈-⎢⎥⎣⎦，故 D 对 14．下列说法正确的是（） A ．函数()23sin 0,42f x x x x π⎛⎫⎡⎤=-∈ ⎪⎢⎥⎣⎦⎝⎭的最大值是1 B ．函数()cos sin tan 0,tan 2x f x x x x x π⎛⎫⎛⎫=⋅+∈ ⎪ ⎪⎝⎭⎝⎭的值域为(C ．函数()1sin 2cos 2f x x a x =+⋅在()0,π上单调递增，则a 的取值范围是(],1-∞- D ．函数()222sin 42cos tx x xf x x x π⎛⎫+++ ⎪⎝⎭=+的最大值为a ，最小值为b ，若2a b +=，则1t =【答案】ACD 【详解】 A 选项，()222311cos cos cos 1442f x x x x x x ⎛⎫=--=-++=--+ ⎪ ⎪⎝⎭，又0,2x π⎡⎤∈⎢⎥⎣⎦可得：[]cos 0,1x ∈，则当cos 2x =时函数()f x 取得最大值1，A 对； B 选项，()2233sin cos sin cos cos sin sin cos x x x xf x x x x x+∴=+=⋅ ()()22sin cos sin cos sin cos sin cos x x x x x x x x++-⋅=⋅()()2sin cos sin cos 3sin cos sin cos x x x x x x x x⎡⎤++-⋅⎣⎦=⋅，设sin cos 4t x x x π⎛⎫=+=+ ⎪⎝⎭，则()22sin cos 12sin cos t x x x x =+=+，则21sin cos 2t x x -⋅=， 0,2x π⎛⎫∈ ⎪⎝⎭，3,444x πππ⎛⎫∴+∈ ⎪⎝⎭，sin 42x π⎛⎤⎛⎫∴+∈ ⎥⎪ ⎝⎭⎝⎦，(t ∴∈，令()223221323112t t t t t g t t t ⎛⎫--⨯ ⎪-⎝⎭==--，(t ∈，()()422301t g t t --'=<-， ()g t ∴在区间(上单调递减，()()32min 1g t g===-所以，函数()f x 的值域为)+∞，B 错； C 选项，()1sin 2cos 2f x x a x =+⋅在区间()0,π上是增函数，()cos2sin 0f x x a x ∴=-⋅≥'，即212sin sin 0x a x --⋅≥，令sin t x =，(]0,1t ∈，即2210t at --+≥，12a t t ∴≤-+，令()12g t t t =-+，则()2120g t t'=--<，()g t ∴在(]0,1t ∈递减，()11a g ∴≤=-，C 对；D选项，()2222 22sin cos222costx t x x xf xx x⎛⎫+++⎪⎝⎭=+()()2222cos sin sin2cos2cost x x t x x t x xtx x x x++⋅+⋅+==+++，所以，()()()()22sin sin2cos2cost x x t x xf x t tx xx x--+-=+=-+⋅-+-，()()2f x f x t∴+-=，所以，函数()f x的图象关于点()0,t对称，所以，22a b t+==，可得1t=，D对. 15．如图是函数()sin()(0,0,||)f x A x Aωϕωϕπ=+>><的部分图象，则下列说法正确的是（）A．2ω=B．π,06⎛⎫- ⎪⎝⎭是函数，()f x的一个对称中心C．2π3ϕ=D．函数()f x在区间4ππ,5⎡⎤--⎢⎥⎣⎦上是减函数【答案】ACD【详解】由题知，2A=，函数()f x的最小正周期11π5π2π1212T⎛⎫=⨯-=⎪⎝⎭，所以2π2Tω==，故A正确；因为11π11π11π2sin22sin212126fϕϕ⎛⎫⎛⎫⎛⎫=⨯+=+=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，所以11ππ2π62kϕ+=+，k Z∈，解得4π2π3kϕ=-，k Z∈，又||ϕπ<，所以2π3ϕ=，故C正确；函数()2π2sin 23f x x ⎛⎫=+ ⎪⎝⎭，因为ππ2ππ2sin 22sin 06633f ⎡⎤⎛⎫⎛⎫-=⨯-+==≠ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，所以π,06⎛⎫-⎪⎝⎭不是函数()f x 的一个对称中心，故B 错误；令π2π3π2π22π232m x m +≤+≤+，m Z ∈，得π5ππ1212m x mx -≤≤+，m Z ∈，当1m =-时，13π7π1212x -≤≤-，因为4π13π7ππ,,51212⎡⎤⎡⎤--⊆--⎢⎥⎢⎥⎣⎦⎣⎦，所以函数()f x 在区间4ππ,5⎡⎤--⎢⎥⎣⎦上是减函数，故D 正确．。

三角函数的图像与性质

三角函数的图像与性质引言三角函数在数学中起着非常重要的作用，它们的图像与性质也是数学学习过程中的基础内容。

本文将介绍三角函数的图像和常见性质，包括正弦函数、余弦函数和正切函数。

正弦函数的图像与性质正弦函数是三角函数中最常见的函数之一，它的图像呈现周期性的波动。

正弦函数的定义域为实数集，值域为[-1, 1]。

正弦函数的图像可以用下面的公式表示：$$y = \\sin(x)$$正弦函数的图像在周期范围内呈现上升和下降的特点，其中最高点和最低点的纵坐标分别为1和-1。

正弦函数的图像以曲线方式连续无间断地进行。

正弦函数的性质包括： - 正弦函数的周期为$2\\pi$，即在每个周期内，正弦函数的图像完整地重复一次。

- 正弦函数的对称轴为x轴。

- 正弦函数的图像在$[\frac{\pi}{2},\frac{3\pi}{2}] $ 上是增函数，在$[0, \frac{\pi}{2}] $ 和$[\frac{3\pi}{2}, 2\pi] $ 上是减函数。

余弦函数的图像与性质余弦函数也是三角函数中常见的函数，它的图像与正弦函数非常相似，但是相位不同。

余弦函数的定义域为实数集，值域为[-1, 1]。

余弦函数的图像可以用下面的公式表示：$$y = \\cos(x)$$余弦函数的图像在周期范围内呈现上升和下降的特点，其中最高点和最低点的纵坐标分别为1和-1。

余弦函数的图像以曲线方式连续无间断地进行。

余弦函数的性质包括： - 余弦函数的周期为$2\\pi$，即在每个周期内，余弦函数的图像完整地重复一次。

- 余弦函数的对称轴为y轴。

- 余弦函数的图像在$[\pi, 2\pi] $ 上是增函数，在$[0, \pi] $ 上是减函数。

正切函数的图像与性质正切函数是另一个重要的三角函数，它的图像在不同的区间内有不同的特点。

正切函数的定义域是除了$\\frac{\\pi}{2} + k\\pi$（其中k是整数）的所有实数，值域是整个实数集。

2三角函数的图像与性质

cos2α＝1，∴5sin2α＝1，sin2α＝15，又 sin α>0，∴sin α＝ 55，故选 B.
【答案】 (1)B
(2)(多选题)[2020·山东师大附中月考]在平面直角坐标系 xOy
中，角 α 顶点在原点 O，以 x 正半轴为始边，终边经过点 P(1，
m)(m<0)，则ห้องสมุดไป่ตู้列各式的值恒大于 0 的是( )
对于 B，将 y＝sin2x＋3π的图象 C2 沿 x 轴方向向右平移1112π个
单位也可得到，y＝sin2x－1112π＋3π＝sin2x－32π＝cos 2x 的图象 C1，故选项 B 正确；
对于 C，先作 C2 关于 x 轴对称，得到 y＝－sin2x＋π3的图象 C3，再将图象 C3 沿 x 轴方向向右平移152π个单位，得到 y＝－
3．[2020·山东枣庄质量检测]在平面直角坐标系 xOy 中，角 α 的顶点是 O ，始边是 x 轴的非负半轴， 0<α<2π ，点 P1＋tan1π2，1－tan1π2是 α 终边上一点，则 α 的值是________.
解析：因为 1＋tan1π2>0,1－tan1π2>0，即 P 点在第一象限，所以 0<α<2π，又 tan α＝11＋－ttaann11ππ22＝1t＋anπ4ta－nπ4ttaann1π1π22＝tanπ6，∴α＝6π.
2x，∴fπ6＝－2sin3π＝－ 3.故选 D. 答案：D
3．[2020·山东临沂期末检测]已知函数 f(x)＝2cos2ωx－1π2(ω>0)
的图象关于直线 x＝4π对称，则 ω 的最小值为( )
1
1
A.3
B.6
4

高中数学三角函数图像和性质

高中数学
三角函数的图象和性质
知识点
一.正弦函数：
1.正弦函数的图象:
2.
定义域为
；值域为•
(1)
当且仅当
时，取得最大值1；
⑵
当且仅当
时，取得最小值1
3.单调性：
在闭区间上都是增函数，其值从1增大到1；
在闭区间上都是减函数，其值从1减小到1.
4.奇偶性：.
5.周期性：最小正周期是，周期是
6.对称性：对称轴是，对称中心是.
r
rK，
(1)将正切函数y tanx在区间(亍'上的图象向左、右扩展，就可以得到正切函y tanx,(x R, x-k , k Z)的图象，我们把它叫做正切曲线.正切曲线是由被互相平行的直线x
(k Z)所隔开的无数多支曲线组成的.这些平行直线x=(k Z)叫做正切曲线各支的
⑵结合正切曲线的特征，类比正弦、余弦函数的“五点法”作图，也可用三点两线作图法作出正切函数
6.对称性：对称轴是，对称中心是.
题型一正弦，余弦函数的图象和性质
【例1】求函数y=g+sinx的定义域
函数y=2sin(4x+^)的对称轴方程为
3
【过关练习】
1•求函数y 3sin x2的值域以及取得最值时x的值
2.判断函数y=xsin( x)的奇偶性
3.求函数y1sinx的单调区间
二.余弦函数：
1.余弦函数的Βιβλιοθήκη 象:2.定义域为值域为
(1)当且仅当
时，取得最大值1；
(2)当且仅当
时，取得最小值1.
3.单调性：
在闭区间
上都是增函数，其值从
1增加到1；
在闭区间
上都是减函数，其值从

三角函数的图象和性质

在区间 [0,
2
]
上是单调函数,
必有
2
≤
,
即 0<≤2.
∴0<
4k+2 3
≤2(kZ).
解得 k=0 或 1.
∴=2
或
2 3
.
综上所述,
=
2
,
=2 或
2 3
.
6.如果函数的值.
y=sin2x+acos2x
的图象关于直线
x=-
8
对称,
求a
解: y=sin2x+acos2x= a2+1 sin(2x+), 其中, tan=a.
3.周期性: ①y=sinx、y=cosx 的最小正周期都是
Asin(x+) 和 f(x)=Acos(x+)的最小正周期都是
2;
T=
2|②| .f(x)=
4.奇偶性与对称性: 正弦函数y=sinx(xR)是奇函数, 对称中心
是 (x(kR),是0)偶(k函Z数),,对对称称轴中是心直是线(kx=+k2,+02)((kkZZ)),;对余称弦轴函是数直y=线coxs=x k (kZ) (正(余)弦型函数的对称轴为过最高点或最低点且垂
性, 如果是周期函数, 求出它的一个周期.
解:
(1)由∴∵∴2kfsfs((iixnx+n))xx=的4--lcoc<定oogxss<21xx义(2s=>ik域n0,x2+为-s即ic5n4o{(xsx,x2|-k)s2≥ik4nlZ)(o≤x+g-21424<2,)x>=<0-2得k12:.+
5
4

专题4 三角函数的图象与性质-重难点题型精讲(举一反三)(新高考地区专用)(解析版)

专题4.7 三角函数的图象与性质-重难点题型精讲1．正弦函数与余弦函数的图象(1)正弦函数的图象①根据三角函数的定义，利用单位圆，我们可以得到函数y=,x∈[0,2π]的图象，如图所示.②五点法观察图，在函数y=,x∈[0,2π]的图象上，以下五个点：,1),( π,0),(-1),(2π,0)在确定图象形状时起关键作用.描出这五个点，函数y=,x∈[0,2π]的图象形状就基本确定了.因此，在精确度要求不高时，常先找出这五个关键点，再用光滑的曲线将它们连接起来，得到正弦函数的简图.这种作图的方法叫做“五点(画图)法”.(2)余弦函数的图象①图象变换法作余弦函数的图象由诱导公式六，我们知道，而函数x∈R的图象可以通过正弦函数y=,x∈R的图象向左平移个单位长度而得到.所以将正弦函数的图象向左平移个单位长度，就得到余弦函数的图象，如图所示.②五点法作余弦函数的图象类似于正弦函数图象的作法，从余弦函数y=,x∈R的图象可以看出，要作出函数y=在[0,2]上的图象，起关键作用的五个点是：(0,1),(,0),(,-1),(,0),(2,1).先描出这五个点，然后把这五个点用一条光滑的曲线连接起来就得到了函数y=在[0,2]上的简图，再通过左右平移(每次移动2个单位长度)即可得到余弦函数y=,x∈R的图象.(3)正弦曲线、余弦曲线正弦函数的图象和余弦函数的图象分别叫做正弦曲线和余弦曲线.它们是具有相同形状的“波浪起伏”的连续光滑曲线.2．正弦函数与余弦函数的性质(1)周期函数①定义：一般地，设函数f(x)的定义域为D，如果存在一个非零常数T，使得对每一个x∈D都有x+T∈D，且f(x+T)=f(x)，那么函数f(x)就叫做周期函数，非零常数T叫做这个函数的周期.②最小正周期：如果在周期函数f(x)的所有周期中存在一个最小的正数，那么这个最小正数就叫做f(x)的最小正周期.(2)正弦函数与余弦函数的性质正弦函数与余弦函数的图象与性质如下表：3．正弦型函数的性质的性质4．正切函数的性质与图象(1)正切函数的图象及性质(2)三点两线法作正切曲线的简图类比于正、余弦函数图象的五点法，我们可以采用三点两线法作正切函数的简图.“三点”是指点(-,-1),(0,0),(,1);“两线”是指直线x=-和x=.在三点、两线确定的情况下,可以大致画出正切函数在区间(-上的简图.5．余切函数的图象及性质正切函数的图象及性质：的图象先向右平移个单位长度，再以x轴为对称轴上下翻折，可得的图象.余切函数的图象与性质如下表：【题型1 三角函数的定义域和值域（最值）】【方法点拨】求与三角函数有关的函数的值域(最值)的常用方法有：(1)借助三角函数的有界性、单调性求解；(2)转化为关于的二次函数求解.注意求三角函数的最值对应的自变量x的值时，要考虑三角函数的周期性.【例1】（2022·甘肃·高二开学考试）函数f(x)=tan(x+π4)的定义域为（）A．{x|x≠kπ+π4,k∈Z}B．{x|x≠2kπ+π4,k∈Z}C．{x|x≠kπ−π4,k∈Z}D．{x|x≠kπ,k∈Z}【解题思路】根据正切函数的定义域可得结果.【解答过程】因为x+π4≠kπ+π2,k∈Z，所以x≠kπ+π4,k∈Z.故f(x)的定义域为{x|x≠kπ+π4,k∈Z}.故选：A.【变式1-1】（2022·四川省高三阶段练习（理））若x∈[π4,2π3]，则函数f(x)=3sin x cos x+√3sin2x的值域为（） A ．[0,3√32]B ．[0,√32] C ．[0,√3]D ．[0,3+√3]【解题思路】利用二倍角公式和辅助角公式化简原式为f (x )=√3sin(2x -π6)+√32，结合正弦函数的图像和性质，求解即可. 【解答过程】由题意，f (x )=3sin x cos x +√3sin 2x =32sin2x +√32(1-cos2x )=√3×(√32sin2x -12cos2x )+√32=√3×(cos π6sin2x -sin π6cos2x )+√32=√3sin(2x -π6)+√32,当x ∈[π4,2π3]时，有2x -π6∈[π3,7π6]，当2x -π6=π2，即x =π3时，f (x )max =f (π3)=√3+√32=3√32；当2x -π6=7π6，即x =2π3时，f (x )min =f (2π3)=0.即函数f (x )的值域为[0,3√32].故选：A.【变式1-2】（2022·福建省高二阶段练习）函数f (x )=sinx +cos (x +π6)的值域为（） A ．[−2,2]B ．[−√3,√3]C ．[−1,1]D ．[−√32,√32] 【解题思路】利用两角和的余弦公式和辅助角公式进行化简，即可得到答案【解答过程】解：函数f (x )=sinx +cos (x +π6)=sinx +√32cosx −12sinx =√32cosx +12sinx =cos (x −π6)，∵x ∈R ，∴cos (x −π6)∈[−1,1]，∴函数的值域为[−1,1]，故选：C ．【变式1-3】（2022·全国·高一单元测试）若x ∈[−π3,2π3]，则函数y =cos 2(x +π6)+sin (x +2π3)的最大值与最小值之和为（）A ．12B ．1C ．74D ．√2【解题思路】利用诱导公式可化简函数为y =(cos (x +π6)+12)2−14，根据余弦型函数值域的求法可求得cos(x+π6)∈[−√32,1]，结合二次函数最值的求法可求得y的最大值和最小值，加和即可求得结果.【解答过程】y=cos2(x+π6)+sin(x+2π3)=cos2(x+π6)+sin(π2+x+π6)=cos2(x+π6)+cos(x+π6)=(cos(x+π6)+12)2−14，当x∈[−π3,2π3]时，x+π6∈[−π6,5π6]，∴cos(x+π6)∈[−√32,1]，∴当cos(x+π6)=1时，y max=94−14=2；当cos(x+π6)=−12时，y min=−14；∴y max+y min=2−14=74.故选：C.【方法点拨】证明一个函数是否为周期函数或求函数周期的大小常用以下方法：(1)定义法：即对定义域内的每一个x值，看是否存在非零常数T使f(x+T)=f(x)成立，若成立，则函数是周期函数且T是它的一个周期.(2)公式法：利用三角函数的周期公式来求解.(3)图象法：画出函数的图象，通过图象直观判断即可.【例2】（2023·广东·高三学业考试）函数f(x)=sin(x2−π4)的最小正周期是（）A．π2B．πC．2πD．4π【解题思路】利用正弦函数的周期求解．【解答过程】f(x)的最小正周期为T=2π12=4π．故选：D．【变式2-1】（2023·广东·高三学业考试）函数f(x)=cos(12x+π6)的最小正周期为（）A．π2B．πC．2πD．4π【解题思路】利用余弦型函数的周期公式进行求解.【解答过程】∵f(x)=cos(12x+π6)，∴f(x)最小正周期T=2π12=4π．故A，B，C错误.故选：D.【变式2-2】（2022·甘肃临夏·高二期末（理））函数f(x)=cos(ωx+π6)(ω>0)的最小正周期为π，则f(π2)=（）A．−√32B．−12C．12D．√32【解题思路】由周期求出ω，从而可求出f(x)，进而可求出f(π2).【解答过程】因为函数f(x)的最小正周期为π，ω>0，所以ω=2ππ=2，得f(x)=cos(2x+π6)，所以f(π2)=cos(2×π2+π6)=−cosπ6=−√32．故选：A.【变式2-3】（2022·广东佛山·高三阶段练习）在下列函数中，最小正周期为π且在(0,π2)为减函数的是（）A．f(x)=sin|2x|B．f(x)=cos(2x+π6)C．f(x)=|cosx|D．f(x)=tan(2x−π4)【解题思路】根据三角函数的图像性质，逐个选项进行判断即可得出答案.【解答过程】对于A，f(x)=sin|2x|的图像关于y轴对称，在(0,π2)为增函数，不符题意，故A错；对于B，f(x)=cos(2x+π6)的最小正周期为π，x∈(0,π2),2x+π6∈(π6,7π6)，不是减函数，不符题意，故B错；对于C，f(x)=|cosx|的最小正周期为π，在(0,π2)为减函数，符合题意，故C对；对于D，f(x)=tan(2x−π4)的最小正周期为π2，不符题意，故D错；故选：C.【题型3 三角函数的奇偶性】【方法点拨】掌握正弦、余弦、正切函数的奇偶性相关知识，结合具体题目，灵活求解.【例3】（2022·广东·高三学业考试）若函数f(x)=sin(x+φ)是偶函数，则φ可取一个值为（）A．−πB．−π2C．π4D．2π【解题思路】根据偶函数的定义得φ=kπ+π2,k∈Z,结合选项可确定答案.【解答过程】∵函数f(x)=sin(x+φ)是偶函数，∴f(−x)=f(x)，即sin(−x+φ)=sin(x+φ).∴−x+φ=x+φ+2kπ或−x+φ+x+φ=π+2kπ,k∈Z.当−x+φ=x+φ+2kπ时，可得x=−kπ，不满足函数定义.当−x+φ+x+φ=π+2kπ时，φ=kπ+π2,k∈Z,若φ=kπ+π2=−π，解得k=−32∉Z，故A错误;若φ=kπ+π2=−π2，解得k =−1∈Z ，故B 正确; 若φ=kπ+π2=π4，解得k =−14∉Z ，故C 错误;若φ=kπ+π2=2π，解得k =32∉Z ，故D 错误;故选:B.【变式3-1】（2022·全国·高一）下列函数中，在其定义域上是偶函数的是（） A ．y =sinxB ．y =|sinx |C ．y =tanxD ．y =cos (x −π2)【解题思路】根据奇偶性定义，结合三角函数的奇偶性可直接得到结果.【解答过程】对于A ，∵y =sinx 定义域为R ，sin (−x )=−sinx ，∴y =sinx 为奇函数，A 错误；对于B ，∵y =|sinx |定义域为R ，|sin (−x )|=|−sinx |=|sinx |，∴y =|sinx |为偶函数，B 正确；对于C ，∵y =tanx 定义域为(kπ−π2,kπ+π2)(k ∈Z )，即定义域关于原点对称，tan (−x )=−tanx ，∴y =tanx 为奇函数，C 错误；对于D ，∵y =cos (x −π2)=sinx 定义域为R ，sin (−x )=−sinx ，∴y =cos (x −π2)为奇函数，D 错误. 故选：B.【变式3-2】（2022·北京高三阶段练习）函数f (x )=cos x +cos2x 是（） A ．奇函数，且最大值为2 B ．偶函数，且最小值为-98 C ．奇函数，且最小值为-98D ．偶函数，且最大值为98【解题思路】利用函数奇偶性的定义可判断出函数f (x )的奇偶性，利用二次函数的基本性质可求得函数f (x )的最值.【解答过程】函数f (x )的定义域为R ，f (-x )=cos (-x )+cos (-2x )=cos x +cos2x =f (x )，故函数f (x )为偶函数，因为-1≤cos x ≤1，则f (x )=2cos 2x +cos x -1=2(cos x +14)2-98，所以，f (x )min =-98，f (x )max =2+1-1=2.故选：B.【变式3-3】（2022·广西·模拟预测（理））若将函数f (x )=sin2x −√3cos2x 的图象向右平移m (m >0)个单位后，所得图象对应的函数为奇函数，则m 的最小值是（） A ．π6B ．π3C ．2π3D ．5π6【解题思路】首先对f (x )化简得到f (x )=2sin (2x −π3)，再写出平移后的解析式y =2sin (2x −2m −π3)，因为其为奇函数，则−2m −π3=k π,k ∈Z ，解出m 即可得到最小值.【解答过程】f (x )=sin2x −√3cos2x =2(12sin2x −√32cos2x)=2sin (2x −π3)，向右平移m(m >0)个单位后得到函数y =2sin [2(x −m )−π3]=2sin (2x −2m −π3)，由于是奇函数，因此，得−2m −π3=k π,k ∈Z ，m =−π6−k π2,k ∈Z.又∵m >0，则当k =−1时，m 的最小值是π3，故选：B.【方法点拨】掌握正弦、余弦、正切函数的对称性相关知识，结合具体题目，灵活求解.【例4】（2022·安徽·高三开学考试）函数f (x )=tan (2x −π3)的图象的一个对称中心为（） A ．(π12,0)B ．(7π12,0)C ．(−5π12,0)D ．(−π12,0)【解题思路】根据正切型函数的对称中心为(k π2,0) k ∈Z ，求解即可. 【解答过程】由2x −π3=k π2,k ∈Z ，可得x =k π4+π6,k ∈Z ，当k =0时，x =π6，当k =1时，x =π4+π6=5π12，当k =2时，x =8π12=23π，当k =−1时，x =−π4+π6=−π12，当k =−2时，x =−4π12=−13π，当k =−3时，x =−7π12，所以(−π12,0)为f (x )图象的一个对称中心，故选：D.【变式4-1】（2022·河南·高三阶段练习（理））已知函数f (x )=2cos (ωx −π6)(ω>0)在[0,2π]内恰有三条对称轴，则ω的取值范围是（） A ．[43,116)B ．(43,116]C ．[1312,1912)D ．(1312,1912]【解题思路】根据余弦函数的性质可得2π≤2ωπ−π6<3π，进而即得. 【解答过程】因为0≤x ≤2π，所以−π6≤ωx −π6≤2ωπ−π6，所以2π≤2ωπ−π6<3π，解得1312≤ω<1912．故选：C.【变式4-2】已知函数f(x)=sin (12x −π6)，则结论正确的是（）A ．f (x )的图象关于点(5π3,0)中心对称B ．f (x )的图象关于直线x =−π3对称C ．f (x )在区间(−π,π)内有2个零点D ．f (x )在区间[−π2,0]上单调递增【解题思路】A 、B 应用代入法判断对称轴和对称中心；C 、D 根据给定区间求12x −π6的范围，结合正弦型函数的性质求零点和单调性. 【解答过程】A ：f(5π3)=sin (12×5π3−π6)=sin2π3≠0，故(5π3,0)不是对称中心，错误；B ：f(−π3)=sin[12×(−π3)−π6]=−sin π3≠±1，故x =−π3不是对称轴，错误；C ：在x ∈(−π,π)，则12x −π6∈(−2π3,π3)，故f(x)=0，可得12x −π6=0，所以x =π3为f (x )在(−π,π)内的唯一零点，错误；D ：在x ∈[−π2,0]，则12x −π6∈[−5π12,−π6]，故f(x)=sin (12x −π6)递增，正确. 故选：D.【变式4-3】（2022·贵州·高三阶段练习（文））已知函数f (x )=2cos (ωx +φ)（ω>0，0<φ<π）的相邻两条对称轴之间的距离为2π，且为奇函数，将f (x )的图象向右平移π3个单位得到函数g (x )的图象，则函数g (x )的图象（） A ．关于点(−5π3,0)对称B ．关于点(π2,0)对称 C ．关于直线x =−π3对称D ．关于直线x =π2对称【解题思路】两个相邻对称轴的为半个周期，奇函数可以确定f (x )为正弦函数，由此条件得出f (x )的解析式，再根据平移得出g (x )的解析式，根据解析式写出对称中心和对称轴的通式即可得出答案.【解答过程】由相邻两条对称轴之间的距离为2π可知T2=2π，即T =4π，ω=2πT ，ω=12, 因为f (x )为奇函数，根据0<φ<π可知φ=π2，f (x )=2sin 12x , g (x )=2sin (12(x −π3))=2sin (12x −π6),对称中心：12x −π6=k π(k ∈Z )，x =2k π+π3(k ∈Z )，故A 正确，B 错误;对称轴：12x −π6=π2+k π(k ∈Z )，x =2k π+4π3(k ∈Z )，故C 、D 错误;故选：A.【方法点拨】三角函数的单调性问题主要有：三角函数的单调区间的求解、比较函数值的大小、根据三角函数的单调性求参数；结合具体条件，根据三角函数的图象与性质进行求解即可.【例5】（2022·江西·高三阶段练习（理））函数y =sin (π6−2x)(x ∈[0,π])为增函数的区间是（） A ．[0,π3]B ．[π12,7π12]C ．[π3,5π6]D ．[5π6,π]【解题思路】根据三角函数单调性的求法求得正确答案. 【解答过程】y =sin (π6−2x)=−sin (2x −π6)，2k π+π2≤2x −π6≤2k π+3π2，k π+π3≤x ≤k π+5π6，k ∈Z ，令k =0可的y =sin (π6−2x)(x ∈[0,π])的递增区间为[π3,5π6]. 故选：C.【变式5-1】（2022·河南信阳·一模（理））已知函数f (x )=2√3cos (x -π2)cos x -2sin 2x ，若f (x )在区间[m ,π4]上单调递减，则实数m 的取值范围（）A ．[π6,π4]B ．[π3,π2]C ．[π6,π4)D ．[π6,π3)【解题思路】利用三角恒等变换，化简三角函数，利用正弦型函数的单调性，建立不等式组，可得答案.【解答过程】f (x )=2√3cos (x -π2)cos x -2sin 2x =2√3sin x cos x -2·1-cos2x 2=√3sin2x -1+cos2x=2(√32sin2x +12cos2x)-1 =2sin (2x +π6)-1，由x ∈[m ,π4]，则2x +π6∈[2m +π6,2π3]，由题意，[2m +π6,2π3]⊆[π2,3π2]，则π2≤2m +π6<2π3，解得π6≤m <π4. 故选：C.【变式5-2】（2022·江苏·高三阶段练习）已知a =log 168，b =πln0.8，c =sin2.5，则a ，b ，c 的大小关系是（） A ．c <a <b B ．c <b <a C ．a <b <cD ．a <c <b【解题思路】由对数的运算法则求出a ，又πln0.8，sin2.5分别可看做y =πx ，y =sinx 的函数值，考虑构造指数函数和正弦函数，利用函数的单调性对其值进行估计，又因为ln0.8估值困难，故考虑利用与函数y =lnx 近似的有理函数y =1−1x 对其大小进行估值，最后求得答案.【解答过程】由题意，a =log 168=log 2423=34=0.75，设f (x )=lnx +1x −1，则f ′(x )=1x −1x 2=x−1x 2，当0<x <1时，f ′(x )<0，函数f (x )在(0,1)上单调递减，当x >1时，f ′(x )>0，函数f (x )在(1,+∞)上单调递增，所以f (0.8)>f (1)，即ln0.8+54−1>0，所以ln0.8>−14，因为函数y =πx 在(−∞,+∞)上单调递增，所以πln0.8>π−14，又(π−14)−4=π，(34)−4=25681≈3.16，所以(34)−4>(π−14)−4，因为y =x−4在(0,+∞)单调递减，所以34<π−14，所以πln0.8>34，故b >a ，因为3π4<2.5<5π6，函数y =sinx 在(π2,π)上单调递减，所以sin 5π6<sin2.5<sin3π4，所以12<sin2.5<√22，所以sin2.5<34，即c <a ，所以c <a <b ，故选：A.【变式5-3】（2022·内蒙古·高三阶段练习（文））若函数f(x)=√2cos (ωx +π4)(ω>0)在(0,7π4)上单调递减，则ω的最大值为（）A ．37 B ．34C ．14D ．1【解题思路】由题知ωx +π4∈(π4,7π4ω+π4)，再根据函数y =√2cosx 在(0,π)上单调递减可得7π4ω+π4≤π，进而解不等式求解即可.【解答过程】解：因为函数f(x)=√2cos (ωx +π4)(ω>0)在(0,7π4)上单调递减，所以7π4≤12T =πω，解得0<ω≤47，因为x ∈(0,7π4)，所以ωx +π4∈(π4,7π4ω+π4)，因为函数y =√2cosx 在(0,π)上单调递减，所以，函数f(x)=√2cos (ωx +π4)(ω>0)在(0,7π4)上单调递减，则有7π4ω+π4≤π，解得ω≤37，所以ω的取值范围是ω∈(0,37]，即ω的最大值为37. 故选：A.【方法点拨】解决正(余)弦型函数性质的综合应用问题的思路： (1)熟练掌握函数或的图象，利用基本函数法得到相应的函数性质，然后利用性质解题.(2)直接作出函数图象，利用图象形象直观地分析并解决问题. 【例6】已知函数f (x )=4sinxcos (x +π6)+1.(1)求f (x )的最小正周期及单调区间； (2)求f (x )在区间[−π6,π4]上的最大值与最小值.【解题思路】（1）先利用三角恒等变换化简得到f (x )=2sin (2x +π6)，从而利用T =2π|ω|求出最小正周期，再利用整体法求解函数的单调区间；（2）根据x ∈[−π6,π4]求出2x +π6∈[−π6,2π3]，从而结合函数图象求出最大值为2，最小值为−1.【解答过程】（1）因为f (x )=4sinx (cosxcos π6−sinxsin π6)+1=2√3sinxcosx −2sin 2x +1 =√3sin2x +cos2x =2sin (2x +π6) 所以f (x )的最小正周期T =2π2=π；令−π2+2k π≤2x +π6≤π2+2k π，k ∈Z ，解得：[−π3+k π,π6+k π]，k ∈Z ，令π2+2k π≤2x +π6≤3π2+2k π，k ∈Z ，解得：[π6+k π,2π3+k π]，k ∈Z ，单调增区间为[−π3+k π,π6+k π]，k ∈Z ，单调减区间为[π6+k π,2π3+k π]，k ∈Z ；（2）已知x ∈[−π6,π4]，所以2x +π6∈[−π6,2π3]，当2x +π6=π2，即x =π6时，f (x )取得最大值，最大值为2，当2x +π6=−π6，即x =−π6时，f (x )取得最小值，最小值为-1，所以f (x )在区间[−π6,π4]上的最大值为2，最小值为−1.【变式6-1】（2022·陕西·高三阶段练习（文））已知函数f (x )=4sin (ωx +φ)（ω>0，|φ|<π2）图象的一条对称轴为直线x =−π12，这条对称轴与相邻对称中心之间的距离为π8．(1)求f (x )；(2)求f (x )在[−π24,π4]上的值域．【解题思路】（1）先求出周期，由此求出ω的值，利用对称轴方程求出φ，即可得到函数的解析式；（2）根据自变量的范围求得4x −π6∈[−π3,5π6]，根据正弦函数的取值求得函数的值域【解答过程】（1）因为函数f(x)图象的对称轴与相邻对称中心之间的距离为π8，所以T =π2，故ω=2πT=4，又f(x)的图象的一条对称轴方程为x =−π12，则4×(−π12)+φ=π2+k π，k ∈Z ，即φ=5π6+k π，k ∈Z ，又|φ|<π2，所以φ=−π6，故f(x)=4sin (4x −π6)；（2）因为x ∈[−π24,π4]，所以4x −π6∈[−π3,5π6]，所以sin (4x −π6)∈[−√32,1]，所以4sin (4x −π6)∈[−2√3,4]，故f (x )在[−π24,π4]上的值域为[−2√3,4].【变式6-2】（2021·天津·高一期末）已知函数f (x )=2√3cos 2(π2+x)-2sin(π+x )cos x -√3 (1)求f (x )的最小正周期及单调递减区间； (2)求f (x )在区间[π4,π2]上的最值；(3)若f (x 0-π6)=1013,x 0∈[3π4,π]，求sin2x 0的值．【解题思路】（1）根据三角恒等变换可得f (x )=2sin (2x -π3)，然后根据三角函数的性质即得；（2）根据正弦函数的性质即得；（3）由题可得sin (2x 0-2π3)=513，然后根据同角关系式及和差角公式即得. 【解答过程】（1）因为f (x )=2sin x cos x +2√3sin 2x -√3 =sin2x -√3cos2x =2sin (2x -π3)．所以f (x )的最小正周期T =2π2=π，∵π2+2k π≤2x -π3≤3π2+2k π,k ∈Z ，∴5π12+k π≤x ≤11π12+k π，所以f (x )的单调递减区间为[5π12+k π,11π12+k π](k ∈Z)；（2）由（1）知f (x )的单调递减区间为[5π12+k π,11π12+k π](k ∈Z)，∵x ∈[π4,π2]，∴f (x )在[π4,5π12]上单调递增，在[5π12,π2]上单调递减，又f (5π12)=2sin π2=2,f (π4)=2sin π6=1,f (π2)=2sin2π3=√3，故f (x )min =1,f (x )max =2；另解：∵x ∈[π4,π2]， ∴t =2x -π3∈[π6,2π3]，∵y =sin t 在t ∈[π6,π2]单调递增，在[π2,2π3]上单调递减， ∴当t =π2时，(sin t )max =1,f (x )max =2×1=2， ∴当t =π6时，(sin t )min =12,f (x )min =2×12=1；（3）∵f (x 0-π6)=1013，∴sin (2x 0-2π3)=513，由x 0∈[3π4,π]，得2x 0-2π3∈[5π6,4π3]，∴cos (2x 0-2π3)=-1213， ∴sin2x 0=sin [(2x 0-2π3)+2π3]=sin (2x 0-2π3)cos2π3+cos (2x 0-2π3)sin 2π3=513×(-12)+(-1213)×√32=-5+12√326．【变式6-3】（2022·黑龙江·高三阶段练习）已知函数f (x )=[(1+√2)sin x -cos x]⋅[(1-√2)sin x -cos x]. (1)求f (x )的最小正周期T 和单调递减区间；(2)四边形ABCD 内接于⊙O ，BD =2，锐角A 满足f (3A4)=-1，求四边形ABCD 面积S 的取值范围.【解题思路】（1）利用三角函数恒等变换公式对函数化简变形得f (x )=√2cos (2x +π4)，从而可求出最小正周期，再由2kπ≤2x +π4≤2kπ+π(k ∈Z )求出其单调区间，（2）由f (3A4)=-1，求得A =π3，再由圆的性质可得C =2π3，设AB =a ，AD =b ，BC =c ，CD =d ，分别在△ABD 和△CBD 中利用余弦定理结合基本不等式可得0<ab ≤4，0<cd ≤43，从而可求出四边形ABCD 面积S 的取值范围.【解答过程】（1）[(1+√2)sin x -cos x]⋅[(1-√2)sin x -cos x]=[(sin x -cos x )+√2sin x]⋅[(sin x -cos x )-√2sin x]=(sin x -cos x )2-2sin 2x =sin 2x -2sin x cos x +cos 2x -2sin 2x=1-2sin 2x -sin2x =cos2x -sin2x=√2cos (2x +π4)， ∴f (x )=√2cos (2x +π4) ∴T =π.由2kπ≤2x +π4≤2kπ+π(k ∈Z )，得kπ-π8≤x ≤kπ+3π8(k ∈Z )，所以f (x )单调递减区间为[kπ-π8,kπ+3π8](k ∈Z ). （2）由于f (3A4)=-1，根据（1）得√2cos (2×3A 4+π4)=-1，∵0<A <π2，∴A =π3，C =2π3.分别设AB =a ，AD =b ，BC =c ，CD =d .因BD =2，分别在△ABD 和△CBD 中由余弦定理得a 2+b 2-2ab cos π3=4，c 2+d 2-2cd cos2π3=4，∴a 2+b 2=4+ab ，c 2+d 2=4-cd .∵a 2+b 2≥2ab ，c 2+d 2≥2cd ，等号在a =b =2，c =d =2√33时成立，∴4+ab ≥2ab ，4-cd ≥2cd ，解得0<ab ≤4，0<cd ≤43. ∴0<ab +cd ≤163.等号在a =b =2，c =d =2√33时成立，∵S =12ab sin A +12cd sin C =√34(ab +cd )，所以S 的取值范围是(0,4√33].。

三角函数的图像和性质(说课案)

三角函数的图像和性质(第一课时说课案) 下面我将从四个方面说明本节课的教学设计。

一、教材分析二、教学方法分析三、教学流程四、教学说明一、教材分析1、地位与作用：本节课是在学生掌握了单位圆中的正弦线和诱导公式的基础上进行的，不仅是对前面所学知识应用的考察，也是后续学习正、余弦函数性质的基础。

对函数图像清晰而准确的掌握也为学生在解题实践中提供了有力的工具。

2、学情分析：（1）知识与技能：学生已掌握了一些初等基本函数的图像和性质，并了解一些函数图像的画法。

（2）心理与生理：高一上学期的学生已经对高中数学体系中函数问题的处理方法和过程有了初步认识，且具有了较强的分析、判断、理解能力和一定层次上的交流沟通能力。

3、教学目标（1）知识与技能目标：通过研究掌握正弦函数图像及其画法；掌握余弦函数图像；深刻理解五点作图法中五点（零点、最高点、最低点）的本质即：图像中走向趋势发生变化的点。

（2）过程与方法：通过主动思考，主动发现，亲历知识的形成过程，使对正弦函数单调、对称、“周而复始”等性质的认知更为深刻。

（3）情感态度与价值观：用联系的观点看待问题，善于类比联想，直观想象，对数形结合有进一步认识，激发学习数学的兴趣，养成良好的数学品质。

4、重、难点分析：（1）重点：用单位圆中的正弦线作正弦函数在]2,0[π的图象、“五点法”作图；（2）难点：如何由正弦函数在]2,0[π上的图象得到正弦函数在R上的图象；如何在正弦函数的图像上找出“五点”。

二、教学方法教学方法：演示法、示范教学法、启发式引导、互动式讨论、反馈式评价。

学习方法：观察发现、合作交流、归纳总结、反馈模仿。

教学手段：运用多媒体网络教学平台，构建学生自主探究的教学环境。

三、教学流程1、复习、引入：复习内容有：描点作函数图像的一般步骤；弧度定义；正、余弦函数定义；正弦线、余弦线；诱导公式。

设置的目的是让学生再次回顾弧度的定义（强调弧度与实数一一对应的关系）与正弦线（实质是函数值），为利用正弦线作出正弦函数的图像做准备。