梁挠曲轴方程的拉普拉斯变换求解
如何在理论力学中解决梁的挠曲问题?

如何在理论力学中解决梁的挠曲问题?在理论力学中,梁的挠曲问题是一个非常重要的研究领域。
梁在受到外力作用时会发生弯曲变形,这种变形会影响梁的强度、刚度以及稳定性等性能。
因此,准确地解决梁的挠曲问题对于工程设计和实际应用具有重要意义。
要解决梁的挠曲问题,首先我们需要了解一些基本的概念和理论。
梁是一种常见的结构构件,其主要承受横向载荷。
当梁受到载荷作用时,梁内会产生弯矩和剪力。
弯矩是导致梁弯曲的主要因素,而剪力则会对梁的剪切变形产生影响。
在研究梁的挠曲时,我们通常会引入一些假设来简化问题。
例如,我们假设梁的材料是均匀、连续和各向同性的,梁的横截面在弯曲过程中始终保持平面,并且忽略梁的横向剪切变形。
这些假设在大多数实际情况中是合理的,可以帮助我们更方便地分析和解决问题。
解决梁挠曲问题的一个重要方法是利用梁的弯曲方程。
梁的弯曲方程描述了梁的挠度与弯矩之间的关系。
对于等截面梁,常见的弯曲方程有欧拉伯努利梁理论和铁木辛柯梁理论。
欧拉伯努利梁理论假设梁的弯曲变形很小,并且忽略了剪切变形的影响。
在这种理论下,梁的弯曲方程可以表示为:$EI\frac{d^2y}{dx^2} = M(x)$其中,$E$ 是梁材料的弹性模量,$I$ 是梁横截面的惯性矩,$y$ 是梁的挠度,$x$ 是梁的轴向坐标,$M(x)$是梁在$x$ 处的弯矩。
通过求解这个微分方程,结合梁的边界条件和连续条件,我们可以得到梁的挠度曲线和转角曲线。
然而,欧拉伯努利梁理论在一些情况下并不适用,例如对于短粗梁或者梁的剪切变形不能忽略的情况。
这时就需要用到铁木辛柯梁理论。
铁木辛柯梁理论考虑了剪切变形的影响,其弯曲方程相对更加复杂。
除了利用弯曲方程求解梁的挠曲问题,还可以采用能量法。
能量法的基本思想是利用梁在变形过程中的能量守恒原理来求解。
常见的能量法有单位载荷法和卡氏定理。
单位载荷法是通过在梁上施加一个单位虚拟载荷,然后根据虚拟载荷所做的功等于实际载荷所产生的应变能来求解梁的挠度和转角。
梁的挠曲线近似微分方程及其积分.

二、结构形式叠加(逐段刚化法):
A a
P q
C a
P
a
a
q
a
a
+
=
例6-4-1 按叠加原理求A点转角 和C点挠度.
解、载荷分解如图
、由梁的简单载荷变形表,
查简单载荷引起的变形。
PA
Pa 2 4 EI
f ( x) M ( x) I0 M ( x)
EI ( x) I0
EI 0
EI 0 f ( x) M ( x)
M(x) M(x) I0
I(x)
:几何形状:长度不变,惯性矩变为I0 。
:实梁对应方程: EI0 f ( x) M ( x)
虚梁对应方程:
M (x) q(x)
:令:q(x) M ( x ) 依此建立虚梁上的分布载荷。
8
2
- q a2
a2
C
a
求虚梁B点的剪力和弯矩
x
13qa 3 RA 72
QB
13qa3 72
1 2
qa2 2
a
5 72
qa3
MB
13qa3 72
a
1 2
qa2 2
a
a 3
7 72
qa4
D
B
5qa 3 72EI
7qa4 f B 72EI
C点左右位移怎样?
四、变截面直梁的共轭梁法: :将截面的变化折算到弯矩之中去。
梁的挠曲线微分:方E程 If ( x) M ( x) 梁的外载与内力的为关 : M系(x) q(x)
上二式形式相同,用类比法,将微分方程从形式上转化为 外载与内力的关系方程。从而把求挠度与转角的问题转化为求 弯矩与剪力的问题。
关于梁的挠曲线方程 -回复的文章

关于梁的挠曲线方程 -回复的文章梁的挠曲线方程 - 探索结构力学的奥秘在结构力学中,梁是一种常见的结构元素,用于支撑和承载荷载。
梁的挠曲是指在受到外力作用下,梁发生弯曲变形的现象。
为了研究和预测梁的挠曲行为,工程师们发展了一种被称为梁的挠曲线方程的数学模型。
梁的挠曲线方程描述了梁在受到外力作用下的变形情况。
这个方程是基于弹性理论和材料力学原理建立起来的。
它考虑了梁材料的弹性特性以及外力对其产生的影响。
一般来说,梁的挠曲线方程可以表示为:y = f(x)其中,y表示横向位移(即垂直于原始位置上下方向上的位移),x表示沿着梁长度方向上的位置坐标。
这个方程描述了在不同位置上,横向位移与位置坐标之间的关系。
具体而言,在弹性理论中,工程师们假设材料具有线弹性行为,并使用弯矩-曲率关系来推导梁的挠曲线方程。
弯矩是指梁在受到外力作用下产生的弯曲力矩,而曲率则是指梁在受到弯矩作用下产生的曲率变化。
根据弯矩-曲率关系,可以得到梁的挠曲线方程为:d²y/dx² = M(x)/EI其中,M(x)表示在位置x处的弯矩大小,E表示梁材料的弹性模量,I表示梁截面的惯性矩。
这个方程描述了横向位移随位置坐标变化的二阶导数关系。
通过求解这个微分方程,工程师们可以得到具体的挠曲线方程。
这个方程可以用来预测和分析梁在受到不同外力作用下的变形情况。
通过对挠曲线方程进行数值计算和仿真模拟,工程师们可以评估和优化梁结构的设计。
除了上述基本形式外,实际工程中还存在许多复杂情况需要考虑。
例如,在考虑非均匀截面、非线性材料行为、动态荷载等因素时,挠曲线方程可能需要进行修正和扩展。
总之,梁的挠曲线方程是结构力学中的重要工具,它帮助工程师们理解和预测梁在受力下的变形行为。
通过研究和应用这个方程,我们能够更好地设计和优化梁结构,确保其在实际工程中的安全可靠性。
同时,挠曲线方程也是探索结构力学奥秘的一部分,它揭示了材料和力学之间复杂而又精妙的关系。
laplace变换的原理和方法

其中 a 1, a 2 , a n 及 b 0, b1 b m 均为实数,
A ( s ) ( s s 1 )( s s 2 ) ( s s n ) s i ( i 1, , n ) 是 A ( s ) 0 的根。
1、 A ( s ) 0 无重根 F (s) C1 s s1 C2 s s2 Ci s si Cn s sn
e
( s j ) t
) dt
1
2 j s j
[
1
s j
]
s
2 2
余弦函数
通理可得: F ( s ) L [cos t ] s s
2 2
6、单位脉冲函数
0 f (t ) (t ) t 0 t 0
(t )
且有
'
一般地,有 F
(n)
( s ) L [( t ) f ( t )], Re( s ) c
n
(3)积分性质
设 L [ f ( t )] F ( s ),则有 L [ f ( t ) dt ]
0 t
1 s
F (s)
t t t
L [ dt
dt
n
f ( t ) dt ]
m
C m 1 ( s s1 )
m 1
C1 s s1
C m 1 s s m 1
Cn s sn
C m 1 , C n 的计算同单根部分,
C 1 , C m 的计算公式:
C m lim ( s s 1 )
讲梁的挠曲线方程与积分解法
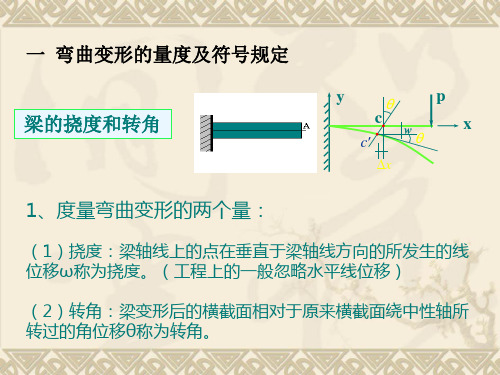
②积分常数的确定——边界条件和连续条件:
边界条件:梁在其支承处的挠度或转角是已知的, 这样的已知条件称为边界条件。 连续条件:梁的挠曲线是一条连续、光滑、平坦 的曲线。因此,在梁的同一截面上不可能有两个 不同的挠度值或转角值,这样的已知条件称为连 续条件。
边界条件
积分常数2n个=2n个
连续条件
列出图示结构的边界条件和连续条件。
8
代入(1)(2)得:
1 ( 1 qx3 1 qL3)
EI 6 6
1 ( 1 qx4 qL3 x qL4 )
EI 24
68
将 x 0 代入得:
A
qL3 6EI
(与C比较知E:I A C)
A
qL4 8EI
(与D比较知E:IA )D
因此
常数C表示起始截面的转角×刚度(EI)
常数D表示起始截面的挠度×刚度(EI)
x L
2
2、
d 2
dx 2
M (x) EI z
EI" 1 qx2
2
积分一次: EI' EI 1 qx3 C (1)
积分二次:
6
EI 1 qx4 Cx D (2)
24
B X``
3、确定常数C、D.
由边界条件: x L, 0 代入(1)得: C 1 qL3
6
x L, y 0 代入(2)得: D 1 qL4
支座反力,分段列弯矩方程; 分段的原则:
①凡载荷有突变处(包括中间支座),应作为分段点;
②凡截面有变化处,或材料有变化处,应作为分段点;
③中间铰视为两个梁段间的联系,此种联系体现为两部分之间 的相互作用力,故应作为分段点;
(2)分段列出梁的挠曲线近似微分方程,并对其积分 两次
梁的挠曲线方程 -回复

梁的挠曲线方程
梁的挠曲线方程描述了在受到外力作用下的梁的弯曲形状。
梁的挠曲方程具体形式取决于梁的几何形状、材料性质、荷载情况等因素。
以下是一些常见的梁的挠曲方程:
1.简支梁的挠曲方程:对于简支梁,载荷集中在梁的两端,
其挠曲方程可以用Euler-Bernoulli梁理论描述,其方程形式如下:y(x) = c1x²/2EI - c2x³/6EI + M₀x/2EI
其中,y(x)是弯曲后梁的垂直偏移,x是梁上的位置,E是梁的弹性模量,I是梁的截面惯性矩,M₀是梁上的弯矩。
2.悬臂梁的挠曲方程:对于悬臂梁,悬臂端受到力矩和剪力
的影响,其挠曲方程可以用Timoshenko梁理论描述,其方程形式如下:y(x) = M₀x/GI+ M₁x²/2GI- M₂x⁴/24GI+ θ₀x²/2GJ + V₀x/GJ
其中,y(x)是弯曲后梁的垂直偏移,x是梁上的位置,G是梁的剪切模量,I是梁的截面惯性矩,J是梁的截面极惯性矩,M₀和M₁是梁上的弯矩,M₂是梁上的剪力,θ₀是梁上的旋转角度,V₀是梁上的剪力。
以上方程仅给出了简支梁和悬臂梁的挠曲方程的简化形式,实际情况中还需考虑更多的因素。
对于更复杂的梁形式和加载情况,可能需要采用更复杂的挠曲方程进行描述。
挠曲线方程

例7-3.图示一简支梁,在梁跨度中点C处作用一个集中力P。求 该跨中点C的挠度及支座A点处横截面的转角。
P
解:[分析]象这样类型习题的传统
解法是:以A点为原点,建立坐标系 A
B
,分AC段,CB段分别列出弯矩方程 RA x
及挠曲线方程,然后根据变形条件
L/2
L
RB
和连续条件确定积分方程。从而求
解,我们的书中用的就是这种解法,但是,我们只要稍微注意一
EIZ
y ''
RAx
q 2
x2
q 2
Lx
q 2
x2
EIZ
y'
q 4
Lx2
q 6
x3
C
EIZ
y
q 12
Lx3
q 24
x4
Cx
D
——(1) ——(2)
(3)利用边界条件确定积分常数C、D
x=0, y A 0 得:D=0
x=L, yB 0
得:C qL3
24
将C、D代入(1)(2)得:
EIZ EIZ
y' q Lx2 4
y q Lx3 12
q x3 qL3 6 24 q x4 qL3 24 24
x
(4) x
L 2
时,(将
x
L 2
代入(4)式得yC
)
EI Z yC
5 384
qL4
yC
5 384 EI Z
我们上面所讲的直接积分法是求梁变形的基本方法, 但在载荷复杂的情况下,要列多段弯矩方程,从而产生很 多的积分常数。运算非常复杂。现在我们将要介绍的叠加 法,基本上克服了这一缺点,为工程上常采用的较方便的 计算方法之一。
梁的挠曲线和变形计算课件

Segment CB:
b M ( x2 ) Px 2 P( x2 a) l
( a x2 l )
(2) The equation of the deflection curve Segment AC
0 x1 a
b Px1 l
RA
1 ql 3 q 4 ql3 qx 3 y ( x x x) (l 2lx 2 x3 ) EI 12 24 24 24EI
(3) Maximum deflection and maximum angle of rotation
5ql 4 yC y | l x 384 EI 2
(g)
Continuity conditions:
y1 |x1 a y2 |x2 a ,
C1 C2 ,
y1' |x1 a y '2 |x2 a
(i)
(h)
Substituting (b), (c) ,(e) and (f) into (h),
D1 D2
Substituting (g) into (c) and (f) , and using (i), we get
(挠曲线的近似微分方程)
Beam deformation ---- The integration method
(梁的变形 -- 积分法)
Beam deformation ---- The method of superposition
(梁的变形 -- 叠加法)
Rigidity condition under bending
Boundary conditions:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
算例对其进行了验证。结果表明, 该方法求解步骤规范, 计算量 小, 方法简捷。
[ 关键词] 静定梁; 挠曲轴方程; 单位阶跃函数; 拉普拉斯变换
[ 中图分类号] T U 311. 4 [ 文献标识码] A
[ 文章编号] 1671-9387( 2006) 09-0176-03
研究梁的变形, 不仅是为了解决梁的刚度问题 与求解静不定梁, 同时也可为研究压杆稳定问题奠 定基础。因此, 求解梁挠曲轴方程是材料力学中的一 项重要内容。目前, 求解梁挠曲轴方程的基本方法有 积分法、奇异函数法及共轭梁法等。积分法是分析梁 位移的最基本方法, 但在工程实际中, 梁上往往作用 多项荷载, 在这种情况下, 需要分段建立与求解梁挠 曲轴方程, 并需要确定许多积分常数, 实际应用很不 方便[ 1-5] 。奇异函数法仍属于积分法, 只是采用奇异 函数建立了弯距统一方程, 其仍然需要积分运算, 也 要应用梁挠曲轴的位移边界条件求解积分常数[ 5-6] 。
式中, 求常数 c 得:
c=
F Pb 6E I l
(
b2
-
l 2)
( 12)
将( 12) 式代入( 11) 式得梁挠曲轴方程为:
w(x) =
FP 6EI
b l
x
3
-
ua( x ) ( x -
a) 3 +
b3 l
bl
2
x
图 2 等截面悬臂梁计算简图 Fig. 2 Calculation diagr am o f unifo rm
( 3)
将单位阶跃函数引入梁分段表达的 弯矩方程
( 2) 式中, 则梁的弯矩方程可表达成一个统一的方程
式:
M(x) =
bF l
P
x
-
ua ( x ) FP ( x -
a)
( 0 ≤x ≤ l)
( 4)
梁的挠曲轴近似微分方程[ 1-5] 为:
d2 w dx 2
=
M ( x) EI
( 5)
式中, EI 为梁截面的弯曲刚度。将( 4) 式代入( 5) 式 可得( 图 1 所示) 梁的挠曲轴近似微分方程的统一表
-
Me s3
-
FPl s3
+
e-
asM s3
e
)
( 19)
17 8
西北农林科技大学学报( 自然科学版)
第 34 卷
对( 19) 式进行拉普拉斯反演变换得:
w(x) =
1 EI
F6Px 3 -
M
e
+ 2
FP l x 2
+
ua( x )
M 2
e
(
x
-
a) 2
( 0 <
x ≤ l)
( 20)
可见, 应用该方法求解悬臂梁的挠曲轴方程时,
cro ss sectio n o f cantilever bea m
梁的支座反力为:
F A = FP M A = M e + Fpl
( 14)
梁的统一弯矩方程为:
M ( x ) = FA x - MA + ua ( x ) Me
( 0 < x ≤ l)
( 15)
将( 14) 式代入( 15) 式得:
达式为:
d2 w dx 2
=
FP EI
b l
x
-
ua ( x ) ( x -
a)
( 6)
由( 6) 式可知, 引用单位阶跃函数可直接建立最
右段梁的弯距方程, 该方程式适用于各个梁段, 避免
了分段求解的弊端。
[ 收稿日期] 2006-03-07 [ 基金项目] 陕西省水利科技计划项目( S K 2003-12) [ 作者简介] 赵毅力( 1957- ) , 男, 陕西澄城人, 讲师, 主要从事工程力学研究。
L [w(x)] =
FP EI
(
b ls4
-
e- as s4
)
+
c s2
( 10)
对上式进行拉普拉斯反演变换, 可得:
w(x) =
L
-
1[
FP EI
(
b ls4
-
es
as 4
)
+
c s2
]
=
F E
P
I
[
bx 3 6l
-
ua ( x )
(x
6
a) 3]
+
cx
( 11)
将梁挠曲轴的另一边界条件 w ( l ) = 0 代入( 11)
可直接将初始边界条件代入, 不需要根据边界条件
求常数。
4 小 结
求解多项荷载作用下的梁挠曲轴方程时, 引入
单位阶跃函数, 可使分段连续的弯距方程表达成一 个统一方程形式。使梁挠曲轴近似微分方程不再分 段, 也可表达成一个统一方程。所以说, 单位阶跃函 数为更好的处理这类问题提供了一个有力的工具。 应用拉普拉斯变换方法求梁挠曲轴方程, 可减少计 算量, 对于悬臂梁可直接将边界条件代入求解; 对于 简支梁和外伸梁最多只需根据边界条件求解一个常 数; 在梁上作用多项荷载时, 求解步骤规范, 计算更 为简便。
1 引入单位阶跃函数表达梁挠曲轴近 似微分方程
图 1 所示等截面简支梁上作用一集中力 FP , 梁 处于平衡状态。设x 轴的原点位于梁的左端A 处, 垂 直于梁轴方向为挠度, 用 w 表示。则梁的支座反力 为:
FA =
bFP l
( 1)
FB =
aF P l
梁A C, CB 段的弯矩方程分别为:
[ 参考文献]
[ 1] 干光瑜, 秦惠民. 材料力学[ M ] . 北京: 高等教育出版社, 1999. [ 2] 任文敏, 陈艳秋, 范钦珊. 材料力学[ M ] . 北京: 清华大学出版社, 2004. [ 3] 李庆华. 材料力学[ M ] . 西安: 西安交通大学出版社, 2005. [ 4] 同济大学航空航天与力学学院基础力学教学研究部. 材料力学[ M ] . 上海: 同济大学出版社, 2005. [ 5] 单辉祖. 材料力学[ M ] . 北京: 高等教育出版社, 1999. [ 6] 纳什( 美) . 材料力学理论与习题[ M ] . 北京: 清华大学出版社, 2003. [ 7] 丁同仁. 常微分方程基础[ M ] . 上海: 上海科学技术出版社, 1981. [ 8] 盖云芙, 包革军. 复变函数与积分变换[ M ] . 北京: 科学出版社, 2004. [ 9] 汪德新. 数学物理方法[ M ] . 武汉: 华中科技大学出版社, 2001. [ 10] 南京工学院数学教研组. 积分变换[ M ] . 北京: 高等教育出版社, 1989.
Solution o f beam deflection curve bas ed on laplace transformation
ZHAO Yi -li, FENG Xu
( Y angling Vocat ional and T echnical College, Y angling, Shaanx i 712100, China)
w ( 0) = 0
w ′( 0) = c
( 9)
式中, w ( 0) 是 x = 0 处的挠度; w ′( 0) 是 x = 0 处截面
的转角, 虽然这一值未知, 但其一定是一个常数 c, 在
解 出挠 曲 轴方 程后, 可 用梁 的 另一 边 界条 件
w ( l ) = 0求解。将边界条件( 9) 式代入( 8) 式得:
用拉普拉斯变换方法求解多项荷载作用的梁时, 可
以少求很多积分常数, 且计算方法简单。
3 算例分析
图 1 等截面简支梁计算简图 F ig . 1 Calculation diag ram o f unifor m cro ss
sectio n of simple suppo rt ed beam
应用拉普拉斯变换求解图 2 所示等截面悬臂梁 的挠曲轴方程。
共轭梁法避免了积分求解, 但要将实梁转换为虚梁, 对于多项荷载作用的梁也要分段求解[ 1] 。这些方法 互补性不强, 不仅计算过程繁琐, 且计算量大, 因此, 寻求更为简便的计算方法显得十分必要。本研究将 单位阶跃函数引入梁挠曲轴近似微分方程中, 并用 拉普拉斯变换方法求解, 以期为梁挠曲轴方程求解 提供简便方法。
第9 期
赵毅力等: 梁挠曲轴方程的拉普拉斯变换求解
1 77
( 0 ≤x ≤ l)
( 13)
对于上述问题, 若用积分法求解时, 则要分A C,
CB 两段进行计算, 还要根据边界条件( w ( 0) = 0, w
( l) = 0 ) 和挠曲轴在x = a 处的连续条件求解4 个积
分常数。弯矩函数分段愈多, 求解愈繁琐。显然, 应
w ′( x ) 在 x = 0 处的值; s 为拉普拉斯变换的参变量。
对( 6) 式两边进行拉普拉斯变换得:
s2L [ w ( x ) ] - sw ( 0) - w ′( 0)
=
F E
P
I
(
b ls2
-
e- as s2
)
( 8)
式中, e 为自然对数的底。对图1 所示的简支梁, 挠曲 轴的初始边界条件为:
M( x ) = FPx - M e - FP l + ua( x ) M eΒιβλιοθήκη ( 0 < x ≤ l)
( 16)
将( 16) 代入( 5) 得梁挠曲轴近似微分方程为:
d2w dx 2
=
1 EI
( FPx
-
Me -
F Pl +
ua( x ) Me)
( 0 < x ≤ l)
