各地中考数学第26题精华

合集下载

中考数学黄金知识点系列专题26四边形26--(附解析答案)

专题26 四边形聚焦考点☆温习理解一、四边形的内角和定理及外角和定理四边形的内角和定理：四边形的内角和等于360°。

四边形的外角和定理：四边形的外角和等于360°。

推论：多边形的内角和定理：n 边形的内角和等于•-)2(n 180°；多边形的外角和定理：任意多边形的外角和等于360°。

二、平行四边形 1、平行四边形的概念两组对边分别平行的四边形叫做平行四边形。

2、平行四边形的性质（1）平行四边形的邻角互补，对角相等。

（2）平行四边形的对边平行且相等。

推论：夹在两条平行线间的平行线段相等。

（3）平行四边形的对角线互相平分。

（4）若一直线过平行四边形两对角线的交点，则这条直线被一组对边截下的线段以对角线的交点为中点，并且这两条直线二等分此平行四边形的面积。

3、平行四边形的判定（1）定义：两组对边分别平行的四边形是平行四边形（2）定理1：两组对角分别相等的四边形是平行四边形（3）定理2：两组对边分别相等的四边形是平行四边形（4）定理3：对角线互相平分的四边形是平行四边形（5）定理4：一组对边平行且相等的四边形是平行四边形三、矩形1、矩形的概念有一个角是直角的平行四边形叫做矩形。

2、矩形的性质（1）具有平行四边形的一切性质（2）矩形的四个角都是直角（3）矩形的对角线相等（4）矩形是轴对称图形3、矩形的判定（1）定义：有一个角是直角的平行四边形是矩形（2）定理1：有三个角是直角的四边形是矩形（3）定理2：对角线相等的平行四边形是矩形四、菱形1、菱形的概念有一组邻边相等的平行四边形叫做菱形2、菱形的性质（1）具有平行四边形的一切性质（2）菱形的四条边相等（3）菱形的对角线互相垂直，并且每一条对角线平分一组对角（4）菱形是轴对称图形3、菱形的判定（1）定义：有一组邻边相等的平行四边形是菱形（2）定理1：四边都相等的四边形是菱形（3）定理2：对角线互相垂直的平行四边形是菱形4、菱形的面积S菱形=底边长×高=两条对角线乘积的一半五、正方形1、正方形的概念有一组邻边相等并且有一个角是直角的平行四边形叫做正方形。

齐齐哈尔中考数学第26题精选

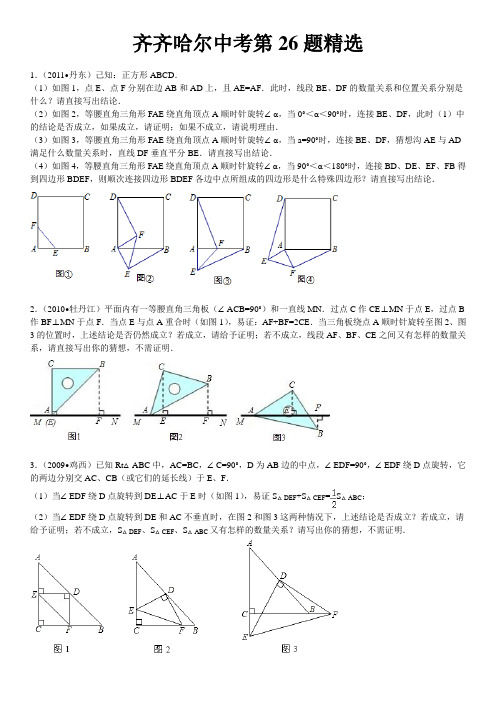
齐齐哈尔中考第26题精选1．（2011•丹东）己知：正方形ABCD．（1）如图1，点E、点F分别在边AB和AD上，且AE=AF．此时，线段BE、DF的数量关系和位置关系分别是什么？请直接写出结论．（2）如图2，等腰直角三角形FAE绕直角顶点A顺时针旋转∠α，当0°＜α＜90°时，连接BE、DF，此时（1）中的结论是否成立，如果成立，请证明；如果不成立，请说明理由．（3）如图3，等腰直角三角形FAE绕直角顶点A顺时针旋转∠α，当a=90°时，连接BE、DF，猜想沟AE与AD满足什么数量关系时，直线DF垂直平分BE．请直接写出结论．（4）如图4，等腰直角三角形FAE绕直角顶点A顺时针旋转∠α，当90°＜α＜180°时，连接BD、DE、EF、FB得到四边形BDEF，则顺次连接四边形BDEF各边中点所组成的四边形是什么特殊四边形？请直接写出结论．2．（2010•牡丹江）平面内有一等腰直角三角板（∠ACB=90°）和一直线MN．过点C作CE⊥MN于点E，过点B作BF⊥MN于点F．当点E与点A重合时（如图1），易证：AF+BF=2CE．当三角板绕点A顺时针旋转至图2、图3的位置时，上述结论是否仍然成立？若成立，请给予证明；若不成立，线段AF、BF、CE之间又有怎样的数量关系，请直接写出你的猜想，不需证明．3．（2009•鸡西）已知Rt△ABC中，AC=BC，∠C=90°，D为AB边的中点，∠EDF=90°，∠EDF绕D点旋转，它的两边分别交AC、CB（或它们的延长线）于E、F．（1）当∠EDF绕D点旋转到DE⊥AC于E时（如图1），易证S△DEF+S△CEF=S△ABC；（2）当∠EDF绕D点旋转到DE和AC不垂直时，在图2和图3这两种情况下，上述结论是否成立？若成立，请给予证明；若不成立，S△DEF、S△CEF、S△ABC又有怎样的数量关系？请写出你的猜想，不需证明．4．（2008•张家界）聪聪用两块含45°角的直角三角尺△ABC、△MNK进行一次探究活动：他将△MNK的直角顶点M 放在△ABC的斜边AB的中点处，让MK经过C点（如图甲），若BC=MK=4．（1）此时两三角尺的重叠部分（△ACM）面积为_________；（2）再将图甲中的△MNK绕顶点M逆时针旋转45°得到图乙，此时两三角尺的重叠部分（四边形MDCG）面积为_________；（3）据此猜想：在MK与BC相交的前提下，将△MNK绕点M旋转到任一位置（如图丙）时两三角尺的重叠部分面积为_________，请说出理由．5．（2007•临沂）如图1，已知△ABC中，AB=BC=1，∠ABC=90°，把一块含30°角的三角板DEF的直角顶点D放在AC的中点上（直角三角板的短直角边为DE，长直角边为DF），将直角三角板DEF绕D点按逆时针方向旋转．（1）在图1中，DE交AB于M，DF交BC于N．①证明DM=DN；②在这一过程中，直角三角板DEF与△ABC的重叠部分为四边形DMBN，请说明四边形DMBN的面积是否发生变化？若发生变化，请说明是如何变化的；若不发生变化，求出其面积；（2）继续旋转至如图2的位置，延长AB交DE于M，延长BC交DF于N，DM=DN是否仍然成立？若成立，请给出证明；若不成立，请说明理由；（3）继续旋转至如图3的位置，延长FD交BC于N，延长ED交AB于M，DM=DN是否仍然成立？若成立，请给出写出结论，不用证明．6．（2006•河北）如图1，一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起．现正方形ABCD保持不动，将三角尺GEF绕斜边EF的中点O（点O也是BD中点）按顺时针方向旋转．（1）如图2，当EF与AB相交于点M，GF与BD相交于点N时，通过观察或测量BM，FN的长度，猜想BM，FN满足的数量关系，并证明你的猜想；（2）若三角尺GEF旋转到如图3所示的位置时，线段FE的延长线与AB的延长线相交于点M，线段BD的延长线与GF的延长线相交于点N，此时，（1）中的猜想还成立吗？若成立，请证明；若不成立，请说明理由．。

2023年北京中考数学26题详解(二)

2023年北京中考数学26题详解(二)
2023年北京中考数学26题详解
题目描述
题目：已知函数f(x)=√x+2，若实数a满足方程f(a+
2)=f(a)，求实数a的值。

解题思路
1.首先，我们来理解函数f(x)=√x+2的意义。

这是一个以直线
y=2为渐近线的平方根函数，即当x的取值趋近于负无穷和
y的取值趋近于正无穷时，函数值将无限接近于0。

2.根据题目描述，已知f(a+2)=f(a)，我们需要找出实数a的
值。

3.将f(a+2)=f(a)代入函数f(x)=√x+2，得到√a+4=
√a。

4.两边平方消去根号，得到a+4=a。

5.将等式化简为4=0。

但是这是一个不可能的情况，所以不存在
满足条件的实数a。

答案
根据解题思路，我们得到结论：不存在满足条件的实数a。

总结
通过解题过程，我们学习到了通过代入函数的定义和方程的条件进行方程求解的方法。

同时，我们也注意到在代数运算中产生矛盾的情况，表示题目中给定的条件是不满足的。

这种方法在解决数学问题时非常实用，帮助我们提高解题的思维能力。

试题解析中考数学第26题解析

③当∠PBE=2∠OBE，当BP在BE轴下方时，如图(3)-2
在x轴上取点Q使得∠QEB=∠QBE，连接EQ，则QE=QB
∠OQE=2∠OBE
设点Q(a，0)由勾股定理：QE =OQ +OE
∴(3-a) =a +3
∴a=
∴tan∠OQE= =
过点E作EM⊥BE交BP 于点M，过点M作MN⊥x轴于点N，
（3）存在
①当∠PBE=2∠OBE，当BP在BE轴上方时，
如图(3)-1，设交y轴于点，
∴∠ BE=2∠OBE，
∴∠ BO=∠EBO，
又∠ OB=∠EOB=90°，BO=BO，
∴△ BO≌△EBO（AAS），
∴ O=EO= ，∴点（0，），
直线BP1过点B、，则求直线B 解析式为：，
解得：，（舍去），
∴
∴
∴直线BC的表达式为：y=-x+3
∵DG∥CB
∴设直线DG的表达式为：y=-x+m
∵直线DG经过经过点G（5，0）
∴0=-5+m
∴m=5
∴直线DG的表达式为：y=-x+5
∴
解得：
∴D（1，4）或（2，3）；
【（3）问分析】：分∠PBE或∠PEB等于2∠OBE四种情况分别求解即可
【（3）解答过程】
【变式训练】
（2019咸宁）如图，在平面直角坐标系中，直线与x轴交于点A，与y轴交于B，抛物线经过A，B两点且与x轴的负半轴交于点C．
（1）求该抛物线的解析式；
（2）若点D为直线AB上方抛物线上的一个动点，当∠ABD=2∠BAC时，求点D的坐标；
（3）已知E，F分别是直线AB和抛物线上的动点，当以B，O，E，F为顶点的四边形是平行四边形时，直接写出所有符合条件的E点的坐标．

2023年深圳中考数学第26题

2023年深圳中考数学第26题在接下来的文章中，我将对2023年深圳中考数学第26题进行全面深入的探讨和评估。

这道题目不仅仅是一道数学题，更是一个概念和方法的综合考验。

我会以从简到繁、由浅入深的方式来解读这道题，以便你能更深入地理解。

让我们来看一下这道题的具体内容和要求。

题目中涉及到了概率、几何、代数等多个数学知识点，要求学生综合运用多种方法来解决问题。

而这也是我们为什么要对这个题目进行全面评估的原因之一：需要考虑它的广度和深度。

要全面评估这个题目，我们需要从几何、代数和概率三个不同的角度来分析和解答。

我们来看一下几何部分。

题目中涉及到的几何知识点包括三角形的面积计算和相似三角形的性质。

在解答这部分内容时，我们需要了解三角形的性质和计算面积的公式，并据此展开解题。

我们来看一下代数部分。

在这道题目中，考查了代数的知识点包括方程的求解和代数式的化简。

需要使用代数方法来解决这部分内容，需要运用方程的求解和代数式的运算法则。

让我们来分析概率部分。

这道题目中，涉及到了概率的知识点，包括概率的计算和事件的相互独立性。

在解答这部分内容时，需要理解概率的概念、计算方法和相关的概率定理。

从上面几个方面的分析可以看出，这道题目的广度和深度都很大。

它涉及到了多个知识点和方法，而且要求学生综合运用这些知识和方法来解决问题，这也是题目的难点所在。

在文章的后半部分，我将共享我对这个题目的个人观点和理解。

我认为这个题目很好地考察了学生的综合运用能力和解决问题的能力。

它要求学生灵活地运用数学知识和方法，不仅仅是死记硬背，而是要求学生深入理解和灵活运用。

这是培养学生数学思维和解决实际问题能力的一个很好的例子。

我认为，这样的题目对学生的数学素养和综合运用能力有很大的促进作用，对他们的学习和发展有着积极的意义。

通过对2023年深圳中考数学第26题的全面评估和探讨，我们不仅对这道题目有了更深入的理解，也更加了解了它所涉及到的数学知识和方法。

23年重庆中考数学a卷26题解析

题目：23年重庆中考数学a卷26题解析在本篇文章中，我将针对23年重庆中考数学a卷26题展开详细的解析，并从浅入深地深入探讨这一题目。

通过本文的阅读，读者将能够更加全面、深刻地理解这道数学题目的解题思路和方法。

【题目简介】题目26的内容是：已知函数f(x) = x^2 - 4x + a，对于任意的实数x，恒有f(x) ≥ -2，则a的取值范围是？【解题思路】我们需要对给出的函数进行分析。

根据题目所给的条件，即f(x) ≥ -2，我们可以列出不等式x^2 - 4x + a ≥ -2。

接下来，我们需要通过一系列的数学推导和分析来确定a的取值范围。

【数学推导】1. 我们将x^2 - 4x + a ≥ -2转化为标准的一元二次不等式形式，即x^2 - 4x + a + 2 ≥ 0。

2. 我们可以利用一元二次不等式的判别式来确定a的取值范围。

判别式的公式为△ = b^2 - 4ac，其中a=1，b=-4，c=a+2。

3. 根据不等式△ ≥ 0，我们可以得出关于a的一元二次不等式，即(-4)^2 - 4*1*(a+2) ≥ 0。

4. 对式子进行化简得到16 - 4a - 8 ≥ 0，进一步化简可得-4a + 8 ≥ -16，即-4a ≥ -24。

5. 最终得到a ≤ 6。

【解题结论】综合以上的数学推导和分析，我们可以得出结论：当a的取值范围为a ≤ 6时，对于任意的实数x，函数f(x) = x^2 - 4x + a恒有f(x) ≥ -2。

a的取值范围为a ≤ 6。

【个人观点】对于这道题目的解析，我认为最关键的是要将给出的不等式转化为标准形式，并利用一元二次不等式的判别式来进行分析。

需要注意对不等式进行化简和推导，以得出最终的结论。

这道题目考查了对一元二次不等式的理解和运用，是一道具有一定难度的数学题目。

总结：通过本文的解析，我们对23年重庆中考数学a卷26题有了更深入的理解。

从转化不等式到求解不等式，我们逐步推导出了a的取值范围，并且对一元二次不等式的应用有了更加清晰的认识。

历年大连市中考数学第26题

历年大连市中考数学第26题(2008·大连)如图，点C 、B 分别为抛物线C 1：121+=x y ，抛物线C 2：22222c x b x a y ++=的顶点．分别过点B 、C 作x 轴的平行线，交抛物线C 1、C2于点A 、D ，且AB = BD ． ⑴求点A 的坐标；⑵如图，若将抛物线C 1：“121+=x y ”改为抛物线“11212c x b x y ++=”．其他条件不变，求CD 的长和2a 的值．附加题：如图，若将抛物线C 1：“121+=x y ”改为抛物线“11211c x b x a y ++=”，其他条件不变，求21b b +的值．(2009·大连)如图，抛物线F ：c bx ax y ++=2的顶点为P ，抛物线：与y 轴交于点A ，与直线OP 交于点B ．过点P 作PD ⊥x 轴于点D ，平移抛物线F 使其经过点A 、D 得到抛物线F ′：'+'+'=c x b x a y 2，抛物线F ′与x 轴的另一个交点为C ．⑴当a = 1，b =－2，c = 3时，求点C 的坐标(直接写出答案)； ⑵若a 、b 、c 满足了ac b 22=①求b ：b ′的值；②探究四边形OABC 的形状，并说明理由． yxO P DCBA2LOCABDx1L (2010·大连)如图，抛物线F ：2(0)y ax bx c a =++>与y 轴相交于点C ，直线1L 经过点C 且平行于x 轴，将1L 向上平移t 个单位得到直线2L ，设1L 与抛物线F 的交点为C 、D ，2L 与抛物线F 的交点为A 、B ，连接AC 、BC （1）当12a =，32b =-，1c =，2t =时，探究△ABC 的形状，并说明理由；（2）若△ABC 为直角三角形，求t 的值（用含a 的式子表示）；（3）在（2）的条件下，若点A 关于y 轴的对称点A ’恰好在抛物线F 的对称轴上，连接A ’C ，BD ，求四边形A ’CDB 的面积（用含a 的式子表示）yx MPO CBA(2011·大连)如图，抛物线c bx ax y ++=2经过A （－1，0）、B （3，0）、C （0，3）三点，对称轴与抛物线相交于点P 、与直线BC 相交于点M ，连接PB ． ⑴求该抛物线的解析式；⑵抛物线上是否存在一点Q ，使△QMB 与△PMB 的面积相等，若存在，求点Q 的坐标；若不存在，说明理由；⑶在第一象限、对称轴右侧的抛物线上是否存在一点R ，使△RPM 与△RMB 的面积相等，若存在，直接写出点R 的坐标；若不存在，说明理由．(2012·大连)如图，抛物线c bx ax y ++=2经过A (-3,0)、B (3,0)、C (0,3)三点，线段BC 与抛物线的对称轴l 相交于点D 。

2023中考数学复习-专题26 一次函数与反比例函数(练透)(学生版)

专题26 一次函数与反比例函数一、单选题1．（2022·全国九年级课时练习）下列函数中，是反比例函数的是（） A ．2x y =-B ．21y x=+ C ．2y x=-D ．21y x =+2．（2022·北京市第十三中学九年级期中）已知点A （1，a ）与点B （3，b ）都在反比例函数y 12x=-的图象上，则a 与b 之间的关系是（） A ．a ＞b B ．a ＜b C ．a ≥b D ．a ＝b3．（2022·哈尔滨风华中学九年级开学考试）如图是甲、乙两车在某时段速度随时间变化的图象，下列结论正确的是（）A ．乙前3秒行驶的路程为15米B ．在0到6秒内甲的速度每秒增加6米/秒C ．两车到第2.5秒时行驶的路程相等D ．在0至6秒内甲的速度都大于乙的速度4．（2022·建昌县教师进修学校九年级）在平面直角坐标系中，函数2y mx m =++的图象如图所示，则m 的取值范围是（）A ．0m ＜B ．2m -＞C ．20m -＜＜D ．02m ＜＜5．（2022·武汉一初慧泉中学九年级月考）下表反映的是某地区用电量x （千瓦时）与应交电费y （元）之间的关系：用电量x （千瓦时） 1 2 3 4 …应交电费y （元）0.55 1.1 1.65 2.2 …下列说法：①x 与y 都是变量，且x 是自变量，y 是x 的函数；②用电量每增加1千瓦时，应交电费增加0.55元；③若用电量为8千瓦时，则应交电费4.4元；④若所交电费为2.75元，则用电量为6千瓦时，其中不正确的是（） A ．①B ．②C ．③D ．④6．（2022·武汉一初慧泉中学九年级月考）已知反比例函数32y x=-，直线24y x =-+交于(),P a b 、(),Q m n 两点，则代数式33m a b n+++的值是（） A ．2 B ．－2 C ．4 D ．－47．（2022·沙坪坝区·重庆八中九年级）如图：四边形ABCD 为菱形，且对角线BD ∥x 轴，A 、C 两点在y 轴上，E 点在BC 上，且BE ＝2CE ，双曲线y ＝k x（x ＞0）经过E 、B 两点，且8EFB S =△，则k 的值为（）A ．3B ．83C ．4D ．68．（2022·江苏泰州中学附属初中）在平面直角坐标系中，一次函数 2y x b =-+（b 为常数）的图像与x 、y 轴分别交于点A 、B ，直线AB 与双曲线4y x= 分别交于点P 、Q ，则AP ·BP 的值是（）A ．4B ．8C ．10D ．与b 的取值有关9．（2022·南宁市天桃实验学校九年级）如图，在平面直角坐标系中，若折线241y x =--+与直线交2y kx k =+（0k >）有且仅有一个交点，则k 的取值范围是（）A ．01k <<或14k =B ．1k >或14k =C ．02k <<或14k =D ．2k >或14k =10．（2022·湖南新田县·九年级期中）如图，11122233,,,OA B A A B A A B △△△…是分别以123,,,A A A …为直角顶点，一条直角边在x 轴正半轴上的等腰直角三角形，其斜边的中点111222333(,),(,),(,),C x y C x y C x y …均在反比例函数4y x=（x ＞0）的图象上，则12100y y y +++的值为（）A ．10B ．20C ．42D ．7二、填空题11．（2022·陕西西安·高新一中九年级月考）如果一个正比例函数的图象与反比例函数y ＝4x的图象交于A （x 1，y 1），B （x 2，y 2）两点，那么（x 2﹣x 1）（y 2﹣y 1）的值为___． 12．（2022·浙江省杭州市上泗中学九年级）如图，在直角坐标系中，第一象限内的点A ，B 都在反比例函数的图象上，横坐标分别是3和1，点C 在x 轴的正半轴上，满足AC BC ⊥．且BC AC =，则k 的值是_______________________．13．（2022·宜兴市实验中学九年级）如图，点B 在x 的正半轴上，且BA OB ⊥于点B ，将线段BA 绕点B 逆时针旋转60︒到BB '的位置，且点B '的坐标为()1,1．若反比例函数ky x=()0x >的图象经过A 点，则k =______．14．（2022·山东济宁学院附属中学九年级期末）如图，在平面直角坐标系中，直线y ＝32x与双曲线y ＝6x相交于A 、B 两点，C 是第一象限内双曲线上一点，连接CA 并延长交y 轴于点P ，连接BP 、BC ，若△PBC 的面积是30，则C 点的坐标为__________________．15．（2022·厦门海沧实验中学九年级开学考试）设函数1y x=与1y x =+的图象的交点坐标为(),m n ，则()()11m n ++的值为___________．三、解答题16．（2022·全国九年级专题练习）已知点A （0，2）和点B （0，－2），点P 在函数1y x=-的图象上，如果△P AB 的面积是6，求P 点的坐标． 17．（2022·广西贺州市·九年级期中）若反比例函数y ＝mx与一次函数y ＝kx +b 的图象都经过点（﹣2，﹣1），且当x ＝1时，这两个函数值相等．（1）求反比例函数的解析式；（2）求一次函数的解析式．18．（2022·哈尔滨市虹桥初级中学校九年级开学考试）在平面直角坐标系中，直线y ＝﹣x ﹣1与直线y 34=x +6交于点A ，直线y ＝﹣x ﹣1与x 轴交于点B ，直线y 34=x +6与x 、y 轴分别交于点D 、C ．（1）求点A 的坐标；（2）求△ABD 的面积．19．（2022·重庆实验外国语学校）如图，直线y kx b =+与双曲线my x=的图象分别交于点(2,2)A ，点B ，与x 轴交于点C ，过点A 作线段AD 垂直x 轴于点D ，1tan 2ACD ∠=，连接AO ，BO ．（1）直线y kx b =+与双曲线my x=的解析式；（2）求AOB ∆的面积；（3）在直线AB 上是否存在点P ，使得3AOB AOP S S ∆∆=？若存在，请直接写出所有满足条件的点P 的坐标，若不存在，请说明理由．20．（2022·福建三明一中）如图，折线ABC 是在某市乘出租车所付车费y （元）与行车里程x （千米）之间的函数关系图象．（1）根据图象，写出射线BC 的函数关系式并写出定义域；（2）某人乘坐2.5千米，应付元；某人乘坐13千米，应付元；（3）若某人付车费30.8元，出租车行驶了多少千米？21．（2022·北京市第十三中学九年级期中）如图，在平面直角坐标系xOy中，直线y＝﹣2x﹣3与双曲线kyx=交于M（a，2），N（1，b）两点．（1）求k，a，b的值；（2）若P是y轴上一点，且△MPN的面积是7，直接写出点P的坐标．22．（2022·哈尔滨市虹桥初级中学校九年级开学考试）在平面直角坐标系中，点O为坐标原点，直线y＝kx+4交x轴、y轴分别于点A、点B，且△ABO的面积为8．（1）如图1，求k的值；（2）如图2，点P是第一象限直线AB上的一个动点，连接PO，将线段OP绕点O顺时针旋转90°至线段OC，设点P的横坐标为t，△AOC的面积为S，求S与t之间的函数关系式（不要求写出自变量t的取值范围）；（3）在（2）的条件下，过点B作直线BM⊥OP，交x轴于点M，垂足为点N，∠PMB＝2∠OPB，求点P的坐标．23．（2022·浙江诸暨市暨阳初级中学）如图，直线483y x=-+分别与x轴，y轴相交于点A，点B，作矩形ABCD，其中点C，点D在第一象限，且满足AB∶BC＝2∶1．连接BD．（1）求点A，点B的坐标．（2）若点E是线段AB（与端点A不重合）上的一个动点，过E作EF∥AD，交BD于点F，作直线AF．①过点B作BG⊥AF，垂足为G，当BE＝BG时，求线段AE的长度．②若点P是线段AD上的一个动点，连结PF，将△DFP沿PF所在直线翻折，使得点D的对应点D落在线段BD或线段AB上．直接写出线段AE长的取值范围．。

初三数学26章试题及答案

初三数学26章试题及答案试题一：代数方程1. 解下列方程：\[x^2 - 5x + 6 = 0\]2. 判断方程\[3x^2 + 5x - 2 = 0\]的根的情况。

3. 计算方程\[2x^3 - 4x^2 + x - 6 = 0\]的根。

试题二：几何问题4. 在直角三角形ABC中，∠A=90°，AB=6cm，AC=8cm，求BC的长度。

5. 在矩形PQRS中，若PS=10cm，PR=4cm，求矩形的面积。

6. 圆O的半径为r，点A在圆上，求圆心O到点A的距离。

试题三：函数与图像7. 已知函数\[y = 3x - 2\]，求当x=1时y的值。

8. 画出函数\[y = x^2 - 4x + 4\]的图像，并找出顶点坐标。

9. 判断函数\[y = 2x + 3\]的增减性。

试题四：概率与统计10. 抛一枚均匀硬币两次，求正面朝上一次的概率。

11. 随机抽取10个学生，求至少有3个学生生日在同一个月的概率。

12. 某班有50名学生，其中30名男生，20名女生。

随机抽取一名学生，求抽到女生的概率。

答案：1. 方程\[x^2 - 5x + 6 = 0\]的根为\[x_1 = 2, x_2 = 3\]。

2. 方程\[3x^2 + 5x - 2 = 0\]的判别式\[Δ = 25 + 24 > 0\]，因此有两个不相等的实根。

3. 方程\[2x^3 - 4x^2 + x - 6 = 0\]的根需要使用高次方程的求解方法，这里不提供具体解法，但可以说明存在三个根。

4. 根据勾股定理，BC的长度为\[BC = \sqrt{AB^2 + AC^2} =\sqrt{6^2 + 8^2} = 10cm\]。

5. 矩形的面积为\[面积 = PS \times PR = 10cm \times 4cm =40cm^2\]。

6. 圆心O到点A的距离为半径r。

7. 当x=1时，y的值为\[y = 3 \times 1 - 2 = 1\]。

山东济南中考数学第25题(反比例函数)、第26题、第27题(二次函数)解答题整理试题以及答案

九年级中考数学解答题练习试题一、解答题。

（第25题反比例函数）（x＞0）的图象经过点A（2√3，1），射1、（2014年济南中考）如图1，反比例函数y=kx线AB与反比例函数图象交于另一点B（1，a），射线AC与y轴交于点C，∠BAC=75°，AD⊥y轴，垂足为D．（1）求k的值；（2）求tan∠DAC的值及直线AC的解析式；（3）如图2，M是线段AC上方反比例函数图象上一动点，过M作直线l⊥x轴，与AC 相交于点N，连接CM，求△CMN面积的最大值．2、（2015年济南中考）如图1，点A（8，1）、B（n，8）都在反比例函数y=m（x＞0）x的图象上，过点A作AC⊥x轴，于点C，过点B作BD⊥y轴于点D。

(1)求m的值和直线AB的函数关系式；(2)动点P从O点出发，以每秒2个单位长度的速度沿折线OD﹣DB向B点运动，同时动点Q从O点出发，以每秒1个单位长度的速度沿折线OC向C点运动，当动点P运动到D 时，点Q也停止运动，设运动的时间为t秒．①设△OPQ的面积为S，写出S与t的函数关系式；②如图2，当的P在线段OD上运动时，如果作△OPQ关于直线PQ的对称图形△O’PQ，是否存在某时刻t，使得点Q’恰好落在反比例函数的图象上？若存在，求Q’的坐标和t的值；若不存在，请说明理由．3、（2016年济南中考）如图1，▱OABC的边OC在x轴的正半轴上，OC=5，反比例函数y=m（x＞0）的图象经过点A（1，4）．x（1）求反比例函数的关系式和点B的坐标；（2）如图2，过BC的中点D作DP∥x轴交反比例函数图象于点P，连接AP、OP．①求△AOP的面积；②在▱OABC的边上是否存在点M，使得△POM是以PO为斜边的直角三角形？若存在，请求出所有符合条件的点M的坐标；若不存在，请说明理由．4、（2017年济南中考）如图1，平行四边形OABC的边OC在y轴的正半轴上，OC=3，A(2，1)，反比例函数y=k（x＞0）的图象经过点B．x（1）求点B的坐标和反比例函数的关系式；（2）如图2，直线MN分别与x轴、y轴的正半轴交于M，N两点，若点O和点B关于直线MN成轴对称，求线段ON的长；（3）如图3，将线段OA延长交y=k（x＞0）于点D，过B，D的直线分别交x轴，y轴于xE，F两点，请探究线段ED与BF的数量关系，并说明理由．5、（2018年济南中考）如图，直线y=ax+2与x轴交于点A（1，0），与y轴交于点B（0，b）．将线段AB先向右平移1个单位长度、再向上平移t（t＞0）个单位长度，得到对应线段CD，反比例函数y=k（x＞0）的图象恰好经过C、D两点，连接AC、BD．x（1）求a和b的值；（2）求反比例函数的表达式及四边形ABDC的面积；（3）点N在x轴正半轴上，点M是反比例函数y=k（x＞0）的图象上的一个点，若△xCMN是以CM为直角边的等腰直角三角形时，求所有满足条件的点M的坐标．6、（2019年济南中考）如图1，点A（0，8）、点B（2，a）在直线y＝﹣2x+b上，反比例函数y＝k（x＞0）的图象经过点B．x（1）求a和k的值；（2）将线段AB向右平移m个单位长度（m＞0），得到对应线段CD，连接AC、BD．的值；①如图2，当m＝3时，过D作DF⊥x轴于点F，交反比例函数图象于点E，求DEEF②在线段AB运动过程中，连接BC，若△BCD是以BC为腰的等腰三形，求所有满足条件的m的值．图1 图27、（2020年济南中考）如图，矩形OABC的顶点A、C分别落在x轴、y轴正半轴上，顶点为（2，2√3），反比例函数y=k x （x ＞0）的图象与BC 、AB 分别交于D 、E ，BD=12. （1）求反比例函数表达式和点E 的坐标；（2）写出DE 、AC 的位置关系，并说明理由；（3）点F 在直线AC 上，点G 是坐标系内一点，当四边形BCFG 是菱形，求出点G 的坐标并判断点G 是否在反比例图象上；8、（2021年济南中考）如图，直线y=32x 与双曲线y=kx 交于A 、B 两点，点A 坐标为（m ，﹣3），点C是双曲线第一象限分支上的一点，连接BC并延长交x轴于点D，且BC=2CD。

中考数学第26题试题解析

中考数学第26题试题解析二次函数、一次函数与简单的几何图形相结合的问题是沈阳市中考的必考题.这种类型题的核心就是点坐标与线段长的转化.数学中考试卷的26题灵活的考查了这一内容.下面，我们通过分析这道题，总结出解解决这类题的策略和方法.26.如图，直线y ＝﹣x +4与x 轴交于点B ，与y 轴交于点C ，抛物线y ＝﹣x 2+bx +c 经过B ，C 两点，与x 轴另一交点为A ．点P 以每秒个单位长度的速度在线段BC 上由点B 向点C 运动（点P 不与点B 和点C 重合），设运动时间为t 秒，过点P 作x 轴垂线交x 轴于点E ，交抛物线于点M ．（1）求抛物线的解析式；（2）如图（1），过点P 作y 轴垂线交y 轴于点N ，连接MN 交BC 于点Q ，当＝时，求t 的值；（3）如图（2），连接AM 交BC 于点D ，当△PDM 是等腰三角形时，直接写出t 的值．【试题解析】（1）求抛物线的解析式；分析：第一问属于“双基”的考查，考查的是：已知函数关系式求与坐标轴的交点、用待定系数法求函数关系式.求函数与坐标轴的交点坐标可化归为两个函数求交点的问题，即：把两个函数关系式联立起来求方程组的解.x 轴直线关系式为y ＝0；y 轴直线关系式为x ＝0.解：（1）由⎩⎨⎧=+-=04x x y ，得：⎩⎨⎧==40y x ∴C （0，4）由⎩⎨⎧=+-=04y x y ，得：⎩⎨⎧==04y x ∴B （4，0） ∵抛物线y ＝﹣x 2+bx +c 经过B ，C 两点∴ 解得：∴抛物线解析式为y ＝﹣x 2+3x +4（2）如图（1），过点P 作y 轴垂线交y 轴于点N ，连接MN 交BC 于点Q ，当＝时，求t 的值；分析：第二问灵活地考查了点坐标与线段长的转化.它需要学生理解函数图形定义，掌握平行于坐标轴的线段长的表示方法、三角形相似、转化的数学思想.解题的基本方法是：已知点在函数图象上，常设出这个点的横坐标，用函数关系式表示出这个点的纵坐标；平行于坐标轴的线段长表示方法：若A （A x ，A y ）,B （B x ，B y ），当AB 平行于x 轴时，A B x x AB -=,当AB 平行于y 轴时，A B y y AB -=；对于不平行坐标轴的线段关系通常转化为平行于坐标轴的线段关系.解（2）如图（3）∵B （4，0），C （0，4），∠BOC ＝90°∴OB ＝OC∴∠OBC ＝∠OCB ＝45°∵ME ⊥x 轴于点E ，PB ＝t∴∠BEP ＝90°∴Rt △BEP 中，sin ∠PBE ＝∴BE ＝PE ＝PB ＝t∴x M ＝x P ＝OE ＝OB ﹣BE ＝4﹣t ，y P ＝PE ＝t∵点M 在抛物线上∴y M ＝﹣（4﹣t ）2+3（4﹣t ）+4＝﹣t 2+5t∴MP ＝y M ﹣y P ＝﹣t 2+4t∵PN ⊥y 轴于点N∴∠PNO ＝∠NOE ＝∠PEO ＝90°∴四边形ONPE 是矩形∴ON ＝PE ＝t∴NC ＝OC ﹣ON ＝4﹣t∵MP ∥CN∴△MPQ ∽△NCQ∴∴解得：t 1＝，t 2＝4（点P 不与点C 重合，故舍去）∴t 的值为（3）如图（2），连接AM 交BC 于点D ，当△PDM 是等腰三角形时，直接写出t 的值．分析：第三问在第二问考查方法的基础上，融入了分类讨论的思想.等腰三角形没明确谁是腰谁是底的情况下，让三条边两两相等分三种情况讨论.解（3）∵∠PEB ＝90°，BE ＝PE∴∠BPE ＝∠PBE ＝45°∴∠MPD ＝∠BPE ＝45°①若MD ＝MP ，则∠MDP ＝∠MPD ＝45°∴∠DMP ＝90°，即DM ∥x 轴，与题意矛盾②若DM ＝DP ，如图（4），则∠DMP ＝∠MPD ＝45°∵∠AEM ＝90°∴AE ＝ME∵y ＝﹣x 2+3x +4＝0时，解得：x 1＝﹣1，x 2＝4∴A （﹣1，0）∵由（2）得，x M ＝4﹣t ，ME ＝M y ＝5t +t ﹣2∴AE ＝4﹣t ﹣（﹣1）＝5﹣t∴5﹣t ＝﹣t 2+5t解得：t 1＝1，t 2＝5（0＜t ＜4，舍去）③若MP ＝DP ，则∠PMD ＝∠PDM解法一：如图（5），记AM 与y 轴交点为F ，过点D 作DG ⊥y 轴于点G∴∠CFD ＝∠PMD ＝∠PDM ＝∠CDF∴CF ＝CD∵A （﹣1，0），M （4﹣t ，﹣t 2+5t ），设直线AM 解析式为y ＝ax +m∴解得：∴直线AM ：y ＝tx +t∴F （0，t ）∴CF ＝OC ﹣OF ＝4﹣t∵tx +t ＝﹣x +4，解得：x ＝∴DG ＝x D ＝ ∵∠CGD ＝90°，∠DCG ＝45°∴CD ＝DG ＝∴4﹣t ＝解得：451>=t （舍），122-=t综上所述，当△PDM 是等腰三角形时，t ＝1或t ＝﹣1．解法二：如图（6），过点A 作AH ⊥x 轴交直线BC 于点H ，则AH ∥ ME.∴∠HAD ＝∠PMD ＝∠PDM ＝∠HDA∴AH ＝HD∵A （﹣1，0），B （4，0）∴AB =5∵∠HAB ＝90°，∠HBA ＝45°∴AH ＝HD=AB=5,HB=2522=+HB AH由（2）得，PB ＝t ，MP ＝y M ﹣y P ＝﹣t 2+4t∴DP=HB-HD-BP=t 2525--∵MP ＝DP∴t t t 425252+-=--解得：451>=t （舍），122-=t综上所述，当△PDM 是等腰三角形时，t ＝1或t ＝﹣1．【反思与总结】本题在考查坐标系中线段关系方面比较灵活，对于不平行坐标轴的线段关系，需要根据具体情况转化到适当的位置。

中考数学狙击重难点系列专题26----双反比例函数图像与几何图形综合(含答案)

双反比例函数图像与几何图形综合1. 如图，直角三角形的直角顶点在坐标原点，∠OAB=30°，若点A在反比例函数y= （x＞0）的图象上，则经过点B的反比例函数解析式为（）A. y=﹣B. y=﹣C. y=﹣D. y=2. 如图，点A在双曲线y= 上，点B在双曲线y= （k≠0）上，AB∥x轴，分别过点A、B向x轴作垂线，垂足分别为D、C，若矩形ABCD的面积是8，则k的值为（）A. 12B. 10C. 8D. 63. 如图，在平面直角坐标系中，∠AOB=90°，∠OAB=30°，反比例函数的图象经过点A，反比例函数的图象经过点B，则下列关于m，n的关系正确的是（）A. m=﹣3nB.C.D.4. 如图，在x轴上方，∠BOA=90°且其两边分别与反比例函数y=﹣、y= 的图象交于B、A两点，则∠OAB的正切值为（）A. B. C. D.5. 如图，∠AOB=90°，且OA，OB分别与反比例函数y= （x＞0）、y=﹣（x＜0）的图象交于A，B 两点，则tan∠OAB的值是（）A. B. C. 1 D.6. 如图，A，B两点在反比例函数y= 的图象上，C、D两点在反比例函数y= 的图象上，AC⊥x轴于点E，BD⊥x轴于点F，AC=2，BD=3，EF= ，则k2﹣k1=（）A. 4B.C.D. 67. 如图，点是反比例函数（是常数，）上的一个动点，过点作轴、轴的平行线交反比例函数（为常数，）于点、．当点的横坐标逐渐增大时，三角形的面积( )A. 先变大再变小B. 先变小再变大C. 不变D. 无法判断8. 如图，过y轴上任意一点P，作x轴的平行线，分别与反比例函数y＝−和y＝的图象交于A点和B点，若C为x轴上任意一点，连接AC，BC，则△ABC的面积为（）A. 3B. 4C. 5D. 69. 如图，点A在反比例函数(x>0)的图象上，点B在反比例函数的图象上，AB⊥x 轴于点M，且AM：MB=1：2，则k的值为（）A. 3B. ﹣6C. 2D. 610. 如图，已知点A 、B分别在反比例函数（），-（）的图象上，且OA⊥OB ，则的值为（）A. B. 2 C. D. 411. 如图，直线l⊥x轴于点P，且与反比例函数y1= （x＞0）及y2= （x＞0）的图象分别交于点A，B，连接OA，OB，已知△OAB的面积为2，则k1﹣k2的值为（）A. 2B. 3C. 4D. ﹣412. 如图，在平面直角坐标系中，已知直线（）分别交反比例函数和在第一象限的图象于点，，过点作轴于点，交的图象于点，连结．若BDO是等腰直角三角形，则的值是________．13. 如图，在平面直角坐标系中，有一宽度为1的长方形纸带，平行于y轴，在x轴的正半轴上移动，交x轴的正半轴于点A、D，两边分别交函数y1＝（x＞0）与y2＝（x＞0）的图像于B、F和E、C，若四边形ABCD是矩形，则A点的坐标为________．14. 如图，是反比例函数和（＜）在第一象限的图象，直线AB∥x轴，并分别交两条曲线于A、B两点，若，则的值为________。

中考数学核心26题答题技巧

中考数学核心26题答题技巧中考数学是学生们备战中考的重中之重，数学作为中考的一项必考科目，对学生的综合能力和数学基础要求较高。

其中，中考数学核心26题是考察学生数学基础知识和解题能力的重要部分。

为了帮助学生们更好地备战中考数学核心26题，以下将介绍一些答题技巧，希望对同学们有所帮助。

首先，对于中考数学核心26题中的选择题，学生在答题时要注意以下几点。

首先，要认真审题，理解题意，确保自己理解题目的要求。

其次，要注意排除干扰项，避免被题目中的干扰项所迷惑。

另外，对于不确定的题目，可以采取排除法，将一些明显错误的选项排除，增加答对的几率。

此外，要注意在有限的时间内迅速做出选择，不要过多地纠结在某一道题目上，以免耽误时间。

其次，对于中考数学核心26题中的填空题，学生在答题时也要注意一些技巧。

首先，要注意对题目中的数据进行整理，明确题目的要求，确保填入的答案是符合题意的。

其次，要注意对题目中的运算符号和计算过程进行细致的分析，避免因为计算错误而导致填空错误。

另外，对于填空题，可以适当利用选项进行辅助，将选项代入题目中进行验证，增加填空题答对的几率。

此外，对于中考数学核心26题中的解答题，学生在答题时也要注意一些技巧。

首先，要注意审题，理清题目的思路，确保自己明白题目的要求。

其次，要注意列出解题步骤，将解题思路进行清晰的展现，以便检查和修改答题过程中的错误。

另外，要注意在解答题中，要对题目中的数据和条件进行合理的利用，准确解题，确保答案的准确性。

总的来说，中考数学核心26题的答题技巧主要包括对题目的认真审题，对题目的要求进行明确理解，对题目中的数据和条件进行合理的分析，对题目中的计算和解题过程进行逻辑性的推理，以及在有限的时间内高效地解题。

希望同学们在中考数学的备考过程中，能够灵活运用这些答题技巧，取得优异的成绩。

祝愿大家在中考中取得理想的成绩，顺利进入理想的高中，为未来的学业道路打下坚实的基础。

加油，同学们！。

初中数学试题分析中考数学第26题

一道中考数学题的分析与思考----- 中考数学第26题2019年葫芦岛中考数学第26题是一道基于二次函数与一次函数为背景，加入了几何中的动点问题，相似三角形的性质和等腰三角形的判定的综合性试题。

同时考查了数形结合思想，分类讨论思想和运动变化等数学思想。

这道题会给学生一种似曾相识的感觉，因为动点问题，等腰三角形分类讨论问题在平时训练中都遇到过，所以要求学生能动中求静，分类讨论时能从简单入手。

此题有三个小问难度是逐渐增加，最后的三种情况分类讨论体现了中考试卷的拔高功能。

现在我们逐问分析（1）求抛物线的解析式；【解】：（1）直线y ＝﹣x +4中，令x ＝0时，y ＝4∴C （0，4）令y ＝0时，解得：x ＝4∴B （4，0）又∵抛物线y ＝﹣x 2+bx +c 经过B ，C 两点∴ 解得：∴抛物线解析式为y ＝﹣x 2+3x +4〖考点分析〗：此小题考查学生直线与两个坐标轴的交点求法和待定系数法求解析式，所以学生是比较容易上手的。

（2）如图①，过点P 作y 轴垂线交y 轴于点N ，连接MN 交BC 于点Q ，当分析：由MP ∥CN ，可知△MPQ ∽△NCQ, 就可以把转化为MP CN，而MP 和CN＝时，求t 的值；【解】：（2）∵B （4，0），C （0，4），∠BOC ＝90°∴OB ＝OC ＝4∴∠OBC ＝∠OCB ＝45°∵ME ⊥x 轴于点E ，PB ＝t ∴∠BEP ＝90°∴Rt △BEP 中，sin ∠PBE ＝∴BE ＝PE ＝PB ＝t∴M x ＝P x ＝OE ＝OB ﹣BE ＝4﹣t ，P y ＝PE ＝t∵点M 在抛物线上∴ M y ＝﹣（4﹣t ）2+3（4﹣t ）+4＝﹣t 2+5t∴MP ＝M y ﹣P y ＝﹣t 2+4t又由题意可知四边形ONPE 是矩形∴ON ＝PE ＝t∴NC ＝OC ﹣ON ＝4﹣t∵MP ∥CN∴△MPQ ∽△NCQ∴∴，即t 1＝，t 2＝4（点P 不与点C 重合，故舍去） ∴t 的值为〖考点分析〗：此小题表面上是动点问题，实际上是“动中有静”，不需要学生动态思考点P ，而是直接用图①静态图即可解决。

中考数学考点总动员系列专题：26 三角形(含解析)

考点二十六：三角形聚焦考点☆温习理解一、三角形1、三角形中的主要线段（1）三角形的一个角的平分线与这个角的对边相交,这个角的顶点和交点间的线段叫做三角形的角平分线。

（2）在三角形中,连接一个顶点和它对边的中点的线段叫做三角形的中线。

（3）从三角形一个顶点向它的对边做垂线,顶点和垂足之间的线段叫做三角形的高线（简称三角形的高）。

2、三角形的三边关系定理及推论（1）三角形三边关系定理：三角形的两边之和大于第三边。

推论：三角形的两边之差小于第三边。

（2）三角形三边关系定理及推论的作用：①判断三条已知线段能否组成三角形②当已知两边时,可确定第三边的范围。

③证明线段不等关系。

3、三角形的内角和定理及推论三角形的内角和定理：三角形三个内角和等于180°。

推论：①直角三角形的两个锐角互余。

②三角形的一个外角等于和它不相邻的来两个内角的和。

③三角形的一个外角大于任何一个和它不相邻的内角。

注：在同一个三角形中：等角对等边；等边对等角；大角对大边；大边对大角。

二、全等三角形1、三角形全等的判定三角形全等的判定定理：（1）边角边定理：有两边和它们的夹角对应相等的两个三角形全等（可简写成“边角边”或“SAS”）（2）角边角定理：有两角和它们的夹边对应相等的两个三角形全等（可简写成“角边角”或“ASA”）（3）边边边定理：有三边对应相等的两个三角形全等（可简写成“边边边”或“SSS”）。

直角三角形全等的判定：对于特殊的直角三角形,判定它们全等时,还有H L 定理（斜边、直角边定理）：有斜边和一条直角边对应相等的两个直角三角形全等（可简写成“斜边、直角边”或“HL ”） 2.全等三角形的性质：三、等腰三角形1、等腰三角形的性质定理及推论：定理：等腰三角形的两个底角相等（简称：等边对等角）推论1：等腰三角形顶角平分线平分底边并且垂直于底边。

即等腰三角形的顶角平分线、底边上的中线、底边上的高重合。

推论2：等边三角形的各个角都相等,并且每个角都等于60°。

广西南宁历年中考数学代几综合压轴题(第26题)

历年中考第26题（2004年—2012年）（2004年）26某生活小区的居民筹集资金1600元，计划在一块上、下底分别为10m ，20m 的梯形空地上种植花木（如图10-1）（1）他们在△AMD 和BMC 地带上种植太阳花，单价为8元/m 2，当△AMD 地带种满花后（图10-1中阴影部分），共花了160元，请计算种满△BMC 地带所需的费用.（2）若其余地带要种的有玫瑰和茉莉花两种花木可供选择，单价分别为12元/m 2和10元/m 2，应选择种哪种花木，刚好用完所筹集的资金？（3）若梯形ABCD 为等腰梯形，面积不变（如图10-2），请你设计一种花坛图案，即在梯形内找到一点P ，使得△APB ≌△DPC 且S △APD = S △BPC ，并说出你的理由.考点：相似三角形的应用；梯形．专题：压轴题．分析：（1）由太阳花的单价和钱数可先求出△AMD 的面积，再由AD ∥BC 证出△AMD ∽△CMB ，根据相似三角形面积之比等于相似比的平方，得出△BMC 的面积，从而算出所要花费的钱数；（2）由△AMD ∽△CMB ，根据相似三角形对应高的比等于它们的相似比，可求出两三角形AD 与BC 边上的高之比，再根据三角形的面积公式可求出AD 边上的高，从而可求出整个梯形的高及面积．进而求出三角形AMB 和三角形DCM 的面积和，然后根据两种花的单价来计算哪种花合算；（3）由（2）可知整个梯形高为12，要保证△APB ≌△DPC 且S △APD =S △BPC ，P 点必须在AD 和BC 的垂直平分线上，且P 到AD 的距离是P 到BC 距离的2倍，即到AD 的距离应该为8．（2005年） 26. OABC是一张放在平面直角坐标系中的矩形纸片，O 为原点，点A 在x 轴上，点C 在y 轴上，OA=10，OC=6。

（1）如图所示，在AB 上取一点M ，使得△CBM 沿CM 翻折后，点B 落在x 轴上，记作B’点，求B’点的坐标；（2）求折痕CM 所在直线的解析式；（3）作B’G//AB 交CM 于点G ，若抛物线y x m =+162过点G ，求抛物线的解析式，并判断以原点O 为圆心，OG 为半径的圆与抛物线除交点G 外，是否还有交点？若有，请直接写出交点的坐标。

2017年南京中考数学第26题详解

2017年南京市中考数学第26题详解
已知函数m x m x y +-+-=)1(2（m 为常数）．
（1）该函数的图像与x 轴公共点的个数是（）
A ．0
B ．1
C ．2
D ．1或2
（2）求证：不论m 为何值，该函数的图象的顶点都在函数2)1(+=x y 的图象上；
（3）当－2≤m ≤3时，求该函数的图象的顶点纵坐标的取值范围．
解：（1）△＝m m 4)1(2+-＝m m m 4122++-＝122++m m ＝2)1(+m ． ∵2)1(+m ≥0， 0)1(2=+-+-m x m x 有两个实数根，
∴抛物线m x m x y +-+-=)1(2与x 轴的公共点的个数是1或2．∴选D ．
（2）∵顶点坐标为)4
)1(,212
+-m m （，把2
1-=m x 代入2)1(+=x y ，得4)1(2+=m y ， ∴不论m 为何值，该函数的图象的顶点都在函数2)1(+=x y 的图象上；
（3）∵顶点的纵坐标为4)1(2+m ，设4
)1(2
+=m z ．画出z 关于m 的函数的图象如答图，结合图象可得：
当m ＝－1时，z 有最小值是0;
当m ＝－2时，41=z ; 当m ＝3时，4=z ．
∴当－2≤m ≤3时，求该函数的图象的顶点纵坐标z 的取
值范围是0≤z ≤4．．
第26题答图。