第04讲 角度计算(含解答)
角度的计算方法

角度的计算方法在日常生活和工作中,我们经常需要计算各种角度,比如建筑设计、工程测量、数学几何等领域都需要用到角度的计算。
本文将介绍角度的计算方法,希望能够帮助大家更好地理解和运用角度的计算。
首先,我们来介绍一下角度的基本概念。
角度是用来衡量两条射线之间夹角大小的单位,通常用度(°)来表示。
一个完整的圆360°,因此角度的计算范围是0°到360°之间。
在实际计算中,我们常常会遇到角度的加减、角度的转换、角度的比较等问题,下面我们将分别介绍这些计算方法。
首先是角度的加减计算。
当我们需要计算两个角度的和或差时,可以直接将两个角度的度数相加或相减。
需要注意的是,如果结果超过360°,则需要将结果减去360°,直到结果在0°到360°之间为止。
例如,计算270°和90°的和,直接相加得到360°,即270°+90°=360°。
再举一个例子,计算300°减去150°,直接相减得到150°,即300°-150°=150°。
其次是角度的转换计算。
有时候我们需要将角度的度数转换成弧度制,或者将弧度制转换成度数。
这时候我们可以利用以下公式进行转换,弧度制=度数×π/180°,度数=弧度制×180°/π。
通过这两个公式,可以很方便地进行角度的转换计算。
比如,将60°转换成弧度制,计算公式为60°×π/180°=π/3 rad。
再比如,将5π/4 rad转换成度数,计算公式为5π/4 rad×180°/π=225°。
最后是角度的比较计算。
当我们需要比较两个角度的大小时,可以直接比较它们的度数大小。
需要注意的是,如果两个角度的度数相等,但是它们的起始位置不同,那么它们并不相等。
角度计算(含详细解析)

4-1-3.角度计算知识点拨一、角1、角的定义:自一点引两条射线所成的图形叫角2、表示角的符号:∠3、角的分类:锐角、直角、钝角、平角、周角、负角、正角、优角、劣角、0角这10种(1)锐角:大于0°,小于90°的角叫做锐角。
(2)直角:等于90°的角叫做直角。
(3)钝角:大于90°而小于180°的角叫做钝角。
(4)平角:等于180°的角叫做平角。
(5)优角:大于180°小于360°叫优角。
(6)劣角:大于0°小于180°叫做劣角,锐角、直角、钝角都是劣角。
(7)周角:等于360°的角叫做周角。
(8)负角:按照顺时针方向旋转而成的角叫做负角。
(9)正角:逆时针旋转的角为正角。
(10)0角:等于零度的角。
4、角的大小:角的大小与边的长短没有关系;角的大小决定于角的两条边张开的程度,张开的越大,角就越大,相反,张开的越小,角则越小。
二、三角形1、三角形的定义:由三条边首尾相接组成的封闭图形叫做三角形2、内角和:三角形的内角和为180度;外角:(1)三角形的一个外角等于另外两个内角的和;(2)三角形的一个外角大于其他两内角的任一个角。
3、三角形的分类(1)按角分:锐角三角形:三个角都小于90度。
直角三角形:有一个角等于90度。
钝角三角形:有一个角大于90度。
注:锐角三角形和钝角三角形可统称为斜三角形(2)按边分:不等腰三角形;等腰三角形(含等边三角形)。
模块一、角度计算【例 1】有下列说法:(1)一个钝角减去一个直角,得到的角一定是锐角,(2)一个钝角减去一个锐姥,得到的角不可能还是钝角.(3)三角形的三个内麓中至多有一个钝角.(4)三角形的三个内角中至少有两个锐角. (5)三角形的三个内角可以都是锐角. (6)直角三角形中可胄邕有钝角.(7)25︒的角用10倍的放大镜看就变成了250︒ 其中,正确说法的个数是【考点】角度计算 【难度】3星 【题型】填空 【解析】 几何问题(1)、(3)、(4)、(5)是正确的说法.【答案】(1)、(3)、(4)、(5)是正确的说法【例 2】 下图是3×3的正方形方格,∠1与∠2相比,较大的是_____。
角度计算公式几何图

角度计算公式几何图在数学中,角度是一个非常重要的概念,它在几何图形中起着至关重要的作用。
角度的大小可以通过角度计算公式来求解,这些公式帮助我们理解和计算各种几何图形中的角度大小。
本文将介绍一些常见的角度计算公式,并通过几何图形来演示这些公式的应用。
首先,让我们来了解一下角度的基本概念。
在数学中,角度是两条射线之间的夹角,通常用度(°)作为单位来表示。
一个完整的圆共有360°,而一个直角则是90°。
在几何图形中,我们经常需要计算各种角度的大小,以便解决各种问题。
在三角形中,角度计算公式是非常常见的。
三角形是几何图形中最基本的形状之一,它由三条边和三个角组成。
在三角形中,角度计算公式可以帮助我们求解三角形的各个角度大小。
例如,在直角三角形中,我们可以利用正弦、余弦和正切函数来计算各个角度的大小。
这些函数是三角函数的基本形式,它们可以帮助我们计算三角形中各个角度的大小。
此外,在矩形和平行四边形中,角度计算公式也起着重要的作用。
矩形是一种特殊的四边形,它有四个直角,因此每个角的大小都是90°。
而平行四边形则有两组相对的平行边,它的对角线相交的角度是相等的。
通过角度计算公式,我们可以轻松地求解矩形和平行四边形中各个角度的大小。
除了三角形、矩形和平行四边形,角度计算公式在其他几何图形中也有着广泛的应用。
例如,在圆形中,圆心角和圆周角的大小可以通过角度计算公式来求解。
圆心角是以圆心为顶点的角,它的大小等于其所对的圆弧的长度与半径的比值。
而圆周角则是指圆周上的两条弧所对的角,它的大小等于其所对的圆弧的长度与半径的比值。
在实际应用中,角度计算公式可以帮助我们解决各种几何问题。
例如,在建筑设计中,我们需要计算各种角度的大小来确定建筑物的结构和形状。
在地理测量中,我们需要计算地球表面上各个角度的大小来确定地理位置和方向。
在工程设计中,我们需要计算各种角度的大小来确定机械零件的形状和位置。
角度计算公式

角度计算公式
角度的计算是几何学中的一个重要概念,它可以帮助我们理解两个线段之间的关系以及形状的形状。
角度的计算公式是描述这种关系的关键。
角度的计算公式是使用三角函数计算的,它通过两个线段的长度和夹角的大小来计算出角度。
首先,我们需要计算出两个线段之间的夹角。
夹角是两个线段之间的角度,它由他们的长度决定,夹角小于180度时,角度小于180度,而大于180度时,角度大于180度。
然后,我们需要使用三角函数来计算角度的大小,它的基本公式是:角度=sin(夹角)/长度。
这个公式表明,夹角和长度共同决定角度的大小。
此外,我们还可以使用反三角函数来求解角度的大小,它的基本公式是:角度=sin-1(夹角)/长度。
这个公式表明,夹角和长度共同决定角度的大小,反三角函数可以从夹角和长度中求出角度。
最后,我们还可以使用三角不等式来计算角度的大小,它的基本公式是:角度<夹角/长度。
这个公式表明,夹角和长度共同决定角度的大小,但是角度的大小不一定等于夹角和长度的乘积。
总之,角度的计算公式是利用三角函数、反三角函数和三角不等式
来计算角度大小的公式,它们都使用夹角和长度来决定角度的大小。
人教版高中化学同步精品讲义(必修一)第04讲 1.4离子反应——离子方程式(含答案解析)
_______________的反应。
1
【答案】
1.
BaCl2 和 Na2SO4 的电离方程式 BaCl2=Ba2++2Cl-、Na2SO4=、SO24-+2Na+
混合前两种溶液中的离子 Ba2+、Cl- Na+、SO24-
混合后数目减少的离子
Ba2+、SO24-
混合后数目不变的离子
Na+、Cl-
3.(2022 年江西省九校期中联考)下列离子方程式改写成化学方程式正确的是
A.Mg2++2OH-=Mg(OH)2↓ B.CO32-+2H+=CO2↑+H2O C.Cl-+Ag+=AgCl↓ D.CO2+2OH﹣=CO32-+H2O
MgCl2+2NaOH=Mg(OH)2↓+2NaCl CaCO3+2HCl=CaCl2+CO2↑+H2O AgNO3+HCl=AgCl↓+HNO3 CO2+Ca(OH)2=CaCO3↓+H2O
第 4 课 离子反应——离子方程式
01
学习目标
1.通过 BaCl2 溶液与 Na2SO4 溶液反应的探究,认识离子反应的本质。 2.通过分析酸、碱、盐之间的反应事实,认识复分解反应离子反应发生的条件。 3.会书写常见反应的离子方程式,能判断给定反应的离子方程式正误。
02
预习导学
自主梳理
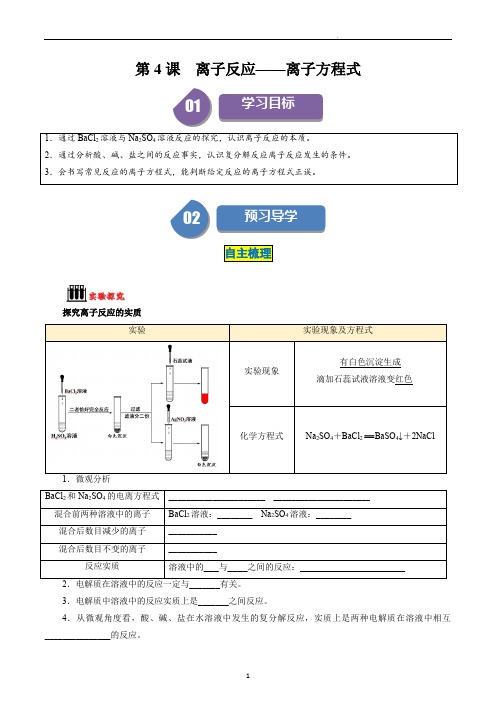
探究离子反应的实质 实验
实验现象及方程式
实验现象
有白色沉淀生成 滴加石蕊试液溶液变红色
化学方程式
Na2SO4+BaCl2=BaSO4↓+2NaCl
1.微观分析
BaCl2 和 Na2SO4 的电离方程式 ______________________ ______________________
混合前两种溶液中的离子 BaCl2 溶液:________ Na2SO4 溶液:________
小学数学四年级讲义:角度计算(精编)

小学数学四年级讲义:角度计算[解题方法和技巧]一.角及其分类:1、角可以分为锐角、直角、钝角、平角、周角。
锐角:大于0°,小于90°的角叫做锐角。
直角:等于90°的角叫做直角。
钝角:大于90°而小于180°的角叫做钝角。
平角:等于180°的角叫做平角。
周角:等于360°的角叫做周角。
2、对顶角:两条直线相交后所得的只有一个公共顶点且两个角的两边互为反向延长线,这样的两个角叫做互为对顶角。
两条直线相交,构成两对对顶角。
互为对顶角的两个角相等。
3、余角和补角:两角之和为90°则两角互为余角,两角之和为180°则两角互为补角。
等角的余角相等,等角的补角相等二、三角形的外角:1、定义:三角形的一条边与另一条边的反向延长线组成的角,叫做三角形的外角。
2、性质:三角形的一个外角等于与它不相邻的两个内角的和。
.三角形的一个外角大于与它不相邻的任一内角.三、折叠图形性质:折叠前后重叠部分完全重合(对应角,对应边,面积相等)[题型一:线与角求角度计算][模型例题1.]如图,直线AB⊥CD于点O,EF为过点O的一条直线。
(1)写出图中与∠1互余的角;(2)若∠2=30°,求∠AOE的度数.答案:(1)∠COE,∠2.(2)120°。
解析:(1)和为90°的两个角互余,故∠COE与∠1互余,又∠2与∠COE为对顶角,相等,故也与∠1互余。
(2)∠2与∠COE为对顶角,相等,故∠AOE=∠AOC+∠COE=90°+30°=120°。
[参照模型做练习1]1.如图1所示,直线AB,CD相交于点O,OE⊥AB,那么下列结论错误的是()A.∠AOC与∠COE互为余角B.∠BOD与∠COE互为余角C.∠COE与∠BOE互为补角D.∠AOC与∠BOD是对顶角2.如图所示,直线AB,CD相交于点O,∠BOE=90°,若∠COE=55°,求∠BOD的度数。
第04讲--相对运动

解:
v
A地
v轮地
v A轮
r
v轮地
(水平向左)
v轮A ? vA地 ?
(向切线右上) (竖直向上)
vA地 v轮地 tan r tan
• 一辆邮车以u=lOm/s旳速度沿平直公路匀速 行驶.在离此公路d=50m处有一种邮递员, 当他与邮车旳连线和公路旳夹角为α=tg-1(1/4) 时开始沿直线匀速奔跑.已知他奔跑旳最大 速度为5m/s.试问:
a杆地 at an a柱地
①
①式旳矢量图如图所示.将①式中旳各矢量向半径方向
上投影,可得
a杆地 cos a柱地 sin an
a杆地
a柱地
• tan
v2
R cos2
1
cos
a
tan
R
v2 cos3
此措施主要!
一种线轴,轮和轴旳半径分别为R和r,目前已 v旳速度将缠绕在轴上旳线水平拉出,已知线轴 和地面之间无滑动,求:线轴
d
v v2 tan
d2 x2 x d
解2: AB L t ,L x2 d 2
BC vOM t , AC vAB t
可得和解1相同成果
• 例:
• 如图所示,在xy平面上有两个半径均为R旳圆, 左圆圆心固定在坐标原点O,右圆圆心O’沿x 轴以速度v0作匀速直线运动,t=O时刻两圆心 重叠,试求两圆交点之一P点旳速率v和向心加 速度an、切向加速度at各与时间t旳关系。
1.列式
V雨人 V雨地 V地水 V水人
A
V地水 V水地
V水人 V人水
2。作图:如右图
,
3。计算
BD DC 2 BC 2 32 42 5m / s AD AB 2 BD 2 102 52 5 5m / s
如何进行角度的四则运算

如何进行角度的四则运算在数学中,角度的四则运算是一个基础且常见的概念。
准确地进行角度的加减乘除运算,对于解决各类问题以及应用到实际生活中具有重要意义。
本文将介绍如何进行角度的四则运算,以帮助读者理解和掌握这一重要技巧。
一、角度的定义与表示方法在开始讨论角度的四则运算之前,首先需要理解角度的定义与表示方法。
简单来说,角度是由两条射线共享一个公共端点而形成的,其度量通常用度数、弧度或百分度来表示。
1. 度数表示法(degree)度数是角度最常用的表示方法。
一个完整的圆共有360°,而半个圆则是180°。
2. 弧度表示法(radian)弧度是另一种角度度量方式,常用于高级数学和物理等领域。
一个完整的圆共有2π弧度,而半个圆则是π弧度。
3. 百分度表示法(grade)百分度是一种不常用的角度度量方式,通常用于测量角度时较小的误差,将一个完整的圆等分为400份。
二、角度的加减运算要进行角度的加法和减法运算,我们需要记住以下两个基本原则:1. 角度的和等于它们的顺时针或逆时针旋转所得到的角度之和。
例如,30° + 60° = 90°,30° - 60° = -30°。
2. 角度的差等于它们的顺时针或逆时针旋转所得到的角度差。
例如,120° - 60° = 60°,60° - 120° = -60°。
当进行角度的加减运算时,我们可以按照以下步骤进行:1. 将所有角度转换为同一种度量方式,通常选择度数制。
2. 将两个角度按照运算规则进行计算,得到结果。
3. 如果结果超过360°或小于0°,则进行相应的调整,使其落在0°到360°之间。
三、角度的乘除运算角度的乘除运算则略微复杂一些,需要记住以下几个关键点:1. 角度的乘法:两个角度的乘积等于它们的弧度乘积(或百分度乘积)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
九年级数学竞赛专题第四讲角度计算一、选择题1.如图1,在△ABC中,∠,∠B的外角平分线分别交对边CB、AC的延长线于D、E,且AD=AB=BE,则∠A的度数是()A.10°B.11°C.12°D.14°(1) (2) (3)2.如图2,P是等边三角形ABC内一点,∠APB,∠BPC,∠CPA的大小之比为5:6:7,则以PA,PB,PC为边的三角形三内角大小之比(从小到大)是()A.2:3:4 B.3:4:5 C.4:5:6 D.以上结果都不对3.如图3,四边形ABCD是正方形,以CD为边作等边三角形CDE,BE与AC相交于点M,则∠AMD的度数是()A.75°B.60°C.54°D.67.5°4.如图4,在△ABC中,AD是BC边上的中线;∠ADB,∠ADC的平分线各交AB,AC 于M,N,MN交AD于P,连结PB,PC,则∠BPC是()A.锐角B.直角C.钝角D.以上都可能(4) (5) (6)5.如图5,点P是正方形ABCD内的一点,若PA=a,PB=2a,PC=3a,(a>0),那么∠APB 的大小是()A.100°B.120°C.135°D.150°二、填空题1.已知一个凸十一边形由若干个边长为1的等边三角形和边长为1的正方形无重叠,无间隙拼成,则该凸十一边形的各内角中,最小的内角大小为____________。
2.如图6,在等腰直角三角形ABC中,∠A=90°,P是△ABC内一点,PA=1,PB=3,PC=7,那么∠CPA=_____________.3.如图7,直角三角形ABC中,∠C=90°,BC被点D、E三等分,且BC=3AC,那么∠AEC+∠ADC+∠ABC=_____________。
(7) (8) (9)4.如图8,等腰三角形ABC中,AB=AC,∠A=20°,D是AB边上一点,AD=BC,连结CD,那么∠BDC的大小是__________。
5.已知:如图9,△ABC中,AC=BC,∠ACB=80°,O为△ABC内一点,∠OAB=10°,∠OBA=30°,那么∠ACO=____________。
三、解答题1.如图,在△ABC中,∠B=90°,M为AB上一点,使得AM=BC,N为BC上一点,使得CN=BM,连结AN,CM相交于点P,试求∠APM的度数。
2.如图,四边形ABCD中,∠DAB=∠CBA,∠CDA=90°,∠BCD=78°,AB=2AD,求∠CAD的度数。
3.如图,梯形ABCD 中,AB ∥CD ,∠D=90°,M 为BC 上一点,且BM=MC=DC ,∠DAM=50°,求∠AMC 的度数。
4.△ABC 中,AD 是△BAC 的角平分线,且有ACABAD111+=,求∠BAC 的度数。
5.如图,正方形被两条与边平行的线段EF ,CH 分割成四个小矩形,P 是EF 与CH 的交点,若矩形PFCH 的面积恰是矩AGPE 面积的2倍,试确定∠HAF 的大小并证明你的结论。
答案 一、选择题 1.C 2.A 3.B 4.C 5.C解答:1. 如图,设∠BAC=x °,则∠BAD=21(180°- x °)∵∠1=21(180°- ∠BAD) = 45°+ 4︒x∠2 = 21∠1 =21( 45°+4︒x ),且∠2 = ∠BAE + ∠E = 2x °,∴21( 45°+ 4︒x )= 2x °解之得 x = 12 即∠BAC=12°2. 如图,将△APB 绕A 点反时针旋转60°得△A 'P C ,显然有△A 'P C ≌△APB ,连P 'P .∵A 'P =AP ,∠'P AP=60°,∴△A 'P P 是等边三角形, ∴P 'P =AP , ∵'P C=PB ,∴△'P CP 的三边长分别为PA ,PB ,PC ,∵∠APB + ∠BPC + ∠CPA = 360°,∠APB :∠BPC :∠CPA=5:6:7,∴∠APB=100°,∠BPC=120°,∠CPA=140°,∴∠P 'P C=∠A 'P C - ∠A 'P P = ∠APB - ∠A 'P P = 100° - 60°= 40° ∠P 'P C=∠APC - ∠AP 'P = 140° - 60°= 80°, ∠PC 'P = 180°- (40°+80°)= 60° ∴∠P 'P C :∠PC 'P :∠'P PC = 2:3:4 3. 如图,连结BD∵∠BCE = ∠BCD + ∠DCE = 90°+60° = 150°,BC=EC , ∴∠EBC=∠BEC=21(180°-∠BCE )=15°∵∠BCM=21∠BCD = 45°,∴∠BMC=180°- (∠BCM +∠EBC )=120°, ∴∠AMB=180°- ∠BMC = 60°∵AC 是线段BD 的垂直平分线,M 在AC 上, ∴∠AMD=∠AMB = 60° 4. 如图,在三角形ABC 中,DM 平分∠BDA ,所以AD :DB=AM :MB 同理AD :DC=AN :NC , 又BD=DC ,所以AM :MB=AN :NC , 所以MN ∥BC所以∠1=∠2=∠3所以PM=PD ,同理PD=PN 所以PM=PN=PD又PM :BD=AP :AD<1, 所以BD>PD所以∠BPD>∠PBD 同理∠CPD>∠PCD所以∠BPC=∠BPD+∠DPC>∠PBD+∠PCD=∠BPM+∠CPN 所以∠BPC>90°,所以∠BPC 是钝角5. 如图,将三角形APB 绕B 点旋转90°得:三角形CPB ,连结PQ 、AC ,则:△CPQ ≌△APB因为∠PBQ=90°,PB+QB=2a ,所以∠PQB=∠BPQ=45°,PQ=22a所以2PC =CQ 2+PQ 2, 所以∠PQC=90° 所以∠APB=∠CQB=∠PQB+∠PQC=135°二、填空题 1.120°; 2.135°; 3.90°; 4.30°; 5.70°; 解答:1.设此凸十一边形的各个内角中有x 个60°,y 个90°角,z 个120°角,t 个150°角,则⎩⎨⎧︒⋅-=+++=+++180)211(150120906011t z y x t z y x消去t 得:3x + 2y + z = 1 因为x,y,z 均为非负整数,所以x = y = 0, z = 1, 所以t = 10.由这个凸十一边形有一个角是120°,其余十个内角均为150°,所以,此凸十一边形中最小内角为120°2.如图,作△ACQ ≌△ABP ,连结PQ ,则AQ=AP=1,CQ=AB=3,∠QAC=∠PAB ,又因为∠PAB+∠PAC=90°,所以∠PAQ=∠QAC+∠CAP=∠PAB+∠PAC=90°所以PQ 2AQ 2+AP 2=2,且∠QPA=45° 在△CPQ 中,PC 2+PQ 2=7+2=9=CQ 2所以∠QPC=90° 所以∠CPA=∠QPA+∠QPC=135°3.如图,以BC 为边作正方形BCMN ,在MN 上取点P 、Q ,使MP=PQ=QN ,连结AP ,PD ,DQ ,则有AM=CD ,MP=AC ,△ACB ≌△PQD ,易得△APM ≌△DCA所以AP=AD 且∠DAC+∠PAM=90°, 即△APD 是等腰直角三角形所以∠ABC+∠ADC=∠PDQ+∠ADC =90°- ∠ADP=90°- 45°= 45° 又由题意知∠AEC=∠EAC=45° 所以∠AEC+∠ADC+∠ABC=90°4.如图,作△AED ≌△BAC ,连结EC ,则∠AEC=∠BAC=20°,∠DAE=∠ADE=∠B=∠°ACB=80°, 所以∠CAE=∠DAE-∠BAC=80°- 20°= 60°又因为AE=AB=AC ,所以△ACE 是一个等边三角形 所以∠DEC=∠AEC-∠AEC=40° 所以∠EDC=21(180°- ∠DEC )=70°所以∠BDC=180°- (∠ADE+∠EDC )=30° 6. 如图,作正△CAQ ,连结BQ ,依题意易得:∠BAQ=60°- 50°=10°=∠OAB ; ∠QCB=80°-60°=20°; CQ = CA = CB所以∠CBQ=80°,∠ABQ = ∠CBQ - ∠CBA = 80°-50°=30°, 所以∠ABQ=∠OBA ,所以△OAB ≌△QAB ,所以AO = AQ = AC 而∠CAO=50°-10°=40°, 所以∠ACO=21(180°-40°)=70°三、解答题1. 解:如图,过A 作AB 的垂线,在其上截取AK=CN=MB ,连KM ,KC ,则因为AM=BC ,AK=BM ,∠KAM=∠B=90°, 所以△KAM ≌△MBC ,所以KM=CM ,∠AMK=∠MCB因为∠CMB+∠MCB=90°,所以∠CMB+∠AMK=90° 所以 ∠KMC=90°所以△KMC 为等腰直角三角形,∠MCK=45° 又因为△AKC ≌△CAN , 所以∠KCA=∠NAC , 所以KC ∥AN ,所以∠APM=∠KCM=45°2. 如图,在四边形ABCD 中,∠DAB=∠ABC=21(360°-90°-78°)=96°,构造含30°角的直角三角形,在形内作∠DAE=60°,易证∠DAC>60°, 可设AE 交CD 于E,在Rt △ADE中知AE=2AD ,由AB=2AD ,得AE=AB ,故连结BE 得等腰三角形AEB ,且顶角∠EAB=96°-60°=36°, 根据顶角36°的等腰三角形特性,考虑作其底角∠ABE 的角平分线BF 交AE 于F , 则BF 把△ABE 分成两个等腰三角形,AF=BF=BE ,在△BEC 中,已知∠BCE=78°,∠BEC=180°-30°-72°=78°,所以∠BEC=∠BCE ,故AF=BF=BE=BC 。
