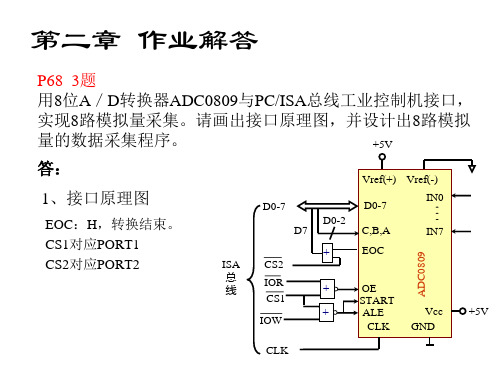
第二章作业解答
第2章_作业 (1)

第二章作业一、单项选择题1、通常以( C )代表时间价值率。
A、通货膨胀补偿率B、风险报酬率C、利息率D、投资利润率2、财务管理的两个基本价值观念是( A )A、时间价值和风险收益B、利润和成本C、风险和利润D、时间价值和成本3、在存本付息的情况下,若想每年都得到利息1000,利率为5%,则现在应存入的本金应为( A )元。
(永续年金的计算问题)A、20000B、50000C、500000D、2000004、一定时期内连续发生在期末的等额支付款项,被称为( B )A、先付年金B、普通年金C、永续年金D、延期年金5、下面有关资金时间价值的表述,正确的是( A )A.资金时间价值的实质是资金周转使用后的增值额B.资金时间价值是推迟消费所获得的报酬C.资金时间价值只能用绝对数来表示D.资金时间价值的量无法进行计量(选择A,严格将来,时间价值是资金周转增值额的一部分,但是因为题目中没有使用“全部”的字样,可以理解为正确;B推迟消费获得的报酬不一定能获得报酬,比如资金不周转的情形。
)6、一项借款,期限一年,年利率8%,按复利计算每半年复利一次,则借款实际利率为( D )A、0.16%B、12.49%C、18.53%D、8.16%(已知名义利率求实际利率的情形)7、永续年金具有下列特征( C )A、每期期初支付B、每期不等额支付C、没有终值D、没有现值8、资金时间价值实质是( B )。
A、资金的自然增值B、资金周转使用后的增值C、不同时间的价值量D、对暂缓消费的报酬9、为在第三年末获得本利和100元,求每年末存入多少资金,计算时应采用(B)。
A、年金现值系数B、年金终值系数C、复利现值系数D、复利终值系数(100元是终值,所以用终值系数计算)10.每年年底存款100元,求第5年末的价值,可用( D )来计算.(终值计算问题)A.PVIF i,n B.FVIF i,n C. PVIFA i,n D.FVIFA i,n11、当利率为10%,计息期为5时,后付年金现值系数为3.791;计息期为6时,后付年金现值系数为4.355,那么利率为10%。
第2章拉压作业参考解答

aEADj + 4.5aEADj = 2aF , Dj = 2F 5.5EA
4. 再由 Hooke 定律:
FN1
=
EADj
=
2F 5.5
=
0.3636F
FN 2
= 1.5EADj
=
1.5´ 2F 5.5
2
(1)图(a)为开槽拉杆,两端受力 F=14kN,b=20mm,b0=10mm,δ=4mm。 (2)图(b)为阶梯形杆,AB 段杆横截面面积为 80mm2,BC 段杆横截面面积为 20mm2, CD 段杆横截面面积为 120mm2。 (3)图(c)为变截面拉杆,上段 AB 的横截面面积为 40mm2,下段 BC 的横截面面积为
DG
=
Dl2
-
2 3
Dl1
-
1 3
Dl3=6.89 ´10-4
m
5
2-15 求附图示圆锥形杆在轴向力 F 作用下的伸长量。弹性模量为 E。
解答 对于截面缓变的圆锥形杆可假设横截面上正应力均匀分布。横截面面积为
A(x)
=
1 4
p [d1l
-
(d1
-
d2 )x]2
/l2
ò ò ò Dl =
l
edx =
FN1
FN3
FN2
D
(2)
(b) 整体分析,示力图见附图(3)。
å M Ai = 0 : FN1 ´1 + 3´ 3´1.5 = 0
FN1 = -13.5kN
FAx A
FAy FN1
B
s1
=
FN 1 A1
=
-13.5 ´103 850 ´10-6
=
-15.88MPa
作业解答第二版
2 F1<0
3 F2<0
4 F3<0
坐标 进给
-x +y +y +y
偏差计算`
F0=0
F1=F0–2X0+1 =–11 F2=F1+2Y1+1 =–10 F3=F2+2Y2+1 =-7
F4=F3+ Y3+1 =–2
坐标计算
X0=6 Y0=0 X1=X0–1=5 Y1=0
X2=5 Y2=Y1+1=1
X3=5 Y3=Y2+1=2
答:(1) 第一象限直线插补程序 设内存中三个单元XE、YE、FM分别存放直线终点横坐标、 终点纵坐标、加工点偏差。
data segment XE DB xe YE DB yz FM DB 0 ZF DB 0
data ends
MOV ADD MOV LAB1:MOV CMP
AL,XE AL,YE CL,AL ;CL存NXY AL,FM AL,00H
1)
(1
z 1)Z
10
s
2
(0.1s
1)
10(1
z
1
)Z
1 s2
0.1 s
0.1 s 10
10(1
z
1
)
(1
z 1 z 1
)
2
0.1
1
1 z
1
0.1 1
1 z 1e101
(1
9z1(1 0.1z1) z1)(1 4.5105
z
1 )
阶跃输入对应 q 1 由被控对象传递函数,得 d 0 由广义对象传递函数,得 v 1, j 1,u 0
修改通道号和计数器 修改采样值缓冲区指针
第二章作业 参考答案
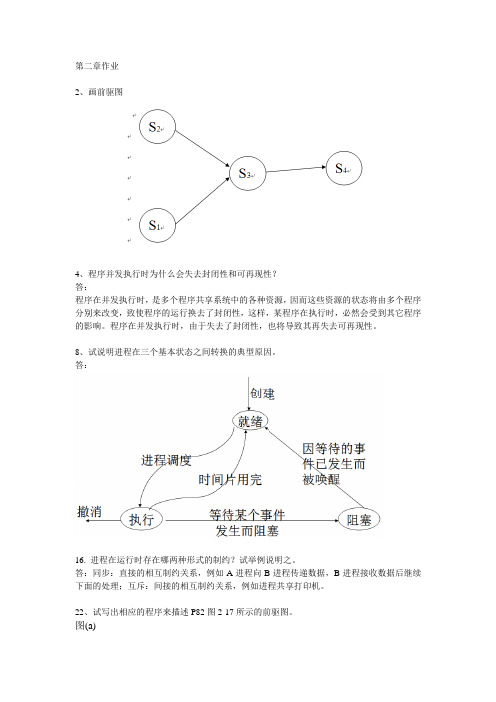
第二章作业2、画前驱图4、程序并发执行时为什么会失去封闭性和可再现性?答:程序在并发执行时,是多个程序共享系统中的各种资源,因而这些资源的状态将由多个程序分别来改变,致使程序的运行换去了封闭性,这样,某程序在执行时,必然会受到其它程序的影响。
程序在并发执行时,由于失去了封闭性,也将导致其再失去可再现性。
8、试说明进程在三个基本状态之间转换的典型原因。
答:16. 进程在运行时存在哪两种形式的制约?试举例说明之。
答:同步:直接的相互制约关系,例如A进程向B进程传递数据,B进程接收数据后继续下面的处理;互斥:间接的相互制约关系,例如进程共享打印机。
22、试写出相应的程序来描述P82图2-17所示的前驱图。
图(a)int a1=0,a2=0,a3=0,a4=0,a5=0,a6=0;a7=0;a8=0;parbeginbegin S1;V(a1);V(a2);end;begin P(a1);S2;V(a3);V(a4);end;begin P(a2);S3;V(a5);end;begin P(a3);S4;V(a6);end;begin P(a4);S5;V(a7);end;begin P(a5);S6;V(a8);end;begin P(a6);P(a7);P(a8);S7;end;parend图(b)int a1=0,a2=0,a3=0,a4=0,a5=0,a6=0;a7=0;a8=0;a9=0;a10=0;parbeginbegin S1;V(a1);V(a2);end;begin P(a1);S2;V(a3);V(a4);end;begin P(a2);S3;V(a5);V(a6);end;begin P(a3);S4;V(a7);end;begin P(a4);S5;V(a8);end;begin P(a5);S6;V(a9);end;begin P(a6);S7;V(a10);end;begin P(a7);P(a8);P(a9);P(a10);S8;end;parend28、在测量控制系统中的数据采集任务,把所采集的数据送一单缓冲区;计算任务从该单缓冲中取出数据进行计算。
第2章作业参考答案

2. 一批晶体管中有个 9 个合格品和 3 个不合格品,从中任取一个安装在电子设备上。若取 出不合格品不再放回,求取得合格品前已取出的不合格品个数的分布律和分布函数。 解:
X0 1 2
3
p 3/4 9/44 9/220 1/220
⎧ 0,
x<0
F (x) = ⎪⎪⎪⎨321/ 4/ ,22,
0≤ x <1 1≤ x < 2
求: (1) 系数 A,B; (2) X 落在区间(-1,1)的概率; (3) X 的概率密度。 解:
x∈R
7. 从一批子弹中任意抽出 5 发试射,若没有一发子弹落在靶心 2 厘米以外,则接受该批子 弹。设弹着点与靶心的距离 X(厘米)的概率密度为
f
(
x)
=
⎪⎧ ⎨
Axe−
x2
,
⎪⎩ 0,
0< x<3 其他
X
~
B
⎛ ⎜⎝
4,
1 5
⎞ ⎟⎠
, 故分布律为
P( X = k) = C4k (0.2)k (0.8)4−k , k = 0,1, 2, 3, 4
( ) (2)P X = k
=
C5k
*
C 4− 20
k
C245
k = 0,1,2,3,4
5. 临床观察表明,某药物产生副作用的概率为 0.002。现在 900 个患者服用该药物,求至 少有3例患者出现副作用的概率.
试求:(1)系数 批子弹被接受的概率。 解:
⎧ 0,
x<0
∫ ∫ (2) F(x) =
x −∞
f
(t)dt
=
⎪⎪ ⎨ ⎪
x2 0 1 − e−9
第二章作业题解答

第二章静电场习题解答2-1.已知半径为F = Cl的导体球面上分布着面电荷密度为A = p s0 cos的电荷,式中的炖0为常数,试计算球面上的总电荷量。
解取球坐标系,球心位于原点中心,如图所示。
由球面积分,得到2用打Q =护= J j p50cos OrsmOd Od(p(S) 0 0In x=j j psQSefsinGded00 0In n=PsF j J cos ageded(p0 0丸=sin20d0 = 0o2-2.两个无限人平面相距为d,分别均匀分布着等面电荷密度的异性电荷,求两平面外及两平面间的电场强度。
解对于单一均匀带电无限人平面,根据对称性分析,计算可得上半空间和卞半空间的电场为常矢量,且大小相等方向相反。
由高斯定理,可得电场大小为E = ^-2e0对于两个相距为的d无限大均匀带电平面,同样可以得到E] = E“耳=E3题2-2图因此,有2-3.两点电荷q、= 8C和q2 = -4C ,分别位于z = 4和),=4处,求点P(4,0,0)处的电场强度。
解根据点电荷电场强度叠加原理,P点的电场强度矢量为点Si和Si处点电荷在P处产生的电场强度的矢量和,即E r = Qi 弘 | ① R?4T V£0/?/ 4TT£0R] = r — r L = 4e v — 4e., R 、= J 4-0 " + 0-4 ~ = 4>/2 R 2 =r —r 2 =4e v -4e v , R 2 = J 4-0 ' + 0-4 ' = 4>/22-7. 一个点电荷+q 位于(-a, 0,0)处,另一点电荷-2q 位于(a,0,0)处,求电位等于零的 面;空间有电场强度等于零的点吗?解根据点电荷电位叠加原理,有々)=丄]鱼+鱼4矶丄忌」式中Rj =r-r L = x-\-a e v + ye v +e. R i = yl x + a 2 + r+^2 R 2 =r-r 2 = x ~a e v + ),e y+e r R? — yj x — ci + )r +代入得到式中代入得到心孟 _______ 1^x + a)2+ y 2+ z 22JaS+b+z 2(3x+d )(x+3a ) + 3),+3z ,=0根据电位与电场强度的关系,有电位为零,即令简化可得零电位面方程为要是电场强度为零,必有E x = 0, E y = 0, E : = 0一 (x+ d)[(x + d)2 + y 2 + ^2p + 2(—d)[(—d)2+ y 2 + 疋 -)^(x+n)2 + y 2 + z 2 2 +2y^(x-a)2 + y 2+ z 2丄-z[(x + d)2 + + 疋 2+2z[(x-d)2 +)*此方程组无解,因此,空间没有电场强度为零的点。
第二章 力学作业答案

第二章 力学一.选择题1【基础训练4】、如图2-14,物体A 、B 质量相同,B 在光滑水平桌面上.滑轮与绳的质量以及空气阻力均不计,滑轮与其轴之间的摩擦也不计.系统无初速地释放,则物体A 下落的加速度是 (A) g. (B) 4g /5 . (C) g /2 . (D) g /3 .,,42,/2,.5b b b a a a b a b a a T m a m g T ma g T T a a a =-==== 2【自测1】、在升降机天花板上拴有轻绳,其下端系一重物,当升降机以加速度a 1上升时,绳中的张力正好等于绳子所能承受的最大张力的一半,问升降机以多大加速度上升时,绳子刚好被拉断(A) 2a 1. (B) 2(a 1+g ).(C) 2a 1+g . (D) a 1+g .[C ]1max max 122T mg ma m a a ma T T T mg maa a g -==+==-==+物对地物对机机对地()3【自测2】、质量为m 的小球,放在光滑的木板和光滑的墙壁之间,并保持平衡,如图2-22所示.设木板和墙壁之间的夹角为,当逐渐增大时,小球对木板的压力将 (A) 增加. (B) 减少. (C) 不变.(D) 先是增加,后又减小.压力增减的分界角为=45°.αm图2-22BA【解答】受力分析如图右所示:垂直于板面的压力sin /sin N mg N mg αα=→=4【自测3】、两个质量相等的小球由一轻弹簧相连接,再用一细绳悬挂于天花板上,处于静止状态,如图2-23所示.将绳子剪断的瞬间,球1和球2的加速度分别为(A) a 1=g,a 2=g. (B) a 1=0,a 2=g. (C) a 1=g,a 2=0. (D) a 1=2g,a 2=0[D ]121211200020T m g F F m g m m F mgT mg F ma a g a --=-====→--==-=弹弹弹弹,(负号表示向下)5【附录A3】.一根细绳跨过一光滑的定滑轮,一端挂一质量为M 的物体,另一端被人用双手拉着,人的质量M m 21=.若人相对于绳以加速度a 0向上爬,则人相对于地面的加速度(以竖直向上为正)是(A) 3/)2(0g a +. (B ) )3(0a g --.图2-23(C3/)2(0g a +- (D)0a()()()()3/2,3/,)(00000a g a a a g a ma a m M g m M a a m mg T MaT Mg +=+∴-=++=-+=-=-二、填空题6【基础训练9】、 质量为m 的小球,用轻绳AB 、BC 连接,如图2-18,其中AB 水平.剪断绳AB 前后的瞬间,绳BC 中的张力比 T : T ′= .A7【自测9】质量分别为m 1、m 2、m 3的三个物体A 、B 、C ,用一根细绳和两根轻弹簧连接并悬于固定点O ,如图2-27.取向下为x 轴正向,开始时系统处于平衡状态,后将细绳剪断,则在刚剪断瞬时,物体B 的加速度B a ϖ=_______;物体A 的加速度A a ϖ=______.()g m m a a g m f g m a m f mg f f g m m B A ab B a ab ab3232232-.0,--.,=====+=+断后,未断时,8【自测10】、一小珠可以在半径为R 的竖直圆环上作无摩擦滑动,如图2-28.今使圆环以角速度绕圆环竖直直径转动.要使小珠离开环的底部停在环上某一点,则角速度最小应大于_____gR________.22min cos sin sin ,cos N mg N m R g gg R RRθθωθωωθ==∴=>∴>三、计算题9【基础训练12】、水平转台上放置一质量M =2 kg 的小物块,物块与转台间的静摩擦系数μs =,一条光滑的绳子一端系在物块上,另一端则由转台中心处的小孔穿下并悬一质量m =0.8 kg 的物块.转台以角速度ω=4 rad/s 绕竖直中心轴转动,求:转台上面的物块与转台相对静止时,物块转动半径的最大值r max 和最小值r min .O x A B Cm 1 m 2m 3ORO图2-28AB?10【自测12】、质量为m 的小球,在水中受的浮力为常力F ,当它从静止开始沉降时,受到水的粘滞阻力大小为f =kv (k 为常数).证明小球在水中竖直沉降的速度v 与时间t 的关系为),e 1(/m kt kFmg ---=v 式中t 为从沉降开始计算的时间。
第二章课后作业答案

第二章线性表习题(答案)1.描述以下三个概念的区别:头指针,头结点,首元素结点。
首元结点是指链表中存储线性表中第一个数据元素a1的结点。
为了操作方便,通常在链表的首元结点之前附设一个结点,称为头结点,该结点的数据域中不存储线性表的数据元素,其作用是为了对链表进行操作时,可以对空表、非空表的情况以及对首元结点进行统一处理。
头指针是指向链表中第一个结点(或为头结点或为首元结点)的指针。
若链表中附设头结点,则不管线性表是否为空表,头指针均不为空。
否则表示空表的链表的头指针为空。
2.填空:(1)在顺序表中插入或删除一个元素,需要平均移动一半元素,具体移动的元素个数与插入或删除的位置有关。
(2)在顺序表中,逻辑上相邻的元素,其物理位置也相邻。
在单链表中,逻辑上相邻的元素,其物理位置不一定相邻。
(3)在带头结点的非空单链表中,头结点的存储位置由头指针指示,首元素结点的存储位置由头结点的next域指示,除首元素结点外,其它任一元素结点的存储位置由其直接前趋的next域指示。
3.已知L是无表头结点的单链表,且P结点既不是首元素结点,也不是尾元素结点。
按要求从下列语句中选择合适的语句序列。
a. 在P结点后插入S结点的语句序列是:(4)、(1)。
b. 在P结点前插入S结点的语句序列是:(7)、(11)、(8)、(4)、(1)。
c. 在表首插入S结点的语句序列是:(5)、(12)。
d. 在表尾插入S结点的语句序列是:(11)、(9)、(1)、(6)。
供选择的语句有:(1)P->next=S; (2)P->next= P->next->next; (3)P->next= S->next;(4)S->next= P->next; (5)S->next= L; (6)S->next= NULL;(7)Q= P; (8)while(P->next!=Q) P=P->next;(9)while(P->next!=NULL) P=P->next; (10)P= Q;(11)P= L; (12)L= S; (13)L= P;4.设线性表存于a[n]中且递增有序。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解:(1)如图所示, 在ϕ处任取微元段ad ϕ,相应微元电荷为ad ρϕ,则其在轴线上z 处产生的电场方向如图所示,大小为
2
2
014ad dE a z
ρϕ
πε=
+
于是,
sin dE dE θ⊥= ,cos dE dE θ=
由对称性易知,0E dE ⊥⊥==⎰
而
cos θ=,
故
()()
23/23/20
2222001124az Qz
E E dE a z a z π
ρεπε====
=++⎰⎰
即
()3/2
22014z
Qz
E e a z πε=+
(2)如图,在r 处任取微元环,其面积为2rdr π,相应微元环上的电荷为(2)s rdr ρπ,则由上面计算的结果,易写出微元环电荷在轴线上z 处产生的电场为
()3/2
220(2)1
4s z
rdr z
dE e r z ρππε=+
所以,
()()(
)2
3/23/2
002222001/2
220
00202414(3/2)1121
2a a s s z z
a
s z s z z z z rdr dr E e e r z r z z e r z z e z Qz e a z
ρρεερερεπε-==++=+-+⎛⎫= ⎝⎛⎫
=
⎝⎰⎰
解:(1)如图, 在x 处取微元段dx ,相应微元电流为z I
e dx w
,则其在中垂面上y 处产生的磁感应强度方向如图所示,大小为
I dx dB =
于是,
cos dB dB θ⊥=- ,sin dB dB θ=-
由对称性易知,0B dB ⊥⊥==⎰
则,
()()()()()02222
22
2
22
00022220
02
02arctan 211arctan 2w w w
w w w w w w
w I dx I ydx B B dB w x y d x y d x y I I I
x y w w w x y x y I w
w y
μπμμμπππμπ----====-+=-=-=-++=-
⎰⎰⎰⎰⎰ 即,
0arctan 2x I
w B e w y
μπ=-
P 61 题2.30
解:由 B
E t
∂∇⨯=-∂ , 可得 ()
B E dt =-∇⨯⎰
而 ()()()()
000cos 00sin sin x y z
x y y x y y e e e E t z E E e e x y z z z E e E t z e E t z ωβωβββωβ∂-⎡⎤∂∂∂∂⎛⎫⎣
⎦∇⨯==--= ⎪∂∂∂∂∂⎝⎭=---=-⎡⎤⎣⎦ 所以, ()()0
0sin cos y y
E B e E t z dt e t z C ββωβωβω
=--=-+⎰ 为方便起见,可取 0C =,
dB
因此, ()
c o s y E B e t z βωβω
=- ()0
00cos y E B H e t z βωβμμω
==-
()
()()
00000cos sin D x x E D J e E t z t t t
e E t z εεωβεωωβ∂∂∂===-⎡⎤⎣⎦∂∂∂=--
P 61 题2.31
解:在自由空间中,0J = , 于是 D H t
∂∇⨯=∂
, 又 ()0
c o s s i n y x
H e H t z a πωβ=- 从而,
()()
000
cos cos sin sin x y z
y y D x z y x z e e e H H D J H e e t x y z z x H H x x e H t z e t z a a a
πππβωβωβ∂∂⎛⎫⎛⎫∂∂∂∂==∇⨯==-
+ ⎪ ⎪∂∂∂∂∂∂⎝⎭⎝⎭
=---
对上式积分,有
()()()()
000
cos cos sin sin cos sin sin cos x z x z H x x D e H t z dt e t z dt
a a a
H H x x e t z e t z a a a
πππβωβωββπππωβωβωω=---=-+-⎰⎰
则 ()()00
000cos sin sin cos x z H H D x x E e t z e t z a a a
βπππωβωβεωεωε==-+-
P 61 题2.34 解:(1) 0
0,,t t r =R r =R
E E =外内
, 即 0
0,r =R r =R
E E θθ=,外内
, 即
300
sin sin A B
R R θθ= 所以, 2
0B R A =
相应地,()()0
2
00
3
cos sin ,2cos sin ,r r A e e r R R E R A e e r R r θθθθθθ⎧-+<⎪⎪
=⎨⎪+>⎪⎩
(2)
2000300
2cos cos S n r n r r=R r=R
R A A
D D D D R R ρεθεθ=-=-=+,外,外,内,内
所以 00
3c o s S A
R ερθ=
()222200
00
22
00000
3sin cos sin 13sin cos 32sin 02S A
Q R d d R d d R AR d d AR π
π
π
π
π
π
π
ερθθϕθθθϕεϕθθθεπ
θ=====⎰
⎰
⎰
⎰
⎰⎰
(3) 在球坐标系中,由哈密顿算子对任意矢量的散度公式可知,
()()2
22002000000
sin 11sin 11cos sin sin sin 22cos cos 0
r r D D D r r r A A r r r R r R A A
rR rR θθρθθ
εεθθθθθεεθθ∂∂=∇=+
∂∂⎛⎫⎛
⎫∂∂=-+ ⎪ ⎪∂∂⎝⎭⎝⎭
=-+= ,内,内内内 ()()2222200002332200002
23
sin 11sin 112cos sin sin sin 2cos 112sin cos sin 0
r r D D D r r r R A R A r r r r r r R A R A r r r r θθρθθ
εεθθθθθεθεθθθ∂∂=∇=+
∂∂⎛⎫⎛
⎫∂∂=+ ⎪ ⎪∂∂⎝⎭⎝⎭
⎛⎫
=
-+ ⎪⎝⎭
= ,外,外外外。
