大学物理7章作业分析
大学物理课后习题答案 第七章
Q
RT1
ln
V2 V1
8.31 400 ln 0.005 0.001
5.35 103 J
（2） 根据卡诺循环的效率公式可得
1 T2 A净 T1 Q吸
A净
（1
T2 T1
)Q吸
(1
300 ) 5.35 103 400
1.34 103 J
（3）由能量守恒 Q吸 A净 Q放 可得
Pa Va )
1 2 (Pb
Pa ) (Vb
Va )
9.5 102 J
A 100 10.5% Q吸 950
B
C 2 V (L)
62
大学物理上习题册参考解答
10、一定质量理想气体（摩尔热容比为 γ）的某循环过程的 T-V 图如下，其中 CA 为绝
热过程，状态 A(T1,V1)和状态 B（T2,V2）为已知，试问：
RT2
ln
VA VB
R(T1 T2) ln
VA VB
T2 T1 T2
14、一台家用冰箱放在室温为 300K 的房间内，做一盘 2.09105 J 的热量。设冰箱为理想卡诺制冷机。 （1）求做一盘冰块所需要的功；
℃的冰块需从冷冻室取走
（2）若此冰箱能以 2.09102 J / s 的速率取出热量，求冰箱的电功率。
mR mR
60
大学物理上习题册参考解答
6、某理想气体在 P-V 图上等温线与绝热线相交于 A
点（如图所示）。 已知 A 点的压强 P1=2×105Pa，体积 V1=0.5 P ×10-3m3 ，而且 A 点处等温线的斜率与绝热线斜率之比为
0.714，现使气体从 A 点绝热膨胀至 B 点，其体积 V2=1×10-3m3。
大学物理第7章习题解答
第七章7-1容器内装有质量为0.lkg 的氧气，其压强为l0atm(即lMPa)，温度为47C 0。
因为漏气，经过若干时间后，压强变为原来的85，温度降到27C 0。
问：(1)容器的容积有多大?(2)漏去了多少氧气? 解：（1）由RT MmpV =把p =10atm, T=(47+273)K=320K.m =0.1kg, M=32×10-3kg R =8.31J ·mol -1·K -1代入.证V =8.31×10-3m 3(2) 设漏气后，容器中的质量为m ′，则漏去的氧气为kg 103.3kg 301kg )1511.0(2-⨯≈=-='-=m m m ∆ 7-2设想太阳是由氢原子组成的理想气体，其密度可当作是均匀的。
若此气体的压强为Pa 141035.1⨯，试估算太阳的温度。
已知氢原子的质量kg H 271067.1-⨯=μ，太阳半径m R S 81096.6⨯=，太阳质量kg M S 301099.1⨯=。
解： 太阳内氢原子数HSm M N =故氢原子数密度为由P =nkT 知)(1015.11038.1105.81035.17232914K nk p T ⨯=⨯⨯⨯⨯==- 7-3 一容器被中间隔板分成相等的两半，一半装有氮气，温度为1T ，另一半装有氧气，温度为2T ，二者压强相等，今去掉隔板，求两种气体混合后的温度。
解： 如图混合前：2221112222111O He T M m T M m RT M m pV RT M m pV =⇒⎪⎪⎭⎪⎪⎬⎫==气有对气有对 ① 总内能 222111212523RT M m RT M m E E E +=+=前 ② ①代入②证混合后：设共同温度为T()RT M m T T EF RT M m M m E 21210221125231,2523⎪⎪⎭⎫ ⎝⎛+=⎪⎪⎭⎫ ⎝⎛+=式得又由后 ③ 题7-2图又后前E E =，故由（2）（3）知)/53(8211T T T T +=7-4 设有N 个粒子的系统，速率分布函数如习题7一4图所示，求：(1))(v f 的表达式；(2)a 与0v 之间的关系；(3)速率在之间的粒子数；(4)最概然速率；(5)粒子的平均速率；(6) 0.50v ~0v 区间内粒子的平均速率。
大学物理习题答案解析第七章
第七章 恒定磁场7 －1 两根长度相同的细导线分别多层密绕在半径为R 和r 的两个长直圆筒上形成两个螺线管，两个螺线管的长度相同，R ＝2r ，螺线管通过的电流相同为I ，螺线管中的磁感强度大小B R 、B r 满足（ ） （A ） （B ） （C ） （D ）分析与解 在两根通过电流相同的螺线管中，磁感强度大小与螺线管线圈单位长度的匝数成正比．根据题意，用两根长度相同的细导线绕成的线圈单位长度的匝数之比因而正确答案为（C ）。
7 －2 一个半径为r 的半球面如图放在均匀磁场中，通过半球面的磁通量 为（ ）（A ） （B ） （C ） （D ）分析与解 作半径为r 的圆S ′与半球面构成一闭合曲面，根据磁场的高斯定理，磁感线是闭合曲线，闭合曲面的磁通量为零，即穿进半球面S 的磁通量等于穿出圆面S ′的磁通量；．因而正确答案为（D ）． 7 －3 下列说法正确的是（ ）（A ） 闭合回路上各点磁感强度都为零时，回路内一定没有电流穿过 （B ） 闭合回路上各点磁感强度都为零时，回路内穿过电流的代数和必定为零 （C ） 磁感强度沿闭合回路的积分为零时，回路上各点的磁感强度必定为零（D ） 磁感强度沿闭合回路的积分不为零时，回路上任意一点的磁感强度都不可能为零分析与解 由磁场中的安培环路定律，磁感强度沿闭合回路的积分为零时，回路上各点的磁感强度不一定为零；闭合回路上各点磁感强度为零时，穿过回路的电流代数和必定为零。
因而正确答案为（B ）．7 －4 在图（ａ）和（ｂ）中各有一半径相同的圆形回路L1 、L2 ，圆周内有电流I1 、I2 ，其分布相同，且均在真空中，但在（ｂ）图中L2 回路外有电流I3 ，P 1 、P 2 为两圆形回路上的对应点，则（ ）r R B B 2=r R B B =r R B B =2r R B B 4=21==R r n n r R B r 2π2B r 2παB r cos π22αB r cos π2S B ⋅=m Φ（A ） ，（B ） ，（C ） ，（D ） ，分析与解 由磁场中的安培环路定律，积分回路外的电流不会影响磁感强度沿回路的积分；但同样会改变回路上各点的磁场分布．因而正确答案为（C ）．*7 －5 半径为R 的圆柱形无限长载流直导体置于均匀无限大磁介质之中，若导体中流过的恒定电流为I ，磁介质的相对磁导率为μｒ （μｒ＜1），则磁介质内的磁化强度为（ ） （A ）（B ） （C ） （D ）分析与解 利用安培环路定理可先求出磁介质中的磁场强度，再由M ＝（μｒ－1）H 求得磁介质内的磁化强度，因而正确答案为（B ）．7 －6 北京正负电子对撞机的储存环是周长为240 m 的近似圆形轨道，当环中电子流强度为8 mA 时，在整个环中有多少电子在运行？ 已知电子的速率接近光速。
(完整版)大学物理学(课后答案)第7章
第七章课后习题解答一、选择题7-1 处于平衡状态的一瓶氦气和一瓶氮气的分子数密度相同，分子的平均平动动能也相同，则它们[ ](A) 温度，压强均不相同 (B) 温度相同，但氦气压强大于氮气的压强 (C) 温度，压强都相同 (D) 温度相同，但氦气压强小于氮气的压强分析：理想气体分子的平均平动动能32k kT ε=，仅与温度有关，因此当氦气和氮气的平均平动动能相同时，温度也相同。
又由理想气体的压强公式p nkT =，当两者分子数密度相同时，它们压强也相同。
故选（C ）。
7-2 理想气体处于平衡状态，设温度为T ，气体分子的自由度为i ，则每个气体分子所具有的[ ](A) 动能为2i kT (B) 动能为2iRT(C) 平均动能为2i kT (D) 平均平动动能为2iRT分析：由理想气体分子的的平均平动动能32k kT ε=和理想气体分子的的平均动能2ikT ε=，故选择（C ）。
7-3 三个容器A 、B 、C 中装有同种理想气体，其分子数密度n 相同，而方均根速率之比为()()()1/21/21/222::2A B Cv v v =1:2:4，则其压强之比为A B C p :p :p[ ](A) 1:2:4 (B) 1:4:8 (C) 1:4:16 (D) 4:2:1=，又由物态方程p nkT =，所以当三容器中得分子数密度相同时，得123123::::1:4:16p p p T T T ==。
故选择（C ）。
7-4 图7-4中两条曲线分别表示在相同温度下氧气和氢气分子的速率分布曲线。
如果()2p O v 和()2p H v 分别表示氧气和氢气的最概然速率，则[ ](A) 图中a 表示氧气分子的速率分布曲线且()()22p p O H /4v v =(B) 图中a 表示氧气分子的速率分布曲线且()()22p p O H /1/4v v =(C) 图中b 表示氧气分子的速率分布曲线且()()22p p O H /1/4v v =(D) 图中b 表示氧气分子的速率分布曲线且()()22p p O H /4v v =分析：在温度相同的情况下，由最概然速率公式p ν=质量22H O M M <，可知氢气的最概然速率大于氧气的最概然速率，故曲线a 对应于氧分子的速率分布曲线。
大学物理答案解析第7～8章
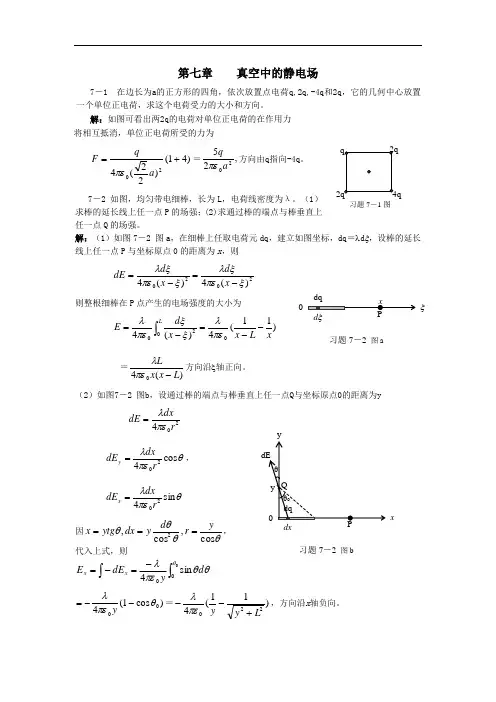
第七章 真空中的静电场7－1 在边长为a 的正方形的四角，依次放置点电荷q,2q,-4q 和2q ，它的几何中心放置一个单位正电荷，求这个电荷受力的大小和方向。
解：如图可看出两2q 的电荷对单位正电荷的在作用力 将相互抵消，单位正电荷所受的力为)41()22(420+=a q F πε＝,2520aqπε方向由q 指向-4q 。
7－2 如图，均匀带电细棒，长为L ，电荷线密度为λ。
（1）求棒的延长线上任一点P 的场强；(2)求通过棒的端点与棒垂直上任一点Q 的场强。
解：（1）如图7－2 图a ，在细棒上任取电荷元dq ，建立如图坐标，dq ＝λd ξ，设棒的延长线上任一点P 与坐标原点0的距离为x ，则2020)(4)(4ξπεξλξπεξλ-=-=x d x d dE则整根细棒在P 点产生的电场强度的大小为)11(4)(4002xL x x d E L--=-=⎰πελξξπελ ＝)(40L x x L-πελ方向沿ξ轴正向。
（2）如图7－2 图b ，设通过棒的端点与棒垂直上任一点Q 与坐标原点0的距离为y204r dxdE πελ=θπελcos 420rdxdE y =， θπελsin 420r dxdE x =因θθθθcos ,cos ,2yr d y dx ytg x ===， 代入上式，则)cos 1(400θπελ--=y ＝)11(4220Ly y+--πελ，方向沿x 轴负向。
习题7－1图dq ξd ξ习题7－2 图ax θθπελθd y dE E x x ⎰⎰-=-=00sin 4xdx习题7－2 图byθθπελθd y dE E y y ⎰⎰==00cos 400sin 4θπελy =＝2204Ly y L+πελ7－3 一细棒弯成半径为R 的半圆形，均匀分布有电荷q ，求半圆中心O 处的场强。
解：如图，在半环上任取d l =Rd θ的线元，其上所带的电荷为dq=λRd θ。
大学物理第07章习题分析与解答
r R r REOr(D)E ∝1/r 222第七章 静电场7-1 关于电场强度与电势的关系，描述正确的是[ ]。
(A) 电场强度大的地方电势一定高； (B) 沿着电场线的方向电势一定降低； (C) 均匀电场中电势处处相等； (D) 电场强度为零的地方电势也为零。
分析与解 电场强度与电势是描述静电场的两个不同物理量，电场强度为零表示试验电荷在该点受到的电场力为零，电势为零表示将试验电荷从该点移到参考零电势点时，电场力作功为零；电场强度等于负电势梯度；静电场是保守场，电场线的方向就是电势降低的方向。
正确答案为（B ）。
7-2 半径为R 的均匀带电球面的静电场中各点的电场强度的大小E 与距球心的距离r 之间的关系曲线为[ ]。
7-3、下分析与解 根据静电场的高斯定理可以求得均匀带电球面的电场强度分布为⎪⎩⎪⎨⎧>πε<=R r rQRr E 2040。
正确答案为（B ）。
7-3 下列说法正确的是[ ]。
（A ）带正电的物体电势一定是正的 (B)电场强度为零的地方电势一定为零 （C ）等势面与电场线处处正交 (D)等势面上的电场强度处处相等分析与解 正电荷在电场中所受的电场力的方向与电场线的切线方向相同，电荷在等势面上移动电荷时，电场力不做功，说明电场力与位移方向垂直。
正确答案为（C ）。
7-4 真空中一均匀带电量为Q 的球壳，将试验正电荷q 从球壳外的R 处移至无限远处时,电场力的功为[ ]。
（A ）24R qQ o πε （B ）R Q o πε4 （C ） R q o πε4 （D ）R qQ o πε4分析与解 静电场力是保守力，电场力做的功等电势能增量的负值，也可以表示成这一过程的电势差与移动电量的乘积，由习题7-2可知电场强度分布，由电势定义式⎰∞⋅=R rE d V 可得球壳与无限远处的电势差。
正确答案为（D ）。
7-5 关于静电场的高斯定理有下面几种说法，其中正确的是[ ]。
大学物理第7章真空中的静电场答案解析
第七章 真空中的静电场7－1 在边长为a 的正方形的四角，依次放置点电荷q,2q,-4q 和2q ，它的几何中心放置一个单位正电荷，求这个电荷受力的大小和方向。
解：如图可看出两2q 的电荷对单位正电荷的在作用力 将相互抵消，单位正电荷所受的力为)41()22(420+=a q F πε＝,2520aqπε方向由q 指向-4q 。
7－2 如图，均匀带电细棒，长为L ，电荷线密度为λ。
（1）求棒的延长线上任一点P 的场强；(2)求通过棒的端点与棒垂直上任一点Q 的场强。
解：（1）如图7－2 图a ，在细棒上任取电荷元dq ，建立如图坐标，dq ＝λd ξ，设棒的延长线上任一点P 与坐标原点0的距离为x ，则2020)(4)(4ξπεξλξπεξλ-=-=x d x d dE则整根细棒在P 点产生的电场强度的大小为)11(4)(40020xL x x d E L--=-=⎰πελξξπελ＝)(40L x x L-πελ方向沿ξ轴正向。
（2）如图7－2 图b ，设通过棒的端点与棒垂直上任一点Q 与坐标原点0的距离为y习题7－1图0 dqξd ξ习题7－2 图a204r dxdE πελ=θπελcos 420rdxdE y =， θπελsin 420r dxdE x =因θθθθcos ,cos ,2yr d y dx ytg x ===， 代入上式，则)cos 1(400θπελ--=y ＝)11(4220Ly y+--πελ，方向沿x 轴负向。
θθπελθd ydE E y y ⎰⎰==000cos 4 00sin 4θπελy =＝2204Ly y L+πελ7－3 一细棒弯成半径为R 的半圆形，均匀分布有电荷q ，求半圆中心O 处的场强。
解：如图，在半环上任取d l =Rd θ的线元，其上所带的电荷为dq=λRd θ。
对称分析E y =0。
θπεθλsin 420RRd dE x =⎰⎰==πθπελ00sin 4RdE E x R02πελ= θθπελθd y dE E x x ⎰⎰-=-=0sin 4xdx习题7－2 图byx习题7－3图2022R q επ=，如图，方向沿x 轴正向。
大学物理习题集答案解析-第七章-磁力
解：( 俯视逆时针旋转. )
h 2mv//
eB
eB h
v//
m
2
R
mv eB
eB v m R
B F
v
v2 v/2/
eB m
R2 h 2
2
由洛伦兹力 F ev B 可判断出 B沿螺旋轴竖直向上( 如图示 ).
7-4 如图示，一条任意形状的载流导线位于均匀磁场 中，试证明它所受到的安培力等于载流直导线ab所 受到的安培力。
为I2且AB与ab在同一平面上，ABab，如图8-2所示，a端距离 AB为ra，b端距离AB为rb，求导线ab受到的作用力。
解的：磁感在应ab上强任度取方一向线: 元B dr,d由rAB产生
A
大小： B 0 I1 2r
I1 r ab
d F I2dr sB i9n 0 I2Bd 同向r叠加
I2 dr
Fe12
q1q2
4 0a2
rˆ1（2 向上）
F12Fe12
v1 q 1
v2
qrˆ12 2
8-5 电流由长直导线1沿平行bc边方向经过a点流入一电阻均匀分布
的正三角形线框，再由b点沿cb方向流出，经长直导线2返回电源，
如图8-5所示，已知导线上的电流为I，三角框的每一边长为L，求三
角框中心O点的磁感应强度的大小。
第七章 磁力
7-1 7-5 7-9 7-2 7-6 7-3 7-7 7-4 7-8
7-1 .有一质量为ｍ的倒Ｕ形导线，两端浸没在水银槽中，导
线的上段长l 处在均匀磁场B中，如果使一个电流脉冲，即
t
电冲量持续q时间与0导id线t跳通起过时导间线相,这比导非线常就小会，跳试起由来导，线假所定达电高脉度
大学物理习题答案解析第七章
第七章恒定磁场7 －1 两根长度相同的细导线分别多层密绕在半径为R 和r 的两个长直圆筒上形成两个螺线管，两个螺线管的长度相同，R ＝2r，螺线管通过的电流相同为I ，螺线管中的磁感强度大小BR 、Br满足（）（A）B R 2B r （B）B R B r （C）2B R B r （D）B R 4B r分析与解在两根通过电流相同的螺线管中，磁感强度大小与螺线管线圈单位长度的匝数成正比．根据题意，用两根长度相同的细导线绕成的线圈单位长度的匝数之比n R r 1n r R 2因而正确答案为（C）。
7 － 2 一个半径为r 的半球面如图放在均匀磁场中，通过半球面的磁通量为（）（A）2πr 2B （B）πr2B22（C）2πr 2Bcosα（D）πr 2Bcosα分析与解作半径为r 的圆S′与半球面构成一闭合曲面，根据磁场的高斯定理，磁感线是闭合曲线，闭合曲面的磁通量为零，即穿进半球面S 的磁通量等于穿出圆面S′的磁通量；Φm B S ．因而正确答案为（D）．7 － 3 下列说法正确的是（）（ A ）闭合回路上各点磁感强度都为零时，回路内一定没有电流穿过（B）闭合回路上各点磁感强度都为零时，回路内穿过电流的代数和必定为零（C）磁感强度沿闭合回路的积分为零时，回路上各点的磁感强度必定为零（D）磁感强度沿闭合回路的积分不为零时，回路上任意一点的磁感强度都不可能为零分析与解由磁场中的安培环路定律，磁感强度沿闭合回路的积分为零时，回路上各点的磁感强度不一定为零；闭合回路上各点磁感强度为零时，穿过回路的电流代数和必定为零。
因而正确答案为（ B ）．7 －4 在图（ａ）和（ｂ）中各有一半径相同的圆形回路L1 、L2 ，圆周内有电流I1 、I2 ，其分布相同，且均在真空中，但在（ｂ）图中L2 回路外有电流I3 ，P1 、P2 为两圆形回路上的对应点，则（A）BL1dl BL2dl，B P1B P2B）BL1dl BL2dl，B P1B P2C）BL1dl BL2dl，B P1B P2D）BLdl BLdl，B P1B P2由磁场中的安培环路定律，积分回路外的电流不会影响磁感强度沿回路的积分；但同样会改变回路上各点的磁场分布．因而正确答案为（C）．*7 － 5 半径为R 的圆柱形无限长载流直导体置于均匀无限大磁介质之中，若导体中流过的恒定电流为质的相对磁导率为μｒ（μｒ<1），则磁介质内的磁化强度为（（A）μr 1 I /2πr （B）μr 1I /2πr（C）μr I /2πr （D）I /2πμr r分析与解利用安培环路定理可先求出磁介质中的磁场强度，再由M＝（μｒ－1）H 求得磁介质内的磁化强度，因而正确答案为（B）．7 － 6 北京正负电子对撞机的储存环是周长为240 m 的近似圆形轨道，当环中电子流强度为8 mA 时，在整个环中有多少电子在运行？已知电子的速率接近光速。
大学物理答案第七章
（3）若沿过程曲线从a到c状态，内能改变为
应用热力学第一定律，系统所作的功为
7-3 2mol的氮气从标准状态加热到373 K，如果加热时（1）体积不变；（2）压强不变，问在这两种情况下气体吸热分别是多少？哪个过程吸热较多？为什么？
分析根据热力学第一定律，系统从外界吸收的热量，一部分用于增加系统的内能，另一部分用于对外作功．理想气体的内能是温度的单值函数，在常温和常压下氮气可视为理想气体，无论经过什么样的准静态过程从标准状态加热到373 K，其内能的变化都相同．在等体过程中气体对外不作功，系统从外界吸收的热量，全部用于系统的内能的增加，而在等压过程中，除增加内能外，还要用于系统对外作功，因此吸热量要多些．
分析气体动理论的能量公式表明，气体的温度是气体分子平均平动动能的量度，而且定义了方均根速率 ．只要温度不变，无论经历什么样的过程，方均根速率都不变．本题中，可以通过等温过程中系统所作的功的表达式确定该过程中系统的温度．
解等温过程中系统所作的功为
7-92 m3的气体等温地膨胀，压强从 变到 ，求完成的功．
第七章热力学基础
7-1 假设火箭中的气体为单原子理想气体，温度为2000 K，当气体离开喷口时，温度为1000 K，（1）设气体原子质量为4个原子质量单位，求气体分子原来的方均根速率 ．已知一个原子质量单位=1.6605×10-27kg；（2）假设气体离开喷口时的流速（即分子定向运动速度）大小相等，均沿同一方向，求这速度的大小，已知气体总的能量不变．
p
p22
p0等温线
1
p1
OV2V1V
图7-12
分析对于双原子理想气体，热容比 ．不论经历什么过程，只要初终态气体的温度相同，就可以应用理想气体状态方程，建立类似于等温过程中初态和终态压强和体积之间的关系．
大学物理答案第七章热力学基础-习题解答
展望
学习方法建议
多做习题，提高解题能力 和综合分析能力。
加强理论学习，深入理解 热力学的物理意义和数学 表达。
关注学科前沿，了解热力 学在最新科研和技术中的 应用。
THANK YOU
感谢聆听
•·
热力学第一定律是能量守恒定律 在热学中的具体表现，它指出系 统能量的增加等于传入系统的热 量与外界对系统所做的功的和。
功的计算：在封闭系统中，外界 对系统所做的功可以通过热力学 第一定律进行计算，这有助于理 解系统能量的转化和利用。
能量平衡：利用热力学第一定律 ，可以分析系统的能量平衡，判 断系统是否处于热平衡状态。
热力学第二定律
热力学第二定律
描述了热力过程中宏观性质的自然方向性，即不可能把热量从低温物体传到高温物体而不引起其它变 化。
表达式
不可能通过有限个步骤将热量从低温物体传到高温物体而不引起其它变化。
03
热力学基础习题解答
热力学第一定律的应用
热量计算：通过热力学第一定律 ，可以计算系统吸收或放出的热 量，进而分析系统的能量变化。
热力学第二定律的应用
01
02
热力学第二定律指出，自
•·
发过程总是向着熵增加的
方向进行，即不可逆过程
总是向着宏观状态更混乱
、更无序的方向发展。
03
04
05
熵增加原理：根据热力学 第二定律，孤立系统的熵 永不减少，即自发过程总 是向着熵增加的方向进行 。
热机效率：利用热力学第 二定律，可以分析热机的 效率，探讨如何提高热机 的效率。
100%
制冷机效率的影响因素
制冷机效率受到多种因素的影响 ，如制冷剂的性质、蒸发温度和 冷凝温度、压缩机和冷却剂的流 量等。
大学物理学(课后答案)第7章
第七章课后习题解答、选择题7-1处于平衡状态的一瓶氦气和一瓶氮气的分子数密度相同，分子的平均平动动能也相同，则它们[](A) 温度，压强均不相同(B)温度相同，但氦气压强大于氮气的压强(C)温度，压强都相同(D)温度相同，但氦气压强小于氮气的压强3分析：理想气体分子的平均平动动能τk= kT，仅与温度有关，因此当氦气和氮2气的平均平动动能相同时，温度也相同。
又由理想气体的压强公式p =nkT ,当两者分子数密度相同时，它们压强也相同。
故选( C)O7-2理想气体处于平衡状态，设温度为T，气体分子的自由度为i ,则每个气体分子所具有的[](A)动能为-kT (B)动能为丄RT2 2(C)平均动能为^kT (D)平均平动动能为^RT分析：由理想气体分子的的平均平动动能3 kT和理想气体分子的的平均动能2T二丄kT ,故选择(C)O27-3三个容器A、B、C中装有同种理想气体，其分子数密度n相同，而方均根1/2 1/2 1/2速率之比为V A : V B : V C 1:2:4 ,则其压强之比为P A : P B : P C[](A) 1:2:4 (B) 1:4:8 (C) 1 : 4 : 16 (D) 4:2:1分析：由分子方均根速率公式= J3RT,又由物态方程p = nkT ,所以当三容器中得分子数密度相同时，得p1: P2： P3 =T1 :T2 :T3 =1:4:16 O故选择(C)O7-4图7-4中两条曲线分别表示在相同温度下氧气和氢气分子的速率分布曲线。
如果(VP O和(V P 分别表示氧气和氢气的最概然速率，则[](A)图中a表示氧气分子的速率分布曲线且V P O z V P H= 4(B) 图中a表示氧气分子的速率分布曲线且V P O/ V P H? =1/4(C) 图中b表示氧气分子的速率分布曲线且V P O / V P H=1/4(D) 图中b表示氧气分子的速率分布曲线且V P O/ V P H2 =4分析：在温度相同的情况下，由最概然速率公式'..P=I j2RT及氢气与氧气的摩尔质量M H2£M o2,可知氢气的最概然速率大于氧气的最概然速率，故曲线a对应于氧分子的速率分布曲线。
大学物理考试习题分析与解答
第七章静电场7-1关于电场强度与电势的关系，描述正确的是[ ]。
(A) 电场强度大的地方电势一定高；(B) 沿着电场线的方向电势一定降低；(C) 均匀电场中电势处处相等；(D) 电场强度为零的地方电势也为零。
分析与解电场强度与电势是描述静电场的两个不同物理量，电场强度为零表示试验电荷在该点受到的电场力为零，电势为零表示将试验电荷从该点移到参考零电势点时，电场力作功为零；电场强度等于负电势梯度；静电场是保守场，电场线的方向就是电势降低的方向。
正确答案为（B）。
7-2半径为R的均匀带电球面的静电场中各点的电场强度的大小E与距球心的距离r之间的关系曲线为[ ]。
7-3、下分析与解根据静电场的高斯定理可以求得均匀带电球面的电场强度分布为。
正确答案为（B）。
7-3下列说法正确的是[ ]。
（A）带正电的物体电势一定是正的(B)电场强度为零的地方电势一定为零（C）等势面与电场线处处正交(D)等势面上的电场强度处处相等分析与解正电荷在电场中所受的电场力的方向与电场线的切线方向相同，电荷在等势面上移动电荷时，电场力不做功，说明电场力与位移方向垂直。
正确答案为（C）。
7-4真空中一均匀带电量为Q的球壳，将试验正电荷q从球壳外的R处移至无限远处时,电场力的功为[ ]。
（A）（B）（C）（D）分析与解静电场力是保守力，电场力做的功等电势能增量的负值，也可以表示成这一过程的电势差与移动电量的乘积，由习题7-2可知电场强度分布，由电势定义式可得球壳与无限远处的电势差。
正确答案为（D）。
7-5 关于静电场的高斯定理有下面几种说法，其中正确的是[ ]。
（A）如果高斯面上电场强度处处为零，则高斯面内必无电荷；（B）如果高斯面内有净电荷，则穿过高斯面的电场强度通量必不为零；（C）高斯面上各点的电场强度仅由面内的电荷产生；（D）如果穿过高斯面的电通量为零，则高斯面上电场强度处处为零分析与解静电场的高斯定理表明，高斯面上的电场强度是由面内外电荷共同产生，而高斯面的电通量只由面内电荷决定。
大学物理习题解答第七章课后习题参考答案
习 题 七7-1 如图所示，O S O S 21=．若在O S 1中放入一折射率为n ，厚度为e 的透明介质片，求O S 1与O S 2之间的光程差．如果1S 和2S 是两个波长为λ的同相位的相干光源，求两光在O 点的相位差．[解] O S1与O S 2的几何路程相等光程差为 ()e n 1-=δ 位相差为 ()e n 122-==∆λπδλπϕ7-2 一束绿光照射到两相距 0.6mm 的双缝上，在距双缝2.5m 处的屏上出现干涉条纹．测得两相邻明条纹中心间的距离为2.27mm ，试求入射光的波长．[解] 由杨氏双缝干涉知 dD x λ=∆ 所以 5448m 10448.55.21060.01027.2733=⨯=⨯⨯⨯=∆=---D xd λÅ7-3 如图所示，在双缝干涉实验中，21SS SS =，用波长为λ的单色光照S ，通过空气后在屏幕E 上形成干涉条纹．已知点P 处为第3级干涉明条纹，求1S 和2S 到点P 的光程差．若整个装置放于某种透明液体中，点P 为第4级干涉明条纹，求该液体的折射率．[解] 1S 和2S 到P 点的光程差满足λλδ312==-=k r r整个装置放置于液体中，1S 和2S 到P 点的光程差满足()λδ412=-=r r nλλ43=n所以得到 33.134==n7-4 如习题7-1图所示，1S 和2S 是两个同相位的相干光源，它们发出波长λ＝5000Å的光波，设O 是它们中垂线上的一点，在点1S 与点O 之间插入一折射率n ＝1.50的薄玻璃，点O 恰为第4级明条纹的中心，求它的厚度e ．[解] 在O 点是第4级明条纹的中心光程差 λδ4=-=e ne所以 410414⨯=-=n e λÅ7-5 初位相相同的两相干光源产生的波长为6000Å的光波在空间某点P 相遇产生干涉，其几何路径之差为6102.1-⨯m ．如果光线通过的介质分别为空气（11=n ）、水（=2n 1.33）或松节油（=3n 1.50）时，点P 的干涉是加强还是减弱．[解] 光在折射率为n 的介质中P 点处光程差为()12r r n -=δ介质为空气时，11=n ，则()λδ2m 102.16121211=⨯=-=-=-r r r r n光程差为半波长的偶数倍，所以P 点处干涉加强． 介质为水时，=2n 1.33，则()m 106.1102.133.1661222--⨯=⨯⨯=-=r r n δ光程差介于两种情况之间，且结果与半波长的奇数倍更接近，所以P 点光强介于明暗条纹中心光强之间，且与暗条纹中心光强更接近．介质为松节油时，=3n 1.50，则()λδ3m 108.1102.15.1661233=⨯=⨯⨯=-=--r r n光程差为半波长的偶数倍，所以P 点处干涉加强．7-6 在双缝干涉实验中，用很薄的云母片（58.1=n ）覆盖在双缝的一条上，如图所示．这时屏上零级明纹移到原来第7级明纹位置上．如果入射光波5000Å，试求云母片的厚度（设光线垂直射入云母片）．[解] 原来的第7级明纹的位置满足λ721=-r r加上云母片后，光程差满足[]()012121=---=+--e n r r ne e r r所以41003.6158.15000717⨯=-⨯=-=n e λ Å7-7 用单色光源S 照射平行双缝1S 和2S 形成两相干光源．在屏上产生干涉图样，零级明条纹位于点O ，如图所示．若将缝光源S 移到S '位置，问零级明条纹向什么方向移动?若使零级明条纹移回点O ，必须在哪个缝的右边插入一薄云母片才有可能? 若以波长为5890Å的单色光，欲使移动了4个明纹间距的零级明纹移回到点O ，云母片的厚度应为多少? 云母片的折射率为1.58．[解] 零级明纹是光程差为0的位置．移动光源后光线2的光程长了，为仍保持光程差为0，必须让1的光程增加以弥补2的增加，只有在下方1才比2长，所以向下．要回到原点，即通过加片的方法使得1的光程增大，所以在1S 后加．在原点时，两光线的光程差满足()λδ41=-=e n得到 m 1006.4158.1105890414610--⨯=-⨯⨯=-=n e λ7-8 用白光作光源观察杨氏双缝干涉，设缝间距为d ，双缝与屏的距离为D ，试求能观察到的无重叠的可见光（波长范围： 4000～7600Å）光谱的级次．[解] k 级明纹的位置为dD k x λ=k 要使光谱无重叠，必须满足 ()()λm i n 1k λm a x k +≤x x 因此 ()min max 1λλ+≤k k 即 ()140007600+≤k k解得 1.1 ≤k 所以只能看到一级无重叠光谱．7-9 白色平行光垂直照射到间距为m m 0.25=d 的双缝上，在距缝cm 50处放一屏幕，若把白光（4000～7600Å）两极端波长的同级明纹间的距离叫做彩色带的宽度，试求第1级和第5级彩色带的宽度．[解] 每一级的宽度()min max min max λλ-=-=∆dDkx x x 1=k 时，()mm 72.0m 102.710400076001025.010*******21=⨯=⨯-⨯⨯⨯⨯=∆----x 5=k 时，()mm 6.3m 106.310400076001025.010505310325=⨯=⨯-⨯⨯⨯⨯=∆----x7-l0 波长为λ的单色光垂直照射在如图所示的透明薄膜上，薄膜厚度为e ．两反射光的光程差是多少?[解]薄膜上下表面的反射光均有半波损失，故没有因半波损失而产生的光程差，因此上下表面反射的光程差为e e n 60.222==δ7-11 白光垂直照射在空气中厚度为71080.3-⨯m 的肥皂膜上，肥皂膜的折射率为1.33，在可见光范围内（4000～7600Å） 哪些波长的光在反射中增强．[解] 光程差 λλδk ne =+=22 所以124-=k neλ 当1=k 时，2021612108.333.1471=-⨯⨯⨯=-λÅ 当2=k 时，同理可得67392=λÅ 当3=k 时，同理可得40433=λÅ所以在可见光范围内波长为4043 Å和6739 Å的光在反射中增强．7-12 在观察肥皂膜的反射光时，表面呈绿色（λ＝5000 Å），薄膜表面法线和视线间的夹角为450，试计算薄膜的最小厚度． [解] 两反射光的光程差为λλδk i n n e =+-=2sin 2221221=k 时对应薄膜厚度最小为m 1011.145sin 33.14105000sin 470221022122--⨯=-⨯⨯=-=in n e λ7-13 用波长连续可调的平行光垂直照射覆盖在玻璃板上的油膜，观察到5000 Å和7000 Å这两个波长的光在反射中消失．油的折射率为1.30，玻璃的折射率为1.50．求油膜的厚度．[解] 某一波长的光在反射中消失，表明光在油膜上下表面反射的光干涉相消，故光程差为 ()21222λδ+==k e n对1λ： ()2122112λ+=k e n对2λ： ()2122222λ+=k e n又因1λ与2λ之间没有其他波长的光消失，故1λ与2λ的干涉级数只可能相差一级 故112-=k k 因此575000700012121211===-+λλk k解得 31=k 22=k以31=k 代入得，()m 1073.630.141050007412710211--⨯=⨯⨯⨯=+=n k e λ7-14 波长为5500 Å的黄绿光对人眼和照像底片最敏感，要增大照像机镜头对此光的透射率，可在镜头上镀一层氟化镁 （2MgF ）薄膜． 已知氟化镁的折射率为1.38，玻璃的折射率为 1.50，求氟化镁的最小厚度．[解] 要增大波长为λ的光的透射率，则须使反射光干涉减弱．那么，光程差应满足()21222λδ+==k e n当0=k 时，e 最小，为m 1096.938.1410550048102min--⨯=⨯⨯==n e λ7-15 如图所示，用波长为λ的单色光垂直照射折射率为2n 的劈尖．图中各部分折射率的关系是1n <2n <3n ，观察反射光的干涉条纹，从劈尖顶端开始向右数第5条暗纹中心所对应的厚度是多少?[解] 因1n <2n <3n ，故在劈尖上下表面的两反射光无因半波损失引起的附加光程差，干涉暗纹应满足()21222λδ+==k e n因棱边为明纹，故从棱边开始向右数第5条暗纹对应上式中4=k所以()()2225494142412n n n k e λλλ=+⨯=+=7-16 用波长为1λ的单色光垂直照射空气劈尖，从反射光的干涉条纹中观察到劈尖装置的点A 处是暗条纹．若连续改变入射光的波长，直到波长为2λ（2λ>1λ）时，点A 将再变成暗条纹．求点 A 处空气层的厚度． [解] 空气劈尖上暗条纹处满足()21222λλδ+=+=k ne因1=n ，所以()21222λλ+=+k e ，即λk e =2 在A 处 11A 2λk e =，22A 2λk e =同一点，e 相同，又2λ>1λ，故2k <1k ，又因1λ到2λ连续可调，中间无其他波长的光干涉形成暗条纹，故112-=k k因此 122111A 212λλλλλ-==k e7-17 用波长为λ的单色光垂直照射到空气劈尖上，从反射光中观察干涉条纹，距顶点为L 处是暗条纹．使劈尖角θ连续慢慢变大，直到该点再次出现暗条纹为止，劈尖角的改变量θ∆是多少?[解] 空气劈尖干涉暗纹，光程差为 ()21222k λλδ+=+=k e劈尖角为θ时，L 处有 ()212221k 1λλ+=+k e 劈尖角为θθ∆+时，有 ()212222k 2λλ+=+k e因为劈尖角连续改变，即e 连续增大，故2k =1k +1 由上述公式得 ()λ=-12k k 2e e又 θθL L e ==sin 1k ，()()θθθθ∆+=∆+=L L e sin 2k 因此 L2λθ=∆7-18 两块长度为l0cm 的平玻璃片，一端相互接触，另一端用厚度为0.004mm 的纸片隔开形成空气劈尖．以波长为5000Å 的平行光垂直照射，观察反射光的等厚干涉条纹．在全部10cm 长度内呈现多少条明纹?[解] 设平玻璃片长为L ，纸片厚为H ，则形成的空气劈尖角为LH ==θθsin 两相邻明纹间距为 HLl 22sin 2λθλθλ===故总条数为 1610500010004.022103=⨯⨯⨯===--λH l L N7-19 为测量硅片上氧化膜的厚度，常用化学方法将薄膜的一部分腐蚀掉，使之成为劈形（又称为台阶），如图所示．用单色光垂直照射到台阶上，就出现明暗相间的干涉条纹，数出干涉条纹的数目，就可确定氧化硅薄膜的厚度．若用钠光照射，其波长λ=5893Å，在台阶上共看到5条明条纹，求膜的厚度（氧化硅的折射率2n ＝1.5，硅的折射率为3n ＝3.42）．[解] 因1n <2n < 3n ，故台阶上下表面反射光的光程差为e n 22=δ明条纹满足的条件为 λk e n =22台阶棱边为明纹，因共看到5条明纹，所以4max =k ，由明纹条件得m 1078575.1105893222101022max max--⨯=⨯⨯===n n k e λλ7-20 检查平板的平整度时，在显微镜下观察到的等厚条纹如图所示，条纹的最大畸变量为1.5条纹间距，所用光波波长为546nm ，试描述待测平面的缺陷．[解] 因每一条干涉条纹上对应的空气厚度相同，故在同一条纹上，畸变部分和平行棱边的直线部分所对应的膜厚度相等，本来离棱边越远膜的厚度越大，而现在同一条纹上，远离棱边的畸变部分厚度并不大，这说明畸变部分是凸起的，因最大畸变是为1.5条纹间距，说明最大畸变处膜厚度比非畸变时膜厚度之差e ∆对应的级数差5.1=∆k由劈尖明纹公式 λλk e =+22得 λk e ∆=∆2所以 m 101.421046.55.1277--⨯=⨯⨯=∆=∆λk e7-21 如图所示，A 、B 是两只块规（块规是两端面经过磨平抛光达到相互平行的钢质长方体）．A 的长度是标准的，B 是相同规格待校准的．A 、B 放在平台上，用一块样板平玻璃压住．（1）设垂直入射光的波长为λ=5893Å，A 、B 相隔cm 5=d ，T 与A 、 B 间的干涉条纹的间距都是0.55 mm ，试求两块规的长度差．（2）如何判断A 、B 哪一块比较长些?（3）如果T 与A 、B 间的干涉条纹间距分别为0.55 mm 和 0.3 mm ，则说明什么问题?[解] （1） 劈尖干涉，相邻条纹间距l 满足l2sin λα=所以A 、B 两只块规的高度差为m 1068.21055.0210893.51052sin 5372----⨯=⨯⨯⨯⨯⨯===∆l d d h λα （2）因空气劈尖棱边处为暗纹，所以若压平板T ，a 、c 处暗纹位置不变，则B 比A 长，若压T ，b 、d 处暗纹位置不变，则A 比B 长．（3） 设平板T 与A 、B 间形成的劈尖角分别为1α、2α．干涉条纹间距分别为1l 和2l ，则 2sin sin 2211λαα==l l已知1l >2l ，则1α<2α，B 的端面与底面不平行，且d 处向下倾斜．7-22 如图所示的观察牛顿环的装置中，设平球面透镜中心恰好和平玻璃接触，透镜球面的半径cm 400=R ，用某单色光垂直入射，观察反射光形成的牛顿环，测得第5个明环的半径是cm 30.0（1）求入射光的波长；（2）设图中OA ＝1.00cm ，求在半径为OA 的范围内可观察到的明环数．[解] （1）牛顿环明环半径公式为()2122k λR k r -=，所以()Rk r 1222k -=λ因中心为暗环，对应第5个明环5=k ，所以()5000104009103.0215222422k =⨯⨯⨯⨯=-⨯=--R r λÅ（2）因为()2122k λR k r -=，所以()5.5010541000.121217222k =⨯⨯⨯+=+≤--λR r k 所以能看到的明环数50个．7-23 用曲率半径为3.00m 的平凸透镜和平板玻璃作牛顿环实验，测得第k 级暗环半径为m m 24.4，第10+k 级暗环的半径为m m 0.6．求所用单色光的波长．[解] 牛顿环暗环半径公式为λkR r =k 故 ()λR k r 1010k +=+因此 ()()323232k 210k 1001.600.3101024.410610⨯=⨯⨯-⨯=-=--+R r r λÅ7-24 用牛顿环实验测单色光的波长．用已知波长为1λ的单色光垂直照射牛顿环装置时，测得第1和第9级暗环的半径之差为1l ；用未知单色光照射时测得第l 和第9级暗环的半径之差为2l ．求单色光的波长2λ．[解] 牛顿环暗环半径公式为 λkR r =k对1λ 11λR r = 199λR r = 所以()19119-=-λR r r又 119l r r =-， 故211⨯=λR l 同理得 222⨯=λR l因此 121222λλl l =7-25 一平凸透镜放在平板玻璃上，在反射光中观察牛顿环．当1λ＝4500Å时，测得第3级明环的半径为31006.1-⨯m ．换用红光，观测到第5级明环的半径为31077.1-⨯m ．求透镜曲率半径和红光的波长．[解] 牛顿环明环半径公式为()2122k λR k r -=，对1λ，3=k 时， 25123λR r =对2λ，5=k 时， 29225λR r =由此得 697145001006.191077.15956262123252=⨯⨯⨯⨯⨯==--λλr r Å由25123λR r =得， m 00.110450051006.12521062123=⨯⨯⨯⨯==--λr R7-26 用牛顿环干涉条纹测定凹球面的曲率半径．将已知曲率半径的平凸透镜放在待测的凹球面上，如图所示．在两曲面之间形成空气层，可以观测到环状干涉条纹．测得第4级暗环的半径4r ＝2.250cm ，已知入射光的波长λ＝5893 Å，平凸透镜的曲率半径1R ＝102.3cm ，求凹球面的曲率半径2R ．[解] 牛顿环k 级暗环条件为 ()21222λλ+=+k e 即 λk e =2由几何关系知 ()2111211212k 2e e R e R R r +=--=因为 11R e << ，故 112k 2e R r = 同理 222k 2e R r = 又 21e e e -= 联立上式得2k 1211r k R R λ-= 以 m 023.11=R ，4=k ，m 10589310-⨯=λ，m 10250.224-⨯=r ，代入得cm 8.1022=R7-27 在观察牛顿环干涉条纹的实验中，用图（a ）、（b ）、（c ）所示的装置代替平凸透镜和平玻璃组合．试画出反射光中的干涉条纹（只画暗条纹）．[解]（a ） （b ） （c ）7-28 用波长为λ的单色光源做迈克尔逊干涉仪实验，在移动反光镜2M 的过程中，视场中的干涉条纹移过k 条，求反射镜移动的距离?[解] 设反射镜移过的距离为d ，则光程差改变量为 λδk d ==∆2所以 2λk d =7-29 迈克尔逊干涉仪的一臂中放有长为100.0mm 的玻璃管，其中充有一个大气压空气，用波长为5850Å的光作光源．在把玻璃管抽成真空的过程中，发现视场中有100.0条干涉条纹从某固定点移过．求空气的折射率．[解] 设空气的折射率为n ，在由空气抽成真空的过程中，光程差改变量为()λk e n ∆=-12所以 00029.1100.10021058500.100121310=⨯⨯⨯⨯+=∆+=--e k n λ7-30 在把迈克尔逊干涉仪的可动反射镜移动0.233mm 过程中，数得条纹移动数为792，求所用光的波长．[解] 设反射镜移动距离为d ，则光程差改变 λδk d ∆==∆25884m 10884.579210233.022103=⨯=⨯⨯=∆=--k d λÅ7-31 常用雅敏干涉仪来测定气体在各种温度和压力下的折射率．干涉仪的光路如图所示．S 为光源，L 为正透镜，1G 、2G 为等厚且相互平行的玻璃板．1T 、2T 为等长的两个玻璃管，长度为l ．进行测量时，先将1T 、2T 抽空，然后把待测气体徐徐导入一管中，在E123451234512345处观察干涉条纹移动数，即可求得待测气体的折射率．设在测量某气体的折射率时，将气体慢慢放入2T 管中，从开始进气到标准状态时，在E 处共看到有98条干涉条纹移过去．所用的钠光波长λ＝5893Å （真空中），l ＝20cm ．求该气体在标准状态下的折射率．[解] 设待测气体在标准状态下的折射率为n ，则在气体导入前后，两条光路中的光程差改变为()λk l n ∆=-1所以00029.110201058939811210=⨯⨯⨯+=∆+=--l k n λ7-32 一单缝宽度4101-⨯=a m ，透镜的焦距m 5.0=f ，若分别用40001=λÅ和76002=λÅ的单色平行光垂直入射，它们的中央明条纹的宽度各是多少?[解] 一级暗纹公式为 λϕ=1sin a 而aλϕϕ==11sin所以 a f f f x λϕϕ===111tan 所以中央明纹的宽度为 af x x λ221==∆对1λ： m 1041011045.02234711---⨯=⨯⨯⨯⨯==∆a f x λ 对2λ： m 106.7101106.75.02234722---⨯=⨯⨯⨯⨯==∆a f x λ7-33 有一单缝宽m m 10.0=a ，在缝后放一焦距cm 50=f 的会聚透镜，用波长λ＝5460 Å的平行绿光垂直照射单缝，求位于透镜焦平面处的屏上的中央亮条纹的宽度．如果把此装置浸入水中，并把屏移动到透镜在水中的焦平面上，中央亮条纹的宽度变为多少?设透镜的折射率54.1='n ，水的折射率33.1=n ．（提示：透镜在水中的焦距()f nn n n f -'-'=1水） [解] （1） 中央明条纹的宽度为m 1046.51010.01046.51050223372----⨯=⨯⨯⨯⨯⨯==∆a f x λ （2） 在水中，透镜焦距为()f nn n n f -'-'=1水 所以中央明条纹的宽度为()()()()m 1040.1101.033.154.11046.550.0154.12122237---⨯=⨯⨯-⨯⨯⨯-⨯=-'-'==∆a n n f n naf x λλ水7-34 用波长λ＝7000Å的平行光垂直照射单缝，缝后放一焦距为70cm 的正透镜，在透镜焦平面处的屏上测得中央亮条纹的宽度为3100.2-⨯m ．试计算： （1）单缝的宽度．（2）当用另一单色光照射时，测得中央亮纹的宽度为3105.1-⨯m ，求此光的波长． [解]中央亮条纹宽度为 af x λ2=∆ （1）由上式可得单缝的宽度为 m 109.41021071070224372----⨯=⨯⨯⨯⨯⨯=∆=x f a λ （2）由前式可得光的波长为5250m 1025.510072105.1109.427234=⨯=⨯⨯⨯⨯⨯='∆='----f x a λÅ7-35 用平行光管把某光源发出的单色光变成平行光后垂直照射在宽度为0.308mm 的单缝上．用焦距为12.62cm 的测微目镜测得中央明条纹两侧第5级暗条纹之间的距离为x ∆＝2.414mm ．求入射光的波长．[解] 单缝衍射暗纹中心到中央亮纹中心距离为 af kx λ= 5=k 时，af x λ55= 两侧第5级暗纹之间的距离为 af x x λ1025==∆ 所以 58921062.121010414.210308.010233=⨯⨯⨯⨯⨯=∆=---f x a λÅ7-36 用波长λ＝6328Å的氦-氖激光垂直照射单缝，其夫琅禾费衍射图样的第1级极小的衍射角为50．试求单缝的宽度．[解] 单缝衍射暗纹条件为λϕk a =sin 当 1=k 时，λϕ=sin a所以 ϕλϕλ==sin a 式中 g r a d1805πϕ= 所以 m 1026.7518010328.667--⨯=⨯⨯=πa7-37 在正常照度下，人眼瞳孔的直径约为mm 2，人眼最敏感的波长为5500Å．眼前m m 250 （明视距离）处的点物在视网膜上形成艾里斑的角半径是多少? 明视距离处能够被分辨的两物点的最小距离是多少?（前房液和玻璃状液的折射率33.1=n ）[解] （1） 因人眼中玻璃状液体的折射率为n ，所以波长变为nλλ='在视网膜上形成爱里斑的角半径为rad 1052.210233.1105.522.122.122.1437---⨯=⨯⨯⨯⨯=='=nD D λλθ （2） 人眼的最小分辨角 Dλθ22.1min =设在距离L 处能分辨的最小距离为d （l d θ=），则m 104.810250102105.522.122.15337----⨯=⨯⨯⨯⨯⨯==D L d λ7-38 已知天空中两颗星对一望远镜的角距离为61084.4-⨯rad ，设它们发出光的波长为5500Å．望远镜的口径至少要多大才能分辨出这两颗星．[解] 设望远镜孔径为D ，当两星对望远镜的角距离大于其最小分辨角时方可分辨，即Dλ22.11084.46≥⨯-所以 cm 9.131084.4105.522.11084.422.1676=⨯⨯⨯=⨯≥---λD7-39 月球距地面约3.86510⨯km ，设月光按λ＝5500Å计算，问月球表面上距离多远的两点才能被直径为5.00m 的天文望远镜所分辨．[解] 设月球上两物点距离为d ，其对望远镜张角大于最小分辨角时，则能分辨该两点即DL d λ22.1≥ 所以 m 8.5100.51086.3105.522.122.187=⨯⨯⨯⨯=≥-D L d λ7-40 用波长为λ＝5893Å的钠光垂直照射光栅，测得第2级谱线的衍射角11102'︒=θ，而用待测波长的单色光照射时，测得第一级谱线的衍射角2441'︒=θ．试求光栅常数和待测光的波长．[解] 光栅方程为 ()λϕk b a =+sin 对1λ有 ()11sin λθ=+b a 对2λ有 ()222sin λθ=+b a由上两式得 546410893.51110sin 244sin 2sin sin 27002211=⨯⨯''⨯==-λθθλÅ 将1λ的数值代入得 m 1067.66-⨯=+b a7-4l 一块每毫米刻痕为500条的光栅，用钠黄光正入射，钠黄光中含有两条谱线，其波长分别为5896Å和5890Å．求在第2级光谱中这两条谱线分开的角度．[解] 光栅常数为 m 10250010163--⨯=⨯=+b a 由光栅方程可得 ()122s i nλϕ=+b a ()222sin λϕ='+b a 因此得到 ⎪⎭⎫⎝⎛+-⎪⎭⎫ ⎝⎛+='-=∆b a b a 21222arcsin 2arcsin λλϕϕϕ6767043.010210890.52arcsin 10210896.52arcsin =⎪⎪⎭⎫⎝⎛⨯⨯⨯-⎪⎪⎭⎫ ⎝⎛⨯⨯⨯=----7-42 一单色平行光投射于衍射光栅，其入射方向与光栅法线夹角为θ，在和法线成︒11和︒53的方向上出现第1级光谱线，并且位于法线的两侧．求θ角的大小．为什么在法线的一侧能观察到第2级谱线，而另一侧却没有?[解]（1） 斜入射时，零级主极大在透镜的与入射光线平行的副光轴方向上．530角的衍射光线和入射光线分别在法线两侧，此衍射角应取负值，而110衍射角应取正值，所以两个第一级光谱线对应的方程分别为 ()()λθ-=-+053sin sin b a （1）()()λθ+=++011sin sin b a （2） 因此求得 3039.0sin =θ 07.17=θ（2） 设法线两侧衍射角为900时对应极大的级数分别为k 和k '在与入射光线异侧有 ()()λk b a -=-+0090sin 7.17sin （3） 在与入射光线同侧有 ()()λk b a '=++0090sin 7.17sin （4）由 （1）、（3）式相除，得 4.17.17sin 53sin 7.17sin 90sin 0000≈--=k 由 （2）、（4）式相除，得 64.27.17sin 11sin 7.17sin 90sin 0000≈++='k 由上面结果知，只有与入射光线同侧可观察到第二级谱线．7-43 一衍射光栅，每厘米有200条透光缝，每条透光缝宽为3102-⨯=a cm ，在光栅后放一焦距为m 0.1=f 的凸透镜．现以λ=6000Å单色平行光垂直照射光栅，试求： （1）透光缝的单缝衍射中央明条纹宽度；（2）在该宽度内有哪几个光栅衍射主极大?[解] （1）单缝衍射第一极小满足 λϕ=s i na （1） 中央明纹宽度为m 1061021060.122sin 2tan 2257---⨯=⨯⨯⨯⨯====∆a f f f x λϕϕ （2） 设该范围内主极大最大级数为k ，则()λϕk b a =+sin （2）由 （1）、（2）式有 5.210220010152=⨯⨯⨯=+=--a b a k 所以在此范围内能看到的主极大级数为210±±=，，k ，共5个光栅衍射主极大．7-44 试指出光栅常数()b a +为下述三种情况时，哪些级数的光谱线缺级？（1）光栅常数为狭缝宽度的两倍，即()a b a 2=+； （2）光栅常数为狭缝宽度的三倍，即()a b a 3=+；（3）光栅常数为狭缝宽度的2.5倍，即()a b a 5.2=+．[解] k 级缺级的条件为k aba k '+=() 3,2,1±±±='k （1）()a b a 2=+时，k k '=2，凡2的倍数级都缺级． （2） ()a b a 3=+时，k k '=3，凡3的倍数级都缺级． （3）()a b a 5.2=+时，k k '=5.2，凡5的倍数级都缺级．7-45 波长λ＝6000Å的单色光垂直入射到一光栅上，测得第2级主极大的衍射角为︒30，且第3级缺级．（1）光栅常数()b a +是多大？（2）透光缝可能的最小宽度是多少？（3）在屏幕上可能出现的主极大的级次是哪些？[解]（1） 由光栅方程得 ()λ230sin 0=+b a所以 m 104.21064430sin 2670--⨯=⨯⨯===+λλb a （2） 当k 级缺级时，满足 k a ba k '+=所以 k kba a '+=当1='k 时，缝宽a 最小，为 m 1083104.276--⨯=⨯=+=k b a a （3） 在屏幕上呈现的主极大的级数由最大级数和缺级情况决定． 因为 ()λφk b a =+sinmax k <4106104.276=⨯⨯=+--λba 因此 m a x k =3又因3=k 缺级，所以在屏上可能出现的级数为 2,1,0±±=k7-46 每厘米刻有400条刻痕的光栅，其透光缝5101-⨯=a m ，用波长为λ＝7000Å的光垂直照射在屏幕上可观察到多少条明条纹?[解] 光栅常数 m 105.240010152--⨯=⨯=+b a 因为 ()λϕk b a =+sinmax k <7.35107105.275=⨯⨯=+--λba 因此35max =k 缺级条件 k k k ab a k '='⨯⨯='+=--5.2101105.255所以 凡能被5整除的级数都缺级，共缺级个数为7535=='N 因此，光栅衍射在屏上呈现明条纹总数为 ()5717352=+-⨯=N7-47 以白光（波长范围4000～7600Å）垂直照射光栅，在衍射光谱中，第2级和第3级发生重叠．求第2级被重叠的范围．[解] 最小波长和最大波长分别为4000min =λ Å 7600max =λ Å第3级光谱中，min λ主极大的位置与第2级某一波长λ的主极大位置相同时，开始重叠，由光栅方程可求此波长 ()λϕ2s i n =+b a ()m i n 3s i n λϕ=+b a因此 600040002323min =⨯==λλÅ 故，第2级光谱中被重叠的光谱波长范围为 6000=λÅ~7600 Å7-48 用两米光栅摄谱仪拍摄氢原子光谱，在可见光范围内有四条谱线，如图所示．光栅上每厘米有4000条缝，光栅后的正透镜的焦距为2.00m ，在其焦平面上放一照相底片，求四条谱线在底片上的间距．[解] 光栅常数为 m 105.2400010162--⨯=⨯=+b a ∞对第一条谱线（1=k ），应用光栅方程，为()λϕ=+sin b a 对αH ， m 10563.671-⨯=λ，在底片上位置为m 543.0arcsin tan tan 1=⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛+==b a f f x λϕ 同理可得δγβH H H ,,三条谱线在照像底片上的位置分别为m 396.02=x m 353.03=x m 333.04=x因此 αH 与βH 之间的间距为 7m 14.01=∆x同理可得βH 与γH 之间的间距为 m043.02=∆x γH 与δH 之间的间距为 m 02.03=∆x7-49 用白光照射每毫米50条刻痕的光栅，在距光栅2m 的屏幕上观察到各色光谱，设可见光的上限波长（红光）r λ＝7800 Å，下限波长（紫光） v λ=4000 Å，试计算屏幕上第1级光谱的宽度．[解] 第一级谱线满足 ()λϕ=+s i nb a 屏幕上红光谱线的位置为 ba f f x +≈≈r1λϕ 紫光谱线的位置为 ba f f x +≈'≈v2λϕ所以第一级光谱的宽度为()()m 108.310400078001015022103v r 21---⨯=⨯-⨯⨯=-+=-=∆λλb a fx x x7-50 一光源发射红双线在波长λ＝6563 Å处，两条谱的波长差λ∆＝1.8 Å．有一光栅可以在第1级中把这两条谱线分辨出来，求光栅的最少刻线总数．[解] 光栅的分辨率为 kN R =∆=λλ所以 1.364618.16563=⨯=∆=k N λλ 即光栅最少刻线总数为3647条．7-51 一光栅宽为6cm ，每厘米有6000条刻线，在第三级光谱中，对λ＝5000 Å处，可分辨的最小波长间隔是多大?[解] 光栅的总缝数为 3600066000=⨯=N因为光栅的分辨本领为kN =∆λλ046.03600035000=⨯==∆kNλλÅ7-52 一束波长为2.96 Å的X 射线投射到晶体上，所产生的第1级衍射线偏离原入射线方向731'︒，求对应此射线的相邻两原子平面之间的距离．[解] 设掠射角为ϕ，衍射线偏离入射线的角度为θ，则2θϕ=由布拉格方程 λϕk d =sin 2 得相邻两原子平面间距为()52.52731sin296.212sin 2sin 20='⨯⨯===θλϕλk k d Å7-53 以波长为1.10Å的X 射线照射岩盐晶面，测得反射光第1级极大出现在X 射线与晶面的夹角为'3011︒处．问：（1）岩盐晶体的晶格常数d 为多大?（2）当以另一束待测的X 射线照岩盐晶面时，测得反射光第一级极大出现在X 射线与晶面的夹角为'3017︒处，求待测X 射线的波长．[解] （1） 由布拉格方程 λϕk d =sin 2 ，所以 76.25.11sin 210.1sin 20===ϕλk d Å （2） 由布拉格方程得待测X 射线的波长为66.115.17sin 76.22sin 20=⨯⨯==k d ϕλÅ7-54 一束部分偏振光垂直入射于一偏振片上，以入射光为轴旋转偏振片，测得透射光强的最大值是最小值的5倍．求部分偏振光中自然光与线偏振光强度之比．[解] 设该束部分偏振光中自然光光强为0I ，线偏振光光强为I ，透过偏振片后自然光光强变为20I ，因此光强最大时I II +=20max , 光强最小时 20m i n I I =所以22500minmaxI I I I I +== 因此 210=I I7-55 两偏振片A 、B 的透振方向成︒45角，如图所示．入射光是线偏振光，其振动方向和A 的透振方向相同．试求这束光线分别从左边入射和从右边入射时，透射光强之比．[解] 设从左右两边入射时透射光强分别为1I 和2I由马吕斯定律得从左边入射时透射光强为002012145cos I I I == 从右边入射，则00202024145cos 45cos I I I =⋅= 所以入射光从左右两边入射，透射光强之比为1:2:21=I I7-56 三个理想偏振片1P 、2P 、3P 叠放在一起，1P 与3P 的透振方向互相垂直，位于中间的2P 与1P 的透振方向间的夹角为︒30．强度为0I 的自然光垂直入射到1P 上，依次透过1P 、2P 和3P ．求通过三个偏振片后的光强．[解] 通过1P 后： 0121I I =通过2P 后： 002128330cos I I I == 通过3P 后： 0022332360cos I I I ==7-57 一束太阳光以某一入射角入射于平面玻璃上，这时反射光为完全偏振光．若透射光的折射角为︒32，试求：（1）太阳光的入射角；（2）这种玻璃的折射率．[解] 因反射光为完全偏振光，所以入射角为布儒斯特角，则 0090=+r i 0000058329090=-=-=r i由布儒斯特定律得 60.158tan tan 00===i n7-58 光从介质1射向介质2时的临界角是︒60．布儒斯特角是多大? [解] 由光的折射定律得 020190sin 60sin n n = 所以2360sin 012==n n 由布儒斯特定律 23tan 120==n n i 由此得 9.400=i7-59 如图所示的各种情况中，以线偏振光或自然光入射于两种介质的界面上．图中0i 为起偏振角， 0i i ．试画出折射光线和反射光线并标出它们的偏振状态．[解] 折射光和反射光及其偏振状态如下图7-60 如图（a ）所示，一束自然光入射在方解石的表面上，入射光线与光轴成锐角，问有几条光线从方解石透射出来? 如果把方解石切割成等厚的A 、B 两块，并平行地移动一点距离，如图（b ）所示，此时光线通过这两块方解石后，有多少条光线射出来? 如果把B 绕入射光线转过一个角度，此时将有几条光线从B 射出来?[答] （1）因入射光不沿光轴方向，也不垂直于光轴，所以在方解石中产生双折射现象，有两条光线透射出来． （2）在A 中为o 光的光线射出来入射到B ，入射面就是B 中o 光的主平面，因此光线通过B 后，只有一条光线射出，同理，在A 中为e 光的光线通过B 后也有一束光线射出，所以从B 中透射出来的仍是两束光．（3）当把B 任意转过一角度时，A 中的o 光和e 透射出来入射到B 中，各自在B 中又发生双折射现象，每条光线在B 中又分为o 光和e 光，因此，总共有四条光线从B 中射出．*7-61 如图所示，一束自然光入射到一方解石晶体上，其光轴垂直于纸面．已知方解石对o 光的折射率o n ＝1.658，对e 光的折射率为=e n 1.486．（1）如果方解石的厚度为t ＝1.0 cm ，自然光的入射角︒=45i ，求a ，b 两透射光之间的垂直距离；（2）两透射光的振动方向如何? 哪一束光在晶体中是o 光? 哪一束光在晶体中是e 光?[解]（1）由折射定律得：i r n sin sin o o = （1）i r n sin sin e e = （2） 设则,,d BC L AB ==()0e tan tan r r t L -= （3）由于 i ABC =∠，所以 i L d cos = （4）由（1）、（2）、（3）、（4）联立得43.0658.145sin sin sin 000===n i r 002.25=r 48.0486.145sin sin 0e ==r 4.28e =r ()cm 07.02.25tan 4.28tan 0.100=-⨯=Lcm 05.045cos 07.00=⨯=d即a 、b 两光线的垂直距离为cm 05.0．（2）两透射光的振动方向见图．（3）a 为e 光，b 为o 光．*7-62 设方解石对钠黄光 （5893=λÅ）和氦氖激光（63282=λÅ）的主折射率相同，把方解石切割成对上述两光的四分之一波片，其最小厚度各是多少? 6584.1o =n ，4864.1e =n ．[解] 设最小厚度分别为1e 和2e ，依题意有()41e o 1λ=-n n e ()42e o 2λ=-n n e所以 ()()m 10565.84864.16584.1410893.5477e 011--⨯=-⨯⨯=-=n n e λ ()()m 10198.94864.16584.1410328.6477e 021--⨯=-⨯⨯=-=n n e λA B C。
大学物理学第3版修订版北京邮电大学出版社上册第七章习题7答案解析
习 题 77、1选择题(1) 容器中贮有一定量的理想气体,气体分子的质量为m ,当温度为T 时,根据理想气体的分子模型与统计假设,分子速度在x 方向的分量平方的平均值就是:(A) 2x υ=. (B) 2x υ=. ［ ］(C) 23x kT m υ= . (D) 2x kT mυ=. [答案:D 。
2222x y z υυυυ=++, 222213x y z υυυυ===,23kT mυ=。
](2) 一瓶氦气与一瓶氮气的密度相同,分子平均平动动能相同,而且都处于平衡状态,则它们 ［ ］ (A) 温度相同、压强相同. (B) 温度、压强都不相同. (C) 温度相同,但氦气的压强大于氮气的压强. (D) 温度相同,但氦气的压强小于氮气的压强.[答案:C 。
由32w kT =,w w =氦氮,得T 氦=T 氮 ; 由molpM RTρ=,ρρ=氦氮,T 氦=T 氮 ,而M M <mol 氦mol 氮,故p p >氦氮。
](3) 在标准状态下,氧气与氦气体积比为V 1 /V 2=1/2,都视为刚性分子理想气体,则其内能之比E 1 / E 2为: ［ ］ (A) 3 / 10. (B) 1 / 2. (C) 5 / 6. (D) 5 / 3.[答案:C 。
由2mol M i E RT M =2ipV =,得111112222256E i pV i V E i pV i V ==⋅=。
](4) 一定质量的理想气体的内能E 随体积V 的变化关系为一直线,其延长线过E ~V 图的原点,题7、1图所示,则此直线表示的过程为: ［ ］ (A) 等温过程. (B) 等压过程. (C) 等体过程. (D) 绝热过程.[答案:B 。
由图得E =kV , 而2i E pV =,i 不变,2ik p =为一常数。
](5) 在恒定不变的压强下,气体分子的平均碰撞频率Z 与气体的热力学温度T的关系为 [ ] (A) Z 与T 无关. (B).Z 与T 成正比 . (C) Z 与T 成反比. (D) Z 与T 成正比.[答案:C。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第七章机械波
一. 选择题
1. 机械波的表示式为（SI），则
(A) 其振幅为3m (B) 其波速为10m/s (C) 其周期为1/3s (D) 波沿x轴正向传播
2. 一平面简谐波沿x轴正向传播，时波形图如图示，
此时处质点的相位为
(A) 0 (B) π
(C) π/2 (D) - π/2
3. 频率为100Hz、波速为300m/s的简谐波，在传播方向上有两点同一时刻振动相位差为π/3，则这两点相距
(A) 2m (B) 21.9m
(C) 0.5m (D) 28.6m
4. 一平面简谐波在介质中传播，某瞬时介质中某质元正处于平衡位置，此时它的能量为
(A) 动能最大，势能为零 (B) 动能为零，势能最大
(C) 动能为零，势能为零 (D) 动能最大，势能最大
5. 一平面简谐波在弹性介质中传播，下述各结论哪个是正确的？
(A) 介质质元的振动动能增大时，其弹性势能减小，总机械能守恒
(B) 介质质元的振动动能和弹性势能做周期性变化，但二者的相位不相同
(C) 介质质元的振动动能和弹性势的相位在任一时刻都相同，但二者的数值不相等
(D) 介质质元在其平衡位置处弹性势能最大
6. 两相干波源S1、S2发出的两列波长为λ的同相位波列在P点相遇，S1到P点的距离是r1，S2到P点的距离是r2，则P点干涉极大的条件是
(A)
(B)
(C)
(D)
7. 两相干波源S 1和S2相距λ/4（λ为波长），S1的相位比S2的相位超前，在S1、S2连线上，S1外侧各点（例如P点）两波干涉叠加的结果是
(A) 干涉极大
(B) 干涉极小
(C) 有些点干涉极大，有些点干涉极小
(D)无法确定
8. 在波长为λ的驻波中，任意两个相邻波节之间的距离为
(A) λ (B) 3λ/4 (C) λ/2 (D) λ/4
二. 填空题
9. 一声波在空气中的波长是0.25m，传播速度时340m/s，当它进入另一种介质时，波长变成了0.37m，则它在该介质中的传播速度为__________________.
10. 平面简谐波沿x轴正向传播，波动方程为，则处质点的振动方程为_________________，处质点与处质点振动的相位差为_______.
11. 简谐波沿x轴正向传播，传播速度为5m/s ，原点O振动方程为
(SI)，则处质点的振动方程为_____________________.
12. 一平面简谐波周期为2s，波速为10m/s，A、B是同一传播方向上的两点，间距为5m，则A、B两点的相位差为_______________.
13. S1、S2是两个相干波源，已知S1初相位为，若使S1S2连线中垂线上各点均干涉相消，S 2的初相位为_______________.
14. 如图，波源S1、S2发出的波在P点相遇，若P点的合振
幅总是极大值，则波源S1的相位比S2的相位领先
_____________________.
三. 计算题
15. 一横波沿绳子传播时的波动表式为 )410cos(05.0x t y ππ-=[SI] . 求：
（1）此波的振幅、波速、频率和波长; （2）绳子上各质点振动的最大速度和最大加速度;
16. 波源做简谐振动，振幅为0.1m ，振动周期为0.01s . 以它经过平衡位置向正方向运动时为计时起点，若此振动以的速度沿直线传播，求距波源8m 处P 点的振动方程.
17. 如图，一平面波在介质中以速度1
s m 20-⋅=u 沿x 轴负方向传播，已知a 点的振动表式为
t y a π4cos 3= [SI]．（1）以a 为坐标原点写出波动方程；
（2）以与a 点相距m 5处的b 点为坐标原点，写出波动方程．
18. 如图所示，已知和时的波形曲线分别为图中实线曲线Ⅰ和虚线曲线Ⅱ，波沿x轴正向传播. 根据图中给出的条件，求：（1）波动方程；（2）P点质元的振动方程.
19. 如图所示，两相干波源分别在P、Q两点，它们发出频率为ν，波长为λ，初相相同的两列相干波，振幅分别为A1和A2 ，设2/
=
PQ，R为PQ连线上的一点．求：
3λ
（1）自P、Q发出的两列波在R处的相位差；
（2）两波在R处干涉时的合振幅．
第七章机械波参考答案
一. 选择题
1. (C)
2. (C)
3. (C)
4.（D）
5. （D）
6. (C)
7.（B）
8.（C）
二. 填空题 9. ( 503 m/s ) 10. (
；
)
11. ( )
12. ( π/2 ) 13. ( - π/2 ) 14. ( - 2π/3 ) 三. 计算题
15. 一横波沿绳子传播时的波动表式为 )410cos(05.0x t y ππ-=[SI] . 求： （1）此波的振幅、波速、频率和波长;
（2）绳子上各质点振动的最大速度和最大加速度; 解：（1）波动方程
可得振幅
频率
波长 波速
（2）绳上各质点振动时的最大速度
绳上各质点振动时的最大加速度
16. 波源做简谐振动，振幅为0.1m ，振动周期为0.01s . 以它经过平衡位置向正方向运动时为计时起点，若此振动以的速度沿直线传播，求距波源8m 处P 点的振动方程.
解: 波源振动方程为
简谐波的波动方程为
代入，可得质点振动方程
m
17. 一平面波在介质中以速度1s m 20-⋅=u 沿x 轴负方向传播，已知a 点的振动表式为
t y a π4cos 3= [SI]．
（1）以a 为坐标原点写出波动方程；
（2）以与a 点相距m 5处的b 点为坐标原点，写出波动方程．
解：（1）已知A = 3m ，
,
因波沿x 轴负方向传播，以a 点为坐标原点的波动方程为
（2）以a 点为坐标原点时，b 点的坐标为
, 代入上式得b 点的振动方程为
若以b 点为坐标原点，则波动方程为
18. 如图所示，已知
和
时的波形曲线分别为图中实线曲线Ⅰ和虚线曲线Ⅱ，
波沿x 轴正向传播. 根据图中给出的条件，求：（1）波动方程；（2）P 点质元的振动方程.
解：(1) 设波动方程为
由图知A= 0.1m，λ= 4m
又时，原点处质点的位移，速度，故该质点的初相
波动方程为
（2）将代入波动方程，得点质元振动方程为
19. 如图所示，两相干波源分别在P、Q两点，它们发出频率为ν，波长为λ，初相相同的两列相干波，振幅分别为A1和A2 ，设2/
PQ，R为PQ连线上的一点．求：
3λ
=
（1）自P、Q发出的两列波在R处的相位差；
（2）两波在R处干涉时的合振幅．
解：（1）两列波的初相位相同，在R处的相位差为
（2）两波在R处的振动方向相同，频率相同，相位差，则合振幅为。