理论力学期末试卷-模拟试卷07(带答案)
大学理论力学期末考试题库及答案

大学理论力学期末考试题库及答案1. 题目:简述牛顿三定律的内容。
答案:牛顿第一定律(惯性定律)指出,物体在没有受到外力作用时,将保持静止或匀速直线运动状态;牛顿第二定律(加速度定律)表明,物体的加速度与作用在物体上的合外力成正比,与物体质量成反比,方向与合外力方向相同;牛顿第三定律(作用与反作用定律)说明,对于任何两个相互作用的物体,它们之间的力是大小相等、方向相反的。
2. 题目:什么是角动量守恒定律?答案:角动量守恒定律是指在没有外力矩作用的情况下,一个系统的总角动量保持不变。
3. 题目:请解释达朗贝尔原理。
答案:达朗贝尔原理是将动力学问题转化为静力学问题的一种方法。
它基于牛顿第二定律,通过引入惯性力,将动力学方程转化为平衡方程。
4. 题目:什么是虚功原理?答案:虚功原理是分析力学中的一个基本原理,它指出,一个保守系统中,如果系统从一个平衡位置发生微小的虚位移,那么系统内所有力对这些虚位移所做的虚功之和为零。
5. 题目:简述拉格朗日方程的一般形式。
答案:拉格朗日方程的一般形式为:\( \frac{d}{dt}(\frac{\partial L}{\partial \dot{q}_i}) -\frac{\partial L}{\partial q_i} = Q_i \),其中 \( L \) 是拉格朗日量,\( q_i \) 是广义坐标,\( \dot{q}_i \) 是广义速度,\( Q_i \) 是广义力。
6. 题目:请解释什么是哈密顿原理。
答案:哈密顿原理,也称为最小作用量原理,它指出在所有可能的路径中,实际发生的过程是使作用量取极小值的路径。
作用量是拉格朗日量 \( L \) 对时间的积分。
7. 题目:什么是刚体的转动惯量?答案:刚体的转动惯量是衡量刚体对旋转运动的抵抗程度的物理量,它与刚体的质量分布和旋转轴的位置有关。
8. 题目:请解释什么是势能。
答案:势能是物体由于其位置或状态而具有的能量形式,它与物体的位形有关,通常与保守力相关。
2021年理论力学期末考试试题题库及参考答案

理论力学 期末考试试题1-1、自重为P=100kNT 字形钢架ABD,置于铅垂面内,载荷图所示。
其中转矩M=20kN.m ,拉力F=400kN,分布力q=20kN/m,长度l=1m 。
试求固定端A 约束力。
解:取T 型刚架为受力对象,画受力图.1-2 图所示,飞机机翼上安装一台发动机,作用在机翼OA 上气动力按梯形分布:1q =60kN/m ,2q =40kN/m ,机翼重1p =45kN ,发动机重2p =20kN ,发动机螺旋桨反作用力偶矩M=18kN.m 。
求机翼处在平衡状态时,机翼根部固定端O 所受力。
解:1-3图示构件由直角弯杆EBD和直杆AB构成,不计各杆自重,已知q=10kN/m,F=50kN,M=6kN.m,各尺寸图。
求固定端A处及支座C约束力。
1-4 已知:图所示构造,a ,M=Fa ,12F F F ==,求:A ,D 处约束力.解:1-5、平面桁架受力图所示。
ABC 为等边三角形,且AD=DB 。
求杆CD 内力。
1-6、图所示平面桁架,A 端采用铰链约束,B 端采用滚动支座约束,各杆件长度为1m 。
在节点E 和G 上分别作用载荷E F =10kN ,G F =7 kN 。
试计算杆1、2和3内力。
解:2-1 图示空间力系由6根桁架构成。
在节点A上作用力F,此力在矩形ABDC平面内,且和铅直线成45º角。
ΔEAK=ΔFBM。
等腰三角形EAK,FBM和NDB在顶点A,B和D处均为直角,又EC=CK=FD=DM。
若F=10kN,求各杆内力。
2-2 杆系由铰链连接,在正方形边和对角线上,图所示。
在节点D沿对角线LD方向作用力F。
在节点C沿CH边铅直向下作用力F。
如铰链B,L和H是固定,杆重不计,求各杆D内力。
2-3 重为1P =980 N ,半径为r =100mm 滚子A 和重为2P =490 N 板B 由通过定滑轮C 柔绳相连。
已知板和斜面静滑动摩擦因数s f =0.1。
《理论力学》模拟试题答案.docx
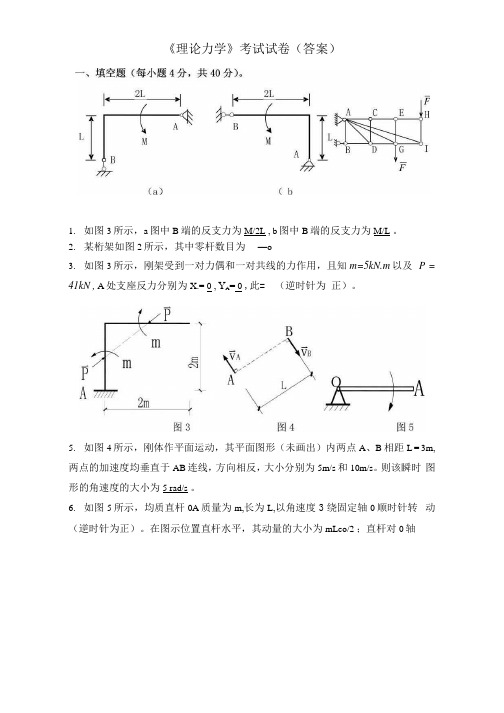
《理论力学》考试试卷(答案)1.如图3所示,a图中B端的反支力为M/2L , b图中B端的反支力为M/L 。
2.某桁架如图2所示,其中零杆数目为—o3.如图3所示,刚架受到一对力偶和一对共线的力作用,且知m=5kN.m以及P = 41kN , A处支座反力分别为X.= 0 ,Y A= 0 ,此= (逆时针为正)。
5.如图4所示,刚体作平面运动,其平面图形(未画出)内两点A、B相距L = 3m, 两点的加速度均垂直于AB连线,方向相反,大小分别为5m/s和10m/s。
则该瞬时图形的角速度的大小为5 rad/s 。
6.如图5所示,均质直杆0A质量为m,长为L,以角速度3绕固定轴0顺时针转动(逆时针为正)。
在图示位置直杆水平,其动量的大小为mLco/2 ;直杆对0轴动量矩的大小为ml? 3/3 ,杆动能大小为ml; 3 76。
二、计算题(共60分)。
1.如图所示,梁AC用三根链杆支承,梁受集中力P和均布荷载作用,已知P=40kN, q=5kN/m,试求各链杆的内力。
(本题15分)解:受力分析如图所示:2.桁架如图所示,试求杆件CD, CE和EF的内力。
(本题15分)解:由图分析可知CD杆为0杆。
……(1分)1)先取整体分析,如图所示分别对A点和B点取矩:Am尸)=o-2x10-4x10-6x10-8x5 + 8x7? = 0D2>*)=°2x10 + 4x10 + 6x10 + 8x5-8x7?^ =0解得:R A =20kN, R B =20kN如图取I - I截面左半部分对A点取矩,取II-11截面右部分对B点取矩£ 〃很了)= 0-2xl0-2x S CE sin(cif)-lx S CE cos(o) = 0£ 〃七(了)= o8X7?A +8X5+6X10+4X10+6X S CE sin(。
)-lx S CE cos(。
)+ 4x S FE = 0上式解得:S^=—11.18KN, S FF = 1QKNCc r Zi3,图示机构中,曲柄04长为r,绕。
理论力学期末试卷-模拟试卷01(带答案)
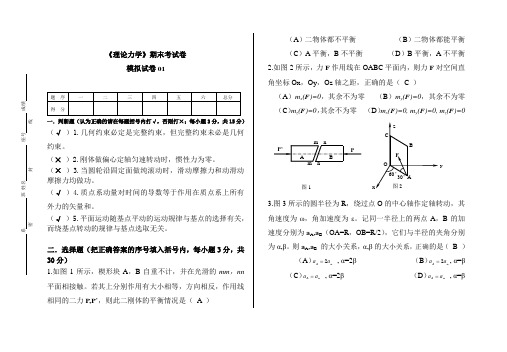
《理论力学》期末考试卷模拟试卷01一.判断题(认为正确的请在每题括号内打√,否则打×;每小题3分,共15分)(√)1.几何约束必定是完整约束,但完整约束未必是几何约束。
(×)2.刚体做偏心定轴匀速转动时,惯性力为零。
(×)3.当圆轮沿固定面做纯滚动时,滑动摩擦力和动滑动摩擦力均做功。
(√)4.质点系动量对时间的导数等于作用在质点系上所有外力的矢量和。
(√)5.平面运动随基点平动的运动规律与基点的选择有关,而绕基点转动的规律与基点选取无关。
二.选择题(把正确答案的序号填入括号内,每小题3分,共30分)1.如图1所示,楔形块A,B自重不计,并在光滑的mm,nn 平面相接触。
若其上分别作用有大小相等,方向相反,作用线相同的二力P,P’,则此二刚体的平衡情况是( A )(A)二物体都不平衡(B)二物体都能平衡(C)A平衡,B不平衡(D)B平衡,A不平衡2.如图2所示,力F作用线在OABC平面内,则力F对空间直角坐标Ox,Oy,Oz轴之距,正确的是( C )(A)m x(F)=0,其余不为零(B)m y(F)=0,其余不为零(C)m z(F)=0,其余不为零(D)m x(F)=0, m y(F)=0, m z(F)=03.图3所示的圆半径为R,绕过点O的中心轴作定轴转动,其角速度为ω,角加速度为ε。
记同一半径上的两点A,B的加速度分别为a A,a B(OA=R,OB=R/2),它们与半径的夹角分别为α,β。
则a A,a B的大小关系,α,β的大小关系,正确的是(B )(A)BAaa2=, α=2β(B)BAaa2=, α=β(C)BAaa=, α=2β(D)BAaa=, α=βy图14.直管AB 以匀角速度ω绕过点O 且垂直于管子轴线的定轴转动,小球M 在管子内相对于管子以匀速度v r 运动。
在图4所示瞬时,小球M 正好经过轴O 点,则在此瞬时小球M 的绝对速度v ,绝对加速度a 是(D )(A )v=0,a =0 (B )v=v r, a =0 (C )v=0,r v a ω2=,← (D )v=v r , r v a ω2=,← 5. 图5所示匀质圆盘质量为m ,半径为R ,可绕轮缘上垂直于盘面的轴转动,转动角速度为ω,则圆盘在图示瞬时的动量是( B ) (A )K=0 (B )K=mR ω,↓ (C )K=2mR ω ,↓ (D )K=mR ω2 ,←6. 条件同前题(5),则圆盘的动能是(D )(A )2221ωmR T = (B )2241ωmR T =(C )22ωmR T = (D )2243ωmR T =7. 匀质半圆盘质量为m ,半径为R ,绕过圆心O 并垂直于盘面的定轴转动(图6),其角速度为ω,则半圆盘对点O 的动量矩的大小L 0 是( C )。
理论力学模拟试题和答案

理论力学模拟试题和答案理论力学模拟试题(一) 单项选择题(每题2分,共4分) 1. 物块重P,与水面的摩擦角o,其上作用一力Q,且已知P=Q,方向如图,则物块的状态为( )。
A 静止(非临界平衡)状态B 临界平衡状态C 滑动状态第1题图第2题图2. 图(a)、(b)为两种结构,则( )。
A 图(a)为静不定的,图(b)为为静定的B 图(a)、(b)均为静不定的C图(a)、(b)均为静定的D图(a)为静不定的,图(b)为为静定的(二) 填空题(每题3分,共12分)1. 沿边长为的正方形各边分别作用有F1,F2,F3,F4,且F1=F2=F3=F4=4kN,该力系向B点简化的结果为:主矢大小为,主矩大小为MB=____________ 向D点简化的结果是什么?____________。
F3DCF4AF2F1B第1题图第2题图2. 图示滚轮,已知R,r,,作用于B点的力F,求力F对A点之矩MA=____________。
3. 平面力系向O点简化,主矢与主矩合力大小及作用线位置,并画在图上。
,MO,求理论力学(MOO第3题图第4题图4. 机构如图,O1A与O2B均位于铅直位置,已知,,2,则杆O1A的角速度,C点的速度。
1(三) 简单计算题(每小题8分,共24分)1. 梁的尺寸及荷载如图,求A、B2. 丁字杆ABC的A端固定,尺寸及荷载如图。
求A端支座反力。
3. 在图示机构中,已知,,O1A杆的角速度角加速度理论力学(五) 2,2,求三角板C点的加速度,并画出其方向。
(四) 图示结构的尺寸及载荷如图所示,q=10kN/m,q0=20kN/m。
求A、C处约束反力。
(五)l=2m,求支座A、D、E处的约束反力。
(六) 复合梁的制成、荷载及尺寸如图所示,杆重不计。
已知q=20kN/m,l=2m,求1、2杆的 3五理论力学(AⅠ)期终试题解答01级土木(80学时类)用(一) 单项选择题1. A2. B (二) 填空题1. 0 ;2.;3. 合力FR4.,合力作用线位置(通过O1)4.5rads ;9ms(三) 简单计算1. 取梁为研究对象,其受力图如图所示。
理论力学(理工大0期末考试试题(题库_带答案)

1-1、自重为P=100kN 的T 字形钢架ABD,置于铅垂面内,载荷如图所示。
其中转矩M=20kN.m ,拉力F=400kN,分布力q=20kN/m,长度l=1m 。
试求固定端A 的约束力。
解:取T 型刚架为受力对象,画受力图.1-2 如图所示,飞机机翼上安装一台发动机,作用在机翼OA 上的气动力按梯形分布:1q =60kN/m ,2q =40kN/m ,机翼重1p =45kN ,发动机重2p =20kN ,发动机螺旋桨的反作用力偶矩M=18kN.m 。
求机翼处于平衡状态时,机翼根部固定端O 所受的力。
解:1-3图示构件由直角弯杆EBD以及直杆AB组成,不计各杆自重,已知q=10kN/m,F=50kN,M=6kN.m,各尺寸如图。
求固定端A处及支座C的约束力。
1-4 已知:如图所示结构,a, M=Fa, 12F F F ==, 求:A ,D 处约束力.解:1-5、平面桁架受力如图所示。
ABC 为等边三角形,且AD=DB 。
求杆CD 的内力。
1-6、如图所示的平面桁架,A 端采用铰链约束,B 端采用滚动支座约束,各杆件长度为1m 。
在节点E 和G 上分别作用载荷E F =10kN ,G F =7 kN 。
试计算杆1、2和3的内力。
解:2-1 图示空间力系由6根桁架构成。
在节点A上作用力F,此力在矩形ABDC平面内,且与铅直线成45º角。
ΔEAK=ΔFBM。
等腰三角形EAK,FBM和NDB在顶点A,B和D处均为直角,又EC=CK=FD=DM。
若F=10kN,求各杆的内力。
2-2 杆系由铰链连接,位于正方形的边和对角线上,如图所示。
在节点D沿对角线LD方向F。
在节点C沿CH边铅直向下作用力F。
如铰链B,L和H是固定的,杆重不计,作用力D求各杆的内力。
2-3 重为1P =980 N ,半径为r =100mm 的滚子A 与重为2P =490 N 的板B 由通过定滑轮C 的柔绳相连。
已知板与斜面的静滑动摩擦因数s f =0.1。
《理论力学》期末考试试题及答案
理论力学部分第一章静力学基础一、是非题(每题3分,30分)1.力有两种作用效果,即力可以使物体的运动状态发生变化,也可以使物体发生变形。
()2.在理论力学中只研究力的外效应。
()3.两端用光滑铰链连接的构件是二力构件。
()4.作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
()5.作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
()6.三力平衡定理指出:三力汇交于一点,则这三个力必然互相平衡。
()7.平面汇交力系平衡时,力多边形各力应首尾相接,但在作图时力的顺序可以不同。
()8.约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
()9. 力偶只能使刚体发生转动,不能使刚体移动。
()10.固定铰链的约束反力是一个力和一个力偶。
()二、选择题(每题4分,24分)1.若作用在A点的两个大小不等的力F1和F2,沿同一直线但方向相反。
则其合力可以表示为。
①F1-F2;②F2-F1;③F1+F2;2.作用在一个刚体上的两个力F A、F B,满足F A=-F B的条件,则该二力可能是。
①作用力和反作用力或一对平衡的力;②一对平衡的力或一个力偶。
③一对平衡的力或一个力和一个力偶;④作用力和反作用力或一个力偶。
3.三力平衡定理是。
①共面不平行的三个力互相平衡必汇交于一点;②共面三力若平衡,必汇交于一点;③三力汇交于一点,则这三个力必互相平衡。
4.已知F1、F2、F3、F4为作用于刚体上的平面共点力系,其力矢关系如图所示为平行四边形,由此。
①力系可合成为一个力偶;②力系可合成为一个力;③力系简化为一个力和一个力偶;④力系的合力为零,力系平衡。
5.在下述原理、法则、定理中,只适用于刚体的有。
①二力平衡原理;②力的平行四边形法则;③加减平衡力系原理;④力的可传性原理;⑤作用与反作用定理。
6.关于约束的说法正确的是 。
① 柔体约束,沿柔体轴线背离物体。
② 光滑接触面约束,约束反力沿接触面公法线,指向物体。
理论力学期末考试和答案
理论力学期末考试和答案一、选择题(每题2分,共20分)1. 质点系的动量守恒定律成立的条件是()。
A. 质点系所受合外力为零B. 质点系所受合外力不为零C. 质点系所受合外力为任意值D. 质点系所受合外力不为零,但合外力矩为零答案:A2. 质心的位置坐标可以通过()计算得到。
A. 质点系中所有质点的位置坐标B. 质点系中所有质点的质量C. 质点系中所有质点的位置坐标和质量D. 质点系中所有质点的动量答案:C3. 刚体绕定轴转动的转动惯量I与刚体的质量M和形状有关,与()无关。
A. 刚体的质量分布B. 刚体的形状C. 刚体绕定轴的转动半径D. 刚体绕定轴的转动速度答案:D4. 刚体平面运动中,角速度与线速度的关系是()。
A. 线速度与角速度成正比B. 线速度与角速度成反比C. 线速度与角速度无关D. 线速度与角速度成正比,且与转动半径成正比答案:D5. 刚体绕定轴转动的动能公式为()。
A. E_k = 1/2 * I * ω^2B. E_k = 1/2 * M * v^2C. E_k = 1/2 * M * ω^2D. E_k = 1/2 * I * v^2答案:A6. 两个质点m1和m2组成的系统,它们之间的万有引力为F,当它们相距为r时,系统的引力势能为()。
A. U = -G * m1 * m2 / rB. U = G * m1 * m2 / rC. U = -G * m1 * m2 * rD. U = G * m1 * m2 * r答案:A7. 质点系的动能守恒定律成立的条件是()。
A. 质点系所受合外力为零B. 质点系所受合外力不为零C. 质点系所受合外力为任意值D. 质点系所受合外力不为零,但合外力矩为零答案:A8. 刚体绕定轴转动的角动量守恒定律成立的条件是()。
A. 刚体所受合外力矩为零B. 刚体所受合外力不为零C. 刚体所受合外力为任意值D. 刚体所受合外力矩不为零答案:A9. 刚体的平行轴定理表明,刚体绕任意轴的转动惯量I与绕通过质心的平行轴的转动惯量I_c之间的关系是()。
大学理论力学期末考试题库及答案
大学理论力学期末考试题库及答案一、选择题(每题2分,共20分)1. 质点系的质心位置取决于()。
A. 质点系的总质量B. 质点系中各质点的质量C. 质点系中各质点的位置D. 质点系中各质点的速度答案:C2. 刚体的转动惯量与()有关。
A. 质量B. 质量分布C. 质量分布和形状D. 形状3. 两个质点组成的系统,若两质点间的作用力大小相等,方向相反,则这两个力()。
A. 是一对平衡力B. 是一对作用力和反作用力C. 是一对内力D. 不能确定答案:B4. 质点沿直线做匀加速运动,加速度为a,初速度为v0,则经过时间t后的速度v为()。
A. v = v0 + atB. v = v0 - atC. v = v0 + 1/2atD. v = v0 - 1/2at5. 两个质点组成的系统,若两质点间的作用力大小相等,方向相反,则这两个力()。
A. 是一对平衡力B. 是一对作用力和反作用力C. 是一对内力D. 不能确定答案:B6. 刚体绕固定轴转动时,其转动惯量与()有关。
A. 质量B. 质量分布C. 质量分布和形状D. 形状答案:C7. 质点沿直线做匀加速运动,加速度为a,初速度为v0,则经过时间t后的位移s为()。
A. s = v0t + 1/2at^2B. s = v0t - 1/2at^2C. s = v0t + at^2D. s = v0t - at^2答案:A8. 刚体绕固定轴转动时,其角加速度与()有关。
A. 质量B. 质量分布C. 质量分布和形状D. 形状答案:B9. 质点沿直线做匀加速运动,加速度为a,初速度为v0,则经过时间t后的位移s为()。
A. s = v0t + 1/2at^2B. s = v0t - 1/2at^2C. s = v0t + at^2D. s = v0t - at^2答案:A10. 两个质点组成的系统,若两质点间的作用力大小相等,方向相反,则这两个力()。
A. 是一对平衡力B. 是一对作用力和反作用力C. 是一对内力D. 不能确定答案:B二、填空题(每题2分,共20分)1. 质点系的质心位置取决于质点系中各质点的________和________。
中国海洋大学理论力学__期末考试试题(题库_带答案)
理论力学 期末考试试题1-1、自重为P=100kN 的T 字形钢架ABD,置于铅垂面内,载荷如图所示。
其中转矩M=20kN.m ,拉力F=400kN,分布力q=20kN/m,长度l=1m 。
试求固定端A 的约束力。
解:取T 型刚架为受力对象,画受力图.1-2 如图所示,飞机机翼上安装一台发动机,作用在机翼OA 上的气动力按梯形分布:1q =60kN/m ,2q =40kN/m ,机翼重1p =45kN ,发动机重2p =20kN ,发动机螺旋桨的反作用力偶矩M=18kN.m 。
求机翼处于平衡状态时,机翼根部固定端O 所受的力。
解:1-3图示构件由直角弯杆EBD 以及直杆AB 组成,不计各杆自重,已知q=10kN/m ,F=50kN ,M=6kN.m ,各尺寸如图。
求固定端A 处及支座C 的约束力。
1-4 已知:如图所示结构,a, M=Fa,12F F F ==, 求:A ,D 处约束力.解:1-5、平面桁架受力如图所示。
ABC为等边三角形,且AD=DB。
求杆CD的内力。
1-6、如图所示的平面桁架,A 端采用铰链约束,B 端采用滚动支座约束,各杆件长度为1m 。
在节点E 和G 上分别作用载荷E F =10kN ,G F =7 kN 。
试计算杆1、2和3的内力。
解:2-1 图示空间力系由6根桁架构成。
在节点A上作用力F,此力在矩形ABDC平面内,且与铅直线成45º角。
ΔEAK=ΔFBM。
等腰三角形EAK,FBM和NDB在顶点A,B和D处均为直角,又EC=CK=FD=DM。
若F=10kN,求各杆的内力。
F。
2-2 杆系由铰链连接,位于正方形的边和对角线上,如图所示。
在节点D沿对角线LD方向作用力D在节点C沿CH边铅直向下作用力F。
如铰链B,L和H是固定的,杆重不计,求各杆的内力。
2-3 重为1P=980 N,半径为r =100mm的滚子A与重为2P=490 N的板B由通过定滑轮C的柔绳相连。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 1 页 共 3 页 《理论力学》期末考试 模拟试卷07 (考试时间:120分钟)
题 序 一 二 三 四 五 六 总分 得 分
一.选择题(每题3分,共15分。请将答案的序号填入划线内。) 1.若平面力系由三个力组成(设这三个力互不平行),下述说法正确的是( D ) (A) 若力系向某点简化,主矩为零,则此三个力必然汇交于一点 (B) 若主矢为零,则此三个力必然汇交于一点 (C) 此力系绝不能简化为一个合力偶 (D) 若三个力不汇交于一点,则此力系一定不平衡
2.物块重kN5,放置于水平面上,与水平面间的摩擦角om35,今用与铅垂线成o60角的力F推动物块,若kNF5,则物块将( A )。 (A) 不动 (B) 滑动 (C) 处于临界状态 (D) 滑动与否无法确定 3.点作曲线运动时,下述说法正确的是( B )。 (A) 若切向加速度为正时,则点作加速运动 (B) 若切向加速度与速度符号相同,则点作加速运动 (C) 若切向加速度与速度符号相反,则点作加速运动 (D)若切向加速度为零,则速度为常矢量 4.均质直杆AB直立在光滑的水平面上,当杆由铅直位置无初速倒下时,杆质心点的轨迹是下述的哪一种( A )。 (A) 是一条直线段 (B) 是一个四分之一的圆弧 (C) 是一个四分之一的椭圆弧 (D) 是上述三种之外的一条曲线段 5.若质点的动能保持不变,则( D )。 (A) 该质点的动量必守恒 (B) 该质点必作直线运动 (C) 该质点必作变速运动 (D) 该质点必作匀速运动 二.填空题(每空2分,共30分。请将答案填入划线内。) 1.作用在刚体上的力可沿其作用线任意移动,而不改变力对刚体的 作用效果 ,所以,
在静力学中,力是 滑移 矢量。 2.作用在刚体上的力平行移动时,必须附加一个力偶,附加力偶的矩等于 原力对新的作用点之矩 。
3.右图所示正方体的边长为a,力F沿AB作用于A点,则该力对y轴之矩
为)(FyM=22Fa 。 4.动点的相对速度是指 动点相对于动系的运动速度 ,绝对速度是指 动点对于定系的运动速度 ,牵连速度是指 动系上与动点相重合的点相对于定系的速度 。 5.刚体的平面运动可以简化为平面图形在自身平面内的运动。可分解为随基点的 平动 和绕基点的 转动 。 6.质点系的 内 力不影响质心的运动。只有 外 力才能改变质心的运动。
7.一等腰直角三角形板OAB在其自身平面内以等角速度绕顶点O转动,某一动点M相对此三角形板以匀速沿AB边运动,当三角形板转一圈时,M点走过了AB。如已知
bOBAB,则当M点在A时的相对速度的大小rv=2b;科氏加速度的大小ca=2b。
8.均质滑轮绕通过O点并垂直于平面Oxy的水平轴Oz作定轴转动,滑轮质量为1m,半径为r,一根绳子跨过滑轮,绳子的两端悬挂质量均为2m的重物A和B,(绳质量不计,绳与滑轮间没有相对滑动),图示瞬时滑轮的角速度为,角加速度为,则此系统在该瞬时的动
量有大小 P=0 ;对Oz轴的动量矩 zL =212(2)2mmr 。
三、简支梁AB的支承和受力情况如下图所示。已知分布载荷的集度mkNq/20,力偶矩的大小mkNM20,梁的跨度ml4。不计梁的自重,求支座A、B的约束反
.
系 班 姓名 座号 成绩 . ...................................................... 密 .................................... 封 ................................ 线 ....................................
..................
o60
F
O F x y
z A B 第 2 页 共 3 页 力。(10分) 解:(1)选梁为研究对象(2分) (2)受力分析如图所示(6分) (3)列平衡方程: 0xF 0AxF (3分)
0yF 02AyBylFFq(3分)
0)(FMA 024ByllFlqM(3分)
联立求解,可得 0AxF 25()AyFkN 15()ByFkN (3分)
四、物体A和B各重AG和BG,BAGG;滑轮重G,并可看作半径为r的匀质圆盘,如下图所示。不计绳索的质量,试求物体A的速度是v时整个系统的动量。(15分) 解:系统的动量等于各物体动量的矢量和。 重物A的动量为
AA
GPvg (3分)
方向垂直向下。重物B的动量为 BB
GPvg (3分)
方向垂直向上。而滑轮的动量等于零。故整个系统的动量为 ABABAB
GGGGPPPvvvggg
方向垂直向下。 (4分)
五、下图所示结构的杆重不计,已知:mkNq/3,kNFP4,mkNM2,ml2,C为光滑铰链。试求铰支座B处及固定端A的约束反力。(15分)
解:(1)分别选整体和CB杆为研究对象 (3分) (2)分别进行受力分析 (6分) (3)分别列平衡方程,有 整体: 0xF 0AxPFqlF 0yF 0AyByFF
0)(FMA 3202AByPlMFlqlFlM(6分)
CB杆:0iM 30ByFlM (3分) 联立求解,可得 10()AxPFqlFkN, 0.577()AyFkN
22()AMkN 0.577()ByFkN (2分)
六、平面机构的曲柄OA长为l2,以匀角速度0绕O轴转动。在图示位置时,BOAB,并且o90OAD。求此时套筒D相对杆BC的速度和加速度。(15分)
r O
A B v
C A
/2l
q B M
/2l AyF AxF ByF
AM AyF
AxF ByF l
M 2l l C
A PF
q B
CyF
ByF M C
B 第 3 页 共 3 页
解:(1)先进行速度分析。以套筒B为动点,杆OA为动系,由aervvv作B的速度图,由图可知:
0o23cos303eavvl; o03sin303ravvl (4分) 再以A为基点分析D点的速度。由DADAvvv作D点的速度合成图。由图可知: 00oo243cos30cos303AD
lv
vl,o023cos603DADvvl
0233DADADAvvADl
(4分)
再以套筒D为动点,杆BC为动系,由111aervvv作D点速度合成图,由图可知: 111aervvv
其中:10433aDvvl,10233eBCavvvl,代入上式可得套筒D相对杆BC的速度为
1110233raevvvl (2分)
(2)再进行加速度分析。以套筒B为动点,杆OA为动系,由naerkaaaa作B的速度图,列ka方向的投影方程,有 ocos30akaa
其中:2002323kravl,代入上式,可得20o4cos303kaaal。 (4分) 再以A为基点分析D点的加速度。由nDADADAaaaa作D点的速度合成图。列nDAa方向的投影方程,有 ocos30nDDAaa
其中:220439nDADAaDAl,代入上式,可得20o8cos309nDADaal (4分) 再以套筒D为动点,杆BC为动系,由111aeraaa作D点加速度合成图,列1aa方向的投影方程,有111aeraaa
其中:21089aDaal,21043eaaal,代入上式,可得
21110209raeaaal (2分)
1111122(sin)sin(sin)sin(3)AyCC
mMmgrdFmvmadtmmr
(1分)
A
B o60
0
O
C D ev av rv Dv
Av
DAv Av A
B o60
0
O
C D
ra
aa nea
D
a
Aa nDAa
ka Aa
DAa
D 1ra 1aa 1ea D
1rv 1av
1ev
