五年级体积与表面积试题(最新整理)
小学五年级长方体正方体表面积体积练习测试题6套

第一套测试题一、填空。
1.4.07立方米=( )立方米( )立方分米2.9.08立方分米=( )升=( )毫升3.一个正方体的表面积是72平方分米,占地面积是( )平方分米。
4.一个长方体的体积是30立方厘米,长6厘米,宽5厘米,高( )厘米。
5.用一根12分米长的铁丝围成一个最大的正方体形状的框架,这个正方体的体积是( )立方分米。
6.用3个棱长4分米的正方体粘合成一个长方体,长方体的表面积比3个正方体的表面积少( )平方分米。
7.一个长方体的体积是96立方分米,底面积是16立方分米,它的高是( )分米。
8.一个棱长是5分米的正方体水池,蓄水的水面低于池口2分米,水的容量是( )升。
9.挖一个长和宽都是5米的长方体菜窖,要使菜窖的容积是50立方米,应该挖( )深。
二、判断。
1.长方体中的三条棱分别叫做长、宽、高。
()2.求一个容器的容积,就是求这个容器的体积。
( ) 3.一个正方体的棱长之和是12厘米,体积是1立方厘米。
( )4.正方体的棱长扩大5倍,它的体积就扩大15倍。
( ) 5.把2块棱长都为2厘米的正方体拼成一个长方体,表面积增加了8平方厘米。
( )三、选择题。
1.用一根52厘米长的铅丝,正好可以焊成长6厘米,宽4厘米,高________厘米的长方体教具。
[ ]①2 ②3 ③4 ④52.如果把长方体的长、宽、高都扩大3倍,那么它的体积扩大________倍。
[ ]①3 ②9 ③27 ④103.加工一个长方体油箱要用多少铁皮,是求这个油箱的[ ] ①表面积②体积③容积4.个长方体水池,长20米,宽10米,深2米,占地________平方米。
[ ]①200 ②400 ③5205.3个棱长是1厘米的正方体小方块排成一行后,它的表面积是[ ].①18平方厘米②14立方厘米③14平方厘米④16平方厘米6.一个棱长是4分米的正方体,棱长总和是________分米。
[ ]①16 ②24 ③32 ④48四、解答应用题。
五年级体积与表面积应用题

长方体和正方体的体积练习题(一)长方体和正方体的体积之-----切1、把一根长 2米的长方体木料,平均截成3段,表面积增加了12平方米,原来长方体木料的体积是多少立方分米2、一个长方体长16分米,高6分米,沿水平方向横切成俩个小长方体,表面积增加160平方分米,求原长方体体积3、有一个正方体被切成24个小长方体,这些长方体的表面积之和为162平方厘米,求原正方体的表面积(二)长方体和正方体的体积之-----增与去4、一个长方体如果高减少3厘米,正好成为一个正方体,表面积少36平方厘米,原长方体的体积5、一个长方体木块,从上部和下部分别截去高为3厘米2厘米的长方体后,便成为一个正方体,表面积减少了120平方厘米,原来长方体体积是多少6、在一个棱长为6厘米的大正方体木块,如果把它锯成棱长为2厘米的小正方体若干块,表面积增加了多少平方厘米7、一个长方体,如果高增加2厘米就成了一个正方体,而且表面积增加56平方厘米,求原长方体的体积8、一个正方体木柱棱长8米,在木柱一头挖去一个棱长2米的正方体,问正方体现在的表面积是多少(三)长方体和正方体的体积之-----底面周长9、一个长方体,表面积是70平方分米,底面积是平方分米,底面周长是分米,这个长方体的高是多少体积是多少10.一个长方体的表面积为16000平方分米,底面是边长为40厘米的正方形,求长方体的体积是多少11、一个长方体的表面积是平方分米,底面积是19平方分米,底面周长是分米,这个乘方体的体积是多少立方分米(四)长方体和正方体的体积之-----锻压12.将一块棱长20厘米的正方体铁块锻压成一块,100厘米长,2厘米厚的铁板,这个铁板的宽是多少13.把一棱长30厘米的正方体钢坯,锻压成高和宽都是5厘米的长方体钢材.能锻造多长14.把一个棱长5厘米的正方体钢材,锻压成长5厘米,宽4厘米的长方体钢材,钢材厚多少厘米(五)长方体和正方体的体积之-----上升水的体积15、在一个长30厘米。
北师大版小学数学五年级长方体表面积和体积测试题
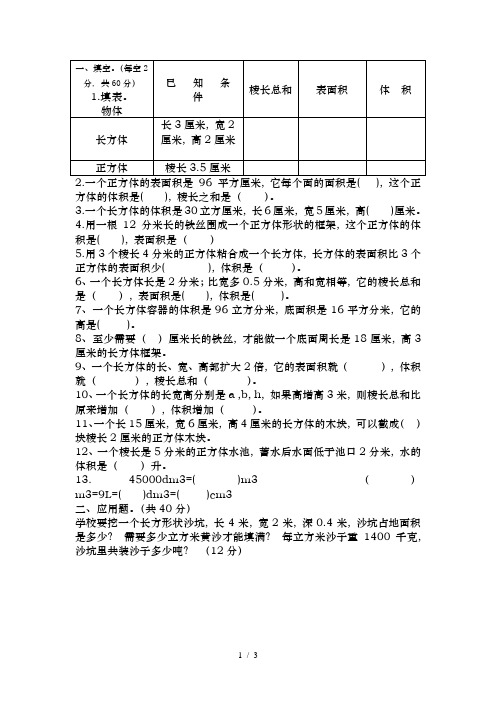
方体的体积是( ), 棱长之和是()。
3.一个长方体的体积是30立方厘米, 长6厘米, 宽5厘米, 高( )厘米。
4.用一根12分米长的铁丝围成一个正方体形状的框架, 这个正方体的体积是( ), 表面积是()5.用3个棱长4分米的正方体粘合成一个长方体, 长方体的表面积比3个正方体的表面积少( ), 体积是()。
6、一个长方体长是2分米;比宽多0.5分米, 高和宽相等, 它的棱长总和是(), 表面积是( ), 体积是( )。
7、一个长方体容器的体积是96立方分米, 底面积是16平方分米, 它的高是( )。
8、至少需要()厘米长的铁丝, 才能做一个底面周长是18厘米, 高3厘米的长方体框架。
9、一个长方体的长、宽、高都扩大2倍, 它的表面积就(), 体积就(), 棱长总和()。
10、一个长方体的长宽高分别是a ,b, h, 如果高增高3米, 则棱长总和比原来增加(), 体积增加()。
11、一个长15厘米, 宽6厘米, 高4厘米的长方体的木块, 可以截成()块棱长2厘米的正方体木块。
12、一个棱长是5分米的正方体水池, 蓄水后水面低于池口2分米, 水的体积是()升。
13. 45000dm3=()m3 ()m3=9L=( )dm3=( )cm3二、应用题。
(共40分)学校要挖一个长方形状沙坑, 长4米, 宽2米, 深0.4米, 沙坑占地面积是多少?需要多少立方米黄沙才能填满?每立方米沙子重1400千克, 沙坑里共装沙子多少吨?(12分)一个长方体的水池, 长8.5米, 宽4米, 深2米, 如果每小时可以放进8立方米, 要放满这一池水需要多少小时?(4分)把一块棱长8厘米的正方体钢坯, 锻造成长1.6分米, 宽5厘米的长方体钢板, 这钢板有多厚?(损耗不计)(4分)在一个长20米, 宽8米, 深2米的长方体蓄水池四周与底面贴瓷砖, 瓷砖是边长为2分米的正方形, 贴完共需瓷砖多少块?需要贴的面积有多大?(8分)一个长方体容器的容积是96升, 内壁高6分米, 装有3分米高的水, 将一石块完全浸入后, 水面上升到5分米, 这个石块的体积是多少?(4分)一个底面是正方形的长方体, 所有棱长的和是100厘米, 它的高是7厘米, 这个长方体的体积是多少立方厘米?(4分)把一个长30厘米、宽24厘米的铁皮的四角分别去掉一个边长为2厘米的正方形, 做成一个无盖的长方体, 这个长方体的体积是多少?(4分)附加题: 一个长方体, 如果高增加3厘米, 就成为一个正方体。
五年级下册数学)计算图形的表面积和体积练习题

五年级下册数学)计算图形的表面积和体积练习题一、计算图形的表面积和体积(每题8分,共16分)一个长方体的长、宽、高分别为L、W、H,它的表面积是2LW+2LH+2WH,它的体积是LWH。
给定的两个图形的尺寸分别为8cm×8cm和5dm×12dm×2dm。
将5dm转换为50cm,那么第二个图形的尺寸为50cm×120cm×20cm。
第一个图形的表面积为2×8×8+2×8×8+2×8×8=384cm²,体积为8×8×8=512cm³。
第二个图形的表面积为2×50×120+2×50×20+2×120×20=cm²,体积为50×120×20=cm³。
二、解答应用题(第1、2、3题每题6分,其它每题5分,共38分)1.加工一个长方体铁皮油桶,长2.5米,宽1.6米,高3米,至少需要多少平方米的铁皮?最多能装多少升油?这个油桶的表面积是2×(2.5×1.6+2.5×3+1.6×3)=33.6平方米。
它的体积是2.5×1.6×3=12立方米,也就是升。
2.学校要挖一个长方形沙坑,长4米,宽2米,深0.4米,它占地多少平方米?需要挖出多少立方米的黄沙?这个沙坑的表面积是2×(4×2+4×0.4+2×0.4)=17.6平方米。
它的体积是4×2×0.4=3.2立方米,需要挖出3.2立方米的黄沙。
3.做一个棱长为6米的正方形无盖鱼缸,需要多少平方米的玻璃?它的容积是多少升?这个鱼缸有6个面,每个面都是一个6×6的正方形,所以需要的玻璃面积是6×6×6=216平方米。
人教版五下长方体、正方体表面积、体积练习题

长方体、正方体练习题班级姓名一、填空:1、长方体或者正方体()叫做它的表面积。
2、一个正方体的棱长是10厘米,它的表面积是()平方厘米。
3、一个长方体长4分米,宽3分米,高2分米,它的表面积是()平方分米。
4、正方体的棱长之和是60分米,它的表面积是()平方分米。
5、用两个长5厘米,宽3厘米,高2厘米的长方体拼成一个表面积尽可能小的正方体,这个拼成的长方体的表面积是()平方厘米。
6、一个正方体的底面积是25平方分米,它的表面积是()平方分米,它的体积是()立方分米。
7、一个长方体,长是5厘米,宽3厘米,高1厘米,这个长方体的棱长总和是,表面积是,体积是。
8、一个正方体的棱长总和是24分米,它的表面积是,体积是。
9、3个棱长是1厘米的正方体小方块排成一行,形成的长方体的表面积是,体积是。
10、用同样的小正方体拼成一个大正方体,至少用个这样的小正方体。
11、一个正方体的表面积是36平方厘米,把它放在桌子上占的面积是()平方厘米。
12、一个长方体长5厘米,宽5厘米,高4厘米,这个长方体有2个面是()形,有()个面的面积相等,长方体的表面积是()。
13、把一根长80厘米、宽5厘米、高5厘米的长方体木材,锯成长度都是40厘米的两段,表面积比原来增加了。
14、把两个同样大小的长方体拼成一个正方体,这个正方体的棱长是10厘米,原来长方体的表面积平方厘米,体积是立方厘米。
15、用3个棱长4分米的正方体粘合成一个长方体,长方体的表面积比3个正方体的表面积少( )平方分米。
16、焊接一个长7cm、宽2cm、高1cm的长方体框架,至少要用()cm的铁丝。
二、判断:1、物体所占空间的大小叫做物体的体积。
()2、正方体的棱长扩大2倍,它的体积就扩大8倍。
()3、容积和体积的计算方法相同,但意义不同。
()4、正方体的棱长是6厘米,它的表面积和体积相等。
()5、相邻的面积单位之间的进率是100。
()6、表面积相等的物体,它们的体积也一定相等。
完整版)五年级下册数学表面积和体积练习题

完整版)五年级下册数学表面积和体积练习题1、计算长方体钢材重量:长2米,横截面是边长为5厘米的正方形,每立方分米钢重7.8千克。
首先计算出长方体的体积为2m × 0.05m × 0.05m = 0.005立方米,然后将体积乘以钢的密度7.8千克/立方分米,得到钢材重量为0.005 × 7.8 =0.039千克。
2、一个棱长为5分米的正方体鱼缸,里面装满水,将水倒入一个底面积为48平方分米,高为6分米的长方体鱼缸里,求水深。
首先计算出正方体鱼缸的体积为0.05m × 0.05m ×0.05m = 0.立方米,然后将体积乘以水的密度1千克/立方分米,得到水的质量为0. × 1000 = 0.125千克。
将水倒入长方体鱼缸后,长方体鱼缸的底面积为48平方分米,高度为6分米,因此长方体鱼缸的体积为0.48立方米。
根据相似三角形的性质,可以得出两个鱼缸中水深的比例为5:12,因此水深为6分米 ×5/12 = 2.5分米。
3、将一块棱长为8厘米的正方体钢坯锻造成长16厘米,宽5厘米的长方体钢板,求钢板的厚度。
由于锻造过程中损耗不计,因此钢坯的体积等于钢板的体积。
钢坯的体积为0.008立方米,钢板的体积为0.016m × 0.05m × h,其中h为钢板的厚度。
将两式相等,解得h=0.16厘米。
4、一个长方形铁皮长30cm,宽25cm,从四个角各切掉一个长为5cm的正方形,然后做成一个无盖的盒子,求铁皮的面积和盒子的容积。
首先计算出四个正方形的面积为4 ×0.05m × 0.05m = 0.01平方米,然后将这个面积从原来的长方形铁皮面积中减去,得到剩余的面积为0.75平方米。
这个面积即为盒子的表面积。
盒子的容积为(30cm-2×5cm)×(25cm-2×5cm)×5cm=2500立方厘米=0.0025立方米。
五年级下册表面积和体积练习题

五年级下册表面积和体积练习题1.正方体的棱长和等于棱长的12倍。
2.长方体的表面积等于长乘以宽再乘以2,再加上长乘以高再乘以2,再加上宽乘以高再乘以2.3.正方体的表面积等于棱长的6次方。
4.长方体的体积等于长乘以宽乘以高。
5.正方体的体积等于棱长的3次方。
6.长方体的体积等于底面积乘以高。
7.三角形的面积等于底乘以高除以2.1.求一个面积为36平方米的正方体所有棱长的和。
2.用一根铁丝焊成一个棱长为8厘米的正方体框架,求用同一根铁丝焊成一个长10厘米、宽7厘米的长方体框架的高。
3.天天游泳池的长、宽、深分别为25米、10米、1.6米,瓷砖的边长为1分米的正方形,求至少需要多少块瓷砖。
4.把棱长为12厘米的正方体切割成棱长为3厘米的小正方体,可以切割成多少块。
5.把棱长为15分米的正方体平均分成三个长方体后,求木块的表面积增加了多少方厘米。
6.求一个长方体的长、宽、高分别为9厘米、6厘米、x 厘米,且棱长和为72厘米的表面积。
7.制作一个长1.2米、宽0.6米、高0.8米的无盖长方体鱼缸,求至少需要多少平方米的玻璃。
8.一块长1.2米、宽6分米、厚3分米的长方体木块,可以截出多少块棱长为3分米的正方体。
9.一个长方体的高增加3厘米后成为正方体,此时表面积比原来增加了96平方厘米,求原来的长方体体积。
10.把棱长为6分米的正方体钢锭熔铸成一个长9分米、宽4分米的长方体钢锭,求这个长方体钢锭的高。
11.做6个口径为2分米、长度为1米的烟囱,求至少需要多少平方米的铁皮。
12.求一个长方体的长、宽、高分别为10厘米、7厘米、x 厘米,且棱长总和为80厘米的高和表面积。
13.求一个长方体的长、宽、高分别为10厘米、8厘米、2厘米的棱长之和、表面积和体积。
14.一根长96厘米的铁丝围成一个正方体,求这个正方体的棱长和表面积。
15.修建长50米、宽42米的长方形操场,先铺10厘米的三合土,再铺5厘米的煤渣,求需要多少立方米的三合土和煤渣。
五年级数学表面积和体积的题

五年级数学表面积和体积的题一、题目。
1. 一个正方体的棱长为5厘米,求它的表面积和体积。
- 解析:- 正方体表面积公式为S = 6a^2(a为棱长),这里a = 5厘米,所以表面积S=6×5^2=6×25 = 150平方厘米。
- 正方体体积公式为V=a^3,所以体积V = 5^3=125立方厘米。
2. 一个长方体,长为8厘米,宽为6厘米,高为4厘米,求它的表面积和体积。
- 解析:- 长方体表面积公式S=(ab + ah+bh)×2(a为长,b为宽,h为高),这里a = 8厘米,b = 6厘米,h = 4厘米。
则S=(8×6 + 8×4+6×4)×2=(48 + 32+24)×2=(80 + 24)×2 = 104×2=208平方厘米。
- 长方体体积公式V=abh,所以体积V=8×6×4 = 192立方厘米。
3. 一个正方体的表面积是216平方厘米,求它的棱长和体积。
- 解析:- 设正方体棱长为a,由正方体表面积公式S = 6a^2,已知S = 216平方厘米,则6a^2=216,a^2=36,解得a = 6厘米。
- 正方体体积公式V=a^3,所以体积V = 6^3=216立方厘米。
4. 一个长方体的体积是360立方厘米,长是10厘米,宽是6厘米,求它的高和表面积。
- 解析:- 由长方体体积公式V = abh,已知V = 360立方厘米,a = 10厘米,b = 6厘米,则h=(V)/(ab)=(360)/(10×6)=6厘米。
- 长方体表面积公式S=(ab + ah+bh)×2=(10×6+10×6 + 6×6)×2=(60+60 + 36)×2=(120+36)×2 = 156×2 = 312平方厘米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
体积和表面积复习一
1、做一个长方体浴缸(无盖),长8分米,宽4分米,高5分米,至少需要多少平方分米的玻璃?如果每平方米
玻璃6元钱,至少需要多少钱买玻璃?
2、小明的房间长5米,宽4.5米,高3米,门窗的面积是3平方米。
现在要在这个房间的四壁和顶面粉刷水泥,
如果每平方米需要水泥5千克,一共要水泥多少千克?
3、一根钢材,横截面是正方形,周长是8分米,钢材长14分米,如果将它熔成棱长为0.5分米的正方形钢材,
可以熔铸多少块?
4、一个长方体无盖的水箱长0.8米,宽0.6米,高0.5米。
做这个水箱至少需要多少平方米铁皮?如果每升水1
千克,这个水箱最多能装多少千克水?
5、用96厘米的铁丝折一个正方形框架,这个正方体棱长是多少?如果用纸糊满框架的表面,至少需要纸多少厘
米?
6、做一节长120厘米,宽和高都是10厘米的通风管,至少需要铁皮多少平方厘米?做12节这样的通风管呢?
7、如果用一根铁丝围成一个长10厘米,宽8厘米,高6厘米的长方体框架。
这根铁丝长多少厘米?如果在这个
框架的表面贴上彩纸,彩纸的面积大约是多少平方厘米?
8、一个长方体玻璃容器,从里面量长8dm,宽5dm,高6dm,,内有水深0.4m,若放入一个棱长为4dm的小正方体,
现在水深多少分米?
9、用一根长48厘米的铁丝折成一个长方体框架,测得长和宽分别是5厘米和3厘米,它的体积和表面积分别是
多少?
10、把2块棱长为1.5dm的正方体木块拼成一个长方体。
这个长方体的体积、表面积分别是多少?
11、一个长方体玻璃缸,从里面量长8dm,宽6dm,高4dm,水深3.5dm。
如果放入一棱长为3dm的正方体铁块,
缸里的水会溢出多少升?
12、王叔叔用120cm长的铁丝焊成了一个底面周长为36cm的长方体框架,这个长方体框架的高是多少厘米?
如果底面长为10cm,这个长方体框架的体积和表面积分别是多少?
13、把一根长2m的长方体木料锯成3段后,表面积比原来增加了144cm2,这根木料的体积是多少立方厘米?
14、一块橡皮泥,先捏成一个棱长6cm的正方体,后来又改捏成一个长8cm,宽3cm的长方体,这时高是多少
厘米?
15、在一个长120cm、宽60cm的长方体水箱里,放入一块长方体的铁块后。
,水面就比原来上升2cm(水淹没
铁块)。
已知铁块的长和宽都是20cm,求铁块的高。
16、在一个棱长为30cm的正方体水箱中,有深15cm的水,将一个长20cm,宽15cm的长方体铁块放入水箱中,
水面高度为20cm,这个铁块高多少厘米?
17、一个棱长为5cm的正方体木块,把它锯成棱长为1cm的正方体若干块,表面积增加多少平方厘米?
18、把一个体积是460cm3的石块放入一个长方体容器中,完全浸入水中后,水面由148cm上升到150cm,这
个容器的底面积是多少平方厘米?
22、把一张长20cm、宽12cm的长方形纸裁成几个同样大小并且面积尽可能大的正方形纸,一共可以裁多少个?
“”
“”
At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。
