哈工大导航原理大作业
哈工大GPS卫星导航实验报告4

实验四接收机位置解算及结果分析(选作)一、实验原理GPS接收机位置的导航解算即解出本地接收机的纬度、经度、高度的三维位置,这是GPS 接收机的核心部分。
GPS接收机位置求解的过程如下:前序实验已经提到,导航电文与测距码(C/A码)共同调制L1载频后,由卫星发出。
卫星上的时钟控制着测距信号广播的定时。
本地接收机也包含有一个时钟,假定它与卫星上的时钟同步,接收机接收到一颗卫星发送的数据后,将导航电文解码得到导航数据。
定时信息就包含在导航数据中,它使接收机能够计算出信号离开卫星的时刻。
同时接收机记下接收到卫星信号的时刻,便可以算出卫星至接收机的传播时间。
将其乘以光速便可求得卫星至接收机的距离R,这样就把接收机定位于以卫星为球心的球面的某一个地方。
如果同时用第二颗卫星进行同样方法的测距,又可将接收机定位于以第二颗卫星为球心的第二个球面上。
因此接收机就处在两个球的相交平面的圆周上。
当然也可能在两球相切的一点上,但这种情况只发生在接收机与两颗卫星处于一条直线时,并不典型。
于是,我们需要同时对第三颗卫星进行测距,这样就可将接收机定位于第三个球面上和上述圆周上。
第三个球面和圆周交于两个点,通过辅助信息可以舍弃其中一点,比如对于地球表面上的用户而言,较低的一点就是真实位置,这样就得到了接收机的正确位置。
在上述求解过程中,我们假定本地接收机与卫星时钟同步,但在实际测量中这种情况是不可能的。
GPS星座内每一颗卫星上的时钟都与一个叫做世界协调时(UTC,即格林尼至时间)的内在系统时间标度同步。
卫星钟差可根据导航电文中给出的有关钟差参数加以修正,其基准频率的频率稳定度为10-13左右。
而本地接收机时钟的频率稳定度只有10-5左右,而且其钟差一般难以预料。
由于卫星时钟和接收机时钟的频率稳定度没有可比性,这样,就会在卫星至接收机的传播时间上增加一个很大的时间误差,严重影响定位精度。
为解决这一问题,我们通常将接收机的钟差也作为一个未知参数,与本地接收机的ECEF坐标(ECEF坐标系的定义在前序实验中已经给出)一起求解。
哈工大自动控制原理大作业

自动控制原理大作业1.题目在通常情况下,自动导航小车(AGV )是一种用来搬运物品的自动化设备。
大多数AGV 都需要有某种形式的导轨,但迄今为止,还没有完全解决导航系统的驾驶稳定性问题。
因此,自动导航小车在行驶过程中有时会出现轻微的“蛇行”现象,这表明导航系统还不稳定。
大多数的AGV 在说明书中都声明其最大行驶速度可以达到1m/s ,但实际速度通常只有0.5m/s ,只有在干扰较小的实验室中,才能达到最高速度。
随着速度的增加,要保证小车得稳定和平稳运行将变得越来越困难。
AGV 的导航系统框图如图9所示,其中12=40ms =21ms ττ, 。
为使系统响应斜坡输入的稳态误差仅为1%,要求系统的稳态速度误差系数为100。
试设计合适的滞后校正网络,试系统的相位裕度达到50 ,并估计校正后系统的超调量及峰值时间。
()R s ()Y s2.分析与校正主要过程2.1确定开环放大倍数K100)1021.0)(104.0(lim )(lim =++==s s s sK s sG K v (s →0) 解得K=100)1021.0)(104.0(100++=s s s G s 2.2分析未校正系统的频域特性根据Bode 图:穿越频率s rad c /2.49=ω相位裕度︒---=⨯-⨯--=99.18)2.49021.0(arctan )2.4904.0(arctan 9018011γ 未校正系统频率特性曲线由图可知实际穿越频率为s rad c /5.34=ω2.3根据相角裕度的要求选择校正后的穿越频率1c ω现在进行计算:︒︒︒--=+=---55550)021.0(arctan )04.0(arctan 901801111c c ωω则取s rad c /101=ω可满足要求2.4确定滞后校正网络的校正函数 由于11201~101c ωω)(=因此取s rad c /110111==ωω)(,则由Bode 图可以列出 40)1lg(20)1lg(40)110lg(2022+=+ωω 解得s rad /1.02=ω于是1.0=β 则滞后网络传递函数为1101)(++=s s s G c ,10=T 2.5验证已校正系统的相位裕度已校正系统的开环传递函数为:)110)(1021.0)(104.0()1(100)()(++++=s s s s s s G s G c 相位裕度︒----=-⨯-⨯-+-=2.51)100(arctan )10021.0(arctan )1004.0(arctan )10(arctan 901801111γ校正后的相位裕度大于50°,满足设计要求。
L1-导航原理(哈工大导航原理、惯性技术课件)讲解学习

陶瓷 壳体
球形 转子
球形电极 自转轴
钛离子泵
缺陷:结构复杂、昂贵
Lecture 1 -- Introduction
23
5.2 低成本、小型化
环形激光陀螺 (Ring laser gyro -- RLG) 1960s 早期开始研制, 1970s 后期进入实用
光纤陀螺 (Fiber Optical Gyro – FOG) 1970s 开始研制, 1980s 早期进入实用
15
4.2 历史: 陀螺罗经
陀螺仪被寄予希望, 但面临着自动寻北 的挑战
1908年, Anschutz (德国) 发明了陀螺罗经 (gyro compass)
1909年, Sperry (美国) 也独 立研制出陀螺罗经.
—— 陀螺罗经的出现标志着陀螺仪技术 的现代应用的发端
Lecture 1 -- Introduction
Lecture 1 -- Introduction
14
4.2 历史: 在航海的应用
磁罗盘 (Magnetic compass) 被用于早期的航海
19世纪后期,大量的木质 轮船被钢铁材质的轮船取代, 使磁罗盘的效能受到影响.
磁罗盘的使用在地球两极 附近受到限制 寻找替代的方向指示装置
Lecture 1 -- Introduction
Exam: Close book, close note Contact: 15204694662
Lecture 1 -- Introduction
28
此课件下载可自行编辑修改,仅供参考! 感谢您的支持,我们努力做得更好!谢谢
t
S
S0
Vdt
0
惯性导航的特点: 自主 (Autonomous, self-contained) 只依赖于对载体的惯性测量 (借助加速度计、陀螺仪) 连续稳定的输出
自01-哈工大机械原理大作业任务书-连杆机构参考模板
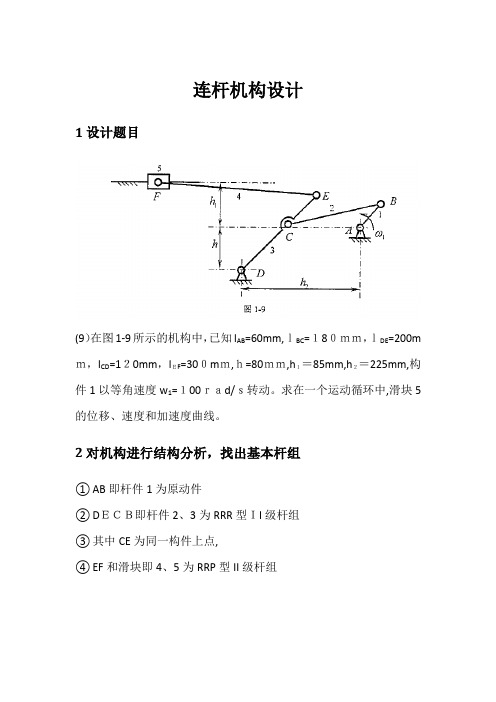
连杆机构设计1设计题目(9)在图1-9所示的机构中,已知l AB=60mm,lBC=180mm,lDE=200m m,l CD=120mm,lEF=300mm,h=80mm,h1=85mm,h2=225mm,构件1以等角速度w1=100rad/s转动。
求在一个运动循环中,滑块5的位移、速度和加速度曲线。
2对机构进行结构分析,找出基本杆组①AB即杆件1为原动件②DECB即杆件2、3为RRR型II级杆组③其中CE为同一构件上点,④EF和滑块即4、5为RRP型II级杆组3各基本杆组的运动分析数学模型② RRR 杆组运动分析的数学模型1.位置分析设两个构件长度1R ,2R 及外运动副1N ,2N 的位置已知,求两个构件的位置角1θ,2θ及内运动副3N 的位置。
选定坐标系及相应的标号如下图,构件的位置角i θ约定从响应构件的外运动副i N 引x 轴的方向线,按逆时针量取。
设外运动副1N ,2N 的位置坐标分别为1N (1x P ,1y P ),2N (2x P ,2y P ),则 12221212[( -)( -)]x x y y d P P P P =+ 222121cos ()/(2 )d R R R d α=++ 212 1arctan(( )/( )y y x x P P P P ϕ=-- 1θϕα=±内运动副3N 点坐标为:3111 cos x x P P R θ=+3111 sin y y P P R θ=+构件2K 的位置角:23232arctan[()/( )]y y x x P P P P θ=--位置分析过程中应注意两个问题:(1) 因为1N ,2N 的位置及杆长1R ,2R 都是给定的,这就可能出现d >12R R +或12d R R <-的情况。
在这两种情况下实际上不可能形成RRR 杆组,计算过程中应及时验算上述条件,如满足上述条件应中止运算并给出相应信息。
(2)在给定1N ,2N ,1R ,2R 的条件下,3N 可能有两个位置如上图中的3N 和3N ',相应的1θϕα=+和1θϕα'=-,我们称为杆组的两种工作状态。
哈工大机械原理大作业连杆

哈工大机械原理大作业-连杆连杆是机械原理中常见的机构之一,也是机械工程中非常重要的部件。
它由两个旋转接头和一个连接两个旋转接头的杆件组成。
连杆广泛应用于各种机械设备中,如汽车发动机、泵、机床等。
本文将介绍连杆的工作原理、应用以及设计要点。
连杆的工作原理是将旋转运动转化为直线运动或将直线运动转化为旋转运动。
它通过两个旋转接头的运动将杆件上的一个点的运动转化为另一个点的运动。
连杆的运动有两种基本形式:一是曲柄连杆机构,二是摇杆连杆机构。
曲柄连杆机构中,一个旋转接头为曲柄,另一个旋转接头为连杆;摇杆连杆机构中,一个旋转接头为摇杆,另一个旋转接头为连杆。
连杆广泛应用于各种机械设备中。
在汽车发动机中,连杆将曲轴的旋转运动转化为活塞的直线运动,从而驱动汽缸的工作;在泵中,连杆将电机的旋转运动转化为柱塞的直线运动,从而产生压力;在机床中,连杆将电机的旋转运动转化为工作台的直线运动,从而实现加工。
设计连杆时需要考虑一些要点。
首先是连杆的材料选择和尺寸设计。
连杆需要承受较大的力和扭矩,因此需要选择具有较高强度和刚度的材料。
同时,根据应用需求和力学原理,设计连杆的尺寸,以确保其能够承受正常工作条件下的负荷。
其次是连杆的润滑和密封。
连杆在工作过程中需要润滑剂来减少摩擦和磨损,同时需要密封装置来防止润滑剂泄漏。
因此,设计连杆时需要考虑润滑剂的供给和密封装置的设计。
最后是连杆的制造和装配。
连杆的制造需要保证其精度和质量,以确保其运转平稳和可靠。
在装配过程中,需要按照设计要求进行装配,同时进行必要的调试和检测,以确保连杆的工作性能符合要求。
总之,连杆是机械工程中非常重要的部件,广泛应用于各种机械设备中。
设计和制造连杆需要考虑材料选择、尺寸设计、润滑和密封以及制造和装配等方面的要点。
通过合理的设计和制造,可以确保连杆的工作性能和可靠性,从而提高机械设备的工作效率和寿命。
哈工大惯性技术(导航原理)大作业讲解

Assignment of Inertial Technology 《惯性技术》作业Autumn 2015Assignment 1: 2-DOF response simulation A 2-DOF gyro is subjected to a sinusoidal torque with amplitude of 4 g.cmand frequency of 10 Hz along its outer ring axis. The angular moment of its rotor is 10000 g.cm/s , and the angular inertias in its equatorial plane are both 4 g.cm/s 2. Please simulate the response of the gyro within 1 second, and present whatever you can discover or confirm from the result.In this simulation, we are going to discuss the response of a 2-DOF gyro to sinusoidal torque input. According to the transfer function of the 2-DOF gyro, the outputs can be expressed as: 12222()()()()yx y x y x y J H s M s M s J J s H s J J s H α=-++ 12222()()()()x y x x y x y J H s M s M s J J s H s J J s H β=+++ The original system transfer function is a 2-input, 2-output coupling system. But the given input only exists one input, we can treat the system as 2 separate FIFO systemAs a consequence, we can establish the block diagram of the system in simulink in Fig 1.1. Substitute the parameters into the system and input, then we have the input signals as follow: 0,4sin(20)y ox M M t π==Then the inverse Laplace transform of the output equals the response of the gyro in timedomain as follows:02222000200222200()sin sin ()()()cos cos ()()ox a ox a x a x a ox ox a ox a a a a a M M t t t J J M M M t t t H H H ωαωωωωωωωωωβωωωωωωωω=-+--=+---Fig 1.1 The block diagram of the system in simulinkAnd the simulation results in time domain within 1 second are shown in the follwing pictures. Fig1.2 is the the output of outer ring ()tα. Fig1.3 is the output of inner ring ()tβ. Fig1.4 is the trajectory of 2-DOF gyro’s response to sinusoidal input. As we can see from the Fig1.3,there are obvious sawtooth wave in the output of the inner ring. It’s a unexpected phenomenon in my original theoretical analysis.Fig1.2 The output of inner ring ()tβFig 1.3 The output of outer ring ()tαI believe the sawtooth wave is caused by the nutation. For the frequency of the nutation isobtained as100002500/3974eHrad s HzJω===≈, which is far higher than the frequencyof the applied sinusoidal torque , namelyaωω.Fig 1.4 Trajectory of 2-DOF gyro’s response to sinusoidal input The trajectory of 2-DOF gyro’s response to sinusoidal input are shown in Fig1.4. As we can see, it’s coupling of X and Y channel scope output. The overall shape is an ellipse, which is not perfect for there are so many sawteeth on the top of it.Note that the major axis of ellipse is in the direction of the forced procession, amplitude of which isoxMHω, whereas the minor axis is in the direction of the torsion spring effects, with amplitude oxaMHω.The nutation components are much smaller than that of the forced vibration, which can be eliminated to get the clear static response.2200222()sin sin()cos(1cos)()ox oxa ax aox ox oxa aa a a aM Mt t tJ HM M Mt t tH H Hαωωωωωωβωωωωωωω≈≈-≈-=--To prove it, we eliminate the effects of the nutation namely the quadratic term in the denominator and get Fig 1.5, which is a perfect ellipse. We can conclude that when input to the 2-DOF gyro is sinusoidal torque, the gyro will do an ellipse conical pendulum as a static response, including procession and the torsion spring effects, together with a high-frequency vibration as the dynamic response.Fig 1.5 Trajectory of the gyro’s response without nutationAssignment 2: Single-axis INS simulation2.1 description of the problemA magnetic levitation train is being tested along a track running north-south. It first accelerates and then cruises at a constant speed. Onboard is a single-axis platform INS, working in the way described by the courseware of Unit 5: Basic problems of INS. The motion information and Earth parameters are shown in table 2-1, and the possible error sources are shown in Table2-2.Fig2.1 The sketch map of the single-axis INS problemYou are asked to simulate the operation of the INS within 10,000 seconds, and investigate, first one by one and then altogether, the impact of these error sources on the performance of the INS.The block diagram in the courseware might be of some help. However, there lurks an inconspicuous error, which you have to correct before you can obtain reasonable results.There are one core relevant formula, to get the specific form of its solution, we should substitute the unknown parameters.(1)()c N ay A K y ga=∆++-Firstly, the input signal is accelerometer of the platform, and the velocity of the platform is the integration of the acceleration./py y ydty Rω=+=-⎰The acceleration along Yp may contains two parts:cos gsin gypf y yααα=-≈-When accelerometer errors are concerned, the output of accelerometer will be:(1)N a yp Na K f A=++When gyro errors concerned:'(1)p g pKωωε=++Only αis unknown:[(1)]tg pttptK dtdtααωεϕϕω=+++-∆∆=⎰⎰And the reference block diagram and simulink block diagram are as follows in Fig2.2, Fig2.3. There is a small fault in the reference block, which is that the sign of the marked add operation should be positive instead of negative.The results of the simulation are shown in Fig 2.4 to Fig 2.13.Fig2.2 The reference block diagram in the courseware(unrectified)Fig2.3 The simulink block diagram for Assignment 22.2 results and analysis of the problemFig.2.4 real acceleration,velocity and displacement output without error sourcesKFig2.5 position bias when only accelerometer scale factor error exists0.0001aFig2.6 position bias output when only gyro scale factor error exists 0.0001g K =Fig2.7 position bias when only acceleromete bias error exists 20.0002/N A m s ∆=Fig2.8 position bias output when only initial velocity error exists 200.01/y m s ∆=Fig2.9 position bias output when only initial position error exists 010y m ∆=Fig2.10 position bias output bias when only gyro bias errorexists 0.000000024240.00681/3/h rad s ε=︒=Fig2.11 position bias output when only initial platform misalignment angle exists0.000012120''345radα==Fig2.12 output considering all the error sourcesFig2.13 position bias output considering all error sourcesAs we can see in the above simulation results, if there is no error we can navigate the train ’s motion correctly, which comes from north to the south as shown in Fig2.4, beginning with an constant acceleration within 60 seconds then cruises at a constant speed, approximately 65 m/s. However, the situation will change a lot when different errors put into the simulation. The initial position error 010y m ∆= effects least as Fig.2.8, for this error doesn ’t enter into the closed loop and it won ’t influence the iterative process. The position bias is constant and can be negligible.In the second case, when the accelerometer scale factor error exists, 0.0001a K =, as shown in Fig2.5, the result are stable and almost accurate, the position bias is a sinusoidal output.So it is with the accelerometer bias error situation, 20.0002/N A m s ∆=, in Fig2.7, the initialvelocity error, 200.01/y m s ∆= in Fig2.9, and the initial platform misalignment angle,05''α=, in Fig2.11. However, the influence degrees of the different factors are not in the samemagnitude. The accelerometer scale factor influences the least with magnitude of 5, then the initial velocity larger magnitude of 8, and the accelerometer bias magnitude of 25. The influence of the initial platform misalignment angle is much more significant with a magnitude of 150. All the navigation bias in the second kind case is sinusoidal, which means they ’re limited and negligible as time passes by.In the third case, such as the gyro scale factor error situation, 0.0001g K =, in Fig2.6, and the gyro bias error,0.01/h ε=︒, results in Fig2.10, effects the most significant, the trajectory of the navigation disvergence accumulated as time goes. The position bias is a combination of sinusoidal signal and ramp signal. They also show that the longitudinal and distance errors resulted from gyro drifts are not convergent in time. It means the errors in the gyroscope do most harm to our navigation. And due to the significant influence of the gyro bias errors and the gyroscope scale factor error, results considering all the error sources disverge, and the navigationposition of the motion will be away from the real motion after a enough long time, as shown in Fig2.10. The gyro bias error is the most significant effect factor of all errors. By the time of 10000s, it has reaches 1600m, and it’s nearly the quantity of the position bias considering all error sources. Through contrasting all the results, We can conclude that the gyro bias error is the main component of the whole position bias.Impression of the Whole simulation experimentThrough contrasting all the results, We can conclude that the gyro bias error is the main component of the whole position bias, and the the gyro bias or the drift error do most harm to our navigation. So it is a must for us to weaken or eliminate it anyway. In spite of all the disadvantages discussed above, the INS still shows us a relatively accurate results of single-axis navigation.Assignment 3: SINS simulation3.1 Task descriptionA missile equipped with SINS is initially at the position of 46o NL and 123 o EL, stationary on a launch pad. Three gyros, GX, GY, GZ, and three accelerometers, AX, AY, AZ, are installed along the axes Xb, Yb, Zb of its body frame respectively.Case 1: stationary testThe body frame of the missile initially coincides with the geographical frame, as shown in the figure, with its pitching axis Xb pointing to the east, rolling axis Yb to the north, and azimuth axis Zb upward. Then the body of the missile is made to rotate in 3 steps:(1) -22o around Xb(2) 78o around Yb(3) –16o around ZbFig 3.1 Introduction to assignment 3After that, the body of the missile stops rotating. You are required to compute the final outputs of the three accelerometers on the missile, using quaternion and ignoring the device errors. It is known that the magnitude of gravity acceleration is g = 9.8m/s2.Case 2: flight tes tInitially, the missile is stationary on the launch pad, 400m above the sea level. Its rolling axis is vertical up,and its pitching axis is to the east. Then the missile is fired up. The outputs of the gyros and accelerometers are both pulse numbers. Each gyro pulse is an angular increment of 0.01arc-sec, and each accelerometer pulse is 1e-7g, with g =9.8m/s2. The gyro output frequency is 200Hz, and the accelerometer’s is 10Hz. The outputs of the gyros and accelerometers within 1315s are stored in a MA TLAB data file named imu.mat, containing matrices gm of 263000× 3 and am of 13150× 3 respectively. The format of the data is as shown in the tables, with 10 rows of each matrix selected. Each row represents the outputs of the type of sensors at each sampling time. The Earth can be seen as an ideal sphere, with radius 6371.00km and spinning rate 7.292× 10-5 rad/s, The errors of the sensors are ignored, so is the effect of height on the magnitude of gravity. The outputs of the gyros are to be integrated every 0.005s. The rotation of the geographical frame is to be updated every 0.1s, so are the velocities and positions of the missile.You are required to:(1) compute the final attitude quaternion, longitude, latitude, height, and east, north, vertical velocities of the missile.(2) compute the total horizontal distance traveled by the missile.(3) draw the latitude-versus-longitude trajectory of the missile, with horizontal longitude axis.(4) draw the curve of the height of the missile, with horizontal time axis.Fig 3.2 simplified navigation algorithm for SINS 3.2Procedure code3.2.1 Sub function code:quaternion multiply code:function [q1]=quml(q1,q2);lm=q1(1);p1=q1(2);p2=q1(3);p3=q1(4);q1=[lm -p1 -p2 -p3;p1 lm -p3 p2;p2 p3 lm -p1;p3 -p2 p1 lm]*q2;endquaternion inversion code:function [qni] =qinv(q)q(1)=q(1);q(2)=-q(2);q(3)=-q(3);q(4)=-q(4);qni=q;end3.2.2case1 DCM algorithm:function ans11cz=[cos(-22/180*pi) sin(-22/180*pi) 0 ;-sin(-22/180*pi) cos(-22/180*pi) 0;0 0 1]; %The third rotation DCMcx=[1 0 0 ;0 cos(78/180*pi) sin(78/180*pi);0 -sin(78/180*pi) cos(78/180*pi)]; %The first rotation DCMcy=[cos(-16/180*pi) 0 -sin(-16/180*pi);0 1 0;sin(-16/180*pi) 0 cos(-16/180*pi)]; %The second rotation DCM A=cz*cy*cx*[0;0;-9.8]end3.2.3case1 quaternion algorithm:function ans12g=[0;0;0;-9.8];q1=[cos(-11/180*pi);sin(-11/180*pi);0;0]; %The first rotation quaternionq2=[cos(39/180*pi);0;sin(39/180*pi);0]; %The second rotation quaternionq3=[cos(-8/180*pi);0;0;-sin(-8/180*pi)]; %The third rotation quaternionr=quml(q1,q2); %call the quaternion multiplication subfunction q=quml(r,q3);P1=[q(1) q(2) q(3) q(4);-q(2) q(1) q(4) -q(3);-q(3) -q(4) q(1) q(2);-q(4) q(3) -q(2) q(1)];P2=[q(1) -q(2) -q(3) -q(4);q(2) q(1) q(4) -q(3);q(3) -q(4) q(1) q(2);q(4) q(3) -q(2) q(1)];P=P1*P2;gn=P*g;gn=gn(2:4)end3.2.4 case2 SINS quaternion algorithm code:function ans2clc;clear;%parameters initializing:T=0.005;K=13150;R=6371000; %radius of earthwE=7.292*10^(-5); %spinning rate of earthQ=zeros(4, 263001) ;%quaternion matrix initializinglongitude=zeros(1,13151);latitude=zeros(1,13151);H=zeros(1,13151); %altitude matrixQ(:,1)=[cos(45/180*pi);-sin(45/180*pi);0;0]; % initial quaternion longitude(1)=123; %initial longitudelatitude(1)=46; % initial latitudeH(1)=400; %initial altitudelength=0;g=9.8;vE = zeros(1,13151); %eastern velocityvN = zeros(1,13151); %northern velocityvH = zeros(1,13151); %upward velocityvE(1)=0;vN(1)=0;vH(1)=0;load imu.mat %data loading%main calculation sectionfor N=1:Kq1=zeros(4,11);q1(:,1)=Q(:,N);for n=1:20 % Attitude iteration wx=0.01/(3600*180)*pi*gm((N-1)*10+n,1); % Angle incrementwy=0.01/(3600*180)*pi*gm((N-1)*10+n,2);wz=0.01/(3600*180)*pi*gm((N-1)*10+n,3);w=[wx,wy,wz]';normw=norm(w); % Norm calculationW=[0,-w(1),-w(2),-w(3);w(1),0,w(3),-w(2);w(2),-w(3),0,w(1);w(3),w(2),-w(1),0];I=eye(4);S=1/2-normw^2/48;C=1-normw^2/8;q1(:,n+1)=(C*I+S*W)*q1(:,n);Q(:,N+1)=q1(:,n+1);endWE=-vN(N)/R; % rotational angular velocity component of a geographic coordinate systemWN=vE(N)/R+wE*cos(latitude(N)/180*pi);WH=vE(N)/R*tan(latitude(N)/180*pi)+wE*sin(latitude(N)/180*pi);attitude=[WE,WN,WH]'*T; %correction of the quaternion by updating the rotation of geographic coordinatenormattitude=norm(attitude);e=attitude/normattitude;QG=[cos(normattitude/2);sin(normattitude/2)*e];Q(:,N+1)=quml(qinv(QG),Q(:,N+1));fx=1e-7*9.8*am(N,1); %specific force measured by accelerometerfy=1e-7*9.8*am(N,2);fz=1e-7*9.8*am(N,3);Fb=[fx fy fz]';F=quml(Q(:,N+1),quml([0;Fb],qinv(Q(:,N+1)))); %The specific force is decomposed into geographic coordinate system.FE(N)=F(2);FN(N)=F(3);FU(N)=F(4);%calculate the velocity of the vehicle:VED(N)=FE(N)+vE(N)*vN(N)/R*tan(latitude(N)/180*pi)-(vE(N)/R+2*wE*cos(latitude(N)/ 180*pi))*vH(N)+2*vN(N)*wE*sin(latitude(N)/180*pi);VND(N)=FN(N)-2*vE(N)*wE*sin(latitude(N)/180*pi)-vE(N)*vE(N)/R*tan(latitude(N)/180 *pi)-vN(N)*vH(N)/R;VUD(N)=FU(N)+2*vE(N)*wE*cos(latitude(N)/180*pi)+(vE(N)^2+vN(N)^2)/R-g;%integration and get the relative velocity of vehicle:vE(N+1)=VED(N)*T+vE(N);vN(N+1)=VND(N)*T+vN(N);vH(N+1)=VUD(N)*T+vH(N);% integration and get the position of vehicle:longitude(N+1)=vE(N)/(R*cos(latitude(N)/180*pi))*T/pi*180+longitude(N);latitude(N+1)=vN(N)/R*T/pi*180+latitude(N);H(N+1)=vH(N)*T+H(N);length=sqrt((vE(N))^2+(vN(N))^2)+length;endfigure(1) %picture the longitude-latitude curve of the motion within 1315 secondstitle(' longitude-latitude ');hold ongrid onplot(longitude,latitude);figure(2) % picture the altitude curve of the motion within 1315 secondstitle('altitude');hold ongrid onplot(0:13150,H);3.3Simulation outputs and results analysisIn case 1, the DCM algorithm and quaternion results are the same as follow:A =7.53165.9788-1.8892And the results suggest the solution of DCM and quaternion is equivalence in this problem.In case 2, the latitude-versus-longitude trajectory of the missile(with horizontal longitude axis) and the altitude curve of the missile are shown as follows in Fig 3.3 and Fig 3.4.Fig3.3 the latitude-versus-longitude trajectory of the missile(with horizontal longitude axis)Fig3.4the altitude curve of the missileImpression of the Assignment 3In this assignment, we simulate the missile navigation situation in a real problem, as the problem we have done before. I did this based on my own original code, but to my surprise, it’s harder than I have expected. For the detailed thoughts for my program I have forgotten. I have to recheck the code line by line, But I am still troubled in correcting the initial parameters for many times. It has taught me a lesson, which is never to be egotistical for your ability to memory and the work you have done or understood.。
哈工大机械原理大作业连杆机构9

机械原理大作业大作业一:连杆机构运动分析学生姓名:学号:指导教师:丁刚完成时间:机电工程学院机械设计系制二〇一八年四月连杆机构运动分析1题目(9)图1 设计题目在图1所示的机构中,已知l AB=60mm,l BC=180mm,l DE=200mm,l CD=120mm,l EF=300mm,h=80mm,h1=85mm,h2=225mm,构件1以等角速度ω1=100rad/s 转动。
求在一个运动循环中,滑块5的位移、速度和加速度曲线。
2分析结构1、杆1为RR主动件,绕A以ω1 转动,自由度1.2、4杆和滑块5为RRP II级杆组.,自由度0.3、2,3杆组成II级杆组RRR,自由度0.总共自由度为F=5*3-2*7=1 .由上述的杆组类型,确认出所需运动分析数学模型:同一构件上的点、RRP、RRR。
3.杆组法对平面连杆机构进行运动分析3.1对主动件杆1 RR I级构件的分析主动杆1转角:φ= [0°,360°) δ=0°,则φ’=ω1=100 rad/s角加速度φ’’=0.已知h2=225mm, h=80mm, l AB=60mm 所以A(225mm,80mm)A点速度(0,0),加速度(0,0)B点位置(x A+l AB*cos(φ), Y A+l AB*sin(φ))B点速度(-l AB*sin(φ), l AB*cos(φ)),加速度(-l AB*cos(φ), -l AB*sin(φ))3.2RRRII 级杆组分析(模型参考教材P37-38)图3 如图所示两个构件组成II 级杆组。
已知了B 的位置(x B ,y B )= (x A +l AB *cos(φ), Y A +l AB *sin(φ)),速度(x ’B ,y ’B ) 和加速度(x ’’B ,y ’’B ), 已知运动副D (0,0), 还可知,x ’D =y ’D =0, x ’’D =y ’’D =0. l BC =180 mm, l CD = 120mm所以,x c =x D +l CD *cos(φi)= x B +l BC *cos(φj) y c =x D +l CD *sin(φi)= x B +l BC *sin(φi) 对于φ的求解: A 0=2*l CD (x B -x D ) B 0=2*l BC (y B -y D ) C 0=l CD 2+ l BD 2- l BC 2为了保证机构的装配正常:l BD ≤l CD + l BC AND l BD ≥Abs (l CD - l BC )可求3杆的转角φi=2*arctan((B 0±sqrt (A 02 + B 02- C 02))/(A 02+ C 02)),角速度w3=φi ’和角加速度α3= φi ’’3.3 同一构件上的点(模型参考书P35-36)Φiφjφi已知D(0,0),速度(0,0),加速度(0,0),3杆转角φi 角速度φi’角加速度φi’’,Φi和它的导数在3.2都有体现LDE= 200mm可求出E的坐标,速度,加速度.x E =x c+lCE*cos(φi)y E =x C+lCE*sin(φi)同样地,速度、加速度通过求导即可得出算式,可以编出程序。
导航原理实验报告

导航原理实验报告院系:班级:学号:姓名:成绩:指导教师签字:批改日期:年月日哈尔滨工业大学航天学院控制科学实验室实验1 二自由度陀螺仪基本特性验证实验一、实验目的1.了解机械陀螺仪的结构特点;2.对比验证没有通电和通电后的二自由度陀螺仪基本特性表观; 3.深化课堂讲授的有关二自由度陀螺仪基本特性的内容。
二、思考与分析1. 定轴性(1) 设陀螺仪的动量矩为H ,作用在陀螺仪上的干扰力矩为M d ,陀螺仪漂移角速度为ωd ,写出关系式说明动量矩H 越大,陀螺漂移越小,陀螺仪的定轴性(即稳定性)越高.答案:d d H M ω=⨯u u u r u u r u u r/sin d dH M θω= 干扰力矩M d 一定时,动量矩H 越大,陀螺仪漂移角速度为ωd 越小,陀螺漂移越小,陀螺仪的定轴性(即稳定性)越高.(2) 在陀螺仪原理及其机电结构方而简要蜕明如何提高H 的量值?答案:H J =Ωu u r u r 由公式2AJ dm r =⎰⎰⎰可知提高H 的量值有四种途径:1. 陀螺转子采用密度大的材料,其质量提高了,转动惯量也就提高了。
2. 改变质量分布特性。
在质量相同的情况下,若质量分布的半径距质心越远,H 越大。
因此将陀螺转子的有效质量外移,如动力谐陀螺将转子设计成环状。
即在陀螺电机定子环中,可做成质量集中分布在环外边缘的环形结构,切边缘部分材质密度大,可提高转动惯量。
3. 增大r,可有效提高转动惯量。
4. 另外可通过采用外转子电机来改变电机质量分布,增大r 。
改变电机定转子结构:采用外转子,内定子结构的转子电机。
4. 增加陀螺转子的旋转速度。
2/602(1)/n s f p ωππ==- ,60(1)/n f s p =-提高电压周波频率 f ↑——〉n ↑——H ↑ f=400Hz适当减少极对数 ,如取p=1适当减少转差率s ,可通过减少转子支承轴承摩擦来实现2.进动性(1) 在外框架施加一沿x 轴正方向作用力矩时,画出动量矩H 的进动方向及矢量M ,ω,H 的关系坐标图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《导航原理》作业(惯性导航部分)一、题目要求 A fighter equipped with SINS is initially at the position of ︒35 NL ︒122X G Y G Z G ,and three accelerometers, X A ,Y A ,Z A are installed along the axes b X ,b Y ,b Z of the body frame respectively.Case 1:stationary onboard testThe body frame of the fighter initially coincides with the geographical frame, as shown in the figure, with its pitching axis b X pointing to the east,rolling axis b Y to the north, and azimuth axis b Z upward. Then the body of the fighter is made to rotate step by step relative to the geographical frame.(1) ︒10around b X(2) ︒30around b Y(3) ︒50-around b ZAfter that, the body of the fighter stops rotating. You are required to compute the final output of the three accelerometers on the fighter, using both DCM and quaternion respectively,and ignoring the device errors. It is known that the magnitude of gravity acceleration is 2/8.9g s m =. Case 2:flight navigationInitially, the fighter is stationary on the motionless carrier with its board 25m above the sea level. Its pitching and rolling axes are both in the local horizon, and its rolling axis is ︒45on the north by east, parallel with the runway onboard. Then the fighter accelerate along the runway and take off from the carrier.The output of the gyros and accelerometers are both pulse numbers,Each gyro pulse is an angular increment of sec arc 1.0-,and each accelerometer pulse is g 6e 1-,with 2/8.9g s m =.The gyro output frequency is 10 Hz,andthe accelerometer’s is 1Hz. The output of gyros and accelerometers within 5400s are stored in MATLAB data files named gout.mat and aout.mat, containing matrices gm of35400⨯ and am of 35400⨯ respectively. The format of data as shown in the tables, with 10 rows of each matrix selected. Each row represents the out of the type of sensors at each sample time.The Earth can beseen as an idealsphere, with radius6368.00km andspinning rate rad/s 10292.75-⨯, Theerrors of sensors areignored, so is theeffect of height onthe magnitude ofgravity. The outputof the gyros are to integrated every 0.1s. The rotation of geographical frame is to be updated every 1s, so are the velocities and position of the figure. You are required to:(1)Compute the final attitude quaternion, longitude, latitude, height, and east, north, vertical velocities of the fighter.(2)Compute the total horizontal distance traveled by the fighter.(3)Draw the latitude-versus-longitude trajectory of the fighter, with horizontal longitude axis.(4)Draw the curve of the height of fighter, with horizontal time axis.二、Case1解答2.1 方向余弦阵法(1) 绕Xb 轴转过ψ︒=10ϕ ⎪⎪⎪⎭⎫ ⎝⎛︒︒-︒︒=⎪⎪⎪⎭⎫ ⎝⎛-=10cos 10sin 010sin 10cos 0001cos sin 0sin cos 0001ϕϕϕϕϕC(2) 绕Yb 轴转过︒=30θ ⎪⎪⎪⎭⎫ ⎝⎛︒︒︒-︒=⎪⎪⎪⎭⎫ ⎝⎛-=30cos 030sin 01030sin 030cos cos 0sin 010sin 0cos θθθθθC(3) 绕Zb 轴转过︒-=50ψ所以变换后的坐标由于初始时刻有 所以计算得( Z Y X )=(3581.86027.2-4054.4-)三个加速度计的输出分别是计算程序见附录一2.2 四元数法(1)绕Xb(2)绕Yb(3)绕Zb 则合成四元数合成四元数的逆由公式计算得 (Z Y X )=(3581.86027.2-4054.4-)三个加速度计的输出分别是由两种计算方法的计算结果可以看出,方向余弦阵法和四元数法的计算结果是一致的。
计算程序见附录二三、Case2解答3.1程序流程图3.2 源程序详见附录三3.3 仿真及结果3.3.1 运行程序可得:(1)战斗机相对当地地理坐标系的姿态四元数为:(2)经度纬度高度(3)战斗机的东部,北部和垂直速度(43.3.2运行程序,绘制纬度-经度战斗机轨迹(以经度为横轴,纬度为纵轴);如图:3.3.3 运行程序,绘制战斗机的高度的曲线(以时间为横轴,高度为纵轴),如图:四、心得体会通过本次的大作业,我对比力、四元数等惯性导航技术中涉及的基本概念有了更深的理解,同时再次复习方向余弦矩阵法和四元数法求解捷联惯导系统,更加熟练地掌握其算法。
除此之外,本次大作业中所有程序均要涉及Matlab编程,在编写程序时,四元数的初始化非常重要,如果四元数的初始化错误,会导致所有的运算结果错误。
在编程过程中,每当遇到问题,我就会上网查一些资料,并与周边同学进行深入讨论,学习并解决问题。
这进一步提高了我的自学能力和对知识综合应用的能力。
五、参考/协助确认本文是根据本人研究成果,并参考相关文献资料整合而成,非本人完全独立研究完成,编程部分很大程度上参考了百度百科及周边同学的研究成果。
另外,报告形式上借鉴了上届学长学姐的形式。
本人对作业中的某些结论不负完全责任,特此声明。
C1=[1,0,00,cos(10/180*pi),sin(10/180*pi)0,-sin(10/180*pi),cos(10/180*pi)]; %第一次转动方向余弦阵C2=[ cos(30/180*pi),0,-sin(30/180*pi)0,1,0sin(30/180*pi),0,cos(30/180*pi)];%第二次转动方向余弦阵C3=[ cos(-50/180*pi),sin(-50/180*pi),0-sin(-50/180*pi),cos(-50/180*pi),00,0,1];%第三次转动方向余弦阵A=C3*C2*C1*[0;0;9.8] %计算转动后加速度的输出norm(A) %检验输出是否正确附录二q1=[cos(10/360*pi);0;0;sin(10/360*pi)];%第一次转动四元数q2=[cos(30/360*pi);sin(30/360*pi);0;0];%第二次转动四元数q3=[cos(-50/360*pi);0;sin(-50/360*pi);0];%第三次转动四元数r=quml(q1,q2);%计算四元数乘积q=quml(r,q3);A1=[q(1) q(2) q(3) q(4)-q(2) q(1) q(4) -q(3)-q(3) -q(4) q(1) q(2)-q(4) q(3) -q(2) q(1)]A2=[q(1) -q(2) -q(3) -q(4)q(2) q(1) q(4) -q(3)q(3) -q(4) q(1) q(2)q(4) q(3) -q(2) q(1)]A=A1*A2;%G=A*[0;0;0;9.8] %计算转动后的弹体加速度计的输出附录三%已知参数k=10;T=1;Gyro_pulse=0.1/3600/180*pi;Acc_pulse=9.8/1000000;R=6368000;g=9.8;W_earth=0.00007292;%初始导航参数和地球参数Q=zeros(5401,4); %定义变换四元数矩阵Q(1,:)=[cos((-45/2)/180*pi),0,0,sin((-45/2)/180*pi)];Longitude=zeros(1,5401); %定义长度为5400的经度数组Latitude=zeros(1,5401); %定义长度为5400的纬度数组Height=zeros(1,5401); %定义长度为5400的高度数组Longitude(1)=122; %初始化经度,纬度,高度Latitude(1)=35;Height(1)=25;%定义速度矩阵,供画图用Ve=zeros(1,5401); %东向速度Vn=zeros(1,5401); %北向速度Vu=zeros(1,5401); %天向速度X=zeros(1,5401);%定义加速度矩阵fe=zeros(1,5400);fn=zeros(1,5400);fu=zeros(1,5400);FE=zeros(1,5400);FN=zeros(1,5400);FU=zeros(1,5400);load gout.mat;load aout.mat;for N=1:K %位置、速度迭代q=zeros(11,4);q(1,:)=Q(N,:);for n=1:k %姿态迭代w=Gyro_pulse*gm((N-1)*10+n,1:3); w_mod=quatmod([w,0]); W=[0,-w(1),-w(2),-w(3);w(1),0,w(3),-w(2); w(2),-w(3),0,w(1);w(3),w(2),-w(1),0];I=eye(4);S=1/2-w_mod^2/48;C=1-w_mod^2/8+w_mod^4/384;q(n+1,:)=((C*I+S*W)*q(n,:)')';endQ(N+1,:)=q(n+1,:);%地理坐标系的转动角速度分量WE=-Vn(N)/R;WN=Ve(N)/R+W_earth*cos(Latitude(N)/180*pi);WU=Ve(N)/R*tan(Latitude(N)/180*pi)+W_earth*sin(Latitude(N)/180*pi);Gama=[WE,WN,WU]*T; %用地理坐标系的转动四元数Gama_mod=quatmod([WE,WN,WU,0]);n=Gama/Gama_mod;Qg=[cos(Gama_mod/2),sin(Gama_mod/2)*n];Q(N+1,:)=quatmultiply(quatinv(Qg),Q(N+1,:));%加速度计测得的比力fb=Acc_pulse*am(N,1:3);f1=quatmultiply(Q(N+1,:),[0,fb]);fg=quatmultiply(f1,quatinv(Q(N+1,:)));fe(N)=fg(2);fn(N)=fg(3);fu(N)=fg(4);%计算载体的相对加速度FE(N)=fe(N)+Ve(N)*Vn(N)/R*tan(Latitude(N)/180*pi)-(Ve(N)/R+2*W_earth*cos(Latitu de(N)/180*pi))*Vu(N)+2*Vn(N)*W_earth*sin(Latitude(N)/180*pi);FN(N)=fn(N)-2*Ve(N)*W_earth*sin(Latitude(N)/180*pi)-Ve(N)^2/R*tan(Latitude(N)/1 80*pi)-Vn(N)*Vu(N)/R;FU(N)=fu(N)+2*Ve(N)*W_earth*cos(Latitude(N)/180*pi)+(Ve(N)^2+Vn(N)^2)/R-g; %积分计算载体的相对速度Ve(N+1)=FE(N)*T+Ve(N);Vn(N+1)=FN(N)*T+Vn(N);Vu(N+1)=FU(N)*T+Vu(N);%积分计算载体的位置Latitude(N+1)=(Vn(N)+Vn(N+1))/2*T/R/pi*180+Latitude(N);Longitude(N+1)=(Ve(N)+Ve(N+1))/2*T/(R*cos(Latitude(N)/180*pi))/pi*180+Longitude (N);Height(N+1)=(Vu(N)+Vu(N+1))/2*T+Height(N);%computing the distance of horizonXe=(Ve(N)+Ve(N+1))/2*T;Xn=(Vn(N)+Vn(N+1))/2*T;X(N+1)=X(N)+sqrt(Xe^2+Xn^2);End%绘制经、纬度变化曲线(以经度为横轴,纬度为纵轴);figure(1);grid on;hold on;plot(Longitude,Latitude);%绘制高度变化曲线(以时间为横轴,高度为纵轴)figure(2);xlabel('时间/秒');ylabel('高度/米');grid on;hold on;plot((0:5400),Height);%绘制总水平位移曲线figure(3);xlabel('时间/秒');ylabel('航程/米');grid on;hold on;plot((0:5400),X)(注:可编辑下载,若有不当之处,请指正,谢谢!)。
