2.1 LTI连续系统的响应
第二章 连续系统的时域分析

du (t ) 整理方程组得:d 2u2 (t ) + 7 2 + 6u2 (t ) = 6e(t ) dt 2 dt 特征方程:a2+7a+6=0 特征根:a=-1, a=-6 齐次解:rh(t) = A1e-t +A2e-6t
5
第二章 连续系统的时域分析
② 选定特解后,将它代入到原微分方程,即得到一个由 yh(t)及其各阶导数以及激励共同组成的一个非齐次微 分方程,依据此方程求出待定系数,然后可确定方程 的特解。
3. 求系统的全响应y(t)
y(t)=方程的全解y(t)=齐次解yh(t) + 特解 yP(t)
=自由响应+强迫响应 将上面方程的全解代入系统的初始条件即可得齐次解中 的待定系数,从而进一步得到系统的全响应。此时, 方程的齐次解yh(t)为系统的自由响应,特解yP(t)为系 统的强迫响应(固有响应)。
解: 由原方程可得
dh 2 (t ) dh(t ) +3 + 2h(t ) = 2δ ′(t ) + 3δ (t ) 2 dt dt
(t ≥ 0)
特征方程: λ2+3λ+2 = 0 特征根: λ1= -1,λ2= -2,且n > m
h (t ) = Ae − t u (t ) + e −2 t (t ) u(t)
20
第二章 连续系统的时域分析
式中A、B为待定系数,将h(t)代入原方程 式,解得A=1,B=1。因此,系统的冲激 响应为 h(t ) = e − t u(t ) + e −2 t (t )
21
第二章 连续系统的时域分析
信号与系统 2.1

所以,特解为
1 2 2 10 y p (t ) = t + t − 3 9 27
8
d 2 y (t ) dt2
+2
d y (t ) d f (t ) + 3 y (t ) = + f (t ) dt dt
7
P1 cos(β t ) + P2 sin (β t )(特征根不等于 ± j β )
Signals & Systems
例:给定微分方程式
d 2 y (t ) dt2
d y (t ) d f (t ) +2 + 3 y (t ) = + f (t ) dt dt
如果已知: (1) f (t ) = t 2 ; (2 ) f (t ) = e t , 方程的特解。 解: (1)由于f(t)=t2,故特解函数式为 代入方程,整理得
10
Signals & Systems
全解举例2.1-1
例 描述某LTI系统的微分方程为 y”(t) + 5y’(t) + 6y(t) = f(t) 求当f(t) = 2e-t,t≥0;y(0)=2,y’(0)= -1时的全解 解: (1) 特征方程为λ2 + 5λ+ 6 = 0 其特征根λ1= – 2, λ2= – 3。齐次解为 yh(t) = C1e – 2t + C2e – 3t (2)当f(t) = 2e – t时,其特解可设为 yp(t) = Pe – t 将其代入微分方程得 Pe – t + 5(– Pe – t) + 6Pe – t = 2e – t 解得 P=1,于是特解为 yp(t) = e – t (3)全解为: y(t) = yh(t) + yp(t) = C1e – 2t + C2e – 3t + e – t 其中 待定常数C1,C2由初始条件确定。 y(0) = C1+C2+ 1 = 2,y’(0) = – 2C1 – 3C2 – 1= – 1 解得 C1 = 3 ,C2 = – 2 最后得全解 y(t) = 3e – 2t – 2e – 3t + e – t , t≥0
信号与系统教案第2章
bm f
( m)
(t ) bm1 f
( m1)
ai 、 bj为常数。
2.1 LTI连续系统的响应
经典时域分析方法 y(t ) yh (t ) yp (t ) 卷积法
y(t) = yzi (t) + yzs (t)
一、经典时域分析方法(微分方程经典解)
微分方程的全解即系统的完全响应, 由齐次解 yh(t)和特解yp(t)组成
信号与系统 电子教案
2.2 冲激响应和阶跃响应
2.2
冲激响应和阶跃响应
一、冲激响应
由单位冲激函数δ(t)所引起的零状态响应称为 单位冲激响应,简称冲激响应,记为h(t)。 h(t)=T[{0},δ(t)]
t
h t T 0 , t
def
h t
t
信号与系统 电子教案
第二章 连续系统的时域分析
《信号与系统》
授课教师:吕晓丽
第2-1页
■
长春工程学院电子信息教研室
信号与系统 电子教案
第二节总结
总
结
1、LTI系统的判定方法 线性性质 时不变性质 2、 LTI系统的分类 因果系统 稳定系统 3、系统的描述 系统框图与系统方程
第2-2页
■
长春工程学院电子信息教研室
[例] 已知某二阶线性时不变连续时间系统的动态方程
y" (t ) 6 y' (t ) 8 y(t ) f (t ), t 0
初始条件y(0)=1, y '(0)=2, 输入信号f (t)=et ε(t),求 系统的完全响应y(t)。
解:
(3) 求方程的全解
y (t ) yh (t ) yp (t ) C1e
信号与系统_2_微分方程求解
第2-11页
■
©三峡大学 电气信息学院 电子工程系
信号与系统 电子教案
说明
•对于一个具体的电网络,系统的 0状 态就是系统中
储能元件的储能情况;
将初始条件代入,得
y(0) = (C1+P0) + C2=1, y’(0)= –2(C1+P0) –3C2+1=0
解得 C1 + P0 = 2 , C2= –1 最后得微分方程的全解 为
y(t) = 2e–2t – e–3t + te–2t, t≥0
上式第一项的系数C1+P0= 2,不能区分C1和P0,因 而也不能区分自由响应和强迫响应。
微分方程的经典解:
y(t)(完全解) = yh(t)(齐次解) + yp(t)(特解)
齐次解是齐次微分方程 y(n)+an-1y(n-1)+…+a1y(1)(t)+a0y(t)=0
的解。yh(t)的函数形式由上述微分方程的特征根 确定。
特解的函数形式与激励函数的形式有关。P41表2-1、 2-2
第2-4页
2.2 冲激响应和阶跃响应 一、卷积代数
一、冲激响应
二、奇异函数的卷积特性
二、阶跃响应
三、卷积的微积分性质
四、卷积的时移特性
第2-3页
■
©三峡大学 电气信息学院 电子工程系
信号与系统 电子教案
2.1 LTI连续系统的响应
一、微分方程的经典解
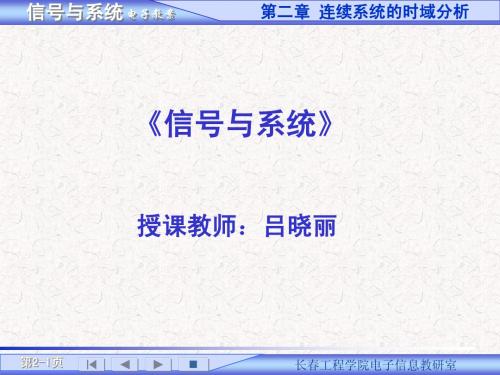
y(n)(t) + an-1y (n-1)(t) + …+ a1y(1)(t) + a0y (t) = bmf(m)(t) + bm-1f (m-1)(t) + …+ b1f(1)(t) + b0f (t)
§2.1LTI连续系统的响应

9 页
y(0+ ) = −1 y' (0+ ) = 4
归纳零负和零正的关系
X
第
三、零输入响应和零状态响应 零输入响应和零状态响应
在一定条件下,激励源与起始状态之间可以等效转换。 在一定条件下,激励源与起始状态之间可以等效转换。 即可以将原始储能看作是激励源。 即可以将原始储能看作是激励源。
特
解:根据微分方程右端函数式形式,设含待定系 根据微分方程右端函数式形式, 数的特解函数式→代入原方程 代入原方程, 数的特解函数式 代入原方程,比较系数 定出特解。 定出特解。 齐次解+特解 特解, 初始条件定出齐次解 解:齐次解 特解,由初始条件定出齐次解 Ak 。
全
X
第
经典法
我们一般将激励信号加入的时刻定义为t=0 ,响应 我们一般将激励信号加入的时刻定义为 时的方程的解, 为 t ≥ 0+ 时的方程的解,初始条件
7 页
E(常数 ) 常数
B(常数 ) 常数
B t p + B2t p−1 +⋯+ Bpt + Bp+1 1
tp eα t
cos(ω t )
Beα t
B cos(ω t ) + B2 sin(ω t ) 1
sin(ω t )
X
第
关于 0 与 0 初始值 二、 + − 起始点的跳变
0−
O
8 页
0+
t
t ≥ 0+
(完整word版)信号与系统(郑君里)复习要点(良心出品必属精品)

信号与系统复习书中最重要的三大变换几乎都有。
第一章信号与系统1、信号的分类①连续信号和离散信号②周期信号和非周期信号连续周期信号f(t)满足f(t) = f(t + mT),离散周期信号f(k)满足f(k) = f(k + mN),m = 0,±1,±2,…两个周期信号x(t),y(t)的周期分别为T1和T2,若其周期之比T1/T2为有理数,则其和信号x(t)+y(t)仍然是周期信号,其周期为T1和T2的最小公倍数。
③能量信号和功率信号④因果信号和反因果信号2、信号的基本运算(+ - ×÷)2.1信号的(+ - ×÷)2.2信号的时间变换运算(反转、平移和尺度变换)3、奇异信号3.1 单位冲激函数的性质f(t) δ(t) = f(0) δ(t) , f(t) δ(t –a) = f(a) δ(t –a)例:3.2序列δ(k)和ε(k)f(k)δ(k) = f(0)δ(k) f(k)δ(k –k0) = f(k0)δ(k –k0) 4、系统的分类与性质4.1连续系统和离散系统4.2 动态系统与即时系统 4.3 线性系统与非线性系统 ①线性性质T [af (·)] = a T [ f (·)](齐次性)T [ f 1(·)+ f 2(·)] = T[ f 1(·)]+T[ f 2(·)] (可加性) ②当动态系统满足下列三个条件时该系统为线性系统:y (·) = y f (·) + y x (·) = T[{ f (·) }, {0}]+ T[ {0},{x(0)}] (可分解性) T[{a f (·) }, {0}] = a T[{ f (·) }, {0}]T[{f 1(t) + f 2(t) }, {0}] = T[{ f 1 (·) }, {0}] + T[{ f 2 (·) }, {0}](零状态线性))0(d )()(f t t t f =⎰∞∞-δ)(d )()(a f t a t t f =-⎰∞∞-δ?d )()4sin(91=-⎰-t t t δπ)0('d )()('f t t f t -=⎰∞∞-δ)0()1(d )()()()(n n n ft t f t -=⎰∞∞-δ4)2(2])2[(d dd )(')2(0022=--=--=-==∞∞-⎰t t t t tt t t δ)(1||1)()()(t aa at n n n δδ⋅=)(||1)(t a at δδ=)(||1)(00at t a t at -=-δδ)0()()(f k k f k =∑∞-∞=δT[{0},{ax 1(0) +bx 2(0)} ]= aT[{0},{x 1(0)}] +bT[{0},{x 2(0)}](零输入线性) 4.4时不变系统与时变系统T[{0},f(t - t d )] = y f (t - t d )(时不变性质) 直观判断方法:若f (·)前出现变系数,或有反转、展缩变换,则系统为时变系统。
第二章 信号与线性系统 吴大正 教材课件

对于t>0时
yf (t ) 3 yf (t ) 2 y f (t ) 6 (t )
第2章 离散信号与系统的Z域分析 连续系统的时域分析
y f (t ) C f 1e t C f 2e 2t 3;
y f (t ) 4e t e 2t 3, t 0
y (t ) an 1 y
(n)
( n 1)
(t ) a0 y (t ) bm f
m j 0
( m)
(t ) b0 f (t )
(2.1-1)
可表示为:
ai y ( i ) (t ) b j f ( j ) (t )
i 0
n
式中an-1,…,a1,a0和bm,…,b1,b0均为常数。该方程的全解由齐 次解和特解组成。齐次方程的解即为齐次解,用yh(t)表示。非齐 次方程的特解用yp(t)表示。即有 y(t)=yh(t)+yp(t) (2.1-2)
例2―3 求微分方程y″(t)+3y′(t)+2y(t)=f(t)的齐次解。 解:由特征方程
2 3 2 0 解得特征根λ1=-1,λ2=-2。
因此该方程的齐次解
yh(t)=c1e-t+c2e-2t
第2章 离散信号与系统的Z域分析 连续系统的时域分析 例2-1 求微分方程y″(t)+2y′(t)+y(t)=f(t)的齐次解。 解 由特征方程 2 2 1 0 解得二重根λ1=λ2=-1,
y x (t ) 4e t 2e 2t , t 0
第2章 离散信号与系统的Z域分析 连续系统的时域分析 2、零状态响应yf(t)
lti连续时间系统零状态响应的求解方法

lti连续时间系统零状态响应的求解方法1. 介绍在连续时间系统的分析中,零状态响应是指某个系统在初始状态为零的情况下,接收到某个输入信号后的输出响应。
在实际问题中,求解零状态响应是一个重要的任务,本文将介绍lti连续时间系统零状态响应的求解方法。
2. 基本思路求解lti连续时间系统的零状态响应的基本思路是将系统输入分解成一组基函数,然后根据基函数的性质求解对应的输出响应,最后将所有响应按照线性叠加原理相加得到系统的总输出响应。
在lti连续时间系统中,常用的基函数包括单位脉冲响应、单位阶跃响应和正弦信号等。
3. 单位脉冲响应法单位脉冲响应法是求解lti连续时间系统零状态响应的常用方法。
具体方法是将系统的初始状态设置为零,输入信号为单位脉冲函数,然后求解系统对单位脉冲函数的响应,得到系统的单位脉冲响应ht(t),最后将ht(t)与输入信号进行卷积计算,得到系统的零状态响应y(t)。
如下图所示:其中,δ(t)表示单位脉冲函数,ht(t)表示系统的单位脉冲响应,x(t)表示系统的输入信号,y(t)表示系统的零状态响应。
4. 单位阶跃响应法单位阶跃响应法也是求解lti连续时间系统零状态响应的一种常用方法。
具体方法是将系统的初始状态设置为零,输入信号为单位阶跃函数,然后求解系统对单位阶跃函数的响应,得到系统的单位阶跃响应h(t),最后将h(t)与输入信号进行卷积计算,得到系统的零状态响应y(t)。
如下图所示:其中,u(t)表示单位阶跃函数,h(t)表示系统的单位阶跃响应,x(t)表示系统的输入信号,y(t)表示系统的零状态响应。
5. 正弦信号法除了单位脉冲响应法和单位阶跃响应法之外,还可以利用正弦信号作为基函数进行求解。
正弦信号法的基本思路是将输入信号分解成一组正弦信号,并求解系统对每个正弦信号的响应,最后将所有响应按照线性叠加原理相加得到系统的总输出响应。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四、零输入响应和零状态响应
对于 LTI 系统,把输出响应分成由激励信号 f(t) 引起 的响应 H[f(t)] 和由系统起始状态 { x(0-)} 引起的响应 H[{x(0-)}]两者的叠加,由此可分别定义零输入响应 和零状态响应。
H[・] f(t) y(t)=H[f(t)]+H[{x(0-)}] {x(0-)}
四、零输入响应和零状态响应
带有起始值的等效电路
i(t) R1=1 iC(t) C=1F + e(t) vC(0-) + R2=3/2 iL(t)
其中: iL(0-) = 4/5 A
L
vC(0-) = 6/5 V
iL(0-)
问题: 如何求解izi(0+)、 izi '(0+) ?
四、零输入响应和零状态响应
R + vc(0-) t − 1 ( t −τ ) RC
+ vc(t) -
vC (t ) = e
−
t RC
完全响应中,第一项只和电容两端的起始储能有 关,与激励无关,被称为零输入响应,第二项与起始 储能无关,只与输入激励有关,被称为零状态响应。
1 vC (0 − ) + RC ∫ e 0−
f (t )dτ
i(t)
iC(t) C=1F
iL(t) L=1/4H R2=3/2
+ e(t)=4V -
+
- e(t)=2V
四、零输入响应和零状态响应
(1) 建立电路的微分方程 i''(t) +7i'(t) +10i(t) = e''(t) + 6e'(t) + 4e(t) (2) 求零输入响应 izi''(t) + 7izi'(t) + 10izi (t) = 0 其解的形式为: izi(t) = Azi1e-2t + Azi2e-5t ,t≥0 要求解Azi1、Azi2,必须首先确定izi(0+)、 izi '(0+)。
y zi (t ) = ∑ Azik e
k =1
n
xk t
由于没有外加激励的作用,因此系统的状态不会发 生变化,即y (k) (0+)= y (k) (0-) ,于是, yzi(t)中的常数 可以由 y (k) (0-)确定。
四、零输入响应和零状态响应
零状态响应的定义:不考虑起始时刻系统的储能作 用(系统起始状态为零),仅由外加激励信号所产 生的响应,记为yzs(t)。它满足方程 an yzs (n) (t) +an-1 yzs (n-1) (t) +…+a1 yzs (1) (t) + a0 yzs (t) = bm f(m) (t) + bm-1 f(m-1) (t) + …+b1 f(1) (t) + b0 f (t) 及起始状态y (k) (0-) (k=0,1,…,n-1) ,其表达式为:
零输入等效电路
i(t) R1=1 C=1F + vC(0-)=6/5V L=1/4
初始值等效电路
izi(0+) R1=1 + vC(0-)=6/5V iL(0+) iC(0+) iL(0-)=4/5A R2=3/2
iL(0-)=4/5A R2=3/2
-
由此可得:izi(0+) = -6/5 A、 izi ‘(0+)= 2 A/s,将该值代 入零输入响应的表达式可求得Azi1 =-4/3 、Azi2 =2/15
第二章 LTI 连续时间系统的时域分析和零状态响应 由时域经典法求解系统完全响应是把响 应分成自由响应和强迫响应,这只是系统响 应的一种分解形式,另一种广泛应用的重要 分解是零输入响应和零状态响应。
四、零输入响应和零状态响应
例 1 、设有如图所示 RC 电路,电容两端 + 有 起 始 电 压 vc(0-), f(t) 激励源为 f(t),求 t>0 时系统的响应vc(t) 。
零输入响应的定义:没有外加激励信号的作用,只 有系统起始状态(起始时刻系统储能)所产生的响 应,记为yzi(t)。
四、零输入响应和零状态响应
零输入响应yzi(t)是满足方程: an yzi(n) (t) +an-1 yzi (n-1) (t) +…+a1 yzi (1) (t) + a0 yzi (t)=0 及起始状态y (k) (0-) (k=0,1,…,n-1)的解,因此,它是 齐次解的一部分,其表达式为:
零输入响应
}
零状态响应
}
四、零输入响应和零状态响应
例3 描述某系统的微分方程为 y''(t) + 3y'(t) + 2y(t) = 2f'(t) + 6f(t) 已知y(0-)=2,y'(0-)=0,f(t)=u(t)。求该系统的 零输入响应和零状态响应。 解:(1)零输入响应 yzi(t) = 4e–t –2e–2t ,t > 0 (2)零状态响应 yzs (t)= – 4e –t + e –2t + 3 ,t≥0
四、零输入响应和零状态响应
系统响应的分解可以表示为:
4 − 2t 2 −5t 8 e + y (t ) = e − 3 15 5
自由响应 强迫响应 (瞬态响应) (稳态响应)
}
}
2 −5t 8 − 2t 4 −5t 8 4 −2t = − e + e + e − e + 15 15 5 3 3
izs''(t) = aδ'(t) + bδ(t) + cu(t) izs'(t) = aδ(t) + bu(t) izs (t) = au(t)
解得:a=4, b=-4, c=4。进而可得:izs(0+)=4、 izs '(0+)=-4 代入解表达式即可求出: Azs1 =8/3 、Azs2 = -4/15。
四、零输入响应和零状态响应
例4 某LTI连续具有一定的起始状态,已知激励为 f1(t)时,系统的全响应为: y1(t)= 7e–t + 2e–3t , t≥0 当起始状态不变,激励为f2(t) =3f1(t)时,全响应为 y2(t)= 17e–t - 2e–2t +6e–3t , t≥0
求: (1) 系统地零输入响应。 (2) 若起始状态不变,激励f3(t) = 5f1(t)时系统 地全响应。
y zs (t ) = ∑ Azsk e
k =1
n
xk t
+ B(t )
其中 B(t) 是特解,可见零状态响应由自由响应的一 部分和特解构成。
四、零输入响应和零状态响应
系统响应的表达式:
y (t ) =
∑
n
k =1
Ak e x k t + B ( t )
强迫响应
自由响应
= ∑ Azik e
k =1
四、零输入响应和零状态响应
零状态等效电路
izs(t) R1=1 iC(t) + e(t)=4u(t) C=1F iL(t) L=1/4H R2=3/2
由于,izs(0-)=0、 izs’(0-)=0,可直接由冲激
函数匹配法求解。
四、零输入响应和零状态响应
将e(t)=4u(t)代入微分方程得: izs''(t) +7izs'(t) +10izs (t) = 4δ'(t) + 24δ(t) + 16u(t) 冲激函数匹配法:
n
}
}
n
xk t
+ ∑ Azsk e
k =1
xk t
+ B (t )
零输入响应
}
零状态响应
}
四、零输入响应和零状态响应
例2 给定电路如图,t<0时开关S处于1的位置,而且 已经达到稳态;t=0时,开关转向2,把t<0时的电路 状态看作起始状态,求t>0时i(t)的零输入和零状态响 应。
2
S
1
R1=1
四、零输入响应和零状态响应
(3) 零状态响应 izs''(t) +7izs'(t) +10izs (t) = e''(t) + 6e'(t) + 4e(t) 其解的形式为: izs(t) = Azs1e-2t + Azs2e-5t + B(t),t≥0 由于,e(t) =4,因此,其特解 B(t) = 8/5。 另外,要求解Azs1、Azs2,必须首先确定izs(0+)、 izs'(0+)。
四、零输入响应和零状态响应
练习 某二阶LTI连续系统的起始状态为x1(0-)和 x2(0-) ,当x1(0-)=1、x2(0-)=0时,其零输入响应为: yzi1(t)= e–t + e–2t , t≥0 当x1(0-)=0、x2(0-)=1时,其零输入响应为: yzi2(t)= e–t - e–2t , t≥0 当x1(0-)=1、x2(0-)=1,输入激励为f(t)时,其零输入 响应为: yzi(t)= 2 + e–t , t≥0 求:当x1(0-)=3、x2(0-)=2,激励为2f(t)时系统的全响应。
