西安电子科技大学数值分析
西安电子科技大学 研究生 电磁场数值分析期末考试题

西安电子科技大学何超电磁场数值分析考点1:矩量法的一般过程(算子方程、离散化过程、选配过程、矩阵方程求解)。
给定算子方程和基函数,采用伽略金法,计算阻抗矩阵和激励电压矩阵,从而求得电流系数矩阵,即得到方程的近似解。
(矩阵维数一般为2×2,或3×3,便于计算)。
1/link?url=oRwkn_6gajdEKC3YUFvvipOKLuZJXnVk43odUwyDWYRao nT1SlZLKEq9PCQba5xPYg_7mXpK8pZW0R-_RfT5EOXLvj0BKqKmQ6cfXMuW8P7有3个矩量法例题考点2:ScaLAPACK 的矩阵分布方式。
给定进程网格,矩阵分块大小,要求能写出按ScaLAPACK矩阵分布方式,每个进程对应的矩阵元素。
?1 并行矩阵填充在PC集群系统中MPI并行矩量法研究36 37考点3:temporary block column 对active block column 分解产生的影响.对于当前活动列块(即正在进行LU分解的列块),要能够分析其左侧临时列块对其LU分解所产生的影响。
?英文书写得很详细了啊45--55有lu分解将系数矩阵A转变成等价两个矩阵L和U的乘积,其中L和U分别是下三角和上三角矩阵。
当A 的所有顺序主子式都不为0时,矩阵A可以分解为A=LU,且当L的对角元全为1时分解唯一。
其中L是下三角矩阵,U是上三角矩阵。
4阶矩阵的LU分解[1]高斯消元法见数值分析教材考点4:积分方程的建立要求掌握EFIE 、MFIF 、PMCHW(电场、磁场、表面积分方程)根据等效原理建立的过程,即对于给定的问题(PEC (理想导体)或介质)能根据等效原理建立积分方程(不要求写出场的位函数表达式,主要考察方程建立的思想)。
看矩量法的书那个英文书只有EFIE 等效原理EFIE考点 5:RWG 基函数考察 RWG 基函数的 表达式,以及其 特点,对于给定的一个三角形网格图要能够标出哪些地方( 公共边上) 存在基函数。
西安电子科技大学数学分析考研大纲 .doc

西安电子科技大学数学分析考研大纲一、考试总体要求与考试要点1.考试对象考试对象为具有全国硕士研究生入学考试资格并报考西安电子科技大学理学院数学科学系硕士研究生的考生。
2.考试总体要求测试考生对数学分析的基本内容的理解、掌握和熟练程度。
要求考生熟悉数学分析的基本理论、掌握数学分析的基本方法,具有较强的抽象思维能力、逻辑推理能力和运算能力。
3.考试内容和要点(一) 实数集与函数1、实数:实数的概念;实数的性质;绝对值不等式。
2、函数:函数的概念;函数的定义域和值域;复合函数;反函数。
3、函数的几何特性:单调性;奇偶性;周期性。
要求:理解和掌握绝对值不等式的性质,会求解绝对值不等式;掌握函数的概念和表示方法,会求函数的定义域和值域,会证明具体函数的几何特性。
(二) 数列极限1、数列极限的概念(N ε-定义)。
2、数列极限的性质:唯一性;有界性;保号性。
3、数列极限存在的条件:单调有界准则;两边夹法则。
要求:理解和掌握数列极限的概念,会使用N ε-语言证明数列的极限;掌握数列极限的基本性质、运算法则以及数列极限的存在条件(单调有界原理和两边夹法则),并能运用它们求数列极限;了解无穷小量和无穷大量的概念性质和运算法则,会比较无穷小量与无穷大量的阶。
(三) 函数极限1、函数极限的概念(εδ-定义、X ε-定义);单侧极限的概念。
2、函数极限的性质:唯一性;局部有界性;局部保号性。
3、函数极限存在的条件:海涅归结原则。
4、两个重要极限。
要求:理解和掌握函数极限的概念,会使用εδ-语言以及X ε-语言证明函数的极限;掌握函数极限的基本性质、运算法则,会使用海涅归结原理证明函数极限不存在;掌握两个重要极限并能利用它们来求极限;了解单侧极限的概念以及求法。
(四) 函数连续1、函数连续的概念:一点连续的定义;区间连续的定义;单侧连续的定义;间断点的分类。
2、连续函数的性质:局部性质及运算;闭区间上连续函数的性质(最值性、有界性、介值性、一致连续性);复合函数的连续性;反函数的连续性。
电子科技大学数值分析研究生期末考试习题二

习 题 二请尽可能提供程序1、假设)(x f 在[]b a ,上连续,求)(x f 的零次最佳一致逼近多项式。
2、选择常数a ,使得ax x x -≤≤310max 达到极小,又问这个解是否唯一?3、如何选取r ,使r x x p +=2)(在[]1,1-上与零偏差最小?r 是否唯一?4、设在[]1,1-上543238401653841524381211)(x x x x x x -----=ϕ,试将)(x ϕ降低到3次多项式.求a 、b 使⎰-+202]sin [πdx x b ax 为最小。
5、设{}x span ,11=ϕ,{}1011002,x x span =ϕ,分别在21,ϕϕ上求一元素,使其为]1,0[2C x ∈的最佳平方逼近,并比较其结果。
6、用最小二乘法求一个形如2bx a y +=的经验公式,使它与下列数据相拟合,并求均方误差。
i x 19 25 31 38 44i y19.0 32.3 49.0 73.3 97.87、确定下列求积公式中的待定参数,使其代数精度尽量高,并指明所构造出的求积公式所具有的代数精度。
)()0()()(101h f A f A h f A dx x f hh++-≈--⎰8、用辛普森公式求积分1x e dx -⎰并估计误差。
9、求近似求积公式)]43(2)21()41(2[31)(10f f f dx x f +-≈⎰的代数精度。
10、用三个节点(2=n )的Gauss 求积公式计算积分)2(14112π=+=⎰-dx x I 。
11、试确定常数A ,B ,C 和α,使得数值积分公式)()0()()(22ααCf Bf Af dx x f ++-=⎰-为Gauss 型公式。
12、用三点公式求2)1(1)(x x f +=在1.1,0.1=x 和1.2处的导数值,并估计误差,)(x f 的值由下表给出:X1.0 1.11.2 1.3 1.4)(x f0.2500 0.2268 0.2066 0.1890 0.173613、就初值问题0)0(,=+='y b ax y 分别导出欧拉方法和改进的欧拉方法的近似解的表达式,并与准确解bx ax y +=221相比较。
电子科技大学-数值分析答案-钟尔杰

| x n +1 − 7 |=
而xn具有n位有效数,故
所以
| x n +1 − 7 |≤
由此得xn+1的误差限
1 2 7
| x n − 7 |2 ≤
1 × × 10 2− 2 n 2 7 4
1
| x n +1 − 7 |≤
1 × 10 1− 2 n 2
故,xn+1是 7 的具有 2n位有效数字的近似值。 三、问题 1.假定 a0,b0是非负实数且a0≠b0,按如下递推公式
∑ [ai ∑ b j ]
i =1 j =1
n,仍为( n + 2 ) ( n – 1) / 2。 ,算法输出 11 试构造一个算法,对输入的数据 x0,x1,x2,……,xn,以及x(均为实数) 为 ( x –x0) ( x –x1) ( x –x2)……( x –xn) 的计算结果。 解 算法如下: 第一步:输入x;x0,x1,x2,……,xn,M Å (x – x0 );k Å 0; 第二步:M Å M×(x – x0 );k Å k+1; 第三步:判断,若 k ≤ n,则转第二步;否则输出 M,结束。 12 利用级数公式
4
π 1 dx = arctan 1 = 可以计算出无理数π 的值。将定积分表示为积分和 2 4 1+ x
R
H
∫
1
0
xn dx ( n = 1,2,…,20) 的递推 5+ x
关系,并研究递推算法的数值稳定性。 6.计算两个多项式Pn(x)和Qm(x)的乘积多项式Tn+m(x)的方法称为向量的卷积方法。设
第一章 习题解答与问题
一、习题解答 1 设 x>0,x 的相对误差限为 δ,求 ln x 的误差。 解:设 x的准确值为x*,则有 ( | x – x* | /|x*| ) ≤ δ 所以 e(ln x)=| ln x – ln x* | =| x – x* | ×| (ln x)’|x=ξ·≈ ( | x – x* | / | x*| ) ≤ δ 另解: e(ln x)=| ln x – ln x* | =| ln (x / x*) | = | ln (( x – x* + x*)/ x*) | = | ln (( x – x* )/ x* + 1) |≤( | x – x* | /|x*| ) ≤ δ 2 设 x = – 2.18 和 y = 2.1200 都是由准确值经四舍五入而得到的近似值。求绝对误差限 ε( x ) 和 ε( y ) 。 解:| e(x) | = |e(– 2.18)|≤ 0.005,| e(y) | = |e( 2.1200)|≤ 0.00005,所以 ε( x )=0.005, ε( y ) = 0.00005。 3 下近似值的绝对误差限都是 0.005,问各近似值有几位有效数字 x1=1.38,x2= –0.0312,x3= 0.00086 解:根据有效数字定义,绝对误差限不超过末位数半个单位。由题设知,x1,x2, x3有效 数末位数均为小数点后第二位。故x1具有三位有效数字,x2具有一位有效数字,x3具有零位 有效数字。 4 已知近似数 x 有两位有效数字,试求其相对误差限。 解:| er(x) | ≤ 5 × 10– 2 。 5 设 y0 = 28,按递推公式 yn = yn-1 –
应用数值分析西安电子科技大学课后答案

应用数值分析西安电子科技大学课后答案1. 大数据中的小数据可能缺失、冗余、存在垃圾数据,但不影响大数据的可信数据,是大数据的()的表现形式。
[单选题] *A. 价值涌现B.隐私涌现C. 质量涌现(正确答案)D. 安全涌现2. 数据科学基本原则中,基于数据的智能的主要特点是()。
[单选题] *A. 数据简单,但算法简单B.数据复杂,但算法简单(正确答案)C. 数据简单,但算法复杂D. 数据复杂,但算法复杂3. ()是数据库管理系统运行的基本工作单位。
[单选题] *A. 事务(正确答案)B.数据仓库C. 数据单元D. 数据分析4. 目前,多数NoSQL 数据库是针对特定应用场景研发出来的,其设计遵循()原则,更强调读写效率、数据容量以及系统可扩展性。
[单选题] *B. READC. BASE(正确答案)D. BASIC5. 数据可视化的本质是()。
[单选题] *A. 将数据转换为知识(正确答案)B.将知识转换为数据C. 将数据转换为信息D.将信息转换为智慧6.下列不属于大数据在社会活动中的典型应用的是()。
[单选题] *A. 美团实现了快速精准的送餐服务B. 共享单车、滴滴打车方便了人们的日常出行C. 快递实现了订单的实时跟踪D. 供电公司提供电费账单查询(正确答案)7.在空间维度上刻画数据连续性是数据的()。
[单选题] *A. 可关联性(正确答案)B.可溯源性C. 可理解性D.可复制性8.将观测值分为相同数目的两部分,当统计结果为非对称分布时经常使用的是()。
[单选题] *B.标准差C. 中位数(正确答案)D.均值9. ()的本质是将低层次数据转换为高层次数据的过程。
[单选题] *A. 数据处理B.数据计算C. 数据加工(正确答案)D.整齐数据10. 在抽样方法中,当合适的样本容量很难确定时,可以使用的抽样方法是()。
[单选题] *A. 有放回的简单随机抽样B. 无放回的简单随机抽样C. 分层抽样D.渐进抽样(正确答案)11.下列关于基本元数据描述正确的是()。
电子科大matlab与数值分析第一次上机实践报告范文

电子科大matlab与数值分析第一次上机实践报告范文实践内容:MATLAB软件操作及程序设计学院:姓名:学号:指导老师:实践日期:题目(一)编程实现以下数列的图像,用户能输入不同的初始值以及系数。
并以某,y为坐标显示图像某(n+1)=a某某(n)-b某(y(n)-某(n)^2);y(n+1)=b某某(n)+a某(y(n)-某(n)^2)题目分析:此题要求是让我们编一个m程序,并且能够实现不同初值和系数画出图像。
这道题的重点有两个,一个是用循环生成两个数列,一个是做出图像。
对于生成数列,我采用for循环,而画出图像,由于某(n)和y(n)是离散的,我采用的是画出一些列点,故用catter(某,y)函数。
试题答案:functionhuatu(某1,y1,a,b,N)%获得变量N表示数列长度%函数huatu(某1,y1,a,b,N)绘制一些列点%参数某1,y1为两个数列的初值,a,b位系数,N为数列长度某(1)=某1;y(1)=y1;forn=1:(N-1)%循环实现递归算出数列某(n+1)=a某某(n)-b某(y(n)-某(n)^2);y(n+1)=b某某(n)+a某(y(n)-某(n)^2);endcatter(某,y,'.','r')%描点法画出图像,图像是一系列点,但有时因为数据%问题点不是很明显题目(二)2.编程实现奥运5环图,允许用户输入环的直径。
题目分析:本题又是一个作图题,重点是如何处理任意半径的问题、图形颜色和保持五个图形。
针对本题,我把圆心坐标设置为和半径有关的量,用循环画五个图形,并用holdon保持图形,而且用a某iequal保持横纵坐标等距。
题目答案:functionf=wuehuan(r)%函数wuehuan(r)能够绘制给定参数的奥运五环t=0:.01:2某pi;%生成一系列角度a=[-2.4某r,0,2.4某r,-1.2某r,1.2某r];%确定五个横坐标b=[0,0,0,-r,-r];%确定五个纵坐标color=['b','k','r','y','g'];%确定五种颜色forn=1:5%循环话五个正园某=r某co(t)+a(n);y=r某in(t)+b(n);plot(某,y,color(n))holdon%保持画过的园不被覆盖a某iequal%保正横纵等距3.实现对输入任意长度向量元素的冒泡排序的升序排列。
电子科技大学数值分析研究生期末考试习题一

电子科技大学数值分析研究生期末考试习题一习题请尽可能提供程序1.用二分法求方程012=--x x 的正根,要求误差05.0<。
2. 为求方程0123=--x x 在5.10=x 附近的一个根,设将方程改写成下列等价形式,并建立相应的迭代公式:1)2/11x x +=,迭代公式21/11k k x x +=+;2)231x x +=,迭代公式3211k k x x +=+;3)112-=x x ,迭代公式1/11-=+k k x x ;4)132-=x x ,迭代公式131-=+k k x x 。
试分析每种迭代公式的收敛性。
3. 给定函数)(x f ,设对一切x ,)(x f '存在且M x f m ≤'≤<)(0,证明对于范围M /20<<λ内的任意定数λ,迭代过程)(1k k k x f x x λ-=+均收敛于)(x f 的根*x 。
4.设a 为正整数,试建立一个求a1的牛顿迭代公式,要求在迭代公式中不含有除法运算,并考虑公式的收敛性。
请提供程序。
5.用Gauss 消去法求解方程组:-=????? ??????? ??----503121312111321x x x (请提供程序)用列主元Gauss 消去法求解下列方程组:(1)=????? ??????? ??13814142210321321x x x (请提供程序)6.用追赶法解三对角方程组b Ax =,其中--------=2100012100012100012100012A ,=00001b 。
7.设n n R P ?∈且非奇异,又设x 为n R 上一向量范数,定义Px xp =。
试证明px 是n R 上向量的一种范数。
8.用平方根法(Cholesky 分解)求解方程组:=????? ??????? ??7351203022323321x x x9.用改进的平方根法(T LDL 分解)求解方程组:=????? ??????? ??3016101795953533321x x x 。
西安电子科技大学数值分析
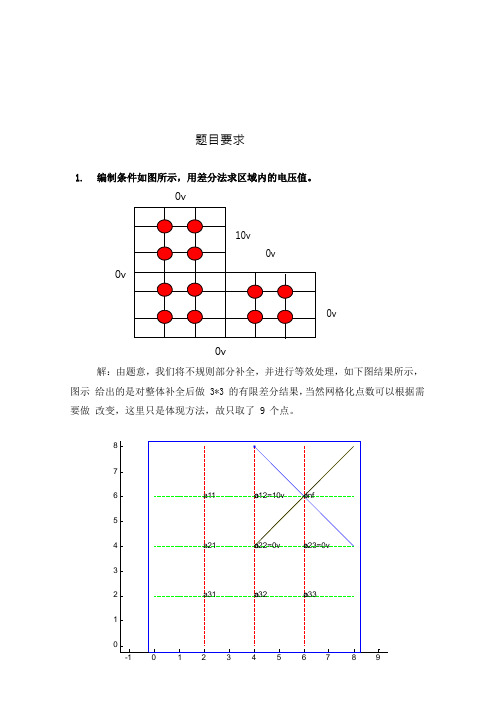
题目要求1. 编制条件如图所示,用差分法求区域内的电压值。
0v10v0v0v0v0v解:由题意,我们将不规则部分补全,并进行等效处理,如下图结果所示,图示给出的是对整体补全后做3*3 的有限差分结果,当然网格化点数可以根据需要做改变,这里只是体现方法,故只取了 9 个点。
876 a11o a12=10v o-inf54 a21o a22=0v o a23=0v32 a31o a32o a331-1 0 1 2 3 4 5 6 7 8 9根据拉普拉斯 5 点差分原理,可知得到关于电压变量 a(i, j 1, 2, 3) 的i , j方程如下:4a 1,1 a 2,110;a 1,1 4a 2,1 a 3,1 0; a 2,1 4a 3,1 a 3,2 0; a 3,1 4a 3,2 a 3,3 0; a 3,2 4a 3,30.4 1 0 0 0 10 1 4 1 00 0 写成矩阵的形式: Ax b ; 其中, A 0 1 4 10 , b 0 。
0 0 1 41 0编写程序可以求得0 01 4a , a , a , a , a , 2.6790.7180.1920.0513 0.0132. 在区域一边有个源,边界为 PML 边界,用 FDTD 法求所研究区域的场分布。
建模说明:二维 TE 波在空间传播,采用 PML 边界吸收,点辐射源验证。
FDTD 基本差分方程Yee 采用矩形网格进行空间离散,将每个节点进行编号,节点的编号和其空 间坐标位置按照下面的方式对应起来()(),,,,i j k i x j y k z =∆∆∆ (2-1) 而该点的任意函数()x,y,z,F t 在时刻n t ∆的值可以表示为:()(),,,,,n F i j k F i x j y k z n t =∆∆∆∆ (2-2)式中x ∆、y ∆、z ∆分别为沿,,x y z 方向上离散的空间步长,t ∆是时间步长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
题目要求
1. 编制条件如图所示,用差分法求区域内的电压值。
0v
10v
0v
0v
0v
0v
解:由题意,我们将不规则部分补全,并进行等效处理,如下图结果所示,图示给出的是对整体补全后做3*3 的有限差分结果,当然网格化点数可以根据需要做改变,这里只是体现方法,故只取了 9 个点。
8
7
6 a11o a12=10v o-inf
5
4 a21o a22=0v o a23=0v
3
2 a31o a32o a33
1
-1 0 1 2 3 4 5 6 7 8 9
根据拉普拉斯 5 点差分原理,可知得到关于电压变量 a
(i, j 1, 2, 3) 的
i , j
方程如下:
4a 1,1 a 2,1
10;
a 1,1 4a 2,1 a 3,1 0; a 2,1 4a 3,1 a 3,2 0; a 3,1 4a 3,2 a 3,3 0; a 3,2 4a 3,3
0.
4 1 0 0 0 10 1 4 1 0
0 0 写成矩阵的形式: Ax b ; 其中, A 0 1 4 1
0 , b 0 。
0 0 1 4
1 0
编写程序可以求得
0 0
1 4
a , a , a , a , a , 2.679
0.718
0.192
0.0513 0.013
2. 在区域一边有个源,边界为 PML 边界,用 FDTD 法求所研究区域的场分布。
建模说明:二维 TE 波在空间传播,采用 PML 边界吸收,点辐射源验证。
FDTD 基本差分方程
Yee 采用矩形网格进行空间离散,将每个节点进行编号,节点的编号和其空 间坐标位置按照下面的方式对应起来
()(),,,,i j k i x j y k z =∆∆∆ (2-1) 而该点的任意函数()x,y,z,F t 在时刻n t ∆的值可以表示为:
()(),,,,,n F i j k F i x j y k z n t =∆∆∆∆ (2-2)
式中x ∆、y ∆、z ∆分别为沿,,x y z 方向上离散的空间步长,t ∆是时间步长。
Yee 采用中心差分来代替对时间和空间的微分,具有二阶精度 ()()()()()
2
,,1/2,,1/2,,n n n F i j k F i j k F i j k x x x
ο∂+--=+∆∂∆ (2-3)
()()()()(
)
1/21/22
,,,,,,n n n F i j k F i j k F i j k t t t ο+-∂-=+∆∂∆ (2-4)
按照式(2-3)和式(2-4),由Maxwell 得差分方程如式(2-5)和式(2-6),其它场量差分格式与此类似。
()()()()()()()()()
11/2,,121/2,,11/2,,1/2,,1/2,,1/2,,1/2,,1121/2,,21/2,,n n x x i j k t i j k t E i j k E i j k i j k t i j k t i j k i j k i j k σεσσεεε++∆-
+∆+=⨯++⨯+∆+∆+++++
()()()()1/21/21/21/21/2,,1/21/2,,1/21/2,1/2,1/2,1/2,n n n n y y z z H i j k H i j k H i j k H i j k y z ++++⎡⎤
++-+-++-+--⎢⎥
∆∆⎢⎥⎣⎦
(2-5)
()()()()()()()()()
1/21/2,1/2,1/212,1/2,1/21
,1/2,1/2,1/2,1/2,1/2,1/2,1/2,1/2,1/2,1/2112,1/2,1/22,1/2,1/2n n x x i j k t i j k t H i j k H i j k i j k t i j k t i j k i j k i j k ρμρρμμμ+-++∆-
++∆++=⨯+++⨯
++∆++∆++++++++
()()()(),1/2,1,1/2,,1,1/2,,1/2n n n n y y z z E i j k E i j k E i j k E i j k z y ⎡⎤
++-+++-+-⎢⎥∆∆⎢⎥⎣⎦
(2-6)
在Yee 的差分格式里,每个网格上各场分量的新值依赖于该点在前一时间步长时刻的值及该点周围邻近点上另一场量的场分量早半个时一间步长时刻的值。
因此,在任一给定时刻,场分量的计算可一次算出一个点,或者采用p 个并行处理器一次算p 个点(并行算法)。
通过这些基本算法,逐个时间步长对模拟区域各网格点的电磁场交替进行计算,在执行适当的时间步数后,即可获得需要的时域数值结果,称这种差分格式为蛙跳格式。
1.4
50
1.2
1
100
0.8
150
0.6
0.4
200
0.2
250
50
100 150 200 250
-0.2
图中给出了当入射波为 TE 波时,所研究区域(2-D )的磁场分布情况。
3.矩量法程序
<1>矩量法(Method of Moments, MoM )是一种将连续方程离散化为代数方程组的方法,对求解微分方程和积分方程均适用。
<2>矩量法包括如下三个基本过程:
(1)离散化过程 主要目的是将算子方程化为代数方程,具体步骤是:①在算子L 定义域内适当的选择一组线性无关的基函数n f ;②将待求函数f 表示为该组基函数的线性组合;③利用算子的线性,将算子方程化为代数方程。
(2)取样检测过程 主要目的是将求解代数方程的问题转化为求解矩阵方程的问题。
基本步骤是:①在算子L 的值域内适当的选择一组线性无关的权函数m W ;②将m W 与代数方程取内积进行N 次抽样检验;③利用算子的线性和内积的性质,将
N 次抽样检验的内积方程化为矩阵方程。
(3)矩阵求逆过程
具体过程如下:
算子方程:()
()()
22
','''4''a b
a b
x y dx dy U x x y y ρπε
--=-+-⎰
⎰
,其中U 为常数
将研究区域D 分成N 个单元n S ,2244a a
b b N N
=⇒=
,b 为单元边长 取()(),1,,n n f x y x y S =∈,其余为零
采样函数:()()m m m w x x y y δδ=--
1
N
n n n a f ρ==∑,带入算子方程,求内积。
即
()()()()()(),221
''4''n n n n a
b
x b y b
mn m n m m a b x b y b
L w L f x x y y dx dy dxdy U x x y y δδπε++----⎡⎤
⎢⎥==--=⎢⎥-+-⎣
⎦
⎰⎰⎰⎰
,m m g w U U ==
[][][]mn n m LA G L a g =⇒=
[]()()()()
()()()()()()()()
()()()()1,11,21312,12,22323,13,2333,1,23,,,,,,,,,,,,n n mn n m m m m n w L f w L f w L f w L f w L f w L f w L f w L f L w L f w L f w L f w L f w L f w L f w L f w L f ⎡⎤
⎢
⎥⎢⎥⎢
⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦
[]123n n a a a a a ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦ ,[]123m m g g g g g ⎡⎤⎢⎥⎢⎥
⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦。
