小学数学思维方法:巧求周长
【精品奥数】三年级下册数学思维训练讲义-第十八讲 巧求周长(二) 人教版(含答案)

第十八讲巧求周长(二)第一部分:趣味数学伸手抓住机会莱斯·布朗因为患有先天性的疾病,说话不清,可他一直有一个梦想:成为一名电台音乐节目主持人。
为了实现自己的梦想,他每天晚上都通过半导体收音机收听当地的摇滚节目。
在自己的小房间里,他虚拟了一个电台:他将一把旧发刷当作麦克风,然后喋喋不休地开始他饶舌的表演,为他假想中的观众介绍各种各样的唱片。
一天,他鼓起勇气,找当地电台台长毛遂自荐,被拒绝后他并没有放弃。
接下来的一星期,他每天都去电台,问是否能给他提供一份工作。
最终台长让莱斯当了一名跑腿的伙计。
他暗暗留心主持人是如何在控制面板上操作的,他就像一块海绵一样,贪婪地吸收着所学的一切知识。
每天在别人的再三催促下才离开工作室。
晚上回去后,他又再三练习。
他在等待机会的到来。
一个星期六的下午,一位名叫洛克的主持人喝得酩酊大醉,可马上就要到他广播的时间了。
电台里只有他和莱斯。
说话已经语无伦次的洛克无疑不能主持长达四个小时的综艺广告节目。
台长打来电话,在不能找到其他主持人的情况下,他给了莱斯机会。
放下电话后,莱斯箭一样冲进直播室,轻轻地把洛克移到一边之后,坐在了他期盼已久的旋转工作台边,激动而自信地开始了他的第一次主持。
这次节目大获成功。
莱斯赢得了听众们的赞扬,当然也包括台长。
莱斯最终得到了他梦寐以求的工作。
【启示】每个人的一生中都会有一些机遇,但我们如果不积累学识,积蓄力量,不懂得如何抓住机遇,机遇就会与你擦肩而过,因为机遇只垂青于那些有准备的人。
知识要点在解答比较复杂的关于长方形、正方形周长计算的问题时,生搬硬套公。
巧算周长(二)--2022-2023学年三年级数学思维拓展(学生)

2022-2023学年小学三年级思维拓展--巧算周长(二)1.知识精讲1专题简析:在解答比较复杂的关于长方形、正方形周长计算的问题时,生搬硬套公式往往行不通,这时灵活地运用所学知识在解题中显得相当的重要。
解答稍复杂的有关长方形、正方形周长的问题,首先要仔细观察,认真思考,想想已知条件和要求问题之间有什么联系,应该先求什么,再求什么,然后灵活运用长方形、正方形周长公式进行计算。
典例分析1把长130厘米的铁丝围成一个长方形,接头处重合2厘米,要使长比宽多18厘米,长和宽各是多少厘米?2一根铁丝长80厘米,围成一个边长为8厘米的正方形,余下的铁丝围成一个长为14厘米的长方形。
这个长方形的宽是多少厘米?3一个长方形的周长是正方形的2倍,正方形的边长与长方形的宽都是4厘米。
长方形的长是多少厘米?4三个同样大小的长方形正好拼成一个正方形,正方形的周长是48厘米,求每个长方形的周长。
5一张长方形的纸,长是28厘米,宽是15厘米,先剪下一个最大的正方形,再从余下的纸片中,再剪下一个最大的正方形。
最后余下的长方形周长是多少?2真题演练一.选择题(共5小题,满分10分,每小题2分)1.(2分)(2022秋•黄州区期末)用长64厘米的铁丝围成一个长是20厘米的长方形,则长方形的宽是()A.24厘米B.22厘米C.12厘米2.(2分)(2022春•德江县期末)在一个边长为6米的正方形的一角剪去一个边长为1米的小正方形,原正方形的周长()A.变小了B.不变C.变大了3.(2分)(2022春•方城县期末)下面两个同样大小的正方形,在不同位置剪去同样大小的长方形后,剩余部分的()A.面积不同,周长不同B.面积不同,周长相同C.面积相同,周长不同4.(2分)(2017秋•端州区期末)一个长方形的周长是32米,宽是7米,它的长是()A.5米B.9米C.11米5.(2分)(2017秋•甘肃期末)学校长方形的操场长120米,宽60米,沿操场跑两圈是( )米.A.180B.360C.720二.填空题(共8小题,满分16分,每小题2分)6.(2分)(2022春•南海区期末)如图是由两个正方形组成,已知大正方形的周长为36厘米,小正方形的周长是厘米。
小学数学寒假训练--------巧算周长

寒假提优
思维训练五 巧算周长
1如图一,你知道右面凸字形的周长怎样算吗?
2. 你能很快算出右面凹字形的周长吗?
3厘米
3 把四个长6厘米,宽2厘米的小长方形拼成一个较大的长方形,你知道拼成的长方形的周长是多少吗?
4将一张长24厘米,宽16厘米的长方形白纸对折两次,折成的小长方形的周长是多少厘米?
5 如图,一张长6分米、宽5分米的长方形纸板,从四个角上,各截去一个边长为1分米的正方形。
所剩部分的周长是多少分米?
6 如图有五个同样的小长方形拼成一个大长方形,如果小长方形的宽是2厘米,那么大长方形周长是多少厘米?
7如图,台阶一共有八级,从点a 到点o 为24分米,从点B 到点o 为16分米,一只蜗牛,从台阶的点a 一级一级向上爬爬到台阶的点B ,这只蜗牛至少要爬多少分米?
B
O A
8把下图中的每个正方形的大小相同,并且每个正方形重合了一部分,其中一个正方形的顶点,在另外两个正方形的中心,如果每个正方形的边长是4厘米,那么这个图形周长是多少厘米?
9如图,把一块长方形菜地平均分成八块同样的小正方形,已知每块小正方形的周长是6厘米,求长方形菜地的周长。
10图中正方形里有一个长方形,求这个长方形的周长(单位:分米)
7
11把边长分别是5厘米4厘米3厘米2厘米的四个正方形从大到小的顺序排成一行(如图),排成的图形周长是多少厘米?。
小学数学竞赛:巧求周长.学生版解题技巧 培优 易错 难

一、基本概念①周长:封闭图形一周的长度就是这个图形的周长.②面积:物体的表面或封闭图形的大小,叫做它们的面积.二、基本公式:①长方形的周长2=⨯(长+宽),面积=长⨯宽.②正方形的周长4=⨯边长,正方形的面积=边长⨯边长.三、常用方法:(1)对于基本的长方形和正方形图形,可以直接用公式求出它们的周长和面积,对于一些不规则的比较复杂的几何图形,我们可以采用转化的数学思想方法割补成基本图形,利用长方形、正方形周长及面积计算的公式求解.(2)转化是一种重要的数学思想方法,在转化过程中要抓住“变”与“不变”两个部分.转化后的图形虽然形状变了,但其周长和面积不应该改变,所以在求解过程中不能遗漏掉某些线段的长度或某部分图形的面积.转化的目标是将复杂的图形转化为周长或面积可求的图形.(3)寻求正确有效的解题思路,意味着寻找一条摆脱困境、绕过障碍的途径.因此,我们在解决数学问题时,思考的着重点就是要把所需解决的问题转化为已经能够解决的问题.也就是说,在直接求解不容易或很难找到解题途径的问题时,我们往往转化问题的形式,从侧面或反面寻找突破口,知道最终把它转化成一个或若干个能解决的问题.这种解决问题的思想在数学中叫“化归”,它是数学思维中重要的思想和方法.(4)在几何中,有许多图形是由一些基本图形组合、拼凑而成的.这样的图形我们称为不规则图形.不规则图形的面积往往无法直接应用公式计算.那么,不规则图形的面积怎样去计算呢?对称、旋转、平移这几种几何变换就是解决这类面积问题的手段.四、几个重要的解题思想 (1)平移在平面图形的计算中,常常要将一个平面图形移动到平面上的另一个位置进行计算.其中,将图形沿一个固定方向的移动叫做平移,一个图形经过平行移动不改变其形状与大小,所以图形面积是保持不变的.利用图形的平移,可以使面积计算问题的解法简捷明快,颇有新意.(2)割补割补法在我国古代叫“出入相补原理”,我国古代魏晋时期著名的数学家刘徽在《九章算术注》中就明确地提出“出入相补,各从其类”的出入相补原理.这个原理的内容是几何图形经过分、合、移、补所拼凑成的新图形,它的面积不变.知识点拨4-2-2.巧求周长(3)旋转在平面图形的割补中,有时要将一个图形绕定点旋转到一个新的位置,产生一种新的图形结构,图形在转动过程中形状大小不发生改变.利用这种新的图形结构可以帮我们解决面积的计算问题.(4)对称平面图形中有许多简单漂亮的图形都是轴对称图形.轴对称图形沿对称轴折叠,轴两侧可以完全重合.也就是说,如果一个图形是轴对称图形,那么对称轴平分这个图形的面积.熟悉轴对称图形这个性质,对面积计算会有很大帮助.(5)代换在几何计算中,对有关数量进行适当的等量代换也是解决问题的已知技巧.小结:本讲主要通过求一些不规则图形的周长,体会一种转化思想,重点在于把不规则图形转化为规则图形的方法,包括平移、旋转、割补、差不变原理,通过这些方法的学习,让学生体会求周长的技巧,提高学生的观察能力、动手操作能力、综合运用能力.例题精讲模块一、图形的周长和面积——割补法【例 1】求图中所有线段的总长(单位:厘米)【例 2】如图所示,点B是线段AD的中点,由A、B、C、D四个点所构成的所有线段的长度均为整数,若这些线段的长度之积为10500,则线段AB的长度是。
第七讲:巧求周长【优质】

知识精讲一、知识点概述我们已经学习了长方形和正方形周长的计算,会运用长方形和正方形周长的计算公式计算长方形和正方形的周长,本周我们要进一步学习和运用长方形和正方形的周长公式,巧求表面上看起来根本不是长方形或正方形的图形的周长,提高我们空间想象能力和解决问题的能力。
2、复习长方形的周长=长×2+宽×2= (长+宽)×2正方形的周长=边长×43、求不规则图形的周长的方法运用长方形和正方形的周长公式,巧求表面上看起来根本不是长方形或正方形的图形的周长,这就必须掌握“转化”的思考方法。
所谓“转化”,这里主要是指把某个图形转变成标准的长方形或正方形,以便计算它们的周长。
特别提示:在运用转化的思维方法时,必须仔细观察题目所给的图形是不是一个直角多边形,即所有的角是不是都为直角。
因为任意直角多边形,总可以弥补成一个长方形或正方形。
三、新授例1、计算右边图形的周长。
(单位:厘米)分析:要想求出这个图形的周长,乍看起来,似乎缺少条件。
因为这个图形不是一个正方形,而是一个六边形。
要求这个六边形的周长,只有把所有的边长相加,然而条件不足。
怎么办呢?我们先仔细观察这个图形,发现它的六个角都是直角,因此,我们可以把图中右上缺角处的线段分别向上、向右平行移到虚线外(见下图)。
这样,正好移补成一个正方形,问题得到了解决。
解答:30×4=120(厘米)答:这个图形的周长是120厘米。
巩固练习:1.如图是由三个长方形组成的。
求这个组合图形的周长。
3、下图是一个楼梯的侧剖面图,已知每步台阶宽3分米,高2分米。
求这个楼梯侧面的周长是多少米。
分析:要求楼梯侧面的周长,表面看起来似乎缺少条件。
但是,如果认真观察,就可以发现把每层台阶的宽度向上移到和最上层同样高的地方,把每层台阶的高度右移到和下层台阶的高度一致的地方,这样原图就转化成一个长方形,这时长方形的长=3×10=30(分米),宽=2×10=20(分米),根据求长方形周长的计算公式(注意将分米换算成米)就可以求出图形的周长了。
三年级下册数学试题-思维训练:巧求周长(无答案)全国通用
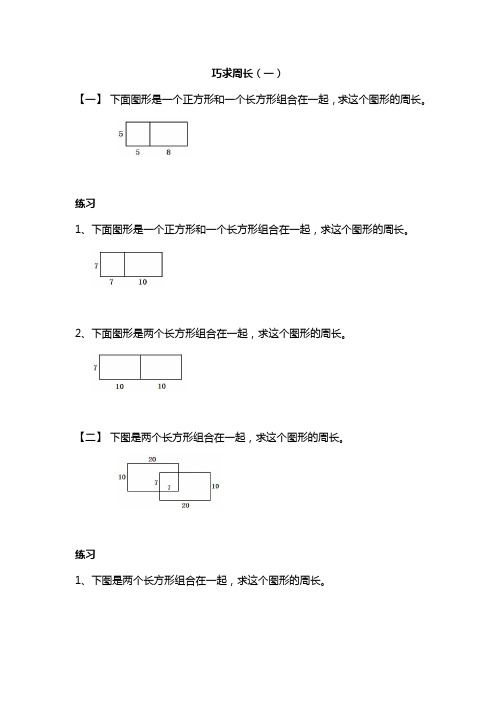
巧求周长(一)【一】下面图形是一个正方形和一个长方形组合在一起,求这个图形的周长。
练习1、下面图形是一个正方形和一个长方形组合在一起,求这个图形的周长。
2、下面图形是两个长方形组合在一起,求这个图形的周长。
【二】下图是两个长方形组合在一起,求这个图形的周长。
练习1、下图是两个长方形组合在一起,求这个图形的周长。
2、从一个边长是10厘米的正方形的一角剪去一个边长是4厘米的小正方形,求剩下图形的周长。
【三】下图是一个楼梯的侧面图,求此图形的周长。
练习1、下图是一个楼梯的侧面图,你能算出它的周长吗?2、如下图所示,丹丹和小玲同时从学校到图书城,丹丹沿A路线行走,小玲沿B路线行走,如果两人速度一样,谁先到图书城?为什么?【四】下图是由6个边长1厘米的正方形拼成的。
这个图形的周长是多少厘米?练习1、下图是由5个边长为3厘米的正方形组成的图形,求这个图形的周长。
2、下图是由6个边长为2厘米的正方形组成,求此图形的周长。
【五】两个大小相同的正方形拼成一个长方形后,周长比原来两个正方形周长的和减少了4米。
原来一个正方形的周长是多少米?练习1、把两个大小相同的正方形拼成一个长方形后,周长比原来两个正方形周长的和减少了8厘米,原来一个正方形的周长是多少厘米?2、把一个正方形剪成两个大小相同的长方形后,两个长方形周长的和比原来正方形周长增加16分米,原来正方形的周长是多少分米?【六】一个正方形的边长是4厘米,将9个这样的正方形如下图一样拼成一个大正方形,问拼成的这个大正方形的周长是多少厘米?练习1、把16个边长是2厘米的小正方形拼成一个大正方形,这个拼成的大正方形周长是多少厘米?2、把8个边长为5分米的小正方形如下图拼成一个长方形,这个长方形的周长为多少厘米?【七】将一张边长为18厘米的正方形纸,剪成4个完全一样的小正方形纸片,问这4个小正方形周长的和比原来的正方形周长增加了多少厘米?练习1、将一张边长为10厘米的正方形纸,剪成2个完全一样的小长方形,那么这2个小长方形周长之和比原来的正方形的周长增加了多少厘米?2、把一个边长为28厘米的正方形,如下图剪成6个完全一样的长方形,这六个长方形周长的和与原来的正方形相比,增加了多少厘米?课外作业1、下面图形是三个相同的正方形组合在一起,求这个图形的周长。
周长—巧求周长(教案)-三年级上册数学 人教版

教案:周长—巧求周长教学目标:1. 让学生理解周长的概念,知道周长是围成封闭图形的所有边的总长度。
2. 培养学生运用测量工具测量图形周长的能力。
3. 引导学生发现并掌握巧求周长的方法,提高解决问题的能力。
教学重点:1. 周长的概念及测量方法。
2. 巧求周长的方法。
教学难点:1. 周长概念的建立。
2. 巧求周长的方法。
教学准备:1. 课件或黑板。
2. 测量工具(如直尺、卷尺等)。
3. 图形卡片。
教学过程:一、导入(5分钟)1. 利用课件或黑板展示各种图形,引导学生观察并说出图形的名称。
2. 提问:这些图形有什么共同特点?引导学生发现图形都是由线段围成的。
二、探究周长的概念(10分钟)1. 引导学生观察图形,提出问题:这些图形的边有什么特点?2. 学生回答:图形的边都是直线。
3. 提问:如果我们要计算这些图形的边长总和,应该怎么计算呢?4. 学生回答:将所有边的长度相加。
5. 总结:将图形的所有边的长度相加,得到的结果就是图形的周长。
三、测量周长(10分钟)1. 分组活动:每组发一张图形卡片,要求学生用测量工具测量图形的周长。
2. 学生操作,教师巡回指导。
3. 各组汇报测量结果,教师点评并总结测量方法。
四、巧求周长(10分钟)1. 出示课件或黑板上的图形,引导学生观察并思考:这些图形的周长有什么规律?2. 学生回答:正方形的周长等于边长乘以4,长方形的周长等于长和宽的和乘以2。
3. 教师总结:正方形和长方形的周长可以通过简单的计算得到,这就是巧求周长的方法。
五、巩固练习(15分钟)1. 出示课件或黑板上的练习题,要求学生独立完成。
2. 学生完成后,教师点评并解答疑问。
六、总结(5分钟)1. 提问:今天我们学习了什么内容?学生回答:周长的概念、测量周长的方法以及巧求周长的方法。
2. 教师总结:周长是围成封闭图形的所有边的总长度,我们可以通过测量工具测量周长,也可以通过巧求周长的方法快速计算正方形和长方形的周长。
专题22 巧算周长(一)(解析)

2022-2023学年小学三年级思维拓展举一反三精编讲义专题22 巧算周长(一)知识精讲专题简析:一个图形的周长是指围成它的所有线段的长度和。
我们已经学会了求长方形、正方形这些标准图形的周长,那么怎样运用长方形、正方形的周长计算公式,巧妙地求一些复杂图形的周长呢?对于一些不规则的比较复杂的几何图形,要求它们的周长,我们可以运用平移的方法,把它转化为标准的长方形或正方形,然后再利用周长公式进行计算。
将一个大长方形或正方形分割成若干个长方形和正方形,那么图形周长就会增加几个长或宽;反之,将若干个小长方形或正方形合成一个大长方形或正方形,图形周长就会减少几个长或宽。
典例分析【典例分析01】下图是一个楼梯的侧面图,求此图形的周长。
2米3米【思路引导】如果把每层台阶的宽度向上移到和最上层台阶同样高的地方,把每层台阶的高度向右移到和最下层的台阶长度一致的地方(如下图),这样楼梯侧面图就转化为一个长方形,然后我们利用长方形周长计算公式求出此图形的周长。
(2+3)×2=10米。
【典例分析02】下图是由6个边长2厘米的正方形拼成的,这个图形的周长是多少厘米?【思路引导】这题我们可以用平移的方法将它转化为一个长方形,如下图:这个长方形的长含有4个小正方形的边长,长为2×4=8厘米;宽含有2个小正方形的边长,宽为2×2=4厘米。
这个长方形的周长为:(2×4+2×2)×2=24厘米。
3米2米【典例分析03】两个大小相同的正方形拼成一个长方形后,周长比原来两个正方形周长的和减少了6厘米。
原来一个正方形的周长是多少厘米?【思路引导】根据题意,画出下图。
当两个正方形拼成一个长方形时,组成两个正方形的8条边就减少了2条,而已知两条边的和是6厘米,那么一条边长就是6÷2=3厘米。
所以,原来正方形的周长是:3×4=12厘米。
【典例分析04】一个正方形,边长是5厘为,将9个这样的正方形如下图一样拼成一个大正方形,问:拼成的大正方形的周长是多少?【思路引导】从图上可以看出,9个小正方形拼成的大正方形共有3排,每排由3个小正方形组成。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
巧求周长
【知识要点】
一、周长公式
正方形周长=边长×4,长方形周长=(长+宽)×2
二、解题方法
1. 通过平移变成已知:把若干段不知道长度的线段通过平移变成知
道长度的线段,把不规则的图形周长化为规则图形周长来求;
2. 图形分割后周长变大:将一个大长方形或正方形分割成若干个图
形后,图形的周长就会增加;
3. 图形拼凑后周长变小:将若干个小长方形或正方形拼凑成大图形
后,图形的周长就会减小。
【典型例题】
1.下图“凸”字的周长是多少厘米?
解: 如图我们发现,它不是一个规则的正方形或长方形,所以不
能直接套用公式.
但如我们把线段AC 放在C A ''、C C '放在A A '、DB 放在B D ''、
D D '放在B B '的位置,
则此图就变成一个正规的长方形,如下图所示.
[5+(3+1)]×2=9×2=18(厘米)
2.下图“E ”字周长是多少厘米?
A ''
解:为了方便,我们把图如下编号,则图形变成下列形式.我们把a移至a'处,把b移至b'处,
图形成为一个大正方形里有4条2厘米长的线段,求“E”形周长就很简单了.
3.下图是由10个边长为3厘米的小正方形组成.每个小正方形的顶点恰在另一个正方形的中心,且边相互平行,求这个图形的周长.
3
分析:此题如仍用平移的方法,不仅移动的次数多且较为麻烦,不妨我们分水平方向和竖直方向两种分别讨论,
水平方向上有(3+1.5⨯9)⨯2=33厘米,
同理,竖直方向也为(3+1.5⨯9)⨯2=33厘米,周长可求.
解:(3+1.5⨯9)⨯2⨯2
=33⨯2
=66(厘米)
答:此图形周长为66厘米.
4.下图是一个零件的平面图,图中每一条最短线段均长5厘米.零件长35厘米,高30厘米,这个零件周长是多少厘米?
分析:我们把图形按右上图所示方向移动,而对于零件下
方的“十”字,则可把“十”字上面的横线移下来,
这时,使图形成为一个大长方形,再看长方形里有
小线段10条,
而每条都长5厘米,所以题目得解.
解:(35+30)⨯2+5⨯10
=65⨯2+50
=130+50
=180(厘米)
答:这个图形的周长是180厘米.
5.在4cm ⨯7cm 的正方形网格(如图)中,所有正方形的
周长的和是多少cm ?
解 分类进行统计,得: 边长为1cm 的正方形周长的
和是1⨯4⨯(4⨯7)=112();
边长为2cm 的正方形周长的
和是:2⨯4⨯(3⨯6)=144(cm );
边长为3cm 的正方形周长的
和是:3⨯4⨯(2⨯5)=120(cm );
边长为4cm 的正方形周长的
和是:4⨯4⨯(1⨯4)=64(cm );
图中所有正方形周长的和
是:112+144+120+64=440(cm ).
6.如下图所示,长方形长4厘米,宽2厘米.现沿其对角线
BD 对折得到一几何图形,试求图形阴影部分周长.
A D F
35厘米30厘米
分析:把图中△BDE 以BD 为轴再转回去,使之与△
ADB 完全重合,不难看出要求的阴影部分的周长正好等于长方形的周长.
阴影部分周长由BE +ED +DC +BC 而BE =AB 、DE =AD .
所以阴影部分周长为AD +AB +BC +DC =(4+2)⨯2=6⨯2=12厘米.
解:(4+2)⨯2
=6⨯2
=12(厘米)
答:它的周长为12厘米.
练习题
1.下图的周长是 厘米.
2.下图是一座楼房的平面图,图中用不同字母
表示长度不同的各条边.已知b =50米,c =30米,g =10米,这座楼房平面的周长
是 米.
3.把边长分别是5厘米、4厘米、3厘米和2厘米的
4个正方形按从大到小的顺序排成一行(如图),排成的图形周长是多少厘米?
4.将一张边长为12厘米的正方形纸对折,再将对折后
的纸沿它的竖直中线(右图虚纸)剪开,得到三个矩形纸片,其中两个较小的矩形
的周长之和是多少厘米?
4
5.如图正方形ABCD的边长为4cm,每边被四等分.求图中所有正方形周长的和.。
