用MATLAB画曲线族
matlab画图设置(坐标轴、曲线、颜色)

matlab画图设置(坐标轴、曲线、颜色)a=linspace(1,2,10)plot(a,'--pr','linewidth',1.5,'MarkerEdgeColor','r','MarkerFaceColor','m','MarkerSize',1 0)legend('a','Location','best')title('a','FontName','Times New Roman','FontWeight','Bold','FontSize',16)xlabel('T','FontName','Times New Roman','FontSize',14)ylabel('a','FontName','Times New Roman','FontSize',14,'Rotation',0)axis auto equalset(gca,'FontName','Times New Roman','FontSize',14)1.曲线线型、颜色和标记点类型plot(X1,Y1,LineSpec, …) 通过字符串LineSpec指定曲线的线型、颜色及数据点的标记类型。
线型颜色数据点标记类型标识符意义标识符意义标识符意义- 实线 r 红色 + 加号-. 点划线 g 绿色 o 圆圈-- 虚线 b 蓝色 * 星号: 点线 c 蓝绿色 . 点m 洋红色 x 交叉符号y 黄色 square(或s) 方格k 黑色 diamond(或d) 菱形w 白色 ^ 向上的三角形v 向下的三角形> 向左的三角形< 向右的三角形pentagram(或p) 五边形hexagram(或h) 六边形2.设置曲线线宽、标记点大小,标记点边框颜色和标记点填充颜色等。
MATLAB数学建模1三角函数的计算和曲线族的画法

三角函数的计算和公式的作图[问题1.1]三角函数的计算求证:三角函数31cos (3cos cos3)4θθθ=+ 用MA TL A B 的符号计算验证,再用曲线验证。
[解析]利用三角公式可得cos3θ = cos2θc o s θ = 11(1cos 2)cos (cos cos 2cos )22θθθθθ+=+ 111[cos (cos cos3)](3cos cos3)224θθθθθ=++=+ 证毕。
[程序]MA TH1_1.m%三角函数的计算和验证clear %清除变量theta =-180:5:180; %角度向量th=theta *pi/180; %化为弧度数figur e %开创图形窗口plot(theta ,cos(th).^3,theta ,(3*cos(th)+cos(3*th))/4,'.')%画线和点syms x %定义符号变量y=1/4*cos(3*x)+3/4*cos(x) %三角函数的展开式expan d (y) %展开三角函数y=cos(x)^3 %三角函数simpl e (y) %展开三角函数M1图练习:验证31sin (3sin sin 3)4θθθ=-[问题1.2] 曲线族的画法根据麦克斯韦速率分布率律,求最概然速率?氧气分子在300K 到600K 温度区间(温度间隔为100K),速率分布曲线有什么异同?最概然速率是多少?氢气、氦气、氖气、氮气、氧气和氟气分子的分子量分别为2、4、20、28、32和38,这些气体分子在300K 时的速率分布曲线有什么异同?最概然速率是多少?[解析]麦克斯韦速率分布函数为23/22()4π()exp()2π2m mv f v v kT kT=- (1.2.1) 其中,k = 1.38×10-23J/K 是玻尔兹兹常数,m 是分子质量,v 是分子速率。
matlab画图设置(坐标轴、曲线、颜色)

matlab画图设置(坐标轴、曲线、颜色)a=linspace(1,2,10)plot(a,'--pr','linewidth',1.5,'MarkerEdgeColor','r','MarkerFaceColor','m','MarkerSize',1 0)legend('a','Location','best')title('a','FontName','Times New Roman','FontWeight','Bold','FontSize',16)xlabel('T','FontName','Times New Roman','FontSize',14)ylabel('a','FontName','Times New Roman','FontSize',14,'Rotation',0)axis auto equalset(gca,'FontName','Times New Roman','FontSize',14)1.曲线线型、颜色和标记点类型plot(X1,Y1,LineSpec, …) 通过字符串LineSpec指定曲线的线型、颜色及数据点的标记类型。
线型颜色数据点标记类型标识符意义标识符意义标识符意义- 实线 r 红色 + 加号-. 点划线 g 绿色 o 圆圈-- 虚线 b 蓝色 * 星号: 点线 c 蓝绿色 . 点m 洋红色 x 交叉符号y 黄色 square(或s) 方格k 黑色 diamond(或d) 菱形w 白色 ^ 向上的三角形v 向下的三角形> 向左的三角形< 向右的三角形pentagram(或p) 五边形hexagram(或h) 六边形2.设置曲线线宽、标记点大小,标记点边框颜色和标记点填充颜色等。
MATLAB曲线绘制大全

一、二维数据曲线图1.1绘制单根二维曲线plot函数的基本调用格式为:plot(x,y)其中x和y为长度相同的向量,分别用于存储x坐标和y坐标数据。
例1-1在0x2p区间内,绘制曲线y=2e-0.5xcos(4x)程序如下:x=0:pi/100:2*pi;y=2*exp(-0.5*x).*cos(4*pi*x);plot(x,y)例1-2绘制曲线。
程序如下:t=0:0.1:2*pi;x=t.*sin(3*t);y=t.*sin(t).*sin(t);plot(x,y);plot函数最简单的调用格式是只包含一个输入参数:plot(x)在这种情况下,当x是实向量时,以该向量元素的下标为横坐标,元素值为纵坐标画出一条连续曲线,这实际上是绘制折线图。
1.2绘制多根二维曲线1.plot函数的输入参数是矩阵形式(1)当x是向量,y是有一维与x同维的矩阵时,则绘制出多根不同颜色的曲线。
曲线条数等于y矩阵的另一维数,x被作为这些曲线共同的横坐标。
(2)当x,y是同维矩阵时,则以x,y对应列元素为横、纵坐标分别绘制曲线,曲线条数等于矩阵的列数。
(3)对只包含一个输入参数的plot函数,当输入参数是实矩阵时,则按列绘制每列元素值相对其下标的曲线,曲线条数等于输入参数矩阵的列数。
当输入参数是复数矩阵时,则按列分别以元素实部和虚部为横、纵坐标绘制多条曲线。
2含多个输入参数的plot函数调用格式为:plot(x1,y1,x2,y2,,xn,yn)(1)当输入参数都为向量时,x1和yl,x2和y2,,xn和yn分别组成一组向量对,每一组向量对的长度可以不同。
每一向量对可以绘制出一条曲线,这样可以在同一坐标内绘制出多条曲线。
(2)当输入参数有矩阵形式时,配对的x,y按对应列元素为横、纵坐标分别绘制曲线,曲线条数等于矩阵的列数。
例1-3分析下列程序绘制的曲线。
x1=linspace(0,2*pi,100);x2=linspace(0,3*pi,100);x3=linspace(0,4*pi,100);y1=sin(x1);y2=1+sin(x2);y3=2+sin(x3);x=[x1;x2;x3]';y=[y1;y2;y3]';plot(x,y,x1,y1-1)3.具有两个纵坐标标度的图形在MATLAB中,如果需要绘制出具有不同纵坐标标度的两个图形,可以使用plotyy绘图函数。
Matlab绘制曲线方法

t=0.1:0.1:3*pi;
y=sin(t);
figure(1)
semilogx(t,y)
grid on
%为图形窗口添加网格
figure(2)
semilogy(t,y)
figure(3)
loglog(t,y)
第4章 Matlab的图形功能
d.双 y 轴图形 绘制左右均有 y 轴的图形 plotyy(x1,y1,x2,y2)
第4章 Matlab的图形功能
三、三维绘图 1. 三维曲线绘图命令 三维函数 plot3主要用来表现单参数的三维曲线,与二维绘 图函数 plot 相比,只多了第三维数据。 其调用格式为: plot3(X1,Y1,Z1,s1,X2,Y2,Z2,s2,…)或 plot3(X,Y,Z,s) 参数的含义如下: Xn、Yn、Zn:第一到三维数据,是尺寸相等的向量/矩阵; s、s1、s2:是字符串,用来设置线型、颜色、数据点标记。
第4章 Matlab的图形功能
4. 坐标系的调整 实现坐标系的调整的命令是 axis 函数。 调用格式为: axis([xmin,xmax,ymin,ymax,zmin,zmax])
坐标的最小值( xmin,ymin,zmin)必须小于相应的最大值 ( xmax,ymax,zmax),否则会出错。
第4章 Matlab的图形功能
用plot(Z)绘制图形。
x=0:pi/20:2*pi; Z=sin(x)+cos(x)*i plot(Z) 等价于plot(real(Z),imag(Z))
用 plot(x1,y1,x2,y2,…) 在 同 一 窗 口中绘制多条曲线,且坐标和 长度都不同。
t1=0:0.1:3*pi; t2=0:0.1:6; plot(t1,sin(t1),t2,sqrt(t2))
matlab中绘制多条曲线的方法

在MATLAB中,绘制多条曲线是非常常见的需求。
通过绘制多条曲线,我们可以直观地比较不同数据之间的关系,分析数据的变化趋势,从而更好地理解数据的特点和规律。
在本文中,我们将介绍在MATLAB中绘制多条曲线的方法,希望能够帮助读者更加熟练地使用MATLAB进行数据可视化和分析。
一、使用plot函数绘制多条曲线在MATLAB中,最常用的绘制曲线的函数是plot函数。
通过plot函数,我们可以轻松地将多组数据绘制成曲线,并在同一张图上进行比较和分析。
下面是使用plot函数绘制多条曲线的基本步骤:1. 准备数据我们需要准备要绘制的多组数据。
假设我们有两组数据x1和y1,以及另外两组数据x2和y2。
这些数据可以是向量、矩阵,甚至是函数表达式。
2. 绘制曲线接下来,我们可以使用plot函数将数据绘制成曲线。
具体的代码如下所示:```matlab绘制第一组数据plot(x1, y1, 'r-'); 'r-'表示红色实线hold on; 将图形保持在同一张图上绘制第二组数据plot(x2, y2, 'b--'); 'b--'表示蓝色虚线hold off; 取消保持图形在同一张图上```通过以上代码,我们可以将两组数据分别绘制成红色实线和蓝色虚线的曲线,并显示在同一张图上。
这样,我们就可以方便地对两组数据进行比较和分析了。
3. 添加图例和标签我们可以通过legend函数添加图例,通过xlabel和ylabel函数添加坐标轴标签,通过title函数添加图标题,使得图像更加清晰和易懂。
二、使用plot3函数绘制三维曲线除了在二维平面上绘制曲线外,MATLAB还提供了plot3函数用于在三维空间中绘制曲线。
使用plot3函数绘制多条三维曲线的步骤与使用plot函数类似,只是需要将数据扩展到三维空间,并指定绘制的坐标系。
具体的代码如下所示:```matlab准备三维数据[x1, y1, z1] = meshgrid(-2:0.2:2, -2:0.2:2, -2:0.2:2);[x2, y2, z2] = meshgrid(-2:0.2:2, -2:0.2:2, -2:0.2:2);v1 = x1.*exp(-x1.^2 - y1.^2 - z1.^2);v2 = x2.*exp(-x2.^2 - y2.^2 - z2.^2);绘制三维曲线plot3(x1, y1, z1, 'r-', 'LineWidth', 2); 'r-'表示红色实线hold on;plot3(x2, y2, z2, 'b--', 'LineWidth', 2); 'b--'表示蓝色虚线hold off;xlabel('X');ylabel('Y');zlabel('Z');legend('Exp(-x^2 - y^2 - z^2)', 'X*Exp(-x^2 - y^2 - z^2)');title('Three-Dimensional Curve');```通过以上代码,我们可以将两组三维数据绘制成红色实线和蓝色虚线的曲线,并显示在同一张图上。
46.matlab绘制空间曲线
46.如何绘制空间曲线的图形?
在 MATLAB 中绘制一条或多条空间曲线用命令 plot3。
它的使用方法类似于绘制平面曲线命令 plot 。
设空间曲线 L 的表达式为
{x=x(t)
y=y(t)
z=z(t)
α≤t≤β
首先确定出曲线中参数 t 的离散点数据,然后根据 t 的数据计算出曲线上坐标x, y, z 的值(所得 x, y, z 是同维数的向量),最后按如下命令格式绘图
plot3(x, y, z)
其中, x, y, z 为空间空间曲线上点的坐标。
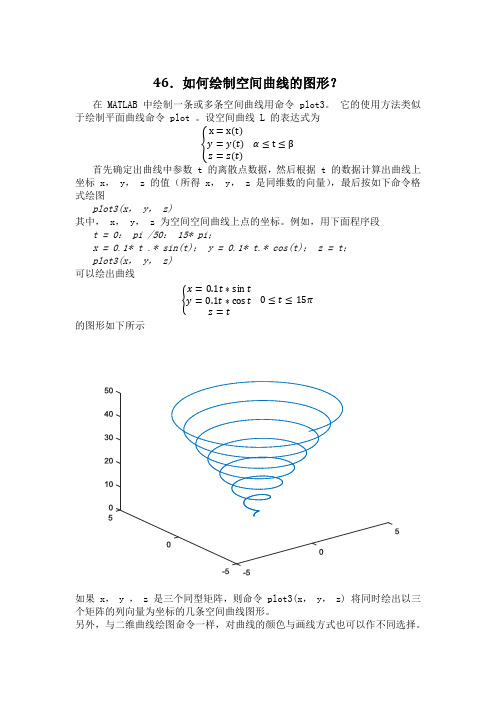
例如,用下面程序段t = 0: pi /50: 15* pi;
x = 0.1* t .* sin(t); y = 0.1* t.* cos(t); z = t;
plot3(x, y, z)
可以绘出曲线
{x=0.1t∗sin t
y=0.1t∗cos t
z=t
0≤t≤15π
的图形如下所示
如果 x, y , z 是三个同型矩阵,则命令 plot3(x, y, z) 将同时绘出以三个矩阵的列向量为坐标的几条空间曲线图形。
另外,与二维曲线绘图命令一样,对曲线的颜色与画线方式也可以作不同选择。
下面命令中
plot3(x, y, z,’ s ’ )
s 是一个或两个选择参数。
对于不同的颜色选取和画线方式选取可以参考二维绘图命令 plot 中的参数列表。
Matlab绘制三维曲线

Matlab绘制三维曲线plot3函数与plot函数用法十分相似,其调用格式为:plot3(x1,y1,z1,选项1,x2,y2,z2,选项2,…,xn,yn,zn,选项n)其中每一组x,y,z组成一组曲线的坐标参数,选项的定义和plot函数相同。
当x,y,z是同维向量时,则x,y,z 对应元素构成一条三维曲线。
当x,y,z是同维矩阵时,则以x,y,z对应列元素绘制三维曲线,曲线条数等于矩阵列数。
例绘制三维曲线。
程序如下:t=0:pi/100:20*pi;x=sin(t);y=cos(t);z=t.*sin(t).*cos(t);plot3(x,y,z);title('Line in 3-D Space');xlabel('X');ylabel('Y');zlabel('Z');三维曲面1.产生三维数据在MATLAB中,利用meshgrid函数产生平面区域内的网格坐标矩阵。
其格式为:x=a:d1:b; y=c:d2:d;[X,Y]=meshgr id(x,y);语句执行后,矩阵X的每一行都是向量x,行数等于向量y的元素的个数,矩阵Y的每一列都是向量y,列数等于向量x的元素的个数。
2.绘制三维曲面的函数surf函数和mesh函数的调用格式为:mesh(x,y,z,c):画网格曲面,将数据点在空间中描出,并连成网格。
surf(x,y,z,c):画完整曲面,将数据点所表示曲面画出。
一般情况下,x,y,z是维数相同的矩阵。
x,y是网格坐标矩阵,z是网格点上的高度矩阵,c用于指定在不同高度下的颜色范围。
例绘制三维曲面图z=sin(x+s in(y))-x/10。
程序如下:[x,y]=meshgrid(0:0.25:4*pi); %在[0,4pi]×[0,4pi]区域生成网格坐标z=sin(x+sin(y))-x/10;mesh(x,y,z);axis([0 4*pi 0 4*pi -2.5 1]);此外,还有带等高线的三维网格曲面函数meshc和带底座的三维网格曲面函数meshz。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用MATLAB画曲线族
(y-c)^2-2/3*(x-c)^3=0的包络线
1 求包络线的方程
syms x y c;
f = (y-c)^2-2/3*(x-c)^3
dfc = diff(f, c)
S = solve(f,dfc)
S1x = S.x
S1y = S.y
计算结果:
该曲线族有两条包络线:
①
x1 = c1 ;
y1 = c1 ;
②
x1 = c1 + 2/3;
y1 = c1 + 4/9;
2 画线
close all
clear,clc
warning('off')
figure
% 曲线族
hold on
for c = -10:0.5:10
x = -10:0.1:10;
y = (2/3)^0.5.*(x-c).^1.5 + c;
plot(x,y)
end
% 包络线
c1 = -10:0.1:10;
x1 = c1 ;
y1 = c1 ;
plot(x1,y1,'r','LineWidth',2)
figure
% 曲线族
hold on
for c = -10:0.5:10
x = -10:0.1:10;
y = -(2/3)^0.5.*(x-c).^1.5 + c; plot(x,y)
end
% 包络线
c1 = -10-2/3:0.1:10-2/3;
x1 = c1 + 2/3;
y1 = c1 + 4/9;
plot(x1,y1,'r','LineWidth',2)
............................
包络线
跳转到:导航, 搜索
在几何学,某个曲线族的包络线(Envelope),是跟该曲线族的每条线都有至少一点相切的一条曲线。
(曲线族即一些曲线的无穷集,它们有一些特定的关系。
)
设一个曲线族的每条曲线C s可表示为
,其中s是曲线族的参数,t是特定曲线的参数。
若包络线存在,它是由
得出,其中h(s)以以下的方程求得:
若曲线族以隐函数形式F(x,y,s) = 0 表示,其包络线的隐方程,便是以下面两个方程消去s得出。
绣曲线是包络线的例子。
直线族(A−s)x + sy = (A−s)(s)(其中A是常数,s是直线族的变量)的包络线为抛物线。
[1]
目录
•1证明
•2参考
•3参见
•4外部链接
[编辑]证明
设曲线族的每条曲线C s为。
设存在包络线。
由于包络线的每点都与曲线族的其中一条曲线的其中一点相切,对于任意的s,设(x(s,h(s)),y(s,h(s)))表示C s和包络线相切的那点。
由此式可见,s是包络线的变量。
要求出包络线,就即要求出h(s)。
在C s的切向量为,其中t = h(s)。
在E的切向量为。
因为x是s和t的函数,而此处t = h(s),局部求导有:
类似地得。
因为E和C s在该点相切,因此其切向量应平行,故有
其中。
可用此两式消去h'(s)。
整理后得:
[编辑]参考
•/~bridger/Envelope/envelope.htm。
