位移法解题步骤例题2(精)
三根杆的位移法例题
三根杆的位移法例题
摘要：
1.介绍三根杆的位移法例题
2.详解三根杆的位移法例题的解法
3.总结三根杆的位移法例题的解法及注意事项
正文：
一、介绍三根杆的位移法例题
三根杆的位移法例题是力学中的一种经典问题，主要涉及到杆的弯曲和应力分布等方面的知识。
这个问题通常描述为：有三根杆固定在一点，并承受一定的力，求杆的位移或应力分布。
这个问题在实际工程中有着广泛的应用，如建筑结构、桥梁设计等。
二、详解三根杆的位移法例题的解法
解三根杆的位移法例题，一般可以分为以下几个步骤：
1.建立模型：首先，根据题目描述，建立三根杆的模型，明确杆的材料、截面形状、边界条件等。
2.列方程：根据力学原理，如力矩平衡、静力平衡等原理，列出方程组。
3.解方程：通过数学方法，如代入法、消元法等，解出方程组中的未知量。
4.计算结果：根据解出的方程，计算出杆的位移或应力分布。
三、总结三根杆的位移法例题的解法及注意事项
解三根杆的位移法例题，需要掌握力学基础知识，熟悉杆的弯曲和应力分
布规律，同时具备一定的数学运算能力。
在解题过程中，要注意以下几点：
1.准确理解题意，明确杆的边界条件和受力情况。
2.在列方程时，要注意单位的统一，保证计算的准确性。
3.在解方程时，要根据方程的特性选择合适的解法，避免盲目尝试。
4.在计算结果时，要注意单位的转换和有效数字的保留。
通过以上步骤和注意事项，可以较好地解决三根杆的位移法例题。
结构力学龙驭球第八章
第八章 位移法总结
A EI
B EI
C
2EI D
一根直杆的刚度不同时, 位移基 本未知量的确定
如图，将BD杆分为BC和CD两根 杆件，则本题有三个未知量 B，
C ，⊿C。
第八章 位移法 总结
(a) E F G
F
C
B l/2
D l
H
A
l
l/2 l/2
(b) C
F B
D
A
(c) C
F D
3 F /28
(3) 在基本结构上分别绘制在各附加约束分别产生单位
位移Δj =1下的弯矩图 及M荷j 载作用下的弯矩图MP
第八章 位移法总结
由平衡条件求出系数kij和自由项Fi P；
(4) 解方程求Δj；
注意：一切计算
(5) 按叠加原理计算杆端弯矩。 都是在基本结构上进
M M 1 1 M 2 2 M n n M p 行!
第八章 位移法总结
MKF112q2a2
qa2
24
MFK11q2a281q2a245q82a
(c) m K
C
q
(d)
F
K
n
q/ 2
(e)
F
K
q/ 2 F
MCK112q2a281q2a2q42a8 M KC
qa2 24
再将图c荷载分解为为正对称与反对称的 叠加，取半结够如图d（正对称 ）、图 e(反对称）所示。由叠加得： （上拉） （上拉） （左拉） （右拉）
三、几个值得注意的问题
1. 位移法的适用条件
(1) 位移法既可以求解超静定结构，也可以求解静定结 构；
(2) 既可以考虑弯曲变形，也可以考虑轴向和剪切变 形；
位移法典型方程、计算举例
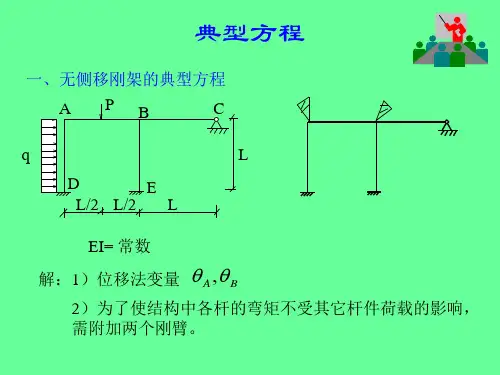
2.78
M M P M 1 C M 2 CH
2.09
0.70
例题2
计算举例
B C
求作弯矩图，EI=常数，各杆长L=6m A
19 kN
D
E
变形图 19 kN
解：1. 位移法变量：θB，ΔAH
2.附加约束作MP图，
并求R1P，R2P R1P=0 ，R2P= –19 kN
R2P
2
你能验算 吗？
例题1
计算举例
16 8
MP
4）位移法方程
r11 C r12 CH R1 P 0 r21 C r22 CH R 2 P 0
3i 4i
C
40 23 i
CH
64 23 i
M1
3i/L
M2
6i/L
5）作M图
2.附加约束（刚臂和支杆）作MP图，并求R1P、R2P
qL2/8
R1P= qL2/16
R2P= – qL
qL2/8
qL2/16
C
R1P
M P图
R2P
例题3
计算举例
2i 3i 4i 4i r21 6i/L r22
3 .作 M 1、 M 2图，求 r11， r21， r12， r22
6i/L
3i r11
n n
图 ，i 1, 2 , , n 。 由
叠 加 原 理 ， 当 n 个 变 量 都 产 生 各 自 实 际 的 位 移（ 角 度 或 侧 移 ） 时 ，在 第 i 个 变 量 处 产 生 的 力 为 ：
r
j 1
ij
Z
j
， 为 消 去 该 处 的 约 束 力 ， 令 ：R iP
结构力学位移法
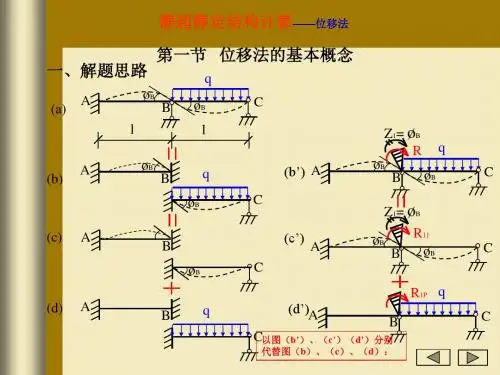
P A
MAB0
B MBA0
2、剪力：QAB表示AB杆A端的剪力。正负号规定同 “材力”。 P A
QAB0
B QBA0
静超静定结构计算——位移法
3、固端弯矩、固端剪力：单跨超静定梁仅由于荷载作 用所产生的杆端弯矩称为固端弯矩，相应的剪力称为固端 剪力。用MAB、MBA、QAB、QBA表示。
EI EI EI f 三、两端固定梁的转角位移方程 M AB 4 A 2 B 6 M AB
A D
B
C
1、写出杆端力的表达式( Z1 B , Z2 c ) ：
M AB 2 M BA M BC EI 30 6 Z1 l 8 EI 30 6 4 Z1 l 8 EI EI 4 Z1 2 Z2 l l
M CB 2 M CD M DC EI EI Z1 4 Z2 l l EI 10 6 2 3 Z2 l 8 0
2 EI 4 EI Z Z 2 22.பைடு நூலகம் 0 1 3 3 2 EI Z 7 EI Z 45 0 1 2 6 3
28.56 Z 1 EI Z 46.73 2 EI
解方程，求得
静超静定结构计算——位移法 2、根据平衡条件列位移法方程 ：
MCB C MCD 30kN B QBA
C QCD
M CB M CD 0 QBA QCD 30 0
即：
3i ( 3 iZ ) ( 4 iZ Z2 ) 0 1 1 2 ( 3i Z 30) ( 3i Z 3i Z ) 0 1 2 16 2 2 4
4、确定线位移的方法
（1）由两个已知不动点所引出的不共线的两杆交点也 是不动点。
位移法—位移法的典型方程和计算实例(建筑力学)
i
18.94kN m
i
2
i
3.158
M CD 6i
18.95kN m
i
3 21.05
M BD i
20 35.79kN m
4
i
作M图，如图示
位移法
位移法计算步骤归纳如下
（1）确定基本未知量。在原结构上加入附加约束，得到
衡条件求出杆端剪力。
M
B
FQAB
M
A
0
2.5 4 2 20
kN 0
4
0
FQBA
2.5 4 2 20
kN 10kN
4
位移法
同理，取杆件BC，由平衡条件得
FQCB FQBC 10kN
取杆件BD，由平衡条件得
FQDB FQBD 7.5kN
1.5i1 0.9375i 2 15 0
1
3.16
i
2
21.05
i
位移法
（6）作M图
利用叠加公式 M M1Z1 M 2 Z 2 M 计算杆端弯矩
3.158 3 21.05
M AC 2i
i
25.26kN m
i
2
i
3.158 3 21.05
k211 k22 2 F2 0
位移法
（3）求系数和自由项
k11＝4i +6 i＝10 i
k12= -1.5 i ＝k21
k12= -1.5 i
k22 0.75i 0.1875 i 0.9375 i
位移法
F1 0
位移法例题
r21=- 24i/l 2
0
6i/l 6i/l
r12= -24i/l 2
r12
Z2=1
-12i/l 2 -12i/l 2 12i/l 2
-12i/l 2 -12i/l 2 r22=48i/l 2 12i/l 2
r22
6i/l
M 2图
FP
说明：水平杆的M图没画，并不是其M=0，而 是EI无穷大的杆能平衡任何弯矩。
R1P FP
R1P=-FP
0 0 0 0 0
FP
R2P FP MP图
R2P=-FP
0
作用在结点上的外力相当于 支座，故杆件无弯矩。 解得
3FP l 2 Z1 = 24i FP l 2 Z2 = 12i
FPl /4 FPl /4 FPl / 2
FPl / 2
M图
(4) 利用叠加法作出弯矩图
例4:用位移法计算图示结构 ,并作弯矩图.EI= 常数. 4:
l
A l
D
（同济大学，2004年考研题）
Z1 = 1
B 4i A 4i 2i l
C 2i l D
Z2 = 1
6i/l
2i/l
B
C
4i/l
M1 图
A
6i/l
D
l
M2 图
l
Z1 = −ql / ( 84i )
2
Z 2 = ql / ( 3i )
3
M 图（× ql ）
2
例2： 位移法求解图示结构。
P
P /2
l A EA = B
Z1
l
l
P
l
注意： M 1图和 M P图的正确作图
例3：用位移法作图示结构的 M 图。EI=常数.
高中物理位移公式大全总结及例题
高中物理位移公式大全总结及例题位移是描述物体位置变化的物理量，是矢量，既有大小又有方向。
在高中物理中，我们主要学习匀速直线运动和匀变速直线运动中的位移公式。
1.匀速直线运动•位移公式：o s = vto其中：▪s：位移（m）▪v：速度（m/s）▪t：时间（s）这个公式表示，在匀速直线运动中，物体在单位时间内通过的距离（即速度）乘以运动时间，就等于物体的位移。
2.匀变速直线运动•位移公式：o s = v₀t + 1/2at²o其中：▪s：位移（m）▪v₀：初速度（m/s）▪t：时间（s）▪a：加速度（m/s²）这个公式表示，在匀变速直线运动中，物体的位移等于初速度乘以时间加上1/2乘以加速度乘以时间的平方。
•其他常用公式：o末速度公式：v = v₀ + ato平均速度公式：v̄= (v₀ + v) / 2o中间时刻速度公式：vₘ = v₀ + 1/2at3.公式的应用这些公式在解决匀速直线运动和匀变速直线运动的问题中非常重要。
我们可以利用这些公式，结合已知条件，求解未知的物理量，如位移、速度、时间、加速度等。
4.注意：•在使用这些公式时，一定要注意单位的统一，一般采用国际单位制。
•对于不同的运动情况，可能需要选择不同的公式进行计算。
•在解决实际问题时，要仔细分析题意，找出已知量和未知量，然后选择合适的公式进行求解。
5.例题一个物体以2m/s的速度匀速运动了5s，求物体的位移。
解：•已知：v = 2m/s，t = 5s•求：s•根据公式s = vt，代入数据得：s = 2m/s × 5s = 10m•答：物体的位移为10m。
6.总结位移公式是高中物理中非常基础且重要的公式。
掌握这些公式，并能灵活运用，对于解决力学问题具有重要意义。
7.温馨提示：•多做练习：通过大量的练习，可以加深对公式的理解和记忆。
•画示意图：在解题过程中，画示意图可以帮助我们更好地理解题意，找出解题思路。
《船舶结构力学》第5章 位移法
Ql01，M10
1 12
Ql01
θ
Mθ12
1 8
Pl12，M 21
1 8
Pl12
θ
θ
图中,因有强迫转θ角存在, 则有转角弯矩：
θ
θ
i
M ij lij 3EI ij
M jilij 6EI ij
j
M ji lij 3EI ij
M ij lij 6EI ij
则：M ij
4EI ij lij
i
2EI ij lij
由题意可知，除了节点4是刚性固定没有转角外,其余四个节点 0、l、2、3在计算过程中都要把它固定然后强迫转动,因此未知转角 有四个，即θ0、θ1、θ2和θ3。
(2)计算固端弯矩：
查附录表A-4,可得杆0-l、1-2和2-4在外荷重作用下的固端弯矩为：
j
M ji
2EI ij lij
i
4EI ij lij
j
同不难得： Nij
M ij M ji lij
N ji
M ij M ji lij
Pre
Next
Exit
则求杆端总弯矩：
M ij
M ij
M ij
M ij
4EI ij lij
i
2EI ij lij
j
M
ji
M ji
M ji
M
ji
2EI ij lij
M10
M10 M10
1 ql2 4EI
12
l
ql 3 168EI
3 ql2 28
0.107ql2
M12
M12
M12
1 12
ql 2
4EI l
ql3 2EI 168EI l
高中物理运动题解题思路及示例
高中物理运动题解题思路及示例一、速度与位移的计算在物理学中，速度和位移是最基本的运动量，它们的计算方法也是解决物理运动题的关键。
下面通过几个具体的例子来说明解题思路。
例题1：一个小球从静止开始沿直线运动，经过2秒后速度为4 m/s，求此时小球的位移。
解析：根据速度的定义，速度等于位移与时间的比值。
所以，我们可以用速度乘以时间来计算位移，即位移等于速度乘以时间。
在本题中，速度为4 m/s，时间为2秒，所以位移等于4 m/s ×2 s = 8 m。
因此，小球在经过2秒后的位移为8米。
例题2：一个物体以10 m/s的速度匀速运动了5秒，求此时物体的位移。
解析：根据速度的定义，速度等于位移与时间的比值。
所以，我们可以用速度乘以时间来计算位移，即位移等于速度乘以时间。
在本题中，速度为10 m/s，时间为5秒，所以位移等于10 m/s × 5 s = 50 m。
因此，物体在经过5秒后的位移为50米。
二、加速度与速度的计算当物体在运动过程中受到外力的作用时，它的速度就会发生变化，这时我们需要考虑加速度的概念。
下面通过几个具体的例子来说明解题思路。
例题3：一个物体以5 m/s^2的加速度匀加速运动了10秒，求此时物体的速度。
解析：根据加速度的定义，加速度等于速度的变化量与时间的比值。
所以，我们可以用加速度乘以时间来计算速度的变化量，即速度的变化量等于加速度乘以时间。
在本题中，加速度为5 m/s^2，时间为10秒，所以速度的变化量等于5 m/s^2× 10 s = 50 m/s。
由于物体是匀加速运动，所以它的初始速度为0 m/s，即物体的速度等于初始速度加上速度的变化量，即速度等于0 m/s + 50 m/s = 50 m/s。
因此，物体在经过10秒后的速度为50 m/s。
例题4：一个物体以2 m/s的速度匀加速运动了5秒，求此时物体的加速度。
解析：根据加速度的定义，加速度等于速度的变化量与时间的比值。
位移法基本原理加例题分析知识分享
3. 位移法的典型方程
Your company slogan
• 位移法基本概念 2. 形常数载常数 • 位移法的典型方程 • 计算步骤和举例
4.1 位移法的计算步骤 4.2 计算举例
Your company slogan
4. 计算步骤和举例
Your company slogan
4.2 计算举例
Your company slogan
1. 位移法基本概念
（2）位移法的基本结构 位移法的基本结构是单跨超静定梁的组合体 假象地： 1）在刚结点上加”附加刚臂”阻止结点转动；
2）在刚结点（或铰结点）沿线位移方向加“附 加链杆”阻止结点移动。
Your company slogan
• 位移法基本概念 2. 形常数载常数
计算出来。常用的载常数表见教材。 已知杆端弯矩，可由杆件的力矩平衡方程求出剪力： 。
其中 是相应的简支梁在荷载作用下的杆端剪力；MAB，MBA的
正负按位移法杆端弯矩正负号规定。
Your company slogan
• 位移法基本概念 2. 形常数载常数 • 位移法的典型方程
3.1 建立基本结构 3.2 典型方程的建立 3.3 方程的物理意义 3.4 系数和自由项的计算
4. 计算步骤和举例
Your company slogan
4. 计算步骤和举例
Your company slogan
4. 计算步骤和举例
Your company slogan
谢谢！
2012.10.20
结束语
谢谢大家聆听！！！
29
Your company slogan
Your company slogan
Your company slogan
位移可以这样求
位移可以这样求先看题，一辆汽车以20m/s 的速度行驶，现因故刹车，并最终停止运动，已知汽车刹车过程的加速度大小是5m/s 2。
则汽车的刹车距离是多少?汽车做匀减速直线运动，刹车距离就是汽车在刹车过程发生的位移的大小，你可以先来想一想？或者动手试一试！1. 利用位移公式来求先算出刹车过程所用的时间t ，因刹车过程汽车做减速运动，所以加速度a 应该取负值，即a=-5m/s 2,时间s 4m/s 5-m/s 20--020===a v t ,经4s 汽车停止。
当然也可以口算，加速度大小是5m/s 2，也就是说汽车的速度每秒减小5m/s ，初速度为20m/s ，所以汽车速度经4s即可减为0，到停止时间s 4=t 。
接下来，再代入位移公式，即可求出刹车距离，即：m 40s)4()m/s 5(21s 420m/s 212220=⨯-⨯+⨯=+=at t v x 2. 利用速度-位移公式可求利用匀变速直线运动的速度-位移公式也可以解出来，什么是速度-位移公式？末速初速平方差，2ax 等于它，即：ax v v 2-202=，所以，0m 4m/s 5-2m/s 20-2-02220=⨯==）（）（a v x 3. 利用汽车运动的逆过程求解我们来个逆向思维，什么意思？就是将整个过程倒过来进行，或者说假如时光可以倒流，我们这个过程将变成初速度为0的反方向的匀加速直线运动。
这样理解,位移大小就等于m 404s)(5m/s 2121222=⨯⨯==at x 。
看看，是不是很简单。
（当然先得算出刹车过程所用的时间t =4s ）。
4. 利用t v =x 求解以上我们介绍了三种解法，想想哪一种最简单？我们认为都不是太简单，最简单的是现在介绍的第4种，利用平均速度乘时间求位移，即：t v =x 。
时间前面算过了t =4s, 而平均速度就等于初速度加末速度除以2，即：0m/s 12020m/s 20=+=+=v v v ，所以，40m s 4m/s 10x =⨯==t v ,希望同学们不要小看这个公式，解起题来很快的。
13.4 位移法计算步骤及算例[19页]
![13.4 位移法计算步骤及算例[19页]](https://img.taocdn.com/s3/m/0d93258cb8d528ea81c758f5f61fb7360b4c2bb0.png)
8i
D 8i
r21 4i
A
4i
8i
D
Z1=1
r11
r 21
4i 4 i
r21
E
4i
4i 8i
E
0
M1 B 2i
C
作出 M 2图
A
r12
0D 0
r12
D
4i
4i
Z2 =1
r22
8i
4i E 4 i
B M2 图 C 2i
r22
E
4i
分别取结点D和结点E为隔离体，由力矩平衡条件得：
r12 4i
r22 8i 4i 12i
(7) 校核。按平衡条件进行校核。
思考：位移法能用于计算静定结构吗？
例13-1 用位移法计算图示的连续梁的内力。EI=常数。
9kN/m
A
80kN
B
解：(1) 确定基本未知量 C ，结点B的角位移Z1。
6m A
3m 3m
(2) 建立基本结构，得
C 到基本体系。
基本结构
9kN/m
B
80kN
(3) 建立位移发典型方程。
63
B F SBC
80kN
C FSCB
(7) 校核 按平衡条件进行校核。
例13-2 试用位移法计算图示刚架，并绘出M图。 各杆的E为常数。
30kN/m
A 2I
D
E
2I
30kN/m Z1
Z2
A
2I
D 2I E
4m
I
I
B
C
I
I
B
C
4m
4m
基本体系
解： (1原) 确结定构基本未知量 结点D、E的角位移Z1和Z2 。
05-3结构力学 第五章 超静定结构的内力和位移计算(5.2节 位移法)ok
如： 1 2
3
1 2
1
3
这样即可使12、13杆 成为单跨超静定梁
2、附加链杆支座约束：为使杆件两端相对线位移被约束而在结点上附加的约 束阻止结点移动的装置。
如：1
3
用“
” 表示
2 1 3
结构变形时，显然13杆可沿水平方向移动， 同时刚结点1也可能发生转角，要使各杆独立成为 单跨超静定梁。 需在1结点上附加刚臂约束 同时还需加附加链杆支座以阻止13杆的水平线 位移。
r11Z 1+ r12Z 2+ · · · · + r1nZ n+R1P=0
位移法 – 刚度法
ri j=rj i
反力互等定理
位移法典型方程，简称为位移法方程 – 结构的刚度方程
主系数，rii>0 r12 ...... r1n Z1 R1P r11 r Z R r ...... r 2P 22 2n 2 21 ri j=rj i 反力互等定理 0 ...... ...... ...... ...... rn 2 ...... rnn Z n RnP rij=rji，Rip，>0，=0，<0 rn1
F M AB ql 2 / 12 F M BA ql 2 / 12
F A l/2 l/2 B
Fl/8 A
Fl/8
F M AB Fl / 8
B
F M BA Fl / 8
q
ql2/8 B A B
F M AB ql 2 / 8
A
F A l/2 l/2 B
3Fl/16 A B
EI=
Z1 Z2
EI=
位移法典型方程、计算举例资料
n
n
rijZj ， 为 消 去 该 处 的 约 束 力 ， 令 ： R iP rijZj =0即 可 。 写 成 方 程 组 的 形 式 为 ：
j 1
j 1
r11Z1 r12Z2 r1n Zn R1P 0
r21
Z1
r22Z2
r2n
Zn
R2P
0
rn1Z1 rn2 Z2 rnnZn RnP 0
六、位移法计算应注意的问题
1. 位移法过程中，判断一个杆件有无弯矩的方法是： 1）该杆有无杆端转角 2）该杆有无杆端相对侧移 3）该杆上有无荷载作用
2. 各图中R1P，r11，r12 的方向应保持一致画出 R2P，r21，r22的方向应保持一致画出
3. r11，r22 均为大于零的值，即施加的单位力与发 生位移的方向协调一致。
这就是位移法的典型方程。
五、位移法的计步骤
1. 确定位移法变量 2. 作MP图，求出R1P、R2P
3 .作 M 1 、 M 2 图r ， 1， 1r2， 1 求 r1， 2r22
4.写出位移法方,程 并求解
rr2111ZZ11rr1222ZZ22
R1P 0 R2P 0
5.依 MM PM 1Z1M 2Z2作出弯矩图
位移法典型方程、计算举例 资料
3、求解思路： “先修改，后复原”
A
B
1）位移法变量
A,B
2）附加2个刚臂，使结点不能转动----各杆弯矩不能相互传递 PL/8
qL2/12
R1P
R2P
R1P，R2P怎么求？
MP图
3）如何消掉附加的刚臂约束？
若令 R1= - R1P、R2= - R2P
P
PL/8
位移法习题-PPT
M
(kN·m)
F1P 80 F2P 80
四、解方程组 7i 1 1.5i 2 80 0 1.5i 1 10i 2 80 0
得 1 13.579 / i 2 10.037 / i
五、作M 图
M M1 1 M2 2 MP
11、21 用位移法作图示刚架得M图。
E
8kN
10kN D
10kN/m 1
Ai B
50kN
iC
10kN 10kNm
6m A
3m
1=k111
3i
B
3m 2m C
解法2: 位移法基本体系 一、撤除静定外伸段,取位移法 基本体系 i =EI/6
二、列位移法基本方程
M1 3i 45
F1P
k111 F1P 0
46.25
20
三、计算系数与自由项
A
B
C
MP (kN·m)
0
得
1 32 / 51i 0.627 / i
2 128 / 17i 7.529 / i
五、作M 图 M M1 1 M2 2 MP
11、23 用位移法计算图示排架与刚架,作M、Q与N图。
20kN/m
C
EI
A
C
A
3i/6
C
QCA
EA
12m
EA
M1
EA
20kN/m EA
1
D
四、支座移动与温度变化----广义固端弯矩
五、最少基本未知量与基本结构
40kN II
II
I
3I
I
2I 2I
4m 2m 2m 4m
• 最少基本未知量
2m
1、去除静定部分
0603位移法典型方程
EA=∞
EA=∞
FP
EA=∞
i1, h1
i2, h2
i3, h3
i4, h4
FP
Δ1
EA=∞ EA=∞
EA=∞
基本体系
EA=∞
EA=∞
EA=∞
基本结构
典型方程：
k111 F1P 0
FP
Δ1
EA=∞ EA=∞
EA=∞
基本体系
k11
Δ1=1
3i1 h1
F1P
3i2 h2
EA=∞
3i3 h3
EA=∞
k21
12i h2
12i h2
24i h2
例4：用位移法计算图示结构。
FP
FP i EI1=∞ i
h
EI1=∞
i
i
h
6i/l 6i/l
Δ1=1
6i/l k11
6i/l k21
M1图
6i/l
6i/l k12
6i/l
k22
kk211111
k12 2 k 22 2
F1P F2P
0 0
6i/l
6i/l
j1 j
F1P FP
1FP 2FP 3FP 4FP
3ik
k
hk2 4 3i j
h2
j1 j
1
FP 4 3i j
h2
j 1 j
M M 11 M P
排架的这种计算方法称剪力分配法。k 称剪力分配系数。柱顶剪
力是按各柱的侧移刚度来分配的。
剪力分配法的使用条件是梁的抗拉刚度无穷大，且仅在柱 顶作用一水平荷载。
h
EI1=∞
i
i
h
6i/h 6i/h
位移法习题与答案
位移法习题与答案位移法是结构力学中常用的一种分析方法，通过计算结构在外力作用下的位移，来求解结构的应力、应变和变形等问题。
在学习位移法时，习题与答案的练习是非常重要的，可以帮助我们加深对位移法的理解和掌握。
下面将给大家介绍一些位移法习题及其答案。
习题一：求解简支梁的弯矩分布已知一根长度为L的简支梁，受到均布载荷q作用，求解弯矩分布。
解答：首先，我们需要根据受力分析确定梁的反力。
对于简支梁，两个支座处的反力相等，且为qL/2。
接下来，我们可以利用位移法求解弯矩分布。
假设梁的弯矩分布为M(x)，则根据位移法的基本原理，可以得到以下方程：d2M(x)/dx2 = -q对该方程进行两次积分，得到：M(x) = -q*x^2/2 + C1*x + C2由于梁两端是简支条件，即位移和转角为零，可以得到边界条件：M(0) = 0M(L) = 0代入上述方程，解得C1 = qL/2，C2 = -qL^2/2。
因此，弯矩分布为：M(x) = -q*x^2/2 + qL/2*x - qL^2/2习题二：求解悬臂梁的挠度已知一根长度为L的悬臂梁，受到集中力F作用在悬臂端点，求解梁的挠度。
解答：首先，我们需要根据受力分析确定梁的反力。
对于悬臂梁，端点处的反力只有一个，即为F。
接下来，我们可以利用位移法求解梁的挠度。
假设梁的挠度为δ(x)，则根据位移法的基本原理，可以得到以下方程：d2δ(x)/dx2 = -F/(EI)对该方程进行两次积分，得到：δ(x) = -F*x^2/(2EI) + C1*x + C2由于梁端点处的位移为零，可以得到边界条件：δ(0) = 0dδ(x)/dx|_(x=L) = 0代入上述方程，解得C1 = 0，C2 = 0。
因此，梁的挠度为：δ(x) = -F*x^2/(2EI)习题三：求解悬臂梁的最大挠度已知一根长度为L的悬臂梁，受到均布载荷q作用，求解梁的最大挠度。
解答：首先，我们需要根据受力分析确定梁的反力。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
位移法解题步骤
例题2
用位移法作例题2图（a ）所示对称刚架的弯矩图（EI 为常数）。
解：⑴取半刚架。
此结构为一对称刚架，且承受对称荷载，故可取半刚架计算，半刚架计算简图如例题2图（b ）所示。
⑵作位移法基本体系图。
半刚架只有一个刚结点C ，只有一个角位移，无线位移。
位移法基本体系如例题2图（c ）所示。
⑶列位移法基本方程。
01111=+P R Z r
⑷求系数和自由项。
令 16===EI i i CE AC ，23
==EI i CK 。
根据载常数和形常数作1M 、P M 图[例题2图(d)、(e)]。
由1M 图及公式可得
1024411=++=r
由P M 图及公式可得
)(1545301m kN R P ⋅-=-=
⑸解算方程。
将系数和自由项代入位移法基本方程中，得
015101=-Z
解方程，得 5.111
11=-=r R Z P ⑹根据叠加法作弯矩图。
计算杆端弯矩。
)(273025.1m kN M AC ⋅-=-⨯=
)(363045.1m kN M CA ⋅=+⨯=
)(424525.1m kN M CK ⋅-=-⨯=
())(5.255.2225.1m kN M KC ⋅-=--⨯=
)(645.1m kN M CE ⋅=⨯=
)(325.1m kN M EC ⋅=⨯=
例题2图。