高中数学第2章数列第17课时等差等比数列复习一教学案苏教版5 精

合集下载

高中数学第2章数列第17课时等差等比数列复习(一)

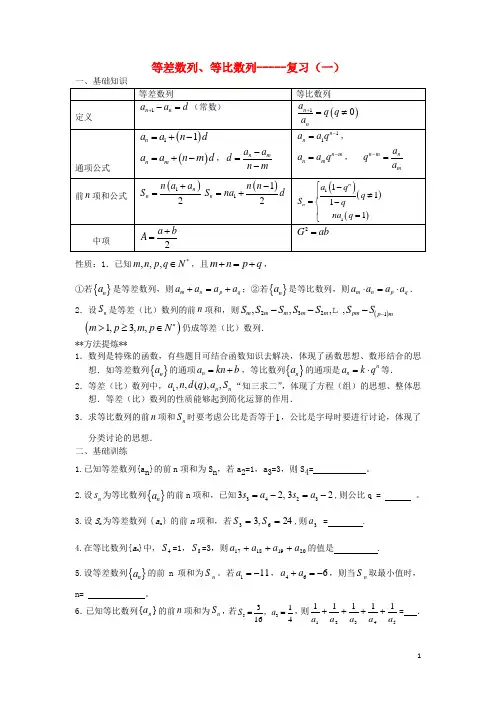
等差数列、等比数列-----复习（一）一、基础知识性质：1．已知,,,m n p q N *∈，且m n p q +=+，①若{}n a 是等差数列，则m n p q a a a a +=+；②若{}n a 是等比数列，则m n p q a a a a ⋅=⋅． 2．设n S 是等差（比）数列的前n 项和，则()2321,,,,m m m m m pm p m S S S S S S S ----L()1,3,,m p m p N *>≥∈仍成等差（比）数列．**方法提炼**1．数列是特殊的函数，有些题目可结合函数知识去解决，体现了函数思想、数形结合的思想．如等差数列{}n a 的通项n a kn b =+，等比数列{}n a 的通项是nn a k q =⋅等．2．等差（比）数列中，1,,(),,n n a n d q a S “知三求二”，体现了方程（组）的思想、整体思想．等差（比）数列的性质能够起到简化运算的作用．3．求等比数列的前n 项和n S 时要考虑公比是否等于1，公比是字母时要进行讨论，体现了分类讨论的思想．二、基础训练1.已知等差数列{a n }的前n 项和为S n ，若a 2=1，a 3=3，则S 4= 。

2.设n s 为等比数列{}n a 的前n 项和，已知3432,s a =-2332s a =-,则公比q = 。

3.设S n 为等差数列｛a n ｝的前n 项和，若24,363==S S ,则3a = .4.在等比数列{a n }中，4S =1，8S =3，则20191817a a a a +++的值是 .5.设等差数列{}n a 的前n 项和为n S 。

若111a =-，466a a +=-，则当n S 取最小值时，n= 。

6．已知等比数列}{n a 的前n 项和为n S ，若5331164S a ==，，则5432111111a a a a a ++++= ．三、典例欣赏：例1. （1）}{n a 是等比数列，21551-=-a a ，54-=s ，求4a （2）在等差数列}{n a 中，105,4,a d ==-则______n S =；（3）在等差数列}{n a 中，41,2,440,n n a d S ===则1______a =；（4）}{n a 是等比数列，,661=+n a a ,126,12812==•-n n s a a 求n 和公比q.例2．已知正数组成的两个数列}{},{n n b a ，若1,+n n a a 是关于x 的方程02122=+-+n n n n b b a x b x 的两根（1）求证：}{n b 为等差数列；（2）已知,6,221==a a 分别求数列}{},{n n b a 的通项公式；（3）求数n nns n b 项和的前}2{。

高中数学《数列复习课》公开课优秀教学设计整理

）
一般特殊
一般特殊
《数列》复习课的点评
在高三的数学复习课上最容易出现的就是“油水分离”式的复习模式，即先对知识点进行梳理，再进行相应的题目训练。

至于这种模式下知识梳理的效果以及相应题目训练是否直指学生学习的困惑或难点，不易得知。

王老师这节复习课的亮点可以用三个字来概括，即“新，准，实”。

一、新
“新”在形式上。

基于教师对学生认知的了解，明确了高三的复习课必须规避“油水分离”式的复习模式，针对怎样才能做到有针对性的复习，王玲老师的这节课给了我们很好的启发。

为了了解学生的情况，王玲老师在本单元复习之前做了章前测，在复习完等差数列后又做了相关的学生调查问卷。

这种新的教学形式正是基于教师对学生的学情分析，有调查问卷提炼出的学生学习难点，有通过课堂前测统计出的解答的正答统计数据和解题过程反馈，教师正是据此确定了本节课的定位并设计了课堂上相关的学生活动。

二、准
“准”在定位上。

正是基于教师对学生的学情分析，有调查问卷提炼出的学生学习难点的聚焦，有通过课堂前测统计出的解答的正答统计数据和解题过程反馈，教师据此确定了本节课的定位并制定了相关的教学目标和重、难点。

使本节课有了很强的指向性。

三、实
“实”在效果上。

王老师这节课真正做到了把课堂还给学生，在学生的自主评价和相互评价中，对知识建构和多角度解读条件的必要性有了感性认识，并且可以比较灵活地应用。

高中数学第二章数列 2.3 等比数列教案苏教版必修5-苏教版高二必修5数学教案

等比数列教学过程一、复习回顾师：前面我们已经学习了有关等差数列的有关知识，请一位同学来回答一下等差数列的定义的文字语言是什么？生：如果一个数列从第二项起，每一项减去它的前一项所得的差都等于同一个常数，那么这个数列就叫做等差数列。

师：等差数列的定义的数学表达式是什么？生：*+∈=-N n d d a n )(a 1n 为常数师：等差数列的通项公式是什么？生：d n a )1(a 1n -+=二、新知探究（一）等比数列的定义师：学完等差数列后，有学生问我：“老师，既然研究了差，我们是不是还要研究等和数列，等积数列，等商数列呢？我充满了好奇！”请问如果一个数列，从第二项起，每一项与它的前一项所得的“和”都等于同一个常数，请同学们举例子。

生：生：师：如果一个数列，从第二项起，每一项与它的前一项所得的“积”都等于同一个常数，请同学们举例子。

生：生：师：如果一个数列，从第二项起，每一项与它的前一项所得的“比”都等于同一个常数，请同学们举例子。

生：生：“等和数列”，“等积数列”，“等比数列”三者中，哪种更具有研究价值呢？生：生：我们的生活中“等比数列”的例子很多，如商品打折，银行存款等。

师：探究，类比等差数列定义同桌之间互相讨论，总结等比数列定义的文字语言。

生：师：定义中你觉得关键的字眼有哪些？生：生：师：你会用数学表达式来表示等比数列定义吗？生：生：例1：观察以下几个数列，回答下面问题：1, 1, 1, 1, 1；0, 1, 2, 4, 8；1, 2, 0, 4, 8；1, 2, 4, 8，0；-3，-9，-27，-81，-243；-1，1/2，1/4，1/8.师：①有哪几个是等比数列？若是，公比等于多少？生：师：②公比q能等于零吗？首项能为零吗？等比数列中会有某一项等于0吗？生：师：③存在公比q=1的等比数列吗？存在公比q=-1的等比数列吗？生：师：④从第三项起，每一项与它的前一项之比是同一个常数，这个数列是否是等比数列？生：师：⑤既是等差数列又是等比数列的数列存在吗？如果存在，请举例！例2：求出下列等比数列中的未知项（1）2，a ，8（2）-4,b ，c ，8（二）等比中项师：由例2中的（1），类比等差中项的概念，你能给出等比中项的概念吗？生：师：2,-6之间是否存在等比中项？生：师：1和4的等比中项是什么？生：师：若ab G =2，则G 是否一定是a 和b 的等比中项吗？生：师：如果把例2中的（2），变为 -4,a,b ，c ，d,e,f,8呢？（三）等比数列的通项公式：这两个等比数列的通项公式。

高中数学第二第15、16课时《数列复习课时》(2课时)教案(学生版) 苏教版必修5

第15、16课时数列复习课(2课时)【学习导航】知识网络【自学评价】（一）数列的概念数列的定义（一般定义，数列与函数）、数列的表示法。

数列的通项公式。

求数列通项公式的一个重要方法：对于任一数列}{n a ,其通项n a 和它的前n 项和n s 之间的关系是（二）等差数列和等比数列的概念、有关公式和性质 1.等差数列(1)定义 (2)通项公式n a =1a +（）d=k a +（）d=dn +1a -d(3)求和公式(4)中项公式A=2ba + 推广：2n a =(5)性质①若m+n=p+q 则②若}{n k 成A.P （其中N k n ∈）则}{nk a 也为A.P 。

③n n n n n s s s s s 232,,-- 成数列。

④1________()1n a a d m n n -==≠- 2.等比数列 (1)定义(2)通项公式 (3)求和公式(4)中项公式ab G =2。

(5)①若②若{N k n ∈③n n s s 2,④1q n -3. (1)(2)(3) 4. (1)当(2)当时,1. 2. :适用于⎭⎬⎫⎩⎨⎧+1n n a a c 其中{ n a }是各项不为0的等差数列，c 为常数；部分无理数列、含阶乘的数列等。

3. :适用于学习札记{}n n b a 其中{}n a 是等差数列，{}n b 是各项不为0的等比数列。

4.倒序相加法: 类似于等差数列前n 项和公式的推导方法。

5.常用结论1） 1+2+3+...+n = _________ 2）1+3+5+...+(2n-1) =3）_________n +++=33312 4） ___________n ++++=2222123 5） __________()n n =+116） (______)()p q pq q p=<-11【精典范例】一函数方程思想在研究数列问题中的运用【例1】（1）首项为正数的等差数列｛a n ｝，其中S 3=S 11，问此数列前几项和最大？（2）等差数列｛a n ｝中，S 10=100，S 20=300，求 S 30。

高中数学第二章数列数列复习1导学案苏教版必修5

必修5 数列复习小结第1课时第 19 课时一、学习目标（1）进一步熟练掌握等差等比数列的通项公式和前n项和公式；（2）提高分析、解决问题能力．二、知识点总结（一）数列的概念1．数列的概念与简单表示法（1）从定义角度看：（2）从函数角度看：数列可以看成以正整数集N*它的有限子集为定义域的函数a n=f(n)当自变量从小到大依次取值时所对应的一列函数值.2．数列的表示（1）列表法；（2）图象法：注意图象是，而不是_______；（3）通项公式：（4）递推公式：如果已知数列｛a n｝的第一项（或前几项）及相邻两项（或几项）间的关系可以用一个公式来表示，那么这个公式就叫做这个数列的递推公式.3．数列的分类1）按数列项数的多少可以分为和。

2）按数列中相邻两项的大小可分为、、和 .4．数列的通项a n与前n项和S n之间的关系对任一数列有a n=（二）等差数列1.等差数列的定义：若数列｛a n｝为等差数列，则有a n-a n-1=(其中n≥2，n∈N*).2.等差中项：3.等差数列的通项公式：a n=，其中a1为首项，d为公差.当d>0时，数列｛a n｝为数列；当d<0时，数列｛a n｝为数列；当d=0时，数列｛a n｝为列.4.等差数列的前n项和公式：_____________________________; _____________________________5.等差数列的性质：（1）等差数列｛a n ｝中，a n -a m = d ；（2）等差数列｛a n ｝中，若m+n=p+q (其中m,n,p,q ∈N *)，则；若m+n=2p ，则a m +a n = p ，也称a p 为a m ，a n 的 .（3）等差数列中依次k 项和成等差数列，即___________________________________成等差数列，其公差为。

6.已知三个数成等差数列，可设这三个数为___________________ 若四个数成等差数列，可设为_____________________________. 7.等差数列的判定方法：1）定义法： ⇔{}n a 是等差数列。

高中数学等比数列教案2 苏教版必修5.doc

第8课时：§2.3 等比数列（2）【三维目标】：一、知识与技能1.进一步熟练掌握等比数列的定义及通项公式；2.深刻理解等比中项概念，掌握等比数列的性质；3.提高学生的数学素质，增强学生的应用意识.二、过程与方法通过自主探究、合作交流获得对等比数列的性质的认识。

三、情感、态度与价值观充分感受数列是反映现实生活的模型，体会数学是来源于现实生活，并应用于现实生活的，数学是丰富多彩的而不是枯燥无味的，提高学习的兴趣。

【教学重点与难点】：重点：等比中项的理解与应用难点：灵活应用等比数列定义、通项公式、性质解决一些相关问题【学法与教学用具】：1.学法：2.教学用具：多媒体、实物投影仪.【授课类型】：新授课【课时安排】：1课时【教学思路】：一、创设情景，揭示课题首先回忆一下上一节课所学主要内容：1.等比数列：如果一个数列从第二项起，每一项与它的前一项的比等于同一个常数，那么这个数列就叫做等比数列.这个常数叫做等比数列的公比；公比通常用字母g表示（（?工0）,即：d=q（gzO）a…-i2.等比数列的通项公式：a n = , a n = a m -q n~m{a m - 0）3.［a n］成等比数列o 也 =g （ " w N+, gHO）“ a…工0”是数列［a n］成等比数列的必要非充分条件a”4.既是等差又是等比数列的数列：非零常数列.二、研探新知1.等比中项：如果在&与方中间插入一个数使a,G,b成等比数列，那么称这个数0为$与方的等比中项.即Q 土y［ab （②方同号）推导：若在仪与方中间插入一个数使a,G,b成等比数列，则—=^>G2= ab^> G = ±y/~ab / a G反之，若G? =ab,则9 = 2,即aGb成等比数列/. a,G,b成等比数列o G? =ab〈ab壬0)a G探究：已知数列｛a”｝是等比数列，(1) af = a3a7是否成立？af = 成立吗？为什么？(2) a； = a”-%](“〉1)是否成立？你据此能得到什么结论？a： = a n_k a n+k(n >k>0)是否成立？你又能得到什么结论？结论：若｛a”｝为等比数列，m + n = p + q (m,n,q,p & NJ ,贝0 a m - a n =a p-a q.由等比数列通项公式得：a m =a l q m^ a n = a x q n^ , a p=a x q p~x ,a^= a x-q q ｛, 故a,” • a n = Q冷2 且勺.仙=a^q p+q 2, '： m + n = p + q, :. a m• a” =a p-a q.2.等比数列的性质：(1)与首末两项等距离的两项积等于首末两项的积。

高中数学第2章数列教案苏教版必修5

本章复习与小结（1）【三维目标】：1.系统掌握数列的有关概念和公式。

2.了解数列的通项公式n a 与前n 项和公式n S 的关系。

3.能通过前n 项和公式n S 求出数列的通项公式n a 。

【授课类型】：复习课【课时安排】：1课时【教学思路】：一、本章知识结构二、知识纲要(1)数列的概念，通项公式，数列的分类，从函数的观点看数列．(2)等差、等比数列的定义．(3)等差、等比数列的通项公式．(4)等差中项、等比中项．(5)等差、等比数列的前n 项和公式及其推导方法．三、方法总结1．数列是特殊的函数，有些题目可结合函数知识去解决，体现了函数思想、数形结合的思想．2．等差、等比数列中，1a 、n a 、n 、)(q d 、n S “知三求二”，体现了方程(组)的思想、整体思想，有时用到换元法．3．求等比数列的前n 项和时要考虑公比是否等于1，公比是字母时要进行讨论，体现了分类讨论的思想．4．数列求和的基本方法有：公式法，倒序相加法，错位相减法，拆项法，裂项法，累加法，等价转化等．四、知识内容：1.数列数列的通项公式：⎩⎨⎧≥-===-)2()1(111n S S n S a a n nn 数列的前n 项和：n n a a a a S ++++= 321 2.等差数列等差数列的定义：如果一个数列从第2项起，每一项与它的前一项的差等于同一个常数，那么这个数列就叫做等差数列，这个常数叫做等差数列的公差，公差通常用字母d 表示。

等差数列的判定方法:（1）定义法：对于数列{}n a ，若d a a n n =-+1(常数)，则数列{}n a 是等差数列。

（2）等差中项：对于数列{}n a ，若212+++=n n n a a a ，则数列{}n a 是等差数列。

等差数列的通项公式：如果等差数列{}n a 的首项是1a ，公差是d ，则等差数列的通项为d n a a n )1(1-+=。

说明：该公式整理后是关于n 的一次函数。

高中数学第2章数列 2.3 等差数列与等比数列的综合应用学案苏教

高中数学第2章数列 2.3 等差数列与等比数列的综合应用学案苏教高中数学第2章数列2.3等差数列与等比数列的综合应用学案苏教算术序列和算术序列的综合应用学习目标：1、进一步熟练掌握等差、等比数列的通项公式和前n项和公式；（2）提高分析、解决问题能力．学习重点：使用相关公式；学习困难：序列I的综合应用研究：●完成下列填空，并写出所用等差数列与等比数列知识(表格)及方法。

1.知道吗？一（an？0）是一个等比序列，那么序列？洛根？是一个数字序列（填入相等的差或相等的比率），如果是log2a5？log2a2？6.那么？一共同的比例是；2.知道吗？1、a1、a2、，？4成等差序列，？1、b1、b2、b3、，？4变成相等的比例序列，然后是3。

如果公差不为零，那么等差序列是什么？一A2、A3和A6的比例顺序相等，然后是其公共比率Q，a1?a3?a5?；a2？a4？a6a2？A1的值为；B224。

2A3在序列{an}中，公差不为零？a7？2a11？0，序列{BN}是等比序列，并且b7?a7,则b6b8=；5.Sn是等比序列吗？一如果S1、2s2和3s3形成一个等差序列，那么？一共同的比率是_;；如果S1、S2和S3形成一个等差序列，那么？一共同的比率是u；6、若数列{an}是等差数列，首项a1?0，a2021?a2021?0，a2021.a2021?0，，则使前n项和sn取最大值时的最大自然数n是；使得sn?0成立的最大自然数n是；定义求和公式、算术序列和算术序列中的一般项公式和项公式的重要属性探究案询问二：●已知数列｛an｝为等差数列，公差d≠0，｛an｝的部分项组成下列数列：ak1，ak2，…，akn，恰为等比数列，其中k1＝1，k2＝5，k3＝17，求kn探索三：●将n个数排成n行n列的一个数阵：二a11a12a13a21a22a23a31a32a33a1na2na3nAn1an2an3ann知道a11=2，A13=A61+1。

2021年高中数学《等比数列》教案1 苏教版必修5

2021年高中数学《等比数列》教案1 苏教版必修5【三维目标】：一、知识与技能1.通过实例，理解等比数列的概念；能判断一个数列是不是等比数列；2.类比等差数列的通项公式，探索发现等比数列的通项公式，掌握求等比数列通项公式的方法。

掌握等比数列的通项公式，并能用公式解决一些简单的实际问题.二、过程与方法1.通过丰富实例抽象出等比数列模型，经历由发现几个具体数列的等比关系，归纳出等比数列的定义；通过与等差数列的通项公式的推导类比，探索等比数列的通项公式．2.探索并掌握等比数列的性质，能在具体的问题情境中，发现数列的等比关系，提高数学建模能力，会等比数列与指数函数的关系。

三、情感、态度与价值观1.培养学生从实际问题中抽象出数列模型的能力．2.充分感受数列是反映现实生活的模型，体会数学是来源于现实生活，并应用于现实生活的，数学是丰富多彩的而不是枯燥无味的，提高学习的兴趣。

【教学重点与难点】：重点：等比数列的定义和通项公式难点：等比数列与指数函数的关系；遇到具体问题时，抽象出数列的模型和数列的等比关系，并能用有关知识解决相应问题。

【学法与教学用具】：1. 学法：首先由几个具体实例抽象出等比数列的模型，从而归纳出等比数列的定义；与等差数列通项公式的推导类比，推导等比数列通项公式。

2. 教学用具：多媒体、实物投影仪.【授课类型】：新授课【课时安排】：1课时【教学思路】：一、创设情景，揭示课题引入：“一尺之棰，日取其半，万世不竭。

”；细胞分裂模型；计算机病毒的传播；印度国王奖赏国际象棋发明者的实例等都是等比数列的实例。

再看下面的例子：①1，2，4，8，16，…②1，，，，，…③1，20，，，，…④，，，，，……观察：请同学们仔细观察一下，看看以上①、②、③、④四个数列有什么共同特征？共同特点：（1）“从第二项起”，“每一项”与其“前一项”之比为常数（2）隐含：任一项（3）时，为常数二、研探新知1．等比数列定义：一般地，如果一个数列从第二项起．．．．，每一项与它的前一项的比等于同一个常数．．，那么这个数列就叫做等比数列，这个常数叫做等比数列的公比；公比通常用字母表示，（注意：等比数列的公比和项都不为零）．注意：（1）“从第二项起”与“前一项”之比为常数,成等比数列=（,）（2）隐含：任一项,“≠0”是数列成等比数列的必要非充分条件．（3）时，为常数。

南京市溧水县第二高级中学高中数学第17课时数列复习专题1教学案苏教版必修5

总课题数列总课时第17课时分课题数列复习专题（一）分课时第 1 课时教学目标系统掌握数列有关概念和公式并会运用解决问题. 重点难点等差、等比数列的概念和公式．南京市溧水县第二高级中学高中数学第17课时数列复习专题1教学案苏教版必修51．数列的概念，通项公式，数列的分类，从函数的观点看数列． 2．等差、等比数列的定义． 3．等差、等比数列的通项公式． 4．等差中项、等比中项．5．等差、等比数列的前n 项和公式及其推导方法．例题剖析（1）已知等差数列的第p n k ，，项构成等比数列的连续3项，如果这个等差数列不是常数列，则等比数列的公比为．（2）182 ，，，，z y x 成等比数列，则=x ．（3）三个数成等比数列，它们的积为512，如果中间一个数加上2，则成等差数列，这三个数是．（4）一个数列的前n 项和为n S n n 1)1(4321+-++-+-= ，例1则=++503317S S S ．（5）一个数列}{n a ，当n 为奇数时，15+=n a n ，当n 为偶数时，22n n a =，则这个数列前m 2项的和为．（6）已知正项等比数列}{n a 共有m 2项，且)(94342a a a a +=⋅，++++ 321a a a)(426422m m a a a a a ++++= ，则=1a ，公比=q ．（7）设}{n a ，}{n b 都是等差数列，它们的前n 项和分别为n S ，n T ，已知1235-+=n n T S n n ，则=n n b a ；=55b a ．（8）已知方程022=++m x x 和022=+-n x x 一共四个根组成一个首项为3的等差数列，则=-n m ．（9）一个直角三角形三边长组成等差数列，则它的三边长从小到大的比值为．例2 某三个互不相等的数组成等差数列，如果适当排列此三数，也可成等比数列，已知这三个数的和等于6，求这三个数．课堂小结等差、等比数列的概念和公式．课后训练班级：高一（）班姓名：____________一基础题1．若直角三角形的三边的长组成公差为3的等差数列，则三边长分别为（） A ．5，8，11 B ．9，12，15 C ．10，13，16 D ．15，18，21 2．设{}n a 是等比数列，有下列四个命题：（1）{}2n a 是等比数列；（2）{}1+n na a 是等比数列；（3）⎭⎬⎫⎩⎨⎧n a 1是等比数列；（4）{}||lg n a 是等比数列；其中正确命题的序号为．3．写出数列的一个通项公式，使它的前4项分别是下列各数：（1）16795431，，，；（2）978756534312⨯⨯ ⨯ ⨯，，，；（3）11，101，1001，10001；（4）818929432- - ，，，；二提高题4．已知四个数依次成等差数列，且四个数的平方和为94，首尾两数之积比中间两数之积少18，求此等差数列．5．等差数列{}n a 中，前m 项（m 为奇数）和为77，其中偶数项之和为33，且181=-m a a ，求通项公式．6．在等差数列{}n a 中，已知)(q p p S q S q p ≠= =，，求q p S +．三能力题7．如图是第七届国际数学教育大会)7(-ICME 的会徽图案轮廓，它是由一串直角三角形组成的，其中18732211=====A A A A A A OA ，记821OA OA OA ，，，的长度所组成的数列为{}n a )81(≤≤ ∈+n N n ，,写出数列{}n a 的通项公式．8．一个正方形被分成九个相等的小正方形，将中间的一个正方形挖掉，再将剩余的每个正方形都分成九个相等的小正方形，并将中间的一个正方形挖掉，如此继续下去…… （1）第三次分割时共挖掉了多少个正方形？（2）设原正方形边长为a ，第n 次分割时共挖掉了多少个正方形？这些正方形的面积和为多少？12 7A 8。

高中数学第2章数列第18课时等差等比数列复习(二)教学案(无答案)苏教版必修5

等差数列、等比数列-----复习（二）例1．根据下面各数列的前n 项的值，写出数列的一个通项公式． ⑴1，0，ΛΛ,71,0,51,0,31 （2）0．9，0．99，0．999，0．9999，…… （3）131116,1089,754,421⨯⨯-⨯⨯-，…… （4）,0 ,2 ,0 ,2 ,0 ........2 ________________例2．（1）已知数列{}n a ，22103n a n n =-+，它的最小项是（2）数列{}n a 中,303-+=n n a n ,当=n _______时，n a 最大（3）已知数列{}n a 中，kn n a n +=2且{}n a 是递增数列，求实数k 的取值范围（4）在数列}{n a 中，前n 项和nn n S )1110)(12(10120+-=。

试问：该数列中有没有最大的项？若有，求其项数；若没有，请说明理由。

例3．（1）已知}{n a 为等差数列，99,105642531=++=++a a a a a a ，则20a 等于（2）设等差数列}{n a 的前n 项之和为n S ，已知10100S =，则47a a +=____________ （3）设{}n a 是公差为正数的等差数列，若12315a a a ++=，12380a a a =，则1211a a +=+13a（4）若等差数列{}n a 的前n 项和为n S ，且310(7)n a n -=>，714S =，72n S =，则n =____例4．（1）数列{}n a 中,,452++=n n S n 则=n a ______________（2）已知等差数列{}n a 的公差0d ≠，且931,,a a a 成等比数列，则1392410a a a a a a ++=++（3）等差数列{}n a 共有2n+1项，其中奇数项之和为319，偶数项之和为290，则其中间项为_____(4)等差数列{}n a 中，,35412=S 前12项中，偶数项之和和奇数项之和之比为,27:32则公差_________=d(5)已知两个等差数列{}n a 和{}n b 的前n 项和分别为n n B A 和且3457++=n n B A n n 则使得nn b a为整数n 的个数是_____________个例5．（1）已知等差数列{}n a 中，,15,652==a a 若n n a b 2=，则数列{}n b 的前5项和等于________（2）已知n S 为等差数列{ n a }的前n 项和，若2415a a a ++是一个确定的常数，则数列{}n S 是常数的项为_____________（3）设n S 是等差数列{}n a 的前n 项和，若,3163=S S 则=126S S____________ (4)在等差数列{}n a 中，满足7473a a =, 且01>a ，若n S 取得最大值，则=n _________例6．设等差数列{}n a 的前n 项和为n S ，若4510,15S S ≥≤，则4a 的最大值为__ ____.例7．等差数列{}n a 中，338,33a s ==，（1）求数列{}n a 的前n 项和的最大值；（2）求数列{||}n a 的前n 项和n T 。

高中数学第2章数列第19课时等差等比数列复习(三)教学案(无答案)苏教版必修5

等差数列、等比数列-----复习（三）例1．（1）已知数列—1，a 1，a 2，—4成等差数列,—1，b 1,b 2,b 3,—4成等比数列，则212b a a -的值为__________（2）设,21=a 数列{}n a 21+是公比为2的等比数列，则=6a __________ （3）若数列{n a }中，1a =3且21n n a a =+（n 是正整数），则它的通项公式是n a =▁▁（4）数列{}n a 中，已知对任意+++∈321*a a ，a N n …,13-=+nn a 则+++232221a a a …2n a +等于例2．（1）已知等比数列｛n a ｝的公比为2，若a a 20032002+=，且A 、B 、C 三点共线（直线不过原点O ），则20052004a a +＝_____________ （2）在等比数列{}n a 中，公比,2=q ,7799321=⋅⋅⋅+++a a a a 则=⋅⋅⋅++9963a a a _______（3）已知数列{}n a 是各项为正数的等比数列，且1818212=⋅⋅⋅⋅a a a ，若2=q ，则=⋅⋅⋅⋅⋅18963a a a a _____________例3．（1）在等比数列}{n a 中，若1049S =，20112S =，则30S = ．（2）已知等比数列{}n a 中前8项的和,308=S 前16项的和,15016=S 求20S例4．数列{}n a 的前n 项和为,n S 已知,11=a n n S n n a 21+=+，证明：⎭⎬⎫⎩⎨⎧n S n 是等比数列例5．在等比数列{}n a 中，110a >，公比()0,1q ∈，且153528225a a a a a a ++=，又3a 与5a 的等比中项为2，①求n a ；②设2l o g n n b a =，数列{}n b 的前n 和为n S ，当1212nS S S n+++最大时，求n 的值。

高中数学第二章数列数列复习2导学案(教师版) 苏教版必修5

必修5 数列复习小结第2课时第 20 课时一、学习目标（1）进一步熟练掌握等差等比数列的通项公式和前n 项和公式；（2）提高分析、解决问题能力．二、例题探究例1（2009浙江文）设n S 为数列{}n a 的前n 项和，2n S kn n =+，*n N ∈，其中k 是常数．I ）求1a 及n a ；II ）若对于任意的*m N ∈，m a ，2m a ，4m a 成等比数列，求k 的值．解（Ⅰ）当1,111+===k S a n ， 12)]1()1([,2221+-=-+--+=-=≥-k kn n n k n kn S S a n n n n （*）经验，,1=n （*）式成立， 12+-=∴k kn a n（Ⅱ）m m m a a a 42,, 成等比数列，m m m a a a 422.=∴，即)18)(12()14(2+-+-=+-k km k km k km ，整理得：0)1(=-k mk ，对任意的*∈N m 成立， 10==∴k k 或例 2 (2009山东卷文)等比数列{n a }的前n 项和为n S ，已知对任意的n N +∈，点(,)n n S ，均在函数(0x y b r b =+>且1,,b b r ≠均为常数)的图像上.（1）求r 的值；（11）当b=2时，记 1()4n nn b n N a ++=∈ 求数列{}n b 的前n 项和n T解:因为对任意的n N +∈,点(,)n n S ，均在函数(0x y b r b =+>且1,,b b r ≠均为常数)的图像上.所以得n n S b r =+,当1n =时,11a S b r ==+,当2n ≥时,1111()(1)n n n n n n n n a S S b r b r b b b b ----=-=+-+=-=-,又因为{n a }为等比数列, 所以1r =-, 公比为b , 所以1(1)n n a b b -=-（2）当b=2时，11(1)2n n n a b b --=-=,111114422n n n n n n n b a -++++===⨯ 则234123412222n n n T ++=++++ 3451212341222222n n n n n T +++=+++++ 相减,得23451212111112222222n n n n T +++=+++++- 31211(1)112212212n n n -+⨯-++--12311422n n n +++=-- 所以113113322222n n n n n n T ++++=--=- 【命题立意】:本题主要考查了等比数列的定义,通项公式,以及已知n S 求n a 的基本题型,并运用错位相减法求出一等比数列与一等差数列对应项乘积所得新数列的前n 项和n T .例3.某企业2008年的纯利润为500万元，因设备老化等原因，企业的生产能力将逐年下降.若不能进行技术改造，预测从今年起每年比上一年纯利润减少20万元，今年初该企业一次性投入资金600万元进行技术改造，预测在未扣除技术改造资金的情况下，第n 年（今年为第一年）的利润为500(1+n21)万元（n 为正整数）.（Ⅰ）设从今年起的前n 年，若该企业不进行技术改造的累计纯利润为A n 万元，进行技术改造后的累计纯利润为B n 万元（须扣除技术改造资金），求A n 、B n 的表达式；（Ⅱ）依上述预测，从今年起该企业至少经过多少年，进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润？解: (Ⅰ)依题意知，数列n A 是一个以500为首项，－20为公差的等差数列，所以2(1)480(20)490102n n n A n n n -=+⨯-=-， 2111500(1)500(1)500(1)600222n n B =++++++-＝2111500500()600222nn ++++- ＝11[1()]22500500600112n n -+⨯--＝5005001002n n -- (Ⅱ)依题意得，n n B A >，即2500500100490102n n n n -->-，可化简得250102n n n <+-， ∴可设n n f 250)(=，2()10g n n n =+- 又+∈N n ，∴可设)(n f 是减函数，)(n g 是增函数，又5050(3)(3)2,(4)(4)8816f g f g =>==<= 则4n =时不等式成立，即4年三、课后作业1.（2007宁夏）已知a b c d ，，，成等比数列，且曲线223y x x =-+的顶点是()b c ，，则ad 等于________22．（2006江西卷）已知等差数列｛a n ｝的前n 项和为S n ，若1O a B ＝200OA a OC ＋，且A 、B 、C 三点共线（该直线不过原点O ），则S 200＝_________1003.（2008江苏）将全体正整数排成一个三角形数阵：12 34 5 67 8 9 10．．．．．．．按照以上排列的规律，第n 行（n ≥3）从左向右的第3 个数为．答案262n n-+四、反思总结。

高中数学等比数列教案5苏教版必修5

高中数学等比数列教案5苏教版必修5教学目标1．明白得等比数列的概念，能用定义判定一个数列是否为等差数列； 2．了解等比数列的推导方法；3．把握等比数列的通项公式，并能用公式解决一些简单的问题．教学重点等比数列的概念q a a nn =+1（q 为常数）；通项公式：11-=n n q a a ．教学难点等比数列的递推公式与通项公式的转化．教学过程复习回忆前面我们共同探讨了等差数列，现在我们再来回忆一下要紧内容．①等差数列定义：d a a n n =--1（n ≥2）． ②等差数列性质：（1）a ，A ，b 成等差数列，由2ba A +=；（2）若m +n =p +q ，则a m +a n =a p +a q ． ③等差数列求和公式：2)(1n n a a n S +=d n n na 2)1(1-+=．问题情境数列：1，3，5，7，…，2n －1，… 2，－1，－4，…，－3n ＋5，… 1，1，1，…，1，…这些数列均为等差数列，满足a n －a n －1＝d ( n ≥2 )．我们来观看下列几个数列，看其又有何共同特点？ 1，2，4，8，16， (263)； ① 5，25，125，625，…； ② 1， ,81,41,21--； ③ 是等差数列吗？假如不是，你能试着总结这些数列的特点吗？特点：关于数列①，12-=n n a ，21=-n na a （n ≥2）；关于数列②，nn a 5=，51=-n na a （n ≥2）；关于数列③，1121)1(-+⋅-=n n n a ，211-=-n n a a （n ≥2）．共同特点：从第二项起，第一项与前一项的比都等于同一个常数．也确实是说，这些数列从第二项起，每一项与前一项的比都具有“相等”的特点．数学理论 1．等比数列定义一样地，假如一个数列从第二项起，每一项与它的前一项的比等于同一个常数，那么那个数列就叫做等比数列，那个常数叫做等比数列的公比；公比通常用字母q 表示（q ≠0），即：)0(:1≠=-q q a a n n （n ≥2）．前面我们观看的数列①，②，③差不多上等比数列，它们的公比依次是2，5，21-.那么数列1，1，1，…，1，…呢？ *说明：（1）“从第2项起”，各项均满足；（2）次序，后项比前项：a n a n －1＝q ，n ≥2，或a n ＋1a n＝q ；（3）q 为常数，表达“等”比；（4）由递推公式，a n ≠0，且q ≠0；a n ＋1＝a n · q ；（5）非零常数列既是等差数列，也是等比数列．例1 判定下列各数列是否为等比数列？假如是，请写出公比：(1) －1，－5，－25，－125； (2) 0，1，2，4，8；(3) 1，－12，14，－18，116； (4) a ，a ，a ，a ，a ．解：(1) 该数列是等比数列，q ＝5．(2) 该数列不是等比数列． (3) 该数列是等比数列，q ＝－12．(4) 当a ＝0时，该数列不是等比数列；当a ≠0时，该数列是等比数列，公比q ＝1．例2 求下列等比数列中的未知项：(1)2，a ，8； (2) －4，b ，c ，12．解：(1)由题意，得 a 2＝8a，⇒ a 2＝16，故a ＝±4．(2)由题意，得 b －4＝c b ＝12 c ，⇒ b 2＝－4c ，b ＝2c 2，解得b ＝2，c ＝－1．推广：假如A ，B ，C 三个数成等比数列，那么B 2＝AC ，我们把B 叫做A ，C 的等比中项．注意（1）与等差中项不同的是同号两数才有等比中项；等比中项有两个．当0>a ，0>b 时，ab G =也叫做a ，b 的几何平均数．（2）关于公比为q 的无穷等比数列{}n a ，假如n a n (≥2)是其中除第1项以外的任意一项，那么它的前一项是q a n ，后一项是q a n ，由)()(2q a qa a n n n ⋅=可知，n a 是它的前一项与后一项的等比中项．事实上等比数列中的任意一项差不多上它的前后等距离的项的等比中项．练习：(1) 2与4的等比中项是_____；(－3)2与(－3)－6的等比中项是______．2．等比数列的通项公式例已知等比数列｛a n ｝的首项a 1＝3，q ＝2，求a 10．若依照递推公式则需求出前9项，则需探求通项公式．此数列的前几项依次为：3，6，12，24，48，利用观看法可得a n ＝3×2n －1，但需证明是否各项均满足．证法一：对等比数列｛a n ｝，若首项为a 1，公比为q ，则a 2a 1＝q ，a 3a 2＝q ，a 4a 3＝q ，…，a n －1a n －2＝q ，a na n －1＝q ．将这n －1个式子左右两边分别相乘，得a na 1＝q n －1，故a n ＝a 1 · qn －1．当n ＝1时，上述等式也成立．证法二：或者由定义得：q a a 12=；21123)(q a q q a q a a ===； 312134)(q a q q a q a a ===；……)0(1111≠⋅⋅==--q a q a q a a n n nn =1时，等式也成立，即对一切*∈N n 成立．等比数列的通项公式沟通了a 1，a n ，n 与q 之间的联系．如：数列①，121-⨯=n n a （n≤64），表示那个等比数列的各点都在函数12-=x y 的图象上.如图所示．数学应用例3 已知在等比数列｛a n ｝中，首项a 1＝3，q ＝－2，求通项公式a n 及a 6；解 a n ＝3×(－2)n －1，a 6＝3×(－2)6－1＝－96．例4 已知在等比数列｛a n ｝中，a 3＝20，a 6＝160，求通项公式a n ．解由题意，a 3＝a 1·q 2＝20，a 6＝a 1·q 5＝160，解得q ＝2，a 1＝5，故a n ＝5×2n －1．或解 a 6＝a 3·q 3，即160＝20q 3，解得q =2．故a n ＝a 3×2n －3＝20×2n －3＝5×2n －1．推广的等比数列通项公式a n ＝a m ·qn －m．从函数的角度看等比数列的通项公式，依照首项和公比的不同取值，考察等比数列中各项的变化特点．专门关于q ＜0时的等比数列，为摆动数列，相邻两项符号相反，但间隔的两项一定同号．例5 一个等比数列的第3项与第4项分别是12与18，求它的第1项与第2项．解设那个等比数列的第1项是1a ，公比是q ，那么1221=q a ，① 1831=q a ， ②由②÷①可得第23=q ，③ 把③代入①可得 3161=a ．∴ 812==q a a ．∴ 那个数列的第1项与第2项分别是316和8．例6 已知{}{}n n b a ,是项数相同的等比数列，求证{}n n b a ⋅是等比数列．证明：设数列{}n a 的首项是1a ，公比为q 1；{}n b 的首项为b 1，公比为q 2，那么数列{}n n b a ⋅的第n 项与第n +1项分别为：nn n n q b q a q b q a 2111121111⋅⋅⋅⋅⋅⋅--与，即为n n q q b a q q b a )()(211112111与-．∵2112111211111)()(q q q q b a q q b a b a b a n n n n n n ==⋅⋅-++，它是一个与n 无关的常数，因此{}n n b a ⋅是一个以q 1q 2为公比的等比数列．例7 在243和3中间插入3个数，使这5个数成等比数列．这3个数依次为多少？解设a 1＝243，a 5＝3，插入的三个数依次为a 2，a 3，a 4．由题意，q 4＝a 5a 1＝181，解得q ＝±13．故此三数依次为81，27，9，或－81，27，－9．借助教材Ｐ50／例3 推广的等比中项的概念：或解设a 1＝243，a 5＝3，插入的三个数依次为a 2，a 3，a 4．a 32＝a 1·a 5＝729，又a 3＞0，因此a 3＝81．a 22＝a 1·a 3，故a 2＝±81，且当a 2＝81时，a 4＝9；当a 2＝－81时，a 4＝－9．故此三数依次为81，27，9，或－81，27，－9．例8 一个边长为1的正三角形，将每边三等分，以中间一段为边向形外作正三角形，并擦去中间一段．如此连续下去，试求第n 个图形的边长和周长．解设第n 个图形的边长为a n ．由题意，a n ＝(13)n －1．第n 个图形的边数为3×4n －1，则第n 个图形的周长为(13)n －1×3×4n －1＝3×(43)n －1．(1) (2)(3)。

高中数学第2章数列 2.3.1 等比数列的概念教案苏教版必修5-苏教版高二必修5数学教案

等比数列的概念教学目标：1. 体会等比数列是用来刻画一类离散现象的重要数学模型，理解等比数列的概念．2. 利用等比数列解决实际问题．教学重点：等比数列的概念．教学难点：理解等比数列“等比〞的特点．可以通过与等差数列进行类比来突破难点．教学方法：启发式、讨论式．教学过程：一、问题情境情境1：某种细胞，如果每个细胞每分钟分裂为2个，那么每过1分钟，1个细胞分裂的个数依次为1,2,4,8,16,情境2：“一尺之棰，日取其半，万世不竭〞的意思为：一尺长的木棒，每日取其一半，永远也取不完．如果将“一尺之棰〞视为1份，那么每日剩下的部分依次为1111,,,,24816情境3：某轿车的售价约为36万元，年折旧率约为10﹪〔就是说这辆车每年减少它的价值的10﹪〕，那么该车从购买当年算起，逐年的价值依次为23⨯⨯⨯36,360.9,360.9,360.9,问题：与等差数列相比，上面这些数列有什么特点？二、学生活动通过观察，发现：1．上述数列的共同特征，从第2项起，每一项都与它的前一项的比等于同一个常数．而等差数列的特征是，从第2项起，每一项都与它的前一项的差等于同一个常数． 2．根据这一规律可以发现任何一项都可以找出来．通过讨论，得到这些问题共同的特点是，每一项与它的前一项的比都等于同一个常数．三、建构教学1. 归纳总结，形成等比数列的概念：一般地，如果一个数列从第2项起，每一项与它的前一项的比都等于同一个常数，那么这个数列就叫做等比数列，这个常数叫做等比数列的公比，公比通常用字母q 表示．2. 符号记法，假设数列{}n a 为等比数列，公比为q ，那么)2(1≥=-n q a a n n ．问题1：以下数列是否为等比数列，如果是，公比是多少？〔1〕1,1,1,1,1；〔2〕8,4,2,1,0；〔3〕161,81,41,21,1--；〔4〕432,,,x x x x ．问题2：一个数列是等比数列，那么它的项和公比必须满足什么条件？问题3：当等比数列的公比为负数的时候，数列每一项有什么样的特征？〔学生讨论回答〕答问题1中〔1〕、〔3〕是等比数列，公比分别是1和21-；〔2〕不是；〔4〕当x 不等于0的时候是，等于0的时候不是．问题2中等比数列的每一项都不能为0，公比也不能等于0．问题3中项是呈正负交替出现，形成摇摆数列．3. 等比中项的概念．假设b G a ,,成等比数列，那么G 叫a 和b 的等比中项，且ab G ab G ±==,2．注：同号的两个数才有等比中项，等比中项有两个，它们互为相反数．四、数学运用1. 例题．例2 〔1〕在等比数列{}n a 中，是否有)2(112≥=+-n a a a n n n ？〔2〕如果数列{}n a 中，对于任意的正整数()2≥n ，都有112+-=n n n a a a ，那么{}n a 一定成等比数列吗？引导学生利用课本P36例3的证明过程对等比数列进行讨论，只是要提醒学生等比数列每一项均不为0．所以〔2〕不一定成立，只有在每一项均不为0的时候才成立．总结判定数列是否是等比数列的两个方法：定义法和等比中项法．例3 等比数列{}n a 的首项为1a ，公比为q ．（1）新数列1221,,,,,a a a a a n n n --也是等比数列吗？如果是，公比是多少？（2）依次取出数列{}n a 所有的奇数项，组成一个新数列，这个数列还是等比数列吗？如果是，它的首项和公比是多少？（3）数列{}()0≠c ca n 是等比数列吗？如果是，它的首项和公比是多少？引导学生讨论，按照等比数列的定义，利用)2(1≥=-n q a a n n 判断．归纳总结一般性的结论：如果取出的项下标成等差数列，按照原来的顺序排列形成的新数列依然是等比数列，公比是d q 〔d 为下标成等差数列时的公差〕2. 练习．（1）以下数列是等比数列，请在括号内填上适当的数：①〔〕，3,27； ②3，〔〕，5； ③1，〔〕，〔〕，881．（2）直角三角形的三边c b a ,,成等比，c 为斜边，那么___________sin =A ．（3）数列{}n a 满足：53lg +=n a n ，试用定义证明{}n a 是等比数列．五、要点归纳与方法小结1. 了解等比数列的概念，形成与等差数列的一个对比；2. 对于等比数列的每一项均不为0要进行讨论；3. 证明一个数列是等比数列要用定义法证明，即()21≥=-n q a a n n ．六、课外作业课本练习P51第1，2，3，6题．。

高中数学 第2章 数列 第17课时 等差等比数列复习一教学案苏教版5 精