2019届河北省中考系统复习:第25讲与圆有关的计算(8年真题训练)
河北省2019届中考数学系统复习第六单元圆滚动小专题(九)与圆有关的计算与证明练习
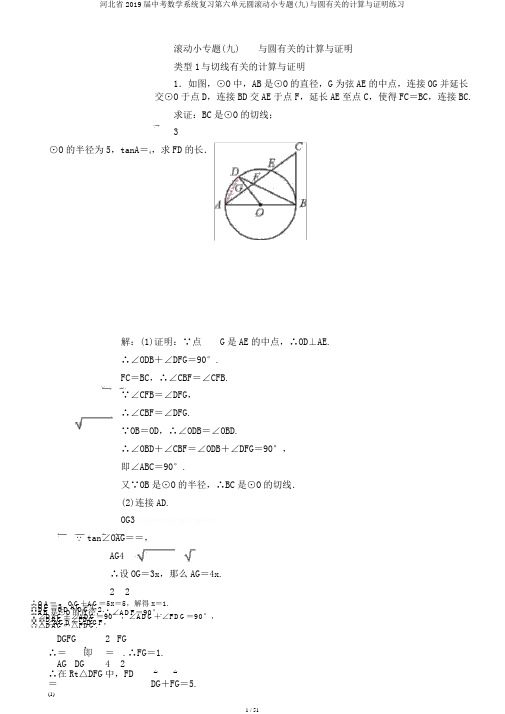
滚动小专题(九) 与圆有关的计算与证明类型1 与切线有关的计算与证明1.如图,⊙O 中,AB 是⊙O 的直径,G 为弦AE 的中点,连接OG 并延长交⊙O 于点D ,连接BD 交AE 于点F ,延长AE 至点C ,使得FC =BC ,连接BC.求证:BC 是⊙O 的切线;3⊙O 的半径为5,tanA =4,求FD 的长.解:(1)证明:∵点 G 是AE 的中点,∴OD⊥AE.∴∠ODB+∠DFG=90°.FC =BC ,∴∠CBF=∠CFB.∵∠CFB=∠DFG,∴∠CBF=∠DFG.∵OB=OD ,∴∠ODB=∠OBD.∴∠OBD+∠CBF=∠ODB+∠DFG=90°,即∠ABC=90°.又∵OB 是⊙O 的半径,∴BC 是⊙O 的切线.(2)连接AD.OG3∵ tan ∠OAG==,AG4∴设OG =3x ,那么AG =4x.2 2∴OA = OG +AG =5x =5,解得x =1. ∴OG =3,AG =4. ∴DG =OD -OG =2. ∵AB 是⊙O 的直径,∴∠ADF =90°. ∵∠DAG +∠ADG =90°,∠ADG +∠FDG =90°, ∴∠DAG =∠F DG. 又∵∠AGD =∠DGF , ∴△DAG ∽△FDG. DGFG 2 FG ∴= ,即 = .∴FG=1.AG DG 4 2 ∴在Rt △DFG 中,FD= 2 2 DG +FG =5.(1)(3)2.如图,四边形ABCD内接于⊙O,∠BAD=90°,过点C作CE⊥AD,垂足为E,且∠EDC=∠BDC.(4)求证:CE是⊙O的切线;假设DE+CE=4,AB=6,求BD的值.1(3)(4)(5)(6)(7)(8)(9)(10) 解:(1)证明:∵∠BAD =90°,(11) ∴∠BCD =90°.(12) ∵CE ⊥AD ,∴∠E =90°.(13) ∵∠EDC +∠DCE =90°,(14) ∠EDC =∠BDC ,(15) ∴∠BDC +∠DCE =90°.(16) ∵OD =OC ,∴∠ODC =∠OCD.(17) ∴∠OCD +∠DCE =90°,即 OC ⊥CE.(18) 又∵OC 是⊙O 的半径,∴CE 是⊙O 的切线.过点O 作OF ⊥AE ,垂足为F ,那么AF =DF ,∴OF =1AB =1×6=3.2 2 23 易证得四边形 OFEC 为矩形,∴CE =OF.4 ∵DE +CE =4,∴DE =1.5 2在Rt △DCE 中,CD =1+3=10.∵∠EDC =∠BDC ,∴Rt △BDC ∽Rt △CDE.BD CDBD10∴= ,即 10 =.CD DE 1∴BD =10.类型2 与弧长及面积有关的计算3.如图,在⊙O 中,半径 OA ⊥OB ,过 OA 的中点C 作FD ∥OB 交⊙O 于D ,F 两点,且 CD = 3,以O 为圆心,OC 为︵半径作CE ,交OB 于E 点.(1)求⊙O 的半径OA 的长;(2)计算阴影局部的面积.解:(1)连接OD.FD ∥OB ,OA ⊥OB ,∴OA ⊥FD.∵C 为OA 的中点,21 1∴OC=2OA=2OD.∴在Rt△OCD中,∠ODC=30°.∴OC=CD·tan30°=1.∴OD=2OC=2,即⊙O的半径OA的长为2.(2)S阴影=S扇形BOD+S△OCD-S扇形COE21230×π×290×π×1=360+2×1×3-360π312+2.4.如图,风车的支杆O E垂直于桌面MN,风车中心O到桌面的距离 OE为25cm,小风车在风吹动下绕着中心O不停地转动,转动过程中,叶片端点A,B,C,D在同一圆O上,⊙O的半径为10cm.风车在转动过程中,当∠AOE=45°时,求点A到桌面的距离(结果保存根号);(2)在风车转动一周的过程中,求点A相对于桌面的高度不超过20cm所经过的路径长(结果保存π).备用图1备用图2解:(1)如图1,当点A运动到点A1的位置时,∠AOE=45°.作A1F⊥MN于点F,A1G⊥OE于点G,∴A1F=GE.在Rt△A1OG中,∵∠A1OG=45°,OA1=10,122.∴OG=OA·cos45°=10×2=5∵OE=25,∴GE=OE-OG=25-5 2.∴A1F=GE=25-52.答:点A到桌面的距离是(25-52).cm(2)如图2,点A在旋转过程中运动到点A2,A3的位置时,点A到桌面的距离等于20.cm作A2H⊥MN于点H,那么A2H=20.作A2D⊥OE于点D,∴DE=A2H.∵OE=25,∴OD=OE-DE=25-20=5.在Rt△A2OD中,∵OA2=10,OD1cos∠A2OD==.OA22∴∠A2OD=60°.由圆的轴对称性可知,∠A3OA2=2∠A2OD=120°.120×π×1020π∴点A所经过的路径长为180=3.答:点A所经过的路径长为203πcm.32π+4π=6π.图1 图25.如图,有一直径 MN =4的半圆形纸片,其圆心为点 P ,从初始位置Ⅰ开始,在无滑动的情况下沿数轴向右翻滚至 位置Ⅴ,其中,位置Ⅰ中的 MN 平行于数轴,且半圆 P 与数轴相切于原点 O ;位置Ⅱ和位置Ⅳ中的 MN 垂直于数轴; 位置Ⅲ中的 MN 在数轴上;位置Ⅴ中的点 N 到数轴的距离为 3,且半圆 P 与数轴相切于点 A. 解答以下问题:位置Ⅰ中的MN 与数轴之间的距离为2;位置Ⅱ中的半圆P 与数轴的位置关系是相切; 求位置Ⅲ中的圆心P 在数轴上表示的数;纸片半圆P 从位置Ⅲ翻滚到位置Ⅳ时,求点N 所经过路径长及该纸片所扫过图形的面积; 求OA 的长.[(2)(3)(4) 中的结果保存 π]︵︵ 解:(2)位置Ⅰ中ON 的长与数轴上线段 ON 相等,︵ 90×π×2∵ON 的长为 =π,NP =2,180∴位置Ⅲ中的圆心 P 在数轴上表示的数为 π+2.90×π×4(3)点N 所经过路径长为 =2π,180 2 2S 半圆=180×π×2 90×π×4 =4π.360 =2π,S 扇形= 360∴半圆P 所扫过图形的面积为作NC 垂直数轴于点C ,作PH ⊥NC 于点H ,连接PA ,那么四边形PHCA 为矩形.在Rt △NPH 中,PN =2,NH =NC -HC =NC -PA =1.NH1∵ sin ∠NPH ==,∴∠NPH =30°.PN2∴∠MPA =60°.︵ 60×π×22∴MA 的长为 180 =π.32 5∴OA =π+4+3π=3π+4.4。
(沪科版)中考数学总复习课件【第25讲】与圆有关的计算

2π -3 . 3 每个圆都经过另一个圆的圆心,则图中阴影部分的面积为________
图25 -9
第25讲┃与圆有关的计算
第24讲┃与圆有关的位置关系
核心练习
6.[ 2014·岳阳] 的弧长为( D ) π A. 2 已知扇形的圆心角为60°,半径为 1,则扇形
B .π
π C. 6
π D. 3 圆心角为120°,弧长为12π 的扇形半径为
7.[ 2014·衡阳] ( C )
A.6 B.9 C.18 D.36
第25讲┃与圆有关的计算
第25讲┃与圆有关的计算
图25 -1
A.(60°,4) B.(45°,4) C.(60°,2 2) D.(50°,2 2)
第25讲┃与圆有关的计算
[解析 ] 取正六边形中心为 M,连接 MA,MB. ∵多边形是正六边形, 360 ° ∴∠OMA=∠AMB=∠BMC= =60°, 6 MO= MA=MB=MC , ∴△MOA,△MAB ,△MBC 都是等边三角形, ∴∠COA=60°, MO=MC=OA =2, ∴CO =4, 即 θ = 60°,m=4 , ∴顶点 C 的极坐标应记为(60°,4).
第25讲┃与圆有关的计算
经典示例
例1 [2014·常德] 阅读理解:如图25-1①,在平面内
选一定点O,引一条有方向的射线Ox ,再选定一个单位长度,那 么平面上任一点M的位置可由∠MOx的度数θ 与OM的长度 m确定, 有序数对(θ ,m)称为点M的“极坐标”,这样建立的坐标系称 为“极坐标系”. 应用:在图②的极坐标系下,如果正六边形的边长为2 ,有 一边OA在射线Ox上,那么正六边形的顶点C的极坐标应记为 ( A )
第25讲┃与圆有关的计算
河北省2019届中考数学系统复习第六单元圆第25讲与圆有关的计算(8年真题训练)练习

第25讲与圆有关的计算命点近8年的命形式考方向高考点型呈形式比丰富,、2021(T25(1)解),2021(T23(2)解、填空、解答三种型都有出,弧的扇形弧、面的算T25(3)解),2021(T25解),2021(T26考重于弧公式的考,算,解),2021(T19填),2021(T14)扇形面的考重在化程中形成的区域面,可用多种方法行化成求扇形面.重于有关正多形面的算,一般都有正多形与2021(T15)技巧性,需要我熟掌握正多形的各个量之的关系,并能把正多形行分割与拼接.命点1扇形弧、面的算1.(2021·河北T14·3分)如,AB是⊙O的直径,弦CD⊥AB,∠C=30°,CD=23.S阴影=(D)A.πB.2π C.23 D.2 33π2.(2021·河北T19·3分)如,将8cm的首尾相接成半径2cm的扇形.S扇形=4cm2.命点2 正多形与S3.(2021·河北T15·3分)如,a的正六形内有两个三角形(数据如),阴影=(C)S空白A.3 B .4 C .5 D .6重点1 弧的算如,△ABC是正三角形,曲CDEFG⋯叫做“正三角形的开〞,曲的各局部弧.1(1)中已有4段弧,接着画出第5段弧GH;2πa10πa(2)△ABC的a,第1段弧的是3;第5段弧的是3;前5段弧的和(即曲CDEFGH的)是10πa;(3)似地有“正方形的开〞“正五形的开〞⋯,a的正方形的开的前5段弧的和是15πa;2(4)猜测:30πa①a的正n形的前5段弧的和是n;m〔m+1〕πa②a的正n形的前m段弧的和是n.【思路点】(1)以点B心,BG半径画弧即可;(2)利用弧公式算.但要先确定弧所的心角都是120度,半径却在不断地增大,第1段弧的半径是a,第2段弧的半径是2a,第3段弧的半径是3a,依此下去第5段弧的半径是5a,和就是把五段弧加起来;(3)先利用正方形的性求出正方形的外角度数,合每段弧所在的半径化律,利用弧公式算每段弧,最后求和;(4)可以利用前面的探究方法,合正n形的性解决.【式1】(2021·淄博)如,⊙O的直径AB=6.假设∠BAC=50°,劣弧AC的(D)8π3π4πA.2π B.3 C.4 D.3【式2】(2021·廊坊模)如,在 6的菱形ABCD中,分以各点心,以的一半半径,在菱形内作四条弧,中阴影局部的周是6π.(果保存π)方法指1.求弧,要先确定两个要素,一是弧所在的半径,二是弧所在扇形的心角,再代入弧公式算即可.2.同一正多形的开每局部弧所的心角不,半径后一段比相的前一段增加一个正多形的.2π×ma模型建立a的正n形的开第m段弧.n重点2 扇形面的有关算如1,直径AB 6的半,点A逆旋60°,此点B到达点B′,求中阴影局部的面.2图1 图2图3【变式1】 (2021·大庆)如图2,在Rt △ABC 中,∠ACB=90°,AC =BC =2,将Rt △ABC 绕点A逆时针旋转30°后得到Rt △ADE,点B 经过的路径为弧BD ,那么图中阴影局部的面积为23π.【变式2】 如图3,在Rt △ABC 中,∠ACB=90°,AC =1,∠ABC=30°,将Rt △ABC 绕A 点逆时针旋转30°后得到Rt △ADE,点B 经过的路径为弧BD ,那么图中阴影局部的面积是1π.3【变式3】 如图4,在△ABC 中,AB =6,将△ABC 绕点B顺时针旋转60°后得到△DBE,点A 经过的路径为弧AD ,那么图中阴影局部的面积是π6.图4图5【变式4】如图5,在Rt △ABC 中,∠ACB=90°,BC =1,将Rt △ABC 绕点C 顺时针旋转60°,此时点B 恰π3好在DE 上,其中点A 经过的路径为弧AD ,那么图中阴影局部的面积是2-4 .(注:所有小题结果保存π)【思路点拨】阴影局部的面积可以看作以旋转点为圆心,旋转角为圆心角, AB 为半径的扇形面积;只有变式4阴影局部的面积是 S-S.扇形ACD△BC E【自主解答】解:∵AB=AB′=6,∠BAB′=60°,∴S=S+S-S=S60 2阴影 扇形B′A B 半圆O′ 半圆 扇形B′A B =360×π×6=6π.O方法指导 在圆中求阴影局部面积大致有以下方法:弓形或弓形的一局部可转化成扇形减去三角形的面积;新月形可以用扇形减去一个弓形的面积;可以利用等积变换求阴影局部的面积;可以利用轴对称、中心对称求阴影局部的面积;旋转形成阴影局部的面积,往往可以转化成求一个扇形的面积.重难点3 正多边形和圆(2021·河北模拟 )如图是由有两个公共顶点的正六边形与正方形组成的一个图形.假设阴影局部的周长为10,那么这个图形的外轮廓线的周长为()AA.18B.183C.22D.223【思路点拨】从图形上能看出,正方形的边长等于正六边形边长的2倍.提示:设正六边形的边长为a,那么正方形的边长为2a,由题意,得5a=10,解得a=2.那么外轮廓线的周长为3a2a×3=9a=18.【变式训练3】(2021·河北模拟 )如图,正六边形与正方形有重合的中心 O.假设∠BOC是正n边形的一个外角,那么n的值为(C)3A.8 B.10 C.12 D.16【变式训练4】(2021·石家庄二模)正六边形ABCDEF与正三角形△ACG按如下图位置摆放,在六边形AGCDEFS阴影中,S空白的值是(D)A.52B.51C.61D.71方法指导1.熟悉常见正多边形边长与对角线的数量关系.360°2.正n边形的中心角与每一个外角相等,都等于(n≥3).n3.研究面积相关问题时可采用割补与拼接等方法,研究周长可采用化曲为直等方法.注:正多边形与圆中,正多边形通常是指正方形,正五边形,正六边形,正八边形等常见的正多边形.1.(2021·盘锦)如图,一段公路的转弯处是一段圆弧︵︵(AB),那么AB的展直长度为(B).3πm .6πm C.9.12πmA Bπm D2.(2021·成都)如图,在?ABCD中,∠B=60°,⊙C的半径为3,那么图中阴影局部的面积是 (C)A.πB.2π C .3πD.6π3.(2021·德州)如图,从一块直径为2m的圆形铁皮上剪出一个圆心角为90°的扇形,那么此扇形的面积为(A)π23222A.2mB.2πm C.πm D.2πm44.(2021·河北模拟)如图,分别把正六边形边AB,EF,CD向两个方向延长,相交于点M,N,Q,那么阴影局部与空白局部的面积比为(A)1121A.2B.3C.5D.45.(2021·河北模拟)如图,六边形ABCDEF和六边形MNPQGH都是正六边形.假设AB=10,那么MN的值可能是(D)53C.52D.53A.B.526.(2021·株洲)如图,正五边形ABCDE和正三角形AMN都是⊙O的内接多边形,那么∠BOM=48°.7.(2021·石家庄藁城区模拟)如图,M,N分别是正五边形ABCDE的边AB,AE的中点,四边形MNHG 是位于该正五边形内的正方形,那么∠BMH的度数是99°.8.(2021·盐城)如图,图1是由假设干个相同的图形(图2)组成的美丽图案的一局部,图2中图形的相关数据:半径OA=2cm,∠AOB=120°.那么图2的图形周长为8πcm(结果保存π).359.(2021·河南)如图,在△ABC中,∠ACB=90°,AC=BC=2,将△ABC绕AC的中点D逆时针旋转90°得到︵53△A′B′C′,其中点B的运动路径为BB′,那么图中阴影局部的面积为4π-2.10.(2021·邢台宁晋县模拟︵︵)如图,半圆O的直径AB=4,P,Q是半圆O上的点,弦PQ的长为2,那么AP与QB的长度之和为()BA.2πB.4πC.5πD.π333︵︵1204提示:连接OP,OQ,易知△OPQ为等边三角形,lAP+lQB=180×π×2=3π.11.(2021·威海)如图,在正方形ABCD中,AB=12,点E为BC的中点,以CD为直径作半圆CFD,点F为半圆的中点,连接AF,EF,那么图中阴影局部的面积是(C)A.18+36π B.24+18π C .18+18πD.12+18π提示:作 FH⊥BC 交BC 延长线于点H ,连接AE ,S 阴影=S +S 半圆 -S -S=12×12+ 2×π×6-2×12×6- 2×65×65=18+18π.正方形ABCD △ABE △AEF1 2 1 112.(2021·河北模拟)如图,点 P 是⊙O 外一点,PA 切⊙O 于点A ,AB 是⊙O 的直径,连接 OP ,过点B 作BC∥OP交⊙O 于点C ,连接AC 交OP 于点D.(1)求证:PC 是⊙O 的切线;6(2)假设PD=16,AC=8,那么图中阴影局部的面积为25π-482;3cm cm2cm︵在(2)的条件下,假设点E是AB的中点,连接CE,求CE的长.解:(1)证明:连接OC,∵PA切⊙O于点A,∴∠PAO=90°.∵OP∥BC,∴∠AOP=∠OBC,∠COP=∠OCB.∵OC=OB,∴∠OBC=∠OCB.∴∠AOP=∠COP.OA=OC,在△PAO和△PCO中,∠AOP=∠COP,OP=OP,∴△PAO≌△PCO(SAS).∴∠PAO=∠PCO=90°.又∵OC是⊙O的半径,∴PC是⊙O的切线.连接AE,BE,过点B作BM⊥CE于点M,∴∠CMB=∠EMB=90°,∠AEB=90°.︵︵︵又∵点E是AB的中点,∴AE=BE.1∴∠ECB=∠ACE=2∠ACB=45°.又∵∠CMB=90°,∴∠CBM=45°.∴BM=CM.在Rt△BCM中,由勾股定理,得∴CM=BM=32cm.又∵∠ABE=∠ACE=45°,2 2 2 2 2CM+BM=BC,即CM+BM=36,∴在Rt△AEB中,BE=AB·cos∠ABE=5 2cm.在Rt△BEM中,由勾股定理,得EM=2222=42(cm),BE-BM=〔52〕-〔32〕∴CE=CM+EM=7 2cm,即CE的长为72cm.13.(2021·宜宾)刘徽是中国古代卓越的数学家之一,他在?九章算术?中提出了“割圆术〞,即用内接或外切正多边形逐步逼近圆来近似计算圆的面积,设圆O的半径为1.假设用圆O的外切正六边形的面积来近似估计圆O的面积,7那么S=2 3.(结果保存根号)8。
河北省2019届中考数学复习第25讲 与圆相关的计算 含答案
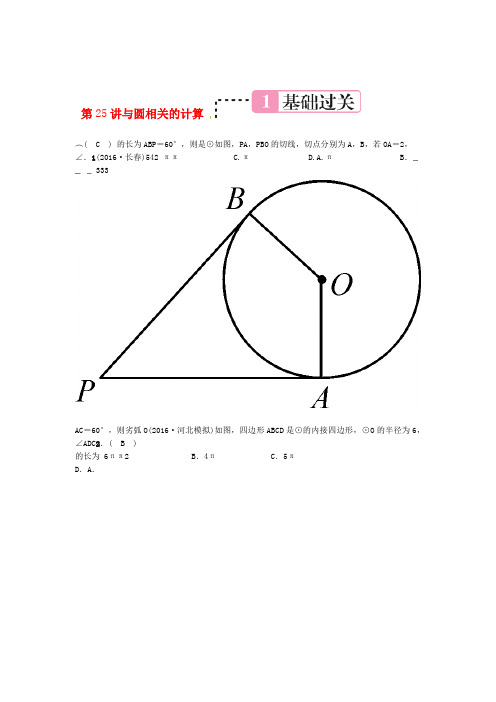
第25讲与圆相关的计算︵( C ) 的长为ABP=60°,则是⊙如图,PA,PBO的切线,切点分别为A,B,若OA=2,∠.1(2016·长春)542 ππ C.π D.A.π B.333AC=60°,则劣弧O(2016·河北模拟)如图,四边形ABCD是⊙的内接四边形,⊙O的半径为6,∠ADC2.( B )的长为 6ππ2 B.4π C.5πD.A.( B ) ,则它的内切圆的半径为3.(2016·南京)已知正六边形的边长为22A.2 1 B.3 C. D.3的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角以半径为14.(2016·泸州)( D ) 形的面积是2323 D.C.A. B. 8484( A )AB90°,连接,则图中阴影部分的面积是5.如图,已知扇形AOB的半径为2,圆心角为4π-π-2 D.442 BA.π-.π-4 C.2,且,其中OA的长度为6 cmπ.(2016·河北模拟)如图,水平地面上有一面积为30 cm的灰色扇形OAB6点2所示,则OOA与地面垂直.若在没有滑动的情况下,将图1的扇形向右滚动至OB垂直地面为止,如图( A )移动了2 图图1cm π1110A.π cm B.3)cm+π(11.3)cm D2+π(10.C.O点移动的距离其实就是优弧AB的长.提示:°,若∠A=70AB,AC分别相交于点D,E.BC7.(2016·张家口模拟)如图,以为直径的⊙O与△ABC的边7 ,则图中阴影部分图形的面积和为π.BC=218=140°,提示:∠DOB +∠EOC7140.1=π∴阴影部分图形的面积和为×π×18360忽略为半径的扇形(的正六边形铁丝框ABCDEF变形为以点A为圆心,AB8.(2016·巴中)如图,将边长为3 18..则所得扇形AFB(阴影部分)的面积为铁丝的粗细)1 求解.提示:利用公式S=lr扇形2,,B(-21)ABC在直角坐标平面内,三个顶点的坐标分别为A(-1,2),)9.(2016·张家界如图,已知:△ 1个单位长度).C(1,1)(正方形网格中每个小正方形的边长是 2);的坐标是逆时针旋转90度得到的,B(1,-绕点B(1)△AC是△ABCC1111 ).求出线段AC旋转过程中所扫过的面积(结果保留π(2)为半径的扇形的面积.AC旋转过程中所扫过的面积为以点C为圆心,AC解:线段2π5·(·π5)9022旋转过程中所扫过的面积为=,∴线段AC.=∵AC=2+15360410.(2016·昆明)如图,AB为⊙O的直径,AB=6,AB⊥弦CD,垂足为G,EF切⊙O于点B,∠A =30°,连( D ),下列结论不正确的是BC,OC,AD接.是等边三角形.△COBA.EF∥CD B︵3 πDG D.CB的长为C.CG=2︵3π××60.=π提示:CB的长为180︵上,点OB在的顶点C是AB的中点,点D·深圳11.(2016)如图,在扇形AOB中∠AOB=90°,正方形CDEF( A ) 2OB的延长线上,当正方形CDEF的边长为时,则阴影部分的面积为2E在4-4π-8 D.π2.π-4 B.4π-8 C.2A的边长为.264如图,正方形ABCD内接于⊙O,其边长为,则⊙O的内接正三角形EFG(201612.·威海),CD=O于D,F两点,且作OA如图,在⊙O中,半径⊥OB,过OA的中点CFD∥OB交⊙·13.(2016新疆)︵于E点.为圆心,OC为半径作CE,交OB以O OA的长;O(1)求⊙的半径 (2)计算阴影部分的面积.OD.(1)连接解:. °,∴∠AOB=90OA∵⊥OB.90OCD=°∵CD∥OB,∴∠,=是AO中点,CD3CRt在△OCD中,∵2CO.OD=∴2221. (2x),解得x==+,∴=设OCxx(3)2.的半径为O,即⊙2=OD∴.1CO.,∴∠°CDO==30CDO(2)∵sin∠=2OD.30°=OB,∴∠DOB=∠ODC∵FD∥22π31×290π×130π×3+-=+.SS=S+S-=×1∴OCE阴影扇形△CDO扇形OBD236036021214.归纳猜想:同学们,让我们一起进行一次研究性学习.(1)如图1,已知正△ABC的中心为O,半径为R,将其沿直线l向右翻滚,当正三角形翻滚一周时,其中心O经过的路程是2πR.图1(2)如图2将半径为R的正方形沿直线l向右翻滚,当正方形翻滚一周时,其中心O经过的路程是2πR.图2(3)猜想:把正多边形翻滚一周,其中心O所经过的路程是多少(R为正多边形的半径,可参看图3)?请说明理由.图3(4)进一步猜想:任何多边形都有一个外接圆,若将任意圆内接多边形翻滚一周时,其外心所经过的路程是否是一个定值(R为多边形外接圆的半径)?为什么?请以任意三角形为例说明(如图4).图4通过以上猜想你可得到什么样的结论?请写出来.120πR解:(1)当正△ABC向右翻滚一周时,其中心O经过的路线是三条等弧,所以其中心O经过的路程为×1803=2πR.90πR(2)中心O经过的路程为×4=2πR.180(3)2πR.理由如下:当正n边形向右翻滚一周时,其中心O经过的路线是n条等弧,这些弧的半径为R,所360°对的圆心角为,n360πR∴中心O经过的路程为××n=2πR.n180(4)是定值2πR,以任意三角形为例说明如下:如图4,在△ABC中,设∠A=α,∠B=β,∠C=γ,△ABC的外接圆⊙O的半径为R,把△ABC沿直线l向右翻滚一周时,其外心O经过的路线是三条弧,当AC边与直线l重合时,C 与C′重合,A与A′重合,B与B′重合,连接CO,C′O′,则∠ACO=∠A′C′O′,所以∠OCO′=∠ACA′=180°-γ,(180-γ)πR(180-α)πR(180-β)πR∴l=,同理,另两条弧长分别为,,180180180∴外心O所经过的路程为2πR.R.π2结论:任何多边形都有一个外接圈,若将任意圆内接多边形翻滚一周时,其外心所经过的路程为。
邢台市2019年中考二轮模块复习《与圆有关的计算》练习解析

与圆有关的计算与圆有关的计算在近7年河北中考中考查5次,选择题、填空题、解答题均有考查。
本节常考的知识点有:(1)扇形的相关计算;(2)圆锥的相关计算 一、选择题 例题精讲1. (2019黄石中考)在长方形ABCD 中,AB = 16,如图所示,裁出一扇形ABE ,将扇形围成一个圆锥(AB 和AE 重合),则此圆锥的底面圆半径为 ( )A .4B .16C .24D .8【答案】A【解析】设所围圆锥的底面半径为r ,则r ππ21801690=⨯,∴r = 4,故选择A . 2. (宜昌中考)如图,圆形薄铁片与直角三角尺、直尺紧靠在一起平放在桌面上.已知铁片的圆心为O ,三角尺的直角顶点C 落在直尺的10cm 处,铁片与直尺的唯一公共点A 落在直尺的14cm 处,铁片与三角尺的唯一公共点为B .下列说法错误的是( )A .圆形铁片的半径是4cmB .四边形AOBC 为正方形 C .弧AB 的长度为4πcmD .扇形OAB 的面积是4πcm²【答案】C【解析】∵圆形铁片与直尺和三角形的直角边都有唯一的公共点,∴圆与直尺和三角形的直角边均相切.∴OB ⊥BC ,OA ⊥AC ,又∠BCA =90°,∴四边形OACB 为矩形,又OA =OB ,∴四边形OACB 为正方形.∴圆形铁片的半径等于正方形的边长,为14-10=4cm ;因此A 、B 正确;利用弧长公式可计算弧AB 的长为9042180ππ⨯⨯=cm ,扇形OAB 的面积是29044360ππ⨯⨯=cm²,故C 选项错误,D 正确.故选C. 针对性训练1. 已知一块圆心角为300°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝忽略不计),圆锥的底面圆的BC直径是80 cm ,则这块扇形铁皮的半径是( ) A .24 cmB .48 cmC .96 cmD .192 cm2. 如图,在矩形ABCD 中,已知AB=4,BC=3,矩形在直线l 上绕其右下角的顶点B 向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,…,依次类推,这样连续旋转次后,顶点A 在整个旋转过程中所经过的路程之和是( )A .2015πB .3019.5πC .3018πD .3024π3.如图,AB 为⊙O 的切线,切点为B ,连接AO ,AO 与⊙O 交于点C ,BD 为⊙O 的直径,连接CD .若∠A =30°,⊙O 的半径为2,则图中阴影部分的面积为( )A.43π B.43π-C.π D.23π4. 将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上.水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8 cm ,水的最大深度是2 cm ,则杯底有水部分的面积是( ) A .2)34316(cm -πB .2)38316(cm -πC .2)3438(cm -πD .2)3234(cm -π5. 若用一张直径为20cm 的半圆形铁片做一个圆锥的侧面,接缝忽略不计,则所得圆锥的高为( )cm D.10cm 答案1-5 B DAAA (二)、填空题例题精讲1. (龙东中考)如图,从直径是2米的圆形铁皮上剪出一个圆心角是90°的扇形ABC(A 、B 、C 三点在⊙O 上),将剪下来的扇形围成一个圆锥的侧面,则该圆锥的底面圆的半径是__________米.CBA【答案】42【解析】方法1:如图1,连接OB,OC,∵∠BAC=90°,∴∠BOC=180°,∴点B,O,C在同一条直线上,∴BC是⊙O直径,∵⊙O的直径为2米,∴BC=2米,在Rt△ABC中,由勾股定理得222AB AC BC+=,∵AB=AC,∴2AC2=22,∴AC,∴圆锥的底面圆的半径=÷(2π).CBACBA图1 图22.(大庆中考)在Rt△ABC中,∠C=90°,A C=BC=1,将其放入平面直角坐标系中,使A点与原点重合,AB在x轴上,△ABC沿x轴顺时针无滑动的滚动,点A再次落在x轴时停止滚动,则点A经过的路线与x 轴围成图形的面积为.【答案】12π+【解析】如图,∵∠C=90°,AC=BC=1,∴AB==∴点A经过的路线与x轴围成图形的面积2190111123602ππ⨯⨯=⨯⨯+=+.故答案为:π +.针对训练1. 一个扇形的半径为3cm,面积为πcm2,则此扇形的圆心角为_______.2. 如图,将一块含30°角的直角三角板和半圆形量角器按如图的方式摆放,使斜边与半圆相切.若半径OA=2,则图中阴影部分的面积是____________.(结果保留π)3. (黄冈中考)如图所示的扇形是一个圆锥的侧面展开图,若∠AOB=120°,弧AB的长为12πcm,则该圆锥的侧面积为__________cm2.【答案】1—3题答案 40°,43π+,108π(三)、解答题例题精讲1. (2019龙东中考)如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内,△ABC的三个顶点坐标分别为A(2,-4),B(4,-4),C(1,-1).(1)画出△ABC关于y轴对称的△A1B1C1,直接写出点A1的坐标:____________.(2)画出△ABC绕点O逆时针旋转90°后的△A2B2C2.(3)在(2)的条件下,求线段BC扫过的面积(结果保留π).解:(1)如图所示,A1坐标为(﹣2,﹣4),故答案为 (﹣2,﹣4).(2)如图所示.(3)∵OC OB =∴△ABC 旋转时线段BC 扫过的面积=22229090360360BOB COC OB OC S S ππ⨯⨯=-扇形扇形﹣=90(322)360π⨯-=152π.2. (怀化中考)如图,在Rt △ABC 中,∠ACB =90°,AC =1,AB =2.(1)求作⊙O ,使它经过点A 、B 、C (要求:尺规作图,保留作图痕迹,不写作法); (2)在(1)所作的图中,求出劣弧BC 的长l.解:(1)如图所示.(2)因为AC =1,AB =2,∠ACB =90°,所以∠B =30°,∠A =60°,连接OC ,则∠BOC =120°,OC =OB =1,所以劣弧BC 的长l =12021803ππ=. 针对练习1. 如图,射线PA 切⊙O 于点A ,连接PO .(1)在PO 的上方作射线PC ,使∠OPC=∠OPA (用尺规在原图中作,保留痕迹,不写作法),并证明:PC 是⊙O 的切线;(2)在(1)的条件下,若PC 切⊙O 于点B ,AB=AP=4,求AB 的长.2.如图①,半径为R ,圆心角为n°的扇形面积是S 扇形=2360n R p .由弧长l =180n Rp ,得S扇形=2360n R p =12180n R R p 创=12lR .通过观察,我们发现S 扇形=12lR 类似于S 三角形=12×底×高.类比扇形,我们探索扇环(如图②,两个同心圆围成的圆环被扇形截得的一部分叫做扇环)的面积公式及其应用.(1)设扇环的面积为S 扇环,AB 的长为l 1,CD 的长为l 2,线段AD 的长为h(即两个同心圆半径R 与r的差).类比S 梯形=12×(上底+下底)×高,用含l 1,l 2,h 的代数式表示S 扇环,并证明. (2)用一段长为40m 的篱笆围成一个如图②所示的扇环形花园,线段AD 的长h 为多少时,花园的面积最大?最大面积是多少?答案;1解:(1)作图如图所示.连接OA ,过O 作OB ⊥PC 于B ,∵PA 切⊙O 于点A , ∴OA ⊥PA ,又∵∠OPC=∠OPA ,OB ⊥PC ,∴易知OA=OB ,即d=r ,∴PC 是⊙O 的切线;(2)∵PA 、PC 是⊙O 的切线,∴PA=PB ,又∵AB=AP=4,∴△PAB 是等边三角形,∴∠APB=60°,∴∠AOB =120°,∠POA=60°.在Rt △AOP 中,tan60°=4OA ,∴∴AB l =1203180π⨯.2解:(1)121().2S l l h =+证法1:S 扇环=S 扇形OAB -S 扇形OCD 2222()360360360n R n r n R r p p p=-=-12111()()()().218021801802n n R n r R r R r h l l h p p p =?-=??+ C n ° OABl 1 l 2 Dh 图②ABO n ° R l 图①证法2:S 扇环=S 扇形OAB -S 扇形OCD 2212111()222180180n R n r l R l r p p =-=-12111()()()().218021801802n n R n r R r R r h l l h p p p =?-=??+ (2)由l 1+l 2+2h =40,得l 1+l 2=40-2h . ∴S 扇环=12×(l 1+l 2)×h =12(40-2h) h =-h 2+20h =-(h -10)2+100(0<h <20). ∴当h =10时,S 扇环的最大值为100m 2.∴当线段AD 的长为10m 时,花园的面积最大,最大面积为100m 2.2019-2020学年数学中考模拟试卷一、选择题1.在1x ,12,212x +,3xy π,3x y +,1a m +中分式的个数有()A .2 个B .3 个C .4 个D .5 个2.如图,平面直角坐标系中,矩形ABCD 与双曲线(0)ky x x=>交于D 、E 两点,将△OCD 沿OD 翻折,点C 的对称C'恰好落在边AB 上,已知OA=3,OC=5,则AE 长为( )A .4B .259C .269D .33.如图,AB ,AC 均为⊙O 的切线,切点分别为B ,C ,点D 是优弧BC 上一点,则下列关系式中,一定成立的是( )A .∠A+∠D =180°B .∠A+2∠D =180°C .∠B+∠C =270°D .∠B+2∠C =270°4.下列事件是随机事件的是( ) A .人长生不老 B .明天就是5月1日C .一个星期有七天D .2020年奥运会中国队将获得45枚金牌5.在一次学校组织的期末考试中,为了了解初二学生的数学水平,随机抽取了部分学生的数学成绩,并计算了他们的样本方差S 2=160[(95﹣70)2+(67﹣70)2+……+(92﹣70)2],请问这次抽取了多少名学生,这些学生的平均成绩是多少?( ) A .60,60B .70,70C .60,70D .70,606.如图,⊙O 与BC 相切于点B ,弦AB ∥OC ,若∠C =40°,则∠AOB 的度数是( )A.60B.70°C.80°D.90°7.下列运算正确的是( )A .﹣(a 3)2=a 5B .a 2+a 2=a 4C .212-⎛⎫ ⎪⎝⎭=4 D .2| 28.下图是由个大小相同的小正方体组成的几何体,它的左视图是( ) [Failed to download image :http://192.168.0.10:8086/QBM/2019/5/18/2206392863694848/2206818096996352/STEM/cbb80a6d7032477fa761eb6258ac924e.png]A. B. C. D.9.已知坐标平面内一点A(2,1),O 为原点,B 是x 轴上一个动点,如果以点B ,O ,A 为顶点的三角形是等腰三角形,那么符合条件的动点B 的个数为( ) A.2个B.3个C.4个D.5个10.如图所示,第1个图案是由黑白两种颜色的六边形地面砖组成的,第2个,第3个图案可以看成是由第1个图案经过平移而得,那么第n 个图案中有白色六边形地面砖( )块.A.6+4(n+1)B.6+4nC.4n ﹣2D.4n+211.在Rt △ABC 中,∠C =90°,sinA =35,BC =6,则AB =( ) A .4B .6C .8D .1012.如图,点A 是直线l 外一点,在l 上取两点B 、C,分别以点A 、C 为圆心,以BC 、AB 的长为半径画弧,两弧交于点D,分别连接AD 、CD,得到的四边形ABCD 是平行四边形.根据上述作法,能判定四边形ABCD 是平行四边形的条件是( )A .两组对边分别平行的四边形是平行四边形B .一组对边平行且相等的四边形是平行四边形C .两组对角分别相等的四边形是平行四边形D .两组对边分别相等的四边形是平行四边形 二、填空题13.用估算的方法求一元二次方程2t 2-t-2=0的解 列表:∴ t ≈_______14.把多项式ax 2+2a 2x+a 3分解因式的结果是_____.15.在ABCD □中,BC 边上的高为4,5AB =,AC =ABCD □的周长等于______.16.如图,正方形ABCD E 、F 分别为边AD 、CD 上一点,将正方形分别沿BE 、BF 折叠,点A 的对应点M 恰好落在BF 上,点C 的对应点N 给好落在BE 上,则图中阴影部分的面积为__________;171的绝对值是_____.18.如图,点A 、B 、C 在半径为2的⊙O 上,BC ∥OA ,∠A =25°,则弧AB 的长为__.三、解答题19.如左图所示的晾衣架,支架主视图的基本图形是菱形,其示意图如右图,晾衣架伸缩时,点G 在射线DP 上滑动,∠CED 的大小也随之发生变化,已知每个菱形边长均等于20cm ,且AH =DE =EG =20cm .当∠CED 由60°变为120°时,点A 向左移动了多少厘米?(结果精确到0.1cm20.如图,ABC 中,∠ACB=90°,D 为AB 中点,四边形BCED 为平行四边形,DE 、AC 相交于点F .求证: (1)点F 为AC 的中点;(2)试确定四边形ADCE 的形状,并说明理由;(3)若四边形ADCE 为正方形,ABC 应添加什么条件?并证明你的结论.21.计算:2sin30°+(π-3.14)0|+(12)-1+(-1)2019 22.如图,O 为△ABC 边AC 的中点,AD ∥BC 交BO 的延长线于点D ,连接DC ,DB 平分∠ADC ,作DE ⊥BC ,垂足为E .(1)求证:四边形ABCD 为菱形;(2)若BD =8,AC =6,求DE 的长.23.为了解某校九年级学生英语口语检测成绩等级的分布情况,随机抽取了该校若干名学生的英语口语检测成绩,按A ,B ,C ,D 四个等级进行统计分析,并绘制尚不完整的统计图;请根据统计图所提供的信息,解答下列问题:(1)求本次抽取的学生一共有多少人?(2)求本次抽取的学生中B 级的学生人数,并补全条形统计图;(3)根据抽样调查结果,请你估计某校860名九年级学生英语口语检测成绩等级为A 级的人数.24.在四边形ABCD 中,AB =AD ,请利用尺规在CD 边上求作一点P ,使得S △PAB =S △PAD ,(保留作图痕迹,不写作法).25.如图,在平面直角坐标系中,点O 为坐标原点,点()0,4A 与点B 关于x 轴对称,点(),0C m 为x 轴的正半轴上一动点.以AC 为边作等腰直角三角形ACD ,90ACD ∠=︒,点D 在第一象限内.连接BD ,交x 轴于点F .(Ⅰ)用含m 的式子表示点D 的坐标;(Ⅱ)在点C 运动的过程中,判断OF 的长是否发生变化?若不变求出其值,若变化请说明理由; (Ⅲ)过点C 作CG BD ⊥,垂足为点G ,请直接写出BF DF -与CG 之间的数量关系式.【参考答案】***一、选择题二、填空题13.114.a (x+a )215.12或2016.617 118.59π. 三、解答题19.点A 向左移动了约43.9cm【解析】【分析】分别求得当∠CED 是60°和120°,两种情况下AD 的长,求差即可.【详解】根据题意得:AB =BC =CD ,当∠CED =60°时,AD =3CD =60cm ,当∠CED =120°时,过点E 作EH ⊥CD 于H ,则∠CEH=60°,CH=HD.在直角△CHE中,sin∠CEH=CH CE,∴CH cm),∴CD=,∴AD=cm).∴103.9﹣60=43.9(cm).即点A向左移动了约43.9cm;【点睛】本题考查了菱形的性质,当菱形的一个角是120°或60°时,连接菱形的较短的对角线,即可把菱形分成两个等边三角形.20.(1)证明见解析;(2)四边形ADCE为菱形,理由见解析;(3)AC=BC,证明见解析.【解析】【分析】(1)根据三角形的中位线,证出即可;(2)由题意容易证明CE平行且等于AD,AD=CD=BD,所以得到四边形ADCE为菱形;(3)应添加条件AC=BC,证明CD⊥AB且相等即可.【详解】证明:(1)∵四边形DBEC是平行四边形,∴DE∥BC,∵D为AB中点,∴DF为△ABC的中位线,即点F为AC的中点;(2)∵平行四边形BDEC,∴CE平行等于BD.∵D为AB中点,∴AD=BD,∴CE平行且等于AD,∴四边形ADCE为平行四边形,又∵AD=CD=BD,∴四边形ADCE为菱形;(3)应添加条件AC=BC.证明:∵AC=BC,D为AB中点,∴CD ⊥AB (三线合一的性质),即∠ADC=90°.∵四边形BCED 为平行四边形,四边形ADCE 为平行四边形,∴DE=BC=AC ,∠AFD=∠ACB=90°.∴四边形ADCE 为正方形.(对角线互相垂直且相等的四边形是正方形)【点睛】此题主要考查平行四边形、正方形的判定.21.【解析】【分析】依次计算特殊角的三角函数值,零次幂,去绝对值,负整数幂,再合并即可.【详解】 原式=2×12-1+2-1【点睛】本题运用了实数的运算法则和三角函数的特殊值,注意运算的准确性.22.(1)见解析;(2)245【解析】【分析】(1)由ASA 证明△OAD ≌△OCB 得出OD =OB ,得出四边形ABCD 是平行四边形,再证出∠CBD =∠CDB ,得出BC =DC ,即可得出四边形ABCD 是菱形; (2)由菱形的性质得出OB =12BD =4,OC =12AC =3,AC ⊥BD ,由勾股定理得出BC5,证出△BOC ∽△BED ,得出OC BC DE BD =,即可得出结果. 【详解】(1)证明:∵O 为△ABC 边AC 的中点,AD ∥BC ,∴OA =OC ,∠OAD =∠OCB ,∠AOD =∠COB ,在△OAD 和△OCB 中,OAD OCB OA OCAOD COB ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△OAD ≌△OCB (ASA ),∴OD =OB ,∴四边形ABCD 是平行四边形,∵DB 平分∠ADC ,∴∠ADB =∠CDB ,∴∠CBD =∠CDB ,∴四边形ABCD是菱形;(2)解:∵四边形ABCD是菱形,∴OB=12BD=4,OC=12AC=3,AC⊥BD,∴∠BOC=90°,∴BC5,∵DE⊥BC,∴∠E=90°=∠BOC,∵∠OBC=∠EBD,∴△BOC∽△BED,∴OC BCDE BD=,即358DE=,∴DE=245.【点睛】本题考查了菱形的判定与性质、平行四边形的判定、全等三角形的判定与性质、勾股定理、相似三角形的判定和性质;熟练掌握菱形的判定与性质是解题的关键.23.(1)本次抽取的学生一共有100人;(2)本次抽取的学生中B等积的学生人数是25人,见解析;(3)某校860名初三学生英语口语检测成绩等级为A级的人数是172人.【解析】【分析】(1)根据A等级的人数和所占的百分比即可求出总人数;(2)用总人数乘以B等级所占的百分比,即可补全统计图;(3)用某校860名初三学生乘以A等级所占的百分比,即可得出答案.【详解】解:(1)2010020%=(人).∴本次抽取的学生一共有100人.(2)10025%25⨯=(人)∴本次抽取的学生中B等积的学生人数是25人.补图如下:(3)86020%172⨯=(人)∴估计某校860名初三学生英语口语检测成绩等级为A级的人数是172人.本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.24.见解析【解析】【分析】作∠P 的平分线交CD 边于点P ,则点P 即为所求.【详解】解:如图,点P 即为所求.【点睛】本题考查的是作图﹣复杂作图,熟知三角形的面积公式及角平分线的性质是解答此题的关键.25.(1) G(4+m,m)(2) OF=4,OF 是不变化的 (3) BF DF -是CG 的两倍【解析】【分析】(1)过D 点作x 轴垂线,垂足为G 点,可知△CDG 相似△OAC ,即可求出D 点坐标.(2)利用B,D 两点的坐标给出直线BD 的解析式,然后令解析式的y=0,给出x 的值,如果x 含有参数,则OF 的长是变化的,若x 不含参数,则OF 的长无变化.(3)用含m 的式子表示出BF DF -和CG 的长,结果就出来了,其中BF DF -的长利用△DFG 相似△OBF 可求,CG 的长直接利用勾股定理可求.【详解】解:(1) 过D 点作x 轴垂线,垂足为H 点,∵90ACD ∠=︒,∴=90ACO DCH ∠+∠︒∵=90ACO CAO ∠+∠︒,∴CAO DCH ∠=∠ ,又∵90ACD CHD ∠=∠=︒,AC=CD,∴在△OAC 和△CDH ,CAO DCH AOC CHD AC CD ∠=∠⎧⎪∠=∠⎨⎪=⎩(AAS)ACO CDH ∴≌,∴CH=OA,DH=OC=m,∴OH=4+m ,∴D(4+m,m).(2)设BD 直线的解析式为:y=kx+b ,将点B(0,-4)与点D(4+m,m)代入方程,()44+m b k b m =-⎧⎨+=⎩, 解得:11k b =⎧⎨=⎩ , BD 的直线解析式为4y x =- ,当y=0时,x=4 ,OF=4,OF 是不变化的;(3)可知△DFH 相似△OBF ,∴::m 4DH OB DF BF ==:,由 B(0,-4)与点D(4+m,m),可以知道)4m +,∴, DF= ,BF DF -m-4,CG === ∴BF DF -是CG 的两倍.【点睛】本题是一道综合习题,第一问考查相似与坐标系中点的表示,第二问考查力一次函数,第三问考查力相似与勾股定理,本题第二问关键是给出直线BD 的解析式,第三问的关键是会表示两个线段的长2019-2020学年数学中考模拟试卷一、选择题1.下列图形既是轴对称图形,又是中心对称图形的是( )A. B.C. D.2.如图,抛物线2y ax bx c =++(a≠0)的对称轴为直线x =1,与x 轴的交点(1x ,0),(2x ,0),且﹣1<1x <0<2x ,有下列5个结论:①abc <0;②b >a+c ;③a+b >k (ka+b )(k 为常数,且k≠1);④2c <3b ;⑤若抛物线顶点坐标为(1,n ),则2b =4a (c ﹣n ),其中正确的结论有( )个.A .5B .4C .3D .23.我们将如图所示的两种排列形式的点的个数分别叫做“平行四边形数”和“正六边形数”.设第n 个“平行四边形数”和“正六边形数”分别为a 和b ,若a+b =103,则a b的值是( )A.619B.837C.1093D.12914.如图,菱形ABCD 的对角线AC 、BD 相交于点O .若周长为20,BD =8,则AC 的长是( )A.3B.4C.5D.65.分式方程的解是( )A.3B.-3C.D.96.若二次函数2(2)4y ax a x a =+++的图像与x 轴有两个交点12(,0),(,0)x x ,且121x x <<,则a 的取值范围是()A .2153a -<<-B .103a -<<C .203a <<D .1233a << 7.一组数据2,3,8,6,x 的唯一众数是x ,其中x 是不等式组26070x x ->⎧⎨-<⎩的解,则这组数据的中位数是( )A .3B .5C .6D .8 8.计算11x -- 1x x -的结果为( ) A .1 B .2 C .﹣1 D .﹣29.一个直角三角形两边长分别为3和4,则它的面积为( )A .6B .12C .6或10D .6或210.对于函数y=-2(x-3)2,下列说法不正确的是( )A.开口向下B.对称轴是3x =C.最大值为0D.与y 轴不相交11.如图,点A (0,2),在x 轴上取一点B ,连接AB ,以A 为圆心,任意长为半径画弧,分别交OA 、AB 于点M 、N ,再以M 、N 为圆心,大于12MN 的长为半径画弧,两弧交于点D ,连接AD 并延长交x 轴于点P .若△OPA 与△OAB 相似,则点P 的坐标为( )A .(1,0)B .0)C .(230)D .(0)12.如图,将一副三角板叠放在一起,使顶点A 在另一直角三角形的斜边DE 上,斜边BC 与直角边EF 在一直线上,则图中∠EAC 的度数为( )A .60°B .75°C .65°D .55°二、填空题 13.如图,△ABC 中,D 、E 、F 分别是各边的中点,随机地向△ABC 中内掷一粒米,则米粒落到阴影区域内的概率是_____.14.如图,某飞机于空中探测某座山的高度,在点A 处飞机的飞行高度是3700AF =米,从飞机上观测山顶目标C 的俯角是45,飞机继续以相同的高度飞行300米到B 地,此时观察目标C 的俯角是50,则这座山的高度CD 是________米(参考数据:sin500.77≈,cos500.64≈,tan50 1.20≈)15.关于x 的一元二次方程x 2+4x ﹣k=0有实数根,则k 的取值范围是__________.16.如图,直线a ,b 与直线c ,d 相交,已知∠1=∠2,∠3=110°,则∠4的度数为________.17.如图,已知正方形ABCD 的边长为1,连接AC ,BD ,CE 平分∠ACD 交BD 于点E ,则DE=_________.18.如果在五张完全相同的纸片背后分别写上平行四边形、矩形、菱形、正方形、等腰梯形,打乱后随机抽取其中一张,那么抽取的图形既是轴对称图形又是中心对称图形的概率等于_____.三、解答题19.解不等式组()3151924x x x x ⎧-≤+⎪⎨-<⎪⎩,并写出它的所有整数解. 20.阅读下列材料,解决问题:12345678987654321这个数有这样一个特点:各数位上的数字从左到右逐渐增大(由1到9,是连续的自然数),到数9时,达到顶峰,以后又逐渐减小(由9到1),它活像一只橄榄,我们不妨称它为橄榄数.记第一个橄榄数为a 1=1,第二个橄榄数为a 2=121,第三个橄榄数为a 3=12321……有趣的是橄榄数还是一个平方数,如1=12,121=112,12321=1112,1234321=11112……而且,橄榄数可以变形成如下对称式:1111⨯= 2222121121⨯=++ 3333331232112321⨯=++++…… 根据以上材料,回答下列问题(1)11111112= ;将123454321变形为对称式:123454321= .(2)一个两位数(十位大于个位),交换其十位与个位上的数字,得到一个新的两位数,将原数和新数相加,就能得到橄榄数121,求这个两位数.(3)证明任意两个橄榄数a m ,a n 的各数位之和的差能被m ﹣n 整除(m =1,2…9,n =1,2…9,m >n )21.某公司用100万元研发一种市场急需电子产品,已于当年投入生产并销售,已知生产这种电子产品的成本为4元/件,在销售过程中发现:每年的年销售量y (万件)与销售价格x (元/件)的关系如图所示,其中AB 为反比例函数图象的一部分,设公司销售这种电子产品的年利润为s (万元).(1)请求出y (万件)与x (元/件)的函数表达式;(2)求出第一年这种电子产品的年利润s (万元)与x (元/件)的函数表达式,并求出第一年年利润的最大值.22.如图,AB ⊥EF ,DC ⊥EF ,垂足分别为B 、C ,且AB =CD ,BE =CF .AF 、DE 相交于点O ,AF 、DC 相交于点N ,DE 、AB 相交于点M .(1)请直接写出图中所有的等腰三角形;(2)求证:△ABF ≌△DCE .23.如图,在菱形ABCD 中,对角线AC 、BD 交于点O ,过点A 作AE ⊥BC 于点E ,延长BC 至F ,使CF =BE ,连接DF .(1)求证:四边形AEFD是矩形;(2)若BF=8,DF=4,求CD的长.24.解方程:213xx x+=-.25.如图,在平行四边形ABCD中,点H为DC上一点,BD、AH交于点O,△ABO为等边三角形,点E在线段AO上,OD=OE,连接BE,点F为BE的中点,连接AF并延长交BC于点G,且∠GAD=60°.(1)若CH=2,AB=4,求BC的长;(2)求证:BD=AB+AE.【参考答案】***一、选择题二、填空题13.1 414.1900 15.k≥﹣4 16.110°17118.3 5三、解答题19.﹣2≤x<1,整数解有﹣2、﹣1、0.【解析】【分析】分别求出各不等式的解集,再求出其公共解集即可.【详解】()3151924x x x x ①②⎧-≤+⎪⎨-<⎪⎩, 解不等式①,得x≥﹣2,解不等式②,得x <1,∴不等式组的解集为﹣2≤x<1,∴不等式组的整数解有﹣2、﹣1、0.【点睛】本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.20.(1)55555555551234567654321,123454321⨯++++++++;(2)65,74,83,92;(3)任意两个橄榄数a m ,a n 的各数位之和的差能被m ﹣n 整除.【解析】【分析】(1)根据题中给出的定义,直接可得:(2)设十位数字是x ,个位数字是y ,根据题意得到x+y=11,进而确定两位数;(3)根据数的规律求得a m 的各数位之和m 2,a n 的各数位之和n 2,然后因式分解证明结论.【详解】(1)根据题中给出的定义,直接可得:11111112=1234567654321,123454321=⨯++++++++5555555555123454321; (2)设十位数字是x ,个位数字是y ,x >y ,10x+y+10y+x =11(x+y )=121,∴x+y =11,∴这个两位数是65,74,83,92;(3)a m 的各数位之和1+2+3+…+m+(m ﹣1)+…+2+1=(1)(1)22m m m m +-+=m 2, a n 的各数位之和1+2+3+…+m+(m ﹣1)+…+2+1=(1)(1)22n n n n +-+=n 2, ∴a m ,a n 的各数位之和的差为m 2﹣n 2=(m+n )(m ﹣n ),∵m >n ,∴m 2﹣n 2=(m+n )(m ﹣n )能被m ﹣n 整除,∴任意两个橄榄数a m ,a n 的各数位之和的差能被m ﹣n 整除.【点睛】本题考查新定义,字母表示数,自然数求和,因式分解;能够理解定义,熟练掌握因式分解,自然数求和方法是解题的关键.21.(1)y =160(48)28(828)x x x x ⎧≤≤⎪⎨⎪-+≤⎩;(2)当每件的销售价格定为16元时,第一年年利润的最大值为44万元.【解析】【分析】(1)依据待定系数法,即可求出y (万件)与x (元/件)之间的函数关系式;(2)分两种情况进行讨论,当x =8时,s max =﹣20;当x =16时,s max =44;根据44>﹣20,可得当每件的销售价格定为16元时,第一年年利润的最大值为44万元.【详解】解:(1)当4≤x≤8时,设y =k x,将A (4,40)代入得k =4×40=160, ∴y 与x 之间的函数关系式为y =160x; 当8<x≤28时,设y =k'x+b ,将B (8,20),C (28,0)代入得,820280k b k b +=⎧⎨+=''⎩, 解得k 1b 28=-⎧⎨='⎩, ∴y 与x 之间的函数关系式为y =﹣x+28,综上所述,y =160(48)28(828)x x x x ⎧⎪⎨⎪-+<≤⎩剟;(2)当4≤x≤8时,s =(x ﹣4)y ﹣160=(x ﹣4)•160x ﹣100=640x-+60, ∵当4≤x≤8时,s 随着x 的增大而增大,∴当x =8时,s max =640x-+60=﹣20; 当8<x≤28时,s =(x ﹣4)y ﹣80=(x ﹣4)(﹣x+28)﹣80=﹣(x ﹣100)2+44,∴当x =16时,s max =44;∵44>﹣20,∴当每件的销售价格定为16元时,第一年年利润的最大值为44万元.【点睛】本题主要考查了反比例函数与二次函数的综合应用,在商品经营活动中,经常会遇到求最大利润,最大销量等问题,解此类题的关键是通过题意,确定出二次函数的解析式,然后确定其最大值,实际问题中自变量x 的取值要使实际问题有意义;解题时注意,依据函数图象可得函数关系式为分段函数,解决问题时需要运用分类思想以及数形结合思想进行求解.22.(1)△EOF ,△AOM ,△DON ;(2)证明见解析【解析】【分析】(1)可以证明△ABF ≌△DCE ,根据全等三角形对应角相等可得∠A =∠D ,∠DEC =∠AFB ,所以△EOF 是等腰三角形,再根据等角的余角相等可得∠A =∠AMO ,∠D =∠DNO ,从而得到△AOM 与△DON 也都是等腰三角形;(2)由BE =CF ,可以证明EC =BF ,然后根据方法“边角边”即可证明△ABF 与△DCE 全等.【详解】(1)解:△EOF ,△AOM ,△DON ;(2)证明:∵AB ⊥EF 于点B ,DC ⊥EF 于点C ,∴∠ABC =∠DCB =90°,∵CF =BE ,∴CF+BC =BE+BC ,即BF =CE…在△ABF 和△DCE 中,AB DC DCB BF CE =⎧⎪⎨⎪=⎩∠ABC=∠, ∴△ABF ≌△DCE ,【点睛】本题主要考查了全等三角形的证明,常用的方法有“边边边”,“边角边”,“角边角”,“角角边”,本题证明得到BF =CE 是解题的关键.23.(1)见解析;(2)CD =5.【解析】【分析】(1)根据菱形的性质得到AD ∥BC 且AD =BC ,等量代换得到BC =EF ,推出四边形AEFD 是平行四边形,根据矩形的判定定理即可得到结论,(2)设BC =CD =x ,则CF =8﹣x 根据勾股定理即可得到结论.【详解】(1)证明:∵在菱形ABCD 中,∴AD ∥BC 且AD =BC ,∵BE =CF ,∴BC =EF ,∴AD =EF ,∵AD ∥EF ,∴四边形AEFD 是平行四边形,∵AE ⊥BC ,∴∠AEF=90°,∴四边形AEFD是矩形.(2)解:设BC=CD=x,则CF=8﹣x,在Rt△DCF中,∵x2=(8﹣x)2+42 ,∴x=5,∴CD=5.【点睛】本题考查了矩形的判定和性质,菱形的性质,勾股定理,正确的识别图形是解题的关键.24.x=65.【解析】【分析】根据分式方程的解法求解即可. 【详解】去分母得:2x﹣6+x2=x2﹣3x,解得:x=65,检验x=65是原方程的解.【点睛】本题主要考查分式方程的解法,注意根的验证.25.(1)BC (2)详见解析【解析】【分析】(1)延长AH、BC相交于点M,可证明△MCH∽△MBA,得出MH=AH,BM=2BC;由∠DOH=∠AOB=60°,∠ODH=∠OBA=60°,∠OHD=∠OAB=60°,可得△DOH是等边三角形,AE=OA-OE=OA-OD=2,得点E是OA的中点,根据“三线合一”可得BE的长度、BE⊥OA,根据勾股定理求出BM的长,而BC=12BM;(2)AB=OB,由(1)知,AE=OE=OD,可证BD=OB+OD=AB+AE.【详解】解:延长AH、BC相交于点M,∵▱ABCD∴CD=AB=4,CD∥AB∴∠MHC=∠MAB,∠MCH=∠MBA∴△MCH∽△MBAMH MC CH∴==MA MB AB∵CH=2MH MC21∴===MA MB42∴MH=AH,BM=2BC∵△ABO为等边三角形∴∠AOB=∠OAB=∠OBA=60°,OA=AB=4∴∠DOH=∠AOB=60°∴∠ODH=∠OBA=60°,∠OHD=∠OAB=60°∴∠DOH=∠ODH=∠OHD∴△DOH是等边三角形∴OH=OD=DH=2∴MH=AH=OA+OH=4+2=6,EM=OE+OH+MH=10 ∵OD=OE=2∴AE=OA﹣OE=4﹣2=2∴点E是OA的中点∵△ABO为等边三角形∴BE⊥OA,∠ABE=30°BE∴==在Rt△BEM中,∠BEM=90°∴BE2+EM2=BM2222∴+=10BM∴=BM∴=BC(2)∵△ABO为等边三角形∴AB=OB由(1)知,AE=OE=OD∵BD=OB+OD∴BD=AB+AE【点睛】本题考查了等边三角形的判定和性质、勾股定理、相似三角形的判定和性质.这道题的关键是证明点E是OA的中点、BM=2BC.。
河北8年中考真题高频考点23.圆的解答题

河北中考圆的解答题22.(2020·河北)如图13,点O为AB中点,分别延长OA到点C,OB到点D,使OC=OD,以点O为圆心,分别以OA,OC为半径在CD上方作两个半圆,点P为小半圆上任一点(不与点A,B重合),连接OP并延长交大半圆于点E,连接AE,CP.(1)①求证:△AOE≌△POC;②写出∠1,∠2和∠C三者间的数量关系,并说明理由.(2)若OC=2OA=2,当∠C最大时,直接指出CP与小半圆的位置关系,并求此时S扇形EOD(答案保留π).备用图图1321BA OBA OC D DCPE解:(1)①证明:∵OA=OB,OE=OC,∠AOE=∠POC,∴△AOE≌△POC;②∠1+∠C=∠2.理由:∵△AOE≌△POC,∴∠E=∠C.∵∠1+∠E=∠2,∴∠1+∠C=∠2.(2)相切.如图,∵CP与小半圆相切,∴CP⊥OP.在Rt△OPC中,∵OP=1,OC=2,∴cos∠COP=12,∴∠COP=60°.∴∠DOE=120°.∴S扇形EOD=2120243603ππ⨯=.25.(2019·河北)如图1和图2,□ABCD中,AB=3,BC=15,tan∠DAB=34.点P为AB延长线上一点,过点A 作⊙O切CP于点P,设BP=x.(1)如图1,x为何值时,圆心O落在AP上?若此时⊙O交AD于点E,直接..指出PE与BC的位置关系;(2)当x=4时,如图2,⊙O与AC交于点Q,求∠CAP的度数,并通过计算比较弦AP与劣弧PQ长度的大小;(3)当⊙O与线段..AD只有一个公共点时,直接..写出x的取值范围.第25题图1 第25题图2 第25题备用图解:(1)∵圆心O落在AP上,∴AP为⊙O的直径,∴∠BEP=90°,∴PE ⊥AD.∵四边形ABCD 是平行四边形, ∴∠BPC=∠DAB ,BC ∥AD , ∴PE ⊥BC.∵作⊙O 切CP 于点P , ∴∠BPC=90°,∵tan ∠DAB =34,设BP =x , ∴PC=BP ·tan ∠DAB =34x ,又∵BC =15, ∴2225)34(=+x x ,解得x=9,即当x=9时,圆心O 落在AP 上. 此时PE ⊥BC .(2)如图所示,作CM ⊥AP 于点M ,∵tan ∠CBP=tan ∠DAB =34,BC=15, ∴BM=9,CM=12,∴AM=AB+BM=3+9=12=CM , ∴∠CAP=45°. ∵AB=3,BP=4, ∴AP=AB+BP=3+4=7.作垂直于AP 的直径EF 于点G ,连接OP 、FP ,则∠FGP=90°,∠F=∠CAP=45°,AG=PG=27, ∴FG=PG=27, ∴OG=OG-FG=OP-FG=OP-27, ∴222)27()27(OP OP =+-,解得OP=27, ∴劣弧PQ 长度为27236090⋅⨯π=π47. ∵π47<7, ∴弦AP 大于劣弧PQ 长度. (3)当⊙O 与线段..AD 只有一个公共点时,x ≥18.25.(2018河北省,25,10)如图,点A 在数轴上对应的数为26,一原点O 为圆心,OA 长为半径作优弧,使点B 在O 右下方,且tan ∠AOB =34.在优弧上任取一点P ,且能过P 作直线l ∥OB 交数轴与点Q ,设Q 在数轴上对应的数为x ,连接OP . (1)若优弧上一段的长为13π,求∠AOP 的度数及x 的值;(2)求x 的最小值,并指出此时直线l 与所在圆的位置关系;(3)若线段PQ 的长为12.5,直接..写出这时x 的值.解:(1)设∠AOP 的度数为n ,则18026·πn =13π.解得n =90. ∴OP ⊥OA .1分∵l ∥OB ,∴∠PQO =∠AOB .∴tan ∠PQO =tan ∠AOB =OQ PO =34. ∵OP =26,∴OQ =239. ∴∠AOP 的度数为90°,x 的值为239.2分(2)如图(1),将l 向左平移,当l 与⊙O 相切时,x 取得最小值.由(1)可知tan ∠PQO =34. ∴sin ∠PQO =54. ∵OP =26, ∴OQ =265. ∴x 的最小值为-265,2分 此时l 与所在圆相切.1分第25题图POQ B l 26A26备用图OB(3)如图(2)当点P 在数轴上方时,过点O 作OC ⊥l ,垂足为C .连接OP . 设QC 的长度为a ,则PC =12.5+a ,OC =34a . 在Rt △OPC 中有(12.5+a )2+(34a )2=262. 解得a 1=9.9,a 2=-18.9(舍).1分∴OQ =35a =35×9.9=16.5. ∴此时x 的值为-16.5.1分 当点P 在数轴的下方时,同理可得x 的值为-31.5. 1分另外,当点Q 在点O 右侧时,同理可得x 的值为31.5.1分综上,x 的值为-16.5或-31.5或31.5.23.(2017·河北)如图,16AB =,O 为AB 中点,点C 在线段OB 上(不与点O ,B 重合),将OC 绕点O 逆时针旋转270︒后得到扇形COD ,AP ,BQ 分别切优弧CD 于点P ,Q ,且点P ,Q 在AB 异侧,连接OP .(1)求证:AP BQ =;(2)当43BQ =时,求QD 的长(结果保留π);(3)若APO ∆的外心在扇形COD 的内部,求OC 的取值范围. 【答案】(1)见解析;(2)143π;(3)4<OC <8. 第25题答图(1) A26OB PQ 第25题答图(2) A 26O B PQ Cl考点:全等三角形的判定与性质,切线的性质,解直角三角形,外心.25.(2016河北,20,10分)如图,半圆O的直径AB=4,以长为2的弦PQ为直径,向点O方向作半圆M,其中P点在AQ(弧)上且不.与A点重合,但Q点可与B点重合.发现AP(弧)的长与QB(弧)的长之和为定值l,求l;思考点M与AB的最大距离为_______,此时点P,A间的距离为_______;点M与AB的最小距离为________,此时半圆M的弧与AB所围成的封闭图形面积为________.探究当半圆M与AB相切时,求AP(弧)的长.(注:结果保留π,cos 35°=6,cos 55°=3)第25题图备用图26. (2015·河北)(本小题满分14分)平面上,矩形ABCD与直径为QP的半圆K如图摆放,分别延长DA和QP交于点O,且∠BOQ=60°,OQ=OD=3,OP=2,OA=AB=1.让线段OD及矩形ABCD位置固定,将线段OQ连带着半圆K一起绕着点O按逆时针方向形如旋转,设旋转角为α(0°≤α≤60°).发现(1)当α=0°,即初始位置时,点P____直线AB上.(填“在”或“不在”)求当α是多少时,OQ经过点B?(2)在OQ旋转过程中.简要说明α是多少时,点P,A间的距离最小?并指出这个最小值:(3)如图,当点P恰好落在BC边上时.求α及S阴影.拓展如图.当线段OQ与CB边交于点M,与BA边交于点N时,设BM=x(x>0),用含x的代数式表示BN的长,并求x的取值范围.探究当半圆K 与矩形ABCD 的边相切时,求sin α的值.【答案】发现:(1)在,15°;(2)当α=60°时,最小距离为1;(3)30°,3=+24S π阴影 。
河北省邢台市2019年中考数学二轮模块复习 与圆有关的计算练习

与圆有关的计算与圆有关的计算在近7年河北中考中考查5次,选择题、填空题、解答题均有考查。
本节常考的知识点有:(1)扇形的相关计算;(2)圆锥的相关计算 一、选择题 例题精讲1. (2016黄石中考)在长方形ABCD 中,AB = 16,如图所示,裁出一扇形ABE ,将扇形围成一个圆锥(AB 和AE 重合),则此圆锥的底面圆半径为 ( )A .4B .16C .24D .8【答案】A【解析】设所围圆锥的底面半径为r ,则r ππ21801690=⨯,∴r = 4,故选择A . 2. (宜昌中考)如图,圆形薄铁片与直角三角尺、直尺紧靠在一起平放在桌面上.已知铁片的圆心为O ,三角尺的直角顶点C 落在直尺的10cm 处,铁片与直尺的唯一公共点A 落在直尺的14cm 处,铁片与三角尺的唯一公共点为B .下列说法错误的是( ) A .圆形铁片的半径是4cm B .四边形AOBC 为正方形 C .弧AB 的长度为4πcm D .扇形OAB 的面积是4πcm ²【答案】C【解析】∵圆形铁片与直尺和三角形的直角边都有唯一的公共点,∴圆与直尺和三角形的直角边均相切.∴OB ⊥BC ,OA ⊥AC ,又∠BCA =90°,∴四边形OACB 为矩形,又OA =OB ,∴四边形OACB 为正方形.∴圆形铁片的半径等于正方形的边长,为14-10=4cm ;因此A 、B正确;利用弧长公式可计BC算弧AB 的长为9042180ππ⨯⨯=cm ,扇形OAB 的面积是29044360ππ⨯⨯=cm ²,故C 选项错误,D 正确.故选C . 针对性训练1. 已知一块圆心角为300°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝忽略不计),圆锥的底面圆的直径是80 cm ,则这块扇形铁皮的半径是( ) A .24 cmB .48 cmC .96 cmD .192 cm2. 如图,在矩形ABCD 中,已知AB =4,BC =3,矩形在直线l 上绕其右下角的顶点B 向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,…,依次类推,这样连续旋转次后,顶点A 在整个旋转过程中所经过的路程之和是( )A .2015πB .3019.5πC .3018πD .3024π3.如图,AB 为⊙O的切线,切点为B ,连接AO ,AO 与⊙O 交于点C ,BD 为⊙O 的直径,连接CD .若∠A =30°,⊙O 的半径为2,则图中阴影部分的面积为( )A .43π B .43π-C .πD .23π4. 将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上.水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8 cm ,水的最大深度是2 cm ,则杯底有水部分的面积是( ) A .2)34316(cm -πB .2)38316(cm -πC .2)3438(cm -πD .2)3234(cm -π5. 若用一张直径为20cm 的半圆形铁片做一个圆锥的侧面,接缝忽略不计,则所得圆锥的高为( )cmcm D.10cm 答案1-5 B DAAA (二)、填空题例题精讲1. (龙东中考)如图,从直径是2米的圆形铁皮上剪出一个圆心角是90°的扇形ABC (A 、B 、C 三点在⊙O 上),将剪下来的扇形围成一个圆锥的侧面,则该圆锥的底面圆的半径是__________米.【答案】42 【解析】方法1:如图1,连接OB ,OC ,∵∠BAC =90°,∴∠BOC =180°,∴点B ,O ,C 在同一条直线上,∴BC 是⊙O 直径,∵⊙O 的直径为2米,∴BC =2米,在Rt △ABC 中,由勾股定理得222AB AC BC +=,∵AB =AC ,∴2AC 2=22, ∴AC,∴圆锥的底面圆的÷(2π).CBACBA图1图22.(大庆中考)在Rt △ABC 中,∠C =90°,AC =BC =1,将其放入平面直角坐标系中,使A 点与原点重合,AB 在x 轴上,△ABC 沿x 轴顺时针无滑动的滚动,点A 再次落在x 轴时停止滚动,则点A 经过的路线与x 轴围成图形的面积为 .CBA【答案】12π+【解析】如图,∵∠C=90°,AC=BC=1,∴AB==∴点A经过的路线与x轴围成图形的面积2190111123602ππ⨯⨯=⨯⨯+=+.故答案为:π +.针对训练1. 一个扇形的半径为3cm,面积为πcm2,则此扇形的圆心角为_______.2. 如图,将一块含30°角的直角三角板和半圆形量角器按如图的方式摆放,使斜边与半圆相切.若半径OA=2,则图中阴影部分的面积是____________.(结果保留π)3. (黄冈中考)如图所示的扇形是一个圆锥的侧面展开图,若∠AOB=120°,弧AB的长为12πcm,则该圆锥的侧面积为__________cm2.【答案】1—3题答案40°,43,108π(三)、解答题例题精讲1. (2016龙东中考)如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内,△ABC的三个顶点坐标分别为A(2,-4),B(4,-4),C(1,-1).(1)画出△ABC关于y轴对称的△A1B1C1,直接写出点A1的坐标:____________.(2)画出△ABC绕点O逆时针旋转90°后的△A2B2C2.(3)在(2)的条件下,求线段BC扫过的面积(结果保留π).解:(1)如图所示,A1坐标为(﹣2,﹣4),故答案为 (﹣2,﹣4).(2)如图所示.(3)∵OCOB=,∴△ABC 旋转时线段BC 扫过的面积=22229090360360BOB COC OB OC S S ππ⨯⨯=-扇形扇形﹣=90(322)360π⨯-=152π.2. (怀化中考)如图,在Rt △ABC 中,∠ACB =90°,AC =1,AB =2.(1)求作⊙O ,使它经过点A 、B 、C (要求:尺规作图,保留作图痕迹,不写作法); (2)在(1)所作的图中,求出劣弧BC 的长l.解:(1)如图所示.(2)因为AC =1,AB =2,∠ACB =90°,所以∠B =30°,∠A =60°,连接OC ,则∠BOC =120°,OC =OB =1,所以劣弧BC 的长l =12021803ππ=. 针对练习1. 如图,射线PA 切⊙O 于点A ,连接PO .(1)在PO 的上方作射线PC ,使∠OPC =∠OPA (用尺规在原图中作,保留痕迹,不写作法),并证明:PC 是⊙O 的切线;(2)在(1)的条件下,若PC 切⊙O 于点B ,AB =AP =4,求AB 的长.2.如图①,半径为R ,圆心角为n °的扇形面积是S 扇形=2360n R p .由弧长l =180n Rp ,得S 扇形=2360n R p=12180n R R p 创=12lR .通过观察,我们发现S 扇形=12lR 类似于S 三角形=12×底×高.类比扇形,我们探索扇环(如图②,两个同心圆围成的圆环被扇形截得的一部分叫做扇环)的面积公式及其应用.(1)设扇环的面积为S 扇环,AB 的长为l 1,CD 的长为l 2,线段AD 的长为h (即两个同心圆半径R 与r 的差).类比S 梯形=12×(上底+下底)×高,用含l 1,l 2,h 的代数式表示S 扇环,并证明.(2)用一段长为40m 的篱笆围成一个如图②所示的扇环形花园,线段AD 的长h 为多少时,花园的面积最大?最大面积是多少?答案;1解:(1)作图如图所示.连接OA ,过O 作OB ⊥PC 于B ,∵PA 切⊙O 于点A , ∴OA ⊥PA ,又∵∠OPC =∠OPA ,OB ⊥PC ,∴易知OA =OB ,即d =r ,∴PC 是⊙O 的切线;(2)∵PA 、PC 是⊙O 的切线,∴PA =PB ,又∵AB =AP =4,∴△PAB 是等边三角形,∴∠APB =60°,∴∠AOB =120°,∠POA =60°.在Rt △AOP 中,tan60°=4OA ,∴OA∴AB l =1203180π⨯.2解:(1)121().2S l l h =+证法1:S 扇环=S 扇形OAB -S 扇形OCD 2222()360360360n R n r n R r p p p=-=-12111()()()().218021801802n n R n r R r R r h l l h p p p =?-=??+ 证法2:S 扇环=S 扇形OAB -S 扇形OCD 2212111()222180180n R n r l R l r p p =-=-C n ° OABl 1 l 2 Dh 图②ABO n ° R l 图①12111()()()().218021801802n n R n r R r R r h l l h p p p =?-=??+ (2)由l 1+l 2+2h =40,得l 1+l 2=40-2h . ∴S 扇环=12×(l 1+l 2)×h =12(40-2h ) h =-h 2+20h =-(h -10)2+100(0<h <20). ∴当h =10时,S 扇环的最大值为100m 2.∴当线段AD 的长为10m 时,花园的面积最大,最大面积为100m 2.。
河北省2019年中考数学专题9圆的有关计算证明与探究精讲试题

2019中考,每年都是原创题,并且出题解题策略解答此类问题要熟练掌握圆的基本性质,垂径定理,弦、弧、圆心角、圆周角之间的关系,能够快速作出辅助线找到解题思路与方法.一般辅助线有:连半径、作垂直、构造直径所对的圆周角等.,重难点突破)圆内定理的应用【例1】如图,AB 是⊙O 的直径,弦CD⊥AB 于点E ,且CD =24,点M 在⊙O 上,MD 经过圆心O ,连接MB.(1)若BE =8,求⊙O 的半径;(2)若∠DMB=∠D,求线段OE 的长.【解析】(1)根据垂径定理求出DE 的长,设出半径,根据勾股定理,列出方程即可求出半径;(2)根据∠DOE=2∠DMB,得出∠DOE=2∠D,根据AB⊥CD,求出∠D 的度数,根据锐角三角函数求出O E 的长.【答案】解:(1)设⊙O 的半径为x ,则OE =x -8. ∵CD =24,由垂径定理得DE =12.在Rt △ODE 中,∵OD 2=DE 2+OE 2,即x 2=(x -8)2+122,解得x =13. ∴⊙O 的半径为13;(2)∵∠DOE=2∠DMB,∠DMB =∠D,∴∠DOE =2∠D.∵∠DOE+∠D=90°,∴∠D =30°. 在Rt △OED 中,∵DE =12,∠OED =90°,∴OE =DE·tan30°=12×33=4 3.1.如图,已知AB 是⊙O 的弦,OB =2,∠B =30°,C 是弦AB 上的任意一点(不与点A ,B 重合),连接CO 并延长CO 交⊙O 于点D ,连接AD.(1)弦长AB =________;(结果保留根号)(2)当∠D=20°时,求∠BOD 的度数;(3)当AC 的长度为多少时,以A ,C ,D 为顶点的三角形与以B ,C ,O 为顶点的三角形相似?请写出解答过程.解:(1)23;(2)连接OA.∵OA=OB =OD ,∴∠BAO =∠B=30°,∠D =∠DAO=20°, ∴∠DAB =∠BAO+∠DAO=50°, ∴∠BOD =2∠DAB=100°; (3)∵∠B CO =∠DAC+∠D, ∴∠BCO>∠DAC,∠BCO>∠D ,∴要使△DAC 与△BOC 相似,只能∠DCA=∠BCO=90°, 此时∠BOC=60°,∠BOD =120°, ∴∠DAC =60°,∴△DAC ∽△BOC.∵∠BCO =90°,即OC⊥AB,∴AC =12AB = 3.【方法指导】熟练掌握圆内的4个定理,根据图形的形状和位置选择合适的定理.圆外定理的应用【例2】(天水中考)如图,点D 为⊙O 上一点,点C 在直径BA 的延长线上,且∠CDA=∠CBD. (1)判断直线CD 和⊙O 的位置关系,并说明理由;(2)过点B 作⊙O 的切线BE 交直线CD 于点E ,若AC =2,⊙O 的半径是3,求BE 的长.【解析】(1)连接OD ,根据圆周角定理求出∠DAB +∠DBA=90°,从而得出∠CDA+∠ADO=90°,再根据切线的判定推出即可;(2)首先利用勾股定理求出DC ,由切线长定理得出DE =EB ,在Rt △CBE 中根据勾股定理得出方程,求出方程的解即可.【答案】解:(1)直线CD 和⊙O 的位置关系是相切. 理由:连接OD.∵AB 是⊙O 的直径,∴∠ADB =90°,∴∠DAB +∠DBA=90°. ∵∠CDA =∠CBD,∴∠DAB +∠CDA=90°. ∵OD =OA ,∴∠DAB =∠ADO ,∴∠CDA +∠ADO=90°,即OD⊥CE, ∴直线CD 是⊙O 的切线,即直线CD 和⊙O 的位置关系是相切;(2)∵AC=2,⊙O 的半径是3,∴OC =2+3=5,OD =3. 在Rt △CDO 中,由勾股定理得CD =4. ∵CE 切⊙O 于点D ,EB 切⊙O 于点B , ∴DE =EB ,∠CBE =90°. 设DE =EB =x ,在Rt △CBE 中,由勾股定理,得CE 2=BE 2+BC 2,则(4+x )2=x 2+(5+3)2,解得x =6,即BE =6.2.(毕节中考)如图,以△ABC 的BC 边上一点O 为圆心的圆,经过A ,B 两点,且与BC 边交于点E ,D 为BE 的下半圆弧的中点,连接AD 交BC 于点F ,AC =FC.(1)求证:AC 是⊙O 的切线;(2)已知圆的半径R =5,EF =3,求DF 的长.解:(1)连接AE ,AO.∵BE 为直径,∴∠BAE =90°. ∵BD ︵=ED ︵,∴∠BAD =∠EAD=45°, ∴∠AFC =∠B+45°, ∴∠CAF =∠EAC+45°.∵AC =FC ,∴∠AFC =∠CAF,∴∠B +45°=∠EAC+45°,∴∠B =∠EAC. ∵OA =OB ,∴∠OAB =∠B,∴∠EAC =∠OAB,∴∠OAC =∠OAE+∠EAC=∠OAE+∠OAB=∠BAE=90°, ∴AC ⊥OA ,∴AC 为⊙O 的切线;(2)连接OD.∵BD ︵=DE ︵, ∴∠BOD =∠DOE=90°.在Rt △OFD 中 ,OF =5-3=2,OD =5,∴DF =OF 2+OD 2=29. 【方法指导】掌握圆外3个定理和2个定义,了解一种证明方法,熟练应用6条辅助线解题.圆中的计算【例3】(2019枣庄中考)如图,在△ABC 中,∠C =90°,∠BAC 的平分线交BC 于点D ,点O 在AB 上,以点O 为圆心,OA 为半径的圆恰好经过点D ,分别交AC ,AB 于点E ,F.(1)试判断直线BC 与⊙O 的位置关系,并说明理由;(2)若BD =23,BF =2,求阴影部分的面积.(结果保留π)【解析】(1)连接OD ,证明OD∥AC,即可证得∠ODB=90°,从而证得BC 是圆的切线;(2)在Rt △BOD 中,设OF =OD =x ,利用勾股定理列出关于x 的方程,求出方程的解得到x 的值,即为圆的半径,求出圆心角的度数,用Rt △ODB 的面积减去扇形DOF 的面积即可确定出阴影部分面积.【答案】解:(1)BC 与⊙O 相切. 证明:连接OD.∵AD 是∠BAC 的平分线, ∴∠BAD =∠CAD. 又∵OD=OA ,∴∠OAD =∠ODA,∴∠CAD =∠ODA,∴OD ∥AC , ∴∠ODB =∠C=90°,即OD⊥BC. 又∵BC 过半径OD 的外端点D , ∴BC 与⊙O 相切;(2)设OF =OD =x ,则OB =OF +BF =x +2,在Rt △BOD 中,由勾股定理得:OB 2=OD 2+BD 2,即(x +2)2=x 2+12, 解得:x =2,即OD =OF =2,∴OB =2+2=4.∵Rt △ODB 中,OD =12OB ,∴∠B =30°,∴∠DOB =60°,∴S 扇形DOF =60π×4360=2π3,∴S 阴影=S △ODB -S 扇形DOF =12×2×23-2π3=23-2π3.故阴影部分的面积为23-2π3.3.(2019襄阳中考)如图,AB 为⊙O 的直径,C ,D 为⊙O 上的两点,∠BAC =∠DAC,过点C 作直线EF⊥AD,交AD 的延长线于点E ,连接BC.(1)求证:EF 是⊙O 的切线;(2)若DE =1,BC =2,求劣弧BC ︵的长l. 解:(1)连接OC.∵OA =OC ,∴∠OAC =∠OCA. 又∵∠BAC=∠DAC,∴∠DAC =∠OCA,∴AD ∥OC. ∵EF ⊥AD ,∴EF ⊥OC , ∴EF 是⊙O 的切线; (2)连接OD ,DC.∵∠DAC =12∠DOC ,∠OAC =12∠BOC ,∵∠DAC =∠OAC.∴∠DOC =∠BOC,∴DC =BC.∵ED =1,DC =BC =2,∴sin ∠ECD =DE DC =12,∴∠ECD =30°,∴∠OCD =60°. ∵OC =OD ,∴△DOC 是等边三角形, ∴∠BOC =∠COD=60°,OC =2,∴l =60π×2180=2π3.【方法指导】熟练应用5个公式,关注与前面知识的综合应用.2019-2020学年数学中考模拟试卷一、选择题1.下列等式从左到右的变形,属于因式分解的是( ) A .8x 2 y 3=2x 2⋅4 y 3B .( x+1)( x ﹣1)=x 2﹣1C .3x ﹣3y ﹣1=3( x ﹣y )﹣1D .x 2﹣8x+16=( x ﹣4)22.如图,在Rt △ABC 中,∠C =90°,∠CBA =30°,AE 平分∠CAB 交BC 于D ,BE ⊥AE 于E ,给出下列结论:①BD =2CD ;②AE =3DE ;③AB =AC+BE ;④整个图形(不计图中字母)不是轴对称图形.其中正确的结论有( )A.1个B.2个C.3个D.4个3.如图所示,在菱形ABCD 中,∠BAD =70°,AB 的垂直平分线交对角线AC 于点F ,垂足为E ,连接DF ,则∠CDF 等于( )A .75°B .70°C .60°D .55°4.如图,正方形ABCD 内接于圆O ,4AB =,则图中阴影部分的面积是( ).A .416π-B .3216π-C .1632π-D .816π-5.如图,已知正方形ABCD 的边长为3cm ,若将这个正方形沿射线AD 方向平移2cm ,则平移前后图形的重叠部分面积为( )A.3cm2B.4.5cm2C.6cm2D.9cm26.下面的统计图表示某体校射击队甲、乙两名队员射击比赛的成绩,根据统计图中的信息,下列结论正确的是()A.甲队员成绩的平均数比乙队员的大B.乙队员成绩的平均数比甲队员的大C.甲队员成绩的中位数比乙队员的大D.甲队员成绩的方差比乙队员的大7.一组2、3、4、3、3的众数、中位数、方差分别是()A.4,3,0.2B.3,3,0.4C.3,4,0.2D.3,2,0.48.如图,在锐角ABC中,延长BC到点D,点O是AC边上的一个动点,过点O作直线MN BC,MN分别交ACB∠的平分线于E,F两点,连接AE、AF.在下列结论中.①∠、ACDCF=,则OC的长为6;④当AO CO=时,四边形CE=,5=;③若12OE OF=;②CE CFAECF是矩形.其中正确的是( )A.①④B.①②C.①②③D.②③④9.如图,△ABC中,下面说法正确的个数是()个.①若O是△ABC的外心,∠A=50°,则∠BOC=100°;②若O是△ABC的内心,∠A=50°,则∠BOC=115°;③若BC=6,AB+AC=10,则△ABC的面积的最大值是12;④△ABC的面积是12,周长是16,则其内切圆的半径是1.A.1 B.2 C.3 D.410.某赛季甲、乙两名篮球运动员各参加10场比赛,各场得分情况如图,下列四个结论中,正确的是()A.甲运动员得分的平均数小于乙运动员得分的平均数 B.甲运动员得分的中位数小于乙运动员得分的中位数C.甲运动员得分的最小值大于乙运动员得分的最小值 D.甲运动员得分的方差大于乙运动员得分的方差11.用直尺和圆规作Rt△ABC斜边AB上的高线CD,甲、乙两人的作法如图:根据两人的作法可判断()A.甲正确,乙错误B.乙正确,甲错误C.甲、乙均正确D.甲、乙均错误12.给出一种运算:对于函数y=x n,规定y'=n×x n﹣1.若函数y=x4,则有y'=4×x3,已知函数y=x3,则方程y'=6x的解是()A.x=2 B.x=3 C.x1=0,x2=2 D.x=﹣2二、填空题13.如图,当小明沿坡度i=1A到B行走了6米时,他实际上升的高度BC=______米.14.已知扇形所在圆半径为4,弧长为6π,则扇形面积为_____15.如图,在平面直角坐标系中,将点P(-4,2)绕原点顺时针旋转90°,求其对应点Q的坐标.16.分解因式:ax2﹣ax=_____.17.今年春节黄金周上海共接待游客约5090000人,5090000这个数用科学记数法表示为______.18.如图,直线a、b被直线c所截,a∥b,∠1=70°,则∠2=_____°.三、解答题19.如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.(1)求证:△AEC≌△ADB;(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.20.下面是两个转盘,每个转盘分成几个相等的扇形,甲、乙两个人做游戏,游戏者同时转动两个转盘一次,如果转盘A转出了红色,转盘B转出了蓝色,则甲赢否则乙赢.(1)甲和乙获胜的概率分别是多少?(2)这个游戏对双方公平吗?说说你的理由.(3)如果你认为不公平,应怎样修改才能使游戏对双方公平?21.如图1,P(m,n)在抛物线y=ax2-4ax(a>0)上,E为抛物线的顶点.(1)求点E的坐标(用含a的式子表示);(2)若点P在第一象限,线段OP交抛物线的对称轴于点C,过抛物线的顶点E作x轴的平行线DE,过点P作x轴的垂线交DE于点D,连接CD,求证:CD∥OE;(3)如图2,当a=1,且将图1中的抛物线向上平移3个单位,与x轴交于A、B两点,平移后的抛物线的顶点为Q,P是其x轴上方的对称轴上的动点,直线AP交抛物线于另一点D,分别过Q、D作x轴、y轴的平行线交于点E,且∠EPQ=2∠APQ,求点P的坐标.22.如图,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE、BF,交点为G.求证:AE⊥BF.23.某水果零售商店,通过对市场行情的调查,了解到两种水果销路比较好,一种是冰糖橙,一种是睡美人西瓜.通过两次订货购进情况分析发现,买40箱冰糖橙和15箱睡美人西瓜花去2000元,买20箱冰糖橙和30箱睡美人西瓜花去1900元.(1)请求出购进这两种水果每箱的价格是多少元?(2)该水果零售商在五一期间共购进了这两种水果200箱,冰糖橙每箱以40元价格出售,西瓜以每箱50元的价格出售,获得的利润为w元.设购进的冰糖橙箱数为a箱,求w关于a的函数关系式;(3)在条件(2)的销售情况下,但是每种水果进货箱数不少于30箱,西瓜的箱数不少于冰糖橙箱数的5倍,请你设计进货方案,并计算出该水果零售商店能获得的最大利润是多少?24.如图,△ABC是正方形网格图中的格点三角形(顶点在格点上),请分别在图1,图2的正方形网格内按下列要求画一个格点三角形.(1)在图1中,以AB为边画直角三角形△ABD(D与C不重合),使它与△ABC全等.(2)在图2中,以AB为边画直角三角形△ABE,使它的一个锐角等于∠B,且与△ABC不全等.25.在一次数学课上,李老师对大家说:“你任意想一个非零数,然后按下列步骤操作,我会直接说出你运算的最后结果.”操作步骤如下:第一步:计算这个数与1的和的平方,减去这个数与1的差的平方;第二步:把第一步得到的数乘以25;第三步:把第二步得到的数除以你想的这个数.(1)若小明同学心里想的是数8,请帮他计算出最后结果:[(8+1)2﹣(8﹣1)2]×25÷8(2)老师说:“同学们,无论你们心里想的是什么非零数,按照以上步骤进行操作,得到的最后结果都相等”小明同学想验证这个结论,于是,设心里想的数是a(a≠0),请你帮小明完成这个验证过程.【参考答案】***一、选择题二、填空题13.314.;15.点Q的坐标为(2,4).16.ax(x﹣1).17.09×10618.三、解答题19.(1)见解析;(2)BF=2.【解析】【分析】(1)由旋转的性质得到三角形ABC与三角形ADE全等,以及AB=AC,利用全等三角形对应边相等,对应角相等得到两对边相等,一对角相等,利用SAS 得到三角形AEC 与三角形ADB 全等即可; (2)根据∠BAC =45°,四边形ADFC 是菱形,得到∠DBA =∠BAC =45°,再由AB =AD ,得到三角形ABD 为等腰直角三角形,求出BD 的长,由BD ﹣DF 求出BF 的长即可. 【详解】解:(1)由旋转的性质得:△ABC ≌△ADE ,且AB =AC , ∴AE =AD ,AC =AB ,∠BAC =∠DAE ,∴∠BAC+∠BAE =∠DAE+∠BAE ,即∠CAE =∠DAB , 在△AEC 和△ADB 中,AE AD CAE DAB AC AB =⎧⎪∠=∠⎨⎪=⎩, ∴△AEC ≌△ADB (SAS );(2)∵四边形ADFC 是菱形,且∠BAC =45°, ∴∠DBA =∠BAC =45°, 由(1)得:AB =AD , ∴∠DBA =∠BDA =45°,∴△ABD 为直角边为2的等腰直角三角形, ∴BD 2=2AB 2,即BD =, ∴AD =DF =FC =AC =AB =2, ∴BF =BD ﹣DF =﹣2. 【点睛】此题考查了旋转的性质,全等三角形的判定与性质,以及菱形的性质,熟练掌握旋转的性质是解本题的关键. 20.(1)1625,925 ;(2)不公平,理由见解析;(3)两次都转蓝色,甲赢;两次都转红色,乙赢.【解析】 【分析】(1)根据题意,用列表法将所有可能出现的结果,再根据概率公式计算可得; (2)由(1)的结果,判断两人获胜的概率是否相等,得到结论不公平. (3)只要使甲、乙获胜的概率相等即可. 【详解】解:(1)列表如下:由表知,共有25种等可能结果,其中转盘A转出了红色,转盘B转出了蓝色有16种结果,∴甲获胜的概率为16 25,则乙获胜的概率为925;(2)不公平,因为1625≠925;(3)两次都转蓝色,甲赢;两次都转红色,乙赢.【点睛】此题考查的是用列表法或树状图法求概率.注意画树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件.21.(1) E(2,﹣4a);(2)见解析;(3) P(2+1).【解析】【分析】(1)将原式提取公因式然后化简即可解答(2)设直线OE的解析式为:y=k x,把E点代入可得直线OE的解析式为:y=﹣2ax,由P(m,n)得直线OP的解析式为:y=nxm,得到C(2,2nm),然后设直线CD的解析式为:y=kx+b,得到:k=﹣2a,即可解答(3)当a=1时,抛物线解析式为:y=x2﹣4x,向上平移3个单位得新的抛物线解析式为:y=x2﹣4x+3=(x﹣2)2﹣1,然后设P(2,t),可得AP的解析式为:y=tx﹣t,D(3+t,t2+2t),Q(2,﹣1),E(3+t,﹣1),再设PE交x轴于F,即可解答【详解】解:(1)y=ax2﹣4ax=a(x2﹣4x+4﹣4)=a(x﹣2)2﹣4a,∴E(2,﹣4a);(2)设直线OE的解析式为:y=kx,把E(2,﹣4a)代入得:2k=﹣4a,k=﹣2a,∴直线OE 的解析式为:y =﹣2ax , 由P (m ,n )得直线OP 的解析式为:y =nxm, ∴当x =2时,y =2n m ,即C (2,2n m), ∵D (m ,﹣4a ),设直线CD 的解析式为:y =kx+b ,将点D 和C 的坐标代入得:422km b an k b m +=-⎧⎪⎨+=⎪⎩(n =am 2﹣4am ), 解得:k =﹣2a , 根据两直线系数相等, ∴OE ∥CD ;(3)如图2,当a =1时,抛物线解析式为:y =x 2﹣4x ,向上平移3个单位得新的抛物线解析式为:y =x 2﹣4x+3=(x ﹣2)2﹣1, ∴Q (2,﹣1),A (1,0),B (3,0), 设P (2,t ),可得AP 的解析式为:y =tx ﹣t ,联立方程组为:243y tx ty x x =-⎧⎨=-+⎩ ,解得:1110x y =⎧⎨=⎩ ,22232x ty t t =+⎧⎪⎨=+⎪⎩ , ∴D (3+t ,t 2+2t ), ∵Q (2,﹣1), ∴E (3+t ,﹣1), ∴PQ =QE =t+1, ∴∠EPQ =45°, ∵∠EPQ =2∠APQ , ∴∠APQ =22.5°, 设PE 交x 轴于F , ∵∠DEP =45°, ∴ME =FM =1,∴∠FPA =∠PAF =67.5°, ∴PF =AF =t+1, ∵FP,t =t+1,t+1,∴P(2+1).【点睛】此题为二次函数综合题,需要熟练掌握运算方法22.证明见解析【解析】【分析】由E,F分别是正方形ABCD边BC,CD的中点知CF=BE,证Rt△ABE≌Rt△BCF得∠BAE=∠CBF,根据∠BAE+∠BEA=90°即可得∠CBF+∠BEA=90°,据此即可得证.【详解】证明:∵E,F分别是正方形ABCD边BC,CD的中点,∴CF=BE,在Rt△ABE和Rt△BCF中,∵AB BCABE BCF BE CF=⎧⎪∠=∠⎨⎪=⎩,∴Rt△ABE≌Rt△BCF(SAS),∴∠BAE=∠CBF,又∵∠BAE+∠BEA=90°,∴∠CBF+∠BEA=90°,∴∠BGE=90°,∴AE⊥BF.【点睛】本题主要考查正方形的性质,全等三角形的的判定与性质,解题的关键是掌握正方形的性质与全等三角形的判定与性质.23.(1)每箱冰糖橙进价为35元,每箱睡美人西瓜进价为40元;(2)w=﹣5a+2000;(3)当购买冰糖橙30箱,则购买睡美人西瓜170箱该水果零售商店能获得的最大利润,最大利润为1850元.【解析】【分析】(1)设每箱冰糖橙x元,每箱睡美人西瓜y元,根据“买40箱冰糖橙和15箱睡美人西瓜花去2000元,买20箱冰糖橙和30箱睡美人西瓜花去1900元”列出方程组并解答;(2)根据(1)的结论以及“利润=售价﹣成本”解答即可;(3)设购买冰糖橙a箱,则购买睡美人西瓜为(200﹣a)箱,根据“每种水果进货箱数不少于30箱,西瓜的箱数不少于冰糖橙箱数的5倍”列出不等式并求得a的取值范围,再根据一次函数的性质解答即可.【详解】(1)设每箱冰糖橙进价为x元,每箱睡美人西瓜进价为y元,由题意,得40152000 20301900x yx y+=⎧⎨+=⎩,解得:3540 xy=⎧⎨=⎩,即设每箱冰糖橙进价为35元,每箱睡美人西瓜进价为40元;(2)根据题意得,w=(40﹣35)a+(50﹣40)(200﹣a)=﹣5a+2000;(3)设购买冰糖橙a箱,则购买睡美人西瓜为(200﹣a)箱,则200﹣a≥5a且a≥30,解得30≤a1 333≤,由(2)得w=﹣5a+2000,∵﹣5,w随a的增大而减小,∴当a=30时,y最大.即当a=30时,w最大=﹣5×30+2000=1850(元).答:当购买冰糖橙30箱,则购买睡美人西瓜170箱该水果零售商店能获得的最大利润,最大利润为1850元.【点睛】本题考查了一次函数的应用和二元一次方程组的应用.解决问题的关键是读懂题意,找到关键描述语,进而找到所求的量的等量关系和不等关系.24.(1)详见解析;(2)详见解析.【解析】【分析】(1)如图1,根据三边对应相等的两三角形全等作图即可;(2)根据三组对应边成比例的两个三角形相似作图.【详解】解:(1)如图1,∴△ACD为所求;(2)如图2,∴△ABD为所求.【点睛】本题考查了作图﹣应用与设计作图:应用与设计作图主要把简单作图放入实际问题中.首先要理解题意,弄清问题中对所作图形的要求,结合对应几何图形的性质和基本作图的方法作图.此题灵活应用相似三角形的判定与性质.25.(1)100;(2)100.【解析】【分析】(1)原式先计算括号中的乘方运算,再计算减法运算,最后算乘除运算即可求出值;(2)列出代数式,计算即可得到结果.【详解】解:(1)原式=(81﹣49)×25÷8=800÷8=100;(2)根据题意得:[(a+1)2﹣(a﹣1)2]×25÷a=4a×25÷a=100.【点睛】此题考查了完全平方公式,熟练掌握完全平方公式是解本题的关键.2019-2020学年数学中考模拟试卷一、选择题1.下列一元二次方程有两个不相等的实数根的是( ) A.2(1)20x ++= B.2251010x x -+= C.230x x -=D.230x -+=2.如图,一块直角三角板和一张光盘竖放在桌面上,其中A 是光盘与桌面的切点,∠BAC =60°,光盘的直径是80cm ,则斜边AB 被光盘截得的线段AD 长为( )A.20cmB.40cmC.80cmD.80cm3.将抛物线向左平移1个单位,再向下平移3个单位得到的解析式是( ).A.B.C.D.4.不等式组21331563x x x +≥-⎧⎪-⎨--⎪⎩>的解集在数轴上表示正确的是( )A .B .C .D .5.如图,AB 是⊙O 的直径,C 是⊙O 上一点,OD ⊥BC 于点D ,AC =4,则OD 的长为( )A.1B.1.5C.2D.2.56.下列交通标志是中心对称图形的为( )A .B .C .D .7.如图是由几个相同的小正方体组成的立体图形的俯视图,图上的数字表示该位置上小正方体的个数,这个立体图形的左视图是()A.B. C. D.8.数据2、5、6、0、6、1、8的中位数是()A.8 B.6 C.5 D.09.港珠澳大桥是中国境内一座连接着香港、珠海和澳门的桥隧工程,工程投资总额1269亿元,1269亿用科学记数法表示为()A.1.269×1010B.1.269×1011C.12.69×1010D.0.1269×101210.分式方程1232x x=-的解为()A.25x=-B.1x=-C.1x=D.25x=11.已知Rt△ABC的三边长为a,4,5,则a的值是()A.3 C.3 D.9或4112.1纳米=10-9米,将50纳米用科学记数法表示为()A.50×10-9米B.5×10-9米C.0.5×10-9米D.5×10-8米二、填空题13.将5700 000用科学记数法表示为______.14.如图,在平面直角坐标系xoy中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B、C在反比例函数3(0)y xx=>的图象上,则△OAB的面积等于_____ .15在实数范围内有意义,则x的取值范围是_____.16.如图,AB∥CD,若∠E=34°,∠D=20°,则∠B的度数为_____.17.如图,直线m∥n,Rt△ABC的顶点A在直线n上,∠C=90°,若∠1=25°,∠2=75°,则∠B=_____.18.若分式12x有意义,则x的取值范围为_____.三、解答题19.如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.(1)求证:△AEC≌△ADB;(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.20.我们约定,在平面直角坐标系中两条抛物线有且只有一个交点时,我们称这两条抛物线为“共点抛物线”,这个交点为“共点”.(1)判断抛物线y=x2与y=﹣x2是“共点抛物线”吗?如果是,直接写出“共点”坐标;如果不是,说明理由;(2)抛物线y=x2﹣2x与y=x2﹣2mx﹣3是“共点抛物线”,且“共点”在x轴上,求抛物线y=x2﹣2mx﹣3的函数关系式;(3)抛物线L1:y=﹣x2+2x+1的图象如图所示,L1与L2:y=﹣2x2+mx是“共点抛物线”;①求m的值;②点P是x轴负半轴上一点,设抛物线L1、L2的“共点”为Q,作点P关于点Q的对称点P′,以PP′为对角线作正方形PMP′N,当点M或点N落在抛物线L1上时,直接写出点P的坐标.21.如图,直线y=x+b与双曲线y=kx(k为常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.(1)求直线和双曲线的解析式;(2)点P在x轴上,且△BCP的面积等于2,求P点的坐标.22.从共享单车,共享汽车等共享出行到共享雨伞等共享物品,各式各样的共享经济模式在各个领域迅速的普及,根据国家信息中心发布的中国分享经济发展报告2017显示,参与共享经济活动超6 亿人,比上一年增加约1亿人.(1)为获得北京市市民参与共享经济活动信息,下列调查方式中比较合理的是;A.对某学校的全体同学进行问卷调查B.对某小区的住户进行问卷调查C.在全市里的不同区县,选取部分市民进行问卷调查(2)调查小组随机调查了延庆区市民骑共享单车情况,某社区年龄在12~36岁的人有1000人,从中随机抽取了100人,统计了他们骑共享单车的人数,并绘制了如下不完整的统计图表.如图所示.骑共享单车的人数统计表根据以上信息解答下列问题:①统计表中的a=;b=;②补全频数分布直方图;③试估计这个社区年龄在20岁到32岁(含20岁,不含32岁)骑共享单车的人有多少人?23.如图,已知AB是⊙P的直径,点C在⊙P上,D为⊙P外一点,且∠ADC=90°,2∠B+∠DAB=180°.(1)证明:直线CD为⊙P的切线;(2)若DC=,AD=4,求⊙P的半径.24.家访是学校与家庭沟通的有效渠道,是形成教育合力的关键,是转化后进生的催化剂.某市教育局组织全市中小学教师开展家访活动活动过程中,教育局随机抽取了部分教师调查其近两周家访次数,将采集到的数据按家访次数分成五类,并分别绘制了下面的两幅不完整的统计图.请根据以上信息,解答下列问题:(1)请把条形统计图补充完整;(2)所抽取的教师中,近两周家访次数的众数是次,平均每位教师家访次;(3)若该市有12000名教师,请估计近两周家访不少于3次的教师有多少名?25.合肥合家福超市为了吸引顾客,设计了一种促销活动:在三等分的转盘上依次标有“合”,“家”,“福”字样,购物每满200元可以转动转盘1次,转盘停下后,指针所指区域是“福”时,便可得到30元购物券(指针落在分界线上不计次数,可重新转动一次),一个顾客刚好消费400元,并参加促销活动,转了2次转盘.(1)求出该顾客可能获得购物券的最高金额和最低金额;(2)请用画树状图法或列表法求出该顾客获购物券金额不低于30元的概率.【参考答案】***一、选择题二、填空题13.7×106.14.9 215.x≥﹣116.54°17.40°18.x≠2.三、解答题19.(1)见解析;(2)BF=2.【解析】【分析】(1)由旋转的性质得到三角形ABC与三角形ADE全等,以及AB=AC,利用全等三角形对应边相等,对应角相等得到两对边相等,一对角相等,利用SAS得到三角形AEC与三角形ADB全等即可;(2)根据∠BAC=45°,四边形ADFC是菱形,得到∠DBA=∠BAC=45°,再由AB=AD,得到三角形ABD为等腰直角三角形,求出BD的长,由BD﹣DF求出BF的长即可.【详解】解:(1)由旋转的性质得:△ABC≌△ADE,且AB=AC,∴AE=AD,AC=AB,∠BAC=∠DAE,∴∠BAC+∠BAE=∠DAE+∠BAE,即∠CAE=∠DAB,在△AEC和△ADB中,AE AD CAE DAB AC AB =⎧⎪∠=∠⎨⎪=⎩,∴△AEC ≌△ADB (SAS );(2)∵四边形ADFC 是菱形,且∠BAC =45°,∴∠DBA =∠BAC =45°,由(1)得:AB =AD ,∴∠DBA =∠BDA =45°,∴△ABD 为直角边为2的等腰直角三角形,∴BD 2=2AB 2,即BD =,∴AD =DF =FC =AC =AB =2,∴BF =BD ﹣DF =﹣2.【点睛】此题考查了旋转的性质,全等三角形的判定与性质,以及菱形的性质,熟练掌握旋转的性质是解本题的关键.20.(1)是,(0,0);(2)2132y x x =--;(3)①m 的值为0或4,②P (﹣3,0)或P (﹣5,0)或P (﹣13,0).【解析】【分析】(1)解方程x 2=﹣x 2得出x =0(2)因为两个抛物线的共点在x 轴上,y =0代入L1中求得交点坐标,分别代入L2中,求得m 的值,获得抛物线的解析式.(3)①两抛物线为共点抛物线时,只有一个交点,运用判别式为零,求出m 的值②设点P 坐标(a ,0),通过Q 点坐标,获得P'点坐标,因为PP'为正方形,利用K 型全等模型建立全等关系,从而求出点M 和N 的坐标,将M 、N 分别代入解析式,获得a 的值,从而求出点P 的坐标.【详解】解:(1)是,(0,0)x 2=﹣x 2∴x =0(2)令y =x 2﹣2x =0解得x 1=0,x 2=2当x =0时,﹣3≠0∴(0,0)不是共点当x =2时,4﹣4m ﹣3=0解得m =14 ∴y =2132x x -- (3)①若两个抛物线是“共点抛物线”则方程﹣x 2+2x+1=﹣2x 2+mx 有两个相等的实数根即x 2+(2﹣m )x+1=0有两个相等的实数根∴△=(2﹣m )2﹣4=0解得m =0或m =4∴m 的值为0或4.②P (﹣3,0)或P (﹣5,0)或P (﹣13,0)设点P (a ,0)当m =0时,Q (﹣1,﹣2)∴P'(﹣2﹣a ,﹣4)∵PM =MP',∠A =∠B ,∠AMP =∠BP'M∴△APM ≌△BMP'(AAS )设M (x ,y ),N (a ,b )42y x a a x y +=-⎧⎨---=⎩解得13x y a =⎧⎨=--⎩24a m n n m a ---=-⎧⎨--=-⎩解得31m n a =-⎧⎨=-⎩∴可得M (1,﹣3﹣a ),N (﹣3,a ﹣1)分别代入L 1解析式可得a 1=﹣5,a 2=﹣13当m =4时,Q (1,2)∴P'(2﹣a ,4)∵PM =MP',∠A =∠B ,∠AMP =∠BP'M∴△APM ≌△BMP'(AAS )设M (m ,n )N (x ,y )240a m n n a --=⎧⎨-=-⎩解得24m n a=-⎧⎨=-⎩ 24a x y y x a --=-⎧⎨-=-⎩解得31x y a =⎧⎨=+⎩∴可得M (﹣2,4﹣a ),N (3,1+a )分别代入L 1解析式可得a 1=﹣3,a 2=11(舍)∴P (﹣3,0)或P (﹣5,0)或P (﹣13,0)【点睛】本题考查了全等模型和抛物线的交点问题,难度适中,难点在于(3)②,需要根据正方形建立K 型全等,从而获得参数a 的值,是一道很好的压轴问题.21.(1)y =2x ;y =x+1;(2)P 点的坐标为(3,0)或(﹣5,0). 【解析】【分析】(1)把A (1,2)代入双曲线以及直线y =x+b ,分别可得k ,b 的值;(2)先根据直线解析式得到BO =CO =1,再根据△BCP 的面积等于2,即可得到P 的坐标.【详解】解:(1)把A (1,2)代入双曲线y =k x ,可得k =2, ∴双曲线的解析式为y =2x; 把A (1,2)代入直线y =x+b ,可得b =1,∴直线的解析式为y =x+1;(2)设P 点的坐标为(x ,0),在y =x+1中,令y =0,则x =﹣1;令x =0,则y =1,∴B(﹣1,0),C(0,1),即BO=1=CO,∵△BCP的面积等于2,∴12BP×CO=2,即12|x﹣(﹣1)|×1=2,解得x=3或﹣5,∴P点的坐标为(3,0)或(﹣5,0).【点睛】本题主要考查了反比例函数与一次函数交点问题,解题时注意:反比例函数与一次函数交点的坐标同时满足两个函数解析式.22.(1)C;(2)①0.15,30;②见解析;③估计这个社区年龄在20岁到32岁(含20岁,不含32岁)骑共享单车的人有700人.【解析】【分析】(1)根据抽样调查的定义可得;(2)①根据“频率=频数÷总数”可分别求得a、b的值;②由①中所求数据可补全图形;③总人数乘以样本中第3、4、5组的频率之和可得答案.【详解】解:(1)调查方式中比较合理的是C,故答案为:C;(2)①a=15÷100=0.15,b=100×0.3=30,故答案为:0.15,30;②补全图形如下:③1000×(0.15+0.25+0.3)=700(人),答:估计这个社区年龄在20岁到32岁(含20岁,不含32岁)骑共享单车的人有700人.【点睛】本题考查条形图、频率分布表、样本估计总体等知识,解题的关键是记住频率=频数÷总数,频率之和为1,属于中考常考题型.23.(1)证明见解析;(2)⊙P的半径为5.【解析】【分析】(1)连接PC,则∠APC=2∠B,可证PC∥DA,证得PC⊥CD,则结论得证;(2)连接AC,先求出AC长,可证△ADC∽△ACB,可求出AB长,则⊙P的半径可求出.【详解】(1)连接PC,∵PC=PB,∴∠B=∠PCB,∴∠APC=2∠B,∵2∠B+∠DAB=180°,∴∠DAC+∠ACP=180°,∴PC∥DA,∵∠ADC=90°,∴∠DCP=90°,即DC⊥CP,∴直线CD为⊙P的切线;(2)连接AC,∵DC=AD=4,∠ADC=90°,∴AC===,∵AP=CP,∴∠PAC=∠ACP,∵AD∥PC,∴∠DAC=∠ACP,∴∠PAC=∠DAC,∵AB是⊙P的直径,∴∠BCA=90°,∴∠BCA=∠ADC,∴△ADC∽△ACB,∴AB AC AC AD=,=∴AB=10,∴⊙P的半径为5.【点睛】本题考查切线的判定、圆周角定理、勾股定理、相似三角形的判定与性质等知识,解题的关键是灵活应用这些知识解决问题.24.(1)补图见解析;(2)3,3.24;(3)9120名.【解析】【分析】(1)家访总人数:54÷36%=150(人),家访4次的人数:150×28%=42(人),家访2次的人数:150﹣6﹣54﹣42﹣18=30(人);(2)根据统计图可知,家访3次的人数最多,所以众数为3,平均每位教师家访:(6×1+30×2+54×3+42×4+18×5)÷150=3.24(次);(3)近两周家访不少于3次的教师有12000×544218150++=9120(名).【详解】解:(1)家访总人数:54÷36%=150(人),家访4次的人数:150×28%=42(人)家访2次的人数:150﹣6﹣54﹣42﹣18=30(人)条形统计图补全如下:(2)根据统计图可知,家访3次的人数最多,所以众数为3,平均每位教师家访:(6×1+30×2+54×3+42×4+18×5)÷150=3.24(次),故答案为3,3.24;(3)近两周家访不少于3次的教师有12000×544218150++=9120(名).【点睛】本题考查了统计图与概率,熟练掌握条形统计图与扇形统计图是解题的关键.25.(1)最高金额为60元、最低金额为0元;(2)5 9【解析】【分析】(1)两次都抽到“福”时可得最高金额,两次都没有抽到“福”时可得最低金额;(2)画出树状图,利用概率公式计算即可;【详解】解:(1)根据题意,该顾客可能获得购物券的最高金额为60元、最低金额为0元;(2)画树状图如下:由树状图知,共有9种等可能结果,其中该顾客获购物券金额不低于30元的有5种结果,所以该顾客获购物券金额不低于30元的概率为59.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第25讲 与圆有关的计算命题点近8年的命题形式考查方向扇形弧长、面积的计算2018(T 25(1)解),2017(T 23(2)解、T 25(3)解),2016(T 25解),2015(T 26解),2014(T 19填),2013(T 14选)题型呈现形式比较丰富,选择题、高频考点填空题、解答题三种题型都有出现,弧长的考查侧重于对弧长公式的考查,计算较简单,扇形面积的考查侧重在动态变化过程中形成的区域面积,可用多种方法进行尝试转化成求扇形面积.正多边形与圆2014(T 15选)侧重于有关正多边形面积的计算,一般都有技巧性,需要我们熟练掌握正多边形的各个量之间的关系,并能把正多边形进行分割与拼接.命题点1 扇形弧长、面积的计算1.(2013·河北T14·3分)如图,AB 是⊙O 的直径,弦CD ⊥AB ,∠C =30°,CD =2.则S 阴影=(D)3A .π B .2π C. D.π233232.(2014·河北T19·3分)如图,将长为8 cm 的铁丝首尾相接围成半径为2 cm 的扇形.则S 扇形=4cm 2.命题点2 正多边形与圆3.(2014·河北T15·3分)如图,边长为a 的正六边形内有两个三角形(数据如图),则=(C)S 阴影S 空白A .3 B .4 C .5 D .6重难点1 弧长的计算 如图,△ABC 是正三角形,曲线CDEFG…叫做“正三角形的渐开线”,曲线的各部分为圆弧.(1)图中已经有4段圆弧,请接着画出第5段圆弧GH ;(2)设△ABC 的边长为a ,则第1段弧的长是;第5段弧的长是;前5段弧长的和(即曲线CDEFGH 的2πa 310πa3长)是10πa ;(3)类似地有“正方形的渐开线”“正五边形的渐开线”…,边长为a 的正方形的渐开线的前5段弧长的和是;15πa 2(4)猜想:①边长为a 的正n 边形的前5段弧长的和是;30πan ②边长为a 的正n 边形的前m 段弧长的和是.m (m +1)πan 【思路点拨】 (1)以点B 为圆心,BG 长为半径画弧即可;(2)利用弧长公式计算.但要先确定弧所对的圆心角都是120度,半径却在不断地增大,第1段弧的半径是a ,第2段弧的半径是2a ,第3段弧的半径是3a ,依此下去第5段弧的半径是5a ,总和就是把五段弧长加起来;(3)先利用正方形的性质求出正方形的外角度数,结合每段弧所在圆的半径变化规律,利用弧长公式计算每段弧长,最后求和;(4)可以利用前面的探究方法,结合正n 边形的性质解决.【变式训练1】 (2018·淄博)如图,⊙O 的直径AB =6.若∠BAC=50°,则劣弧AC 的长为(D )A .2πB .C .D .8π33π44π3【变式训练2】 (2018·廊坊模拟)如图,在边长为6的菱形ABCD 中,分别以各顶点为圆心,以边长的一半为半径,在菱形内作四条圆弧,则图中阴影部分的周长是6π.(结果保留π)方法指导1.求弧长,要先确定两个要素,一是弧所在圆的半径,二是弧所在扇形的圆心角,再代入弧长公式计算即可.2.同一正多边形的渐开线每部分弧所对的圆心角不变,半径后一段比相邻的前一段增加一个正多边形的边长.边长为a 的正n 边形的渐开线第m 段弧长为.模型建立2π×man 重难点2 扇形面积的有关计算 如图1,直径AB 为6的半圆,绕点A 逆时针旋转60°,此时点B 到达点B′,求圆中阴影部分的面积.图1 图2 图3【变式1】 (2018·大庆)如图2,在Rt △ABC 中,∠ACB=90°,AC =BC =2,将Rt △ABC 绕点A 逆时针旋转30°后得到Rt △ADE,点B 经过的路径为弧BD ,则图中阴影部分的面积为π.23【变式2】 如图3,在Rt △ABC 中,∠ACB=90°,AC =1,∠ABC=30°,将Rt △ABC 绕A 点逆时针旋转30°后得到Rt △ADE,点B 经过的路径为弧BD ,则图中阴影部分的面积是π.13【变式3】 如图4,在△ABC 中,AB =6,将△ABC 绕点B 顺时针旋转60°后得到△DBE,点A 经过的路径为弧AD ,则图中阴影部分的面积是6π.图4 图5【变式4】 如图5,在Rt △ABC 中,∠ACB=90°,BC =1,将Rt △ABC 绕点C 顺时针旋转60°,此时点B 恰好在DE 上,其中点A 经过的路径为弧AD ,则图中阴影部分的面积是-.(注:所有小题结果保留π)π234【思路点拨】 阴影部分的面积可以看作以旋转点为圆心,旋转角为圆心角,AB 为半径的扇形面积;只有变式4阴影部分的面积是S 扇形ACD -S △BCE .【自主解答】 解:∵AB=AB′=6,∠BAB′=60°,∴S 阴影=S 扇形B′AB +S 半圆O′-S 半圆O =S 扇形B′AB =×π×62=6π.60360在圆中求阴影部分面积大致有以下方法:方法指导(1)弓形或弓形的一部分可转化成扇形减去三角形的面积;(2)新月形可以用扇形减去一个弓形的面积;(3)可以利用等积变换求阴影部分的面积;(4)可以利用轴对称、中心对称求阴影部分的面积;(5)旋转形成阴影部分的面积,往往可以转化成求一个扇形的面积.重难点3 正多边形和圆 (2017·河北模拟)如图是由有两个公共顶点的正六边形与正方形组成的一个图形.若阴影部分的周长为10,则这个图形的外轮廓线的周长为(A )A .18B .18C .22D .2233【思路点拨】 从图形上能看出,正方形的边长等于正六边形边长的2倍.提示:设正六边形的边长为a ,则正方形的边长为2a ,由题意,得5a =10,解得a =2.则外轮廓线的周长为3a +2a×3=9a =18.【变式训练3】 (2017·河北模拟)如图,正六边形与正方形有重合的中心O.若∠BOC 是正n 边形的一个外角,则n 的值为(C )A .8B .10C .12D .16【变式训练4】 (2018·石家庄二模)正六边形ABCDEF 与正三角形△ACG 按如图所示位置摆放,在六边形AGCDEF中,的值是(D )S 阴影S 空白A . B . C . D .25151617方法指导1.熟悉常见正多边形边长与对角线的数量关系.2.正n 边形的中心角与每一个外角相等,都等于(n≥3).360°n 3.研究面积相关问题时可采用割补与拼接等方法,研究周长可采用化曲为直等方法.注:正多边形与圆中,正多边形通常是指正方形,正五边形,正六边形,正八边形等常见的正多边形.1.(2018·盘锦)如图,一段公路的转弯处是一段圆弧(),则的展直长度为(B )AB ︵ AB︵ A .3π m B .6π m C .9π m D .12π m2.(2018·成都)如图,在▱ABCD 中,∠B=60°,⊙C 的半径为3,则图中阴影部分的面积是(C )A .πB .2πC .3πD .6π3.(2018·德州)如图,从一块直径为2 m 的圆形铁皮上剪出一个圆心角为90°的扇形,则此扇形的面积为(A )A . m 2B .π m 2C .π m 2D .2π m 2π2324.(2018·河北模拟)如图,分别把正六边形边AB ,EF ,CD 向两个方向延长,相交于点M ,N ,Q ,则阴影部分与空白部分的面积比为(A )A .B .C .D .121325145.(2018·河北模拟)如图,六边形ABCDEF 和六边形MNPQGH 都是正六边形.若AB =10,则MN 的值可能是(D )A .B .5C .5D .5532236.(2018·株洲)如图,正五边形ABCDE 和正三角形AMN 都是⊙O 的内接多边形,则∠BOM=48°.7.(2018·石家庄藁城区模拟)如图,M ,N 分别是正五边形ABCDE 的边AB ,AE 的中点,四边形MNHG 是位于该正五边形内的正方形,则∠BMH 的度数是99°.8.(2018·盐城)如图,图1是由若干个相同的图形(图2)组成的美丽图案的一部分,图2中图形的相关数据:半径OA =2 cm ,∠AOB=120°.则图2的图形周长为cm (结果保留π).8π39.(2018·河南)如图,在△ABC 中,∠ACB=90°,AC =BC =2,将△ABC 绕AC 的中点D 逆时针旋转90°得到△A′B′C′,其中点B 的运动路径为,则图中阴影部分的面积为π-.BB ′︵543210.(2018·邢台宁晋县模拟)如图,半圆O 的直径AB =4,P ,Q 是半圆O 上的点,弦PQ 的长为2,则与的长AP ︵ QB︵ 度之和为(B )A .πB .πC .πD .π234353提示:连接OP ,OQ ,易知△OPQ 为等边三角形,l +l =×π×2=π.AP ︵ QB︵ 1201804311.(2018·威海)如图,在正方形ABCD 中,AB =12,点E 为BC 的中点,以CD 为直径作半圆CFD ,点F 为半圆的中点,连接AF ,EF ,则图中阴影部分的面积是(C )A .18+36πB .24+18πC .18+18πD .12+18π提示:作FH⊥BC 交BC 延长线于点H ,连接AE ,S 阴影=S 正方形ABCD +S 半圆-S △ABE -S △AEF =12×12+×π×62-×12×6-×6×6=18+18π.1212125512.(2018·河北模拟)如图,点P 是⊙O 外一点,PA 切⊙O 于点A ,AB 是⊙O 的直径,连接OP ,过点B 作BC∥OP 交⊙O 于点C ,连接AC 交OP 于点D.(1)求证:PC 是⊙O 的切线;(2)若PD = cm ,AC =8 cm ,则图中阴影部分的面积为 cm 2;16325π-482(3)在(2)的条件下,若点E 是的中点,连接CE ,求CE 的长.AB︵解:(1)证明:连接OC ,∵PA 切⊙O 于点A ,∴∠PAO=90°.∵OP∥BC,∴∠AOP=∠OBC,∠COP=∠OCB.∵OC=OB ,∴∠OBC=∠OCB.∴∠AOP=∠COP.在△PAO 和△PCO 中,{OA =OC ,∠AOP =∠COP ,OP =OP ,)∴△PAO≌△PCO(SAS ).∴∠PAO=∠PCO=90°.又∵OC 是⊙O 的半径,∴PC 是⊙O 的切线.(3)连接AE ,BE ,过点B 作BM⊥CE 于点M ,∴∠CMB=∠EMB=90°,∠AEB=90°.又∵点E 是的中点,∴=.AB ︵ AE ︵ BE︵ ∴∠ECB=∠ACE=∠ACB=45°.12又∵∠CMB=90°,∴∠CBM=45°.∴BM=CM.在Rt △BCM 中,由勾股定理,得CM 2+BM 2=BC 2,即CM 2+BM 2=36,∴CM=BM =3 cm .2 又∵∠ABE=∠ACE=45°,∴在Rt △AEB 中,BE =AB·cos ∠ABE=5 cm .2在Rt △BEM 中,由勾股定理,得EM ===4(cm ),BE2-BM2(52)2-(32)22∴CE=CM +EM =7 cm ,2即CE 的长为7 cm .213.(2018·宜宾)刘徽是中国古代卓越的数学家之一,他在《九章算术》中提出了“割圆术”,即用内接或外切正多边形逐步逼近圆来近似计算圆的面积,设圆O 的半径为1.若用圆O 的外切正六边形的面积来近似估计圆O 的面积,则S =2.(结果保留根号)3。
