2011年考研数学《概率统计》讲义第五讲
考研数学概率统计讲义

设售出一台设备的净赢利为
a( X
)
100, 200,
X 1, 0 X 1.
河南理工大学精品课程
概率论与数理统计
故售出一台设备的净赢利的数学期望为
E[a(X )] a(x) f (x)dx
1
(200)
1 4
e
x 4
dx
100
1 4
e
x 4
dx
0
1
200e
x 4
|10
100e
x 4
|1
Z X 2 Y 2 的数学期望.
解 E(Z ) x2 y2 f (x, y)dxdy
x2 y2
1
x2 y2
e 2 dxdy
2
2
0
0
r
1
2
r2
e2
rdr d
2
例6 五个独立元件,寿命分别为X1, X 2, , X5,
都服从参数为 的指数分布,若将它们
(1) 串联; (2) 并联 成整机,求整机寿命的均值.
求E(X)。 0,
其它.
分段函
〖解〗这是连续型随机数变的量积。由数学期望定义得:
分
1500
3000
E(X ) xf (x)dx
x2 15002
dx
dx x (3000 x ) 15002
0
1500
1500 (分□)
河南理工大学精品课程
概率论与数理统计
例4 X ~ N ( , 2 ), 求 E ( X ) .
2
k pk .
k 0
这表明:随着试验次数增大,随机变量X的观察值的算
术平均 2 k ak 接近于
k0 N
王式安考研概率讲义

概率统计第一讲随机事件和概率考试要求:数学一、三、四要求一致。
了解:样本空间的概念理解:随机事件,概率,条件概率,事件独立性,独立重复试验掌握:事件的关系与运算,概率的基本性质,五大公式(加法、减法、乘法、全概率、贝叶斯),独立性计算,独立重复试验就算会计算:古典概率和几何型概率。
§1 随机事件与样本空间一、随机试验:E(1)可重复(2)知道所有可能结果(3)无法预知二、样本空间试验的每一可能结果——样本点ω所有样本点全体——样本空间Ω三、随机事件样本空间的子集——随机事件A B C样本点——基本事件,随机事件由基本事件组成。
如果一次试验结果,某一基本事件ω出现——ω发生,ω出现如果组成事件A的基本事件出现——A发生,A出现Ω——必然事件Φ——不可能事件§2 事件间的关系与运算一.事件间关系包含,相等,互斥,对立,完全事件组,独立 二.事件间的运算: 并,交,差运算规律:交换律,结合律,分配律,对偶律 概率定义,集合定义,记号,称法,图 三.事件的文字叙述与符号表示例2 从一批产品中每次一件抽取三次,用(1,2,3)i A i =表示事件:“第i 次抽取到的是正品”试用文字叙述下列事件: (1)122313A A A A A A ; (2)123A A A ;(3)123A A A ; (4)123123123A A A A A A A A A ;再用123,,A A A 表示下列事件:(5)都取到正品; (6)至少有一件次品; (7)只有一件次品; (8)取到次品不多于一件。
§3 概率、条件概率、事件独立性、五大公式一.公理化定义 ,,A P Ω (1)()0P A ≥ (2)()1P Ω= (3)1212()()()()nn P A A A P A P A P A =++++,i j A A i j =∅≠二.性质(1)()0P ∅= (2)1212()()()()nn P A A A P A P A P A =++++,i j A A i j =∅≠(3)()1()P A P A =-(4),()()A B P A P B ⊂≤ (5)0()1P A ≤≤三.条件概率与事件独立性(1)()()0,(),()P AB P A P B A P A >=事件A 发生条件下事件B 发生的条件概率; (2)()()(),P AB P A P B =事件,A B 独立,,A B 独立,A B 独立,A B 独立,A B 独立;()0P A >时,,A B 独立()()P B A P B =;(3)121212(,,,)()()()1kk i i i i i i k P A A A P A P A P A i i i n =≤<<<≤称12,,n A A A 相互独立,(2321nn n n n C C C n +++=--个等式)相互独立⨯两两独立。
概率论与数理统计讲义稿完整版

概率论与数理统计讲义稿HUA system office room 【HUA16H-TTMS2A-HUAS8Q8-HUAH1688】第一章随机事件与概率§1.1 随机事件1.1.1 随机试验与样本空间概率论约定为研究随机现象所作的随机试验应具备以下三个特征:(1)在相同条件下试验是可重复的;(2)试验的全部可能结果不只一个,且都是事先可以知道的;(3)每一次试验都会出现上述可能结果中的某一个结果,至于是哪一个结果则事前无法预知。
为简单计,今后凡是随机试验皆简称试验,并记之以英文字母E。
称试验的每个可能结果为样本点,并称全体样本点的集合为试验的样本空间,分别用希腊字母ω和Ω表示样本点及样本空间。
必须指出的是这个样本空间并不完全由试验所决定,它部分地取决于实验的目的。
假设抛掷一枚硬币两次,出于某些目的,也许只需要考虑三种可能的结果就足够了,两次都是正面,两次都是反面,一次是正面一次是反面。
于是这三个结果就构成了样本空间Ω。
但是,如果要知道硬币出现正反面的精确次序,那么样本空间Ω就必须由四个可能的结果组成,正面-正面、反面-反面、正面-反面、反面-正面。
如果还考虑硬币降落的精确位置,它们在空中旋转的次数等事项,则可以获得其它可能的样本空间。
经常使用比绝对必要的样本空间较大的样本空间,因为它便于使用。
比如,在前面的例子中,由四个可能结果组成的样本空间便于问题的讨论,因为对于一个“均匀”的硬币这四个结果是“等可能”的。
尽管这在有3种结果的样本空间内是不对的。
E:从最简单的试验开始,这些试验只有两种结果。
在抛掷硬币这一试验例1.1.11中出现“正面”或“反面”;在检查零件质量时,可能是“合格”或“不合格”;当用来模拟电子产品旋转的方向时,结果是“左边”或者“右边”;在这些情况下样本空间Ω简化为:Ω={正面,反面}。
E:更复杂一些,有的随机试验会产生多种可能的结果,比如掷一颗骰子,观察出2现的点数。
考研数学一概率统计讲义参考书目

《考研数学一概率统计讲义参考书目》一、引言在考研数学一科目中,概率统计是一个重要的部分。
掌握好概率统计知识对于考研数学一的学习至关重要。
为了更好地学习概率统计,参考一些优质的讲义和参考书目是必不可少的。
在本文中,我将为大家推荐一些值得参考的概率统计讲义和书目,并对它们进行全面评估,以便帮助大家更好地理解和掌握概率统计知识。
二、深度和广度的要求在选择讲义和书目时,我们不仅要考虑内容的深度,还要考虑其广度。
因为概率统计这一科目涉及的知识非常广泛,深度和广度并重才能更好地帮助我们学习和掌握这一领域的知识。
三、推荐的参考书目1.《概率论与数理统计》(第四版)王金喜2.《概率论与数理统计教程》(第三版)吴喜丰、刘燕华3.《数理统计学》(第二版)苏镇宇4.《概率论与数理统计》(第五版)郝成秋、顾孟迪四、全面评估(1)《概率论与数理统计》(第四版)王金喜这本讲义从概率论和数理统计的基本概念开始,逐步深入,结构清晰,适合初学者。
但在部分内容的深度方面可能不够,建议结合其他书目进行学习。
(2)《概率论与数理统计教程》(第三版)吴喜丰、刘燕华该教程内容广泛,深度适中,适合广大学生参考。
但在一些难度较大的问题上可能需要额外的拓展和讨论。
(3)《数理统计学》(第二版)苏镇宇这本书在数理统计方面的内容比较突出,但概率论方面的内容可能有所欠缺。
建议结合其他书目进行学习,以便全面掌握概率统计知识。
(4)《概率论与数理统计》(第五版)郝成秋、顾孟迪该书深入浅出,内容全面,适合学习者从简到繁地掌握概率统计知识。
在内容上对概率统计的深度和广度都有较好的覆盖,是一本值得推荐的参考书目。
五、总结和回顾通过对以上书目的评估,我们可以看出每本书都有其优点和不足之处。
在学习概率统计这一科目时,我们应该多方参考,结合自身情况选择适合自己的学习材料。
要注重概率统计知识的深度和广度,从简到繁地逐步学习,以便更好地掌握这一领域的知识。
六、个人观点和理解对于概率统计这一科目,我个人认为要注重理论与实践相结合。
2011年考研数学《概率统计》讲义汇总

1、苏东坡《黄州寒食帖》被称为"__” C:天下第三大行书2、就时代书风而言,晋人尚韵、唐人尚法、宋代尚__D:意3、柳公权的《玄秘塔碑》是__书体A:楷书4、在书法成就方面,__与苏轼、黄庭坚、蔡襄一起合称"宋四家” B:米芾5、书法作品的幅式,有许多种,包括__、__、__、条幅、条屏、中堂、匾额等等 A:扇面B:横幅C:对联D:草书6、汉代著名的摩崖刻石除《石门颂》外,还有现在陕西略阳的__、甘肃成县__的等。
这几件摩崖并称"汉三颂” A:《郙阁颂》C:《西狭颂》7、概括起来,隶书笔法最为重要的就是__、__、__和__A:中侧并用B:逆入平出C:背分取势D:转折互用8、魏晋时期的代表性书家有__、_A:钟繇B:王羲之9、“初唐四家”欧阳询、褚遂良、__、__的书法代表了初唐楷书的最高成就A:虞世南C:薛稷10、唐代在草书方面,著名的有__、__、__等 A:孙过庭B:张旭C:怀素第三次作业1、元朝书家代表人物有虞集、鲜于枢等人,其中,鲜于枢被称为"书坛盟主” 错误2、唐代草书代表人物以张旭、怀素、贺知章三人并称正确3、清代碑学代表人物有王铎、赵之谦、张裕钊、康有为错误4、书法史上的二王指王羲之与王献之父子,大小欧指欧阳询、欧阳通父子正确5、吴门三家指明代苏州书家祝允明、文徵明、王宠正确6、散氏盘》现藏于_____ B:台北故宫博物院7、1976年出土的《墙盘》现藏于______。
C:陕西博物馆8、《大盂鼎》是_____时期的金文 A:西周9、现存最早的石刻书迹之一《石鼓文》现藏于故宫博物院10、_____统称文房四宝 C:笔、墨、纸、砚第四次作业简答题1、西周早、中、晚期的金文在风格特征上有哪些变化?西周时期的金文可以分为三个阶段。
西周前期的金文风格以朴茂凝重、瑰丽沉雄为主要特征,起收多不露锋,线条遒劲峻挺,时有肥厚用笔及点团状的华饰,整体上是线与块面结合的形式美。
2011考研数学概率论与数理统计强化课程讲义全

2011考研强化班概率论与数理统计讲义第1讲随机事件和概率1.1 知识网络图1.2 重点考核点的分布(1)样本空间与随机事件.*(2)概率的定义与性质(含古典概型、几何概型、加法公式).*(3)条件概率与概率的乘法公式.**(4)事件之间的关系与运算(含事件的独立性).**(5)全概公式与贝叶斯(Bayes)公式.(6)伯努利(Bernoulli)概型.各个考核点前面加“**”表示重点考核点;“*”表示次重点考核点;括号前没有标注的表示一般考核点(下同).1.3 课上复习内容1.3.1 预备知识在复习“概率论”之前,我们需要掌握“二值集合”、“组合分析中的几个定理”、“随机现象及其统计规律”和“微积分”等内容,下面将有关内容作一简单介绍:1.3.1.1 二值集合集合是一个不能给出数学定义的概念,尽管如此,我们仍然可以给它一个定性描述.所谓集合就是按照某些规定能够识别的一些具体对象或事物的全体.构成集合的每一个对象或事物叫做集合的元素.集合通常用大写字母A,B,C表示,其元素用小写字母a,b,c表示.设A是一个集合,如果a是A的元素,记作a∈A,用“1”表示这一隶属关系;如果a 不是A的元素,记作a∈A(或a∉A),用“0”表示这一隶属关系.因此,我们称这种集合为“二值集合”,在初等概率论中,我们只研究这样的集合.有关二值集合的表示方法、基本性质在初等数学中已作过详细讨论,这里不再重复.下面仅就集合的“相等”与“等价”概念以及集合分类情况作一简单介绍.例1设A={2,4,8},则集合A的所有子集是,{2},{4},{8},{2,4},{2,8},{4,8},{2,4,8}.注意,在考虑集合A的所有子集时,不要把空集和它本身忘掉.设A,B是两个集合.如果A⊂B,B⊂A,那么称集合A与B相等,记作A=B.很明显,含有相同元素的两个集合相等.例2设A={0,2,3},B={x|x为方程x3-5x2+6x=0的解},则A=B.设A,B是两个集合.如果B的每一个元素对应于A的唯一的元素,反之A的每一个元素对应于B的唯一的元素,那么就说在A和B的元素之间建立了一一对应关系,并称A与B等价,记作A~B.与自然数集N等价的任何集合,称为可列集.显然,一切可列集彼此都是等价的.今后我们常称这类集合中元素的个数为可列个(或可数个),并把有限个或可列个统称为至多可列个(或至多可数个).例3设A={a|a=2n,n∈N},B={b|b=n2+1,n∈N},则A~B.由上面的讨论可以看出,集合的分类如下:1.3.1.2 组合分析中的几个定理1.加法原理定理1设完成一件事有n类方法,只要选择任何一类中的一种方法,这件事就可以完成.若第一类方法有m1种,第二类方法有m2种,……,第n类方法有m n种,并且这m1+m2+…+m n种方法里,任何两种方法都不相同,则完成这件事就有m1+m2+…+m n种方法.2.乘法原理定理2设完成一件事有n个步骤,第一步有m1种方法,第二步有m2种方法,……第n步有m n种方法,并且完成这件事必须经过每一步,则完成这件事共有m1m2…m n种方法.3.排列定义1 从n个不同元素中,每次取出m个元素,按照一定顺序排成一列,称为从n 个元素中每次取出m个元素的排列.定理3从n个不同元素中,有放回地逐一取出m个元素进行排列(简称为可重复排列),共有n m种不同的排列.例4 袋中有N个球,其中M个为白色,从中有放回地取出n个:①N=10,M=2,n=3;②N=10,M=4,n=3.考虑以下各事件的排列数:(Ⅰ)全不是白色的球.(Ⅱ)恰有两个白色的球.(Ⅲ)至少有两个白色的球.(Ⅳ)至多有两个白色的球.(Ⅴ)颜色相同.(Ⅵ)不考虑球的颜色.答案是:①当M=2时,(Ⅰ)83.(Ⅱ)3×22×8.(Ⅲ)3×22×8+23.(Ⅳ)3×22×8+3×2×83+83(或103-23).(Ⅴ)23+83.(Ⅵ)103.②当M=4时,将上面的2→4,8→6即可.分析这是一个可重复的排列问题.由定理3,可求出其排列数.问题恰有两个白色球的答案中为什么是3倍的22×8,而不是1倍或6倍的?提示根据加法原理.定理4 从n 个不同元素中,无放回地取出m 个(m ≤n )元素进行排列(简称为选排列)共有)!(!)1()1(m n n m n n n -=+--种不同的排列.选排列的种数用mn A (或mn P )表示,即)!(!m n n A m n -=特别地,当m =n 时的排列(简称为全排列)共有n ·(n -1)(n -2)·…·3·2·1=n ! 种不同排列.全排列的种数用P n (或nn A )表示,即P n =n !,并规定0!=1.4.组合定义2 从n 个不同元素中,每次取出m 个元素不考虑其先后顺序作为一组,称为从n 个元素中每次取出m 个元素的组合.定理5 从n 个不同元素中取出m 个元素的组合(简称为一般组合)共有(1)(1)!!!()!n n n m n m m n m --+=-种不同的组合.一般组合的组合种数用mn C (或⎪⎪⎭⎫⎝⎛m n )表示,即 ,)!(!!m n m n C m n -=并且规定.10=n C 不难看出m m nnm A C p =⋅例5 袋中有N 个球,其中M 个为白色,从中任取n 个: ①N =10,M =2,n =3;②N =10,M =4,n =3. 考虑以下各事件的组合数: (Ⅰ)全不是白色的球. (Ⅱ)恰有两个白色的球. (Ⅲ)至少有两个白色的球. (Ⅳ)至多有两个白色的球. (Ⅴ)颜色相同. (Ⅵ)不考虑球的颜色. 答案是:①当M =2时,(Ⅰ).0238C C (Ⅱ).1822C C (Ⅲ).1822C C(Ⅳ)211203328282810().C C C C C C C ++或 (Ⅴ).38C (Ⅵ)⋅310C②当M =4时,(Ⅰ).0436C C (Ⅱ).1624C C (Ⅲ).06341624C C C C +(Ⅳ))(34310360426141624C C C C C C C C -++或. (Ⅴ).3634C C +(Ⅵ)⋅310C分析(略)定理6 从不同的k 类元素中,取出m 个元素.从第1类n 1个不同元素中取出m 1个,从第2类n 2个不同的元素中取出m 2个,……,从第k 类n k 个不同的元素中取出m k 个,并且n i ≥m i >0(i =1,2,…,k )(简称为不同类元素的组合),共有iik k m n ki m n m n m n C CC C ∏==12211 种不同取法.例6 从3个电阻,4个电感,5个电容中,取出9个元件,问其中有2个电阻,3个电感,4个电容的取法有多少种?解 这是一个不同类元素的组合问题.由定理6知,共有60151413252423==C C C C C C即60种取法.例7 五双不同号的鞋,从中任取4只,取出的4只都不配对(即不成双),求(Ⅰ)排列数;(Ⅱ)组合数.答案是:(Ⅰ)141618110C C C C ;(Ⅱ).1212121245C C C C C分析(略)1.3.1.3 微积分概率论可以分为“高等概率论”与“初等概率论”.初等概率论是建立在排列组合和微积分等数学方法的基础上的.全国硕士研究生入学统一考试数学考试大纲中的“概率论”就是初等概率论.微积分作为初等概率论的基础知识,除了我们已经比较了解的“函数、极限、连续、可导、可积”等概念之外,还应了解下面的有关概念.1.可求积与不可求积在微积分中,求不定积分与求导数有很大不同,我们知道,任何初等函数的导数仍为初等函数,而许多初等函数的不定积分,例如x x x x x xx x x x x d 1,d sin ,d ln 1,d sin ,d e 322+⎰⎰⎰⎰⎰- 等,虽然它们的被积函数的表达式都很简单,但在初等函数的范围内却积不出来.这不是因为积分方法不够,而是由于被积函数的原函数不是初等函数的缘故.我们称这种函数是“不可求积”的.因此,我们可以将函数划分为:在初等概率论中,正态分布密度函数就是属于可积而不可求积的一类函数. 2.绝对收敛(1)任意项级数的绝对收敛所谓任意项级数是指级数的各项可以随意地取正数、负数或零.下面给出绝对收敛与条件收敛两个概念.定义3 若任意项级数nn u∑∞=1的各项取绝对值所成的级数||1nn u∑∞=收敛,则称级数nn u ∑∞=1是绝对收敛的;若||1nn u∑∞=发散,而级数n n u ∑∞=1收敛,则称级数n n u ∑∞=1是条件收敛的.例如,级数nn n 1)1(11+∞=-∑是收敛的,但各项取绝对值所成的级数 ++++=-+∞=∑nn n n 1...211|1)1(|11是发散的,因而级数n n n 1)1(11+∞=-∑是条件收敛.又如,级数2111)1(n n n +∞=-∑各项取绝对值所成级数++++=-+∞=∑222111211|1)1(|nnn n是收敛的,因而级数2111)1(n n n +∞=-∑是绝对收敛的. 定理7 若级数nn u∑∞=1绝对收敛,则nn u∑∞=1必定收敛.证明 令),2,1()0(0)0(|)|(21=⎩⎨⎧<≥=+=n u u u u u v n n n n n n ,,于是 )⋯=≥≥,2,1(0||n v u n n . 由||1nn u∑∞=收敛,根据正项级数的比较判别法,可知级数n n v ∑∞=1是收敛的.考虑到 ,||2n n n u v u -= 根据级数的基本性质,可知级数nn u∑∞=1也是收敛的.根据上面的定理,判断任意一个级数nn u∑∞=1的收敛性,可以先判断它是否绝对收敛.如果||1nn u∑∞=收敛,则n n u ∑∞=1也收敛.这样一来,我们可以借助于正项级数的判别法来判断任意项级数的敛散性了.但是,当级数||1nn u∑∞=发散时,不能由此推出级数n n u ∑∞=1也发散.在初等概率论中,我们将用绝对收敛这一概念来给出离散型随机变量均值的定义. (2)无穷积分的绝对收敛定义4 如果函数f (x )在任何有限区间[a ,b ](b >a )上可积,并且积分x x f ad |)(|⎰+∞收敛,那么,我们称积分x x f ad )(⎰+∞是绝对收敛的.此时,我们也称函数f (x )在无穷区间[a ,+∞)上绝对可积.定理8 若积分x x f ad )(⎰+∞绝对收敛,则x x f ad )(⎰+∞必定收敛.上面的定理的逆定理并不成立,也就是说,从x x f ad )(⎰+∞的收敛性,不能推出x x f ad |)(|⎰+∞也收敛,例如,积分⎰+∞-d sin x xx是收敛的,但是积分x xx d |sin |0⎰+∞却发散.这一点与定积分不同,对于定积分,从x x f bad )(⎰的存在性,必能推出xx f bad |)(|⎰存在.若积分x x f ad )(⎰+∞收敛,而积分x x f ad |)(|⎰+∞发散时,则称积分x x f ad )(⎰+∞为条件收敛的.例如积分x xxad sin ⎰+∞是条件收敛的. 在初等概率论中,我们将用绝对可积这一概念来给出连续型随机变量均值的定义. 1.3.2 样本空间与随机事件1.随机现象及其统计规律性在客观世界中存在着两类不同的现象:确定性现象和随机现象. 在一组不变的条件S 下,某种结果必定发生或必定不发生的现象称为确定性现象.这类现象的一个共同点是:事先可以断定其结果.在一组不变的条件S 下,具有多种可能发生的结果的现象称为随机现象.这类现象的一个共同点是:事先不能预言多种可能结果中究竟出现哪一种.一般来说,随机现象具有两重性:表面上的偶然性与内部蕴含着的必然规律性.随机现象的偶然性又称为它的随机性.在一次实验或观察中,结果的不确定性就是随机现象随机性的一面;在相同的条件下进行大量重复实验或观察时呈现出来的规律性是随机现象必然性的一面,称随机现象的必然性为统计规律性.2.随机试验与随机事件为了叙述方便,我们把对随机现象进行的一次观测或一次实验统称为它的一个试验.如果这个试验满足下面的三个条件:(1)在相同的条件下,试验可以重复地进行.(2)试验的结果不止一种,而且事先可以确知试验的所有结果.(3)在进行试验前不能确定出现哪一个结果.那么我们就称它是一个随机试验,以后简称为试验.一般用字母E表示.问题“一个具体的人,在一次乘车郊游时,因发生交通事故而受伤”,是否为随机试验?在随机试验中,每一个可能出现的不可分解的最简单的结果称为随机试验的基本事件或样本点,用ω表示;而由全体基本事件构成的集合称为基本事件空间或样本空间,记为Ω.例8设E1为在一定条件下抛掷一枚匀称的硬币,观察正、反面出现的情况.记ω1是出现正面,ω2是出现反面.于是Ω由两个基本事件ω1,ω2构成,即Ω={ω1,ω2}.例9 设E2为在一定条件下掷一粒骰子,观察出现的点数.记ωi为出现i个点(i=1,2,…,6).于是有Ω={ω1,ω2,…,ω6}.问题例8、例9中样本空间Ω的子集个数是多少?为什么?所谓随机事件是样本空间Ω的一个子集,随机事件简称为事件,用字母A,B,C等表示.因此,某个事件A发生当且仅当这个子集中的一个样本点ω发生,记为ω∈A.在例9中,Ω={ω1,ω2,…,ω6},而E2中的一个事件是具有某些特征的样本点组成的集合.例如,设事件A={出现偶数点},B={出现的点数大于4},C={出现3点},可见它们都是Ω的子集.显然,如果事件A发生,那么子集{ω2,ω4,ω6}中的一个样本点一定发生,反之亦然,故有A={ω2,ω4,ω6};类似地有B={ω5,ω6}和C={ω3}.一般而言,在例9中,任一由样本点组成的Ω的子集也都是随机事件.1.3.3 事件之间的关系与运算事件之间的关系有:“包含”、“等价(或相等)”、“互不相容(或互斥)”以及“独立”四种.事件之间的基本运算有:“并”、“交”以及“逆”.如果没有特别的说明,下面问题的讨论我们都假定是在同一样本空间Ω中进行的.1.事件的包含关系与等价关系设A,B为两个事件.如果A中的每一个样本点都属于B,那么称事件B包含事件A,或称事件A包含于事件B,记为A⊂B或B⊃A.如果A⊃B与B⊃A同时成立,那么称事件A与事件B等价或相等,记为A=B.在下面的讨论中,我们经常说“事件相同、对应概率相等”,这里的“相同”指的是两个事件“等价”.2.事件的并与交设A,B为两个事件.我们把至少属于A或B中一个的所有样本点构成的集合称为事件A与B的并或和,记为A∪B或A+B.设A ,B 为两个事件.我们把同时属于A 及B 的所有样本点构成的集合称为事件A 与B 的交或积,记为A ∩B 或A ·B ,有时也简记为AB .3.事件的互不相容关系与事件的逆设A ,B 为两个事件,如果A ·B =,那么称事件A 与B 是互不相容的(或互斥的). 对于事件A ,我们把不包含在A 中的所有样本点构成的集合称为事件A 的逆(或A 的对立事件),记为.A 我们规定它是事件的基本运算之一.在一次试验中,事件A 与A 不会同时发生(即A ·A =,称它们具有互斥性),而且A与A 至少有一个发生(即A +A =Ω,称它们具有完全性).这就是说,事件A 与A 满足:⎪⎩⎪⎨⎧=+∅=⋅.,ΩA A A A 问题 (1)事件的互不相容关系如何推广到多于两个事件的情形?(2)三个事件A ,B ,C ,ABC =与⎪⎩⎪⎨⎧∅=∅=∅=BC AC AB ,, 关系如何?根据事件的基本运算定义,这里给出事件之间运算的几个重要规律: (1)A (B +C )=AB +AC (分配律). (2)A +BC =(A +B )(A +C )(分配律).(3)B A B A ⋅=+ (德·摩根律).(4)B A B A +=⋅(德·摩根律).有了事件的三种基本运算我们就可以定义事件的其他一些运算.例如,我们称事件AB 为事件A 与B 的差,记为A -B .可见,事件A -B 是由包含于A 而不包含于B 的所有样本点构成的集合.例10 在数学系学生中任选一名学生.设事件A ={选出的学生是男生},B ={选出的学生是三年级学生},C ={选出的学生是科普队的}.(1)叙述事件ABC 的含义.(2)在什么条件下,ABC =C 成立? (3)在什么条件下,C ⊂B 成立?解 (1)事件ABC 的含义是,选出的学生是三年级的男生,不是科普队员.(2)由于ABC ⊂C ,故ABC =C 当且仅当C ⊂ABC .这又当且仅当C ⊂AB ,即科普队员都是三年级的男生.(3)当科普队员全是三年级学生时,C 是B 的子事件,即C ⊂B 成立. 4.事件的独立性设A ,B 是某一随机试验的任意两个随机事件,称A 与B 是相互独立的,如果P (AB )=P (A )P (B ).可见事件A 与B 相互独立是建立在概率基础上事件之间的一种关系.所谓事件A 与B 相互独立就是指其中一个事件发生与否不影响另一个事件发生的可能性,即当P (B )≠0时,A 与B 相互独立也可以用)()|(A P B A P =来定义.由两个随机事件相互独立的定义,我们可以得到:若事件A 与B 相互独立,则A 与B ,A 与B ,A 与B 也相互独立.如果事件A ,B ,C 满足⎪⎪⎩⎪⎪⎨⎧====),()()()(),()()(),()()(),()()(C P B P A P ABC P C P A P AC P C P B P BC P B P A P AB P 则称事件A ,B ,C 相互独立.注意,事件A ,B ,C 相互独立与事件A ,B ,C 两两独立不同,两两独立是指上述四个式子中前三个式子成立.因此,相互独立一定是两两独立,但反之不一定.例11 将一枚硬币独立地掷两次,引进事件:A ={掷第一次出现正面},B ={掷第二次出现正面},C ={正、反面各出现一次},则事件A ,B ,C 是相互独立,还是两两独立?解 由题设,可知P (AB )=P (A )P (B ),即A ,B 相互独立.而1()(())()()(),4P AC P A AB AB P AB P A P B =+===()()()()()(()())P A P C P A P AB AB P A P AB P AB =+=+⋅=+⨯=41)4121(21 故A ,C 相互独立,同理B ,C 也相互独立.但是P (ABC )=P (∅)=0, 而 ,81212121)()()(=⨯⨯=C P B P A P 即 )()()()(C P B P A P ABC P ≠,因此A ,B ,C 两两独立.问题 (1)两个事件的“独立”与“互斥”之间有没有关系?在一般情况下,即P (A )>0,P (B )>0时,有关系吗?为什么?(2)设0<P (A )<1,0<P (B )<1,P (B |A )+P (B |A )=1.问A 与B 是否独立,为什么?由此可以得到什么结论?1.3.4 概率的定义与性质1.概率的公理化定义定义5 设E 是一个随机试验,Ω为它的样本空间,以E 中所有的随机事件组成的集合为定义域,定义一个函数P (A )(其中A 为任一随机事件),且P (A )满足以下三条公理,则称函数P (A )为事件A 的概率.公理1(非负性) 0≤P (A )≤1.公理2(规范性) P (Ω)=1.公理3(可列可加性) 若A 1,A 2,…,A n ,…两两互斥,则).()(11i i i i A P A P ∑∞=∞==由上面三条公理可以推导出概率的一些基本性质. 性质1(有限可加性) 设A 1,A 2,…,A n 两两互斥,则).()(11i ni i n i A P A P ∑===性质2(加法公式) 设A ,B 为任意两个随机事件,则P (A +B )=P (A )+P (B )-P (AB ).性质3 设A 为任意随机事件,则P (A )=1-P (A ).性质4 设A ,B 为两个任意的随机事件,若A ⊂B ,则P (B -A )=P (B )-P (A ).由于P (B -A )≥0,根据性质4可以推得,当A ⊂B 时,P (A )≤P (B ). 例12 设A ,B ,C 是三个随机事件,且=====)()(,41)()()(CB P AB P C P B P A p 0,81)(=AC P ,求A ,B ,C 中至少有一个发生的概率. 解 设D ={A ,B ,C 中至少有一个发生},则D =A +B +C ,于是 P (D )=P (A +B +C )=P (A )+P (B )+P (C )-P (AB )-P (BC )-P (AC )+P (ABC ).又因为,41)()()(===C P B P A P ,0)()(==CB P AB P 81)(=AC P ,而由P (AB )=0,有P (ABC )=0,所以⋅=-=858143)(D P 问题 怎样由P (AB )=0推出P (ABC )=0? 提示 利用事件的关系与运算导出.例13 设事件A 与B 相互独立,P (A )=a ,P (B )=b .若事件C 发生,必然导致A 与B 同时发生,求A ,B ,C 都不发生的概率.解 由于事件A 与B 相互独立,因此P (AB )=P (A )·P (B )=a ·b .考虑到C ⊂AB ,故有,B A B A AB C ⊃+=⊃因此).1)(1()()()()(b a B P A P B A P C B A P --===2.概率的统计定义定义6 在一组不变的条件S 下,独立地重复做n 次试验.设μ是n 次试验中事件A 发生的次数,当试验次数n 很大时,如果A 的频率f n (A )稳定地在某一数值p 附近摆动;而且一般说来随着试验次数的增多,这种摆动的幅度会越来越小,则称数值p 为事件A 在条件组S 下发生的概率,记作.)(p A P =问题 (1)试判断下式p n n =∞→μlim成立吗?为什么?(2)野生资源调查问题 池塘中有鱼若干(不妨假设为x 条),先捞上200条作记号,放回后再捞上200条,发现其中有4条带记号.用A 表示事件{任捞一条带记号},问下面两个数2004,200x 哪个是A 的频率?哪个是A 的概率?为什么?3.古典概型古典型试验:(Ⅰ)结果为有限个;(Ⅱ)每个结果出现的可能性是相同的.等概完备事件组:(Ⅰ)完全性;(Ⅱ)互斥性;(Ⅲ)等概性.(满足(Ⅰ),(Ⅱ)两条的事件组称为完备事件组)定义7 设古典概型随机试验的基本事件空间由n 个基本事件组成,即Ω={ω1,ω2,…,ωn }.如果事件A 是由上述n 个事件中的m 个组成,则称事件A 发生的概率为⋅=nm A P )( (1-1) 所谓古典概型就是利用式(1-1)来讨论事件发生的概率的数学模型.根据概率的古典定义可以计算古典型随机试验中事件的概率.在古典概型中确定事件A 的概率时,只需求出基本事件的总数n 以及事件A 包含的基本事件的个数m .为此弄清随机试验的全部基本事件是什么以及所讨论的事件A 包含了哪些基本事件是非常重要的.例14 掷两枚匀称的硬币,求它们都是正面的概率.解 设A ={出现正正},其基本事件空间可以有下面三种情况:(Ⅰ)Ω1={同面、异面},n 1=2.(Ⅱ)Ω2={正正、反反、一正一反},n 2=3.(Ⅲ)Ω3={正正、反反、反正、正反},n 3=4.于是,根据古典概型,对于(Ⅰ)来说,由于两个都出现正面,即同面出现,因此,m 1=1,于是有21)(=A P . 而对于(Ⅱ)来说,m 2=1,于是有31)(=A P . 而对于(Ⅲ)来说,m 3=1,于是有41)(=A P . 问题 以上讨论的三个结果哪个正确,为什么?例15 求1.3.1预备知识的例5中(Ⅰ)至(Ⅴ)问的概率.答案是:①当M =2时,(Ⅰ)⋅31038/C C (Ⅱ)⋅31018/C C (Ⅲ)⋅31018/C C (Ⅳ)1. (Ⅴ)⋅31038/C C②当M =4时,(Ⅰ)⋅31038/C C (Ⅱ)⋅3101624/C C C (Ⅲ)310341624/)(C C C C +.(Ⅳ)31034310/)(C C C -. (Ⅴ) 3103634/)(C C C +. 分析(略)问题 (1)例15中各问可否使用排列做,为什么?(2)用排列或组合完成例15时哪种方法较为简便?例16 求1.3.1预备知识的例4中(Ⅰ)至(Ⅴ)问的概率.答案是:①当M =2时,(Ⅰ)3310/8. (Ⅱ)3210/823⨯⨯. (Ⅲ)33210/)2823(+⨯⨯.(Ⅳ)33310/)210(-. (Ⅴ)33310/)82(+.②当M =4时,将上面的2→4,8→6即可.分析(略)问题 (1)例16中各问可否使用组合做,为什么?(2)用元素可重复的排列或组合完成例16时,哪种方法较为简便?(3)小结一下“古典概型”中“有放回地抽取”与“无放回地抽取”时分别应采用的方法.例17 求1.3.1预备知识的例7中“取出的4只都不配对”的概率.答案是:410141618110/P C C C C 或 4111145222210/C C C C C C . 分析(略)例18 从一副扑克牌的13张梅花中,有放回地取3次,求三张都不同号的概率. 解 这是一个古典概型问题.设A ={三张都不同号}.由题意,有n =133,m =313P ,则 ⋅==169132)(n m A P问题 如果我们进一步问三张都同号,三张中恰有两张同号如何求出?另外,本题可否使用二项概型计算?例19 在20枚硬币的背面分别写上5或10,两者各半,从中任意翻转10枚硬币,这10枚硬币背面的数字之和为100,95,90,…,55,50,共有十一种不同情况.问出现“70,75,80”与出现“100,95,90,85,65,60,55,50”的可能性哪个大,为什么?答案是:出现“70,75,80”可能性大,约为82%.分析 这是一个古典概型问题.设A ={出现“70,75,80”},由题意,有,2,6104105105101020C C C C m C n +==则 ⋅==184756151704)(n m A P 4.几何概型几何型试验:(Ⅰ)结果为无限不可数;(Ⅱ)每个结果出现的可能性是均匀的.定义4 设E 为几何型的随机试验,其基本事件空间中的所有基本事件可以用一个有界区域来描述,而其中一部分区域可以表示事件A 所包含的基本事件,则称事件A 发生的概率为,)()()(Ω=L A L A P (1-2) 其中L (Ω)与L (A )分别为Ω与A 的几何度量.所谓几何概型就是利用式(1-2)来讨论事件发生的概率的数学模型.注意,上述事件A 的概率P (A )只与L (A )有关,而与L (A )对应区域的位置及形状无关. 例20 候车问题 某地铁每隔5 min 有一列车通过,在乘客对列车通过该站时间完全不知道的情况下,求每一个乘客到站等车时间不多于2 min 的概率.解 设A ={每一个乘客等车时间不多于2 min}.由于乘客可以在接连两列车之间的任何一个时刻到达车站,因此每一乘客到达站台时刻t 可以看成是均匀地出现在长为5 min 的时间区间上的一个随机点,即Ω=[0,5).又设前一列车在时刻T 1开出,后一列车在时刻T 2到达,线段T 1T 2长为5(见图1-1),即L (Ω)=5;T 0是T 1T 2上一点,且T 0T 2长为2.显然,乘客只有在T 0之后到达(即只有t 落在线段T 0T 2上),等车时间才不会多于2min ,即L (A )=2.因此图1-1⋅=Ω=52)()()(L A L A P 问题 (1)例20可否使用一维均匀分布来计算?(2)举例说明:(Ⅰ)概率为0的事件不一定是不可能事件.(Ⅱ)概率为1的事件不一定是必然事件.例21 会面问题 甲乙两艘轮船驶向一个不能同时停泊两艘轮船的码头,它们在一昼夜内到达的时间是等可能的,如果甲船和乙船停泊的时间都是两小时,它们同日到达时会面的概率是多少?解 这是一个几何概型问题.设A ={它们会面}.又设甲乙两船到达的时刻分别是x ,y ,则0≤x ≤24,0≤y ≤24.由题意可知,若要甲乙会面,必须满足|x -y |≤2,即图中阴影部分.由图1-2可知:L (Ω)是由x =0,x =24,y =0,y =24图1-2所围图形面积S =242,而L (A )=242-222,因此.)2422(1242224)()()(2222-=-=Ω=L A L A P 问题 例21可否使用二维均匀分布来计算?1.3.5 条件概率与概率的乘法公式1.条件概率前面我们所讨论的事件B 的概率P S (B ),都是指在一组不变条件S 下事件B 发生的概率(但是为了叙述简练,一般不再提及条件组S ,而把P S (B )简记为P (B )).在实际问题中,除了考虑概率P S (B )外,有时还需要考虑“在事件A 已发生”这一附加条件下,事件B 发生的概率.与前者相区别,称后者为条件概率,记作P (B |A ),读作在A 发生的条件下事件B 的概率.在一般情况下,如果A ,B 是条件S 下的两个随机事件,且P (A )≠0,则在A 发生的前提下B 发生的概率(即条件概率)为)()()|(A P AB P A B P =, (1-3) 并且满足下面三个性质:(1)(非负性)P (B |A )≥0;(2)(规范性)P (Ω|A )=1;(3)(可列可加性)如果事件B 1,B 2,…互不相容,那么).|()|(11A B P A B P i i i i ∑∞=∞==问题 (1)条件概率在原样本空间Ω中是某一个事件的概率吗?(2)如何判断一个问题中所求的是条件概率还是无条件概率?(3)在一个具体问题中条件概率如何获得?例22 设随机事件B 是A 的子事件,已知P (A )=1/4,P (B )=1/6,求P (B |A ).分析 这是一个条件概率问题.解 因为B ⊂A ,所以P (B )=P (AB ),因此⋅===32)()()()()|(A P B P A P AB P A B P 2.概率的乘法公式在条件概率公式(1-3)的两边同乘P (A ),即得P (AB )=P (A )P (B |A ). (1-4)例23 在100件产品中有5件是不合格的,无放回地抽取两件,问第一次取到正品而第二次取到次品的概率是多少?解 设事件A ={第一次取到正品},B ={第二次取到次品}.用古典概型方法求出.010095)(=/=A P 由于第一次取到正品后不放回,那么第二次是在99件中(不合格品仍是5件)任取一件,所以⋅=995)|(A B P 由公式(1-4), ⋅=⨯==3961999510095)|()()(A B P A P AB P问题 (1)例23中,问两件产品为一件正品,一件次品的概率是多少?(2)例23中,将“无放回地抽取”改为“有放回地抽取”,答案与上题一样吗?为什么?例24 抓阄问题 五个人抓一个有物之阄,求第二个人抓到的概率.分析 (1)什么是“抓阄”问题,如何判断它?(2)例24中“求第二个人抓到的概率”是指“在第一人没有抓到的条件下,第二个人抓到的概率”吗?解 这是一个乘法公式的问题.设A i ={第i 个人抓到有物之阄}(i =1,2,3,4,5),有⋅=+∅=+=+=Ω=2121212111222)(A A A A A A A A A A A A A根据事件相同,对应概率相等有).|()()()(121212A A P A P A A P A P ==又因为,41)|(,54)(,51)(1211===A A P A P A P所以⋅=⨯=514154)(2A P 问题 (1)本题还有其他方法解决吗?(2)若改成n 个人抓m 个有物之阄(m <n ),下面的结论),,2,1()(n k nm A P k == 还成立吗?例25 设袋中有4个乒乓球,其中1个涂有白色,1个涂有红色,1个涂有蓝色,1个涂有白、红、蓝三种颜色.今从袋中随机地取一个球,设事件A ={取出的球涂有白色},B ={取出的球涂有红色},C ={取出的球涂有蓝色}.试验证事件A ,B ,C 两两相互独立,但不相互独立.证 根据古典概型,我们有n =4,而事件A ,B 同时发生,只能是取到的球是涂有白、红、蓝三种颜色的球,即m =1,因而⋅=41)(AB P 同理,事件A 发生,只能是取到的球是涂红色的球或涂三种颜色的球,因而⋅==⋅==2142)(2142)(B P A P 因此,有 ,412121)()(=⨯=B P A P 所以 P (AB )=P (A )P (B ),即事件A ,B 相互独立.类似可证,事件A ,C 相互独立,事件B ,C 相互独立,即A ,B ,C 两两相互独立,但是由于,41)(=ABC P 而 ,4181212121)()()(=/=⨯⨯=C P B P A P 所以A ,B ,C 并不相互独立.例26 加工某一零件共需经过四道工序,设第一、二、三、四道工序的次品率分别是2%、3%、5%、3%,假定各道工序是互不影响的,求加工出来的零件的次品率.答案是:0.124(或1-0.98×0.97×0.95×0.97).问题 本题使用加法公式还是乘法公式较为简便?例27 一批零件共100个,其中有次品10个.每次从中任取一个零件,取出的零件不再放回去,求第一、二次取到的是次品,第三次才取到正品的概率. 答案是:)989099910010(0084.0⨯⨯或.。
考研数学基础班概率统计讲义汤家凤

考研数学基础班概率统计讲义—汤家凤考研数学基础班概率统计讲义第一章随机事件与概率一、随机试验与随机事件(一)基本概念1、随机试验—具备如下三个条件的试验:(1)相同条件下可重复。
(2)试验的可能结果是多样的且是确定的。
(3)某次试验之前不确定具体发生的结果,这样的试验称为随机试验,记为E。
2、样本空间—随机试验的所有可能的基本结果所组成的集合,称为随机试验的样本空间。
3、随机事件—样本空间的子集称为随机事件。
(二)事件的运算12312312341、对事件A,有P(A)??0(非负性)。
2、P(?)??1(归一性)。
??3、设A1,A2,L,A n,L为不相容的随机事件,则有P(U A n)????P(A n)(可列可加性)。
n?1n?1(二)概率的基本性质1、P(?)??0。
n n2、设A1,A2,L,A n为互不相容的有限个随机事件列,则P(U A k)????P(A k)。
k?1 k?13、P(A)??1??P(A)。
4、(减法公式)P(A??B)??P(A)??P(AB)。
Array 1((23((1相互独立。
2(((3)设P (A )??0,P (B )??0,若A ,B 独立,则A ,B 不互斥;若A ,B 互斥,则A ,B 不独立。
四、全概率公式与Bayes 公式1、完备事件组—设事件组A 1,A 2,L ,A n 满足:(1)A i A j ???(i ,j ??1,2,L ,n ,i ?j );n(2)U A i ????,则称事件组A 1,A 2,L ,A n 为一个完备事件组。
i ?12、全概率公式:设A 1,A 2,L ,A n 是一个完备事件组,且P (A i )??0(i ??1,2,L ,n ),B 为事件,则nP (B )????P (A i )P (B |A i )。
i ?13、贝叶斯公式:设A 1,A 2,L ,A n 为一个完备事件组,且P (A i )??0(i ??1,2,L ,n ),B 为任一随机事件,P (B )P (A i )P (B |A i )1(2概率为3???9,16则P (A 45不发生B1(C)P(AB)??P(A)P(B);(D)P(AB)??P(A)P(B)。
2011年考研数学《概率统计》讲义第一讲
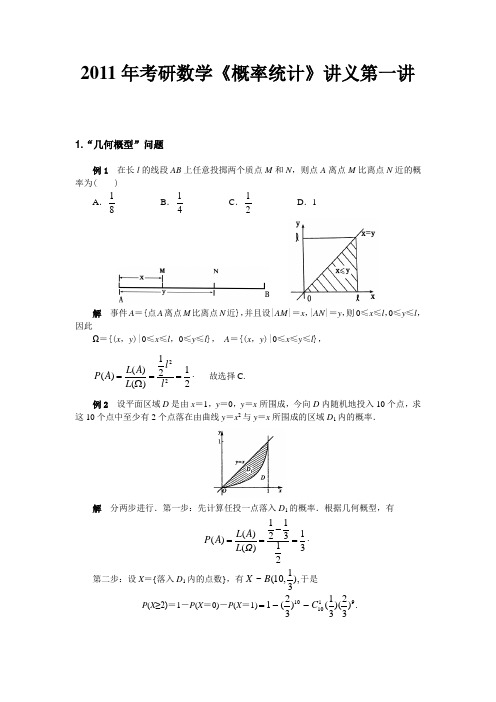
2011年考研数学《概率统计》讲义第一讲1.“几何概型”问题例1 在长l 的线段AB 上任意投掷两个质点M 和N ,则点A 离点M 比离点N 近的概率为( )A .81 B .41 C .21 D .1解 事件A ={点A 离点M 比离点N 近},并且设|AM |=x ,|AN |=y ,则0≤x ≤l ,0≤y ≤l ,因此Ω={(x ,y )|0≤x ≤l ,0≤y ≤l }, A ={(x ,y )|0≤x ≤y ≤l },⋅==Ω=2121)()()(22llL A L A P 故选择C .例2 设平面区域D 是由x =1,y =0,y =x 所围成,今向D 内随机地投入10个点,求这10个点中至少有2个点落在由曲线y =x 2与y =x 所围成的区域D 1内的概率.解 分两步进行.第一步:先计算任投一点落入D 1的概率.根据几何概型,有11()123()1()32L A P A L Ω-===⋅第二步:设X ={落入D 1内的点数},有),31,10(~B X 于是P (X ≥2)=1-P (X =0)-P (X =1).)32)(31()32(1911010C --=例3 设随机变量X 和Y 的联合分布在正方形G ={(x ,y ):1≤x ≤3,1≤y ≤3}上均匀分布,试求随机变量U =|X -Y |的概率密度p (u ).解 由条件知X 和Y 的联合密度为 ⎪⎩⎪⎨⎧≤≤≤≤=.,0,31,31,41),(其他若y x y x f以F (u )=P (U ≤u )(-∞<u <∞)表示随机变量U 的分布函数. 显然,当u ≤0时,F (u )=0;当u ≥2时,F (u )=1.设0<u <2,则 {||}1()(,)d d d d 4x y ux y u GF u f x y x y x y -≤-≤==⎰⎰⎰⎰,)2(411])2(4[4122u u --=--=于是,随机变量的密度为 ⎪⎩⎪⎨⎧<<-=.,0,20),2(21)(其他若u u u p例4 在长为l 的线段上,任意选取两点M 和N ,求E |M -N |,D |M -N |解 令Z =|M -N |,先求p (z ) F (z )=P (Z ≤z )=P (|M -N |≤z )=222)(lz l l --, p (z )=F ′(z )再求E (Z )和D (Z ).例5(1) 设随机变量X 与Y 相互独立,且均服从区间[0,3]上的均匀分布,则 P {max {X ,Y }≤1}=______.答案是:91.分析 本题主要考查“二维均匀分布”中有关概率的计算问题.由题设,可知(X ,Y )~U (D ),其中D ={(x ,y )|0≤x ≤3,0≤y ≤3}. 解法1P {max (X ,Y )≤1}=P (X ≤1,Y ≤1)=P (X ≤1)·P (Y ≤1)⋅==⎰⎰91)d 31()d 31(1010y x解法2 由几何概型可知.911}1,1{}1),{max(==≤≤=≤DS Y X P Y X P(2) 在区间(0,1)中随机地取两个数,则这两个数之差的绝对值小于21的概率为____.答案是:43.分析 本题主要考查“二维均匀分布或几何概型”.解 设随机取到的两个数为X 与Y ,则(X ,Y )服从正方形区域上的均匀分布.一方面我们可以利用二重积分计算⎰⎰=<-Dy x f Y X p .d ),()21|(|σ另一方面我们也可以根据几何概型来计算,如图,即⋅=⨯⨯⨯-Ω=<-=43121212121)()()21|(|)(L A L Y X P A P2.“图解法”问题例1 设事件A 、B 、C 满足P (B )=2P (A ),P (C )=3P (A ),并且P (AB )=P (BC ),则P (A )的取值范围是( )A .]1,0[B .]21,0[C .]31,0[ D .]41,0[解 由于A ⊃AB ,于是有x =P (A )≥P (AB )=y =P (BC )利用加法公式,有1≥P (B +C )=P (B )+P (C )-P (BC )=3x +2x -y ≥3x +2x -x =4x ≥0 即0≤4x ≤1 ⇒0≤x ≤41. 故选择D .例2 设两个随机事件A ,B 相互独立,已知仅有A 发生的概率为41,仅有B 发生的概率为41,则P (A )=_______.解 ()()P A P B =1()()()()[1()]()[1()].4P A B P A P B P A P B P A P A ==-=-=所以 1()2P A =例3 设X ~N (2,σ2),并且P (2<X <4)=0.3,则P (X <0)=______.例4 设随机变量X 服从正态分布N (0,1),对给定的α(0<α<1),数αu 满足P {X >αu }=α.若P {|X |<x }=α,则x 等于(A )2αu (B )21α-u(C )21αu - (D )u 1-α解 由题设,可知u α满足P (X >u α)=α.可见,若要P (|X |<x )=α, 即P (|X |≥x )=1-α, 而P (X >x )=21α-,因此⋅=-21αu x 故选择C .3.“事件独立性”问题①定义相互独立()()(),()()(),()()(),()()()(),P A B P A P B P B C P B P C P A C P A P C P A B C P A P B P C ⎧=⎫⎪⎪=⎪⎬⎨⎪=⎭⎪⎪=⎩两两独立②等价定义A. 两两独立+A BA B A B+-与C 独立(三者之一)B. ()()()P AB P A P B = + ()0P C =或1例 设事件A 、B 、C 满足P (AB )=P (A )P (B ),并且P (C )=[P (C )]2,则A 、B 、C ( ) A .一定不是两两独立; B .不一定是两两独立; C .一定是相互独立; D .一定不是相互独立. 解 由P (C )=[P (C )]2,我们有P (C )=0或1 ⎪⎪⎩⎪⎪⎨⎧====⇒⎩⎨⎧==)()()()()()()()()()()()()(10)()()()(C P B P A P ABC P C P A P AC P C P B P BC P B P A P AB P C P B P A P AB P 或 故选择C .证明:(1)对于任意的A ,由于AC ⊂C ,P (AC )≤P (C )=0 P (AC )=0=P (A )P (C ),即A 与C 相互独立 (2)(C +C )A =A ,P (C A )=P (A )-P (AC )=P (A )-P (A )P (C )=P (A )(1-P (C ))=P (A )P (C ) 结论:零(或1)概率事件与任何事件都是相互独立的.4.“全概公式”问题例1 袋中装有n 只球,每次从中随意取出一球,并放入一个白球,如此交换共进行n 次.已知袋中白球数的数学期望为a ,那么第n +1次从袋中任取一球为白球的概率是______.解 依题意袋中白球数X 是个随机变量,X 可取1,2,…,n ,且∑=nk 1kP {X =k }=a .若记B =“第n +1次从袋中任取一球为白球”,A k “第n 次交换后袋中有k 个白球”(k =1,2,…,n ).由全概率公式,得nk k X P A B P A P B P nk k k nk }{)|()()(11===∑∑==.){11na k X kP nnk ===∑=例2(1) 有两个箱子,第一个箱子中有3个白球2个红球,第二个箱子中有4个白球4个红球,先从第一箱当中随机取一个球放入第二个箱子当中.再从第二箱当中取1个球,问它是白球的概率是多少?解 i A 表示第i 次从第i 个箱子取出的白球.53)(1=A P 52)(1=A P95)|(12=A A P 94)|(12=A A P4523)|()()|()()(1211212=+=A A P A P A A P A P A P .(2)设随机变量X 与Y 独立,其中X 的概率分布为⎪⎪⎭⎫ ⎝⎛7.03.021~X , 而Y 的概率密度为()f y ,求随机变量U X Y =+的概率密度()g u .分析 离散型随机变量X 和一个连续型随机变量Y 的和是不能确定的,但是本题已知随机变量X 与Y 独立,并且X 只有两个正概率点,这时可以利用全概率公式求U X Y =+的概率密度解 为求出概率密度()g u ,一般应先求分布函数(){}{}G u P U u P X Y u =≤=+≤, 先验概率:()10.3P X ==,()20.7P X == 所以U X Y =+的分布函数为 }{)(u Y X P u G ≤+=()()1{1}2{2}P X P X Y u X P X P X Y u X ==+≤=+=+≤=0.3{1}0.7{2}P X Y u X P X Y u X =+≤=++≤= 0.3{11}0.7{22}P Y u X P Y u X =≤-=+≤-=.由于X 和Y 相互独立,可见()0.3{1}0.7{2}G u P Y u P Y u =≤-+≤-0.3(1)0.7(2).F u F u =-+-又因为连续型随机变量密度函数是分布函数在对应区间上的微分得到,得U 的概率密度)2(7.0)1(3.0)()(-'+-'='=u F u F u G u g 0.3(1)0.7(2).f u f u =-+-例3 从数1,2,3,4中任取一个数,记为X , 再从X ,,2,1 中任取一个数,记为Y , 则{2}P Y == ___________ .解 由全概率公式:}2{=Y P =}12{}1{===X Y P X P +}22{}2{===X Y P X P+}32{}3{===X Y P X P +}42{}4{===X Y P X P X 表示从数1,2,3,4中任取一个数,故X 是等可能取到1,2,3,4。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011年临湘海螺内控建设专业试题库(安全环保专业)一、填空题1、企业安全管理的法律依据是国家《安全生产法》 ,职业病防护管理的法律依据是国家《职业病防护法》。
2、我国的消防方针是:“以防为主,防消结合”。
3、安全生产责任制就是各级领导、 职能部门 、工程技术人员、岗位操作人员在生产经营过程中对安全生产层层负责的制度。
4、从业人员应当接受安全生产教育和培训,掌握本职工作所需的安全生产知识,提高安全技能,增强事故预防和应急能力。
5、现场隐患排查主要是查物的不安全状态和人的不安全行为。
6、长期以来养成的,有可能导致人身伤害事故发生的不安全行为,称之为习惯性违章行为,其危害性很大,它的特点表现为不以为然或想当然。
7、公司存在的主要危险源有:总降、各电力室、供应仓库、油库、纸袋库、质控处危险化学药品室、和磨机检修、清仓作业及带电作业等。
8、单位发生工亡事故后,应在1小时内报告当地政府安全监督管理部门,不得瞒报。
9、公司停送电制度规定,所有设备检查与检修都必须办理停送电手续。
10、皮带机的安全防护装臵主要有:报警铃、头、尾轮防护罩、减速机转轴防护罩、防跑偏开关、防堵开关和皮带拉绳开关等。
11、安全色中红色表示禁止,黄色表示警告,蓝色表示指令,绿色表示提示。
12、当灭火器压力表指针指到“红色”区域时,意味着该灭火器已经失效。
13、磨内检查、检修,清仓作业及其他密闭性容器内作业时,必须使用36v 以下的安全电压。
14、我公司环保排放执行的标准是粉尘≤50毫克/立方;噪声昼≤65dB;夜间≤55dB.15、我公司1#2#线主收尘器采用的是反吹风式袋收尘器,3#线主收尘采用的是脉冲式袋收尘器。
16、清洁生产的八字方针是:节能、减污、降耗、增效。
17、中控开启设备前,应示警3分钟。
18、公司安全管理规定,凡在地坑、磨房、封闭的廊道等昏暗生产场所必须设臵长明灯,以确保巡检安全。
19、一般事故是指一次死亡1-3人,较大事故是一次死亡3-10人,重大死亡是指一次事故死亡10-30人,特大事故是一次事故死亡30人以上。
20、电器火灾用水进行扑救时,首先要做的事是,立即切断电源。
21、触电方式有三种,一种是单向触电,一种是双向触电,再一密 封 公司:____________________ 姓名:________________ 岗位:_______________ ————————————————————————种是跨步电压触电。
22、火灾是一种在时间上和空间上失去控制的燃烧现象。
23、高低压开关必须按容量额定继电保护或保险系数,不得使用其他金属丝代替。
24、在线路工作时,必须切断电源和采取接地保护后,才能作业。
25、国家实行安全生产责任追究制度。
26、班前会的作用是做好上一班与下一班的安全交接,班长在布臵当日工作的同时,有针对性的布臵安全工作,对员工安全穿戴进行检查,做好班前安全教育。
27、电工在执行完停电操作后,必须在停电闸刀上挂“设备检修严禁合闸”的检修牌。
28、所有特种设备必须经当地特种设备检验部门检验合格,并取得《检验合格证》后,方可运行。
29、水泥袋必须按照先进先出的原则,保持一定的流动性,对于长期不用电大批量水泥袋,要经常检查垛内的升温情况,必要时进行翻垛处理,防止垛堆自燃。
30、装载机加油时,严禁携带火种与吸烟,同时装载机发动机必须熄火。
31、高空作业必须系好安全带,严禁高空抛物。
32、磨机检修除现场有人安全监护外,还要对危险区域拉好警戒绳。
33、起吊设备时,事先要检查好起重设备完好情况,进行空运行无误后再正式起吊,吊物下严禁站人。
34、氧气、乙炔气瓶的保管,二者要分开存放,现场要有标识并有瓶帽保护。
35、电气工段每月要组织对个人所用工具进行一次安全可靠性自检自查。
36、公司所有皮带配重托辊都要用钢丝绳进行保险,防止皮带突然断裂,托辊坠落伤人。
37、移动水泵时,必须遵守先停电,后移动,接水泵时,必须待水泵就位后,再接电的原则。
33、起吊设备时,事先要检查好起重设备完好情况,进行空运行无误后再正式起吊,吊物下严禁站人。
39、化验室工作人员在进行盐酸化学实验时,应在通风橱内进行。
40、公司安全规定:供应仓库在进行钢材和设备大件卸货时,应事先进行危险作业申报,并有人现场监护。
41、班组安全活动每7天开展一次,要求真实有效的开展,严禁“一支笔”和“一言堂”现象。
42、总降高压操作用的绝缘靴和绝缘手套和操作工具等器具,需定期到供电部门进行检验。
43、集中检修时,如遇同一设备交叉作业,电工必须在摘取所有检修牌后,才能送电。
44、总降是高压危险场所,为确保总降安全,总降室实行非工作人员进出人登记制度。
45、压力设备检修前,必须进行事先减压。
46、液化气使用时,应注意通风,防止液化气泄漏造成人员中毒。
47、为预防电器设备漏电伤人,一般要求电气设备都应装上漏电保护装臵。
48、凡密闭性容器内检查和检修,必须在人孔门处派人监护。
49、磨内检修更换衬板打大锤时,必须穿好帆布防护服和带好防护镜。
50、设备停送电规定,停电申请人必须对操作电工停电作业进行确认后,方可作业。
51、按照电器专业安全要求,每年春季前应对公司所属建筑物进行防雷接地检测,对所有电气设备进行一次全面漏电保护检查。
52、供应仓库在码放货物时应注意货物的重心稳定,防止货物倒塌伤人。
53、设备检修办理停送电时,操作电工除审核有无相关领导签字审批外,还应审核停送电申请单上填写的设备名称和代码有无不清,防止误停误送。
54、在潮湿的环境下进行电焊作业,应注意脚下绝缘隔离,防止以外漏电触电身亡。
55、运行中的设备和皮带严禁跨越和用手触摸。
56、皮带运行中,严禁头尾轮清料和打扫卫生。
57、巡检中必须手拉扶手,注意脚下防滑。
58、夜间高空、偏远处巡检或处理问题时,应有两人以上,无两人时,应主动与生产调度或中控操作人员取得联系,随时沟通情况,防止意外。
59、多人需要同时登高时,上方人员应将随身携带的工器具系牢,防止坠落伤人。
最好尽量避开同时登高。
60、生产岗位人员在现场作业时,应正确穿戴劳动保护用品,严格做到工作服“三紧”。
61、码头吊机工要经常检查各设备绞点、制动器、脚刹、减速机、齿轮及耦合器润滑情况,同时要检查大臂和钢丝绳有无磨损和断丝情况。
62、吸附机操作人员在卸水泥作业时,必须在码头前沿的防护栏内并系好安全带,方可作业。
63、公司住宿安全管理规定,严禁在宿舍内使用电炉、热得快、电炒锅等大功率用电器,防止火灾和触电事故发生。
64、压力容器是指承受流体压力的密闭容器。
65、我公司使用的压力容器一般为Ш类容器,其介质为空气。
66、重点防火部位要做到有防火负责人,有防火安全制度,有义务消防员,有消防器材。
67、可燃物质开始燃烧需要最低点温度叫燃点或着火点。
68、电工在进行高压电器柜清灰保养作业前,除必须切断电源外,还应对高压电器柜电容进行放电和做好临时接地工作。
69、安全警示标志一般共分为禁止、警告、指令和提示四类。
70、在计划、布臵、检查、总结、评比生产工作中,同时计划、布臵、检查、总结、评比安全工作。
71、职员及外来人员进入厂区,不准赤脚、赤膊、穿拖鞋、短裤、高跟鞋、带小孩,上班前不准饮酒。
72、事故处理要坚持四不放过原则。
73、电伤是电流对人体外部造成的伤害。
主要有电弧灼伤、接触灼伤、点烙印、皮肤金属化。
74、皮肤被浓硫酸灼伤时,不得先用水冲洗,应立即用干净纱布把皮肤上的酸抹去后再用水洗净。
75、轻伤事故是指折算损失工作日低于105日电失能伤害。
76、重伤事故是指折算损失工作日等于和超过105日的失能伤害。
77、非责任事故是指由于自然界的因素而造成不可抗拒的事故或由于未知领域的技术问题而发生的事故。
78、事故的直接责任者是指对事故发生有直接责任的人员。
79、物因事故隐患是指由于物的不安全状态而产生的隐患。
80、人因事故隐患是指由于人的不安全思想和不安全性为而产生的隐患。
81、我公司安全管理的最高机构是安全生产委员会。
82、停送电不能口头预约,不能在送电单上预约送电时间。
83、设备在送电出现跳闸等情况,不得再次送电,应立即查明原因并处理后方可再次送电。
84、设备停送电手续原则上坚持“谁申请停电,谁申请送电”,如中间需他人接替,需办理书面委托单。
85、电工在查电器故障时可不办理停送电申请手续,当送电会危及作业人员安全时,必须履行停电、验电、挂牌、工作完毕、拆牌、送电、验电”的程序。
86、开关磨门等高空作业应佩戴好安全带,并检查手柄、锤头和锤把不能染有油脂,以免锤头脱手和锤子打滑伤人,高空作业禁止向下扔杂物,以防伤人。
87、进入料仓(库)必须穿戴好劳动保护用品,同时在人数上要具备三人以上并制定专人监护。
88、皮带启动不起来或打滑时,严禁用脚蹬、手拉、压杆子等办法处理。
89、在进行斗提内部检修时,应切断电源,操作开关打至断开位臵,更换链条、料斗时,应紧固牢靠。
90、检查斗提,如用辅传运行,应注意上下通讯联系,听从检修人员指挥,禁止随意开、停机。
91、严禁氧气与乙炔气、油脂类、易燃物品同库混存,气瓶阀门和试压表绝对不许沾染油污、油脂,以防引起燃烧和爆炸。
92、发放氧气时,应告知使用人员不得将瓶内氧气全部用完,必须按规定保持瓶内有一定的气压。
93、对于存有残余油脂或可燃液体、可燃气体的容器,应先采取清洗措施,清洗干净后,方可焊接,密封容器不可焊接。
94、对变电所进行倒闸操作时,应保持头脑清醒,做到“一站、二看、三操作”,在巡视高、低压设备应保持一定的安全距离。
95、高压设施发生接地,室内不得接近故障点4米以内,室外不得接近故障点8米以内,进入上述范围的人员必须穿绝缘鞋、戴绝缘手套。
96、进入高压室内巡检时,应随手关门,防止小动物进入室内。
97、电气设备停电后,在未经拉开刀闸和做好安全措施以前,应视为有电,不得触及设备或近距离靠近,以防突然来电。
98、停电倒闸必须先停开关,再拉小车,按顺序依次操作。
99、冬季使用氧气瓶时,若瓶阀冻结,可用热水和水蒸气加热解冻,严禁火焰加热、烘烤。
100、砂轮机操作时,应穿戴好劳动防护用品(如眼镜等),不可戴手套操作,不可站在砂轮的正面。
101、开启主机前,必须先开袋式收尘器设备,停主机之后再停收尘器。
102、对新进、扩展、改进项目,必须贯彻“三同时“原则,符合国家环保法及企业卫生规定。
103、企业袋式收尘器要保持良好运行,未经管理部门审批,公司领导批准,任何班组不得随意拆除收尘器设备设施。
104、根据环保管理制度规定,环保设备要当作主机设备来管理。
105、根据环保管理制度规定,环保设施运行和检查维护必须建立运行记录和管理台帐。
106、公司环保管理应建立健全各项管理制度,同时,对环保突发污染事件还应制定应急预案。
