中学教学资料三视图专项练习题
2019-2020届初三 中考复习 三视图 综合题 专项练习(含答案解析)教学提纲
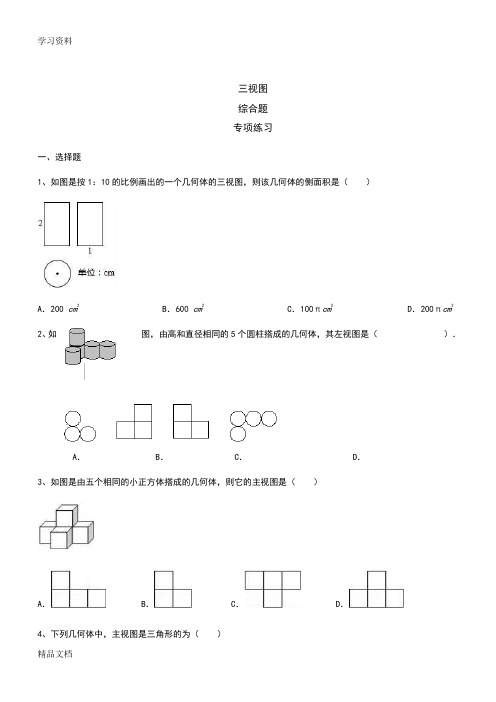
三视图综合题专项练习一、选择题1、如图是按1:10的比例画出的一个几何体的三视图,则该几何体的侧面积是()A.200 cm2 B.600 cm2 C.100πcm2 D.200πcm2 2、如图,由高和直径相同的5个圆柱搭成的几何体,其左视图是().A. B. C. D.3、如图是由五个相同的小正方体搭成的几何体,则它的主视图是()A. B. C. D.4、下列几何体中,主视图是三角形的为()A. B. C. D.5、观察下列几何体,主视图、左视图和俯视图都是矩形的是()A. B. C. D.6、如图是某几何体的三视图及相关数据,则判断正确的是()A.a>c B.b>c C.4a2+b2=c2 D.a2+b2=c27、如图是由一些相同的小正方体搭成的几何体的三视图,搭成这个几何体的小正方体个数是( ) A.2个B.3个C.4个D.6个8、如图所示的几何体的俯视图是()9、如图是一个由5个相同的正方体组成的立体图形,它的三视图是()A. B.C. D.10、已知某几何体的三视图如图所示,则该几何体的体积为()A. B. C. D.二、填空题11、如图是由两个长方体组合而成的一个立体图形的三视图,根据图中所标尺寸(单位:cm),计算出这个立体图形的表面积是________cm2.12、如图,方桌正上方的灯泡(看作一个点)发出的光线照射方桌后,在地面上形成阴影(正方形)示意图,已知方桌边长1.2 m,桌面离地面1.2 m,灯泡离地面3.6 m,则地面上阴影部分的面积为________.13、如图是由几个相同的小立方块组成的三视图,小立方块的个数是 .14、长方体的主视图与俯视图如图297,则这个长方体的体积是________.图29715、三棱柱的三视图如图6226,在△EFG中,EF=8 cm,EG=12 cm,∠EGF=30°,则AB的长为____________cm.16、.图11-1是三个直立于水平面上的形状完全相同的几何体(下底面为圆面,单位:cm).将它们拼成如图11-2的新几何体,则该新几何体的体积为_______________cm3.(计算结果保留)17、一位美术老师在课堂上进行立体模型素描教学时,把14个棱长为1分米的正方体摆在课桌上成如图6形式,然后他把露出的表面都涂上不同的颜色,则被他涂上颜色部分的面积为______.18、一个长方体的主视图和左视图如图所示(单位:cm),则其俯视图的面积是_______________.19、如图,分别是由若干个完全相同的小正方体组成的一个物体的主视图和俯视图,则组成这个物体的小正方体的个数是个.20、如图所示是用小立方块搭成的几何体的主视图、俯视图,它最少需要___________个小立方块,最多需要_____________个小立方块.三、简答题21、一个零件的主视图、左视图、俯视图如图所示(尺寸单位:厘米),(1)这个零件是什么几何体?(2)求这个零件的表面积、体积(结果保留π)22、某几何体的主视图、左视图和俯视图分别如图,试求该几何体的体积.23、由6个相同的小立方块搭成的几何体如图所示,请画出从三个方向看所得到的形状图.24、如图,下列是一个机器零件的毛坯,请将这个机器零件的三视图补充完整.25、已知图为一几何体从不同方向看的图形:(1)写出这个几何体的名称;(2)任意画出这个几何体的一种表面展开图;(3)若长方形的高为10厘米,三角形的边长为4厘米,求这个几何体的侧面积.26、画图:(1)画出圆锥的三视图.已知∠AOB,用直尺和圆规作∠A′O′B′=∠AOB(要求:不写作法,保留作图痕迹)27、如图是一个几何体的二视图(左图为正视图,右图为俯视图),求该几何体的体积(л取3.14).28、由一些大小相同的小正方体组成的简单几何体的主视图和俯视图(如图11). (1)请你画出这个几何体的一种左视图;(2分)(2)若组成这个几何体的小正方体的块数为n,请你写出n的所有可能值.(4分)29、如图是一个由若干个棱长相等的正方体构成的几何体的三视图。
三视图(20个含答案)
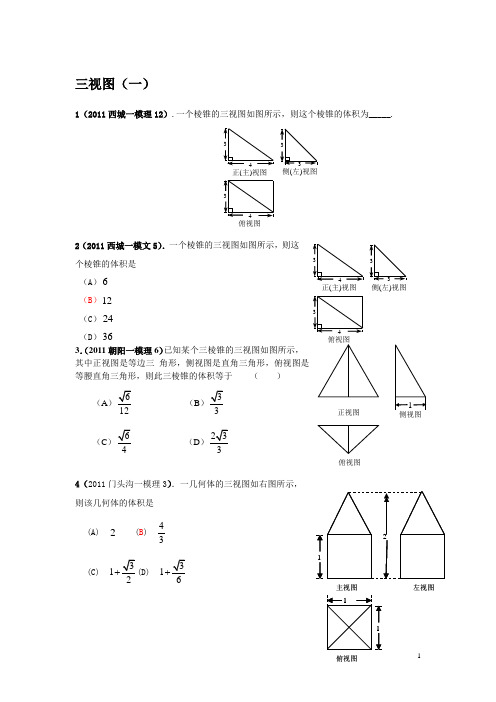
三视图(一)1(2011西城一模理12).一个棱锥的三视图如图所示,则这个棱锥的体积为_____.2(2011西城一模文5).一个棱锥的三视图如图所示,则这个棱锥的体积是(A)6(B)12(C)24(D)363.(2011朝阳一模理6)已知某个三棱锥的三视图如图所示,其中正视图是等边三角形,侧视图是直角三角形,俯视图是等腰直角三角形,则此三棱锥的体积等于()(A )612(B )33(C )64(D )2334(2011门头沟一模理3).一几何体的三视图如右图所示,则该几何体的体积是(A) 2 (B) 4 3(C)312+(D)316+正(主)视图俯视图侧(左)视图3443 33正(主)视图俯视图侧(左)视图3443 33侧视图正视图1俯视图2主视图左视图111ABC DO EA 1B 1C 1D 1 5(2011石景山一模理4).一个空间几何体的三视图及部分数据如图所示(单位:cm ),则这个几何体的体积是( ) A . 33cm B .352cm C . 32cm D .332cm6(2011朝阳一模文6.)已知三棱锥的三视图如图所示,其中侧视图为直角三角形,俯视图为等腰直角三角形,则此三棱锥的体积等于()(A )23(B )33(C )223 (D )2337(2011丰台文5).如图所示,O 是正方体ABCD -A 1B 1C 1D 1对角线A 1C 与AC 1的交点,E 为棱BB 1的中点,则空间四边形OEC 1D 1在正方体各面上的正投影不可能...是( )8(2011海淀一模文11). 如图,在正方体1111ABCD A B C D -中,点P 是上底面1111A B C D 内一动点,则三棱锥P ABC -的主视图与左视图的面积的比值为_____.(A) (B) (C) (D)正视图俯视图侧视图13PDCBA1A 1D 1B 1C 左视主视9(2011门头沟一模文10).一几何体的三视图如左下图所示,则该几何体的体积是10(2011石景山一模文4).一个空间几何体的三视图及部分数据如图所示 (单位:cm ),则这个几何体的表面积是( ) A .29πcm B .212πcm C .215πcm D .224πcm参考答案:1.122.B3.B4.B5.D6.B7.A _8._1__9. 3710.D俯视23主视左视11(第10题(二)1(10。
三视图练习题含答案
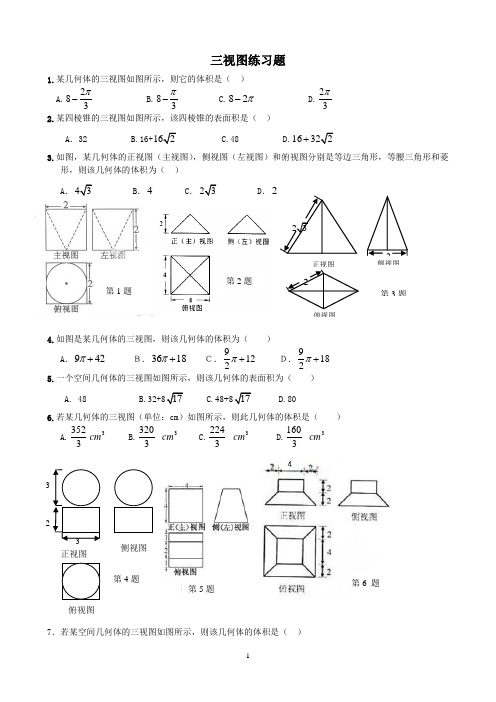
23正视图侧视图2俯视图2第3题三视图练习题1.某几何体的三视图如图所示,则它的体积是( ) A.283π-B.83π-C.π28-D.23π 2.某四棱锥的三视图如图所示,该四棱锥的表面积是( )A .32 B.16+162 C.48 D.16322+3.如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是等边三角形,等腰三角形和菱形,则该几何体的体积为( ) A .43 B .4 C .23 D .24.如图是某几何体的三视图,则该几何体的体积为( )A .942π+ B.3618π+ C.9122π+ D.9182π+ 5.一个空间几何体的三视图如图所示,则该几何体的表面积为( )A. 48B.32+817C.48+817D.806.若某几何体的三视图(单位:cm )如图所示,则此几何体的体积是( ) A.35233cm B.3203 3cm C.2243 3cm D.16033cm7.若某空间几何体的三视图如图所示,则该几何体的体积是( )3 32正视图侧视图俯视图第4题第5题第1题 第2题第6 题A.2B.1C.23D.138.某几何体的三视图如图所示,则该几何体的体积为( )A.π816+B. π88+C. π1616+D. π168+ 9. 某四棱台的三视图如图所示,则该四棱台的体积是( ) A.4 B.314 C.316D.610. 某三棱锥的三视图如图所示,已知该三视图中正视图和俯视图均为边长为2的正三角形,侧视图为如图所示的直角三角形,则该三棱锥的体积为( ) A .1 B .3 C .4D .511. 一个几何体的三视图如图所示,则这个几何体的体积为( )A .(8)36π+ B .(82)36π+ C .(6)36π+ D .(92)36π+12.某几何体的底面为正方形,其三视图如图所示,则该几何体的体积等于( )A .1B .2C .3D .413.某几何体的三视图如图所示,则其体积为______.14.若某几何体的三视图(单位:cm )如图所示,则此几何体的体积等于______3cm . 15.某几何体的三视图如图所示,则该几何体的体积是______.第7题第8题第9题第10题3122第11题 211俯视图正视图13第12题16.已知某三棱锥的三视图(单位:cm )如图所示,则该三棱锥的体积是 17.一个空间几何体的三视图如图所示,则这个空间几何体的体积是 .18.如图所示,一个三棱锥的三视图是三个直角三角形,则该三棱锥外接球的表面积为19.若某空间几何体的三视图如下图所示,则该几何体的表面积是_______________.20.一个正方体的内切球与它的外接球的体积比是( ).A .1∶33B .1∶22C .1∶383D .1∶4221.已知球面上A 、B 、C 三点的截面和球心的距离都是球半径的一半,且AB =BC =CA =2,则球表面积是( ) A.π964 B. π38 C. π4 D. π91622. P 、A 、B 、C 是球O 面上的四点,且PA 、PB 、PC 的两两垂直,PA=PB=PC=9,则球心O 到截面ABC 的距离为23.半径为5的球被一个平面所截,截面面积为16π,则球心到截面的距离为 ( ) A. 4 B.3 C.2.5 D. 224.表面积为3π的圆锥,它的侧面展开图是一个半圆,则该圆锥的底面直径为________.第17题 24 3正视图 侧视图 俯视图第18题 第15题第14题第13题第16题 第19题25. 当圆锥的侧面积与底面积的比值是2时,圆锥的轴截面的顶角等于 26.一平面截一球得到直径是6的圆面,球心到这个平面的距离是4,则该球的体积为 27.一个正四面体的棱长为2,四个顶点在同一个球面上,则此球的表面积为 28.已知一个三棱锥ABC P -的三条侧棱PC PB PA ,,两两垂直,且长度分别为2,3,4,则 该棱锥的外接球的表面积为29.已知用斜二测画法得到的正方形的直观图的面积为218,则原来正方形的面积为 30.正三棱锥的高为1,底面边长为62,正三棱锥内有一个球与其四个面相切.求该棱锥的表面积与体积,内切球的半径.31. 在球心同侧有相距cm 9的两个平行截面,它们的面积分别为249cm π和2400cm π.求球的表面积.32. 球面上有三点A 、B 、C 组成这个球的一个截面的内接三角形三个顶点,其中18=AB ,24=BC 、30=AC ,球心到这个截面的距离为球半径的一半,求球的表面积.答案1.A2.B3.C4.D5.C6.B7.B8.A9.B 10.A 11.A 12.A 13.3π 14.24 15.1616-π 16.1 17.67π 18.29π 19. 20+8220.A 21.A 22.233 23.B 24. 2 25.︒9026.3500π 27.π628.π29 29.72 30. 3629+32 26-31.2500π 32.π1200。
中考三视图练习题

中考三视图练习题一、选择题1. 下列哪个选项是正确的主视图?A. 左视图B. 俯视图C. 右视图D. 仰视图2. 三视图包括哪三个视图?A. 俯视图、左视图、右视图B. 主视图、俯视图、左视图C. 仰视图、俯视图、左视图D. 仰视图、右视图、左视图3. 观察一个物体时,哪个视图可以提供物体的宽度信息?A. 主视图B. 俯视图C. 左视图D. 仰视图4. 下列哪个选项是正确的俯视图?A. 显示物体的顶面形状B. 显示物体的侧面形状C. 显示物体的正面形状D. 显示物体的底面形状5. 当物体的主视图和左视图都相同,且都是矩形时,该物体可能是:A. 立方体B. 圆柱体C. 长方体D. 球体二、填空题6. 在三视图中,______视图显示物体的正面形状。
7. 当物体的主视图和俯视图都是圆形时,该物体可能是______。
8. 一个物体的三视图可以提供物体的______、______和______三个方向的信息。
9. 俯视图通常显示物体的______面形状。
10. 如果一个物体的主视图和左视图都是正方形,那么该物体可能是______。
三、判断题11. 一个物体的主视图和左视图可能完全不同。
()12. 三视图中的任何一个视图都不能单独表示物体的全部信息。
()13. 俯视图可以提供物体的高度信息。
()14. 物体的三视图是相互独立的,没有联系。
()15. 一个物体的三视图可以完全相同的情况是不存在的。
()四、简答题16. 请简述三视图在工程制图中的应用意义。
17. 描述如何通过三视图来确定一个物体的形状。
五、绘图题18. 根据以下描述,绘制一个物体的三视图:- 主视图:一个矩形,长为10cm,宽为5cm。
- 俯视图:一个矩形,长为8cm,宽为6cm。
- 左视图:一个矩形,长为10cm,宽为8cm。
19. 假设你面前有一个立方体,其边长为4cm,请绘制其三视图。
六、综合应用题20. 你是一名工程师,需要根据客户提供的三视图来制作一个零件。
三视图习题(含答案)

几何体的三视图练习题1、若某空间几何体的三视图如图所示,则该几何体的体积是 ( )(A )2(B )1(C )23(D )132、一个几何体的三视图如图,该几何体的表面积是 ( ) (A )372 (B )360 (C )292 (D )2803、若某几何体的三视图(单位:cm )如图所示,则此几何体的体积是 (A )3523cm 3 (B )3203cm 3 (C )2243cm 3 (D )1603cm 34、一个长方体去掉一个小长方体,所得几何体的正(主)视图与侧(左)视图分别如右图所示,则该几何体的俯视图为: ( )5、若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积...等于 ( ) A.2 C..66、图2中的三个直角三角形是一个体积为20cm 2的几何体的三视图,则h= cm第2题第5题7、一个几何体的三视图如图所示,则这个几何体的体积为 。
8、如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为______.9、如图1,△ ABC 为正三角形,AA '//BB ' //CC ' , CC ' ⊥平面ABC 且3AA '=32BB '=CC '=AB,则多面体△ABC -A B C '''的正视图(也称主视图)是( )10、一空间几何体的三视图如图所示,的体积为().A.2π+B. 4π+C. 23π+D. 43π+11、上图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )A .9πB .10πC .11πD .12π12、一个棱锥的三视图如图,则该棱锥的全面积(单位:c 2m )为 ( )第7题侧(左)视图正(主)视俯视图俯视图 正(主)视图 侧(左)视图(A )(B )(C )(D )13、若某几何体的三视图(单位:cm )如图所示,则此几何体的体积是 3cm .14、设某几何体的三视图如上图所示。
九年级数学三视图专项测试(含答案)

学生做题前请先回答以下问题问题1:观察一个几何体的形状通常从三个方面看,从_____看(主视图),从____看(____),从______看(____).问题2:正方形的展开图有哪几种?三视图专项测试一、单选题(共7道,每道14分)1.如图是由若干个大小相同的小正方体堆砌而成的几何体.那么其三种视图中面积最小的是( )A.主视图B.左视图C.俯视图D.三种一样答案:B解题思路:试题难度:三颗星知识点:几何体的三视图2.如图是由若干个同样大小的立方体搭成的几何体的俯视图,小正方形中的数字表示该位置立方体的个数,则这个几何体的左视图是( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:几何体的三视图3.一个铁制零件(正方体中间挖去一个圆柱形孔)如图放置,它的左视图是( )A. B.C. D.解题思路:试题难度:三颗星知识点:简单几何体的三视图4.如图是每个面上都有一个汉字的正方体的一种平面展开图,那么在原正方体中和“国”字相对的面上的字是( )A.中B.钓C.鱼D.岛答案:C解题思路:试题难度:三颗星知识点:正方体的展开图5.如图是每个面上都有一个汉字的正方体的一种展开图,那么在原正方体中与“着”字相对的面上的汉字是( )A.冷B.静C.应D.考解题思路:试题难度:三颗星知识点:正方体展开图---相对面6.如图所示的正方体的展开图可能是( )A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:正方体的展开与折叠7.长方体的主视图与左视图如图所示(单位:m),则其俯视图的面积是( )A.12m2B.8m2C.6m2D.4m2答案:A解题思路:试题难度:三颗星知识点:三视图的面积应用。
三视图专项练习-九年级数学下册基础知识专项讲练浙教版

专题3.2 三视图(专项练习)一、单选题1.下面的几何体的左视图是()A.B.C.D.2.如图所示的几何体,它的左视图是()A.B.C.D.3.下面两幅图是由5个小正方体搭成的几何体的主视图与俯视图,则搭成这个几何体的左视图为()A.B.C.D.4.如图所示几何体的俯视图是()A.B.C.D.5.下列四种说法,正确的是()A.圆柱的侧面是长方形B.射线AB与射线BA表示同一条射线C.两点之间,直线最短D.两点确定一条直线6.如图,由4个完全相同的小正方体组合成一个立体图形,它的俯视图是( )A.B.C.D.7.如图所示的几何体的俯视图是( )A.B.C.D.8.用小立方块搭一个几何体,使得它的主视图和俯视图如图所示,则最少需要小立方块的个数为( )A.6B.7C.10D.139.观察下列几何体,主视图、左视图和俯视图都是矩形的是()A.B.C.D.10.如图所示的是由几个棱长为1的小立方体块搭成的几何体从上往下看的平面图形,小正方形中的数字表示该位置上小立方块的个数,则这个几何体的体积是()A.12B.46C.60D.1311.如图所示的几何体的俯视图是()A.B.C.D.12.如图,矩形的长与宽分别为a和b,在矩形中截取两个大小相同的圆作为圆柱的上下底面,剩余的矩形作为圆柱的侧面,刚好能组合成一个没有空隙的圆柱,则a和b要满足的数量关系是( )A .B .C .D .121a b π=+221ab π=+122a b π=+21a b π=+二、填空题13.用小立方块搭成的几何体从正面和上面看的视图如图,这个几何体中小立方块的个数最多有_________个.14.有一个正方体,六个面上分别写有数字1,2,3,4,5,6,如图是我们能看到的三种情况,如果记6的对面数字为a ,2的对面数字为b ,那么a +b 的值为_____.15.如图是某个几何体的三视图,该几何体是____.16.如图是一个几何体从三个不同方向看得到的形状图.根据图中数据(单位:cm ),可求它的表面积为_____cm 2.(结果保留π)17.如图是由一些相同的小正方体构成的立体图形的三种视图,则构成这个立体图形的小正方体的个数是______个.18.一个几何体由若干大小相同的小立方块搭成的,如图分别是从它的左面,上面看到的平面图形,则组成这个几何体的小立方块最多有_____个.19.如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是___________.20.如果按图中虚线对折可以做成一个上底面为无盖的盒子,那么该盒子的下底面的字母是________.21.把下图折成正方体后,如果相对面所对应的值相等,那么xy的值为_________.三、解答题22.用相同的小立方体搭一个几何体,从正面、上面看到的形状图如图所示,从上面看到的形状图中小正方形的字母表示在该位置上小立方体的个数,请回答下列问题:(1)a ,b ,c 各表示的数字是几?(2)这个几何体最多由几个小立方体搭成?最少呢?(3)当,时,画出这个几何体从左面看得到的形状图.1d e ==2f =23.如图所示的是从上面看12个小立方体所搭几何体的平面图形,小正方形中的数字表示在该位置的小立方体的个数,请画出从正面和左面看这个几何体的形状.参考答案1.D【分析】根据几何体的特点即可求解.【详解】从左边看,第一排三个正方形,第二排两个,第三排一个.即D故选.【点睛】此题主要考查三视图的判断,解题的关键是熟知左视图的定义.2.A【分析】根据从左边看得到的图形是左视图,能够看到的线用实线,看不到的线用虚线,可得答案.【详解】解:从左边看是一个矩形,矩形上方有一条水平的虚线,故选:A.【点睛】本题考查了简单组合体的三视图,从左边看得到的图形是左视图.3.A【分析】由已知条件可知,左视图有2列,每列小正方形数目分别为1,2,据此可画出图形.【详解】这个几何体的左视图为.故选:A.本题考查了几何体的三视图画法.由几何体的俯视图及小正方形内的数字,可知主视图的列数与俯视数的列数相同,且每列小正方形数目为俯视图中该列小正方形数字中的最大数字.左视图的列数与俯视图的行数相同,且每列小正方形数目为俯视图中相应行中正方形数字中的最大数字.4.D【分析】直接找出从上面看到的图形即可.【详解】解:该几何体的俯视图为,故选:D.【点睛】本题考查几何体的三视图,注意看不到的边要用虚线表示出来.5.D【分析】根据几何体的侧面展开图,射线的定义,两点间的距离,直线的性质依次判断.【详解】A、圆柱的侧面展开图是长方形,故该项错误;B、射线AB与射线BA不表示同一条射线,故该项错误;C、两点之间,线段最短,故该项错误;D、两点确定一条直线,故该项正确;故选:D.【点睛】此题考查几何体的侧面展开图,射线的定义,两点间的距离,直线的性质,综合掌握各知识点是解题的关键.6.D【分析】根据俯视图的定义从上向下看几何体,即可得到其俯视图.解:∵从上向下看该几何体,可得到下图:∴选项D符合题意.故选:D【点睛】本题考查了简单组合体的三视图的知识,俯视图是从上往下看得到的平面图形.7.C【分析】根据三视图中俯视图的画法以及注意事项画图即可得解.【详解】解:∵∴该几何体的俯视图是:.故选:C【点睛】本题考查了几何体的三视图,掌握三视图的画法是解题的关键,同时需要注意:在三视图中,分界线和可见轮廓线都用实线画出,不可见的轮廓线用虚线画出;还需明确所选的图为该几何体的俯视图,而不是主视图或者左视图.8.C【分析】从主视图和左视图考查几何体的形状,从俯视图看出几何体的小立方块最少与最多的数目.【详解】解:由主视图可知,它自下而上共有3列,第一列3块,第二列2块,第三列1块.由俯视图可知,它自左而右共有3列,第一列与第二列各3块,第三列1块,从空中俯视的块数只要最底层有一块即可.因此,综合两图可知这个几何体的形状不能确定;并且最少时为第一列中有一个三层,其余为一层,第二列中有一个二层,其余为一层,第三列一层,共10块.故选:C.【点睛】本题考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,主视图疯狂盖,左视图拆违章”就更容易得到答案.9.B【分析】根据这些几何体的三视图判断选项的正确性.【详解】A、主视图为矩形,俯视图为圆,错误;B、主视图为矩形,左视图为矩形,俯视图为矩形,正确;C、主视图为等腰梯形,俯视图为圆环,错误;D、主视图为三角形,俯视图为有对角线的矩形,错误.故选B.【点睛】本题考查几何体的三视图,解题的关键是掌握一些常见几何体的三视图.10.A【分析】先根据正方体的体积公式:V=L3,计算出一个正方体的体积,再数出几何体中小立方块的个数,相乘即可求解.【详解】解:(1×1×1)×(2+3+1+2+4)=1×12答:这个几何体的体积是12cm 3.故选择:A .【点睛】考查了由三视图判断几何体,关键是熟悉正方体的体积公式,通过几何体中小立方块的个数求得体积.11.B 【分析】根据俯视图的定义判断即可.【详解】由题意得:该几何体的俯视图为一个长方形,中间有一个圆形.故选B .【点睛】本题考查三视图的辨别,灵活的空间想象能力是解题关键.12.D 【分析】利用圆柱的底面周长等于剩余长方形的长,列出方程,整理可得答案.【详解】解:组成圆柱后,圆柱的底面周长=剩余长方形的长. 即,22a a b π∴=-()12,a b π+=整理得:.21a b π=+故选:D .【点睛】本题考查的是圆柱的展开图,解决本题的关键是得到圆柱的底面周长和剩余长方形的长之间的等量关系.13.10.根据俯视图和主视图,确定每一层正方体可能有的个数,最后求和即可.【详解】解:从俯视图可以看出,下面的一层有6个,由主视图可以知道在中间一列的一个正方体上面可以放2个或在一个上放2个,另一个上放1或2个.所以小立方块的个数可以是个,个,个.所以最多的628+=6219++=62210++=有10个.故答案为10.【点睛】本题主要考查了通过三视图确定立方体的数量,正确理解俯视图和主视图以及较好的空间想象能力是解答本题的关键.14.7【分析】从图形进行分析,结合正方体的基本性质,得到对面的数字,即可求得结果.【详解】一个正方体已知1,4,6,第二个正方体已知1,2,3,第三个正方体已知2,5,6,且不同的面上写的数字各不相同,可求得1的对面数字为5,6的对面数字为3,2的对面数字为4∴a +b =7故答案为:7.【点睛】本题考查正方体相对两个面的数字,根据相邻的面确定出对面上的数字是解题的关键.15.圆锥.【分析】根据主视图与左视图均是三角形,俯视图是圆,可判断出几何体是圆锥.【详解】主视图与左视图均是三角形,俯视图是圆,可知几何体是圆锥,故答案为:圆锥.【点睛】本题考察几何体的三视图,解题关键是熟悉常见几何体的三视图.16.8π【分析】先根据三视图判断几何体的形状,然后根据表面积计算即可.【详解】解:根据三视图可得该几何体是圆柱;则圆柱表面积2×π×12+2π×3=8π(cm 2).故答案是:8π【点睛】本题考查三视图,几何体的表面积,体积等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.17.8【分析】易得这个几何体共有2层,由俯视图可得第一层正方体的个数,由主视图和左视图可得第二层正方体的个数,相加即可.【详解】解:由俯视图易得最底层有6个正方体,第二层有2个正方体,那么共有个正方628+=体组成.故答案为:8.【点睛】考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查,如果掌握口诀“俯视图打地基,主视图疯狂盖,左视图拆违章”就更容易得到答案.18.5【分析】从左面看与上面看的图形,得到俯视图中最左的一列都为2层,第2列都为1层,得到最多共3+2=5个小正方体.【详解】根据左面看与上面看的图形,得到俯视图中最左的一列都为2层,第2列都为1层,得到最多共3+2=5个小正方体.解:根据俯视图发现最底层由3个小立方块,从左视图发现第二层最多有2个小立方块,故最多有3+2=5个小立方块,故答案为:5.【点睛】本题考查几何体的三视图,是重要考点,难度较易,掌握相关知识是解题关键.19.明【分析】这种展开图是属于“1,4,1”的类型,其中,上面的1和下面的1是相对的2个面.【详解】由正方体的展开图特点可得:“建”和“明”相对;“设”和“丽”相对;“美”和“三”相对;故答案为:明.【点睛】此题考查正方体相对两个面上的文字的知识;掌握常见类型展开图相对面上的两个字的特点是解决本题的关键.20.C【解析】正方体的表面展开图,相对的面之间一定相隔一个正方形,利用正方体及其表面展开图的特点解题.正方体的表面展开图,相对的面之间一定相隔一个正方形,“A”与“C”是相对面,“E”与“D”是相对面,“B”与盒盖是相对面,故答案为B.“点睛”本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.21.2.【解析】正方体的表面展开图,相对的面之间一定相隔一个正方形,“x”与“1”是相对面,“y”与“3”是相对面,“5”与“空白空格”是相对面,∵相对面所对应的值相等,∴x=1,y=3,∴xy=3.故答案是:3.22.(1),,;(2)最多由11个小立方体搭成;最少由9个小立方体搭3a =1b =1c =成;(3)见解析.【解析】【分析】(1)由主视图可知,第二列小立方体的个数均为1,第3列小正方体的个数为3,那么b=1,c=1,a=3;(2)第一列小立方体的个数最少为2+1+1,最多为2+2+2,那么加上其它两列小立方体的个数即可;(3)左视图有3列,每列小正方形数目分别为3,1,2.【详解】(1),,;3a =1b =1c =(2)(个),(个).62311++=4239++=这个几何体最多由11个小立方体搭成;最少由9个小立方体搭成.(3)如图所示.【点睛】本题考查由三视图判断几何体及作三视图,解题关键在于熟练掌握几何体的三视图的相关知识.23.见解析.【分析】由已知条件可知,主视图有3列,每列小正方数形数目分别为2,3,4;左视图有2列,每列小正方形数目分别为4,2.据此可画出图形.【详解】如图所示【点睛】考查画几何体的三视图,用到的知识点为:主视图,左视图分别是从物体的正面,左面看得到的图形;看到的正方体的个数为该方向最多的正方体的个数.。
三视图练习题

三视图练习题一、基本概念题1. 请简述三视图的概念及其作用。
2. 三视图包括哪三个视图?分别表示物体的哪些信息?3. 在三视图中,主视图、俯视图和左视图之间的位置关系是怎样的?二、识图题(1)正方体(2)长方体(3)圆柱体(1)球体(2)圆锥体(3)圆环体(1)三棱柱(2)四棱锥(3)六棱柱三、绘图题(1)一个长方体,长、宽、高分别为10cm、6cm、4cm。
(2)一个圆柱体,底面直径为8cm,高为10cm。
(3)一个圆锥体,底面直径为6cm,高为8cm。
(1)一把直尺(2)一个手机(3)一个茶壶四、分析题(1)主视图为矩形,俯视图为圆形,左视图为矩形。
(2)主视图为三角形,俯视图为矩形,左视图为三角形。
(1)主视图、俯视图和左视图均为正方形。
(2)主视图、俯视图和左视图均为圆形。
五、应用题(1)主视图为长方形,长、宽、高分别为10cm、6cm、4cm。
(2)主视图为圆形,直径为8cm,高为10cm。
(1)一个长方体木箱,长、宽、高分别为60cm、40cm、20cm。
(2)一个圆柱形水桶,底面直径为40cm,高为50cm。
六、综合题(1)一个长方体上放置一个正方体。
(2)一个圆柱体和一个圆锥体组合在一起。
(1)一个长方体挖去一个圆柱体形成的组合体,长方体的长、宽、高分别为20cm、10cm、5cm,圆柱体直径为5cm,高为10cm。
(2)一个正方体和一个四棱锥组合在一起,正方体边长为8cm,四棱锥底面边长为6cm,高为4cm。
七、判断题1. 三视图中,主视图和俯视图的长度方向一定相同。
()2. 在三视图中,左视图的宽度方向与主视图的高度方向一致。
()3. 任何物体的三视图都可以通过旋转和翻转得到。
()八、选择题A. 主视图B. 俯视图C. 正视图D. 左视图A. 主视图B. 俯视图C. 左视图D. 所有视图A. 主视图反映了物体的长度和高度B. 俯视图反映了物体的长度和宽度C. 左视图反映了物体的宽度和高度D. 三视图中的每个视图都包含了物体的所有尺寸信息九、填空题1. 三视图是用于表达物体______、______和______三个方向尺寸的图样。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三视图专项练习
1.(2012年高考福建卷理科4)一个几何体的三视图形状都相同,大小均相等,那么这个几何体不可以是( )
A .球
B .三棱锥
C .正方体
D .圆柱
2.(2012年高考湖南卷理科3)某几何体的正视图和侧视图均如图1所示,则该几何体的俯视图不可能是( )
3.(2012年高考广东卷理科6)某几何体的三视图如图1所示,它的体积为( ) A .12π B.45π C.57π D.81π
4.已知某几何体的三视图如图所示,则它的体积为( ) A .
38π B.3π C. 3
10
π D.6π
5. (2012年高考北京卷理科7)某三棱锥的三视图如图所示,该三梭锥的表面积是( )
6.(课本习题改编)用任意一个平面截一个几何体,各个截面都是圆面,则这个几何体一定是( ).
A .圆柱
B .圆锥
C .球体
D .圆柱、圆锥、球体的组合体
7.(经典习题)某几何体的三视图如图所示,则它的体积是( ). A .8-2π3 B .8-π3 C .8-2π D.2π
3
8..(2012届高三年级第二次综合练习文)如图,一个空间几何体的正视
图、侧视图、俯视图均为全等的等腰直角三角形,如果直角三角形的直角边长都为1,那么这个几何体的表面积为
A .
6
1
B .23
C .
32+ D .32+
9.(北京市西城区2012届高三4月第一次模拟考试试题理)已知正六棱柱
的底面边长和侧棱长相等,体积为3.其三视图中的俯视图如图所示,则其左视图的面积是( )
(A )2(B )2(C )2
8cm (D )2
4cm
10.(2012年云南省第一次统一检测理)下图是一个几何体的三视图,其中正视图是边长为2的等边三角形,侧视图是直角边长分别为1与3的直角三角形,俯视图是半径为1的半圆,则该几何体的体积等于
(A )
π63 (B )π33 (C )π334 (D )π2
1
11. (山西省2012年高考考前适应性训练文)已知某几何体的体积为4
π,它的正视图、侧视图均为边长为1
的正方形,则该几何体的俯视图可以为( )
D
C
B A
12.(湖北武汉2012适应性训练理)一个多面体的三视图如图所示,其中正视
图是正方形,侧视图是等腰三角形. 则该几何体的表面积为 A . 88 B .98 C .108 D .158
13.(湖北省武汉市
2012届高中毕业生五月供题训练(二)理) 某几何体的正视图如左图所示,则该几何体的俯视图不可能的是
14.(湖北文科数学冲刺试卷(二))
15.(襄阳五中高三年级第一次适应性考试文)一个四棱锥的三视图如图所示,其左视图是等边三角形,该四棱锥的体积等于
A
B .
C .
D .
16.(北京市东城区2011-2012学年度第二学期高三综合练习(二)
理)若一个三棱柱的底面是正三角形,其正(主)视图如图所示,则它的体积为 ( )
(A (B )2
(C )
(D )4
17.已知某几何体的三视图如图所示,则它的体积为( ) A .
21 B.1 C. 43
D.
2
3
18.(河北省唐山市2011—2012学年度高三年级第二次模拟考试理)已知某几何体的三视图如图所示,则其体积为 A .1 B. 34 C. 3
5
D. 2
19.(2012年石家庄市高中毕业班教学质量检测(二)文)已知某几何体的三视图如图所示,则该几何体的表面积为
20.(2012河南豫东豫北十所名校毕业班阶段性测试(三)文) 下图是某宝石
饰物的三视图,已知该饰物的正视图、侧视图都是面积为,且一个内
角为60°的菱形,俯视图为正方形,那么该饰物的表面积为 (A) (B) (C) (D)4
21.(中原六校联谊2012年高三第一次联考文)若某空间几何体的三视图如图所示,则该几何体的体积 A .202π- B . 2203π- C .2403π- D .4
403
π-
22.(2012洛阳示范高中联考高三理)一个棱锥的三视图如图(尺寸的长度单位为m ),则该棱锥的全面积是(单位:m 2
).
正视图 侧视图 俯视图 (A )624+ (B )64+
(C )224+ (D )24+
23.(浙江省2012届重点中学协作体高三第二学期高考仿真试题理)如图为一个几何体的三视图,尺寸如图所示,则该几何体的表面积为
A .π++36
B .π++326
C . π4318++
D .π++3218
24.(怀化2012高三第三次模拟考试文)一个几何体的三视图如右图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该几何体的外接球的表面积为
A .π
B . 2π
C .3π
D .4π
25. (2012东城区普通高中示范校高三综合练习(二)理)一个几何体的三视图如图所示,则此几何体的体积是( )
A .112 B.80 C.72 D.64
26.(2012年石家庄市高中毕业班教学质量检测(二) 理)已知某几何体的三视图如图所示,则该几何体的体积为
A .
364 B .32 C .380 D .3
8+28
27..某几何体的正视图与侧视图如图所示,若该几何体的体积为
1
3
,则该几何体的俯视图可以是
28.一个体积为312的正三棱柱的三视图如图所示,则这个正三棱柱的侧视图的面积为
A 36
B 8
C 38
D 12
二.填空题:
1.(2012年高考辽宁卷理科13)一个几何体的三视图如图所示,则该几何体的表面积为_________。
2.(2011·山东高考改编)如图是长和宽分别相等的两个矩形.给定下列三个命题:①存在三棱柱,其正视图、 俯视图如图;②存在四棱柱,其正视图、俯视图如图; ③存在圆柱,其正视图、俯视图如图.其中真命题的序号是________.
3. (东城区普通高中示范校高三综合练习(二) (文))已知某几何体的三视图如图所示, 则几何体的体积为 .
4.(北京市西城区2012届高三下学期二模试卷理)一个几何体的三视
图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,该几何体的体积是_____;若该几何体的所有顶点在同一球面上,则球的表面积是_____.
5.(长安一中、高新一中、交大附中、师大附中、西安中学高2012届第三次模拟文)已知某几何体的三视图如左图所示,根据图中的尺寸(单位:cm)则此几何体的体积是.
6.(2012年大连沈阳联合考试第二次模拟试题理)如图所示,一个三棱锥
的三视图是三个直角三角形(单位:cm),则该三棱锥的外接球的表面积
为___________cm2.
7.一个几何体的三视图如果所示,则这个几何体的表面积与其外接球面
积之比为。
8.已知某几何体的三视图如图,则该几何体的表面积为__________ .
试题答案:一、选择题:1D;2D;3C;4B;5B;6C;7A;8D;9A;10A;11B;12A;13C;14D;15A;16A;17A;18C;19D;20D;21B;22A;23D;24C;25B;26C;27A;28A;。
