北京市育才学校2014届高三上学期期中考试 理科数学 Word版含答案
北京市海淀区2014届高三上期中考试数学试题(理)及答案

海淀区高三年级第一学期期中练习数学(理科) 答案2013.11一、选择题1、A2、C3、B4、C5、B6、B7、D8、C二、填空题:本大题共6小题,每小题5分,共30分。
9.210..211. a b c >> 12..2π3,π613..2λ>14. 4;6(31)n -三、解答题: 本大题共6小题,共80分。
解答应写出文字说明, 演算步骤或证明过程。
15.解:(Ⅰ)由60A = 和332ABC S ∆=可得133sin6022bc = , ---------------------------2分 所以6bc =, --------------------------------------3分又32,b c =所以2,3b c ==. ------------------------------------5分(Ⅱ)因为2,3b c ==,60A = ,由余弦定理2222cos a b c bc A =+-可得 ------------------------------------7分2222367a =+-=,即7a =. ------------------------------------9分 由正弦定理sin sin a b A B=可得------------------------------------11分 72sin sin60B= ,------------------------------------12分 所以21sin 7B =.------------------------------------13分 16. 解:(I )π()3cos4cos(4)2f x x x =-+------------------------------------2分 3cos4sin 4x x =+------------------------------------4分π2sin(4)3x =+------------------------------------6分()f x 最小正周期为πT 2=,------------------------------------8分 (II )因为ππ64x -≤≤,所以ππ4π4333x -≤+≤-----------------------------------10分 所以3πsin(4)123x -≤+≤-----------------------------------12分 所以π32sin(4)23x -≤+≤, -----------------------------------13分 所以()f x 取值范围为[3,2]-. ------------------------------------14分17.解:(I )由已知11,1AH t PH t =-=+ -------------------------------------1分所以APH ∆的面积为1()(11)1,1112f t t t t =-+-<<. ---------------------4分 (II )解法1. 111'()1(11)2221f t t t t =-++⨯-⨯+ 3(3)41t t -=+ -------------------------------------7分 由'()0f t =得3t =, -------------------------------------8分 函数()f t 与'()f t 在定义域上的情况下表: t(1,3)- 3 (3,11) '()f t+ 0 - ()f t ↗ 极大值 ↘-----------------------------------12分所以当3t =时,函数()f t 取得最大值8. ------------------------------------13分解法2.由211()(11)1(11)(1),11122f t t t t t t =-+=-+-<< 设2()(11)(1),111g t t t t =-+-<<, -------------------------------------6分 则2'()2(11)(1)(11)(11)(1122)3(3)(11)g t t t t t t t t t =--++-=--++=--.-------7分 函数()g t 与'()g t 在定义域上的情况下表: t(1,3)- 3 (3,11) '()g t+ 0 - ()g t ↗ 极大值 ↘------------------------------------11分所以当3t =时,函数()g t 取得最大值, -----------------------------------12分所以当3t =时,函数()f t 取得最大值1(3)82g =.------------------------------------13分 18.解:(I )由②可得2112a a ⋅=,3122a a ⋅= -------------------------------2分由①可得12a =. -------------------------------3分(II )由②可得112n n a a +⋅=, ------------------------------6分所以数列{}n a 的通项公式2n n a =. ------------------------------7分(III )由(II )可得21(1)421n n n n b a +=+=++,易得1{4},{2}n n +分别为公比是4和2的等比数列,------------------------------8分 由等比数列求和公式可得124(14)4(12)1(416)214123n n n n n S n n ++--=++=-++--.--13分19.解:(I )因为1a =,2()42ln f x x x x=-+, 所以2242'()(0)x x f x x x-+=>, ------------------------------1分 (1)3f =-,'(1)0f =, ------------------------------3分 所以切线方程为3y =-. ------------------------------4分(II )222(1)22(1)()'()(0)x a x a x x a f x x x x-++--==>, ----------------------------5分 由'()0f x =得12,1x a x ==, ------------------------------6分 当01a <<时,在(0,)x a ∈或(1,)x ∈+∞时'()0f x >,在(,1)x a ∈时'()0f x <,所以()f x 的单调增区间是(0,)a 和(1,)+∞,单调减区间是(,1)a ; ---------------7分 当1a =时,在(0,)x ∈+∞时'()0f x ≥,所以()f x 的单调增区间是(0,)+∞;-----8分 当1a >时,在(0,1)x ∈或(,)x a ∈+∞时'()0f x >,在(1,)x a ∈时'()0f x <.所以()f x 的单调增区间是(0,1)和(,)a +∞,单调减区间是(1,)a . ---------------10分 (III )由(II )可知()f x 在区间[1,e]上只可能有极小值点,所以()f x 在区间[1,e]上的最大值在区间的端点处取到,-------------------------12分 即有(1)12(1)0f a =-+≤且2(e)e 2(1)e 20f a a =-++≤, 解得2e 2e 2e 2a -≥-. ---------------------14分 20.解:(I )27,9,3;8,9,3;6,2,3. --------------------------------------3分(II )若k a 被3除余1,则由已知可得11k k a a +=+,2312,(2)3k k k k a a a a ++=+=+; 若k a 被3除余2,则由已知可得11k k a a +=+,21(1)3k k a a +=+,31(1)13k k a a +≤++;若k a 被3除余0,则由已知可得113k k a a +=,3123k k a a +≤+; 所以3123k k a a +≤+, 所以312(2)(3)33k k k k k a a a a a +-≥-+=- 所以,对于数列{}n a 中的任意一项k a ,“若3k a >,则3k k a a +>”. 因为*k a ∈N ,所以31k k a a +-≥.所以数列{}n a 中必存在某一项3m a ≤(否则会与上述结论矛盾!)若3m a =,则121,2m m a a ++==;若2m a =,则123,1m m a a ++==,若1m a =,则122,3m m a a ++==, 由递推关系易得{1,2,3}A ⊆. ---------------------------------------8分 (III )集合A 中元素个数()Card A 的最大值为21.由已知递推关系可推得数列{}n a 满足:当{1,2,3}m a ∈时,总有3n n a a +=成立,其中,1,2,n m m m =++ .下面考虑当12014a a =≤时,数列{}n a 中大于3的各项:按逆序排列各项,构成的数列记为{}n b ,由(I )可得16b =或9,由(II )的证明过程可知数列{}n b 的项满足:3n n b b +>,且当n b 是3的倍数时,若使3n n b b +-最小,需使2112n n n b b b ++=-=-, 所以,满足3n n b b +-最小的数列{}n b 中,34b =或7,且33332k k b b +=-, 所以33(1)13(1)k k b b +-=-,所以数列3{1}k b -是首项为41-或71-的公比为3的等比数列, 所以131(41)3k k b --=-⨯或131(71)3k k b --=-⨯,即331k k b =+或3231k k b =⨯+, 因为67320143<<,所以,当2014a ≤时,k 的最大值是6,所以118a b =,所以集合A 重元素个数()Card A 的最大值为21.---------------13分。
北京市海淀区2014届高三上期中考试数学试题(理)(有答案)

海淀区高三年级第一学期期中练习数学(理科) 答案2013.11一、选择题1、A2、C3、B4、C5、B6、B7、D8、C二、填空题:本大题共6小题,每小题5分,共30分。
9.210..211. a b c >> 12..2π3,π6 13..2λ> 14. 4;6(31)n - 三、解答题: 本大题共6小题,共80分。
解答应写出文字说明, 演算步骤或证明过程。
15.解:(Ⅰ)由60A =和332ABC S ∆=可得133sin6022bc =, ---------------------------2分 所以6bc =, --------------------------------------3分又32,b c =所以2,3b c ==. ------------------------------------5分(Ⅱ)因为2,3b c ==,60A =,由余弦定理2222cos a b c bc A =+-可得 ------------------------------------7分2222367a =+-=,即7a =. ------------------------------------9分由正弦定理sin sin a b A B=可得------------------------------------11分 72sin sin60B =,------------------------------------12分 所以21sin B =.------------------------------------13分 16. 解:(I )π()3cos4cos(4)2f x x x =-+------------------------------------2分 3cos4sin 4x x =+------------------------------------4分π2sin(4)3x =+------------------------------------6分 ()f x 最小正周期为πT 2=,------------------------------------8分 (II )因为ππ64x -≤≤,所以ππ4π4333x -≤+≤-----------------------------------10分 所以3πsin(4)13x -≤+≤-----------------------------------12分 所以π32sin(4)23x -≤+≤, -----------------------------------13分 所以()f x 取值范围为[3,2]-. ------------------------------------14分17.解:(I )由已知11,1AH t PH t =-=+ -------------------------------------1分所以APH ∆的面积为1()(11)1,1112f t t t t =-+-<<. ---------------------4分(II )解法1. 111'()1(11)2221f t t t t =-++⨯-⨯+ 3(3)41t t -=+ -------------------------------------7分 由'()0f t =得3t =, -------------------------------------8分 函数()f t 与'()f t 在定义域上的情况下表:t (1,3)-3 (3,11) '()f t +0 - ()f t↗ 极大值 ↘-----------------------------------12分 所以当3t =时,函数()f t 取得最大值8. ------------------------------------13分 解法2.由211()(11)1(11)(1),11122f t t t t t t =-+=-+-<< 设2()(11)(1),111g t t t t =-+-<<, -------------------------------------6分则2'()2(11)(1)(11)(11)(1122)3(3)(11)g t t t t t t t t t =--++-=--++=--.-------7分函数()g t 与'()g t 在定义域上的情况下表:t (1,3)-3 (3,11) '()g t +0 - ()g t↗ 极大值 ↘------------------------------------11分 所以当3t =时,函数()g t 取得最大值, -----------------------------------12分 所以当3t =时,函数()f t 取得最大值1(3)82g =.------------------------------------13分18.解:(I )由②可得2112a a ⋅=,3122a a ⋅= -------------------------------2分 由①可得12a =. -------------------------------3分(II )由②可得112n n a a +⋅=, ------------------------------6分所以数列{}n a 的通项公式2n n a =. ------------------------------7分(III )由(II )可得21(1)421n n n n b a +=+=++,易得1{4},{2}n n +分别为公比是4和2的等比数列,------------------------------8分由等比数列求和公式可得124(14)4(12)1(416)214123n n n n n S n n ++--=++=-++--.--13分19.解:(I )因为1a =,2()42ln f x x x x =-+,所以2242'()(0)x x f x x x-+=>, ------------------------------1分 (1)3f =-,'(1)0f =, ------------------------------3分所以切线方程为3y =-. ------------------------------4分(II )222(1)22(1)()'()(0)x a x a x x a f x x x x-++--==>, ----------------------------5分 由'()0f x =得12,1x a x ==, ------------------------------6分 当01a <<时,在(0,)x a ∈或(1,)x ∈+∞时'()0f x >,在(,1)x a ∈时'()0f x <,所以()f x 的单调增区间是(0,)a 和(1,)+∞,单调减区间是(,1)a ; ---------------7分 当1a =时,在(0,)x ∈+∞时'()0f x ≥,所以()f x 的单调增区间是(0,)+∞;-----8分 当1a >时,在(0,1)x ∈或(,)x a ∈+∞时'()0f x >,在(1,)x a ∈时'()0f x <.所以()f x 的单调增区间是(0,1)和(,)a +∞,单调减区间是(1,)a . ---------------10分 (III )由(II )可知()f x 在区间[1,e]上只可能有极小值点,所以()f x 在区间[1,e]上的最大值在区间的端点处取到,-------------------------12分 即有(1)12(1)0f a =-+≤且2(e)e 2(1)e 20f a a =-++≤,解得2e 2e 2e 2a -≥-. ---------------------14分 20.解:(I )27,9,3;8,9,3;6,2,3. --------------------------------------3分(II )若k a 被3除余1,则由已知可得11k k a a +=+,2312,(2)3k k k k a a a a ++=+=+; 若k a 被3除余2,则由已知可得11k k a a +=+,21(1)3k k a a +=+,31(1)13k k a a +≤++; 若k a 被3除余0,则由已知可得113k k a a +=,3123k k a a +≤+; 所以3123k k a a +≤+, 所以312(2)(3)33k k k k k a a a a a +-≥-+=- 所以,对于数列{}n a 中的任意一项k a ,“若3k a >,则3k k a a +>”.因为*k a ∈N ,所以31k k a a +-≥.所以数列{}n a 中必存在某一项3m a ≤(否则会与上述结论矛盾!)若3m a =,则121,2m m a a ++==;若2m a =,则123,1m m a a ++==,若1m a =,则122,3m m a a ++==, 由递推关系易得{1,2,3}A ⊆. ---------------------------------------8分 (III )集合A 中元素个数()Card A 的最大值为21.由已知递推关系可推得数列{}n a 满足:当{1,2,3}m a ∈时,总有3n n a a +=成立,其中,1,2,n m m m =++.下面考虑当12014a a =≤时,数列{}n a 中大于3的各项:按逆序排列各项,构成的数列记为{}n b ,由(I )可得16b =或9,由(II )的证明过程可知数列{}n b 的项满足: 3n n b b +>,且当n b 是3的倍数时,若使3n n b b +-最小,需使2112n n n b b b ++=-=-, 所以,满足3n n b b +-最小的数列{}n b 中,34b =或7,且33332k k b b +=-,所以33(1)13(1)k k b b +-=-,所以数列3{1}k b -是首项为41-或71-的公比为3的等比数列, 所以131(41)3k k b --=-⨯或131(71)3k k b --=-⨯,即331k k b =+或3231k k b =⨯+, 因为67320143<<,所以,当2014a ≤时,k 的最大值是6,所以118a b =,所以集合A 重元素个数()Card A 的最大值为21.---------------13分。
2014年北京市高考理科数学试卷及答案解析(word版)
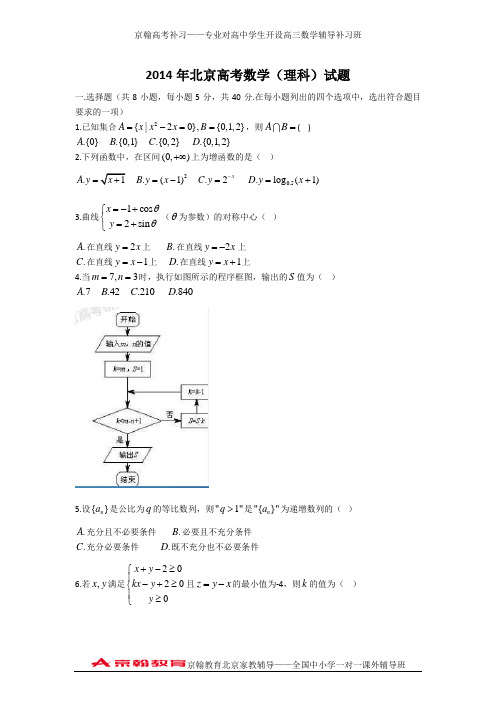
2014年北京高考数学(理科)试题一.选择题(共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项)1.已知集合2{|20},{0,1,2}A x x x B =-==,则AB =( ).{0}A .{0,1}B .{0,2}C .{0,1,2}D2.下列函数中,在区间(0,)+∞上为增函数的是( ).1A y x =+ 2.(1)B y x =- .2x C y -= 0.5.log (1)D y x =+3.曲线1cos 2sin x y θθ=-+⎧⎨=+⎩(θ为参数)的对称中心( ).A 在直线2y x =上 .B 在直线2y x =-上.C 在直线1y x =-上 .D 在直线1y x =+上4.当7,3m n ==时,执行如图所示的程序框图,输出的S 值为( ).7A .42B .210C .840D5.设{}n a 是公比为q 的等比数列,则"1"q >是"{}"n a 为递增数列的( ).A 充分且不必要条件 .B 必要且不充分条件 .C 充分必要条件 .D 既不充分也不必要条件6.若,x y 满足20200x y kx y y +-≥⎧⎪-+≥⎨⎪≥⎩且z y x =-的最小值为-4,则k 的值为( ).2A .2B - 1.2C 1.2D -7.在空间直角坐标系Oxyz 中,已知()2,0,0A ,()2,2,0B ,()0,2,0C ,(2D ,若1S ,2S ,3S 分别表示三棱锥D ABC -在xOy ,yOz ,zOx 坐标平面上的正投影图形的 面积,则( )(A )123S S S == (B )12S S =且 31S S ≠ (C )13S S =且 32S S ≠ (D )23S S =且 13S S ≠8.有语文、数学两学科,成绩评定为“优秀”“合格”“不合格”三种.若A 同学每科成绩不 低于B 同学,且至少有一科成绩比B 高,则称“A 同学比B 同学成绩好.”现有若干同学,他们之间没有一个人比另一个成绩好,且没有任意两个人语文成绩一样,数学成绩也一样 的.问满足条件的最多有多少学生( )(A )2 (B )3 (C )4 (D )5 二、填空题(共6小题,每小题5分,共30分)9.复数211i i +⎛⎫= ⎪-⎝⎭________.10.已知向量a 、b 满足1a =,()2,1b =,且()0a b R λλ+=∈,则λ=________.11.设双曲线C 经过点()2,2,且与2214y x -=具有相同渐近线,则C 的方程为________; 渐近线方程为________.12.若等差数列{}n a 满足7890a a a ++>,7100a a +<,则当n =________时{}n a 的前n 项和最大.13. 把5件不同产品摆成一排,若产品A 与产品C 不相邻,则不同的摆法有_______种. 14. 设函数)sin()(ϕω+=x x f ,0,0>>ωA ,若)(x f 在区间]2,6[ππ上具有单调性,且 ⎪⎭⎫⎝⎛-=⎪⎭⎫ ⎝⎛=⎪⎭⎫⎝⎛6322πππf f f ,则)(x f 的最小正周期为________.三.解答题(共6题,满分80分)15. (本小题13分)如图,在ABC ∆中,8,3==∠AB B π,点D 在BC 边上,且71cos ,2=∠=ADC CD (1)求BAD ∠sin(2)求AC BD ,的长16. (本小题13分).李明在10场篮球比赛中的投篮情况如下(假设各场比赛互相独立):(1)从上述比赛中随机选择一场,求李明在该场比赛中投篮命中率超过6.0的概率. (2)从上述比赛中选择一个主场和一个客场,求李明的投篮命中率一场超过6.0,一 场不超过6.0的概率.(3)记x 是表中10个命中次数的平均数,从上述比赛中随机选择一场,记X 为李明 在这比赛中的命中次数,比较)(X E 与x 的大小(只需写出结论)17.(本小题14分)如图,正方形AMDE 的边长为2,C B ,分别为MD AM ,的中点,在五棱锥ABCDE P -中,F 为棱PE 的中点,平面ABF 与棱PC PD ,分别交于点H G ,. (1)求证:FG AB //;(2)若⊥PA 底面ABCDE ,且PE AF ⊥,求直线BC 与平面ABF 所成角的大小,并 求线段PH 的长.18.(本小题13分)已知函数()cos sin ,[0,]2f x x x x x π=-∈,(1)求证:()0f x ≤; (2)若sin xa b x<<在(0,)2π上恒成立,求a 的最大值与b 的最小值.19.(本小题14分) 已知椭圆22:24C xy +=,(1)求椭圆C 的离心率. (2)设O 为原点,若点A 在椭圆C 上,点B 在直线2y =上,且OA OB ⊥,求直线AB 与圆222x y +=的位置关系,并证明你的结论.20.(本小题13分)对于数对序列1122(,),(,),,(,)n n P a b a b a b ,记111()T P a b =+,112()max{(),}(2)k k k k T P b T P a a a k n -=++++≤≤,其中112max{(),}k k T P a a a -+++表示1()k T P -和12k a a a +++两个数中最大的数,(1)对于数对序列(2,5),(4,1)P P ,求12(),()T P T P 的值.(2)记m 为,,,a b c d 四个数中最小值,对于由两个数对(,),(,)a b c d 组成的数对序列(,),(,)P a b c d 和'(,),(,)P a b c d ,试分别对m a =和m d =的两种情况比较2()T P 和2(')T P 的大小.(3)在由5个数对(11,8),(5,2),(16,11),(11,11),(4,6)组成的所有数对序列中,写出一个数对序列P 使5()T P 最小,并写出5()T P 的值.(只需写出结论).2014北京高考(理科)数学题解析1.集合{}{}2|2002A x x x =-==,.故{}02AB =,,选C .2. A .1y x =+[)1-+∞,上为增函数,符合题意. B .2(1)y x =-在(01),上为减函数,不合题意. C .2x y -=为()-∞+∞,上的减函数,不合题意. D .0.5log (1)y x =+为(1)-+∞,上的减函数,不合题意. 故选A .3. 参数方程1cos 2sin x y θθ=-+⎧⎨=+⎩所表示的曲线为圆心在(12)-,,半径为1的圆.其对称中心为圆心(12)-,.逐个代入选项可知,(12)-,在直线2y x =-上,即选项B .4. 当m 输入的7m =,3n =时,判断框内的判断条件为5k <.故能进入循环的k 依次为7,6,5.顺次执行S S k =⋅,则有765210S =⋅⋅=,故选C . 5.D对于等比数列{}n a ,若1q >,则当10a <时有{}n a 为递减数列. 故“1q >”不能推出“{}n a 为递增数列”.若{}n a 为递增数列,则{}n a 有可能满足10a <且01q <<,推不出1q >. 综上,“1q >”为“{}n a 为递增数列”的既不充分也不必要条件,即选D . 6.D若0k ≥,z y x =-没有最小值,不合题意. 若0k <,则不等式组所表示的平面区域如图所示.由图可知,z y x =-在点20k ⎛⎫- ⎪⎝⎭,处取最小值.故204k ⎛⎫--=- ⎪⎝⎭,解得12k =-,即选项D 正确.7.D (23S S =且13S S ≠)D ABC -在xOy 平面上的投影为ABC △,故12S =,设D 在yOz 和zOx 平面上的投影分别为2D 和3D ,则D ABC -在yOz 和zOx 平面上的投影分别为2OCD △和3OAD △.∵(2012D ,,,(3102D ,,.D 1O D 3D 2DCB A zyx +y -2=0-2kkx -y +2=022O y x故232S S == 综上,选项D 正确. 8.B用ABC 分别表示优秀、及格和不及格。
2014年普通高等学校招生全国统一考试(北京卷)数学试题(理科)解析版

2014年普通高等学校招生全国统一考试(北京卷)数学(理科)一.选择题:本大题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 已知集合2{|20}A x x x =-=,{0,1,2}B =,则A B =I ( )A.{0} B .{0,1} C .{0,2} D .{0,1,2} 【答案】C【解析】∵{}2,0=A ,∴{}{}{}2,02,1,02,0==I I B A .2. 下列函数中,在区间(0,)+∞为增函数的是( )A .1y x =+B .2(1)y x =-C .2x y -=D .0.5log (1)y x =+【答案】A【解析】由初等函数的性质得选项B 在()1,0上递减,选项C 、D 在()+∞,0为减函数,所以排除B 、C 、D.3.曲线1cos 2sin x y θθ=-+⎧⎨==⎩,(θ为参数)的对称中心( )A .在直线2y x =上B .在直线2y x =-上C .在直线1y x =-上D .在直线1y x =+上 【答案】B【解析】试题分析:参数方程⎩⎨⎧+=+-=θθsin 2cos 1y x 所表示的曲线为圆心在)2,1(-,半径为1的圆,其对称中心为)2,1(-,逐个代入选项可知,点)2,1(-满足x y 2-=,故选B. 4. 当7,3m n ==时,执行如图所示的程序框图,输出的S 值为( )A .7B .42C .210D .8405.设{}n a 是公比为q 的等比数列,则“1>q ”是“{}n a 为递增数列”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件 【答案】D 【解析】试题分析:对等比数列}{n a ,若1>q ,则当0,1a 时数列}{n a 是递减数列;若数列}{n a 是递增数列,则}{n a 满足01<a 且10<<q ,故当“1>q ”是”数列}{n a 为递增数列的既不充分也不必要条件.故选C.6. 若x 、y 满足20200x y kx y y +-≥⎧⎪-+≥⎨⎪≥⎩,且z y x =-的最小值为4-,则k 的值为( )A .2B .2-C .12 D .12- 【答案】D【解析】可行域如图所示,当0>k 时,知x y z -=无最小值,当0<k 时,目标函数线过可行域内A 点时z 有最小值,联立⎩⎨⎧=+-=020y kx y ,解之得⎪⎭⎫⎝⎛-0,2k A ,420min -=+=k z ,即21-=k .7.在空间直角坐标系Oxyz 中,已知(2,0,0)(2,2,0),(0,2,0),(1,1,2)A B C D .若123,,S S S 分别是三棱锥D ABC -在,,xOy yOz zOx 坐标平面上的正投影图形的面积,则( ) A .123S S S == B .21S S =且23S S ≠ C .31S S =且32S S ≠ D .32S S =且31S S ≠ 【答案】D【解析】设顶点D 在三个坐标面xoy 、yoz 、zox 的正投影分为'1D 、'2D 、'3D ,则211='='BD AD ,2=AB ,∴2222211=⨯⨯⨯=S ,2222122=⨯⨯=='OCD S S ,2222133=⨯⨯=='OAD S S .8.学生的语文、数学成绩均被评为三个等级,依次为“优秀”“合格”“不合格”.若学生甲2=-+y x 02=+-y kx A=-x y的语文、数学成绩都不低于学生乙,且其中至少有一门成绩高于乙,则称“学生甲比学生乙成绩好”.如果一组学生中没有哪位学生比另一位学生成绩好,并且不存在语文成绩相同、数学成绩也相同的两位学生,那么这组学生最多有( )A .2人B .3人C .4人D .5人 【答案】B【解析1】试题分析:用A 、B 、C 分别表示优秀、及格和不及格,依题意,事件A 、B 、C 中都最多只有一个元素,所以只有AC ,BB ,CA 满足条件,故选B.【解析2】假设AB 两个同学的数学成绩一样,由题意知他们语文成绩不一样,这样他们的语文成绩总有人比另一个人高,语文成绩较高的同学比另一个同学“成绩好”,与已知条件“他们之中没有一个比另一个成绩好”相矛盾.因此,没有任意两个同学数学成绩是相同的.因为数学成绩只有3种,因而同学数量最大为3.即 3位同学成绩分别为(优秀,不合格)、(合格,合格)、(不合格,优秀)时满足条件.二.填空题:本大题共6小题,每小题5分,共30分.请将答案填在答题卡对应题号的位置上,答错位置,书写不清,模棱两可均不得分.二、填空题9. 复数211i i +⎛⎫= ⎪-⎝⎭________.【答案】1-【解析】()()()122111112222-=⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛+-+=⎪⎭⎫ ⎝⎛-+i i i i i i . 10.已知向量a r 、b r 满足1a =r,()2,1b =r ,且()0a b R λλ+=∈r r ,则λ=________.【答案】5【解析】∵0=+b a λ,∴b a -=λ,∴515||||===a b λ. 11.设双曲线C 经过点()2,2,且与2214y x -=具有相同渐近线,则C 的方程为________; 渐近线方程为________.【答案】112322=-y x ;x y 2±= 【解析】设双曲线C 的方程为λ=-224x y ,将()2,2代入λ=-=-324222,∴双曲线方程为112322=-y x .令0422=-x y 得渐近线方程为x y 2±=.12.若等差数列{}n a 满足7890a a a ++>,7100a a +<,则当n =________时{}n a 的前n 项和最大. 【答案】8【解析】∵038987>=++a a a a ,098107<+=+a a a a ,∴0,098<>a a ,∴8=n 时数列{}n a 前n 和最大.13. 把5件不同产品摆成一排,若产品A 与产品B 相邻,产品A 与产品C 不相邻,则不同的摆法有_____种. 【答案】36【解析】36326132233=⨯⨯=A A A .14.设函数)sin()(ϕω+=x x f ,0,0>>ωA ,若)(x f 在区间]2,6[ππ上具有单调性,且⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=⎪⎭⎫⎝⎛6322πππf f f ,则)(x f 的最小正周期为________. 【答案】π【解析】结合图象得26223224ππππ+-+≥T ,即π≥T .三、解答题共6小题,共80分。
北京市朝阳区2014届高三上学期期中考试理科数学Word版含解析试题

北京市朝阳区2013-2014学年度高三年级第一学期期中统一考试理科数学第Ⅰ卷〔共40分〕一、选择题:本大题共8个小题,每题5分,共40分.在每题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{0,1,2}A =,{1,}B m =.假设AB B =,则实数m 的值是( )A .0B .2C .0或2D .0或1或22.命题p :对任意x ∈R ,210x+>的否认是( )A .p ⌝:对任意x ∈R ,210x+≤ B .p ⌝:不存在0x ∈R , 0210x+≤ C .p ⌝:存在0x ∈R , 0210x+≤ D .p ⌝:存在0x ∈R , 0210x +>3.执行如下列图的程序框图,则输出的T 值为( ) A .91B . 55C .54D .304.假设01m <<, 则( )A .log (1)log (1)m m m m +>-B .log (1)0m m +>C .2)1(1m m +>- D .1132(1)(1)m m ->-考点:5.由直线0x =,3x 2π=,0y =与曲线2sin y x =所围成的图形的面积等于( ) A .3 B .32 C .1 D .12【答案】A【解析】试题分析:考点:定积分6.已知平面向量(1,2)=-a ,(2,1)=b ,(4,2)--c =,则以下结论中错误的选项是......( ) A .向量c 与向量b 共线B .假设12λλ=+c a b 〔1λ,2λ∈R 〕,则10λ=,22λ=-C .对同一平面内任意向量d ,都存在实数1k ,2k ,使得12k k =d b +cD .向量a 在向量b 方向上的投影为07.假设函数2()f x x k =-的图象与函数()3g x x =-的图象至多有一个公共点,则实数k 的取值范围是( ) . .A. (,3]-∞B. [9,)+∞C. (0,9]D. (,9]-∞ 【答案】D 【解析】试题分析:函数()2f x x k =-是将函数2y x =的图像先向下平移k 个单位,然后将x 轴下方的图像向上翻折得到的,如下列图:8.同时满足以下4个条件的集合记作k A :〔1〕所有元素都是正整数;〔2〕最小元素为1;〔3〕最大元素为2014;〔4〕各个元素可以从小到大排成一个公差为k ()k *∈N 的等差数列.那么6133A A 中元素的个数是( )A .96B .94C .92D .90【答案】B 【解析】第Ⅱ卷〔共110分〕二、填空题〔每题5分,总分值30分,将答案填在答题纸上〕9.在公比小于零的等比数列{}n a 中,12a =,532a =,则数列{}n a 的前三项和3S = .10.函数43y x x =++(3)x >-的最小值是 . 【答案】1 【解析】 试题分析:()()444332331333y x x x x x x =+=++-≥+⨯=+++,当且仅当12.已知平面向量a 与b 的夹角为6π,3=a ,1=b ,则-=a b ;假设平行四边形ABCD 满足AB =+a b ,AD =a -b ,则平行四边形ABCD 的面积为 .13.已知函数222,0,()2,0.x x x f x x x x ⎧--≥=⎨-<⎩ 假设2(3)(2)f a f a -<,则实数a 的取值范围是 .【答案】31a -<< 【解析】试题分析:根据所给的分段函数,画图像如下:可得135a a a <<<,246a a a >>>,所以函数1()n n a f a +=从第一项开始,函数值先增大后减小再增大再减小,最后趋于平稳值,奇数项的值慢慢变大趋于平稳值,偶数项慢慢变小趋于平稳值,所以偶数项的值总是大于奇数项的值,所以20a ,25a ,30a 的大小关系是253020a a a <<. 考点:三、解答题 〔本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.〕15.(本小题总分值13分)已知函数2π()2sin(2)4cos 4f x x x =-+.(Ⅰ)求函数()f x 的最小正周期及最小值; (Ⅱ)假设π[0,]2α∈,且()3f α=,求α的值.sin 2cos 22x x =++π2)24x =++. ………4分(Ⅰ) 函数()f x 的最小正周期为2ππ2=, 函数()f x 的最小值为22- ………6分(Ⅱ)由()3f α=π)234α++=.所以πsin(2)42α+=………8分 又因为π[0,]2α∈,所以ππ5π2444α≤+≤, ………10分所以ππ244α+=或π3π244α+=.所以0α=或π4α=. ………13分考点:16.(本小题总分值13分)在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c ,且cos2A =. (Ⅰ)假设5=bc ,求ABC ∆的面积; (Ⅱ)假设1a =,求b c +的最大值.〔Ⅱ〕因为,552sinA17.(本小题总分值13分)已知等差数列{}n a 的前n 项和为n S ,*n ∈N ,且364a a +=,55S =-. (Ⅰ)求n a ;(Ⅱ)假设123n n T a a a a =++++,求5T 的值和n T 的表达式.试题解析:(Ⅰ)等差数列{}n a 的公差为d ,则1112545(51)552a d a d a d +++=⎧⎪⎨-+=-⎪⎩18.(本小题总分值14分)已知函数2()43f x x x a =-++,a ∈R . (Ⅰ)假设函数()y f x =的图象与x 轴无交点,求a 的取值范围; (Ⅱ)假设函数()y f x =在[1,1]-上存在零点,求 a 的取值范围;(Ⅲ)设函数()52g x bx b =+-,b ∈R .当0a =时,假设对任意的1[1,4]x ∈,总存在2[1,4]x ∈,使得12()()f x g x =,求b 的取值范围.【答案】(Ⅰ)1a >;(Ⅱ) 80a -≤≤ ;(Ⅲ) 6b ≥或3b ≤-. 【解析】试题分析:(Ⅰ) 函数()y f x =的图像与x 轴无交点,那么函数对应的方程的判别式0∆<,解不等式即可;(Ⅱ)先判断函数()y f x =在闭区间[1,1]-的单调性,然后根据零点存在性定理,可知(1)0(1)0f f ≤⎧⎨-≥⎩,解方程组求得同时满足两个表达式的的取值范围;(Ⅲ) 假设对任意的1[1,4]x ∈,总存在2[1,4]x ∈,使12()()f x g x =,只需函数()y f x =的值域为函数()y g x =值域的子集()y f x =在区间[1,4]上的值域是[1,3]-,然后判断函数()y g x =0b =,0b >,0b <三种情况进行分类讨论,当0b ≠时,函数()y g x =是一次函数,最值在两个区间端点处取得,所以假设其值域是[],m n ,那么就有13mn -≥⎧⎨≤⎩成立,解相应的不等式组即可. 试题解析:(Ⅰ)假设函数()y f x =的图象与x 轴无交点,则方程()0f x =的判别式0∆<, 即164(3)0a -+<,解得1a >. ………3分52153b b +≤-⎧⎨-≥⎩,解得3b ≤-; 综上:实数b 的取值范围6b ≥或3b ≤-. ………14分 考点:19.(本小题总分值14分)已知函数21()(3)3ln 2f x x m x m x =-++,m ∈R .(Ⅰ)求函数()f x 的单调递增区间;(Ⅱ)设1(A x ,1())f x ,2(B x ,2())f x 为函数()f x 的图象上任意不同两点,假设过A ,B 两点的直线l 的斜率恒大于3-,求m 的取值范围.试题解析:(Ⅰ) 依题意,()f x 的定义域为()0,+∞,3()(3)m f x x m x '=-++2(3)3x m x m x-++=(3)()x x m x --=.(ⅰ)假设0m ≤,当3x >时,()0f x '>,()f x 为增函数. (ⅱ)假设3m =,2(3)()0x f x x-'=≥恒成立,故当0x >时,()f x 为增函数.20.(本小题总分值13分)如果项数均为()*2,n n n N≥∈的两个数列{}{},n n a b 满足()1,2,...,k k a b k k n -==且集合{}{}1212,,...,,,,...,1,2,3,...,2n n a a a b b b n =,则称数列{}{},n n a b 是一对 “n 项相关数列”.(Ⅰ)设}{},{n n b a 是一对“4项相关数列”,求1234a a a a +++和1234b b b b +++的值,并写出一对“4项相 关数列” {}{},n n a b ;(Ⅱ)是否存在 “15项相关数列” }{},{n n b a ?假设存在,试写出一对}{},{n n b a ;假设不存在,请说明理由;(Ⅲ)对于确定的n ,假设存在“n 项相关数列”,试证明符合条件的“n 项相关数列”有偶数对. 【答案】(Ⅰ) 23;13;}{n a :8,4,6,5;}{n b :7,2,3,1 ;(Ⅱ)不存在,理由见解析;(Ⅲ)证明见解析. 【解析】试题分析:(Ⅰ) 依题意有,112233441,2,3,4a b a b a b a b -=-=-=-=,以及1234123436a a a a b b b b +++++++=,求得1234a a a a +++以及1234b b b b +++的值,写出符合条件的数列即可,答案不唯一;(Ⅱ)先假设存在,利用反证法证明得出矛盾,即可证明满足已知条件的“10项相关数列”112215151,2,,15a b a b a b -=-=-=,以及12101210465a a a b b b +++++++=成立,解出12155852a a a +++=与已知矛盾,即证;(Ⅲ) 对于确定的n ,任取一对 “n 项相关数列”}{},{n n b a ,构造新数对k k b n c -+=12,k k a n d -+=12),,2,1(n k =,则可证明新数对也是“n 项相关数列”,但是数列}{n c 与}{n a 是不同的数列,可知“n 项相关数列”都是成对对应出现的,即符合条件的 “n 项相关数列”有偶数对.试题解析:(Ⅰ)依题意,112233441,2,3,4a b a b a b a b -=-=-=-=,相加得,12341234()10a a a a b b b b +++-+++=,又1234a a a a +++123436b b b b ++++=,则123423a a a a +++=, 123413b b b b +++=.“4项相关数列”}{n a :8,4,6,5;}{n b :7,2,3,1〔不唯一〕………3分又因为。
北京市育才学校2024-2025学年高三上学期期中考试数学试卷

北京市育才学校2024-2025学年高三上学期期中考试数学试卷一、单选题1.已知集合2{|320},{|1}A x x x B x x =-+<=≥,则A B = A .(,2]-∞B .(1,)+∞C .(1,2)D .[1,)+∞2.下列函数中,在定义域上既是奇函数又是增函数的是()A .12y x =B .3y x =C .e x y =D .lg y x=3.若0,0a b >>,且220a b +-=,则ab 的最大值为A .1 2B .1C .2D .44.函数()2sin y x ωϕ=+在一个周期内的图象如图所示,则此函数的解析式是()A .3π2sin 8y x ⎛⎫=+ ⎪⎝⎭B .π2sin 24y x ⎛⎫=- ⎪⎝⎭C .7π2sin 216x y ⎛⎫=+ ⎪⎝⎭D .π2sin 24y x ⎛⎫=+ ⎪⎝⎭5.在ABC V 中,“π4A >”是“sin 2A >”的()A .充要条件B .充分不必要条件C .必要不充分条件D .既不充分也不必要条件6.已知函数()log a f x x =,()x g x b =,的图像都经过点1(,2)4,则ab 的值为A .1B .2C .4D .87.已知函数()f x 的部分对应值如表所示.数列{}n a 满足11a =,且对任意*n ∈N ,点()1,n n a a +都在函数()f x 的图象上,则2024a 的值为().x1234()f x 3124A .1B .2C .3D .48.已知向量()sin ,cos a θθ= ,()3,4b = ,若//a b ,则tan 2θ等于()A .247B .67C .2425-D .247-9.在直角梯形ABCD 中,已知//BC AD ,AB AD ⊥,4AB =,2BC =,4=AD ,若P 为CD的中点,则P ⋅P 的值为()A .5-B .4-C .4D .510.已知集合{(,)()}M x y y f x ==∣,若对于任意()11,x y M ∈,存在()22,x y M ∈,使得12120x x y y +=成立,则称集合M 是“好集合”.给出下列4个集合:①1(,) M x y y x ⎧⎫==⎨⎬⎩⎭②{}(,)e 2x M x y y ==-∣③{(,)cos }M x y y x ==∣④{(,)ln }M x y y x ==∣其中所有“好集合”的序号是()A .②③B .①②④C .③④D .①③④二、填空题11.41(2)x x+的展开式中的常数项为.12.若向量,a b 满足||1,||2a b == ,且,a b 的夹角为π3,则a b ⋅=,||a b +=.13.已知0a ≥,函数()2,xx af x x a⎧≤⎪=>若0a =,则()f x 的值域为;若方程()20f x -=恰有一个实根,则a 的取值范围是.14.已知数列{}n a 满足1n n a a +>,且其前n 项和n S 满足1n n S S +<,请写出一个符合上述条件的数列的通项公式n a =.15.已知函数2cos ()1xf x x π=+,给出下列四个结论:①()f x 是偶函数;②()f x 有无数个零点;③()f x 的最小值为12-;④()f x 的最大值为1.其中,所有正确结论的序号为.三、解答题16.已知等差数列{}n a 满足1241,10a a a =+=.(1)求{}n a 的通项公式;(2)若等比数列{}1122,0,0n b b a b a -=+=,求{}n b 的通项公式;17.已知函数32()1f x x ax bx =++-在1x =处有极值-1.(1)求实数a ,b 的值;(2)求函数()ln 2g x ax x =+的单调区间.18.在ABC V 中,sin cos 6b A a B π⎛⎫=- ⎪⎝⎭.(1)求B ;(2)若5c =,___________.求a .从①7b =,②4C π=这两个条件中任选一个,补充在上面问题中并作答.注:如果选择多个条件分别解答,按第一个解答计分.19.为了增强学生的冬奥会知识,弘扬奥林匹克精神,北京市多所中小学校开展了模拟冬奥会各项比赛的活动.为了了解学生在越野滑轮和旱地冰壶两项中的参与情况,在北京市中小学学校中随机抽取了10所学校,10所学校的参与人数如下:(Ⅰ)现从这10所学校中随机选取2所学校进行调查.求选出的2所学校参与越野滑轮人数都超过40人的概率;(Ⅱ)现有一名旱地冰壶教练在这10所学校中随机选取2所学校进行指导,记X 为教练选中参加旱地冰壶人数在30人以上的学校个数,求X 的分布列和数学期望;(Ⅲ)某校聘请了一名越野滑轮教练,对高山滑降、转弯、八字登坡滑行这3个动作进行技术指导.规定:这3个动作中至少有2个动作达到“优”,总考核记为“优”.在指导前,该校甲同学3个动作中每个动作达到“优”的概率为0.1.在指导后的考核中,甲同学总考核成绩为“优”.能否认为甲同学在指导后总考核达到“优”的概率发生了变化?请说明理由.20.已知函数e ()xf x x=.(1)求函数()y f x =的图象在点(1,(1))P f 处的切线l 的方程;(2)当0x >时,求证:()f x x >;(3)讨论函数()y f x bx =-(b ∈R 且为常数)零点的个数.21.在一个有穷数列的每相邻两项之间插入这两项的和,形成新的数列,我们把这样的操作称为该数列的一次“Z 拓展”.如数列1,2第1次“Z 拓展”后得到数列1,3,2,第2次“Z 拓展”后得到数列1,4,3,5,2.设数列a ,b ,c 经过第n 次“Z 拓展”后所得数列的项数记为Pn ,所有项的和记为Sn .(1)求P 1,P 2;(2)若Pn ≥2020,求n 的最小值;(3)是否存在实数a ,b ,c ,使得数列{Sn }为等比数列?若存在,求a ,b ,c 满足的条件;若不存在,说明理由.。
2014年北京高考数学理科(含答案)
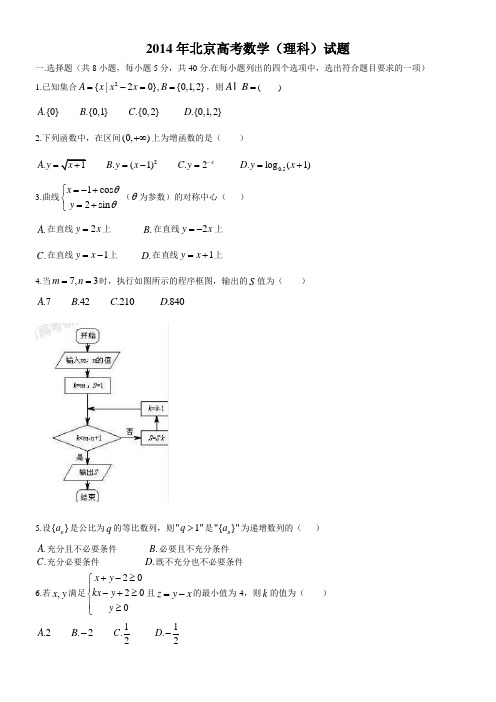
2014年北京高考数学(理科)试题一.选择题(共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项) 1.已知集合2{|20},{0,1,2}A x x x B =-==,则A B =I ( ).{0}A .{0,1}B .{0,2}C .{0,1,2}D2.下列函数中,在区间(0,)+∞上为增函数的是( ).1A y x =+ 2.(1)B y x =- .2xC y -= 0.5.log (1)D y x =+3.曲线1cos 2sin x y θθ=-+⎧⎨=+⎩(θ为参数)的对称中心( ).A 在直线2y x =上 .B 在直线2y x =-上 .C 在直线1y x =-上 .D 在直线1y x =+上4.当7,3m n ==时,执行如图所示的程序框图,输出的S 值为( ).7A .42B .210C .840D5.设{}n a 是公比为q 的等比数列,则"1"q >是"{}"n a 为递增数列的( ).A 充分且不必要条件 .B 必要且不充分条件.C 充分必要条件 .D 既不充分也不必要条件6.若,x y 满足20200x y kx y y +-≥⎧⎪-+≥⎨⎪≥⎩且z y x =-的最小值为-4,则k 的值为( ).2A .2B - 1.C 1.D -7.在空间直角坐标系Oxyz 中,已知()2,0,0A ,()2,2,0B ,()0,2,0C ,(D ,若 1S ,2S ,3S 分别表示三棱锥D ABC -在xOy ,yOz ,zOx 坐标平面上的正投影图形的 面积,则( )(A )123S S S == (B )12S S =且 31S S ≠ (C )13S S =且 32S S ≠ (D )23S S =且 13S S ≠8.有语文、数学两学科,成绩评定为“优秀”“合格”“不合格”三种.若A 同学每科成绩不 低于B 同学,且至少有一科成绩比B 高,则称“A 同学比B 同学成绩好.”现有若干同学, 他们之间没有一个人比另一个成绩好,且没有任意两个人语文成绩一样,数学成绩也一样 的.问满足条件的最多有多少学生( )(A )2 (B )3 (C )4 (D )5二、填空题(共6小题,每小题5分,共30分)9.复数211i i +⎛⎫= ⎪-⎝⎭________.10.已知向量a r 、b r 满足1a =r ,()2,1b =r ,且()0a b R λλ+=∈r r,则λ=________.11.设双曲线C 经过点()2,2,且与2214y x -=具有相同渐近线,则C 的方程为________; 渐近线方程为________.12.若等差数列{}n a 满足7890a a a ++>,7100a a +<,则当n =________时{}n a 的前n 项和最大.13. 把5件不同产品摆成一排,若产品A 与产品C 不相邻,则不同的摆法有_______种.14. 设函数)sin()(ϕω+=x x f ,0,0>>ωA ,若)(x f 在学科网区间]2,6[ππ上具有单调性,且 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛6322πππf f f ,则)(x f 的最小正周期为________.三.解答题(共6题,满分80分)15. (本小题13分)如图,在ABC ∆中,8,3==∠AB B π,点D 在BC 边上,且71cos ,2=∠=ADC CD (1)求BAD ∠sin (2)求AC BD ,的长16. (本小题13分).李明在10场篮球比赛中的投篮情况如下(假设各场比赛互相独立):(1)从上述比赛中随机选择一场,求李明在该场比赛中投篮命中率超过6.0的概率. (2)从上述比赛中选择一个主场和一个客场,求李明的投篮命中率一场超过6.0,一 场不超过6.0的概率.(3)记x 是表中10个命中次数的平均数,从上述比赛中随机选择一场,记X 为李明 在这比赛中的命中次数,比较)(X E 与x 的大小学科网(只需写出结论)17.(本小题14分)如图,正方形AMDE 的边长为2,C B ,分别为MD AM ,的中点,在五棱锥ABCDE P - 中,F 为棱PE 的中点,平面ABF 与棱PC PD ,分别交于点H G ,. (1)求证:FG AB //;(2)若⊥PA 底面ABCDE ,且PE AF ⊥,求直线BC 与平面ABF 所成角的大小,并 求线段PH 的长.已知函数()cos sin ,[0,]2f x x x x x π=-∈,(1)求证:()0f x ≤;(2)若sin x a b x <<在(0,)2π上恒成立,求a 的最大值与b 的最小值.已知椭圆22:24C xy +=,(1)求椭圆C 的离心率.(2)设O 为原点,若点A 在椭圆C 上,点B 在直线2y =上,且OA OB ⊥,求直线AB 与圆222x y +=的位置关系,并证明你的结论.对于数对序列1122(,),(,),,(,)n n P a b a b a b L,记111()T P a b =+,112()max{(),}(2)k k k k T P b T P a a a k n -=++++≤≤L ,其中112max{(),}k k T P a a a -+++L 表示1()k T P -和12k a a a +++L 两个数中最大的数,(1)对于数对序列(2,5),(4,1)P P ,求12(),()T P T P 的值.(2)记m 为,,,a b c d 四个数中最小值,对于由两个数对(,),(,)a b c d 组成的数对序列(,),(,)P a b c d 和'(,),(,)P a b c d ,试分别对m a =和m d =的两种情况比较2()T P 和2(')T P 的大小.(3)在由5个数对(11,8),(5,2),(16,11),(11,11),(4,6)组成的所有数对序列中,写出一个数对序列P 使5()T P 最小,并写出5()T P 的值.(只需写出结论).2014年普通高等学校招生全国统一考试数学(理)(北京卷)参考答案一、选择题(共8小题,每小题5分,共40分) (1)C (2)A (3)B (4)C (5)D (6)D (7)D (8)B二、填空题(共6小题,每小题5分,共30分) (9)-1 (10(11)221312x y -= 2y x =± (12)8(13)36 (14)π三、解答题(共6小题,共80分) (15)(共13分)解:(I )在ADC ∆中,因为17COS ADC∠=,所以sin ADC ∠=。
2014北京高考数学(理科)含答案

2014年普通高等学校招生全国统一考试数学(理)(北京卷)房山区良乡中学 任宝泉录入整理一、选择题(共8道小题,每小题5分,共40分,在每小题的四个选项中,选出符合题目要求的一项)1.已知集合{}2|20A x x x =-=,{}0,1,2B =,则AB =( )A .{}0 B.{}0,1 C.{}0,2 D.{}0,1,2 2.下列函数中,在区间()0,+∞上为增函数的是( ) A.y =B.2(1)y x =-C.2x y -=D.0.5log (1)y x =+3.曲线1cos 2sin x y θθ=-+⎧⎨=+⎩,(θ为参数)的对称中心( )A .在直线2y x =上 B.在直线2y x =-上 C.在直线1y x =-上 D.在直线1y x =+上4.当7,3m n ==时,执行如图所示的程序框图,输出的S 值为( )5.设{}n a 是公比为q 的等比数列,则“1q >”是“{}n a ”为递增数列的( )A .充分且不必要条件 B.必要且不充分条件 C .充分必要条件 D.既不充分也不必要条件6.若,x y 满足20200x y kx y y +-≥⎧⎪-+≥⎨⎪≥⎩且z y x =-的最小值为4-,则k 的值为( )A .2 B.2- C.12 D.12- 7.在空间直角坐标系O x y z 中,已知(2,0,0)A ,(2,2,0)B ,(0,2,0)C,(1,1D ,若123,,S S S 分别表示三棱锥D ABC -在,,xOy yOz zOx 坐标平面上的正投影图形的面积,则( )A .123S S S == B. 12S S =且31S S ≠ C. 13S S =且32S S ≠ D. 23S S =且13S S ≠ 8.有语文、数学两学科,成绩评定为“优秀”、“合格”、“不合格”三种。
若A 同学每科成绩不低于B 同学,且至少有一科成绩比B 高,则称“A 同学比B 同学成绩好”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013-2014学年度第一学期北京育才学校高三数学(理科)期中考试试卷一、选择题(8道小题,每小题5分,共40分)1. 已知全集=R U ,集合2{|1}A x x =≥,则=UC A ( ) A. (,1)-∞ B. (1,1)- C. (1,)+∞ D.(,1)(1,)-∞-+∞ 2. 下面是关于复数21z i=- 的四个命题: 1p :2z =, 2:p 22z i = 3:p z 的共轭复数为1i -+ 4:p z 的虚部为1其中真命题为 ( ).A 23,p p .B 12,p p .C 24,p p .D 34,p p3. 下列函数中,既是奇函数又是增函数的是 ( ).A 3y x =- .B cos y x = .C y x x = .D x y e =4. 执行如图1所示的程序框图,输出的i 值为( ).A 5 .B 6 .C 4 .D 35. 用5,6,7,8,9组成没有重复数字的五位数,其中恰好有一个奇数夹在两个偶数之间的五位数的个数为( ) A 120 B 72 C 48 D 36 6. 函数满足对任意成立,则a 的取值范围是( )A B (0,1) C D7. 在长为10cm 的线段AB 上任取一点C ,分别以线段图1⎩⎨⎧≥+-<=)0(4)3(),0()(x a x a x a x f x 0)()(,212121<--≠x x x f x f x x 都有1(0,)410,4⎛⎤ ⎥⎝⎦1[,1)4,AC CB 的长为邻边做一个矩形,则该矩形面积大于29cm 的概率为( ).A 110 .B 45 .C 310 .D 158. 已知函数()()()22,20,f x x x g x ax a =-=+>对任意的[]11,2x ∈-都存在[]01,2x ∈-,使得()01(),=f x g x 则实数a 的取值范围是( ).A 10,2⎛⎤ ⎥⎝⎦ .B 1,32⎡⎤⎢⎥⎣⎦ .C [)3,+∞ .D (]0,3二、填空题(6道小题,每小题5分,共30分)9. 在()7a x +展开式中4x 的系数为35,则实数a 的值为 .10. 已知向量(4,5cos ),(4tan ,3),αα==a b //b ,则2αcos =_______11. 已知直线l 的参数方程为12x y ⎧=⎪⎪⎨⎪=+⎪⎩ (t 为参数),圆C 的参数方程为c o s2s i nx y θθ=+⎧⎨=⎩ (θ为参数), 则圆心C 到直线l 的距离为 . 12. 不等式20-+>xx 的解集为(),a b ,则)2b ax dx =⎰______13. 如图2,AB ,CD 是半径为a 的圆O 的两条弦,它们相交 于AB 的中点P ,PD =2a3,∠OAP =30°,则CP =_________.14. 我们可以利用数列{}n a 的递推公式2,,n n n n a a n ⎧⎪=⎨⎪⎩为奇数时,为偶数时(n ∈*N )求出这个数列各项的值,使得这个数列中的每一项都是奇数.则2425a a +=_________;研究发现,该数列中的奇数都会重复出现,那么第8个5是该数列的第_______项.三、解答题(6道小题,共80分) 15. 设函数x x f a log )(=(1,0≠>a a a 为常数且),已知数列图3),(1x f ),(2x f ),(n x f 是公差为2的等差数列,且21a x =.(Ⅰ)求数列}{n x 的通项公式; (Ⅱ)当21=a 时,求证:3121<+++n x x x .16. 在锐角ABC ∆中,角A 、B 、C 所对的边长分别为a 、b 、,c 向量()()3,s i n ,c o s ,1-==B n B m ,且m n ⊥.(1)求角B 的大小;(2)求函数()sin(2)=+f x x B 的单调减区间; (3)若ABC ∆2253b ac -=, 求,a c 的值。
17. 电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,如图3是根据调查结果绘制的观众日均收看该类体育节目时间的频率分布直方图,其中收看时间分组区间是:[)[)[)0,10,10,20,20,30,[)30,40,[)40,50,[]50,60.将日均收看该类体育节目时间不低于40分钟的观众称为“体育迷”. (1)求图中x 的值;(2)从“体育迷”中随机抽取2人, 该2人中日均收看该类体育节目时间 在区间[]50,60内的人数记为X , 求X 的数学期望()E X .18. 设函数()sin cos 1=-++f x x x ax(1)当1=a ,[0,2]π∈x 时,求函数()f x 的单调区间与极值; (2)若函数()f x 为单调函数,求实数a 的取值范围。
19. 已知函数()(1)ln 1,=+-+f x b x x x 斜率为1的直线与函数()f x 的图象相切于(1,0)点。
(Ⅰ)求()()ln h x f x x x =-的单调区间;(Ⅱ)当实数01a <<时,讨论21()()()ln 2g x f x a x x ax =-++的极值点.20. 如果由数列{}n a 生成的数列{}n b 满足对任意的n ∈*N 均有1n n b b +<,其中1n n n b a a +=-,则称数列{}n a 为“Z 数列”.(Ⅰ)在数列{}n a 中,已知2n a n =-,试判断数列{}n a 是否为“Z 数列”; (Ⅱ)若数列{}n a 是“Z 数列”,10a =,n b n =-,求n a ;(Ⅲ)若数列{}n a 是“Z 数列”,设,,s t m ∈*N ,且s t <,求证:t m s m t s a a a a ++-<-.9、1 10、725 1112、13 13、98a 14、28,64015、(13分)解:(Ⅰ)n n x f d a x f n a 22)1(2)(22log )(21=⋅-+=∴===n n n a a x nx 22log :==即 …………………6分(Ⅱ)当21=a 时,nn x ⎪⎭⎫⎝⎛=41…………………13分16、(13分)解(1) : =⋅()()3,sin cos ,1-⋅B B ()3cos sin 1-⨯+⨯=B BB B cos 3sin -= ,0m n m n ⊥∴⋅=∴0c o s 3s i n=-B B ABC ∆为锐角三角形,cos 0B ∴≠ ∴3tan =B ,02B π<< 3π=∴B . …………4分(2)7[,],1212k k k Z ππππ++∈ …………8分 (3)由B ac c a b cos 2222-+=,得ac c a b -+=222,代入2253b ac -=得ac c a ac +--=22253,得5=+c a .11sin sin 223ABC S ac B ac π∆==⨯==,得6ac = 联立56a c ac +=⎧⎨=⎩, 解得2,3a c =⎧⎨=⎩或3.2a c =⎧⎨=⎩ …………13分17、解:(1)由题设可知()0.0050.0120.020.0250.028101x +++++⨯=,314113141141414121<⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-=-⋅⎪⎭⎫ ⎝⎛-=+++nnn x x x解之得0.01.x = …………………4分(2)由题设知收看该类体育节目时间在区间[]50,60内的人数为0.005101005⨯⨯=人, “体育迷”的人数为()0.010.0051010015+⨯⨯=, 所以X 的可能取值为0,1,2,()025********C C p X C ===, ()1151021510121C C p X C === ()205102152221C C p X C === ∴X 的数学期望()31022012721213E X =⨯+⨯+⨯=. ………… 13分18、(13分)(1),,,()1().43()0()422()x x x x x x x x πππππ=++=+===解:由f(x)=sinx-cosx+x+1,0<x<2,知f 令f ,从面sin ,或,当变化时,f ,f(x)变化情况如下表:3223332222πππππππππ+因此,由上表知f(x)的单调递增区间是(0,)与(,),单调递增区间是(,),极小值为f()=,极大值为f()=…………………8分(2)()sin()4f x x a π'=++()0f x '≥ 恒成立 或()0f x '≤恒成立(,)a ∴∈-∞+∞ …………13分19、(14分)20、(14分)解:(Ⅰ)因为2n a n =-,所以221(1)21n n n b a a n n n +=-=-++=--,n ∈*N , …………………2分 所以12(1)1212n n b b n n +-=-+-++=-,所以1n n b b +<,数列{}n a 是“Z 数列”. …………………4分 (Ⅱ)因为n b n =-,所以2111a a b -==-,3222a a b -==-,…,11(1)n n n a a b n ---==--, 所以1(1)12(1)2n n na a n --=-----=- (2n ≥),…………………6分 所以(1)2n n na -=-(2n ≥), 又10a =,所以(1)2n n n a -=-(n ∈*N ). …………………8分(Ⅲ)因为 111()()s m s s m s m s s s m s a a a a a a b b +++-++--=-++-=++ ,111()()t m t t m t m t t t m t a a a a a a b b +++-++--=-++-=++ ,………………10分又,,s t m ∈*N ,且s t <,所以s i t i +<+,s i t i b b ++>,n ∈*N ,所以1122,,,s m t m s m t m s t b b b b b b +-+-+-+->>> , …………………12分 所以t m t s m s a a a a ++-<-,即t m s m t s a a a a ++-<-. …………………14分。
