高考数学难点突破_难点27__求空间的角
求解空间角问题的两个技巧

探索探索与与研研究究求空间角问题在高中数学立体几何中比较常见.常见的命题形式有求异面直线所成的角、求直线与平面所成的角、求二面角及其余弦值.此类题目对同学们的空间想象与逻辑思维能力有较高的要求.解答此类问题的常用技巧主要有巧用定义和构造向量.一、巧用定义空间角包括异面直线所成的角、直线和平面所成的角及二面角.运用定义法求解空间角问题,需首先仔细观察几何图形,根据异面直线所成的角、直线和平面所成的角、二面角的定义添加辅助线,确定对应的平面角,然后运用勾股定理、正余弦定理求出空间角的大小.例1.在三棱锥P -ABC 中,△ABC 为等腰直角三角形,AB =AC =1,PB =PC =5.设点E 为PA 的中点,D 为AC 的中点,F 为PB 上一点,且PF =2FB ,PA ⊥AC ,求直线CE 与平面PBC 所成角的正弦值.解:因为AB =AC =1,PB =PC =5,PA =PA ,所以△PAB ≅△PAC ,因为PA ⊥AC ,所以PA ⊥AB ,PA =PC 2-AC 2=2,所以PA ⊥平面ABC ,过点E 作EH ⊥平面PBC 于点H ,连接CH ,则∠ECH 即为直线CE 与平面PBC 所成角,易知BC =2,设点A 到平面PBC 的距离为h ,由V P -ABC =V A -PBC 得13∙S △ABC ∙PA =13∙S △PBC ∙h ,解得h =23,因为点E 为PA 的中点,所以EH =12h =13,因为CE =2,所以sin ∠ECH =EH CE =.解答本题,需首先明确各个点、线段、平面的位置及其关系,然后根据直线与平面所成角的定义,过点E 作EH ⊥平面PBC 于点H ,连接CH ,便可找到直线CE 与平面PBC 所成角对应的平面角∠ECH .然后根据等体积法求得EH 、CE ,再根据正弦函数的定义就能求得问题的答案.二、构造向量对于空间角问题,我们也可以采用向量法来求解.在建立空间直角坐标系或选定基底后,求得各个点的坐标、各个向量的方向向量,便可通过向量的坐标运算求得空间角的大小.对于异面直线所成的角,只需求得两条直线的方向向量,运用数量积公式求解;对于直线与平面所成的角,需求得直线的方向向量和平面的法向量,运用数量积公式求得其夹角,则该夹角的余角即为所求的角;对二面角,需分别求得两个半平面的法向量,则其夹角或补角即为二面角的平面角.例2.如图,在三棱柱ABC -A 1B 1C 1中,CA =CC 1=2CB ,求直线BC 1与直线AB 1夹角的余弦值.解:设 AC =a , CB =b , CC 1=c,且||a =||c =2,||||b =1,则 AB 1= AB + BB 1=a +b+c ,BC 1=c -b ,则|| AB 1=(a +b +c )2=a 2+b 2+c 2+2a b +2a c +2b c ,因为2a b =2b c =2a c =0,所以||AB 1=3.同理可得 BC 1=(c -b )2=5,又 AB 1∙BC 1=(c -b )∙(a +b +c )=3故cos < AB 1, BC 1>= AB 1∙BC 1||AB 1|| BC 1=>0,所以 AB 1与 BC 1的夹角的余弦值,即为直线 AB 1与直线BC 1夹角的余弦值.我们以 AC 、 CB 、 CC 1为基底,将 AB 1与 BC 1用三个基底表示出来,便可直接运用向量的数量积公式求得两异面直线所成角的余弦值.一般来说,定义法的适用范围较广,向量法的适用范围较窄.在使用向量法时,需特别注意题目中所给的图形是否方便建立空间直角坐标系.有时解答空间角问题可以同时运用上述两种方法.(作者单位:江苏省射阳中学)52。
高考数学复习第十二讲立体几何之空间角

第十二讲立体几何之空间角一、基本知识回顾空间的角主要包括两条异面直线所成的角、直线与平面所成的角以及二面角。
1.范围:0,1)异面直线所成角2)直线与平面所成角20,2.求法:平移相交(找平行线替换)2向量法1.范围0 ,20,定义22.求法向量法m narcsin若 m n 则 a //或a若m // n则a m n1.范围:0.定义法(即垂面法)3)二面角 2.作二面角平面角的方法:三垂线定理及逆定理垂线法直接法3. 求二面角大小的方法射影面积法向量法S S cos( S为原斜面面积, S为射影面积 ,为斜面与射影所成锐二面角的平面角)m n当为锐角时,arccosm nm n当为锐角时,arccosm n二、例题讲解1.在正三棱柱 ABC A 1 B 1C 1 中,若 AB 2 BB 1 , 求 AB 1 与 C 1 B 所成的角的大小。
解:法一:如图一所示,设 O 为 B 1 C 、 C 1 B 的交点, D 为 AC 的中点,则所求角是 DOB 。
设 BB 1a , 则 AB 2 a ,于是在DOB 中,O B1 3a , BD 3 2 a6BC 12a,2 22O D1 3 2222AB 1 a , BD OBOD,2即DOB90 ,DOB90法二: 取 A 1 B 1 的中点 O 为坐标原点, 如图建立空间直角坐标系1O xyz , AB 的长度单位,2则由AB2BB1有A 0,1,2,B0,1, 2 , B10,1, 0, C 13,0,0AB 10, 2, 2 ,C1B 3 ,1, 2 ,AB1 C1B 2 2 0, AB1 C 1 B2.如图二所示,在四棱锥P ABCD 中,底面 ABCD 是一直角梯形,BAD90 ,AD // BC,AB BC a , AD 2 a , 且 PA底面 ABCD ,P D 与底面成 30角。
⑴若 AE PD , E 为垂足,求证:BE PD ;⑵求异面直线AE , CD 所成角的大小。
2023年高考数学----空间角问题规律方法与典型例题讲解

2023年高考数学----空间角问题规律方法与典型例题讲解【规律方法】1、用综合法求空间角的基本数学思想主要是转化与化归,即把空间角转化为平面角,进而转化为三角形的内角,然后通过解三角形求得.求解的一般步骤为:(1)作图:作出空间角的平面角.(2)证明:证明所给图形是符合题设要求的. (3)计算:在证明的基础上计算得出结果. 简称:一作、二证、三算.2、用定义作异面直线所成角的方法是“平移转化法”,可固定一条,平移另一条;或两条同时平移到某个特殊的位置,顶点选在特殊的位置上.3、求直线与平面所成角的常见方法(1)作角法:作出斜线、垂线、斜线在平面上的射影组成的直角三角形,根据条件求出斜线与射影所成的角即为所求.(2)等积法:公式θ=sin hl,其中θ是斜线与平面所成的角,h 是垂线段的长,是斜线段的长,其中求出垂线段的长(即斜线上的点到面的距离)既是关键又是难点,为此可构造三棱锥,利用等体积法来求垂线段的长.(3)证垂法:通过证明线面垂直得到线面角为90°. 4、作二面角的平面角常有三种方法(1)棱上一点双垂线法:在棱上任取一点,过这点分别在两个面内作垂直于棱的射线,这两条射线所成的角,就是二面角的平面角.(2)面上一点三垂线法:自二面角的一个面上一点向另一面引垂线,再由垂足向棱作垂线得到棱上的点(即垂足),斜足与面上一点连线和斜足与垂足连线所夹的角,即为二面角的平面角.(3)空间一点垂面法:自空间一点作与棱垂直的平面,截二面角得两条射线,这两条射线所成的角就是二面角的平面角.【典型例题】例19.(2022·浙江金华·高三期末)已知正方体1111ABCD A B C D −中,P 为1ACD △内一点,且1113PB D ACD S S =△△,设直线PD 与11AC 所成的角为θ,则cos θ的取值范围为( )A .⎡⎢⎣⎦B .⎤⎥⎣⎦C .10,2⎡⎤⎢⎥⎣⎦D .1,12⎡⎤⎢⎥⎣⎦【答案】C【解析】如图1,设1B D 与平面1ACD 相交于点E ,连接BD 交AC 于点O ,连接11B D , ∵1BB ⊥平面ABCD ,AC ⊂平面ABCD ,则1BB AC ⊥,AC BD ⊥,1BD BB B ⋂=,1,BD BB ⊂平面11BDD B∴AC ⊥平面11BDD B ,由1B D ⊂平面11BDD B ,则1AC B D ⊥, 同理可证:11AD B D ⊥, 1AD AC A =,1,AD AC ⊂平面1ACD ,∴1B D ⊥平面1ACD ,∵111111AC AD CD AB B D B C =====,由正三棱锥的性质可得:E 为1ACD △的中心, 连接1OD ,∵O 为AC 的中点,∴1OD 交1B D 于点E ,连接PE ,由1B D ⊥平面1ACD ,PE ⊂平面1ACD ,则1B D PE ⊥,即PE 是1PB D 的高,设AB a =,PE d =,则1,B D AC =,且1ACD △的内切圆半径r OE ==,则1112PB D S B D PE =⋅=△,))1212ACD S =⨯=△,∵1113PB DACD S S =△△213=,则13d a r =<, ∴点P 的轨迹是以E 为圆心,13a 为半径的圆.∵1B D ⊥平面1ACD ,1OD ⊂平面1ACD ,则11B D OD ⊥,∴DE , 故PD 为底面半径为13a,高为=DE 的圆锥的母线,如图2所示,设圆锥的母线与底面所成的角α,则3tan 13a α== 所以π3α=,即直线PD 与平面1ACD 所成的角为π3. 直线AC 在平面1ACD 内,所以直线PD 与直线AC 所成角的取值范围为ππ,32⎡⎤⎢⎥⎣⎦,因为11AC AC ∥,所以直线PD 与直线11AC 所成角的取值范围为ππ,32⎡⎤⎢⎥⎣⎦,即ππ,32θ⎡⎤∈⎢⎥⎣⎦, 所以10cos 2θ≤≤. 故选:C.例20.(2022·浙江·效实中学模拟预测)在等腰梯形ABCD 中,AD BC ∥,12AB AD CD BC ===,AC 交BD 于O 点,ABD △沿着直线BD 翻折成1A BD ,所成二面角1A BD C −−的大小为θ,则下列选项中错误的是( )A .1A BC θ∠≤B .1AOC θ∠≥ C .1A DC θ∠≤ D .11A BC A DC θ∠+∠≥【答案】C【解析】等腰梯形ABCD 中,AD BC ∥,12AB AD CD BC ===,可知:30,ACB ACD BD DC ∠=∠=⊥取BD 中点N ,BC 中点M 连接1,A N NM ,则1A N BD ⊥,NM BC ⊥,所以1A NM ∠为 二面角1A BD C −−的平面角,即1A NM θ∠=设122AB AD CD BC ====,则1111,1,2,2A N MN A B A D ==== 2222211111111cos 1222A N NM A M A M A M A N NM θ+−+−∴===−⋅,2222222111111221cos 122228A B BM A M A M A BC A M A B BM +−+−∴∠===−⋅⨯⨯,因为在[]0,π上余弦函数单调递减,又2211111111cos cos 82A M A M A BC A BC θθ−≥−⇒∠≥⇒∠≤,故A 对. 2222222111111221cos 122228A D DC AC AC A DC AC A D CD +−+−∴∠===−⋅⨯⨯222122221111153cos 2416AC AO OC AC AOC AC AO OC +−+−∴∠===−⋅ 当0θ=时,1A 与M 重合,此时160A DC ∠=,故C 不对. 1A DC ∠在翻折的过程中,角度从120减少到60 1AOC ∠在翻折的过程中,角度从180减少到30BD 选项根据图形特征及空间关系,可知正确.. 故选:C例21.(2022·浙江·湖州中学高三阶段练习)如图,ABC 中,90C ∠=︒,1AC =,BC D 为AB 边上的中点,点M 在线段BD (不含端点)上,将BCM 沿CM 向上折起至'B CM △,设平面'B CM 与平面ACM 所成锐二面角为α,直线'MB 与平面AMC 所成角为β,直线MC 与平面'B CA 所成角为γ,则在翻折过程中,下列三个命题中正确的是( )①tan βα,②γβ≤,③γα>. A .① B .①② C .②③ D .①③【答案】B 【解析】如图,设直线BN 与直线CM 垂直相交于点N ,在折叠图里,线段B T '与平面ACM 垂直相交于点T ,,(0,30)BCM θθ∠=∈,由图像知:;B NT B MT αβ''∠=∠=,B N BN θ==', ()sin ;/sin 30B T B M θαθθ=*='︒+',cos NT θα*,()tan 60MN θθ=*︒−,()()2sin 30CM θ=︒+,①tan β==,tan β=≤≤,所以tan βα;② ()Δ1sin 902ACM S CM CA θ=*︒−= 设ACB δ∠'=,则()()()2cos cos cos 90sin sin 90cos cos 0.5sin2δθθθθααθ=*︒−+*︒−=*,Δsin ACB S δ'== 由ΔΔ1133ACM M ACB ACB B T S d S −''**=**',得M ACB d −'=()sin sin 30sin M ACB d B TMC B M γβθα'−====︒+*'',则()()sin sin 2tan 21sin 2sin 30cos 22sin 30γθθβθθθ=≤=≤︒+︒+, 由sin sin γβ≤得γβ≤; ③sin sin sin γγα=⇒,则sin sin 2tan 2sin 2cos 22γθθαθ≤=<sin γα<,所以sin sin γα<,则γα<.故选:B例22.(2022·浙江·高三专题练习)已知等边ABC ,点,E F 分别是边,AB AC 上的动点,且满足EF BC ∥,将AEF △沿着EF 翻折至P 点处,如图所示,记二面角P EF B −−的平面角为α,二面角P FC B −−的平面角为β,直线PF 与平面EFCB 所成角为γ,则( )A .αβγ≥≥B .αγβ≥≥C .βαγ≥≥D .βγα≥≥【答案】A【解析】在等边ABC 中,取BC 边中点D ,连接AD ,交EF 于O ,连接PO , 则,EF PO EF DO ⊥⊥,=PO DO O ⋂,PO ⊂平面POD ,DO ⊂平面POD 故EF ⊥平面POD ,又EF ⊂平面EFCB ,则平面POD ⊥平面EFCB 在POD 中,过P 做PM 垂直于OD 于M ,则PM ⊥平面EFCB ,连接MF , 在等边ABC 中,过M 做MN 垂直于AC 于N ,连接PN.由,EF PO EF DO ⊥⊥,则POM ∠为二面角P EF B −−的平面角即POM α∠=, 由PM ⊥平面EFCB ,MN AC ⊥,则PNM ∠为二面角P FC B −−的平面角即PNM β?由PM ⊥平面EFCB ,则PFM ∠直线PF 与平面EFCB 所成角,即PFM γ?,设AO ,则PO ,=FO a ,sin PM α,cos MO αFM ,)1=cos (1cos )2MN αα+=+, 则有FM OM >,FM NM >由cos MO MN α-(1cos )(cos 1)0αα-+=-<可得MO MN <,则有FM MN OM >>,则111FM MN OM<< 又tan tan ,tan PM PM PMOM NM FMαβγ,=== 故tan tan tan αβγ>>,又0,2παβγ⎛⎫∈ ⎪⎝⎭、、故αβγ>> 故选:A例23.(2022·全国·高三专题练习)设三棱锥V ABC −的底面是正三角形,侧棱长均相等,P 是棱VA 上的点(不含端点),记直线PB 与直线AC 所成的角为α,直线PB 与平面ABC 所成的角为β,二面角P AC B −−的平面角是γ则三个角α,β,γ中最小的角是( ) A .α B .β C .γD .不能确定【答案】B【解析】如图,取BC 的中点 D ,作VO ⊥平面ABC 于点O , 由题意知点O 在AD 上,且AO =2OD .作PE //AC ,PE 交VC 于点E ,作PF ⊥AD 于点F ,连接BF ,则PF ⊥平面ABC 取AC 的中点M ,连接BM ,VM ,VM 交 PE 于点H , 连接BH ,易知BH ⊥PE , 作于点G ,连接FG ,由PG ⊥AC ,PF ⊥AC ,PG PF =P ,由线面垂直判定定理可得AC ⊥平面PGF ,又FG ⊂平面PGF ∴ FG ⊥AC , 作FN ⊥BM 于点N . ∵ PG ∥VM ,PF ∥VN∴ 平面PGF ∥平面VMB , 又 PH ∥FN , 四边形PFNH 为平行四边形, 所以PH =FN因此,直线PB 与直线AC 所成的角=BPE α∠, 直线PB 与平面ABC 所成的角PBF β=∠, 二面角P -AC -B 的平面角PGF γ=∠, 又cos cos PH FN BFPB PB PBαβ==<=又,[0,]2παβ∈,∴ αβ> 因为 tan =tan PF PFGF BF γβ>= ,(0,)2πβγ∈∴ γβ>综上所述,,,αβγ中最小角为β,故选 B.。
高三数学空间角的求法静安高考补习班恒高教育

高三数学空间角的求法静安高考补习班恒高教育一、异面直线所成的角:1、异面直线所成的角的定义:已知两条异面直线,a b ,经过空间任一点O 作直线//,//a a b b '',,a b ''所成的角的大小与点O 的选择无关,把,a b ''所成的锐角(或直角)叫异面直线,a b 所成的角(或夹角).为了简便,点O 通常取在异面直线的一条上2、异面直线所成的角的范围:]2,0(π。
3、异面直线垂直:如果两条异面直线所成的角是直角,则叫两条异面直线垂直.两条异面直线,a b 垂直,记作a b ⊥.4、异面直线所成的角的求法:(1)平移法:即根据定义,以“运动”的观点,用“平移转化”的方法,使之成为相交直线所成的角。
在图中选一个恰当的点(通常是线段端点或中点)作a 、b 的平行线,构造一个三角形,并解三角形求角。
(2)向量法:可适当选取异面直线上的方向向量,利用公式ba b a b a ⋅=><=,cos cos θ 求解。
方法1:利用向量计算。
选取一组基向量,分别算出 b a ⋅,a ,b 代入上式 方法2:利用向量坐标计算,建系,确定直线上某两点坐标进而求出方向向量),,(111z y x a = ),,(222z y x b =222222212121212121c o s z y x z y x z z y y x x ++++++=∴θ(3)三线角公式 用于求线面角和线线角斜线和平面内的直线与斜线的射影所成角的余弦之积等于斜线和平面内的直线所成角的余弦 即:θθθcos cos cos 21=二、直线和平面所成的角1.直线和平面所成的角的定义:平面的一条斜线和它在平面上的射影所成的锐角叫做这条斜线和这个平面所成的角2、直线和平面所成的角的范围:[0,2π]; 当一条直线垂直于平面时,所成的角θ=2π, 即直线与平面垂直;当一条直线平行于平面或在平面内,所成角为θ=0。
高三数学 立体几何的难点突破 用向量方法求空间角和距离
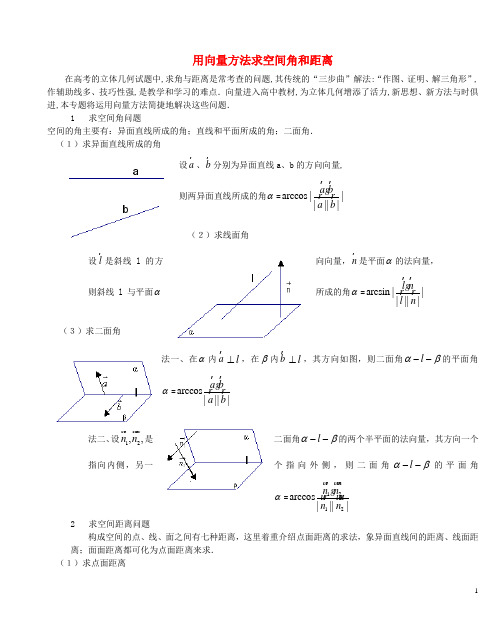
用向量方法求空间角和距离在高考的立体几何试题中,求角与距离是常考查的问题,其传统的“三步曲”解法:“作图、证明、解三角形”,作辅助线多、技巧性强,是教学和学习的难点.向量进入高中教材,为立体几何增添了活力,新思想、新方法与时俱进,本专题将运用向量方法简捷地解决这些问题.1 求空间角问题空间的角主要有:异面直线所成的角;直线和平面所成的角;二面角. (1)求异面直线所成的角设a r 、b r分别为异面直线a 、b 的方向向量,则两异面直线所成的角α=arccos ||||||a ba b r r g r r(2)求线面角向向量,n r是平面α的法向量,设l r是斜线l 的方所成的角α=arcsin ||||||l nl n r r g r r则斜线l 与平面α(3)求二面角法一、在α内a r l ⊥,在β内b rl ⊥,其方向如图,则二面角l αβ--的平面角α=arccos ||||a ba b r r g r r法二、设12,,n n u r u u r是二面角l αβ--的两个半平面的法向量,其方向一个个指向外侧,则二面角l αβ--的平面角指向内侧,另一α=1212arccos ||||n n n n u r u u rg ur u u r 2求空间距离问题构成空间的点、线、面之间有七种距离,这里着重介绍点面距离的求法,象异面直线间的距离、线面距离;面面距离都可化为点面距离来求. (1)求点面距离法一、设n r是平面α的法向量,在α内取一点B, 则 A 到α的距离|||||cos |||AB n d AB n θ==u u u r ru u u r g r 法二、设AO α⊥于O,利用AO α⊥和点O 在α内 的向量表示,可确定点O 的位置,从而求出||AO uuu r.(2)求异面直线的距离法一、找平面β使b β⊂且a βP ,则异面直线a 、b 的距离就转化为直线a 到平面β的距离,又转化为点A 到平面β的距离.法二、在a 上取一点A, 在b 上取一点B, 设a r、b r 分别为异面直线a 、b 的方向向量,求nr 的距离|||||cos |||AB n d AB n θ==u u u r ru u u r g r (此方法移(n r a ⊥r ,n r b ⊥r ),则异面直线a 、b植于点面距离的求法).例1.如图,在棱长为2的正方体1111ABCD A B C D -中,E 、F 分别是棱1111,A D A B 的中点.(Ⅰ)求异面直线1DE FC 与所成的角; (II )求1BC 和面EFBD 所成的角; (III )求1B 到面EFBD 的距离解:(Ⅰ)记异面直线1DE FC 与所成的角为α,则α等于向量1DE FC u u u r u u u u r与的夹角或其补角,11||||111111cos ||()()||||||DE FC DE FC DD D E FB B C DE FC α∴=++=u u u r u u u u rg u u u r u u u u r g u u u u r u u u u r u u u r u u u u r g u u u r u u u u r g(II )如图建立空间坐标系D xyz -,则(1,0,2)DE =u u u r ,(2,2,0)DB =u u u r设面EFBD 的法向量为(,,1)n x y =r 由0DE n DB n ⎧⋅=⎪⎨⋅=⎪⎩u u u r ru u u r r得(2,2,1)n =-r 又1(2,0,2)BC =-u u u u r记1BC 和面EFBD 所成的角为θ则 1112sin |cos ,|||2||||BC n BC n BC n θ⋅=〈〉==u u u u r ru u u u r r u u u u r r∴ 1BC 和面EFBD 所成的角为4π. (III )点1B 到面EFBD 的距离d等于向量1BB u u u r在面EFBD 的法向量上的投影的绝对值, 1||||BB n d n ∴==u u u r u u r g u ur 13 设计说明:1.作为本专题的例1,首先选择以一个容易建立空间直角坐标系的多面体―――正方体为载体,来说明空间角和距离的向量求法易于学生理解.2.解决(1)后,可让学生进一步求这两条异面直线的距离,并让学生体会一下:如果用传统方法恐怕很难(不必多讲,高考对公垂线的作法不作要求).3.完成这3道小题后,总结:对于易建立空间直角坐标系的立几题,无论求角、距离还是证明平行、垂直(是前者的特殊情况),都可用向量方法来解决, 向量方法可以人人学会,它程序化,不需技巧.例2.如图,三棱柱中,已知A BCD 是边长为1的正方形,四边形B B A A '' 是矩形,。
最新高中数学难点突破_难点28__求空间距离

1难点28 关于求空间距离2空间中距离的求法是历年高考考查的重点,其中以点与点、点到线、点到3面的距离为基础,求其他几种距离一般化归为这三种距离.4●难点磁场5(★★★★)如图,已知ABCD是矩形,AB=a,AD=b,PA⊥平面ABCD,PA=2c,Q 6是PA的中点.78求:(1)Q到BD的距离;9(2)P到平面BQD的距离.10●案例探究11[例1]把正方形ABCD沿对角线AC折起成直二面角,点E、F分别是AD、12BC的中点,点O是原正方形的中心,求:13(1)EF的长;14(2)折起后∠EOF的大小.15命题意图:考查利用空间向量的坐标运算来解决16立体几何问题,属★★★★级题目.17知识依托:空间向量的坐标运算及数量积公式.18错解分析:建立正确的空间直角坐标系.其中必须保证x 轴、y 轴、z 轴两19 两互相垂直.20技巧与方法:建系方式有多种,其中以O 点为原点,以、、的方21 向分别为x 轴、y 轴、z 轴的正方向最为简单.22解:如图,以O 点为原点建立空间直角坐标系O —xyz ,设正方形ABCD 边长23 为a ,则A (0,-22a ,0),B (22a ,0,0),C (0, 22a ,0),D (0,0, 22a ),E (0,-24 42a , a ),F (42a , 42a ,0) 2521||||,cos ,2||,2||8042)42)(42(420)0,42,42(),42,42,0()2(23,43)420()4242()042(||)1(22222-=>=<==-=⋅+-+⨯=⋅=-==∴=-+++-=OF OE a a a a a a a a a a a a EF a a a a a26∴∠EOF =120°27[例2]正方体ABCD —A 1B 1C 1D 1的棱长为1,求异面直线A 1C 1与AB 1间的距离. 28命题意图:本题主要考查异面直线间距离的求法,属★★★★级题目. 29知识依托:求异面直线的距离,可求两异面直线的公垂线,或转化为求线30 面距离,或面面距离,亦可由最值法求得.31错解分析:本题容易错误认为O 1B 是A 1C 与AB 1的距离,这主要是对异面直32 线定义不熟悉,异面直线的距离是与两条异面直线垂直相交的直线上垂足间的33 距离.34技巧与方法:求异面直线的距离,有时较难作出它们的公垂线,故通常采35 用化归思想,转化为求线面距、面面距、或由最值法求得.36解法一:如图,连结AC 1,在正方体AC 1中,∵A 1C 1∥AC ,∴A 1C 1∥平面AB 1C ,37 ∴A 1C 1与平面AB 1C 间的距离等于异面直线A 1C 1与AB 1间的距离.3839 连结B 1D 1、BD ,设B 1D 1∩A 1C 1=O 1,BD ∩AC =O 40∵AC ⊥BD ,AC ⊥DD 1,∴AC ⊥平面BB 1D 1D41∴平面AB 1C ⊥平面BB 1D 1D ,连结B 1O ,则平面AB 1C ∩平面BB 1D 1D =B 1O 42作O 1G ⊥B 1O 于G ,则O 1G ⊥平面AB 1C43∴O 1G 为直线A 1C 1与平面AB 1C 间的距离,即为异面直线A 1C 1与AB 1间的距离. 44在Rt △OO 1B 1中,∵O 1B 1=22,OO 1=1,∴OB 1=21121B O OO += 2645∴O 1G =331111=⋅OB B O O O ,即异面直线A 1C 1与AB 1间距离为33. 46解法二:如图,在A 1C 上任取一点M ,作MN ⊥AB 1于N ,作MR ⊥A 1B 1于R ,连47 结RN ,4849 ∵平面A 1B 1C 1D 1⊥平面A 1ABB 1,∴MR ⊥平面A 1ABB 1,MR ⊥AB 1 50∵AB 1⊥RN ,设A 1R =x ,则RB 1=1-x 51∵∠C 1A 1B 1=∠AB 1A 1=45°, 52∴MR =x ,RN =NB 1=)1(22x - 5331)31(23)1(2122222+-=-+=+=x x x RN MR MN (0<x <1) 54∴当x =31时,MN 有最小值33即异面直线A 1C 1与AB 1距离为33. 55●锦囊妙记56空间中的距离主要指以下七种: 57(1)两点之间的距离. 58(2)点到直线的距离. 59(3)点到平面的距离. 60(4)两条平行线间的距离. 61(5)两条异面直线间的距离.62(6)平面的平行直线与平面之间的距离.63(7)两个平行平面之间的距离.64七种距离都是指它们所在的两个点集之间所含两点的距离中最小的距离.65 七种距离之间有密切联系,有些可以相互转化,如两条平行线的距离可转化为66 求点到直线的距离,平行线面间的距离或平行平面间的距离都可转化成点到平67 面的距离.68在七种距离中,求点到平面的距离是重点,求两条异面直线间的距离是难69 点.70求点到平面的距离:(1)直接法,即直接由点作垂线,求垂线段的长.(2)转71 移法,转化成求另一点到该平面的距离.(3)体积法.72求异面直线的距离:(1)定义法,即求公垂线段的长.(2)转化成求直线与平73 面的距离.(3)函数极值法,依据是两条异面直线的距离是分别在两条异面直线74 上两点间距离中最小的.75●歼灭难点训练 76一、选择题771.(★★★★★)正方形ABCD 边长为2,E 、F 分别是AB 和CD 的中点,将正78 方形沿EF 折成直二面角(如图),M 为矩形AEFD 内一点,如果∠MBE =∠MBC ,MB 79 和平面BCF 所成角的正切值为21,那么点M 到直线EF 的距离为( )8081 21 D. 23C. B.1 22A.822.(★★★★)三棱柱ABC—A1B1C1中,AA1=1,AB=4,BC=3,∠ABC=90°,设平83面A1BC1与平面ABC的交线为l,则A1C1与l的距离为( )84A.10B.11C.2.6D.2.485二、填空题863.(★★★★)如左下图,空间四点A、B、C、D中,每两点所连线段的长都87等于a,动点P在线段AB上,动点Q在线段CD上,则P与Q的最短距离为88_________.89904.(★★★★)如右上图,ABCD与ABEF均是正方形,如果二面角E—AB—C 91的度数为9230°,那么EF与平面ABCD的距离为_________.93三、解答题945.(★★★★★)在长方体ABCD—A1B1C1D1中,AB=4,BC=3,CC1=2,如图:9596(1)求证:平面A1BC1∥平面ACD1;97(2)求(1)中两个平行平面间的距离;98(3)求点B 1到平面A 1BC 1的距离.996.(★★★★★)已知正四棱柱ABCD —A 1B 1C 1D 1,点E 在棱100 D 1D 上,截面EAC ∥D 1B 且面EAC 与底面ABCD 所成的角为101 45°,AB =a ,求:102(1)截面EAC 的面积;103(2)异面直线A 1B 1与AC 之间的距离; 104(3)三棱锥B 1—EAC 的体积.1057.(★★★★)如图,已知三棱柱A 1B 1C 1—ABC 的底面是边长为2的正三角形,106 侧棱A 1A 与AB 、AC 均成45°角,且A 1E ⊥B 1B 于E ,A 1F ⊥CC 1于F .107108 (1)求点A 到平面B 1BCC 1的距离;109(2)当AA 1多长时,点A 1到平面ABC 与平面B 1BCC 1的距离相等. 1108.(★★★★★)如图,在梯形ABCD 中,AD ∥BC ,∠ABC =2,AB = 31AD =a ,111∠ADC =arccos552,PA ⊥面ABCD 且PA =a . 112113(1)求异面直线AD 与PC 间的距离;114(2)在线段AD 上是否存在一点F ,使点A 到平面PCF 的距离为36. 115参考答案116难点磁场117解:(1)在矩形ABCD 中,作AE ⊥BD ,E 为垂足 118连结QE ,∵QA ⊥平面ABCD ,由三垂线定理得QE ⊥BE 119∴QE 的长为Q 到BD 的距离 120在矩形ABCD 中,AB =a ,AD =b ,121∴AE =22ba ab +122在Rt △QAE 中,QA =21PA =c123∴QE =22222ba b a c ++124∴Q 到BD 距离为22222ba b a c ++.125(2)解法一:∵平面BQD 经过线段PA 的中点, 126∴P 到平面BQD 的距离等于A 到平面BQD 的距离 127在△AQE 中,作AH ⊥QE ,H 为垂足128∵BD ⊥AE ,BD ⊥QE ,∴BD ⊥平面AQE ∴BD ⊥AH129∴AH ⊥平面BQE ,即AH 为A 到平面BQD 的距离.130在Rt △AQE 中,∵AQ =c ,AE =22ba ab +131∴AH =22222)(ba cb a abc ++132∴P 到平面BD 的距离为22222)(ba cb a abc ++133解法二:设点A 到平面QBD 的距离为h ,由134V A —BQD =V Q —ABD ,得31S △BQD ·h =31S △ABD ·AQ135h =22222)(ba cb a abc S AQS BQDABD ++==⋅∆∆136歼灭难点训练137一、1.解析:过点M 作MM ′⊥EF ,则MM ′⊥平面BCF 138∵∠MBE =∠MBC139∴BM ′为∠EBC 为角平分线, 140∴∠EBM ′=45°,BM ′=2,从而MN =22141答案:A1422.解析:交线l 过B 与AC 平行,作CD ⊥l 于D ,连C 1D ,则C 1D 为A 1C 1与l 143 的距离,而CD 等于AC 上的高,即CD =512,Rt △C 1CD 中易求得C 1D =513=2.6144答案:C145二、3.解析:以A 、B 、C 、D 为顶点的四边形为空间四边形,且为正四面体,146 取P 、Q 分别为AB 、CD 的中点,因为AQ =BQ =22a ,∴PQ ⊥AB ,同理可得PQ ⊥CD ,147 故线段PQ 的148长为P 、Q 两点间的最短距离,在Rt △APQ 中,149PQ =22)2()23(2222=-=-a a AP AQ a 150答案:22a 1514.解析:显然∠FAD 是二面角E —AB —C 的平面角,∠FAD =30°,过F 作FG 152 ⊥平面ABCD 于G ,则G 必在AD 上,由EF ∥平面ABCD .153∴FG 为EF 与平面ABCD 的距离,即FG =2a . 154答案:2a155三、5.(1)证明:由于BC 1∥AD 1,则BC 1∥平面ACD 1 156同理,A 1B ∥平面ACD 1,则平面A 1BC 1∥平面ACD 1157(2)解:设两平行平面A 1BC 1与ACD 1间的距离为d ,则d 等于D 1到平面A 1BC 1158 的距离.易求A 1C 1=5,A 1B =25,BC 1=13,则cos A 1BC 1=652,则sin A 1BC 1=6561,159则S 111C B A ∆=61,由于111111D C A B BC A D V V --=,则31S 11BC A ∆·d =)21(31111D C AD ⋅·BB 1,代入160 求得d =616112,即两平行平面间的距离为616112.161(3)解:由于线段B 1D 1被平面A 1BC 1所平分,则B 1、D 1到平面A 1BC 1的距离相162 等,则由(2)知点B 1到平面A 1BC 1的距离等于616112. 1636.解:(1)连结DB 交AC 于O ,连结EO ,164∵底面ABCD 是正方形 165∴DO ⊥AC ,又ED ⊥面ABCD 166∴EO ⊥AC ,即∠EOD =45° 167又DO =22a ,AC =2a ,EO =︒45cos DO =a ,∴S △EAC =22a 168(2)∵A 1A ⊥底面ABCD ,∴A 1A ⊥AC ,又A 1A ⊥A 1B 1 169∴A 1A 是异面直线A 1B 1与AC 间的公垂线 170又EO ∥BD 1,O 为BD 中点,∴D 1B =2EO =2a 171∴D 1D =2a ,∴A 1B 1与AC 距离为2a172(3)连结B 1D 交D 1B 于P ,交EO 于Q ,推证出B 1D ⊥面EAC 173∴B 1Q 是三棱锥B 1—EAC 的高,得B 1Q =23a17432422322311a a a V EAC B =⋅⋅=-1757.解:(1)∵BB 1⊥A 1E ,CC 1⊥A 1F ,BB 1∥CC 1 176∴BB 1⊥平面A 1EF 177即面A 1EF ⊥面BB 1C 1C 178在Rt △A 1EB 1中, 179∵∠A 1B 1E =45°,A 1B 1=a 180∴A 1E =22a ,同理A 1F =22a ,又EF =a ,∴A 1E =22a 181同理A 1F =22a ,又EF =a 182∴△EA 1F 为等腰直角三角形,∠EA 1F =90°183过A 1作A 1N ⊥EF ,则N 为EF 中点,且A 1N ⊥平面BCC 1B 1 184即A 1N 为点A 1到平面BCC 1B 1的距离 185∴A 1N =221a =186又∵AA 1∥面BCC 1B ,A 到平面BCC 1B 1的距离为2a187∴a =2,∴所求距离为2188(2)设BC 、B 1C 1的中点分别为D 、D 1,连结AD 、DD 1和A 1D 1,则DD 1必过点N ,189 易证ADD 1A 1为平行四边形.190∵B 1C 1⊥D 1D ,B 1C 1⊥A 1N 191∴B 1C 1⊥平面ADD 1A 1 192∴BC ⊥平面ADD 1A 1193得平面ABC ⊥平面ADD 1A 1,过A 1作A 1M ⊥平面ABC ,交AD 于M , 194若A 1M =A 1N ,又∠A 1AM =∠A 1D 1N ,∠AMA 1=∠A 1ND 1=90° 195∴△AMA 1≌△A 1ND 1,∴AA 1=A 1D 1=3,即当AA 1=3时满足条件. 1968.解:(1)∵BC ∥AD ,BC ⊂面PBC ,∴AD ∥面PBC197从而AD 与PC 间的距离就是直线AD 与平面PBC 间的距离. 198过A 作AE ⊥PB ,又AE ⊥BC199∴AE ⊥平面PBC ,AE 为所求. 200在等腰直角三角形PAB 中,PA =AB =a 201∴AE =22a 202(2)作CM ∥AB ,由已知cos ADC =552 203∴tan ADC =21,即CM =21DM204∴ABCM 为正方形,AC =2a ,PC =3a205过A 作AH ⊥PC ,在Rt △PAC 中,得AH =36206下面在AD 上找一点F ,使PC ⊥CF207取MD 中点F ,△ACM 、△FCM 均为等腰直角三角形 208∴∠ACM +∠FCM =45°+45°=90°209∴FC ⊥AC ,即FC ⊥PC ∴在AD 上存在满足条件的点F .210211[学法指导]立体几何中的策略思想及方法212立体几何中的策略思想及方法213近年来,高考对立体几何的考查仍然注重于空间观点的建立和空间想象能214力的培养.题目起点低,步步升高,给不同层次的学生有发挥能力的余地.大题215综合性强,有几何组合体中深层次考查空间的线面关系.因此,高考复习应在抓216好基本概念、定理、表述语言的基础上,以总结空间线面关系在几何体中的确217定方法入手,突出数学思想方法在解题中的指导作用,并积极探寻解答各类立218体几何问题的有效的策略思想及方法.219一、领悟解题的基本策略思想220高考改革稳中有变.运用基本数学思想如转化,类比,函数观点仍是考查中221心,选择好典型例题,在基本数学思想指导下,归纳一套合乎一般思维规律的222解题模式是受学生欢迎的,学生通过熟练运用,逐步内化为自己的经验,解决223一般基本数学问题就会自然流畅.224二、探寻立体几何图形中的基面225立体几何图形必须借助面的衬托,点、线、面的位置关系才能显露地“立”226起来.在具体的问题中,证明和计算经常依附于某种特殊的辅助平面即基面.这227个辅助平面的获取正是解题的关键所在,通过对这个平面的截得,延展或构造,228纲举目张,问题就迎刃而解了.229三、重视模型在解题中的应用230学生学习立体几何是从认识具体几何模型到抽象出空间点、线、面的关系,231从而培养空间想象能力.而数学问题中许多图形和数量关系都与我们熟悉模型232存在着某种联系.它引导我们以模型为依据,找出起关键作用的一些关系或数233量,对比数学问题中题设条件,突出特性,设法对原图形补形,拼凑、构造、234嵌入、转化为熟知的、形象的、直观的模型,利用其特征规律获取优解. 235236。
高考数学难点突破与解题方法

高考数学难点突破与解题方法随着高考日益逼近,数学作为一门重要的科目,成为许多考生头疼的难题。
其中,存在着一些难点,对于许多考生来说是必须要突破的难关。
本文将介绍一些高考数学难点的突破方法和解题技巧,帮助考生在考试中取得更好的成绩。
一、代数与函数代数与函数是高考数学中的一大难点,其中包括方程、函数和不等式。
首先,要熟练掌握基本的代数知识,比如一元二次方程、分式方程等,切忌死记硬背,要通过大量的练习来加深理解。
其次,要了解各类函数的性质,包括基本初等函数的图像、性质和变化规律等。
高考中常见的函数类型有线性函数、二次函数和指数函数等,掌握它们的性质和变化规律能够解决不少难题。
最后,对于不等式的解法,要掌握常见的不等式性质,比如绝对值不等式、二次式不等式等,通过画图或代入法来解决。
二、立体几何立体几何也是高考数学中的难点之一。
在解题时,要注重对图形性质的理解和几何关系的把握。
了解常见几何图形的特征和性质,包括正方体、正四面体和圆锥等,会对解题有很大帮助。
同时,还需要掌握立体几何的投影问题,如求柱体、圆柱和圆锥的截面面积和体积等。
通过多做一些相关的题目进行练习,能够提高解决立体几何难题的能力。
三、概率与统计概率与统计在高考数学中占有一定的比重,也是一些考生容易忽视的部分。
在解题时,要注意理解概率与统计的基本概念和原理。
掌握概率计算的方法,包括排列组合、事件的计算和条件概率等。
对于统计的问题,要熟悉常见统计量的计算,如均值、中位数和标准差等。
此外,还要注意对数据的分析与解读,包括直方图和折线图的解读,以及数据的比较和推断分析。
四、解题技巧在考试时,掌握一些解题技巧对于突破数学难点是非常有效的。
首先,要学会研读题目,理解题目所给的条件和要求,抓住关键信息。
其次,学会尝试多种解题方法,从不同的角度入手,比较其优劣并选择最合适的方法。
此外,要善于归纳总结,在做题过程中,记录解题思路和方法,方便日后进行复习和总结。
空间角问题高三数学知识点

空间角问题高三数学知识点空间角问题是高三数学中的重要知识点之一。
在解决空间角问题时,我们需要熟练掌握一系列概念、定理和计算方法。
本文将系统介绍空间角问题的相关内容,包括空间角的定义、分类和性质,以及求解空间角问题的具体方法和技巧。
一、空间角的定义和分类1.1 空间角的定义空间角是在三维空间中由两条射线形成的角。
它可以看作是平面角在立体空间中的推广。
通常用小写的希腊字母表示空间角,如α、β、γ等。
1.2 空间角的分类根据空间角的大小和位置关系,空间角可以分为以下几种类型:1) 零角:两条射线重合,形成的角为零角。
2) 锐角:两条射线夹角小于90度,形成的角为锐角。
3) 直角:两条射线夹角等于90度,形成的角为直角。
4) 钝角:两条射线夹角大于90度但小于180度,形成的角为钝角。
5) 平角:两条射线夹角等于180度,形成的角为平角。
二、空间角的性质空间角具有一系列重要的性质,掌握这些性质有助于我们解决空间角问题。
2.1 垂直性质若两个空间角互为互补角,则它们所对的两条射线垂直。
2.2 同位角性质若两个空间角由相同的两条射线所形成(其中一条射线相互重合),则这两个空间角互为同位角。
同位角具有以下性质:1) 同位角相等:若两个同位角中的一个角为α,则另一个角也为α。
2) 同位角的补角关系:若两个同位角中的一个角为α,则另一个角为180度减α的补角。
2.3 对顶角性质若两个空间角互为对顶角,则它们所对的两条射线互相重合。
三、求解空间角问题的方法和技巧3.1 判断空间角的类型在解决空间角问题时,首先要能够准确地判断空间角的类型。
可以通过观察两条射线的位置关系和夹角的大小来判断空间角是锐角、直角、钝角还是平角。
3.2 应用对顶角和同位角的性质对顶角和同位角的性质在求解空间角问题时经常被应用。
通过利用对顶角和同位角的性质,可以得到空间角的相关信息,进而解决问题。
3.3 运用向量方法在空间角问题的求解中,向量方法也是一种重要的技巧。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
难点27 求空间的角空间的角是空间图形的一个要素,在异面直线所成的角、线面角、二面角等知识点上,较好地考查了学生的逻辑推理能力以及化归的数学思想.●难点磁场(★★★★★)如图,α—l—β为60°的二面角,等腰直角三角形MPN的直角顶点P在l上,M∈α,N∈β,且MP与β所成的角等于NP与α所成的角.(1)求证:MN分别与α、β所成角相等;(2)求MN与β所成角.●案例探究[例1]在棱长为a的正方体ABCD—A′B′C′D′中,E、F分别是BC、A′D′的中点.(1)求证:四边形B′EDF是菱形;(2)求直线A′C与DE所成的角;(3)求直线AD与平面B′EDF所成的角;(4)求面B′EDF与面ABCD所成的角.命题意图:本题主要考查异面直线所成的角、线面角及二面角的一般求法,综合性较强,属★★★★★级题目.知识依托:平移法求异面直线所成的角,利用三垂线定理求作二面角的平面角.错解分析:对于第(1)问,若仅由B ′E =ED =DF =FB ′就断定B ′EDF 是菱形是错误的,因为存在着四边相等的空间四边形,必须证明B ′、E 、D 、F 四点共面.技巧与方法:求线面角关键是作垂线,找射影,求异面直线所成的角采用平移法.求二面角的大小也可应用面积射影法.(1)证明:如上图所示,由勾股定理,得B ′E =ED =DF =FB ′=25a ,下证B ′、E 、D 、F 四点共面,取AD 中点G ,连结A ′G 、EG ,由EG ABA ′B ′知,B ′EGA ′是平行四边形.∴B ′E ∥A ′G ,又A ′FD G ,∴A ′GDF 为平行四边形.∴A ′G ∥FD ,∴B ′、E 、D 、F 四点共面 故四边形B ′EDF 是菱形.(2)解:如图所示,在平面ABCD 内,过C 作CP ∥DE ,交直线AD 于P ,则∠A ′CP (或补角)为异面直线A ′C 与DE 所成的角. 在△A ′CP 中,易得A ′C =3a ,CP =DE =25a ,A ′P =213a 由余弦定理得cos A ′CP =1515故A ′C 与DE 所成角为arccos1515. (3)解:∵∠ADE =∠ADF ,∴AD 在平面B ′EDF 内的射影在∠EDF 的平分线上.如下图所示.又∵B ′EDF 为菱形,∴DB ′为∠EDF 的平分线, 故直线AD 与平面B ′EDF 所成的角为∠ADB ′ 在Rt △B ′AD 中,AD =2a ,AB ′=2a ,B ′D =2a则cos ADB ′=33 故AD 与平面B ′EDF 所成的角是arccos33. (4)解:如图,连结EF 、B ′D ,交于O 点,显然O 为B ′D 的中点,从而O 为正方形ABCD —A ′B ′C ′D 的中心.作OH ⊥平面ABCD ,则H 为正方形ABCD 的中心, 再作HM ⊥DE ,垂足为M ,连结OM ,则OM ⊥DE , 故∠OMH 为二面角B ′—DE ′—A 的平面角.在Rt △DOE 中,OE =22a ,OD =23a ,斜边DE =25a ,则由面积关系得OM =1030=⋅DE OE OD a 在Rt △OHM 中,sin OMH =630=OM OH 故面B ′EDF 与面ABCD 所成的角为arcsin 630.[例2]如下图,已知平行六面体ABCD —A 1B 1C 1D 1中,底面ABCD 是边长为a 的正方形,侧棱AA 1长为b ,且AA 1与AB 、AD 的夹角都是120°.求:(1)AC 1的长;(2)直线BD 1与AC 所成的角的余弦值.命题意图:本题主要考查利用向量法来解决立体几何问题,属★★★★★级题目. 知识依托:向量的加、减及向量的数量积.错解分析:注意<AA ,1>=<1AA ,>=120°而不是60°,<,>=90°. 技巧与方法:数量积公式及向量、模公式的巧用、变形用.221122211111212211111122122211111222221112221111111212222||||||))((||))((,2||,)2(.22||,22||,0,21120cos ,21120cos 90,,120,,||||,|:|222||||||))(())((||)1(:b a AA AA AB AD AA AA AA BD BD ab AB AD AA AA AA BD AA BD a ab b a AC ab b a AC ab a b AA ab a b AA AA AA a b AA AA AA AA AA AA AA AA AC AC AC +=⋅-⋅-⋅+++=-+-+=⋅=-=⋅--+⋅+⋅+⋅=-++=⋅∴-+=+=+==-+=∴-+=∴=⋅-=︒⋅=⋅-=︒⋅=⋅∴︒>=<︒>=>=<<===⋅+⋅+⋅+++=++++=++=⋅=依题意得由已知得解2212||b a BD +=∴ 2211124||||,cos b a b AC BD BD +-=>=<∴BD 1与AC 所成角的余弦值为2224ba b +.●锦囊妙计空间角的计算步骤:一作、二证、三算1.异面直线所成的角 范围:0°<θ≤90° 方法:①平移法;②补形法.2.直线与平面所成的角 范围:0°≤θ≤90° 方法:关键是作垂线,找射影.3.二面角方法:①定义法;②三垂线定理及其逆定理;③垂面法. 注:二面角的计算也可利用射影面积公式S ′=S cos θ来计算 ●歼灭难点训练 一、选择题1.(★★★★★)在正方体ABCD —A 1B 1C 1D 1中,M 为DD 1的中点,O 为底面ABCD 的中心,P 为棱A 1B 1上任意一点,则直线OP 与直线AM 所成的角是( )A.6π B.4π C.3π D.2π 2.(★★★★★)设△ABC 和△DBC 所在两平面互相垂直,且AB =BC =BD =a ,∠CBA = ∠CBD =120°,则AD 与平面BCD 所成的角为( )A.30°B.45°C.60°D.75°二、填空题3.(★★★★★)已知∠AOB=90°,过O点引∠AOB所在平面的斜线OC,与OA、OB分别成45°、60°,则以OC为棱的二面角A—OC—B的余弦值等于_________.4.(★★★★)正三棱锥的一个侧面的面积与底面积之比为2∶3,则这个三棱锥的侧面和底面所成二面角的度数为_________.三、解答题5.(★★★★★)已知四边形ABCD为直角梯形,AD∥BC,∠ABC=90°,P A⊥平面AC,且P A=AD=AB=1,BC=2(1)求PC的长;(2)求异面直线PC与BD所成角的余弦值的大小;(3)求证:二面角B—PC—D为直二面角.6.(★★★★)设△ABC和△DBC所在的两个平面互相垂直,且AB=BC=BD,∠ABC= ∠DBC=120°求:(1)直线AD与平面BCD所成角的大小;(2)异面直线AD与BC所成的角;(3)二面角A—BD—C的大小.7.(★★★★★)一副三角板拼成一个四边形ABCD,如图,然后将它沿BC折成直二面角.(1)求证:平面ABD⊥平面ACD;(2)求AD与BC所成的角;(3)求二面角A—BD—C的大小.8.(★★★★★)设D是△ABC的BC边上一点,把△ACD沿AD折起,使C点所处的新位置C′在平面ABD上的射影H恰好在AB上.(1)求证:直线C′D与平面ABD和平面AHC′所成的两个角之和不可能超过90°;(2)若∠BAC=90°,二面角C′—AD—H为60°,求∠BAD的正切值.参考答案难点磁场(1)证明:作NA ⊥α于A ,MB ⊥β于B ,连接AP 、PB 、BN 、AM ,再作AC ⊥l 于C ,BD ⊥l 于D ,连接NC 、MD .∵NA ⊥α,MB ⊥β,∴∠MPB 、∠NP A 分别是MP 与β所成角及NP 与α所成角,∠MNB ,∠NMA 分别是MN 与β,α所成角,∴∠MPB =∠NP A .在Rt △MPB 与Rt △NP A 中,PM =PN ,∠MPB =∠NP A ,∴△MPB ≌△NP A ,∴MB =NA . 在Rt △MNB 与Rt △NMA 中,MB =NA ,MN 是公共边,∴△MNB ≌△NMA ,∴∠MNB =∠NMA ,即(1)结论成立.(2)解:设∠MNB =θ,MN =2a ,则PB =PN =a ,MB =NA =2a sin θ,NB =2a cos θ,∵MB ⊥β,BD ⊥l ,∴MD ⊥l ,∴∠MDB 是二面角α—l —β的平面角,∴∠MDB =60°,同理∠NCA =60°,∴BD =AC =3633=MB a sin θ,CN =DM =63260sin 6=︒MB a sin θ,∵MB ⊥β,MP ⊥PN ,∴BP ⊥PN∵∠BPN =90°,∠DPB =∠CNP ,∴△BPD ∽△PNC ,∴PBBDPN PC =22222222)cos 2(3sin 6)sin 362(,aa a aa aBN DB aCN a -=-∴-=-θθθ即整理得,16sin 4θ-16sin 2θ+3=0 解得sin 2θ=4341或,sin θ=2321或,当sin θ=23时,CN =632a sin θ= 2a >PN 不合理,舍去.∴sin θ=21,∴MN 与β所成角为30°. 歼灭难点训练一、1.解析:(特殊位置法)将P 点取为A 1,作OE ⊥AD 于E ,连结A 1E ,则A 1E 为OA 1的射影,又AM ⊥A 1E ,∴AM ⊥OA 1,即AM 与OP 成90°角.答案:D2.解析:作AO ⊥CB 的延长线,连OD ,则OD 即为AD 在平面BCD 上的射影,∵AO =OD =23a ,∴∠ADO =45°. 答案:B二、3.解析:在OC 上取一点C ,使OC =1,过C 分别作CA ⊥OC 交OA 于A ,CB ⊥OC 交OB 于B ,则AC =1,,OA =2,BC =3,OB =2,Rt △AOB 中,AB 2=6,△ABC 中,由余弦定理,得cos ACB =-33. 答案:-33 4.解析:设一个侧面面积为S 1,底面面积为S ,则这个侧面在底面上射影的面积为3S ,由题设得321=S S ,设侧面与底面所成二面角为θ,则cos θ=2133111==S S S S,∴θ=60°.答案:60°三、5.(1)解:因为P A ⊥平面AC ,AB ⊥BC ,∴PB ⊥BC ,即∠PBC =90°,由勾股定理得PB =222=+AB PA .∴PC =622=+PC PB.(2)解:如图,过点C 作CE ∥BD 交AD 的延长线于E ,连结PE ,则PC 与BD 所成的角为∠PCE 或它的补角.∵CE =BD =2,且PE =1022=+AE PA∴由余弦定理得cos PCE =632222-=⋅-+CE PC PE CE PC ∴PC 与BD 所成角的余弦值为63.(3)证明:设PB 、PC 中点分别为G 、F ,连结FG 、AG 、DF ,则GF ∥BC ∥AD ,且GF =21BC =1=AD ,从而四边形ADFG 为平行四边形,又AD ⊥平面P AB ,∴AD ⊥AG ,即ADFG 为矩形,DF ⊥FG .在△PCD 中,PD =2,CD =2,F 为BC 中点,∴DF ⊥PC从而DF ⊥平面PBC ,故平面PDC ⊥平面PBC ,即二面角B —PC —D 为直二面角. 6.解:(1)如图,在平面ABC 内,过A 作AH ⊥BC ,垂足为H ,则AH ⊥平面DBC , ∴∠ADH 即为直线AD 与平面BCD 所成的角.由题设知△AHB ≌△AHD ,则DH ⊥BH ,AH =DH ,∴∠ADH =45°(2)∵BC ⊥DH ,且DH 为AD 在平面BCD 上的射影, ∴BC ⊥AD ,故AD 与BC 所成的角为90°.(3)过H 作HR ⊥BD ,垂足为R ,连结AR ,则由三垂线定理知,AR ⊥BD ,故∠ARH 为二面角A —BD —C 的平面角的补角.设BC =a ,则由题设知,AH =DH =2,23aBH a =,在△HDB 中,HR =43a ,∴tan ARH =HRAH=2 故二面角A —BD —C 大小为π-arctan2.7.(1)证明:取BC 中点E ,连结AE ,∵AB =AC ,∴AE ⊥BC ∵平面ABC ⊥平面BCD ,∴AE ⊥平面BCD , ∵BC ⊥CD ,由三垂线定理知AB ⊥CD .又∵AB ⊥AC ,∴AB ⊥平面BCD ,∵AB ⊂平面ABD . ∴平面ABD ⊥平面ACD .(2)解:在面BCD 内,过D 作DF ∥BC ,过E 作EF ⊥DF ,交DF 于F ,由三垂线定理知A F ⊥DF ,∠ADF 为AD 与BC 所成的角.设AB =m ,则BC =2m ,CE =DF =22m ,CD =EF =36m 321arctan ,321tan 22=∠∴=+==∴ADF DF EF AE DFAFADF即AD 与BC 所成的角为arctan321(3)解:∵AE ⊥面BCD ,过E 作EG ⊥BD 于G ,连结AG ,由三垂线定理知AG ⊥BD , ∴∠AGE 为二面角A —BD —C 的平面角∵∠EBG =30°,BE =22m ,∴EG =42m 又AE =22m ,∴tan AGE =GEAE=2,∴∠AGE =arctan2.即二面角A —BD —C 的大小为arctan2.8.(1)证明:连结DH ,∵C ′H ⊥平面ABD ,∴∠C ′DH 为C ′D 与平面ABD 所成的角且平面C ′HA ⊥平面ABD ,过D 作DE ⊥AB ,垂足为E ,则DE ⊥平面C ′HA .故∠DC ′E 为C ′D 与平面C ′HA 所成的角∵sin DC ′E =D C DE '≤DC DH'=sin DC ′H∴∠DC ′E ≤∠DC ′H ,∴∠DC ′E +∠C ′DE ≤∠DC ′H +∠C ′DE =90° (2)解:作HG ⊥AD ,垂足为G ,连结C ′G ,则C ′G ⊥AD ,故∠C ′GH 是二面角C ′—AD —H 的平面角即∠C ′GH =60°,计算得tan BAD =22.。
