2012学年二模卷和08-12中考真题中填空第18题汇编(附答案)
2012届中考二模联考语文试卷(修改)

全国内地西藏班(校)2012届毕业班二模联考语文试卷主命题学校:广东惠州八中时间:120分钟总分:100分注意事项:1.本试卷的选择题和非选择题都在答题纸上作答,不能答在试卷上。
2.答卷前,考生务必将自己的姓名、考试号写在答题纸上。
3.选择题与非选择题必须在指定的区域内,用黑色字迹的签字笔或钢笔作答,不能超出指定区域或在非指定区域作答,否则答案无效。
一、基础知识与运用(20分)1、下面各组词语的字形及加点字的注音全对的一项是()(2分)A.揣.摩(chuǎi)蓦.然(mù)轩.然大波(xuān)大气磅礴.(bò)B.魁梧.(wú)污秽.(huì)荒谬.绝伦(miù)提纲挈.领(qiè)C.濒.临(bīng)栈.桥(zhàn)拈.轻怕重(zhān)蜂涌.而至(yǒng)D.惬.意(qiè)亢.奋(kàng)同仇敌忾.(qì)繁华嫩.叶(nèn)2、下列词语书写全部正确的一项是()(2分)A.一代天娇不省人事不可思义B.锋芒必露不言而喻与日具增C.相形见拙任劳任怨心无旁鹜D.因地制宜叹为观止别出心裁3、下列各句中,加点成语使用恰当的一项是()(2分)A.人类的智慧与大自然的智慧相比实在是相形见...绌.。
B.今年早春,西南地区的旱情非常严峻,据称是60年未遇。
难怪有父母官急中生智....,怒批气象预报不该说天气晴好,应叫天气晴坏!C.女儿今天要出嫁了,妈妈亲手为女儿乔装打扮....。
D.爬上天堂寨才知道它有多高,只见周围的群山鳞次栉比....,都在它的脚下了。
4、下面各句中,没有语病的是()(2分)A.全班同学都去参加阳光体育活动了,只有我没有去。
B.通过老师的精心指导,我终于理解了这篇文章的内涵。
C.有没有健康的身体,是能做好工作的前提。
D.假期里,大家外出游玩时一定要注意交通安全,防止不要发生意外事故。
中考数学二模第18题精选练习25题

中考数学二模第 18 题精选练习 25 题题1:如图,在△ABC 中,∠ACB=90°,sin B=,将△ABC 绕顶点C 顺时针旋转,得到△A1B1C,点A、B 分别与点A1、B1 对应,边A1B1 分别交边AB、BC 于点D、E,如果点E 是边A1B1 的中点,那么=.题2:定义:如果P 是圆O 所在平面内的一点,Q 是射线OP 上一点,且线段OP、OQ 的比例中项等于圆O 的半径,那么我们称点P 与点Q 为这个圆的一对反演点.已知点M、N 为圆O 的一对反演点,且点M、N 到圆心O 的距离分别为4 和9,那么圆O 上任意一点到点M、N 的距离之=.题3:一个正多边形的对称轴共有10 条,且该正多边形的半径等于4,那么该正多边形的边长等于.题4:如图,在△ABC 中,已知AB=AC,∠BAC=30°,将△ABC 绕着点A 逆时针旋转30°,记点C 的对应点为点D,AD、BC 的延长线相交于点E.如果线段DE 的长,那么边AB 的长为.题5:如图,点M 的坐标为(3,2),动点P 从点O 出发,沿y 轴以每秒1 个单位的速度向上移动,且过点P 的直线l:y=﹣x+b 也随之移动,若点M 关于l 的对称点落在坐标轴上,设点P 的移动时间为t,则t 的值是.题6:如图,在△ABC 中,AB=AC=5,BC=8,将△ABC 绕着点C 旋转,点A、B 的对应点分别是点A'、B',若点B'恰好在线段AA'的延长线上,则AA'的长等于.题7:如图,在△ABC 中,AB=AC=5,BC=2,D为边AC 上一点(点D与点A、C 不重合).将△AB D 沿直线BD 翻折,使点A 落在点E 处,连接CE.如果CE∥AB,那么AD:CD=.题8:如图,在平面直角坐标系xOy 中,已知,0),B(0,6),M(0,2).点Q 在直线AB 上,把△BMQ 沿着直线MQ 翻折,点B 落在点P 处,联结PQ.如果直线PQ 与直线AB 所构成的夹角为60°,那么点P 的坐标是.题9:如图,在矩形ABCD 中,AB=6,点E 在边AD 上且AE=4,点F 是边BC 上的一个动点,将四边形ABFE 沿EF 翻折,A、B 的对应点A1、B1 与点C 在同一直线上,A1B1 与边AD 交于点G,如果DG =3,那么BF 的长为.题10:如图,已知Rt△ABC 中,∠ACB=90°,AC=8,BC=6.将△ABC 绕点 B 旋转得到△DBE,点A 的对应点D 落在射线BC 上.直线AC 交DE 于点F,那么CF 的长为.题11:如图,矩形ABCD,AD=a,将矩形ABCD 绕着顶点B 顺时针旋转,得到矩形EBGF,顶点A、D、C 分别与点E、F、G 对应(点D 与点F 不重合).如果点D、E、F 在同一条直线上,那么线段DF 的长是.(用含a 的代数式表示)题12:如图,在Rt△ABC 中,∠ACB=90°,AB=6,cos B=,先将△ACB 绕着顶点C 顺时针旋转90°,然后再将旋转后的三角形进行放大或缩小得到△A′CB(′点A′、C、B′的对应点分别是点A、C、B),连接A′A、B′B,如果△AA′B 和△AA′B′相似,那么A′C 的长是.题13:如图,在矩形ABCD 中,过点A 的圆O 交边AB 于点E,交边AD 于点F,已知AD=5,AE=2,AF=4.如果以点D 为圆心,r 为半径的圆D 与圆O 有两个公共点,那么r 的取值范围是.题14:如图,点M 的坐标为(3,2),点P 从原点O 出发,以每秒1 个单位的速度沿y 轴向上移动,同时过点P 的直线l 也随之上下平移,且直线l 与直线y=﹣x 平行,如果点M 关于直线l 的对称点落在坐标轴上,如果点P 的移动时间为t 秒,那么t 的值可以是.题15:我们把满足某种条件的所有点组成的图形,叫做符合这个条件的点的轨迹,如图,在Rt△ABC 中,∠C=90°,AC=8,BC=12,动点P 从点A 开始沿射线AC 方向以1 个单位秒的速度向点C 运动,动点Q 从点C 开始沿射线CB 方向以2 个单位/秒的速度向点运动,P、Q 两点分别从点A、C 同时出发,当其中一点到达端点时,另一点也随之停止运动,在整个运动过程中,线段PQ 的中点M 运动的轨迹长为.题16:如图,AD 是△ABC 的中线,点E 在边AB 上,且DE⊥AD,将△BDE 绕着点D 旋转,使得点B 与点C 重合,点E 落在点F 处,连接AF 交BC 于点G,如,那的值等于.题17:在直角梯形ABCD 中,点E 在线段AD 上,将△ABE 沿BE 翻折,点A 恰巧落在对角线BD 上点P 处,那么PD=.题18:如图,在Rt△ABC 中,∠C=90°,AB=5,BC=3,点P、Q 分别在边BC、AC 上,PQ∥AB,把△PCQ 绕点P 旋转得到△PDE(点C、Q 分别与点D、E 对应),点D 落在线段PQ 上,若AD 平分∠BAC,则CP 的长为.题19:如图,在△ABC 中,点D 是AB 的中点,如果把△BCD 沿直线CD翻折,使得点B 落在同一平面内的B′处,联结AB′,那么AB′的长为.题20:如图,Rt△ABC 中,∠C=90°,AC=6,BC=8,D 是AB 的中点,P 是直线BC 上一点,把△BDP 沿PD 所在的直线翻折后,点B 落在点Q 处,如果QD⊥BC,那么点P 和点B 间的距离等于.题21:如图,△ABC 中,∠BAC=90°,AB=6,AC=8,点D 是BC 的中点,将△ABD,将△ABD 沿AD 翻折得到△AED,连接CE,那么线段CE 的长等于.题22:如图,已知平行四边形ABCD 中,AC=BC,∠ACB=45°,将三角形ABC 沿着AC 翻折,点B 落在点E 处,联结DE,那的值为.题23:如图,将△ABC 的边AB 绕着点A 顺时针旋转α(0°<α<90°)得到AB′,边AC 绕着点A 逆时针旋转β(0°<β<90°)得到AC′,联结B′C′.当α+β=90°时,我们称△AB′C′是△ABC 的“双旋三角形”.如果等边△ABC 的边长为a,那么它的“双旋三角形”的面积是(用含a 的代数式表示).题24:如图,将矩形ABCD 沿对角线AC 折叠,使点B 翻折到点E 处,如果DE:AC=1:3,那么AD:AB=.题25:如图,在△ABC 中,AB=AC=5,BC=6,点D 在边AB 上,且∠BDC=90°.如果△ACD 绕点A 顺时针旋转,使点C 与点B 重合,点D 旋转至点D1,那么线段DD1 的长为.参考答案一.填空题(共 25 小题)1.【分析】设 AC =3x ,AB =5x ,可求 BC =4x ,由旋转的性质可得 CB 1=BC =4x ,A 1B 1=5x ,∠ACB = ∠A 1CB 1,由题意可证△CEB 1∽△DEB ,可得 ,即可求解.【解答】解:∵∠ACB =90°,sin = ,∴设 AC =3x ,AB =5x ,∴BC ==4x ,∵将△ABC 绕顶点 C 顺时针旋转,得到△A 1B 1C ,∴CB 1=BC =4x ,A 1B 1=5x ,∠ACB =∠A 1CB 1,∵点 E 是 A 1B 1 的中点,∴CE =A 1B 1=2.5x =B 1E ,∴BE =BC ﹣CE =1.5x ,∵∠B =∠B 1,∠CEB 1=∠BED∴△CEB 1∽△DEB=2.【分析】分三种情形分别求解即可解决问题.【解答】解:由题意⊙O 的半径 r 2=4×9=36,∵r >0,∴r =6,当点 A 在 NO 的延长线上时,AM =6+4=10,AN =6+9=15,∴==,当点 A ″是 ON 与⊙O 的交点时,A ″M =2,A ″N =3,∴=,当点 A ′是⊙O 上异与 A ,A ″两点时,易证△OA ′M ∽△ONA ′,∴ = = = ,∴ 故答案为:综上所述=.故答案为.3.【分析】根据轴对称图形的性质得到这个正多边形是正十边形,求出正十边形的中心角,作AC 平分∠OAB 交OB 于C,根据相似三角形的性质列出比例式,计算即可.【解答】解:∵正多边形的对称轴共有10 条,∴这个正多边形是正十边形,设这个正十边形的中心为O,则OA=OB=4,∠AOB==36°,∵OA=OB,∴∠OAB=∠B=72°,作AC 平分∠OAB 交OB 于C,则∠OAC=∠O,∠ACB=∠B,∴OC=CA=AB,△ABC∽△OAB,∴=,即AB2=4×(4﹣AB),解得﹣2,AB2=﹣2﹣2(舍去),∴AB=2﹣2,故答案为﹣2.4.【分析】作DF⊥BE 于F,CH⊥AD 于H,由题意,可得AD=AC=AB,∠CAD=∠BAC=30°,可得∠DCE=30°,∠E=45°,根据,可得,即+1,在Rt△CHE中,CH=HE=,AH=,根据AD=AH+HE﹣DE,可求出AD 的长,进而得出,AH=,E=AB 的长.【解答】解:如图,作DF⊥BE 于F,CH⊥AD 于H,∵将△ABC 绕着点A 逆时针旋转30°,记点C 的对应点为点D,AD、BC 的延长线相交于点E,∴AD=AC=AB,∠CAD=∠BAC=30°,∴∠ACB=∠ACD=∠ADC=75°,∴∠DCE=30°,∠E=45°,∵DE=,∴DF=EF=1,CF=,∴CE=+1,∴CH=HE=∴AD=AH+HE﹣D ,∴AB=.故答案为:.5.【分析】找出点M 关于直线l 在坐标轴上的对称点E、F,如图所示.求出点E、F 的坐标,然后分别求出ME、MF 中点坐标,最后分别求出时间t 的值.【解答】解:如图,过点M 作MF⊥直线l,交y 轴于点F,交x 轴于点E,则点E、F 为点M 在坐标轴上的对称点.过点M 作MD⊥x 轴于点D,则OD=3,MD=2.由直线l:y=﹣x+b 可知∠PDO=∠OPD=45°,∴∠MED=∠OEF=45°,则△MDE 与△OEF 均为等腰直角三角形,∴DE=MD=2,OE=OF=1,∴E(1,0),F(0,﹣1).∵M(3,2),F(0,﹣1),∴线段MF 中点坐标为,).直线y=﹣x+b 过点(,),则=﹣+b,解得:b=2,∴t=2.∵M(3,2),E(1,0),∴线段ME 中点坐标为(2,1).直线y=﹣x+b 过点(2,1),则1=﹣2+b,解得:b=3,∴t=3.故点M 关于l 的对称点,当t=2 时,落在y 轴上,当t=3 时,落在x 轴上.故答案为2 或3.6.【分析】由旋转的性质可得AC=A'C=5,AB=A'B'=5,BC=B'C=8,由等腰三角形的性质可得AF=A'F,由勾股定理列出方程组,可求AF 的长,即可求AA'的长.【解答】解:如图,过点C 作CF⊥AA'于点F,∵旋转∴AC=A'C=5,AB=A'B'=5,BC=B'C=8∵CF⊥AA',∴AF=A'F在Rt△AFC 中,AC2=AF2+CF2,在Rt△CFB'中,B'C2=B'F2+CF2,∴B'C2﹣AC2=B'F2﹣AF2,∴64﹣25=(5+AF)2﹣AF2,∴AF=∴AA'=故答案为7.【分析】作辅助线,构建平行线和直角三角形,先根据勾股定理计算AG 的长,证明△BCH∽△ABG,列比例式可得BH=4,CH=2,根据勾股定理计算EH 的长,从而得CE 的长,最后根据平行线分线段成比例定理得=.【解答】解:如图,过A 作AG⊥BC 于G,过B 作BH⊥CE,交EC 的延长线于H,延长BD 和CE 交于点F,∵AC=AB=5,∴BG=CG===2 ,∵FH∥AB,∴∠ABG=∠BCH,∵∠H=∠AGB=90°,∴△BCH∽△ABG,∴=,∴==,∴BH=4,CH=2,由折叠得:AB=BE=5,∴EH===3,CE=3﹣2=1,∵FH∥AB,∴∠F=∠ABD=∠EBD,∴EF=BE=5,∴FC=5+1=6,∵FC∥AB,∴=,故答案为:5:6.8.【分析】先求出,OB=6,OM=2,BM=OB﹣OM=4,tan∠BAO=,得出∠BAO=60°,AB=2OA=4,分∠PQB=120°或∠PQB=60°两种情况,(1)当∠PQB=120°时,又分两种情况:①延长PQ 交OB 于点N,则∠BQN=60°,QN⊥BM,由折叠得出BM=MP=4,求出BM=2,由勾股定理得出NP==2 ,ON=OM+NM=4,即可得出P 点的坐标;②QM⊥OB,BM=MP,OP=PM﹣OM=BM﹣OM=4﹣2=2,即可得出P 点的坐标;(2)当∠PQB=60°时,Q 点与A 点重合,OP=AP﹣OA=2,即可得出P 点的坐标;综上情况即可P 点的坐标.【解答】解,0),B(0,6),M(0,2),∴OA=2,OB=6,OM=2,BM=OB﹣OM=4,∴tan∠BAO===,∴∠BAO=60°,∵∠AOB=90°,∴∠ABO=30°,∴AB=2OA=4,∵直线PQ 与直线AB 所构成的夹角为60°,∴∠PQB=120°或∠PQB=60°,(1)当∠PQB=120°时,分两种情况:①如图1 所示:延长PQ 交OB 于点N,则∠BQN=60°,∴∠QNB=90°,即QN⊥BM,由折叠得:BM=MP=4,∠BQM=∠PQM,∵∠PQB=120°,∴∠BQM=∠PQM=120°,∴∠BQN=∠MQN=60°,∵QN⊥BM,∴BN=NM=BM=2,在Rt△PNM 中==2,ON=OM+NM=4,∴P 点的坐标为,4);②如图2 所示:QM⊥OB,BM=MP,OP=PM﹣OM=BM﹣OM=4﹣2=2,∴P 点的坐标为:(0,﹣2);(2)当∠PQB=60°时,如图3 所示:Q 点与A 点重合,由折叠得,OP=AP﹣OA=4 ﹣2=2,∴P 点的坐标为,0);综上所述:P 点的坐标为:(2 ,4)或(0,﹣2)或(﹣2 ,0).9.【分析】由DG=3,CD=6 可知△CDG 的三角函数关系,由△CDG 分别与△A'EG,△B'FC 相似,可求得CG,CB',由勾股定理△CFB'可求得BF 长度.【解答】解:∵△CDG∽△A'EG,A'E=4∴A'G=2∴B'G=4由勾股定理可知CG'=则CB'=由△CDG∽△CFB'设BF=x∴解得x=故答案10.【分析】由题意,可得,所以CD=4,在Rt△FCD 中,∠DCF=90°,tan D=,,可得CF=3.【解答】解:∵如图,已知Rt△ABC 中,∠ACB=90°,AC=8,BC=6.∴AB=,∵将△ABC 绕点B 旋转得到△DBE,点A 的对应点D 落在射线BC 上,直线AC 交DE 于点F,∴BD=AB=10,∠D=∠A,∴CD=BD﹣BC=10﹣6=4,在Rt△FCD 中,∠DCF=90°,∴tan D=,,∴CF=3.故答案为:3.11.【分析】连接BD,证明Rt△EDB≌Rt△CBD,可得DE=BC=AD=a,因为EF=AD=a,根据DF =DE+EF 即可得出DF 的长.【解答】解:如图,连接BD,∵将矩形ABCD 绕着顶点B 顺时针旋转,得到矩形EBGF,且D、E、F 在同一条直线上,∴∠DEB=∠C=90°,BE=AB=CD,∵DB=BD,∴Rt△EDB≌Rt△CBD(HL),∴DE=BC=AD=a,∵EF=AD=a,∴DF=DE+EF=a+a=2a.故答案为:2a.12.【分析】由题意当点A′在线段BC 上且AA′平分∠BAC 时,△AA′B 和△AA′B′相似,作A′H⊥AB 于H.证明△AA′H≌△AA′C(AAS),推出,设A′C=A′H=x,根据勾股定理构建方程即可解决问题.【解答】解:由题意当点A′在线段BC 上且AA′平分∠BAC 时,△AA′B 和△AA′B′相似,作A′H⊥AB 于H.在Rt△ABC 中=,AB=6,∴BC=4,AC==2,∵∠A′AH=∠A′AC,∠AHA′=∠ACA′=90°,AA′=AA′,∴△AA′H≌△AA′C(AAS),∴A′C=A′H,AC=AH=2,设A′C=A′H=x,在Rt△A′BH 中)2,∴x=3﹣5,∴A′C=3﹣5,故答案为﹣5.13.【分析】连接EF,知EF 是⊙O 的直径,取EF 的中点O,连接OD,作OG⊥AF,知点G 是AF 的中点,据此可得AF=2,OG=AE=1,继而求得OF==,OD==,最后根据两圆的位置关系可得答案.【解答】解:如图,连接EF,∵四边形ABCD 是矩形,∴∠BAC=90°,则EF 是⊙O 的直径,取EF 的中点O,连接OD,作OG⊥AF,则点G 是AF 的中点,∴GF=AF=2,∴OG 是△AEF 的中位数,∴OG=AE=1,∴OF==,OD==,∵圆D 与圆O 有两个公共点,∴﹣<r<+,故答案为﹣<r<+.14.【分析】找出点M 关于直线l 在坐标轴上的对称点E、F,如图所示.求出点E、F 的坐标,然后分别求出ME、MF 中点坐标,最后分别求出时间t 的值.【解答】解:设直线l:y=﹣x+b.如图,过点M 作MF⊥直线l,交y 轴于点F,交x 轴于点E,则点E、F 为点M 在坐标轴上的对称点.过点M 作MD⊥x 轴于点D,则OD=3,MD=2.由直线l:y=﹣x+b 可知∠PDO=∠OPD=45°,∴∠MED=∠OEF=45°,则△MDE 与△OEF 均为等腰直角三角形,∴DE=MD=2,OE=OF=1,∴E(1,0),F(0,﹣1).∵M(3,2),F(0,﹣1),∴线段MF 中点坐标为,).直线y=﹣x+b 过点,),则+b,解得:b=2,∴t=2.∵M(3,2),E(1,0),∴线段ME 中点坐标为(2,1).直线y=﹣x+b 过点(2,1),则1=﹣2+b,解得:b=3,∴t=3.故点M 关于l 的对称点,当t=2 时,落在y 轴上,当t=3 时,落在x 轴上.故答案为:2 或3(答一个即可).15.【分析】先以C 为原点,以AC 所在直线为x 轴,建立平面直角坐标系,由题意知0≤t≤6,求得t=0及t=6 时M 的坐标,得到直线M1M2 的解析式为y=﹣2x+8.过点M2 作M2N⊥x 轴于点N,则M2N=6,M1N=3,M1M2=3,线段PQ 中点M 所经过的路径长为个单位长度.【解答】解:以C 为原点,以AC 所在直线为x 轴,建立平面直角坐标系:依题意,可知0≤t≤6,当t=0 时,点M1 的坐标为(4,0);当t=6 时,点M2 的坐标为(1,6),设直线M1M2 的解析式为y=kx+b,∴,解得:,∴直线M1M2 的解析式为y=﹣2x+8.设动点运动的时间为t 秒,则有点Q(0,2t),P(8﹣t,0),∴在运动过程中,线段PQ 中点M3 的坐标为,t),把代入y=﹣2x+8,得+8=t,∴点M3 在M1M2 直线上,过点M2 作M2N⊥x 轴于点N,则M2N=6,M1N=3,∴M1M2=3,∴线段PQ 中点M 所经过的路径长为个单位长度.故答案为.16.【分析】连接FC,证明△EDB≌△FDC,可得ED=DF,∠EBD=∠FCD,FC=BE,即FC∥AB,所以△CFG∽△BAG,可,所以AF,因为DE⊥AD,DE=DF,所以AE=AF,进而可得的值.【解答】解:如图,连接FC,∵将△BDE 绕着点D 旋转,使得点B 与点C 重合,点E 落在点F 处,∴BD=CD,ED=FD,∵∠EDB=∠FDC,∴△EDB≌△FDC(SAS),∴ED=DF,∠EBD=∠FCD,FC=BE,∴FC∥AB,∴△CFG∽△BAG,∴,∴FG=AF,∵DE⊥AD,DE=DF,∴AE=AF,∴=.故答案为.17.【分析】过点C 作CF⊥AB 于点F,则四边形AFCD 为矩形,根据矩形的性质可得出BF=5,结合cos∠ABC=,可得出CF 的长度,进而可得出AD 的长度,在Rt△BAD 中利用勾股定理可求出BD 的长度,由折叠的性质可得出BP=BA=12,再由PD=BD﹣BP 即可求出PD 的长度.【解答】解:过点C 作CF⊥AB 于点F,则四边形AFCD 为矩形,如图所示.∵AB=12,DC=7,∴BF=5.又,∴BC=13,CF==12.∵AD=CF=12,AB=12,∴BD==12.∵△ABE 沿BE 翻折得到△PBE,∴BP=BA=12,∴PD=BD﹣BP=12﹣12.故答案为﹣12.18.【分析】连接AD,根据PQ∥AB 可知∠ADQ=∠DAB,再由点D 在∠BAC 的平分线上,得出∠DAQ =∠DAB,故∠ADQ=∠DAQ,AQ=DQ.在Rt△CPQ 中根据勾股定理可知,AQ=12﹣4x,故可得出x 的值,进而得出结论;【解答】解:连接AD,∵PQ∥AB,∴∠ADQ=∠DAB.∵点D 在∠BAC 的平分线上,∴∠DAQ=∠DAB,∴∠ADQ=∠DAQ,∴AQ=DQ.在Rt△ABC 中,∵AB=5,BC=3,∴AC=4,∵PQ∥AB,∴△CPQ∽△CBA,∴CP:CQ=BC:AC=3:4,设PC=3x,CQ=4x,在Rt△CPQ 中,PQ=5x,∵PD=PC=3x,∴DQ=2x.∵AQ=4﹣4x,∴4﹣4x=2x,解得,∴CP=3x=2;故答案为2.19.【分析】如图,作AE⊥BC 于E,DK⊥BC 于K,连接BB′交CD 于H.只要证明∠AB′B=90°,求出AB、BB′,理由勾股定理即可解决问题;【解答】解:如图,作AE⊥BC 于E,DK⊥BC 于K,连接BB′交CD 于H.∵AB=AC,AE⊥BC,∴BE=EC=4,在Rt△ABE 中=,∴AE=6,AB==2,∵DK∥AE,BD=AD,∴BK=EK=2,∴DK=AE=3,在Rt△CDK 中=3,∵B、B′关于CD 对称,∴BB′⊥CD,BH=HB′∵S△BDC=•BC•DK=•CD•BH,∴BH=,∴BB′=,∵BD=AD=DB′,∴∠AB′B=90°,∴AB′=,故答案.20.【分析】在Rt△ACB 中,根据勾股定理可求AB 的长,根据折叠的性质可得QD=BD,QP=BP,根据三角形中位线定理可得AC,BD=AB,BE=BC,再在Rt△QEP 中,根据勾股定理可求QP,继而可求得答案.【解答】解:在Rt△ACB 中,∠C=90°,AC=6,BC=8,AB==10,由折叠的性质可得QD=BD,QP=BP,又∵QD⊥BC,∴DQ∥AC,∵D 是AB 的中点,∴DE=AC=3,BD=AB=5,BE=BC=4,①当点P 在DE 右侧时,∴QE=5﹣3=2,在Rt△QEP 中,QP2=(4﹣BP)2+QE2,即QP2=(4﹣QP)2+22,解得QP=2.5,则BP=2.5.②当点P 在DE 左侧时,同①知,BP=10故答案为:2.5 或10.21.【分析】如图连接BE 交AD 于O,作AH⊥BC 于H.首先证明AD 垂直平分线段BE,△BCE 是直角三角形,求出BC、BE,在Rt△BCE 中,利用勾股定理即可解决问题.【解答】解:如图连接BE 交AD 于O,作AH⊥BC 于H.在Rt△ABC 中,∵AC=8,AB=6,∴BC==10,∵CD=DB,∴AD=DC=DB=5,∵BC•AH=AB•AC,∴AH=,∵AE=AB,∴点A 在BE 的垂直平分线上.∵DE=DB=DC,∴点D 在BE 使得垂直平分线上,△BCE 是直角三角形,∴AD 垂直平分线段BE,∵AD•BO=BD•AH,∴OB=,∴BE=2OB=,在Rt△BCE 中,EC==,故答案为.22.【分析】依据△ACF 和△DEF 都是等腰直角三角形,设EF=DF=1,则,设AF=CF=x,则AC=EC=1+x,在Rt△ACF 中,依据AF2+CF2=AC2,可得x2+x2=(x+1)2,解得,即可得到AC=2+ ,进而得==.【解答】解:如图,设AD 与CE 交于点F,由折叠可得,∠ACE=∠ACB=45°,而∠DAC=∠ACB=45°,∴∠AFC=90°,∠EFD=90°,AF=CF,由折叠可得,CE=AD,∴EF=DF,∴△ACF 和△DEF 都是等腰直角三角形,设EF=DF=1,则,设AF=CF=x,则AC=EC=1+x,∵Rt△ACF 中,AF2+CF2=AC2,∴x2+x2=(x+1)2,解得或(舍去),∴AC=2+,∴==.故答案为.23.【分析】首先根据等边三角形、“双旋三角形”的定义得出△A B′C′是顶角为150°的等腰三角形,其中AB′=AC′=a.过C′作C′D⊥AB′于D,根据30°角所对的直角边等于斜边的一半得出AC′=a,然后根据S△AB′C′=AB′•C′D 即可求解.【解答】解:∵等边△ABC 的边长为a,∴AB=AC=a,∠BAC=60°.∵将△ABC 的边AB 绕着点 A 顺时针旋转α(0°<α<90°)得到AB′,∴AB′=AB=a,∠B′AB=α,∵边AC 绕着点A 逆时针旋转β(0°<β<90°)得到AC′,∴AC′=AC=a,∠CAC′=β,∴∠B′AC′=∠B′AB+∠BAC+∠CAC′=α+60°+β=60°+90°=150°.如图,过C′作C′D⊥AB′于D,则∠D=90°,∠DAC′=30°,∴C′D=AC′=a,∴S△AB′C′=AB′•C′D=a•a=a2.故答案a2.24.【分析】根据翻折的性质可得∠BCA=∠ECA,再根据矩形的对边平行可得AD∥BC,根据两直线平行,内错角相等可得∠DAC=∠BCA,从而得到∠ECA=∠DAC,设AD 与CE 相交于F,根据等角对等边的性质可得AF=CF,再求出DF=EF,从而得到△ACF 和△DEF 相似,根据相似三角形对应边成比例求===,设DF=x,则AF=FC=3x,在Rt△CDF 中,利用勾股定理列式求出CD,再根据矩形的对边相等求出AB,然后代入进行计算即可得解.【解答】解:∵矩形沿直线AC 折叠,点B 落在点E 处,∴∠BCA=∠ECA,AE=AB=CD,EC=BC=AD,∵矩形ABCD 的对边AD∥BC,∴∠DAC=∠BCA,∴∠ECA=∠DAC,设AD 与CE 相交于F,则AF=CF,∴AD﹣AF=CE﹣CF,即DF=EF,∴=,又∵∠AFC=∠DFE,∴△ACF∽△DEF,∴===,设DF=x,则AF=FC=3x,在Rt△CDF 中=2x,又∵BC=AD=AF+DF=4x,∴==.故答案.25.【分析】作AE⊥BC 于E.根据等腰三角形三线合一的性质得出BC=3,利用勾股定理求出AE=4.根据三角形的面积得出=,那么AD=.再根据旋转的性质可知AD=AD1,∠CAD=∠BAD1,那么△ABC∽△ADD1,利用相似三角形的性质可求出DD1.【解答】解:如图,作AE⊥BC 于E.∵AB=AC=5,BC=6,∴BE=EC=BC=3,∴AE==4.∵S△ABC=AB•CD=BC•AE,∴CD===,∴AD=.∵△ACD 绕点A 顺时针旋转,使点C 与点B 重合,点D 旋转至点D1,∴AD=AD1,∠CAD=∠BAD1,∵AB=AC,∴△ABC∽△ADD1,∴,∴=,∴DD1=.故答案为.31。
2012年语文中考二模测试卷参考答案及评分意见

2012年语文中考二模测试卷参考答案及评分意见一、单项技能考查(每题3分,共15分)1.D(A赝品yàn;C在燕然yān,草木长zhǎng;B诘问jié。
)2.B(不能自已:不能控制自己的感情。
已,停止、控制。
)3.A(“不是”“而是”“这时候”对这几句话之间的逻辑关系有很强的提示作用。
)4.C(此题涉及到病句的三种类型:A“科学的学习方法”不能养成,属搭配不当;B “通过”和“让”,去其一;D项关联词语误用,“只要·就”“只有·才”。
)5.B(B应为“假设关系”。
)二、古诗文能力考查(22分)(一)课内文言文阅读能力考查(10分)6.A(A除“薄暮冥冥”“义薄云天”,“日薄西山”的“薄”也是“迫近”之意。
B“期在必醉”的“期”意为希望、期望,同今义;“期年之后”的“期”意为“一周(年、月)”,读jī,古代也写作“朞”。
C“衡”虽均通“横”,但前一个“横”与“竖”相对,用的是本义;后一个“横”用的是引申义,梗塞、阻塞、不顺。
故C项不是这个题目的最佳选择。
D前一个“诣”意为“报告”,后一个“诣”指“学问等所达到的境界”。
)(2分)7.你太不聪明了!(汝、惠各0.5分,“甚矣”倒装后的强调意味1分。
)(2分)8.山高且大;移山人数少;路途遥远;工具简陋;劳动效率低下;旁人讽刺(不能用原文,一点1分,能任意答出两点即得满分。
)9.①说话的方式不同:愚公妻是“献疑”,即担心又关心;智叟是“笑而止之”,讽刺嘲笑加阻止。
②对愚公的称谓不同:愚公妻称“君”,语气尊敬;智叟称“汝”,语气很不尊重。
③即使说同样的话气不同:愚公妻是民存疑虑,“如太行王屋何”;智叟是语含挖苦,“其如土石何”。
④对愚公的评价不同:愚公妻没说愚公不明智,智叟讽刺愚公“甚矣,汝之不惠”。
⑤对愚公能力的评判不同:愚公妻只是指出事实,愚公个人人能力不够,以君之力,曾不能损魁父之丘;智叟则故意强调“残年”和“毛”,语带讥讽。
北京2012中考英语二模试卷(附答案)

北京2012中考英语二模试卷(附答案)北京2012年中考英语二模试卷(附答案)知识运用(共25分)四、单项填空。
(共13分,每小题1分)22. Taylor Swift is very popular now, and she is ____ favorite singer.A. weB. usC. ourD. ours23. The Spring Festival is coming. It comes ____ January 23 this year. A. in B. onC. atD. for24. The film was so____that the children couldn't stop laughing.A. funnyB. funnierC. funniestD. the funniest25. I like cartoons,____ I didn't go to watch The Adventures of Tintin last week because of the test.A. soB. andC. butD. or26. Although she added salt, it stillwasn't____.A. enouugh saltB. salt enoughC. enough saltyD. salty enough27. Jimmy is a kindboy.He____others fix up the bikes for ten years.A. helpsB. will helpC. helpedD. has helped 28. —When____you____reading the book Steve Jobs?—It's hard to say. Maybe next week.A. did; finishB. have;finishedC. will;finishD. do;finish29. The microwave oven is usedfor____food.A. heatB. heatingC. heatedD. heats30. We like making friends with the people____like helping others.A. whenB. whereC. whoD. what31. By the time I got into theclassroom, the teacher____the test papers.A. had handed outB. handed outC. has handed outD. hands out32. They hope____to London during the Olympics this summer.A. to goB. goC. goingD. gone33. The mobile phone____by Martin Cooper in 1973.A. inventsB. inventedC. is inventedD. was invented34. —Can you tell me____the old people's home?—Last Sunday.A. when they will visitB. when they visitedC. when did they visitD. when will they visit五、阅读下面的短文,掌握其大意,然后从短文后各题所给的A、B、C、D四个选项中,选择最佳选项。
2012年中招模拟试卷及答案

2012年中招模拟试题及答案试卷满分120分考试时间120分钟一、积累与运用(共25分)1.下列词语中加点字的读音完全相同的一项是:()(2分)A.参.天参.军参.观参.差不齐B.清澈.撤.退彻.底天寒地坼.C.简称.称.道称.职拍手称.快D.锦衾.钦.赐侵.吞沁.人心脾2.下列词语书写完全正确的一项是()(2分)A.诓骗精巧绝伦略胜一筹张皇失错B.狼籍郑重其事明察秋毫心无旁骛C.嗔怒毛骨悚然根深蒂固与日具增D.琐屑苦心孤诣相形见绌销声匿迹3.下列句子中加点成语或俗语使用正确的一项是()(2分)A.小沈阳的表演幽默滑稽,每每使大人笑得忍俊不禁....,使孩子笑得前俯后仰。
B.数不胜数的树根在大地里面触类旁通....,吸收着大地母亲给予的营养。
C.解放战争中,我们从东北一直打到江南,不但占领了天津,解放了武汉,还要直捣南京,真是吃着碗里,看着锅里.........。
D.你们不能一叶障目....,不见泰山,仅仅因为一些小的失误就全盘否定我们所取得的成就。
4.下列句子中有语病的一项是()(2分)A.阅读优秀的文学作品,既能增长知识,又能丰富情感。
B.“春城无处不飞花”的诗句虽然不是为昆明而作,却也能贴切地反映昆明的特征。
C.情绪污染指的是一个人心情的好坏影响了其他人的好心情。
D.在英国《泰晤士报》的“2005全球大学排行榜”上,北大跃升至第15位,成为亚洲第一。
5.下列关于文学名著的表述,有误的一项是:()(2分)A.《骆驼祥子》是老舍的代表作,以人力车夫祥子的坎坷、悲惨的生活遭遇为主要情节,深刻揭露了旧中国的黑暗,控诉了统治阶级对劳动者的剥削、压迫,表达了作者对劳动人民的深切同情。
B.吴敬梓的《儒林外史》,是我国清代一部杰出的章回体长篇讽刺小说,全书共五十六回,约四十万字,描写了近二百个人物。
小说假托明代,实际描写了康乾时期科举制度下读书人的功名与生活。
C.在《春水》里,冰心虽然仍旧在歌颂母爱,歌颂亲情,歌颂童心,歌颂大自然,但是,她却用了更多的篇幅,来含蓄地表述她本人和她那一代青年知识分子的烦恼和苦闷。
北京市2012年中考二模试题汇编.
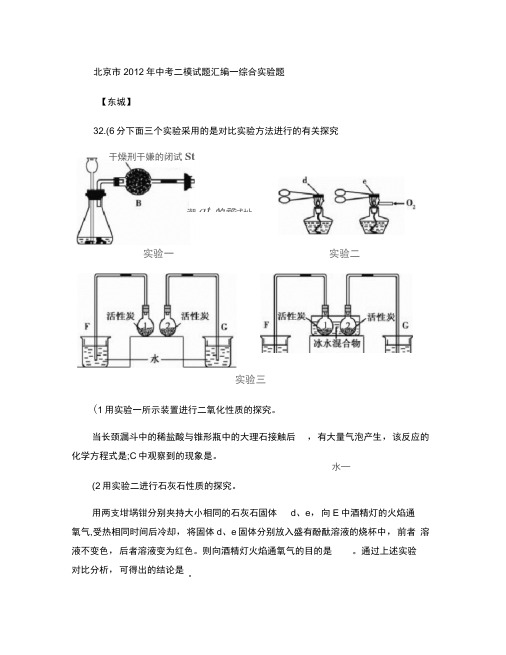
0 北京市2012年中考二模试题汇编一综合实验题【东城】32.(6分下面三个实验采用的是对比实验方法进行的有关探究实验三(1用实验一所示装置进行二氧化性质的探究。
当长颈漏斗中的稀盐酸与锥形瓶中的大理石接触后 ,有大量气泡产生,该反应的 化学方程式是;C 中观察到的现象是。
(2用实验二进行石灰石性质的探究。
用两支坩埚钳分别夹持大小相同的石灰石固体 d 、e ,向E 中酒精灯的火焰通 氧气,受热相同时间后冷却,将固体d 、e 固体分别放入盛有酚酞溶液的烧杯中,前者 溶液不变色,后者溶液变为红色。
则向酒精灯火焰通氧气的目的是。
通过上述实验对比分析,可得出的结论是 潮at 的祁试址实验一实验二 干燥刑干嫌的闭试St水—(3用实验三所示装置进行活性炭吸附能力的实验探究。
实验开始时,在常温常压条件下,烧瓶1内为氮气,烧瓶2内为相同体积的氯气,将相同质量的活性炭装入两支烧瓶后,F侧导管中的液面与烧杯内水的液面基本一致,G 侧导管中的液面高于烧杯内水的液面。
当将两只烧瓶放入冰水混合物中,观察到两侧导管中液面都有所上升,且G侧上升的高度比F侧明显。
通过该对比实验可以得出的结论是。
答案:(1CaC0 3 + 2HCI = CaCI 2 + H 20 + CO 2T干燥的试纸不变色,湿润的试纸变色(2提高酒精灯火焰的温度石灰石在加热时不能分解,在高温时能分解(3活性炭对不同气体的吸附能力不同、活性炭对气体的吸附能力随温度降低而增强(2分【西城】32.(5分某小组同学用下图所示的装置进行了两组兴趣实验(a、b管的体积相等,夹持装置已略去。
图1a b K白磷红磷铜铜a b图2 K 1 2 1 2【资料】(1白磷的着火点为40C ,红磷的着火点为240C(22NaOH + MgCI 2 = Mg(0H2 J + 2NaCI(1如图1所示进行实验。
关闭K ,向烧杯中注入一定量的90C的热水至图中虚线处一段时间后,观察到a管中的现象是。
根据最新考试说明---2012年中考模拟考试卷二(含听力材料和答案)

2012年中考模拟考试卷(二)英语(考试时间共120分钟,全卷满分120分)注意事项:1、答题前,考生先将自己的学校、姓名、考号(准考证号),填写在答题卡指定地方,将条形码准确粘贴在条形码区域内。
2、选择题必须使用2B铅笔填涂,非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整,笔迹清楚。
3、非选择题按照题号顺序在各题目的答题卡区域内作答,超出答题区域书写答案无效。
在草稿纸、试题卷上答题无效。
第I卷(选择题,共80分)一、听力测试(本大题共30小题,每小题1分,共30分)第一节:听音辨图。
听句子,选择与你所听到的句子内容相符的图画。
每个句子读两遍。
(4小题,每小题1分,共4分)A B C D第二节:情景反应。
听句子,选择恰当的答语。
每个句子读两遍。
(6小题,每小题1分,共6分)5. A. I’m 15. B. Fine, thank you. C. No, I don’t.6. A. Some bread. B. Some oranges. C. A bottle of water.7. A. She works at a restaurant. B. She works very hard. C. She works for eight hours a day.8. A. Oh dear! What’s wrong? B. That’s all right. C. It doesn’t matter.9. A. That’s a good idea. B. Wait a moment. C. OK. No problem.10. A. Don’t go there. B. That sounds good. C. It doesn’t matter.第三节:对话理解。
题号一二三四五六七八总分得分1.2.3.4.(一)听五组对话和五个问题,选择正确答案。
每组对话读两遍。
(5小题,每小题1分,共5分)11. A. They’re white. B. They’re blue. C. They’re black.12. A. He likes fishing. B. He likes eating fish. C. He likes reading.13. A. Sports shows. B. TV plays. C. Animal World.14. A. For three hours. B. For five hours. C. For two hours.15. A. Beer. B. Wine. C. A soft drink.(二)听三段长对话,根据对话内容选择正确答案。
2012年中考二模考试

2012年初三年级第二次调研考试初三语文试卷(考试时间:150分钟卷面总分:150分考试形式:闭卷)一、积累与运用。
(35分)1.古诗文名句默写。
(10分)(1)凡是豫则立,▲。
(《孙子》)(2)_____ __ ▲_________,欲上青天揽明月。
(李白《宣州谢眺楼饯别校书叔云》)(3)潭中鱼可百许头,▲。
(柳宗元《小石潭记》)(4)▲,似曾相识燕归来。
(晏殊《浣溪沙》)(5)诗人总能从大自然生生不息的规律中得到启发:朱熹面对一池碧水,感悟“▲?为有源头活水来”;龚自珍凝视一地花瓣,顿悟“落红不是无情物,▲”。
(6)登高望远,古人往往诗兴大发,壮志满怀。
《望岳》中“____ _▲_____________,▲”与“不畏浮云遮望眼,自缘身在最高层”两句诗有异曲同工之妙。
(7)关注民生,是古今仁人志士胸怀的深厚情感。
请写出范仲淹《岳阳楼记》中“忧国忧民”的千古名句:▲,▲__。
(1)不豫则废。
(2)俱怀逸兴壮思飞(3)皆若空游无所依(4)无可无奈何花落去(5)问渠哪得清如许化作春泥更护花(6)会当凌绝顶,一览众山小(7)先天下之忧而忧,后天下之乐而乐(每空1分,计10分)2.阅读下面一段话,完成后面的问题。
(6分)古人不但喜好歌声的高亢.、liáo亮,而且注重吐字清楚,行腔流畅,发声自然圆润,以达到表意之目的。
唱歌既要唱声,又要唱情。
“声情并mào”这个成语,就反映了古人对歌唱的更高追求,只要用这样的歌声,恰当表现歌曲的情感内蕴.,才能产生极大的艺术感染力。
(1)给加点的字注音,或根据拼音写出汉字。
(4分)高亢.▲ liáo亮▲内蕴.▲声情并mào ▲kàng 嘹 yùn 茂(每空1分,计4分)(2)画横线的句子是一个病句,请改正。
(2分)▲3.下列各句中,加点的成语使用错误..的一项是(▲) (2分)A.硅谷的创始者之一肖克利与他八个学生意见不和,八位年轻人毅然与这位诺贝尔奖金获得者分道扬镳....。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012学年二模卷和08-12中考真题中填空题第18题综合汇编
(后附答案)
18.(黄浦)如图3,在Rt ACB ∆中,90ACB ∠=︒,点O 在AB 上,且6CA CO ==,
1
cos 3
CAB ∠=,若将ACB ∆绕点A 顺时针旋转得到Rt ''AC B ∆,且'C 落在CO 的延长线上,
联结'BB 交CO 的延长线于点F ,则BF = ▲ .
18.(长宁)如图,矩形纸片ABCD 沿EF ,GF 同时折叠,C B ,两点恰好同时落在AD 边的P 点处,若∠FPH =
90,PF =8,PH =6,则四边形ABCD 的面积为 .
18.(奉贤)矩形ABCD 中,4AD =,2CD =,边AD 绕A 旋转使得点D 落在射线CB 上P 处,那么DPC ∠的度数为 .
18. (虹口)如图,在△ACB 中,∠CAB=90°,AC=AB =3,将△ABC 沿直线BC 平移,顶点A 、C 、B 平移后分别记为A 1、C 1、B 1,若△A CB 与△A 1C 1B 1重合部分的面积2,则CB 1= ▲ .
18.(嘉定)如图2,在平面直角坐标系中,点A 在x 轴上,点B 的坐标
为(4,2),若四边形OABC 为菱形,则点C 的坐标为 ▲ .
图3
C
A
B
O F
'
C '
B
(图2)
18.(静安)如图,在△ABC 中,∠C=90°,点D 为AB 的中点,BC=3,3
1
cos =
B ,△DB
C 沿着C
D 翻折后, 点B 落到点
E ,那么AE 的长为 ▲ .
17.(浦东)如图,在矩形ABCD 中,点F 为边CD 上一点,沿AF 折叠,点D 恰好落在BC 边上的E 点处,若AB =3,BC =5,则EFC ∠tan 的值为 .
18.(浦东)如图,在直角坐标系中,⊙P 的圆心是P (a ,2)(a >0),半径为2;直线y=x 被⊙P 截得的弦长为23,则a 的值是 .
18.(普陀)如图5,将边长为4的正方形ABCD 沿着折痕EF 折叠,使点B 落在边AD 的中点G 处,那么四边形BCFE 的面积等于 ▲ .
18.(青浦) 如果线段CD 是由线段AB 平移得到的,且点A (-1,3)的对应点为 C (2,5),那么点 B (-3,-1)的对应点 D 的坐标是
18.(金山) 在Rt △ABC 中,∠C =90º ,BC =4 ,AC =3,将△ABC 绕着点B 旋转后点A 落
在直线BC 上的点A ',点C 落在点C '处,那么'
tan AAC 的值是 .
第17题图
F E
D
C
B
A
第18题图
图5
H
G
F C
D
E
B
A
18.(闵行)如图,把一个面积为1的正方形等分成两个面积为
12的矩形,接着把其中一个面积为1
2
的矩形等分成两个面积为14的矩形,再把其中一个面积为1
4的矩形等分成两个
面积为1
8
的矩形,如此进行下去,试利用图形所揭示的规
律计算:
111111111248163264128256
++++++++= .
17.(徐汇)如图2,矩形ABCD 中,4,2==BC AB ,点B A 、分别在y 轴、x 轴的正
半轴上,点C 在第一象限,如果︒=∠30OAB ,那么点C 的坐标是 . 18.(徐汇)如图3,在菱形ABCD 中,3=AB ,︒=∠60A ,点E 在射线CB 上,1=BE ,如果AE 与射线DB 相交于点O ,那么=DO .
18.(松江)将一个平面图形分成面积相等的两部分的直线叫做该平面图形的“面线”,“面线”被这个平面图形截得的线段叫做该图形的“面径”,例如圆的直径就是它的“面径”.已知等边三角形的边长为2,则它的 “面径”长可以是 ▲ (写出2个).
17.(杨浦)如图,以O 为圆心,任意长为半径画弧,与射线OM 交于点A ,再以A 为圆心,AO 长为半径画弧,两弧交于点B ,画射线OB ,则cos ∠AOB 的值等于 .
(第18题图)
A
C
B
图1
A
18.(杨浦)如图,把Rt △ABC 放在直角坐标系内,其中∠CAB =90°,BC =5,点A 、B 的坐标分别为(1,0)、(4,0),将△ABC 沿x 轴向右平移,当点C 落在直线y =2x -6上时,线段BC 扫过的面积为 cm 2.
17.(2008)如图2,圆O 1与圆O 2相交于A 、B 两点,它们的半径都为2,
圆O 1经过点O 2,则四边形O 1AO 2B 的面积为 .
18.(2008)如图3,矩形纸片ABCD ,BC=2,∠ABD=30°.将该纸片沿 对角线BD 翻折,点A 落在点E 处,EB 交DC 于点F ,则点F 到直线
DB 的距离为 .
18.(2009)在Rt ABC △中,903BAC AB M ∠==°,,为边BC 上的点,联结AM (如
图3所示).如果将ABM △沿直线AM 翻折后,点B 恰
好落在边AC 的中点处,那么点M 到AC 的距离是 .
(第17题图) B A M
O
F
C
B
A
图3
D
E O 1 O 2
A
图2
A
图3
B
M C
18.(2010)已知正方形ABCD 中,点E 在边DC 上,DE = 2,EC = 1(如图4所示) 把线段AE 绕点A 旋转,使点E 落在直线BC 上的点F 处,则F 、C 两点的距离为__________.
18.(2011)Rt ABC ∆中,已知
90C ∠= ,50B ∠= ,点D 在边BC 上,2BD CD =,把ABC ∆绕点D 逆时针旋转
()0180m m <<度后,如果点B 恰好落在初始Rt ABC ∆的边上, 那么m =
17、我们把两个三角形的中心之间的距离叫做重心距,在同一平面内有两个边长相等的等边三角形,如果当它们的一边重合时重心距为2,那么当它们的一对角成对顶角时重心距为
18、(2012)如图3,在,90,30,1Rt ABC C A BC ∆∠=∠== ,点D 在AC 上,将ADB ∆沿直线BD 翻折后,将点A 落在点E 处,如果AD ED ⊥,那么线段DE 的长为
图3
C
A
B
F
1
E
D
C
B
A
2012学年中二模卷和08-12中考中的填空题第18题综合汇编训 练针对翻折和旋转 答案
黄浦 18.14. 长宁:18. 115.2
分析: 首先根据勾股定理求得FH 的长,根据折叠的性质,得BC=PF+PH+FH ,再根据直角三角形的面积公式求得直角三角形FPH 斜边上的高,即为AB 的长,进一步求得矩形ABCD 的面积.
阴影部分面积即矩形面积。
解答: 解:作PM ⊥BC 于M .
∵∠FPH=90°,PF=8,PH=6,
∴FH=10,AB=PM=PF*PH/FH =4.8.
∴BC=PF+PH+FH=24,
∴矩形ABCD 的面积=AB•BC=115.2.
奉贤 18. 750或150 .
虹口: 18..
嘉定: 18、(
2,2
3
,) 静安: 18.7. 浦东: 17.
4
3; 18.22-
或22+.
普陀:18. 6 青浦: 18、(0,1) 金山: 18.3或13
闵行: 18.
511
256
. 徐汇:17.)2,321(+; 18.
49或2
9. 松江: 18.2,3,(或介于2和3之间的任意两个实数). 杨浦: 17、
1
2
;18、16
2008: 17、32; 182009: 18. 2 2010:18. 1,5
【解析】题目里只说“旋转”,并没有说顺时针还是逆时针,而且说的是“直线BC 上的点”,所以有两种情况如图所示: 顺时针旋转得到1F 点,则1F C=1
逆时针旋转得到2F 点,则22F B DE ==,225F C F B BC =+= 2011: 18 . 80, 120 2012: 17.. 4 18. 3 -1。
