自控实验二
自控实验报告二 控制系统的暂态特性分析

运行结果为:
T =
80
--------------
s^2 + 2 s + 80
绘制系统的单位阶跃响应曲线:
>> step(T)
>>grid on
系统的单位阶跃响应曲线如下:
2.已知二阶系统
(1)ζ=0.6, =5,试用MATLAB绘制系统单位阶跃响应曲线,并求取系统的暂
[y,t] = step(…)该调用格式不绘出响应波形,而是返回响应的数值向量及其对应的时间向量。
系统的暂态性能指标可以根据上述定义,在响应曲线上用鼠标读取关键点或通过搜索曲线对应的数值向量中关键点来确定。
2. LTI Viewer工具
在MATLAB中提供了线性时不变系统仿真的工具LTI Viewer,可以方便地观察系统的响应曲线和性能指标。在命令窗口中键入litview即可启动LTI Viewer。这里简要介绍LTIViewer工具的使用方法。
三、实验内容
1.已知单位负反馈系统前向通道的传递函数为
试用MATLAB绘制系统的单位阶跃响应曲线。
实验过程与实验结果:
首先建立系统的传递函数模型:
num=80;
den=[1 2 0];
G=tf(num,den)
运行结果为:
G =
80
---------
s^2 + 2 s
在利用feedback命令求出系统的单位阶跃响应:
(5)超调量σ:响应曲线的最大值和稳态值之差,通常用百分比表示
其中y(t)为响应曲线。
在MATLAB中求取单位阶跃响应的函数为step,其使用方法如下
step(sys)在默认的时间范围内绘出系统响应的时域波形
自动控制原理实验报告

自动控制原理实验报告实验目的,通过本次实验,掌握自动控制原理的基本概念和实验操作方法,加深对自动控制原理的理解和应用。
实验仪器与设备,本次实验所需仪器设备包括PID控制器、温度传感器、电磁阀、水槽、水泵等。
实验原理,PID控制器是一种广泛应用的自动控制设备,它通过对比设定值和实际值,根据比例、积分、微分三个控制参数对控制对象进行调节,以实现对控制对象的精确控制。
实验步骤:1. 将温度传感器插入水槽中,保证传感器与水温充分接触;2. 将水泵接通,使水槽内的水开始循环;3. 设置PID控制器的参数,包括比例系数、积分时间、微分时间等;4. 通过调节PID控制器的参数,使得水槽中的水温稳定在设定的目标温度;5. 观察记录PID控制器的输出信号和水温的变化情况;6. 分析实验结果,总结PID控制器的控制特性。
实验结果与分析:经过实验操作,我们成功地将水槽中的水温控制在了设定的目标温度范围内。
在调节PID控制器参数的过程中,我们发现比例系数的调节对控制效果有着明显的影响,适当增大比例系数可以缩小温度偏差,但过大的比例系数也会导致控制系统的超调现象;积分时间的调节可以消除静差,但过大的积分时间会导致控制系统的超调和振荡;微分时间的调节可以抑制控制系统的振荡,但过大的微分时间也会使控制系统的响应变慢。
结论:通过本次实验,我们深入理解了PID控制器的工作原理和调节方法,掌握了自动控制原理的基本概念和实验操作方法。
我们通过实验操作和数据分析,加深了对自动控制原理的理解和应用。
总结:自动控制原理是现代控制工程中的重要内容,PID控制器作为一种经典的控制方法,具有广泛的应用前景。
通过本次实验,我们不仅学习了自动控制原理的基本知识,还掌握了PID控制器的调节方法和控制特性。
这对我们今后的学习和工作都具有重要的意义。
自动控制原理实验二阶系统的阶跃响应

自动控制原理实验二阶系统的阶跃响应一、实验目的通过实验观察和分析阶跃响应曲线,了解二阶系统的动态特性,掌握用MATLAB仿真二阶系统阶跃响应曲线的绘制方法,提高对二阶系统动态性能指标的计算与分析能力。
二、实验原理1.二阶系统的传递函数形式为:G(s)=K/[(s+a)(s+b)]其中,K为系统增益,a、b为系统的两个特征根。
特征根的实部决定了系统的稳定性,实部小于零时系统稳定。
2.阶跃响应的拉氏变换表达式为:Y(s)=G(s)/s3.阶跃响应的逆拉氏变换表达式为:y(t)=L^-1{Y(s)}其中,L^-1表示拉氏逆变换。
三、实验内容1.搭建二阶系统,调整增益和特征根,使系统稳定,并记录实际的参数数值。
2.使用MATLAB绘制二阶系统的阶跃响应曲线,并与实际曲线进行对比分析。
四、实验步骤1.搭建二阶系统,调整增益和特征根,使系统稳定。
根据实验要求,选择适当的数字电路元件组合,如电容、电感、电阻等,在实际电路中搭建二阶系统。
2.连接模拟输入信号。
在搭建的二阶系统的输入端接入一个阶跃信号发生器。
3.连接模拟输出信号。
在搭建的二阶系统的输出端接入一个示波器,用于实时观察系统的输出信号。
4.调整增益和特征根。
通过适当调整二阶系统的增益和特征根,使系统达到稳定状态。
记录实际调整参数的数值。
5.使用MATLAB进行仿真绘制。
根据实际搭建的二阶系统参数,利用MATLAB软件进行仿真,绘制出二阶系统的阶跃响应曲线。
6.对比分析实际曲线与仿真曲线。
通过对比分析实际曲线与仿真曲线的差异,分析二阶系统的动态特性。
五、实验结果与分析1.实际曲线的绘制结果。
根据实际参数的输入,记录实际曲线的绘制结果,并描述其特点。
2.仿真曲线的绘制结果。
利用MATLAB软件进行仿真,绘制出仿真曲线,并与实际曲线进行对比分析。
3.实际曲线与仿真曲线的对比分析。
通过对比实际曲线与仿真曲线的差异,分析二阶系统的动态特性,并讨论影响因素。
六、实验讨论与结论1.实验过程中遇到的问题。
实验二北京科技大学自控实验(3)
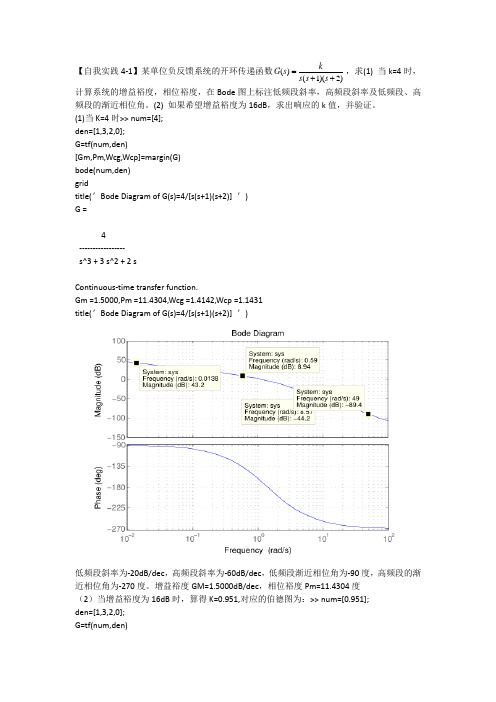
【自我实践4-1】某单位负反馈系统的开环传递函数()(1)(2)kG s s s s =++,求(1) 当k=4时,计算系统的增益裕度,相位裕度,在Bode 图上标注低频段斜率,高频段斜率及低频段、高频段的渐近相位角。
(2) 如果希望增益裕度为16dB ,求出响应的k 值,并验证。
(1)当K=4时>> num=[4]; den=[1,3,2,0]; G=tf(num,den)[Gm,Pm,Wcg,Wcp]=margin(G) bode(num,den) gridtitle(′Bode Diagram of G(s)=4/[s(s+1)(s+2)] ′) G =4----------------- s^3 + 3 s^2 + 2 sContinuous -time transfer function.Gm =1.5000,Pm =11.4304,Wcg =1.4142,Wcp =1.1431 title(′Bode Diagram of G(s)=4/[s(s+1)(s+2)] ′)低频段斜率为-20dB/dec ,高频段斜率为-60dB/dec ,低频段渐近相位角为-90度,高频段的渐近相位角为-270度。
增益裕度GM=1.5000dB/dec ,相位裕度Pm=11.4304度 (2)当增益裕度为16dB 时,算得K=0.951,对应的伯德图为:>> num=[0.951]; den=[1,3,2,0]; G=tf(num,den)[Gm,Pm,Wcg,Wcp]=margin(G) bode(num,den) gridtitle(′Bode Diagram of G(s)=4/[s(s+1)(s+2)] ′) G = 0.951 ----------------- s^3 + 3 s^2 + 2 sContinuous -time transfer function.Gm =6.3091,Pm =54.7839,Wcg =1.4142,Wcp =0.4276 title(′Bode Diagram ′)【自我实践4-2】系统开环传递函数()(0.51)(0.11)kG s s s s =++,试分析系统的稳定性。
自动控制原理实验——二阶系统的动态过程分析

实验二二阶系统的动态过程分析一、 实验目的1. 掌握二阶控制系统的电路模拟方法及其动态性能指标的测试技术。
2. 定量分析二阶系统的阻尼比ξ和无阻尼自然频率n ω对系统动态性能的影响。
3. 加深理解“线性系统的稳定性只与其结构和参数有关,而与外作用无关”的性质。
4. 了解和学习二阶控制系统及其阶跃响应的Matlab 仿真和Simulink 实现方法。
二、 实验内容1. 分析典型二阶系统()G s 的ξ和n ω变化时,对系统的阶跃响应的影响。
2. 用实验的方法求解以下问题:设控制系统结构图如图2.1所示,若要求系统具有性能:%20%,1,p p t s σσ===试确定系统参数K 和τ,并计算单位阶跃响应的特征量d t ,r t 和s t 。
图2.1 控制系统的结构图3. 用实验的方法求解以下问题:设控制系统结构图如图2.2所示。
图中,输入信号()r t t θ=,放大器增益AK 分别取13.5,200和1500。
试分别写出系统的误差响应表达式,并估算其性能指标。
图2.2 控制系统的结构图三、实验原理任何一个给定的线性控制系统,都可以分解为若干个典型环节的组合。
将每个典型环节的模拟电路按系统的方块图连接起来,就得到控制系统的模拟电路图。
通常,二阶控制系统222()2nn nG ssωξωω=++可以分解为一个比例环节、一个惯性环节和一个积分环节,其结构原理如图 2.3所示,对应的模拟电路图如图2.4所示。
图2.3 二阶系统的结构原理图图2.4 二阶系统的模拟电路原理图图2.4中:()(),()()r cu t r t u t c t==-。
比例常数(增益系数)21RKR=,惯性时间常数131T R C=,积分时间常数242T R C=。
其闭环传递函数为:12221112()1()(1)crKU s TTKKU s T s T s K s sT TT==++++(0.1) 又:二阶控制系统的特性由两个参数来描述,即系统的阻尼比ξ和无阻尼自然频率n ω。
《自动控制》一二阶典型环节阶跃响应实验分析报告

《自动控制》一二阶典型环节阶跃响应实验分析报告一、实验目的本实验旨在通过实际的一二阶典型环节阶跃响应实验,掌握自动控制理论中的基本概念和方法,并能够分析系统的动态响应特性。
二、实验原理1.一阶惯性环节:一阶惯性环节是工程实际中常见的系统模型,其传递函数为G(s)=K/(Ts+1),其中K为传递函数的增益,T为时间常数。
2.二阶惯性环节:二阶惯性环节是另一类常见的系统模型,其传递函数为G(s)=K/((Ts+1)(αTs+1)),其中K为传递函数的增益,T为时间常数,α为阻尼系数。
3.阶跃响应:阶跃响应是指给定一个单位阶跃输入,观察系统的输出过程。
根据系统的阶数不同,其响应形式也不同。
实验仪器:电动力控制实验台,控制箱,计算机等。
三、实验步骤1.将实验台上的一阶惯性环节模型接入控制箱和计算机,并调整增益和时间常数的初始值。
2.发送一个单位阶跃信号给控制器,观察实验台上的输出响应,并记录时间和输出值。
3.根据记录的数据,绘制一阶惯性环节的阶跃响应图像。
4.类似地,将实验台上的二阶惯性环节模型接入控制箱和计算机,并调整增益、时间常数和阻尼系数的初始值。
5.发送一个单位阶跃信号给控制器,观察实验台上的输出响应,并记录时间和输出值。
6.根据记录的数据,绘制二阶惯性环节的阶跃响应图像。
四、实验结果与分析1.一阶惯性环节的阶跃响应图像如下:(在此插入阶跃响应图像)根据图像可以看出,随着时间的增加,输出逐渐趋于稳定。
根据实验数据,可以计算出一阶惯性环节的增益K和时间常数T的估计值。
2.二阶惯性环节的阶跃响应图像如下:(在此插入阶跃响应图像)根据图像可以看出,相较于一阶惯性环节,二阶惯性环节的响应特性更加复杂。
根据实验数据,可以计算出二阶惯性环节的增益K、时间常数T和阻尼系数α的估计值。
五、实验结论通过本实验,我们成功地进行了一二阶典型环节阶跃响应实验,并获得了实际的响应数据。
通过对实验数据的分析,我们得到了一阶惯性环节和二阶惯性环节的估计参数值。
自控实验—二三阶系统动态分析

自控实验—二三阶系统动态分析在自控实验中,二、三阶系统动态分析是非常重要的一部分。
通过对系统的动态性能进行分析,可以评估系统的稳定性、响应速度和稳态误差等方面的性能。
本次实验将使用PID控制器对二、三阶系统进行实时控制,并通过实验数据对系统进行动态分析。
首先,我们先了解什么是二、三阶系统。
在控制系统中,系统的阶数表示系统传递函数的阶数,也可以理解为系统动态特性的复杂程度。
二阶系统由两个极点和一个零点组成,三阶系统由三个极点和一个零点组成。
二、三阶系统的动态响应特性与极点位置有关,不同的极点位置对系统的稳定性、响应速度和稳态误差等性能有着不同的影响。
在实验中,我们将使用PID控制器对二、三阶系统进行控制。
PID控制器是一种经典的比例-积分-微分控制器,可以根据误差信号进行调节,通过调整比例系数、积分时间和微分时间来控制系统的响应特性。
实验中,我们将根据二、三阶系统的实时数据进行PID参数调整,以达到控制系统的稳定和快速响应的目的。
在进行实验前,我们首先需要对二、三阶系统进行建模。
二、三阶系统的传递函数通常表示为:二阶系统:G(s) = K / (s^2 + 2ξω_ns + ω_n^2)三阶系统:G(s) = K / (s^3 + 3ξω_ns^2 + 3ω_n^2s + ω_n^3)其中,K表示系统的增益,ξ表示系统的阻尼比,ω_n表示系统的自然频率。
通过实验数据的统计和分析,我们可以估计出系统的K、ξ和ω_n的值,并据此进行PID参数的调整。
接下来,我们进行实验。
我们首先将PID控制器的参数设为初始值,然后对系统进行实时控制,并记录系统输出的数据。
通过对这些数据进行分析,我们可以得到系统的稳态误差、响应时间和超调量等性能指标。
对于二阶系统,我们将分析以下几个方面的性能:1.稳态误差:通过比较实际输出值与目标值之间的差异,可以得到系统的稳态误差。
常见的稳态误差有零稳态误差、常数稳态误差和比例稳态误差等。
心理学自控力试验

心理学自控力试验以心理学自控力实验为标题的文章引言:自控力是指个体能够控制或抑制自己的冲动、欲望或情绪的能力。
它在我们的日常生活中扮演着重要的角色,影响着我们的决策和行为。
为了更好地理解和培养自控力,心理学家们进行了许多自控力实验。
本文将介绍一些典型的心理学自控力实验,并探讨实验结果对我们的日常生活的启示。
实验一:棉花与巧克力实验这个实验由心理学家沃尔特·米舍尔设计。
实验中,参与者被要求坐在一张桌子前,桌上放着一块巧克力和一些棉花。
他们被告知,如果能够抑制吃掉巧克力,可以得到更多的奖励。
实验结果显示,那些能够成功抑制吃掉巧克力的参与者,在后续的任务中表现出更好的自我控制能力。
实验二:棋盘实验这个实验由心理学家巴迪斯特和肖恩·麦康奈尔设计。
实验中,参与者被要求在一张棋盘上进行思考和决策。
其中,棋盘上的一侧代表即时满足,另一侧代表长期利益。
实验结果表明,那些更能够考虑长期利益的参与者,在生活中更容易实现自己的目标。
实验三:马太效应实验这个实验由心理学家柯克·奥斯顿设计。
实验中,参与者被随机分成两组,每组人数相等。
两组参与者分别被要求进行一项任务,完成任务后,他们会得到一定的奖励。
然而,在给予奖励时,实验者采取了不同的方式:对一组参与者,奖励与表现成正比;而对另一组参与者,奖励与表现成反比。
实验结果显示,那些在奖励与表现成正比的组别中的参与者,表现出更好的自我控制能力。
实验四:马戏团大象实验这个实验由心理学家罗伯特·马尔舍设计。
实验中,年幼的大象被用绳子绑在一棵树上,它们尝试挣脱绳子,但很快就放弃了。
当大象长大后,即使只用一根细绳子绑住它们,它们也不再尝试挣脱。
实验结果表明,早期的经历和习惯对个体的自控力有着重要的影响。
结论:通过以上实验,我们可以看到自控力的重要性以及如何培养和提升自控力。
在日常生活中,我们可以通过一些方法来增强自己的自控力,比如设定明确的目标、制定合理的计划、培养良好的习惯和寻求他人的支持等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
本次实验结果与理论结果基本一致,可以说本次实验较为成功。
实验中应该注意的一些事项:每次在示波器观察波形时要点击运行按钮。改变电路参数运行时要先将示波器暂停之后再继续操作。实验操作时不要死搬电路图,要学会对其进行一定的等效改变才可以在电路箱上接线。
总体来说实验让我对TD-ACC设备的操作有了近一步的认识,并且锻炼的自己独立操作,解决问题的能力。对自己的锻炼帮助很大。
实 验 报 告
实验名称典型系统的时域响应和稳定性分析
系
信息院
专业
电气专业
班
试验班
姓名
学号
授课老师
谭冠政
预定时间
实验时间
4月9日
实验台号
一、目的要求
1.研究二阶系统的特征参量 (ξ、ωn) 对过渡过程的影响。
2.研究二阶对象的三种阻尼比下的响应曲线及系统的稳定性。
3.熟悉Routh 判据,用Routh 判据对三阶系统进行稳定性分析。
二、原理简述
1.典型的二阶系统稳定性分析
(1) 结构框图:如下图所示。
(2) 对应的模拟电路图:如下图所示。
系统开环传递函数为:开环增益
(4) 实验内容
先算出临界阻尼、欠阻尼、过阻尼时电阻R 的理论值,再将理论值应用于模拟电路中,
观察二阶系统的动态性能及稳定性,应与理论分析基本吻合。在此实验中
系统闭环传递函数为:
四、线路示图
见二、原理简述。
五、内容步骤
1.将信号源单元的“ST”端插针与“S”端插针用“短路块”短接。由于每个运放单元均
设臵了锁零场效应管,所以运放具有锁零功能。将开关设在“方波”档,分别调节调幅和调频
电位器,使得“OUT”端输出的方波幅值为1V,周期为10s 左右。
2. 典型二阶系统瞬态Байду номын сангаас能指标的测试
算出)。将实验结果填入表1.2-1 中。表1.2-2 中已填入了一组参考测量值,供参照。
3.典型三阶系统的性能
(1) 按图1.2-4 接线,将1 中的方波信号接至输入端,取R = 30K。
(2) 观察系统的响应曲线,并记录波形。
(3) 减小开环增益 (R = 41.7K;100K),观察响应曲线,并将实验结果填入表1.2-3 中。表
1.2-4 中已填入了一组参考测量值,供参照。
六、数据处理
1. 在不同条件下二阶系统的响应曲线
R=10K
R=50K
R=160K
R=200K
典型二阶系统瞬态性能指标实验参考测试值见下表
2.在不同条件下二阶系统的响应曲线
R=30K
R=41.7K
R=100K
典型三阶系统在不同开环增益下的响应情况实验参考测试值见下表
其中自然振荡角频率: 阻尼比:
2.典型的三阶系统稳定性分析
(1) 结构框图:如下图所示。
(2) 模拟电路图:如下图所示。
(3) 理论分析
系统的开环传函为:
系统的特征方程为:
(4) 实验内容
实验前由Routh 判断得Routh 行列式为:
为了保证系统稳定,第一列各值应为正数,所以有
三、仪器设备
PC 机一台,TD-ACC+(或TD-ACS)教学实验系统一套。
(1) 按模拟电路图1.2-2 接线,将1 中的方波信号接至输入端,取R = 10K。
(2) 用示波器观察系统响应曲线C(t),测量并记录超调MP、峰值时间tp 和调节时间tS。
(3) 分别按R = 50K;160K;200K;改变系统开环增益,观察响应曲线C(t),测量并记录
性能指标MP、tp 和tS,及系统的稳定性。并将测量值和计算值进行比较 (实验前必须按公式计
