3.2_一元二次不等式根的分布整理
不等式一元二次方程根的分布

布2023-11-07•定义和公式•根的分布情况•图像表示目录•实例分析•解题技巧和注意事项•练习题与答案01定义和公式定义一元二次方程的标准形式是$ax^2 + bx + c = 0$,其中$a \neq 0$。
说明一元二次方程的标准形式是解决一元二次方程问题的基础,通过配方等方法可以将非标准形式的一元二次方程转化为标准形式,便于分析其根的分布情况。
一元二次方程的标准形式一元二次方程的解是满足方程的根,记作$x_{1}, x_{2}$。
定义根据判别式的性质,一元二次方程的解的情况分为三种:有两个不相等的实数根、有两个相等的实数根和没有实数根。
判别式$b^2 - 4ac$是判断一元二次方程解的分布情况的依据。
说明一元二次方程的解02根的分布情况当判别式Δ大于0时,一元二次方程有两个不相等的实根。
两根不等实根与系数关系图像表示两个实根的和为-b/a,两个实根的积为c/a。
在实数平面上表示为两个不相交的直线。
030201当判别式Δ等于0时,一元二次方程有两个相等的实根。
两根相等两个实根的和为-b/a,两个实根的积为c/a。
实根与系数关系在实数平面上表示为一条直线。
图像表示当判别式Δ小于0时,一元二次方程有两个不相等的虚根。
两根不等且虚根两个虚根的实部为0。
实部为0两个虚根的虚部为√(-Δ)/a。
虚部与系数关系在复数平面上表示为两个相交的直线。
图像表示当Δ < 0时,方程的根的分布03图像表示图像表示一元二次方程的解实数根对于一元二次方程 $ax^2 + bx + c = 0$,如果 $a > 0$,那么该方程有两个实数根,分别是 $x_1 = \frac{-b + \sqrt{\Delta}}{2a}$ 和 $x_2 = \frac{-b - \sqrt{\Delta}}{2a}$。
虚数根如果 $a < 0$,那么该方程有两个共轭虚数根,分别是 $x_1 = \frac{-b + i\sqrt{4ac - b^2}}{2a}$ 和 $x_2 = \frac{-b - i\sqrt{4ac - b^2}}{2a}$。
二次不等式,根的分布

二次不等式恒成立问题、二次方程根的分布、二次函数在闭区间最值一、恒成立问题“恒成立问题”一般是针对不等式而言的一个概念(本处主要研究二次不等式的恒成立),是指在已知不等式的解集为R 或Φ等的条件下,求解参数(异于变量的待定系数)的取值范围,不是解所给的不等式。
☆恒成立问题的解决方案:⎩⎨⎧易于作图的情况)、数形结合处理(针对理(本方法是通法)、转化为最值问题来处21)(x f y =在D x ∈上有最值,那么①a x f <)(恒成立a x f <⇔max )(②a x f >)(恒成立a x f >⇔min )(【注意】在计算最值时应该明确,不等式恒成立的范围,有的是R 上的恒成立,有些是某些区间上的恒成立,关系到最值的求解,故应关注到函数的定义域。
【例题1】已知不等式a x x >-+352在]2,1[上恒成立,求a 的取值范围。
【例题2】已知不等式1)42lg(2+>+-m x x 在]4,1[∈x 上恒成立,求m 的范围。
思考【例题3】已知a x x <--122,在],1[a x ∈上恒成立,求a 的取值范围。
基本思路:结合图像的相对位置关系,列出适合于条件的不等式求解参数的范围【例题4】已知不等式03)1(4)54(22>+---+x m x m m 对一切实数x 恒成立,求参数m 的取值范围. 【例题5】当m 取何值时,关于x 的不等式m x x a ax x a >+++++1)1(22对任意的x ∈R恒成立. 【例题6】x 取一切实数时,使3472+++kx kx kx 恒有意义,求实数k 的取值范围. 二、二次方程根的分布二次方程根的分布是研究二次方程根的特殊性质的知识,该知识最终目标还是求某些参数 的取值范围,主要有以下两种研究方法:⎩⎨⎧、数形结合解答点:数的关系)该方法的特、韦达定理(即根与系21图像的锁定依赖于:_____ _____ _____ _____等几个方面一些准备知识:1、方程()0f x =有实数根⇔函数()y f x =的图象与x 轴有 ⇔函数()y f x =有2、连续函数()y f x =在[,]a b 上存在零点⇔ ()()___0f a f b ⋅3、函数21y x mx =++在(,2]-∞为减函数⇔_________ 4、方程02=++c bx ax (0≠a )根的个数与24b ac ∆=-有怎样的关系?5、韦达定理:若方程02=++c bx ax (0≠a )的实根为1x 、2x ,则12x x +=12x x ⋅=【例题7】:已知2(3)0x m x m +-+=,根据一下条件求m 的取值范围⑴方程有两个不同实数根 ⑵方程有两正根⑶方程有两负根 ⑷两根都小于1⑸两根都大于12⑹一个根大于1,一个根小于1⑺两根都在(0,2) ⑻两根仅有1根在(0,2)⑼两根一个在(2,0)-另一根在(1,2)内 ⑽两根异号,且负根绝对值大于正根不论哪种题型,最关键的地方在于数形结合【练习】(1)已知关于x 的方程 2(2)(36)60k x k k --++=有两个负根,求k 的取值范围.(2)已知二次方程2(2)310m x mx -++=的两个根分别属于(-1,0)和(0,2),则m 的取值范围是(3)已知集合A ={x |x 2-5x +4≤0}与B ={x |x 2-2ax +a +2≤0,a ∈R},若A ∪B =A ,求a 的取值范围.(4)已知函数3211()32f x x ax bx =++在区间[11)-,,(13],内各有一个极值点.求24a b - 的最大值;三、二次函数在闭区间上的最值问题(值域问题)该部分知识同学们自我学习巩固1.二次函数在指定区间上的最值(值域)的解决方法:数形结合,切忌直接代入端点求解(只有当函数在区间上单调的时候方可代端点求最值)2.基本思路是:先作出二次函数在指定区间上的有效图像,从有效图像观察最值在何处取得才是最稳妥的方法。
不等式一元二次方程根的分布

不等式一元二次方程根的分布xx年xx月xx日•不等式与一元二次方程的联系•不等式在一元二次方程中的应用•不等式与一元二次方程的综合应用•不等式在一元二次方程中的拓展应用目录01不等式与一元二次方程的联系如果a>b,c>d,那么a+c>b+d。
不等式的基本性质不等式的性质1如果a>b,c>0,那么ac>bd。
不等式的性质2如果a>b,c<0,那么ac<bd。
不等式的性质3一元二次方程的根的判别式Δ=b²-4ac,当Δ>0时,方程有两个不同的实根;当Δ=0时,方程有两个相同的实根;当Δ<0时,方程没有实根。
一元二次方程的根与系数的关系x₁,x₂=[-b±√(b²-4ac)]/2a,其中x₁,x₂为一元二次方程ax²+bx+c=0的两个根。
一元二次方程的根与系数的关系不等式与一元二次方程的关联01不等式和一元二次方程的联系在于一元二次方程的根的分布情况可以由不等式来表示。
02对于一元二次方程ax²+bx+c=0,如果判别式Δ>0,那么这个方程有两个不同的实根,这两个实根可以用不等式来表示。
03如果a>0,那么方程的两个实根x₁和x₂满足x₁<x₂;如果a<0,那么方程的两个实根x₁和x₂满足x₁>x₂。
02不等式在一元二次方程中的应用利用不等式求根公式通过求解不等式,可以求得一元二次方程的实数根。
确定不等式的解集根据一元二次方程的系数和判别式的值,可以确定不等式的解集,进而求得一元二次方程的根。
利用不等式求解一元二次方程的根通过构造不等式,可以证明一元二次方程在某个区间内至少有一个实数根。
利用不等式证明根的存在通过构造不等式,可以证明一元二次方程在某个区间内只有一个实数根。
利用不等式证明根的唯一性利用不等式证明一元二次方程的根的分布利用不等式判断根的实数性质通过求解不等式,可以判断一元二次方程的实数根是否为整数、有理数、无理数等。
高中数学一元二次不等式根的分布
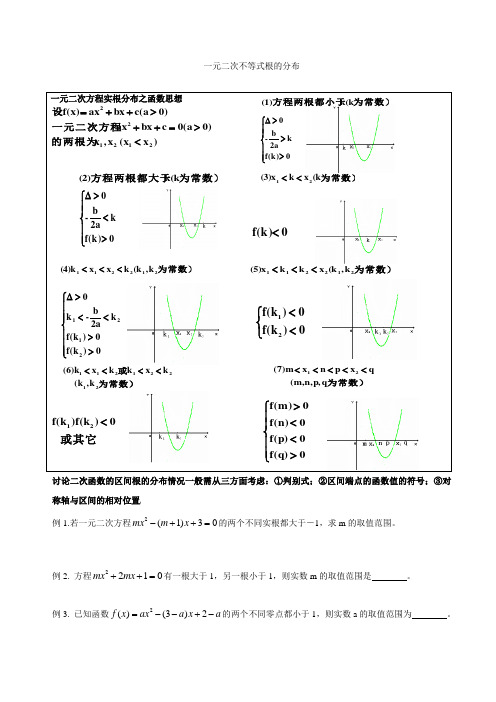
一元二次不等式根的分布讨论二次函数的区间根的分布情况一般需从三方面考虑:①判别式;②区间端点的函数值的符号;③对称轴与区间的相对位置 例1.若一元二次方程2(1)30mx m x -++=的两个不同实根都大于-1,求m 的取值范围。
例2. 方程2210mx mx ++=有一根大于1,另一根小于1,则实数m 的取值范围是 。
例3. 已知函数2()(3)2f x ax a x a =--+-的两个不同零点都小于1,则实数a 的取值范围为 。
一元二次方程实根分布之函数思想 )x (x x ,x 0)0(a c bx ax 0)c(a bx ax f(x)212122<>=++>++=的两根为一元二次方程设为常数)212211k ,(k k x x (4)k <<<⎪⎪⎪⎩⎪⎪⎪⎨⎧>><<>∆0)f(k 0)f(k k 2a b -k 02121为常数)212211k ,(k x k k (5)x <<<⎩⎨⎧<<0)f(k 0)f(k 21为常数)或21221211k ,(k k x k k x (6)k <<<<或其它))f(k f(k 21<为常数)q p,n,(m, q x p n x (7)m 21<<<<<⎪⎪⎩⎪⎪⎨⎧><<>0f(q)0f(p)0f(n)0f(m)⎪⎪⎩⎪⎪⎨⎧>>>∆0f(k)k 2a b -0为常数)方程两根都小于k(k (1)为常数)方程两根都大于k(k (2)⎪⎪⎩⎪⎪⎨⎧><>∆0f(k)k2a b -0为常数)(k x k (3)x 21<<0f(k)<例4.若函数2()(2)(21)f x m x mx m =-+++的两个零点分别在区间(1,0),(1,2)-内,求m 的取值范围.例 5.已知方程2(1)40x a x a ++++=的两个实根为12,x x ,且1201x x <<<,则实数a 的取值范围为 .答案:例1. 令2()(1)3f x mx m x =-++,则方程2()(1)30f x mx m x =-++=有两个不同实根且都大于2(1)120112(1)0m m b m am mf ⎧∆=+->⎪+⎪-⇔-=>-⎨⎪->⎪⎩,解得5m >+或2m <-或05m <<-故实数m 的取值范围为(,2)(0,5(5)-∞-⋃-⋃++∞。
一元二次方程根的分布问题

而另一根不小于 1. 试求:
(1)参数 m 的取值范围; (2)方程两根的平方和的最大值和最小值.
5.设 m 是整数, 且方程 3x2 mx 2 0 的两根都大于
9 7 而小于 ,求 m 得值。 5 3
二次方程的应用 二次方程最重要的性质是判别式和韦达定理 . 下面通过一些例题给出关于二次方程性 质的应用. 对于与二次方程有关的问题,通常可以利用判别式、韦达定理和求根公式解决. 例 1 已知实数 a , b ( a b ) ,且满足
练习: 1.若方程 x2 3x 1 0 的两根 α , β 也是方程 x
4
px2 q 0的根,求 p q 的值。
2.设 x1 , x2 二次方程 x2 x 3 0 的两个根,求 x1
3
4x2 19 的值。
3.已知 b , c 满足 c b 0 的整数,方程 x2 bx c 0 有两个不等的实根 x1 , x2 ,在
例 3 若实数 x ,
y 满足
x y x y 1,求 x y 得值。 3 3 3 1, 3 3 3 3 4 3 6 5 4 5 63
3
求根公式法 例 4 已知 a 0, b 0 , c 0,且
b2 4ac b 2ac,求 b2 4ac的最小值。
一元二次方程根的分布问题 一元二次方程根的分布问题是初中数学竞赛的一个热点问题, 它包括根的分布、 求参数 的范围等内容,涉及函数、不等式等知识,综合性较强。 例 1 当 a 满足什么条件时,方程 (a 值较大?
2
1)x2 6(3a 1)x 72 0 的两根异号且负根的绝对
例 2 设关于
2b 3c 得 a
3.2.2《一元二次不等式的应用》课件(北师大版必修5)

• [策略点睛]
[规范作答]
(1)要 mx2-mx-1<0 恒成立,
若 m=0,显然-1<0. 若
m<0, m≠0, Δ=m2+4m<0
⇒-4<m<0.
∴-4<m≤0.
(2)方法一:∵f(x)=mx
方法二:原不等式即 f(x)+m-5<0, 即 令
12 3 mx-2 +4m-6<0,x∈[1,3] 12 3 g(x)=mx-2 +4m-6,x∈[1,3],
当 m>0 时,g(x)是增函数,∴g(x)max=g(3), 6 6 ∴7m-6<0,得 m<7.∴0<m<7. 当 m=0 时,-6<0 恒成立. 当 m<0 时,g(x)是减函数. ∴f(x)max=g(1)=m-6<0,得 m<6.∴m<0.
x-3x+2≥0 x+2≠0
⇒x<-2 或 x≥3.
所以原不等式的解集为{x|x<-2 或 x≥3}, 即(-∞,-2)∪[3,+∞).
4 (2)原不等式⇒ -(x-1)≤0 x-1
x-3x+1x-1≥0 x-3x+1 ⇒ ≥0⇒ x-1≠0 x-1
• (2)解分式不等式注意的问题: • ①解分式不等式一定要等价变形为标准形式,
就是右边为零,左边为分式再等价转化为不等 式组或高次不等式来求解. • ②若分式不等式含等号,等价转化为整式不等 式时,其分母不为零最易丢掉,这一点一定要 注意. • ③当分式不等式分母正负不确定时不可通过不 等式两边同乘以分母的方法转化为整式不等 式.
• . • 2.若ax2+bx+c<0(a≠0)的解集是∅,则a,b,
c满足的条件是 . a>0,b2-4ac<0 • 3.二次函数y=ax2 +bx+c(x∈R)的部分对应 值如表: x -3 -2 -1 0 1 2 3 4 y 6 0 -4 -6 -6 -4 0 6
一元二次方程实根的分布

一元二次方程实根的分布一元二次方程实根的分布是二次方程中的重要内容,在各类竞赛和中考中经常出现。
这部分知识在初中代数中虽有所涉及,但尚不够系统和完整,且解决的方法偏重于一元二次方程根的判别式和根与系数关系(韦达定理)的运用。
本文将在前面方法的基础上,结合二次函数图象的性质,分两种情况系统地介绍一元二次方程实根分布的情况及其运用。
一.一元二次方程实根的基本分布——零分布一元二次方程实根的零分布,指的是方程的根相对于零的关系。
比如二次方程有一正根,有一负根,其实就是指这个二次方程一个根比零大,一个根比零小,或者说,这两个根分布在零的两侧。
对于这类问题,用一元二次方程根的判别式和根与系数关系(韦达定理)即可判别。
一元二次方程02=++c bx ax (0≠a )的两个实数根为1x 、2x ,则1x 、2x 均为正⇔△≥0,1x +2x >0,1x 2x >0; 1x 、2x 均为负⇔△≥0,1x +2x <0,1x 2x >0;1x 、2x 一正一负⇔1x 2x <0。
例1.关于x 的一元二次方程28(1)70x m x m +++-=有两个负数根,求实数m 取值范围。
解:设两个实数根为1x 、2x ,依题意有1212000x x x x ∆⎧⎪+< ⎨⎪> ⎩≥ ①②③由①得:2(1)32(7)0m m +--≥,2(15)0m -≥,恒成立。
由②得:18m +-<0,解之,m >1-。
由③得:78m ->0,解之,m >7。
综上,m 的取值范围是m >7。
例2.若n >0,关于x 的方程21(2)04x m n x mn --+=有两个相等的正实数根,求mn 的值。
解:设两个实数根为1x 、2x ,依题意有1212000x x x x ∆= ⎧⎪+⎨⎪> ⎩①> ②③由①得:2(2)0m n mn --=,()(4)0m n m n --=,∴m n =或4m n =。
若m n =,则1x +2x 22m n n n n =-=-=-<0,不符合②,舍去。
一元二次方程根的分布

【定理 4】 有且仅有 k1<x1(或 x2)<k2(在(k1,k2)内有且仅有 一个根)⇔f(k1)·f(k2)<0.
【定理 5】 k1<x1≤x2<k2(两个根都在(k1,k2)内)⇔ ffkΔa( (>1=<0kk-,b122) )2-ba>><400ka, ,2c≥0,或Δaffk( (<1=<0kk-,b122) )2-ba<<<400ka, ,2c.≥0,⇔aakΔff1≥( (<-0kk,122) )ba<>>k002, ,.
f(-2)=0, 上恰有一个零点,需满足①f(-2)·f(2)<0 或②-2<41m<0 或 ③0f(<24)1m<=20.,解①得-18<m<0 或 0<m<38;②无解;解③得 m=38.综上可知-18<m≤38,故选 D.
例3 关于x的一元二次方程(m-1)x2+2(m+1)x-m=0 根据下列条件求实数m的取值范围
【定理 1】 x1>0,x2>0
Δ=b2-4ac≥0, (两个正根)⇔x1+x2=-ba>0, x1x2=ca>0.
Δ=b2-4ac≥0, Δ=b2-4ac≥0,
推论:x1>0,x2>0⇔af(>00,)=c>0, 或fa(<00,)=c<0,
b<0
b>0.
上述推论结合二次函数图象不难得到.
【定理 2】 x1<0,x2<0
(m-1)f(2)<0 即m(m-1)<0
解得0<m<1
所以m的取值范围是0<m<1
(2)两根都在区间[-1,3)内
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
f ( k1 ) 0 f (k 2 ) 0
练习Biblioteka 3.已知集合A={x|x2-7x+10≤0}, B={x|x2-(2-m)x+5-m≤0}, 且B A,求实数m的取值范围.
(5) x1 k1 k2 x2 (k1 , k2为常数)
f ( k1 ) 0 f ( k2 ) 0
例:x2+(m-3)x+m=0 求m的范围
(9) 一个根在(-2 ,0)内,另一个根在(1 , 3)内
f (2) m 10 0 f (0) m 0 m f (1) 2m 2 0 f (3) 4m 0
y
c0
0 x1
b 0 2a
x2 O
x
例:x2+(m-3)x+m=0 求m的范围
(3) 一个正根,一个负根且正根绝对值较大
0 x1 x2 0 x x 0 1 2
m m 0
结论3 一元二次方程ax2 bx c 0(a〉 有两异号根. 0)
x1 0 x 2 0
b 2 4ac 0 b x1 x2 0 a c x1 x 2 a 0
a0
b 2 4ac 0 f (0) c 0 b 0 2a
b 2 4ac 0 a 0 x1 0 c x2 0 x1 x2 0 f (0) c 0 a
a 0 0 x1 x
y
2
O
c 0
x
例:x2+(m-3)x+m=0 求m的范围
(4) 两个根都小于1
(m 3) 4m 0 b 3 m 1 2 2a f (1) 2m 2 0
0 x1 O x2 a0
k
x
b 0 2a
例:x2+(m-3)x+m=0 求m的范围
1 (5) 两个根都大于 2 ( m 3) 2 4m 0 b 3 m 1 m 2 2 2a 1 6m 5 0 f ( 2) 4
0 b x1 x 2 0 a c x1x 2 0 a
一正一负,且 负的绝对值大
0 b x1 x 2 0 a c x1x 2 0 a
0 c x1x 2 0 a
0 b k 2a f (k ) 0
f(k)<0
一元二次方程ax2+bx+c=0 (a>0)的 根的分布
两个根都在(k1 y
, k2 )内
x1<k1 < k2 <x2 y o k1 k2
k1 o
k2
x
x
0 b k1 k2 2a f (k1 ) 0 f (k 2 ) 0
y
a0
f ( k1 ) 0 x1 x2
f (k 2 ) 0
O
k1
k2 x
x
b 2a
例:x2+(m-3)x+m=0 求m的范围
(8)一个根小于2,一个根大于4
f (2) 3m 2 0 f (4) 5m 4 0
4 m m 5
2
x1 k x2
a 0 f (k ) 0
y
a0
O
f (k ) 0
k
x1
x2
x
f (k ) 0
例:x2+(m-3)x+m=0 求m的范围
(7) 两个根都在(0 , 2)内
(m 3) 4m 0 3 m 0 2 2 f (0) m 0 f (2) 3m 2 0
2
m m 9
结论4:一元二次方程有两个小于k的根
b 2 4ac 0 b 2 4ac 0 b x1 k ( x1 k ) ( x2 k ) 0 2a k x2 k ( x k )(x k ) 0 2 1 f (k ) 0 y
2
2 m m 1 3
结论4 一元二次方程ax 2 bx c 0(a〉的根满足 0)
b 2 4ac 0 a 0 f (k1 ) 0 f (k ) 0 2 b k1 2a k 2
k1 x1 x2 k 2
5 m 1 6
结论5:一元二次方程有两个大于k的根
b 2 4ac 0 b 4ac 0 x1 k b x k x k 0 k 1 2 x2 k 2a ( x k )(x k ) 0 2 f (k ) 0 1 y
a0
c0 O x1
0
x2
b 0 2a
x
例:x2+(m-3)x+m=0 求m的范围
(2)有两个负根
(m 3) 4m 0 m x1 x2 3 m 0 m 9 x x m 0 1 2
2
结论2 一元二次方程ax2 bx c 0(a0)有两个负根.
3.2
一元二次根的分布
一元二次方程 ax2+bx+c=0 (a>0)的 根的分布
例:x2+(m-3)x+m=0 求m的范围
(1) 两个正根
(m 3) 4m 0 x1 x2 3 m 0 m 0 m 1 x x m 0 1 2
0 b x 1 x 2 0 a c x1x 2 0 a
一元二次方程ax2+bx+c=0 (a>0)的 根的分布
两个根都小于k 两个根都大于k
y y 一个根小于k,一个根 大于k y
k
o
k
x
k o
x
o
x
0 b k 2a f (k ) 0
2
结论1 一元二次方程ax2 bx c 0(a0)有两个正根.
x1 0 x 2 0
y
b2 x1 x 2 x1 x 2 4ac 0 b 0 a c 0 a
b 2 4ac 0 b 0 2a f (0) c 0
2
y
a0 0 x2 b k 2a
a0 0 x2 O b 0 k 2a
k x1 O
x
k x1
x
例:x2+(m-3)x+m=0 求m的范围
(6) 一个根大于1,一个根小于1
f(1)=2m-2 <0
m m 1
结论3 一元二次方程ax bx c 0(a〉 有两个根, 且. 0)
(7)m x1 n p x2 q ( m , n, p, q为常数)
f (m ) 0 f ( n) 0 f ( p) 0 f (q ) 0
课堂小结
一元二次方程 ax2+bx+c=0 (a>0)的 根的分布
两个正根 两个负根 一正根 一负根
