吉首大学-2008 数学建模-B题
2008高教社杯全国大学生数学建模竞赛

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): B我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):同济大学参赛队员(打印并签名) :1. 徐玉华2. 徐子婷3. 冯慰君指导教师或指导教师组负责人(打印并签名):陈雄达日期: 2008 年 9 月 22 日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):现阶段高等教育学费统计模型摘要高等教育学费标准须兼顾学校和社会两方面。
一方面要考虑到经济增长因素、家庭对学费的承受能力;另一方面又要考虑到学校财政收支,以保证教育质量。
所以,我们从两方面探讨高等教育学费标准问题。
先从教育机构(学校)角度出发,以学校财政收支平衡为前提,定性研究高校办学性质、专业划分、地域差异、国民经济四个因素对学费的影响,再建立模型定量地讨论学费和办学性质、专业划分、地域三方面的关系。
通过大量数据的收集,采用0,1级别划分使得这些抽象因素量化,既而易得出它们对学费的具体影响。
对这三个方面,分别建立两个多元线性回归统计模型。
模型一:办学性质、地域性结合教育经费的明细支出、收入得出学费线性回归模型。
模型二:仅从学科专业角度建立学费线性回归模型。
然后,在上述统计线性回归模型的基础上,从国民经济层面(如:城、乡人均年收入)对上述2个模型进行分析,以判别学费的定价是否合理。
数学建模案例分析-2008年B题“高等教育学费标准探讨”

大学数学建模竞赛系列讲座
案例分析—2008B“高等教育学费标准探讨” 主讲:王纪城 2019年7月19日星期五
NORTH UNIVERSITY OF CHINA
大学数学建模竞赛系列讲座
案例分析—2008B“高等教育学费标准探讨” 主讲:王纪城 2019年7月19日星期五
NORTH UNIVERSITY OF CHINA
一、摘要(10分)
• 抓住问题(学费问题) • 数据的收集 • 针对问题和模型的数据整理 • 模型的建立 • 结果及分析
清晰、扼要、规范 (从论文组织、论文评阅-至关重要)
NORTH UNIVERSITY OF CHINA
大学数学建模竞赛系列讲座
案例分析—2008B“高等教育学费标准探讨” 主讲:王纪城 2019年7月19日星期五
案例分析—2008B“高等教育学费标准探讨” 主讲:王纪城 2019年7月19日星期五
高等教育学费标准是社会关注的热点之一,是一个 相当开放的问题,许多媒体的讨论都缺乏数据的支持和 定量的分析。评阅中除了题目中的明确要求外,要特别 注意以下问题:
NORTH UNIVERSITY OF CHINA
大学数学建模竞赛系列讲座
本25%来收取的准则
NORTH UNIVERSITY OF CHINA
大学数学建模竞赛系列讲座
大学数学建模竞赛系列讲座
案例分析—2008B“高等教育学费标准探讨” 主讲:王纪城 2019年7月19日星期五
NORTH UNIVERSITY OF CHINA
大学数学建模竞赛系列讲座
案例分析—2008B“高等教育学费标准探讨” 主讲:王纪城 2019年7月19日星期五
NORTH UNIVERSITY OF CHINA
2008年全国数学建模竞赛C题

二、问题1的分析
1、对题意的理解
(1)搜索完整个区域的时间,是指最后一名队员从 出发点到达集结点所用的时间.
(2)能否在48小时内完成搜索任务,是指“纯工作” 时间能否控制在48小时内,不包括进餐或休息时间. (3)题目仅给出了搜索时的平均行进速度,并未 给出队员停顿下来搜索一个半径为20米的圆形区域 需要花费多少时间,因此对于搜索方式理解为在行 进中连续或分段连续进行搜索.
四、问题2简解
分析: 为了尽量利用第一问的解法,将50人分为 20;20;10三组;对20人的组可直接利用 前面的网格划分;对10人的组,可将前面 的800ⅹ800的网格细分为400ⅹ400的网格. 在分配各组任务时,尽量做到均衡,两个 20人的组分配的搜索区域最好是对称的.
20人组
转向8次,“直穿”42 格 5次,内拐3次 20号外拐
20号搜索用时:
42 800 3 87.38 5 2620 .71 69365 .95秒 19.268小时 0.6
20号“空走”用 时: 420 380 666 .67秒 0.185小时 1.2 1号总用时:18.222小时 20号总用时: 19.453小时
10人组 转向31次,“直穿”69 格 17次,内拐14次;10号外拐14,内拐17次 1号外拐 1号搜索用时: 69 400 17 1287 .38 14 87.38 69108 .72秒 0.6 19.197小时 1号“空走”用时: 1 号总用时: 380 800 20 1000 秒 0.278小时 19.475小时 1.2 综上讨论,全部50名队员中10人组的1号最 后到达,总用时:19.475小时
报告结束,谢谢组委会和各位 专家!
2008年研究生数学建模竞赛题目(D)

中央空调系统节能设计问题一、问题的来源及意义大型建筑物中使用的中央空调系统(以下简称中央空调)工作方式与普通的家用空调有所不同,普通的家用空调是在一个封闭的环境中,利用冷媒完成室内外的能量交换。
而中央空调是利用冷冻水、冷却水和制冷机完成整个建筑物的能量交换。
普通家用空调可以简单地根据温度控制空调的启停,而理论上中央空调只要有一个用户需要,就应该继续工作。
中央空调都是按照最大负荷进行设计和选择设备的,但实际上中央空调大多数时间都在低负荷下运行,有时甚至在设计负荷的10%下运行。
若中央空调的控制方案设计得不好,在低负荷下却按高负荷需求运行时就会造成中央空调系统运行效率下降,产生浪费。
现在的中央空调系统一般是根据温度控制冷冻水系统的流量(温差或压力随之变化),虽然考虑了节能因素,但并未把节能作为首要的目标,而且都是瞬时控制(温度稍有变化,调节系统就起作用),但真正决定建筑物内温度的是中央空调系统所传递冷量(和热量是一个概念,只是因温差方向不同,冷量和热量都可以视为能量)的累加。
中央空调系统从制冷机产生冷量到传送至末端发挥作用,有较大的延迟,通常为20-30分钟。
另外由于大型商场的人流变化很大,瞬时就会引起冷负荷的较大变化,所以传统的基于参数瞬时变化的控制模型对于中央空调所产生的节能效果有限。
为提高中央空调系统的运行效率,应该将中央空调系统的控制由单参数控制改变为建立建筑物冷量需求模型,根据末端在一定时间内冷量需求总量或冷量需求变化率,控制中央空调系统的冷量输出,以实现节能。
二、问题描述大型商场只要营业新风机组就不停地向商场提供新风以改善商场内的空气质量,当然夏季在提供新风的同时也将商场外部的热量带进商场中。
除了新风带入的热量外,商场中的冷负荷还包括通过建筑物围护结构传入的热量,顾客散发的热量,商场内照明、水泵等电气设备产生的热量等。
其中通过建筑物围护结构和新风传入的热量与商场内外的温差有关,可通过附式1进行估算,也可以将其视作一系列对应不同外部温度的常量。
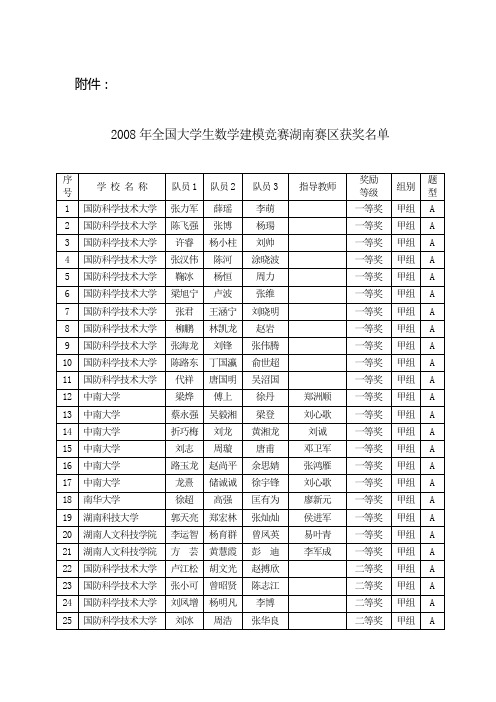
2008年全国大学生数学建模竞赛湖南赛区获奖名单
刘建华
二等奖
甲组
A
45
湘潭大学
李震乾
聂鹏鹏
张恒
刘红良
二等奖
甲组
A
46
长沙理工大学
苏召斌
曹学栋
尹存祥
梁小林
二等奖
甲组
A
47
南华大学
张逆进
黄沼军
粟青
李东
二等奖
甲组
A
48
湖南科技大学
颜永明
廖爱福
李明媛
张剑尘
二等奖
甲组
A
49
湖南科技大学
钟世奇
吴社新
刘雄伟
刘辉亚
二等奖
甲组
A
50
湖南科技大学
殷培孟
孙志跃
郭敏
周鋆
张博
于苑
二等奖
甲组
B
132
中南大学
詹德坚
徐超
齐政亮
方秋莲
二等奖
甲组
B
133
中南大学
王振飞
冯燕茹
刘鹏
秦宣云
二等奖
甲组
B
134
中南大学
魏太云
卜超
沈玉芳
刘建华
二等奖
甲组
B
135
中南大学
伍莎
谭晓畅
何兆强
刘诚
二等奖
甲组
B
136
中南大学
都晓宁
林志军
林孔斌
张鸿雁
二等奖
甲组
B
137
中南大学
张颖娟
赵涛
颜鑫
刘建华
二等奖
卢政贺
孔维玮
三等奖
甲组
B
《2024年2016年全国大学生数学建模竞赛B题解题分析与总结》范文

《2016年全国大学生数学建模竞赛B题解题分析与总结》篇一一、引言全国大学生数学建模竞赛(CUMCM)是衡量各高校数学类学科学生学习与实践能力的标志性竞赛之一。
其中,B题以真实问题的复杂性吸引了广大参赛选手的关注。
本文将对B题的具体题目内容、解题过程、常见方法和误区进行分析,并结合实例对竞赛结果进行总结,以期为其他参赛同学提供一定的参考。
二、题目分析B题通常关注某一实际领域的复杂问题,涉及多个因素的综合考量。
其要求参赛者通过建立数学模型,解决实际问题。
具体问题包括某个地区的旅游经济预测和资源合理配置。
针对此问题,首先需要对旅游业的各项数据进行详细分析,然后构建适当的数学模型,并使用合适的数学工具和软件进行计算和模拟。
三、解题过程1. 数据收集与分析:收集该地区的历史旅游数据,包括游客数量、消费水平、旅游景点分布等。
同时,分析该地区的经济、文化、交通等影响旅游业的因素。
2. 模型构建:根据收集的数据和实际情况,选择合适的数学模型进行建模。
常见的模型包括时间序列预测模型(如ARIMA 模型)、多元回归模型等。
3. 模型求解与验证:利用数学软件(如MATLAB、SPSS等)对模型进行求解,并对模型的预测结果进行验证。
验证方法包括与历史数据进行对比、进行敏感性分析等。
4. 资源合理配置:根据预测结果和实际情况,制定合理的资源分配方案,如旅游景点的开发策略、交通设施的优化配置等。
四、常见方法与误区1. 常见方法:在建模过程中,应选择合适的数学模型和方法。
对于时间序列预测问题,常用的有ARIMA模型、指数平滑法等;对于多元回归问题,则需要考虑各因素之间的相互关系。
同时,还应充分利用计算机技术进行数据分析和模拟。
2. 误区提示:在建模过程中,要避免陷入一些常见的误区。
例如,过分追求模型的复杂性和精确度而忽视模型的实用性和可解释性;忽视数据的预处理和清洗工作;忽略模型的验证和修正等。
五、实例分析以某次B题竞赛的优秀解决方案为例,详细分析其解题过程和关键点。
全国数学建模竞赛C题-文档在线预览

下面是一个简化的搜索问题。有一个平地矩形目 标区域,大小为11200米×7200米,需要进行全境搜 索。假设:出发点在区域中心;搜索完成后需要进 行集结,集结点(结束点)在左侧短边中点;每个 人搜索时的可探测半径为20米,搜索时平均行进速 度为0.6米/秒;不需搜索而只是行进时,平均速度为 1.2米/秒。每个人带有GPS定位仪、步话机,步话机 通讯半径为1000米。搜索队伍若干人为一组,有一个 组长,组长还拥有卫星电话。每个人搜索到目标, 需要用步话机及时向组长报告,组长用卫星电话向 指挥部报告搜索的最新结果。
6
2、问题的分析 (1)搜索时间下限的估计 需要搜索的面积为11200米×7200米=8064ⅹ104平方米 一个队员的搜索半径为20米,若将上述矩形区域划分成 40ⅹ40的小正方形,共有50400个小正方形,20个队员 平均每个队员要搜索2520个小正方形.
一个队员搜索一个小正方形的最短用时
“直穿”40/0.6=66.67秒
“转向”66.67秒+“扫
“扫
角”
角”
7
“直穿”2520个小正方形需用时 (下限)
(2)小组搜索方式的确定 队员之间要相互联络,不能分得太开,20个队员一 字排开能搜索的宽度为800米,将待搜索的矩形区 域分成126个800ⅹ 800的正方形,依次完成这126 个正方形的搜索.
“直穿”一个方 块,每个队员需 要搜索800米
21
五、学生答卷中存在的问题
1 .对题意缺乏理解 “跳跃式瞬间搜索” “进餐、休息问题”
2 . 文章表述不清 许多无搜索线路图
3 . 遗漏部分区域 4. 计算有误 5. 结果普遍偏大 6. 对搜索线路未作可行性验证
22
以上是对于2008年全国大学生数学建模 竞赛C题的一点思考,难免有不成熟或错误 之处,愿意以此求教于各位专家与同仁,共 同推动全国大学生数学建模竞赛活动的蓬勃 开展.
数学建模 2008B题自习教室开放的优化管理

B题自习教室开放的优化管理近年来,大学用电浪费比较严重,集中体现在学生上晚自习上,一种情况是去某个教室上自习的人比较少,但是教室内的灯却全部打开,第二种情况是晚上上自习的总人数比较少,但是开放的教室比较多,这要求我们提供一种最节约、最合理的管理方法。
下面是某学校收集的部分数据,请完成以下问题.00开放(如果哪个教室被开放,则假设此教室的所有灯管全部打开)。
完成以下问题:1.假如学校有8000名同学,每个同学是否上自习相互独立,上自习的可能性为0.7.要使需要上自习的同学满足程度不低于95%,开放的教室满座率不低于4/5,同时尽量不超过90%。
问该安排哪些教室开放,能达到节约用电的目的. 2.假设这8000名同学分别住在10个宿舍区,现有的45个教室分为9个自习区,按顺序5个教室为1个区,即1,2,3,4,5为第1区,…,41,42,43,44,45为第9区。
这10个宿舍区到9个自习区的距离见表2。
学生到各教室上自习的满意程度与到该教室的距离有关系,距离近则满意程度高,距离远则满意程度降低。
假设学生从宿舍区到一个自习区的距离与到自习区任何教室的距离相同。
请给出合理的满意程度的度量,并重新考虑如何安排教室,既达到节约用电目的,又能提高学生的满意程度。
另外尽量安排开放同区的教室。
3.假设临近期末,上自习的人数突然增多,每个同学上自习的可能性增大为0.85,要使需要上自习的同学满足程度不低于99%,开放的教室满座率不低于4/5,同时尽量不超过95%。
这时可能出现教室不能满足需要,需要临时搭建几个教室。
假设现有的45个教室仍按问题2中要求分为9个区。
搭建的教室紧靠在某区,每个区只能搭建一个教室,搭建的教室与该区某教室的规格相同(所有参数相同),学生到该教室的距离与到该区任何教室的距离假设相同。
问至少要搭建几个教室,并搭建在什么位置,既达到节约用电目的,又能提高学生的满意程度.所有数据仅供计算参考.并非完全真实.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B题:私家车保有量增长及调控问题
我国经济的快速发展为私人汽车提供了巨大的发展空间。
据中国汽车工业协会估算,截止到2006年底,中国私人汽车保有量约为2650万辆,占全国汽车保有量的60%左右。
在2006年,我国汽车销量为710多万辆,私人购买比例超过77%,中国已经成为仅次于美国的全球第二大新车市场。
据世界银行的研究,汽车保有量 (尤其是私人汽车)与人均国民收入成正比。
2003年,我国国内人均GDP首次突破1000美元,这预示着中国汽车开始进入家庭消费阶段。
而事实表明,随着中国人均GDP的稳健增长,近年来,我国的家用汽车销量以两位数的增速急剧扩大。
汽车特别是用于消费的私人汽车保有量的多少,与经济发展程度、居民收入以及道路建设等有着密切的联系。
随着私人汽车消费时代的到来,汽车保有量上升的一个重要因素就是国内汽车消费的快速增长。
消费者购买力的增强和个体私营经济的快速发展,也带动了私人汽车的大发展。
私人汽车保有量与一个国家或地区的社会经济发展的有关数据有着密切关系。
附表提供了我国某一经济发达地区的一些相关统计数据。
然而,当我们快速迈进以私人汽车为主体的汽车社会的时候,也面临着新的考验,除了能源紧缺、燃油价格上涨、土地资源有限等诸多不利因素对汽车发展带来巨大的压力外,环境污染也对汽车工业的发展提出了严格的要求。
我国于上世纪1999年对生产的小汽车废气CO、HC、NOX和PM允许排放量制订了国家标准(相当于欧洲标准)。
规定生产的汽车从2000年1月1日起实施国Ⅰ排放标准,从2005年1月1日起实施国Ⅱ排放标准,从2007年7月1日起实施国Ⅲ排放标准,从2010年1月1日起实施国Ⅳ和国Ⅴ排放标准(实现基本与欧洲标准同步)。
据有关资料介绍,在城市交通中,小汽车与公共汽车相比,单位小汽车排放的污染物比公共汽车高9倍。
如果对这种快速增长不从战略的高度加以科学引导和调整,汽车的迅猛增长将不再单纯体现经济建设成就,巨大的负面效应也将成为社会发展的阻碍因素。
请研究下述问题:
问题1、根据附表中的相关数据建立数学模型,分析影响该地区私人汽车保有量的因素,并预测到2010年该地区私人汽车保有量有多少?
问题2、自2007年以来,CPI指数累创新高,为了稳定宏观经济,控制投资与物价的过快上涨,防止过大的资产价格泡沫和过度的投机, 政府决定自去年开始及今后一段时期内采取从紧的货币政策,如,加息、提高人民币存款准备金等等. 据统计, 2007年政府5次升息,9次上调存款准备金率,分析这些措施对该地区私人汽车保有量有什么样的影响?
问题3、假设私人汽车的年运行公里数是公交车年运行公里数的五分之一。
按照汽车废气国III排放标准(欧III)(要求CO排放量每公里不超过2.3克,HC+NOX排放量每公里不超过0.56克,PM排放量每公里不超过0.05克), 如何根据该地区的汽车废气的排放情况,来调控公交车和私人汽车保有量?
1996-2008年某地区相关的统计数据。
