八年级数学重心
【初中数学】初中数学知识点:重心

【初中数学】初中数学知识点:重心重心定义:物体的重心与物体的形状有关,规则图形的重心就是它的几何中心。
如:线段,平行四边形,三角形,正多边形等等。
其它图形重心:注:下面的几何体都是均匀的,线段指细棒,平面图形指薄板。
三角形的重心就是三边中线的交点。
线段的重心就是线段的中点。
平行四边形的重心就是其两条对角线的交点,也是两对对边中点连线的交点。
平行六面体的重心就是其四条对角线的交点,也是六对对棱中点连线的交点,也是四对对面重心连线的交点。
圆的重心就是圆心,球的重心就是球心。
锥体的重心是顶点与底面重心连线的四等分点上最接近底面的一个。
四面体的重心同时也是每个定点与对面重心连线的交点,也是每条棱与对棱中点确定平面的交点。
正多边形的重心是其对称轴的交点。
由物理方法,我们可以找出任意四边形的重心。
三角形重心:重心是三角形三边中线的交点,三线交一点可用燕尾定理证明。
三角形重心性质:1.重心到顶点的距离与重心到对边中点的距离之比为2:1。
2.重心和三角形3个顶点组成的3个三角形面积相等。
3.重心到三角形3个顶点距离的平方和最小。
4.在平面直角坐标系中,重心的坐标是顶点坐标的算术平均,即其坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3);空间直角坐标系??横坐标:(X1+X2+X3)/3纵坐标:(Y1+Y2+Y3)/3 竖坐标:(Z1+Z2+Z3)/3。
5.重心是三角形内到三边距离之积最大的点。
6.(莱布尼兹公式)三角形ABC的重心为G,点P为其内部任意一点,则3PG2=(AP2+BP2+CP2)-1/3(AB2+BC2+CA2)。
7.在三角形ABC中,过重心G的直线交AB、AC所在直线分别于P、Q,则AB/AP+AC/AQ=3。
8.从三角形ABC的三个顶点分别向以他们的对边为直径的圆作切线,所得的6个切点为Pi,则Pi均在以重心G为圆心,r=1/18(AB2+BC2+CA2)为半径的圆周上。
三角形“五心歌”三角形有五颗心;重、垂、内、外和旁心,五心性质很重要,认真掌握莫记混。
人教版 初中数学 八年级上册课题学习重心_课题学习重心
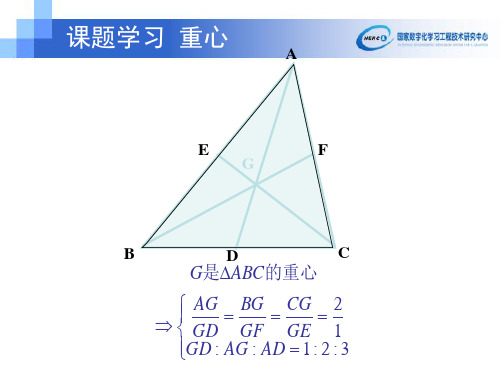
∵EF是△ABC的中位线
F
E
∵∴HEIF是=∥△G12BBCC的中位线
G
∴HI
=∥
1 2
BC
H
I
∴ EF =∥ HI
B
D
C∴四边形EFHI是平行四边形
∴EG=HG,FG=IG
∴EG:GB=1:2,FG:GC=1:2
三角形的重心把中线分成1:2的两部分。
A
E G
B
?
D
C
课题学习 重心
已知ABC的中线CD、BE相交于点G;
A
32145.... SS ::SS SS : S DDDDGGGGEBEEE DEDAAEGDGBCCCB;;;
D
E
GG
B
C
课题学习 重心
归纳有关三角形面积解题方法:
A 1.三角形的中线把三角形 分成面积相等的两个三角
形;
E G
A
求:点G到直角顶点C的距离GC;
解:RtACB,ACB 90o
4
D G
AC 4,BC 3
G是ABC的重心
AB
5
CCGD是 中32 C线D
CD
5 2
C
3
B CG 5 3
课题学习 重心
已知:ABC中AB AC, AD BC, AD与 中线BE相交于点G; AD 18cm,GE 5cm, 求:BC的长。
课题学习 重心 A
E
F
G
B
D
C
G是ABC的重心
AG GD
BG GF
CG GE
2 1
GD : AG : AD 1: 2 : 3
初中数学 什么是三角形的重心

初中数学什么是三角形的重心、垂心和外心三角形是几何学中最基本的形状之一,它由三条线段连接的三个顶点组成。
在三角形中,有一些特殊的点,它们与三角形的顶点和边有着特殊的关系,分别称为重心、垂心和外心。
下面将详细介绍这些三角形中心的定义、性质和应用。
1. 重心:重心是通过三角形的三条中线的交点确定的。
中线是连接三角形的顶点和对边中点的线段。
重心被平分为三个部分,每个部分的长度等于从重心到对边顶点的距离。
重心与三角形的顶点的距离的乘积等于三角形的面积。
重心有以下性质和应用:-重心是三角形内部的点,它将三角形分成三个面积相等的部分。
-重心到三角形的顶点的距离相等,重心到对边的距离最短。
-重心是稳定的,当三角形发生形变时,重心的位置保持不变。
-重心广泛应用于力学和结构分析中,用于确定物体的平衡点和质心。
2. 垂心:垂心是通过三角形的三条高线的交点确定的。
高线是从三角形的顶点垂直于对边的线段。
垂心与三个顶点之间的连线构成的三角形称为垂心三角形。
垂心有以下性质和应用:-垂心到三角形的顶点的距离相等,垂心到对边的距离最短。
-垂心是三角形内部的点,它将三角形分成三个角度相等的部分。
-垂心是稳定的,当三角形发生形变时,垂心的位置保持不变。
-垂心广泛应用于三角形的垂心定理和欧拉线的研究中。
3. 外心:外心是通过三角形的三个顶点的垂直平分线的交点确定的。
垂直平分线是从顶点垂直于对边并平分对边的线段。
外心是三角形内切圆和外接圆的圆心。
外心有以下性质和应用:-外心到三角形的顶点的距离相等,外心到对边的距离最大。
-外心是三角形外接圆的圆心,它是三条边的垂直平分线的交点。
-外心是稳定的,当三角形发生形变时,外心的位置保持不变。
-外心广泛应用于三角形的外心定理和外接圆的研究中。
这些三角形中心点的定义、性质和应用可以帮助我们更好地理解和解决与三角形相关的问题,同时也为几何学和物理学的研究提供了重要的基础。
人教版八年级数学《重心》ppt

课题学习(1)
重 心
你能保持平衡吗?
பைடு நூலகம்
你能完美的做出此动作吗?
能在平衡木上保持平衡吗?
活动 1
你知道杂技演员头上的碗为什么掉不下来吗?
活动 1
碟子为什么不会从顶杆上掉下来呢?
活动 1
杂技演员头上的碗,顶杆上的碟子掉不 下来是由于它们保持着一种平衡.
怎样才能达到平衡?
试一试:怎样用一根手指平衡地顶起一支笔? 一本书呢?
活动 6
物体的重心与物体的形状有关,规则图
形的重心就是它的几何中心.如:线段,平
行四边形,三角形,正多边形等等.
1.线段重心是线段中点.
2.平行四边形的重心是对角线的交点. 3. 三角形的重心是三条中线的交点. 4.正多边形的重心是对称轴的交点.
拓
展
任何有固定形状的物体,不论其在地 球表面如何放置,其平行分布重力的合 力(通常所说的物体的重力)作用线, 都通过物体上一个确定的点,这一点称 为物体的重心.
三、解答题
画出图中各图形的重心O.
手指顶在钢笔、书本的中心就可以平 衡,这个平衡点叫做钢笔、书本的重 心.
你会找出常见的几何图形的重心吗? 如线段、平行四边形、任意多边形等.
活动 2 探究线段的重心.
(1)找出平衡点的位置.
如图所示,两手分开,把均匀木条水平地架在左右手的食 指上,把两食指相对交替靠拢,直到并在一起为止.用一个食指 支在此处,木条能呈水平平衡.
结论:平行四边形的重心就是它 的两条对角线的交点.
(3)由以上发现能找到矩形、菱形、一 般平行四边形的重心的所在位置吗?
O
O
O
(4)将钉子定在所找到的重心处,将细 绳系在钉子上将它们吊起,观察它们是否保 持平衡。 悬挂法
八年级数学《课题学习 -重心1》教案
19.4、课题学习《重心》教学设计
flash演示悬线法测定线段平衡点位置。
教学反思:
本节“课题学习”,主要是让学生多动手、多实践、多猜想、多论证、多总结。
对于其中一些结论,大胆地鼓励学生进行说理甚至证明,说理证明的形式多样,可口述,可书写,可交流探讨,通过学习,进一步让学生了解规则的几何图形的几何图形的重心就是它的几何中心,体会数学和物理学科之间的联系。
注重对学生以下各能力训练培养:学生的空间想象能力;动手操作能力;实践探究能力;猜想发现能力;说明理由逻辑推理能力。
八年级数学上册《找重心》优秀教学案例

1.重心定义:讲解重心的定义,让学生了解重心是几何图形内部的一个重要点,它具有使图形保持平衡的特性。
2.重心的性质:通过讲解和示例,让学生掌握重心在几何图形中的位置特点,如三角形重心位于三边中线的交点,矩形重心位于对角线的交点等。
3.寻找重心的方法:介绍寻找三角形、矩形等简单几何图形重心的方法,如中线法、对角线法等。
3.培养学生的团队协作能力和问题解决能力,提高他们的数学素养。
二、教学目标
(一)知识与技能
1.知识目标:通过本节课的学习,使学生掌握重心的定义,理解重心在几何图形中的位置特点,并能够运用数学语言描述重心的性质。同时,让学生掌握寻找三角形、矩形等简单几何图形重心的方法。
2.技能目标:培养学生运用数学知识解决实际问题的能力,提高他们的空间想象力和逻辑思维能力。通过小组合作、讨论交流等方式,锻炼学生的团队协作能力和沟通表达能力。
八年级数学上册《找重心》优秀教学案例
一、案例背景
《找重心》这一课题是八年级数学上册的教学内容,旨在让学生通过探究几何图形的重心概念,培养他们的空间想象能力和逻辑思维能力。在教学过程中,我将结合课本知识,以实际问题为载体,引导学生运用数学方法解决实际问题。本案例以学生为主体,关注学生的参与度和思考过程,通过小组合作、讨论交流等形式,激发学生的学习兴趣,提高他们的数学素养。
(二)过程与方法
1.过程目标:在教学过程中,注重学生的参与度和主体地位,引导他们通过观察、猜想、验证、总结等环节,探索几何图形重心的性质和寻找方法。让学生在探究过程中,体验数学知识的形成过程,培养他们的探究精神和问题解决能力。
2.方法目标:采用任务驱动法、小组合作法、讨论交流法等多种教学方法,引导学生积极参与教学活动。同时,注重培养学生的自主学习能力,使他们能够在教师的引导下,运用所学知识解决实际问题。
湘教版数学八年级上册 综合与实践找重心 一等奖创新教案

湘教版数学八年级上册综合与实践找重心一等奖创新教案综合与实践找重心一、教学内容分析《找重心》是湘教版教材八年级上册“综合与实践领域”的内容,“综合与实践领域”的内容与其他三个领域的内容不同,它有着自身特定的内涵。
《义务教育数学课程标准》强调“综合与实践”的实施是以问题为载体,以学生自主参与为主的学习活动。
强调问题情境与学生所学的数学知识、各学科知识以及生活经验相结合,鼓励学生独立思考,合作交流,自主设计解决问题的方案,经历发现问题、提出问题、分析问题和解决问题的过程,感悟数学与生活实际之间的联系,以及数学知识在生活实际中的应用,并积累数学活动经验,培养学生的应用意识和能力。
本节课的主题是找平面几何图形的重心。
“重心”这个概念在探究三角形的性质时已出现过,但实际上,“重心”本身是一个物理概念,即物体所受重力的作用点。
要研究平面几何图形的重心,我们有必要先研究物体(如木棒、三角形纸板等)的重心位置,进而抽象出平面几何图形的重心,并从中发现规律。
因此本节课教材中围绕“重心”问题展开,从比萨斜塔开始(让学生感受到重心的神奇)——找均匀物体的重心(数学知识与生活经验相结合)——抽象出平面几何图形的重心(线段、三角形、平行四边形、长方形、正方形)——发现规律(规则的几何图形的重心就是它的几何中心)——重心的应用(感受数学知识在实际生活中的应用),教材中设计了一系列活动,目的就是让学生通过动手操作、自主探究、合作交流等方式获得知识,让学生经历了一个发现知识、探索知识、获得知识的过程,发展和丰富了学生的数学活动经验,促进学生的思考,培养了学生的实践能力和创新意识。
二、教学目标设计1、理解重心的意义,体会数学与物理学科之间的联系,并获得研究问题和解决问题的方法和经验。
2、通过寻找均匀物体的重心位置,抽象出平面几何图形的重心,归纳总结出规则的几何图形的重心就是它的几何中心。
3、通过试验,进一步发展学生的动手操作能力,体验合作交流、自主探究的学习方式,积累数学活动经验,反思数学活动过程。
初二数学重心知识点

初二数学重心知识点
初二数学重心知识点如下:
1. 重心定义:一个平面图形的重心是指平面图形内所有点的坐
标平均值的点,即平面图形的质心。
2. 重心的位置:对于一个均匀分布的平面图形,重心位于几何
图形的对称轴上。
3. 三角形的重心:三角形的重心是三条中线的交点,即三个顶
点与对应中线交点的中点。
4. 四边形的重心:四边形的重心是对角线的交点的中点。
5. 合并图形的重心:当两个或多个平面图形合并成一个新图形时,新图形的重心可以由原来图形的重心根据面积的加权平均得到。
6. 求重心的方法:根据不同几何图形,求重心可以采用不同的
方法。
例如,对于三角形可以使用中线的交点,对于四边形可以使用
对角线的交点,对于不规则图形可以将其分解成多个规则图形来求解。
7. 重心的应用:重心是很多实际问题中的重要概念,例如在工
程设计中确定物体的平衡点、计算物体的形心位置等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
等于这边上中线长的三分之一。
G是ABC的重心
EG F
AG BG CG 2 GD GF GE 1
GD : AG : AD 1 : 2 : 3 B
D
C
已知:ABC中AB AC, AD BC, AD与
中线BE相交于点G; AD 18cm,GE 5cm,
求:BC的长。
A
E G
பைடு நூலகம்
B
?
D
C
5、如图,在梯形ABCD中,AB∥CD, ∠A+∠B=900,E、F分别是AB、CD的中点,
结论:三角形的三条中线交于一点,这一 点就是三角形的重心.
探索四:寻找多边形的重心
请大家找出下列图形的重心位置. 正五边形,正六边形,………
……… …
一个规则的多边形的重心就是它 的几何中心.
物体的重心与物体的形状有关,规则的图 形重心就是它的几何中心。如;线段,平行 四边形,三角形,正多边形,等等。 1.线段重心是线段中点。 2.平行四边形的重心是对角线的交点。 3. 三角形的重心是三条中线的交点。
重心就是能使物体保持平衡的那个点.
1,在三角形的一个顶点处钉
A
一个小钉子作为悬挂点. 2,用下端系有小重物的细线
F
E
缠绕在一个小钉上,吊起硬纸 三角板,记下铅垂线的“痕迹”
B
O D
C
3,重复1,2的步骤.找到两条铅垂线的交点O.
4,在第三个小钉上重复1,2的步骤.仔细观察此时的铅 垂线是否经过交点O?通过顶点与交点O作射线,再观 察测量这三条线与对边的交点有什么特点?
四边形PQCD是平行四边形?成为等腰梯形?
D
PA
C
Q
B
练习
A
1、如图,在梯形ABCD中,AD∥BC, AD=AB=DC,BD⊥CD,则∠C=?
B
2、如图,在梯形ABCD中,AD∥BC,
A
AD=8,BC=17,∠C=70°, ∠B=55°,
则DC=? B
3、如图,在等腰梯形ABCD中, AD∥BC,AD=5cm,BC=11cm,高
探究一: 如何确定线段的重心? 1.平衡法: 2.悬挂法:
小结:线段重心是线段中点。
探究二: 如何确定平行四边形的重心? 1.平衡法:
小结:平行四边形的重心是对角线的交点。
探索二:寻找平行四边形的重心
重心就是能使物体保持平衡的那个点.
结论:平行四边形的重心就是
它的两条对角线的交点.
探索三:寻找三角形的重心
3,三角形的重心把它所在的中线分成了2:1的两部分.
玩梯子游戏方法和心得 https:///view/09382a1c86c24028915f804d2b160b4e767f81b5.html vcg27wfv
下午,太阳还有一杆子高的时候,耿家父子四人乘坐驴车来到了黄河边儿上。第一次上了堤岸见到波浪滔滔的黄河,耿正、耿英和耿直都非常激 动。耿直兴奋地说:“呵,好大的河哇,可比俺们家的那条小河大多了!”而耿英看了一会儿,却有点儿惋惜地说:“可这大河里的水怎么不清 澈呢?怎么洗衣裳啊!”耿正新奇兴奋了一会儿后,挠挠头犯愁地说:“怎么过去呢?俺们还有驴和车!”耿老爹笑了,说:“不用愁,有渡船 呢!”“驴和车也能渡过去?”“都能渡过去!”大家放心了,又观赏游玩一会儿。抬头看看日头即将落山了,耿老爹对耿正兄妹三人说:“娃 儿们,今儿个别再玩儿了,俺们得去旁边的村儿里找个地儿住下来呢。明儿个咱不着急过河,你们没有玩儿够,就多玩儿两天!”远远望去,往 西大约一里多远的岸边上,有一个约莫五、六十户人家的小村庄。走近了发现,村口一棵高大的椿树枝桠上挂着一个大木牌,木牌上面刻有三个 大字:滩头村。进了村一打听,才知道村子里并没有客栈可住。在村子的最南端,一对年长的老夫妇正坐在自家个儿门前的井台边儿上闲坐着聊 天呢。耿老爹恭恭敬敬地走上前去说明情况,请求能在老人家里留宿两日。和善的老爷子笑笑还没有开口,老妇人就爽快地说:“行啊,出门在 外的不容易,还带着三个娃娃呢。俺们家现成着就有两间空着的干净房子呢,平时留给女儿们回来住的,只要简单打扫一下就行啦!”如此顺利 就问得了可以留宿的地方,真正让耿老爹喜出望外,不免千恩万谢几句。而这一对慈眉善目的老夫妇并不多说什么,只是赶快起身推开大门让耿 家父子们进院儿。没有门槛的大门相当宽敞。征得老夫妇同意后,耿老爹将驴车停在了老人家的院子里。耿正帮着爹卸了车后,耿老爹随手把驴 子拴在院里的一棵滩枣树上。树上的枣儿已经打了,但地上有不少枣树叶子,驴子就使劲地够着添吃周围的枣叶。老妇人看着笑了,对耿老爹说: “你把大门关上,放开它哇!看它可怜的!”耿老爹说:“它倒是不会跑了的,但到处走动怕糟践了您老人家的院子呢!”“不碍事,不碍事, 你放开它,让它自己吃枣叶,看它香得!”耿老爹心里暗想:真正遇上好人啦!于是放开毛驴,把院子里散乱的家什和柴火规整一番。完了又问 两位老人家:“有什么需要力气的活儿?俺闲着也是闲着,不如帮您二老做做!”老爷子连忙摆摆手说:“不用,不用,女儿女婿们常来的,家 里现在没有什么需要使力气的活儿。你们赶路辛苦,歇着哇!”。老妇人则说:“俺这就做饭去,给你们好好吃一顿哇。看你们爷儿几个这一路 上分餐露宿的!”耿英听老妇人说要去做饭,马上过来说:“奶奶,俺来帮您做哇!”老妇人乐了,笑着说:“真是个好闺女!俺要
B
C F
6、梯形ABCD的周长为40cm,上底
C
CD=7cm,DE∥BC,G、F分别为AD、AE
中点,且GF=0.5BC,求△AED与△AFG
的周长。
BE
D G
FA
收获季节
谈谈本节课你知道了什么?
1,如何找出一个物体的重心. 2,线段的重心是它的中点.
三角形的重心是它的三条中线的交点. 平行四边形的重心是它对角线的交点. 一个规则多边形的重心就是它的几何中心.
直角三角形重心在斜边中点 等边三角形重心是高或中线或角平 分线交点 4.正多边形的重心是对称轴的交点。 不规则的图形(物体)可以通过悬挂法来 确定它的重心。
三角形的三条中线的交点叫做三角形的重心。
三角形的重心定理
或 三角形的重心与顶点的距离等
于它与 对边中点距离的两倍。
A
三角形的重心到一边中点的距离
A
DE=4cm,则梯形的周长与面积各是
多少?
B
D
C D
C D
C E
4、如图,在等腰梯形ABCD中,
A
D
AB=DC,∠D=120°,对角线CA平分
∠BCD,且梯形的周长为20,则梯形
的上、下底长分别是多少? B
C
5、如图,在等腰梯形ABCD中,
AED
∠B+∠C=90°,AB=6,DC=8,E、
F分别为AD、BC中点,则EF=
求证:EF 1 AB CD
2
D
F
C
A
ME N
B
拓展训练
已知:四边形ABCD是直角梯形, AB=8cm,B 900
AD=24cm,BD=26cm,点P从A出发,以1cm/s
的速度向D运动,点Q从C出发,以3cm/s的速
度向B运 动,其中一动点达到端点时,另一动
点随之停止运动。从运动开始,经过多少时间,
