九年级数学三角形重心垂心专题辅导
初中数学解题模型专题讲解39---三角形“垂心”定理的7种证法

C
-2-
则 A、B、D、E 四点共圆, ∴∠1 = ∠2 又 ∠1与 ∠3互余, ∠2 与 ∠4 互余. ∴∠3 = ∠4 又 C、E、H、D 四点共圆, , 。又 , ∴∠4 = ∠5 ∴∠3 = ∠5 ∠5 + ∠BHC = 1800
, ∴∠3 + ∠BHC = 1800 ∴C、H、F 三点共线。 即 AB 边上的高 CF 经过 H 点。因而三条高 、 、 AD BE CF 相交于一点.
1.2 预备定理:
B
D
1.塞瓦(Ceva)定理:设 D、E、F 分别是 ∆ABC 三边 、 、 BC CA AB
图( 1 )
C
上的点,若
则 交于一点 AF • BD • CE = 1, AD,BE,CF
.
FB DC EA
2.三角形“外心”定理:三角形三边的中垂线相交于一点,此点与三顶点等距,这点叫做 三角形的外心.
、 BE CF 相交于一点.
证法 1.3.3 3 如图(3)连结 , , , DE EF FD
A
则 A、B、D、E 四点共圆,
E
在 和 中, ∴∠1 = ∠2. Rt∆ABE Rt∆ACF
F
易知 , ∠2 = ∠3 ∴∠1 = ∠3.
又 A、F、D、C 四点共圆,∴∠3 = ∠4 ,∴∠1 = ∠4 . 可平见分,∠AEFDD平.在分∆∠DEEDFF中.同,理可得,BE 平分∠DEF ,CF 由“内心”定理可得,AD,BE,CF 相交于一点.
2 41
B
D
图( 3 )
3
C
1如.3图.4(证4法)设4 AB 边上的高 CF 与 BC 边上的高 AD 相交于 H,连结 BH 并延长交 于 AC E. 连结 DF,因 A、F、D、C 四点共圆, ∴∠1 = ∠2又 B、D、H、F 四点共圆, , ∴∠2 = ∠3 在 ∴∠1 = ∠3 ∆BAE 和中 ∆CAF 中,
三角形的重心、垂心、外心和内心的认识(二)2024

三角形的重心、垂心、外心和内心的认识(二)引言:三角形是一种基本的几何图形,它具有独特的性质和特点。
在三角形中,重心、垂心、外心和内心是四个重要的点,它们分别具有不同的特性和作用。
在本文中,我们将进一步探讨三角形的重心、垂心、外心和内心的认识,帮助读者更好地理解和应用它们。
正文:一、重心(Center of Gravity)重心是三角形内部所有点的平均位置。
它具有以下性质:1. 重心所在的直线称为重心线,它经过三角形的顶点与对边的中点。
2. 重心将三角形分成三个面积相等的小三角形。
3. 如果一个三角形均匀分布质量,则它的重心就是质心。
二、垂心(Orthocenter)垂心是三角形三条高线的交点。
它具有以下性质:1. 垂心到三角形三个顶点的距离相等。
2. 垂心到三角形三条边的距离乘积最小。
3. 如果一个三角形是锐角三角形,则垂心在三角形内部;如果是直角三角形,则垂心是直角的顶点;如果是钝角三角形,则垂心在三角形外部。
三、外心(Circumcenter)外心是三角形外接圆的圆心。
它具有以下性质:1. 外心到三角形三个顶点的距离相等。
2. 外心到三角形三条边的距离相等,且等于外接圆的半径。
3. 一个三角形的外心可以通过三条边的垂直平分线的交点确定。
四、内心(Incenter)内心是三角形内切圆的圆心。
它具有以下性质:1. 内心到三角形三条边的距离相等,且等于内切圆的半径。
2. 内心到三角形的三个顶点的距离之和等于三角形的周长。
3. 一个三角形的内心可以通过三条边的角平分线的交点确定。
总结:三角形的重心、垂心、外心和内心是三角形内部的特殊点,它们在三角形的性质和计算中扮演着重要的角色。
重心代表了平均位置,垂心代表了高线的交点,外心代表了外接圆的圆心,内心代表了内切圆的圆心。
通过深入理解和认识这些点的性质,我们可以更好地应用它们解决问题,进一步研究和探索三角形的奥秘。
三角形五心定理
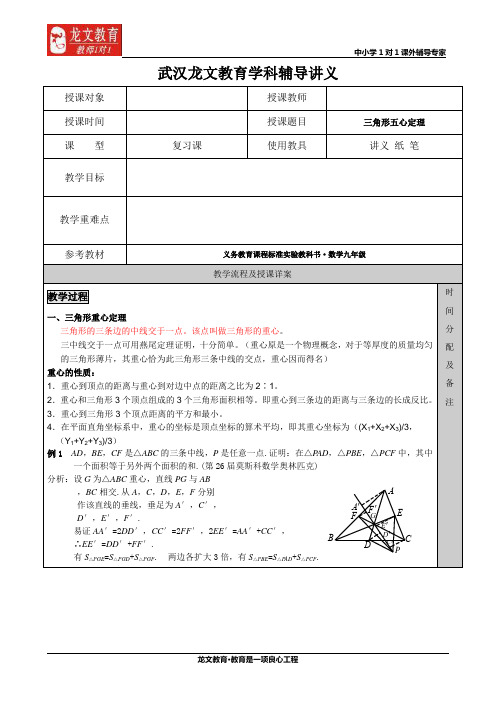
中小学1对1课外辅导专家武汉龙文教育学科辅导讲义授课对象授课教师授课时间授课题目三角形五心定理课型复习课使用教具讲义纸笔教学目标教学重难点参考教材义务教育课程标准实验教科书·数学九年级教学流程及授课详案教学过程一、三角形重心定理三角形的三条边的中线交于一点。
该点叫做三角形的重心。
三中线交于一点可用燕尾定理证明,十分简单。
(重心原是一个物理概念,对于等厚度的质量均匀的三角形薄片,其重心恰为此三角形三条中线的交点,重心因而得名)重心的性质:1.重心到顶点的距离与重心到对边中点的距离之比为2∶1。
2.重心和三角形3个顶点组成的3个三角形面积相等。
即重心到三条边的距离与三条边的长成反比。
3.重心到三角形3个顶点距离的平方和最小。
4.在平面直角坐标系中,重心的坐标是顶点坐标的算术平均,即其重心坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3)例1 AD,BE,CF是△ABC的三条中线,P是任意一点.证明:在△PAD,△PBE,△PCF中,其中一个面积等于另外两个面积的和.(第26届莫斯科数学奥林匹克)分析:设G为△ABC重心,直线PG与AB,BC相交.从A,C,D,E,F分别作该直线的垂线,垂足为A′,C′,D′,E′,F′.易证AA′=2DD′,CC′=2FF′,2EE′=AA′+CC′,∴EE′=DD′+FF′.有S△PGE =S△PGD+S△PGF. 两边各扩大3倍,有S△PBE=S△PAD+S△PCF.时间分配及备注AA'FF'G EE'D'C'PCBD例2 如果三角形三边的平方成等差数列,那么该三角形和由它的三条中线围成的新三角形相似.其逆亦真.分析:将△ABC 简记为△,由三中线AD ,BE ,CF 围成的三角形简记为△′.G 为重心,连DE 到H ,使EH =DE ,连HC ,HF ,则△′就是△HCF .(1)a 2,b 2,c 2成等差数列⇒△∽△′. 若△ABC 为正三角形,易证△∽△′. 不妨设a ≥b ≥c ,有 CF =2222221c b a -+, BE =2222221b a c -+, AD =2222221ac b -+.将a 2+c 2=2b 2,分别代入以上三式,得 CF =a 23,BE =b 23,AD =c 23.∴CF :BE :AD =a 23:b 23:c 23=a :b :c .故有△∽△′.(2)△∽△′⇒a 2,b 2,c 2成等差数列. 当△中a ≥b ≥c 时, △′中CF ≥BE ≥AD . ∵△∽△′, ∴∆∆S S '=(aCF )2.据“三角形的三条中线围成的新三角形面积等于原三角形面积的43”,有∆∆S S '=43.∴22aCF =43⇒3a 2=4CF 2=2a 2+b 2-c 2⇒a 2+c 2=2b 2.二、三角形外心定理三角形外接圆的圆心,叫做三角形的外心。
三角形重心、垂心、内心、外心的向量性质及简单应用

中学数学研究
41
三角形重心、垂心、内心、外心的向量性质及简单应用
广东省珠海市斗门区第一中学 (519100) 陈水松
一、三角形四心的表述与性质
(一) 重心——三角形三条边上的中线的交点叫做三角
形的重心. 重心将中线长度分成 2: 1 的两部分. 1. −O→A + −O−→B + −O−→C = −→0 ⇔O 是 △ABC 的重心.
AC BC −→ + −−→
.
|AC| |BC|
|−B−B+−−→ →CCb| −B)−→C, 所
= 以
4.
−−→ PO
=
−→ aP A
−−→ + bP B + a+b+c
−−→ cP C
⇔
O
为
△ABC
的内心,
P 为平面上任意点.
(二) 垂心——三角形三条高线的交点叫做三角形的垂
证明
因为
O
为
△ABC
证 法 1 设 O(x, y), A(x1, y1), B(x2, y2), C(x3, y3),
−→ −−→ −−→ OA+OB+OC
=
−→0
⇔
x=
x1 + x2 + x3
(x1 − x) + (x2 − x) + (x3 − x) = 0 (y1 − y) + (y2 − y) + (y3 − y) = 0
=
−→0 ,
所以
−→ AO
=
2−O−→D,
所以
A、O、D
三点共线,
初三数学备考

初三数学备考:三角形的垂心的性质1.锐角三角形的垂心在三角形内;直角三角形的垂心在直角顶点上;钝角三角形的垂心在三角形外。
2.三角形的垂心是它垂足三角形的内心;或者说,三角形的内心是它旁心三角形的垂心。
例如在△ABC中3.垂心O关于三边的对称点,均在△ABC的外接圆圆上。
4.△ABC中,有六组四点共圆,有三组每组四个相似的直角三角形。
5.H、A、B、C四点中任一点是其余三点为顶点的三角形的垂心并称这样的四点为一—垂心组。
6.△ABC,△ABO,△BCO,△ACO的外接圆是等圆。
7.在非直角三角形中,过O的直线交AB、AC所在直线分别于P、Q,则AB/AP?tanB+AC/AQ tanC=tanA+tanB+tanC8.三角形任一顶点到垂心的距离,等于外心到对边的距离的2倍。
9.设O,H分别为△ABC的外心和垂心,则∠BAO=∠HAC,∠ABH=∠OBC,∠BCO=∠HCA.10.锐角三角形的垂心到三顶点的距离之和等于其内切圆与外接圆半径之和的2倍。
11.锐角三角形的垂心是垂足三角形的内心;锐角三角形的内接三角形顶点在原三角形的边上中,以垂足三角形的周长最短。
12.西姆松Simson定理西姆松线:从一点向三角形的三边所引垂线的垂足共线的重要条件是该点落在三角形的外接圆上。
13.设H为非直角三角形的垂心,且D、E、F分别为H在BC,CA,AB上的射影,H1,H2,H3分别为△AEF,△BDF,△CDE的垂心,则△DEF≌△H1H2H3.14.三角形垂心H的垂足三角形的三边,分别平行于原三角形外接圆在各顶点的切线。
:分式与分式方程1、指数的扩充2、分式和分式的基本性质设f,g是一元或多元多项式,g的次数高于零次,则称f,g之比f/g为分式。
分式的基本性质分数的分子与分母都乘以或除以同一个不等于0的数,分数的值不变。
3、分式的约分和通分分式的约分是将分子与分母的公因式约去,使分式化简如果一个分式的分子与分母没有一次或一次以上的公因式,且各系数没有大于1的公约数,则此分式成为既约分式既约分式也就是最简分式。
三角形的五心-第3讲重心与垂心教师版

第三讲 三角形的重心与垂心一、 基础知识1.重心的定义:三角形的三中线(或二中线)的交点叫做三角形的重心.2.重心的性质 1)三角形的重心必在三角形的內部; 2)三角形的重心到顶点的距离等于过这顶点的中线长的三分之二; 3)三角形三中线分原三角形为六个等面积的三角形; 4)三角形重心到三顶点的连线分原三角形为三个等面积的三角形; 5)到三角形的三个顶点距离的平方和最小的点是这个三角形的重心;3.垂心的定义:三角形的三条高线的交点叫做三角形的垂心.4.垂心的性质 1) 锐角三角形垂心在三角形内部,直角三角形垂心在三角形直角顶点,钝角三角形垂心在三角形外部;2) 垂心会在三角形内部产生很多相似直角三角形;同时会出现四点共圆问题;二、 例题部分第一部分 重心例1. 如图34-2,已知△ABC 与△CDA 全等,点G 、H 分别是△ABC、△CDA 的重心,则△AGH的面积与△ABC 的面积的比为 ( )A .4:9B .2:3C .1:3D .1:6解答:C.设AC 的中点为O ,可证B 、G 、O 、H 、D 在同一直线上,由重心性质得GO =13BO ,OH =13OD , ∵BO =DO ,∴GH=23BO. AGH S =23ABO S .又 ABO S =12ABC S . ∴AGH S =23×12ABC S =13ABC S .例2. 在△ABC 中,BC=3,AC=4,BC 和AC 的中线AE 、BD 互相垂直,则AB 等于 ( )A .36B .5C .22D .7解答:.B.设在AE 与BD 相交于G ,且AE=3m,BD=3n,在Rt△AGD 中.由勾股定理,得()22222m n += (1)同理在Rt△BGE 中,可得 ()222322n m ⎛⎫+= ⎪⎝⎭(2)由(1)、(2),得2244m n +=5又在Rt△ABG 中,2AB = 2244m n + =5.∴AB=5.例3. 在直角三角形ABC 中. ∠A=90,G 为重心,且GA=2,则22GB GC += .解答:20.如图,过G 作GE ⊥BC 则 2GB =142BC +BC·DE+2DE +2GE ,2GC =142BC 一BC·DE+2DE +2GE ∴2GB +2GC =122BC +22GD ∵BC=2AD=2·32AG=3AG ,GD=12AG ∴2GB +2GC =12 (92AG +2AG )=52AG =20例4. 设M 是△ABC 的重心,过M 的线段交AB ,AC 于P 、Q ,且AP PB =m ,AQ QC =n ,则11m n + =( )A .2B .1C .12D .13解答:B.延长AM 交BC 于D ,作BG ∥PQ 交AD 的延长线于G ,作CE ∥PQ 交AD 、AB 于F 、E ,则△BDG ≌△CDF ∴1m +1n =BP AP +CQ AQ =CM MA +FM MA=AD DG AM AM +-+AD DF AM AM --=22AD AM AM- =2DM AM =1第二部分 垂心例5. (2000年,四川省中考题)如图34-1,已知△ABC 的内切圆0与各边相切于D 、E 、F ,那么点0是△DEF 的 ( )A .三条中线的交点B .三条高的交点C .三条角平分线的交点D .三条边的垂直平分线的交点解答:D.提示:因为⊙O 是△DEF 的外接圆。
正三角形重心中心垂心外心内心的知识点

正三角形重心中心垂心外心内心的知识点一、知识概述《正三角形重心、中心、垂心、外心、内心》①基本定义:- 重心:说实话,这就像是正三角形的平衡点。
如果把正三角形看作是一块均匀的薄板,从重心这个点吊起来,薄板会水平平衡。
它是三条中线(连接一个顶点和对边中点的线段)的交点。
- 中心:在正三角形里,重心、垂心、外心、内心这四个心是重合的,这个重合的点就叫做中心。
- 垂心:想象一下,从正三角形的每个顶点向对边作垂线,三条垂线的交点就是垂心,这就好比是三角形三条高线(过顶点作对边的垂线段)相交的地方。
- 外心:它是正三角形外接圆的圆心,这个点到三个顶点的距离是相等的。
就像用一个圆刚好把正三角形圈在里面,这个圆的圆心就是外心。
- 内心:这是正三角形内切圆的圆心,内心到三条边的距离相等。
就好像在正三角形里面画一个正好能挨着三条边的圆,这个圆的圆心就是内心。
②重要程度:在三角形相关的几何知识里,这些概念非常重要。
无论是解决几何证明题,还是计算三角形的一些数值,它们都是关键的要素。
就像建房子的基石一样,如果这些概念不清楚,很多关于正三角形更复杂的问题就做不了。
③前置知识:得先把三角形的基础概念搞清楚,像三角形的边、角、顶点这些。
另外,得知道线段的中点怎么找,垂线怎么作,还有圆的一些基本概念,像圆心、半径什么的。
④应用价值:在建筑设计里,如果要设计一个正三角形结构的建筑,这些心的位置可以帮助确定建筑的力学结构平衡点,稳定性布局等。
在机械制造中,处理正三角形形状的零件,这些概念有助于精准定位和设计加工工艺。
二、知识体系①知识图谱:在几何学科里,正三角形的这几个心是三角形性质这一板块的重要内容,和三角形的全等、相似等概念也有着千丝万缕的联系。
②关联知识:和三角形的内角和、等腰三角形的性质等知识是紧密相联的。
比如说,正三角形内角都是60度,这一性质在研究这几个心的位置关系或者计算与这几个心相关的线段长度时有时候也会用到。
③重难点分析:- 掌握难度:我觉得对于初学者来说还是有点难度的。
三角形重心外心垂心内心的向量表示及其性质

三角形重心外心垂心内心的向量表示及其性质三角形是几何学中的基础概念之一,具有丰富的性质和特点。
其中,重心、外心、垂心和内心是三角形重要的特殊点,它们在三角形的研究和计算中起着重要的作用。
本文将介绍三角形重心、外心、垂心和内心的向量表示及其性质。
一、三角形重心的向量表示及性质重心是三角形三条中线的交点,记为G。
设三角形的三个顶点分别为A、B、C,对应的向量为a、b、c。
则三角形重心G的向量表示为:G = (a + b + c)/3重心G的性质如下:1. 重心到三角形各顶点的向量和为0向量,即AG + BG + CG = 0。
2. 重心将中线分成2:1的比例,即AG : GM = 2:1,BG : GN = 2:1,CG : GP = 2:1,其中M、N、P分别为中线BC、AC、AB的中点。
3. 重心是三角形内切圆和外接圆的同一个圆心。
二、三角形外心的向量表示及性质外心是三角形三条垂直平分线的交点,记为O。
设三角形的三个顶点分别为A、B、C,对应的向量为a、b、c。
则三角形外心O的向量表示为:O = (a⊥ + b⊥ + c⊥)/3其中,a⊥、b⊥、c⊥分别表示向量a、b、c的垂直平分线的向量。
外心O的性质如下:1. 外心到三角形各顶点的距离相等,即OA = OB = OC。
2. 外心是三角形外接圆的圆心,且外接圆的半径为OA、OB、OC中的一个。
三、三角形垂心的向量表示及性质垂心是三角形三条高线的交点,记为H。
设三角形的三个顶点分别为A、B、C,对应的向量为a、b、c。
则三角形垂心H的向量表示为:H = (a⊥ + b⊥ + c⊥)/3其中,a⊥、b⊥、c⊥分别表示向量a、b、c的高线的向量。
垂心H的性质如下:1. 垂心到三角形各顶点的距离相等,即HA = HB = HC。
2. 垂心是三角形内接圆的圆心,且内接圆的半径为HA、HB、HC中的一个。
四、三角形内心的向量表示及性质内心是三角形三条角平分线的交点,记为I。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形重心垂心形内点的共性
读者都知道,三角形中三条边上的中线交于一点,这个点就是三角形的重心,重心
与一边中点的线段的长是对应中线长的1
3,即:如果G是△ABC三条中线AD、BE、CF的交点,
那么
DG DA
EG
EB
FG
FC
===
1
3
如图1,从而可得:
DG DA
EG
EB
FG
FC
++=1
这个结果说明三组线段的比的和为1,非常奇妙的是三角形的垂心也有类似的性质请看:
设H是△ABC三条高线AD、BE、CF的交点,因为
DH DA S S
EH EB S S
FH FC
S
S
BCH
ABC
ACH
ABC
ABH
ABC =
=
=
∆
∆
∆
∆
∆
∆
所以DH
DA
EH
EB
FH
FC
S S S
S
BCH ACH ABH
ABC
++=
++
=
∆∆∆
∆
1
更为奇妙的是三角形内的任意一点也有这样的性质:
设Q是△ABC内任意一点,连结AQ、BQ、CQ并分别延长交对边于D、E、F
过Q作QP∥AB,QH∥AC分别交BC于P、H,则:
FQ FC
BP
BC
EQ
EB
CH
BC ==
,
又由于△DPQ∽△DBA及△QPH∽△ABC
可得:DQ
DA
PQ
AB
PH
BC
==
所以DQ
DA
EQ
EB
FQ
FC
PH
BC
CH
BC
BP
BC ++=++=1
读者看到这里,是不是感到:数学,真奇妙!。
