高等级道路竖曲线的精确计算方法
道路曲线高程计算公式

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道) 一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:。
竖曲线外矢距

竖曲线外矢距摘要:一、引言二、竖曲线外矢距的定义与计算1.定义2.计算公式三、竖曲线外矢距的应用1.在道路工程中的应用2.在铁路工程中的应用四、竖曲线外矢距的意义五、总结正文:一、引言竖曲线外矢距,作为道路工程和铁路工程中的一个重要概念,对于保证线路平顺、提高行驶舒适性和安全性具有重要意义。
本文将对竖曲线外矢距的定义、计算方法及其在工程中的应用进行详细阐述。
二、竖曲线外矢距的定义与计算1.定义竖曲线外矢距,又称超高缓和段外矢距,是指在道路或铁路的竖曲线上,从曲线起点到曲线终点,垂直于曲线切线方向上的距离。
简单来说,它表示在竖曲线上,车辆行驶过程中,车体中心线与轨道或路面中心线之间的距离。
2.计算公式竖曲线外矢距的计算公式为:外矢距= A * (1 - e^(-k * (L - d)))其中,A为外矢距设计值;e为自然对数的底数;k为曲线超高缓和段长度与外矢距设计值的比值;L为曲线长;d为曲线起点到曲线终点的距离。
三、竖曲线外矢距的应用1.在道路工程中的应用在道路工程中,竖曲线外矢距主要用于指导道路的平面设计。
通过合理设置竖曲线外矢距,可以保证车辆在行驶过程中,车体中心线与路面中心线之间的距离始终保持在一定范围内,从而提高行驶舒适性和安全性。
2.在铁路工程中的应用在铁路工程中,竖曲线外矢距是铁路线路平面设计的重要依据。
通过对竖曲线外矢距的精确计算和合理设置,可以确保列车在行驶过程中,车体中心线与轨道中心线之间的距离符合设计要求,从而保证列车行驶的平稳性和安全性。
四、竖曲线外矢距的意义竖曲线外矢距在道路和铁路工程中具有重要意义。
合理设置竖曲线外矢距,可以提高线路的平顺性,降低车辆和列车在行驶过程中的震动和噪音,从而提高行驶舒适性和安全性。
此外,竖曲线外矢距的设置还有助于优化道路和铁路的空间利用,提高线路的运行效率。
五、总结竖曲线外矢距是道路工程和铁路工程中的一个重要概念,对于保证线路平顺、提高行驶舒适性和安全性具有重要意义。
道路竖曲线计算

道路竖曲线计算 Hessen was revised in January 2021第二节 竖曲线设计纵断面上相邻两条纵坡线相交的转折处,为了行车平顺用一段曲线来缓和,这条连接两纵坡线的曲线叫竖曲线。
竖曲线的形状,通常采用平曲线或二次抛物线两种。
在设计和计算上为方便一般采用二次抛物线形式。
纵断面上相邻两条纵坡线相交形成转坡点,其相交角用转坡角表示。
当竖曲线转坡点在曲线上方时为凸形竖曲线,反之为凹形竖曲线。
一、竖曲线如图所示,设相邻两纵坡坡度分别为i 1 和i 2,则相邻两坡度的代数差即转坡角为ω= i 1-i 2 ,其中i 1、i 2为本身之值,当上坡时取正值,下坡时取负值。
当 i 1- i 2为正值时,则为凸形竖曲线。
当 i 1 - i 2 为负值时,则为凹形竖曲线。
(一)竖曲线基本方程式我国采用的是二次抛物线形作为竖曲线的常用形式。
其基本方程为:Py x 22=若取抛物线参数P 为竖曲线的半径 R ,则有:Ry x 22= Rx y 22=(二)竖曲线要素计算公式竖曲线计算图示1、切线上任意点与竖曲线间的竖距h 通过推导可得:==PQ h )()(2112li y l x R y y A A q p ---=-Rl 22=2、竖曲线曲线长: L = R ω3、竖曲线切线长: T= T A =T B ≈ L/2 =2ωR 4、竖曲线的外距: E =RT 22⑤竖曲线上任意点至相应切线的距离:Rx y 22=式中:x —为竖曲任意点至竖曲线起点(终点)的距离, m ;R —为竖曲线的半径,m 。
二、竖曲线的最小半径(一)竖曲线最小半径的确定1.凸形竖曲线极限最小半径确定考虑因素 (1)缓和冲击汽车行驶在竖曲线上时,产生径向离心力,使汽车在凸形竖曲线上重量减小,所以确定竖曲线半径时,对离心力要加以控制。
(2)经行时间不宜过短当竖曲线两端直线坡段的坡度差很小时,即使竖曲线半径较大,竖曲线长度也有可能较短,此时汽车在竖曲线段倏忽而过,冲击增大,乘客不适;从视觉上考虑也会感到线形突然转折。
公路测量曲线和竖曲线要素计算方法

1.某山岭区一般二级公路,变坡点桩号为K5+030,高程为427.68m ,%51=i ,%42-=i ,竖曲线半径R =2000m 。
试计算竖曲线各要素以及桩号为k5+000和K5+100处的设计高程。
解:⑴计算竖曲线要素09.005.004.012-=--=-=i i ω,为凸形竖曲线。
曲线长20000.09180L R m ω==⨯=切线长m L T 9021802=== 外距2290 2.03222000T E m R ===⨯ ⑵计算设计高程竖曲线起点桩号=(K5+30)-90=K4+940竖曲线起点高程=427.68-90×0.05=423.18m桩号K5+000处:横距m K K x 60)9404()0005(1=+-+= 竖距m R x h 9.040006022211=== 切线高程=423.18+60×0.5=426.18m设计高程=426.18-0.9=425.28m桩号K5+100处:横距m K K x 160)9404()1005(2=+-+= 竖距m R x h 4.6400016022222=== 切线高程=423.18+160×0.05=431.18m设计高程=431.18-6.4=424.78m2.某山岭区二级公路,已知JD1、JD2、JD3的坐标分别为(40961.914,91066.103)、(40433.528,91250.097)、(40547.416,91810.392),并设JD2的R=150m ,Ls=40m ,求JD2的曲线要素。
解:⑴计算出JD2、JD3形成的方位角fwj2,︒=--=48966.11528.40433416.40547097.91250392.91810arctan 2fwj 计算出JD1、JD2形成的方位角fwj1, ︒=--=19908.289914.40961528.40433103.91066097.91250arctan1fwj 曲线的转角为α=360+fwj2-fwj1=82.29058°⑵由曲线的转角,计算出曲线的切线长T ,曲线长L 及超距J3322402019.9882240240150s s L L q R =-=-=⨯ 24243340400.444242384241502384150s s L L p R R =-=-=⨯⨯ ︒===639.7150406479.286479.280R L s β 438.151988.19229058.82tan )444.0150(2tan )(=++=++=q p R T α 0150(2)2(82.2905827.639)240290.526180180s RL L ππαβ⨯=-+=-⨯+⨯= 781.49150229058.82sec )444.0150(2sec )(=-+=-+=R p R E α下面总结范文为赠送的资料不需要的朋友,下载后可以编辑删除!祝各位朋友生活愉快!员工年终工作总结【范文一】201x年就快结束,回首201x年的工作,有硕果累累的喜悦,有与同事协同攻关的艰辛,也有遇到困难和挫折时惆怅,时光过得飞快,不知不觉中,充满希望的201x年就伴随着新年伊始即将临近。
竖曲线公式(实用的工程计算方法)PPT课件

3.角度交会法 根据两个或两个以上的已知角度 的方向交出点的平面位置,称为角度交会法。
4.距离交会法 根据两段已知距离交会出点的平 面位置,称为距离交会法。
.
三、已知坡度的测设
在道路、渠道、给排水工程中经常要测设指 定的坡度线,又称放坡。
对竣工后的土石方工程、路面工程、桥隧工程、 排水工程、挡土墙、防护及其它砌石工程的平面 位置、纵向高程和几何尺寸均应进行实地测量以 确定其质量之优劣。在上述的各项测量内容中, 又以公路中线偏位的检测最为重要。因为各种构 造物的放样,往往是以道路中线为基准进行的。 所以,在竣工测量中应该把对中线偏位放在首位。
.
2、横坡度的测量 横坡度的测量不同于宽度 的测量,横坡度是通过间接法测量,而宽度是 通过直接法测量。所谓间接法测量,是指通过 检测高程,计算两点高差,再计算两点横坡, 用设计值与测量值之差不超过有关规定。
3、路基边坡的测量 抽查每200米测4处,可用 边坡样板或坡度尺沿横断面方向进行检查。
4、排水设施、防护工程等几何尺寸及外观测 量 排水、支挡、防护等工程的几何尺寸是指 断面尺寸的长、宽、高等,另外还包括竖直角 或坡度。
.
已知坡度的放样
.
§11-3 道路施工测量
道路施工测量主要包括恢复路线中线、路 基边桩的测设、竖曲线的测设等项工作。
.
一、路线中线的恢复
从路线勘测到开始施工这段时间里,往 往会有一些中桩丢失,故在施工之前, 应根据设计文件进行恢复工作,并对原 来的中线进行复核,以保证路线中线位 置准确可靠。恢复中线所采用的测量方 法与路线中线测量方法基本相同。此外, 对路线水准点也应进行复核,必要时还 应增设一些水准点以满足施工需要。
竖曲线、缓和曲线计算公式
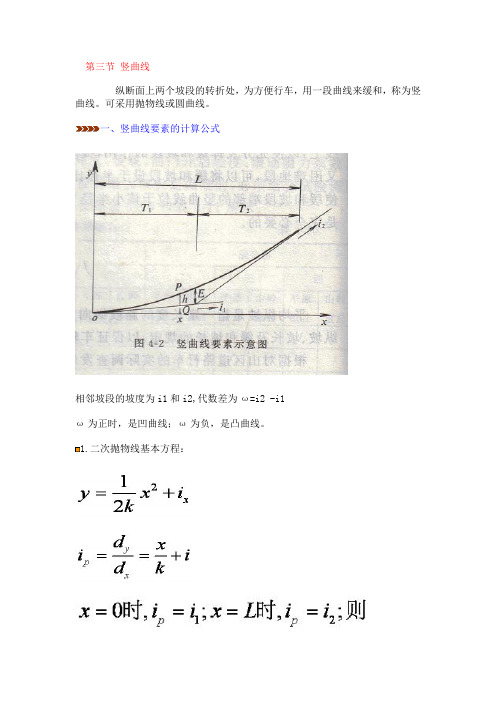
第三节竖曲线纵断面上两个坡段的转折处,为方便行车,用一段曲线来缓和,称为竖曲线。
可采用抛物线或圆曲线。
一、竖曲线要素的计算公式相邻坡段的坡度为i1和i2,代数差为ω=i2 -i1ω为正时,是凹曲线;ω为负,是凸曲线。
1.二次抛物线基本方程:或ω:坡度差(%);L:竖曲线长度;R:竖曲线半径2.竖曲线诸要素计算公式竖曲线长度或竖曲线半径R: (前提:ω很小)L=Rω竖曲线切线长:T=L/2=Rω/2竖曲线上任一点竖距h:竖曲线外距:二、竖曲线最小半径(三个因素)1.缓和冲击对离心加速度加以控制。
ν(m/s)根据经验,a=0.5~0.7m/s2比较合适。
我国取a=0.278,则Rmin=V2/3.6 或Lmin=V2ω/3.62.行驶时间不过短 3s的行程Lmin=V.t/3.6=V/1.23.满足视距的要求分别对凸凹曲线计算。
(一)凸形竖曲线最小半径和最小长度按视距满足要求计算1.当L<ST时,Lmin = 2ST - 4/ω2.当L≥ST时,ST为停车视距。
以上两个公式,第二个公式计算值大,作为有效控制。
按缓和冲击、时间行程和视距要求(视距为最不利情况)计算各行车速度时的最小半径和最小长度,见表4-13。
表中:(1)一般最小半径为极限最小半径的1.5~2倍;(2)竖曲线最小长度为3s行程的长度。
(二)凹曲线最小半径和长度1.夜间行车前灯照射距离要求:1)L<ST2) L≥STL<ST Lmin = 2ST - 26.92/ω (4-14)L≥STω /26.92 (4-15)3s时间行程为有效控制。
例:设ω=2%=0.02;则L=ωR竖曲线最小长度L=V/1.2速度V=120km/h V=40km/h 一般最小半径R凸17000 700一般最小半径R凹6000 700 L凸340 14L凹120 14 例题4-3ω=-0.09 凸形;L=Rω=2000*0.09=180mT=L/2=90mE=T2/2R=2.03m起点桩号=k5+030 - T =K4+940起始高程=427.68 - 5%*90=423.18m桩号k5+000处:x1=k5+000-k4+940=60m切线高程=423.18+60*0.05=426.18m h1=x21/2R=602/2*2000=0.90m设计高程=426.18 - 0.90=425.28m 桩号k5+100处:x2=k5+100-k4+940=160m切线高程=423.18+160*0.05=431.18m h2=x22/2R=1602/2*2000=6.40m设计高程=431.18 - 6.40=424.78m第一节平面线形概述一、路线路线指路的中心线;路线在水平面上的投影叫路线的平面;路线设计:确定路线空间位置和各部分几何尺寸的工作;可分为平面设计、纵断面设计、横断面设计。
竖曲线高程计算excel表

竖曲线高程计算通常涉及到纵坡设计,可以用于计算道路或其他线性结构的竖向变化。
如果你想创建一个Excel表格来进行竖曲线高程计算,以下是一个简单的步骤指南:
1. 打开Excel
首先,打开Microsoft Excel软件。
2. 创建表格
在Excel中创建一个新的工作表。
在这个表中,你可以创建两列,一列是里程(或水平距离),另一列是高程。
3. 输入已知数据
在里程列中输入已知的里程点,在对应的高程列中输入相应里程点的高程。
4. 使用公式进行计算
对于每个里程点,你可以使用以下公式来计算其高程:
(H = H_{0} + i \times d)
其中:
•(H) 是当前里程点的高程。
•(H_{0}) 是前一个里程点的高程。
•(i) 是纵坡的坡度(单位为米/米或米/公里)。
•(d) 是当前里程与前一个里程之间的水平距离。
你可以在每个里程点的高程单元格中输入这个公式,并使用拖放功能将公式应用到其他里程点。
5. 保存和分享表格
完成计算后,保存你的Excel表格。
你可以将这个表格分享给其他人,或者将其导入到其他软件中进行进一步的分析和可视化。
示例:
假设你有以下里程和对应的高程数据:
你可以在里程为1和2的单元格中使用上述公式来计算对应的高程。
然后,使用拖放功能将这个公式应用到其他里程点。
道路曲线计算公式

高速公路线路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式时间:2009-12-27 21:40:34 来源:本站作者:未知我要投稿我要收藏投稿指南高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z,y Z为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z,y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:S Z④变坡点高程:H Z⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x<0时sgn(x)=-1,当x>0时sgn(x)=1,当x=0时sgn(x)=0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高等级道路竖曲线的精确计算方法
孙银聪
【摘要】本文从竖曲线的严密计算公式入手,推导竖曲线上点的设计高程和里程的精确计算方法。
分析和比较了近似公式和严密公式的差别及对设计高程和里程的影响。
在道路勘测设计中用本方法可取得精确、方便、迅速的效果,建议取代传统的近似方法。
一、引言
在传统的道路纵断面设计中,竖曲线元素及对应桩号里程和设计高程均采用近似公式计算,在低等级道路及计算工具很落后的时代曾起到过很大的作用。
但是随着高级道路的快速发展,道路竖曲线半径的不断加大,设计和施工的精度要求越来越高,因此,对勘测设计工作提出了很高的要求。
采用近似的方法进行勘测设计已难以满足高精度、高效灵活的要求。
为此本文给出了实用、精确的竖曲线计算公式,以解决实际工作中存在的问题。
二、计算原理
1. 近似计算公式
如图1所示,设道路纵坡的变坡点为I,其设计高程为H
I ,里程为D
I
,
两侧的纵坡度分别为i
1、i
2
,竖曲线设计半径为R,竖曲线各元素的近似
计算公式如下:
图 1
2. 精确计算公式
如图2所示,在图中建立以水平距离为横坐标轴d,铅垂线为纵坐标
轴H′的dOH′直角坐标系,A点的坐标为(d
A ,0),Z点的坐标为(0,H
Z
′),
竖曲线各元素的精确计算公式如下:
α
1=arctani
1
(1)
α
2=arctani
2
(2)
ω=α
1-α
2
(3)
T=Rtan(4) E=R(sec-1) (5)
d I =Tcosα
1
(6)
d A =Rsinα
1
(7)
H Z ′=Rcosα
1
(8)
竖曲线在直角坐标系中的方程为:(d-d
A
)2+H′2=R2 (9)
图 2
由式(9)可推算出竖曲线上任一与Z点的里程差为d的点的纵坐标值H′,则
0≤d≤d
Y (10)
并可立即推算点的设计高程和里程:
H=H′-ΔH
(11)
D=D
Z +d (D
Z
=D
I
-d
I
)
(12)
式中,α
1,α
2
分别为纵坡线与水平线的夹角;ω为变坡角;Τ为
切线长;Ε为外矢距;d
I 为纵坡变坡点I与Z点的里程差;d
A
为竖圆曲
线圆心A与Z点的里程差;H′为竖圆曲线上任一点的纵坐标值;d为竖圆曲线上任一点与Z点的里程差;H为竖圆曲线上任一点的设计高程;ΔH=H′Z-H Z为Z点纵坐标值与Z点设计高程之差(H Z=H I-d I.i1);D为竖曲线上任一点的里程。
由式(10)可知,当d=d
A 时,则里程D
N
=D
Z
+d
A
的N点为竖圆曲线的变
坡点,其高程H
N =H
N
′-ΔH=R-ΔH=max,N点在现场施工中具有很重要
的指导意义。
三、计算实例
某山岭重丘的二级公路的纵坡变坡点I,其设计高程H
I
=68.410 m,
里程D
I
=6+710.280,两侧纵坡分别为7%和-5%,凸形竖曲线的设计半径R=3 500 m,其计算结果见表1。
表1
四、结论
采用传统的近似计算公式推算竖圆曲线上点的设计高程和里程,存在着一定的误差,并且随着道路纵坡的增大而增大。
特别对于大纵坡又有超高横坡的外边线的竖曲线(有超高的外边线纵坡比中线纵坡更大)以及风景区和校区、别墅区等的竖曲线(纵坡常在10%左右),若用近似方法计算,误差更大,而且没有勘测设计竖圆曲线的变坡点N,直接影响路面施工精度和质量。
而采用本文介绍的方法计算,计算公式精确严密,不受坡度和半径大小的影响,方便迅速,又可计算和测设具有重要作用的竖曲线变坡点N。
采用本方法具有较高的应用价值和施工实际指导意义。
