圆度误差分离的三点法及其演化形式与精度分析
求圆度的方法

求圆度的方法在几何学中,圆度是指一个物体与其最佳圆形形状之间的偏差程度。
对于工程和制造领域来说,圆度的控制是非常重要的,因为它直接影响到产品的质量和性能。
本文将介绍一些常用的方法和技术,用于求取物体的圆度。
1. 三点法三点法是一种常见的求取圆度的方法。
该方法通过在物体的表面上选择三个点,并测量它们与物体中心的距离来计算圆度。
通过多次测量不同位置的三个点,可以得到整个物体的圆度信息。
然后,可以将这些测量值进行统计分析,得出物体的圆度指标。
2. 二维投影法二维投影法是一种通过将物体投影到平面上来求取圆度的方法。
首先,将物体放置在一个平面上,然后使用光线或激光进行投影。
通过测量投影图形的直径和周长,可以计算出物体的圆度。
这种方法适用于较大的物体或无法直接测量的物体。
3. 三维扫描法三维扫描法是一种先进的求取圆度的方法。
该方法使用激光或光学传感器对物体进行高精度的扫描,并生成物体的三维模型。
通过分析三维模型中的数据,可以得出物体的圆度。
这种方法可以应用于各种复杂形状的物体,并且具有较高的精度和准确性。
4. 数学拟合法数学拟合法是一种通过数学模型来求取圆度的方法。
该方法基于最小二乘法,将测量点拟合到最佳圆形模型上。
通过计算残差和拟合误差,可以得出物体的圆度。
这种方法适用于各种测量点的分散性较大的情况。
5. 基于计算机视觉的方法基于计算机视觉的方法是一种使用图像处理和计算机算法来求取圆度的方法。
通过对物体的图像进行分析,可以提取出物体的轮廓,并计算出圆度。
这种方法可以自动化地进行圆度测量,并具有较高的效率和准确性。
在实际应用中,选择合适的求取圆度的方法取决于具体的需求和条件。
不同的方法有其优缺点,需要根据实际情况进行选择。
此外,还需要注意测量设备的精度和准确性,以及操作人员的技术水平,以保证圆度测量的可靠性和准确性。
求取圆度是一项重要的工作,对于产品的质量和性能有着直接的影响。
通过合适的方法和技术,可以准确地求取物体的圆度,并为工程和制造领域提供有效的质量控制手段。
圆度的范围

圆度的范围圆度是指一个圆形物体表面的平滑程度和几何形状的规整程度。
在工业制造和机械加工中,圆度是一个非常重要的指标,因为它直接影响到零件的质量和性能。
圆度的范围是指在实际生产中,圆度的允许误差范围。
下面将详细介绍圆度的范围及其影响因素。
一、圆度的定义和测量方法圆度是指一个圆形物体表面的平滑程度和几何形状的规整程度。
在工业制造和机械加工中,圆度是一个非常重要的指标,因为它直接影响到零件的质量和性能。
圆度的测量方法有很多种,其中比较常用的是三点法和两点法。
三点法是指用三个测量点来确定圆形物体的圆心和半径,从而计算出圆度误差。
两点法是指用两个测量点来确定圆形物体的直径,从而计算出圆度误差。
二、圆度的范围圆度的范围是指在实际生产中,圆度的允许误差范围。
不同的零件和工艺要求对圆度的要求不同,因此圆度的范围也有所不同。
下面将介绍一些常见的圆度范围。
1. 一般圆度范围一般情况下,圆度的允许误差范围为0.01mm~0.05mm。
这个范围适用于一些一般的机械零件,如轴承、齿轮、轴等。
在这个范围内,圆度误差对零件的性能影响较小,可以满足一般的使用要求。
2. 高精度圆度范围对于一些高精度的零件,如精密机床、光学仪器等,圆度的允许误差范围要求更高,一般为0.001mm~0.005mm。
在这个范围内,圆度误差对零件的性能影响较大,需要采用更加精密的加工工艺和测量方法来保证圆度的精度。
3. 超高精度圆度范围对于一些超高精度的零件,如半导体芯片、光学元件等,圆度的允许误差范围更加严格,一般为0.0001mm~0.001mm。
在这个范围内,圆度误差对零件的性能影响非常大,需要采用最先进的加工工艺和测量方法来保证圆度的精度。
三、影响圆度的因素圆度的精度受到很多因素的影响,下面将介绍一些常见的影响因素。
1. 加工工艺加工工艺是影响圆度精度的最重要因素之一。
加工工艺的不同会导致零件表面的粗糙度、形状和尺寸等方面的差异,从而影响圆度的精度。
常用高精度测量仪测量圆度误差分析

常用高精度测量仪测量圆度误差分析高精度测量仪器在现代制造业中是不可或缺的。
其中,测量圆度误差是一个重要的指标。
圆度误差是指一个物体表面的离心偏差,即物体表面所表示的半径与物体中心不同的情况。
测量圆度误差的时候,我们通常采取高精度测量仪,如千分尺、三坐标测量仪等。
这些高精度测量仪可以帮助我们准确测量物体的圆度误差,从而在生产加工中避免问题的发生。
除了测量工具,我们还需要了解一些基本概念,例如如何定义圆度误差的范围和如何确定实际误差。
当我们确定了这些指标后,我们就可以开始实际的测量工作。
在测量圆度误差的时候,我们需要选取适合的测量点,通常选用的有以下几种点位:1、两点万分仪测量点:该方法可以测量径向的圆度误差,同时也可以测量圆跳动的误差。
为了减小误差,我们通常需要到数个测量点,最终取其平均值作为最终结果。
2、三点坐标测量仪测量点:该方法能够测量周向圆度误差。
它不仅可以获得圆边缘坐标,还可以获得中心坐标。
通过三点坐标的测量结果,我们可以获得准确的圆度误差值。
3、有向圆形轮廓测量仪测量点:该方法适用于具有完整有向圆形的物体。
通过该仪器,可以获得物体圆度误差、垂直度误差、平行度误差等数据。
出现圆度误差的原因很多,常见的有机床误差、测量仪器误差、材料精度误差等。
在实际工作中,我们还需要注意一些测量误差的因素。
例如,在测量的过程中应考虑加工误差和材料变形误差,根据实际情况对这些误差进行校正。
此外,在测量时我们还需要考虑测量的恒定条件,如温度、湿度等,以确保数据的准确性和可重复性。
总的来说,高精度测量仪是现代制造业中必不可少的工具,测量圆度误差更是其中的重要指标。
通过测量圆度误差,我们可以准确地确定物体表面的离心偏差,为产业界提供精确的数据支持。
回转误差论文:回转误差圆度误差高速主轴误差分离仿真分析

回转误差论文:基于频域三点法的主轴回转误差测量方法与应用研究【中文摘要】精密测量技术是精密和超精密加工技术中的关键一环,也是精密和超精密加工技术中备受国内外重视的热点和难点。
特别是基于误差分离技术的形状误差和回转误差的测量和评定,一直是国内外研究的重点。
主轴回转精度的测量不可避免会混入被测件本身的形状误差,偏心误差以及随机性误差。
而对于高精度主轴回转精度的测量,混入的形状误差不能忽略,同时要去除偏心和减小随机误差的影响,因此主轴回转精度测量技术的研究焦点在于误差分离技术的研究。
本课题对频域三点法误差分离技术进行了研究,并进一步推导出了近似三点法。
鉴于频域三点法误差分离原理的复杂性,从提高算法运行速度和优化用户界面方面入手,通过Matlab和VC++联合编程,运用模块化程序设计思想,编写了主轴回转误差测量软件系统。
为确保频域三点法回转误差分离技术的可行性和准确性,对其进行了更加深入的研究。
首先根据误差信号各组成部分的几何特征,建立了一个模拟误差数据模型。
其次通过模拟误差数据运用Matlab对频域三点法进行仿真分析,分析结果验证了频域三点法的可行性。
再次探讨了频域三点法主轴回转误差分离技术的误差来源和抑制方法,并运用Matlab对主要误差来源进行仿真分析,在仿真分析的基础上,...【英文摘要】Precision measurement technology is a key ring of precision and ultra-precision processing technology, andalso the hot and difficult field of precision andultra-precision machining technology. Especially the measurement and evaluation of the form error and rotational error based on the error separation technique has been always the focus of the study at home and abroad. Spindle error measurement inevitably mixed with the form of the device, eccentric error and random error. For high-precision measurement ...【关键词】回转误差圆度误差高速主轴误差分离仿真分析【英文关键词】Spindle error Artifact form High speed spindle Error separation Simulation【目录】基于频域三点法的主轴回转误差测量方法与应用研究摘要4-5ABSTRACT5-6目录7-10CONTENTS10-13第一章绪论13-19 1.1 课题研究背景及意义13-14 1.2 国内外研究现状14-17 1.3 本课题的来源与主要研究内容17-19 1.3.1 课题的来源17 1.3.2 课题研究内容和目的17-19第二章频域三点法主轴回转误差分离技术19-28 2.1 主轴回转精度的定义及误差分离技术19-20 2.1.1 主轴回转精度的定义19-20 2.1.2 主轴回转误差分离技术20 2.2 频域三点法和近似三点法20-24 2.2.1 频域三点法圆度误差分离21-23 2.2.2 近似三点法23-24 2.3 主轴圆度误差及回转误差的评定方法24-27 2.3.1 主轴圆度误差的评定25-27 2.3.2 主轴回转误差的评定27 2.4 本章小结27-28第三章测量系统的软件设计28-34 3.1 测量系统的模块化设计28-30 3.1.1 测量系统的功能模块28 3.1.2 程序的处理流程28-30 3.2 测量系统的软件设计平台30 3.3 系统开放性接口30-31 3.4 测量软件界面及特点31-33 3.5 本章小结33-34第四章频域三点法误差分析34-56 4.1 数据采集及去噪34-41 4.1.1 集合平均35-37 4.1.2 数字滤波37-40 4.1.3 减直流分量40-41 4.2 频域三点法分离误差的理论分析41-43 4.2.1 频域三点法的谐波抑制及自动消偏41-42 4.2.2 频域三点法的灵敏度分析42-43 4.3 频域三点法分离精度影响因素的仿真分析43-55 4.3.1 三点法的频域分析43-50 4.3.2 定位误差及标准球精度量级对频域三点法分离精度的影响50-52 4.3.3 频域三点法与近似三点法的对比分析52-55 4.4 本章小结55-56第五章测量系统的硬件设计及实验研究56-71 5.1 测量系统的基本组成56 5.2 精密滚珠螺母机床主轴回转精度测量系统56-63 5.2.1 测量装置设计57-59 5.2.2 数据采集板59-60 5.2.3 精密电容位移传感器60-63 5.3 空气静压轴承主轴回转精度测量系统63-69 5.3.1 高速空气静压轴承主轴64-65 5.3.2 LMS数据采集装置65 5.3.3 电涡流微位移传感器65-66 5.3.4 增量式编码器66 5.3.5 实验结果66-69 5.4 本章小结69-71总结与展望71-73参考文献73-75攻读学位期间发表的论文75-77致谢77。
圆度测量
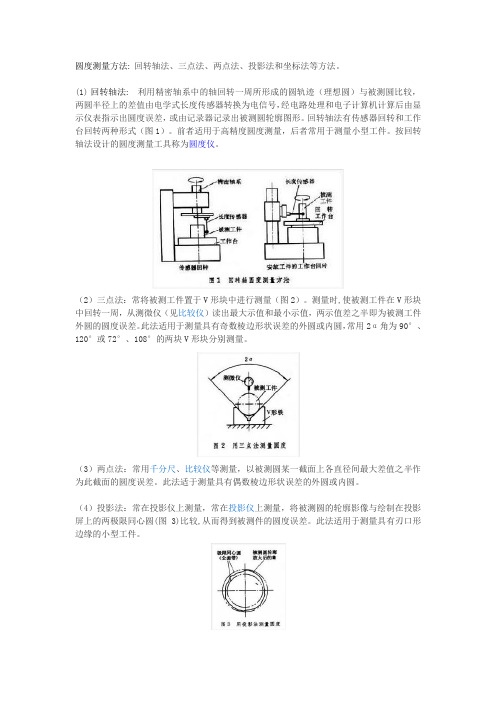
圆度测量方法: 回转轴法、三点法、两点法、投影法和坐标法等方法。
(1)回转轴法: 利用精密轴系中的轴回转一周所形成的圆轨迹(理想圆)与被测圆比较,两圆半径上的差值由电学式长度传感器转换为电信号,经电路处理和电子计算机计算后由显示仪表指示出圆度误差,或由记录器记录出被测圆轮廓图形。
回转轴法有传感器回转和工作台回转两种形式(图1)。
前者适用于高精度圆度测量,后者常用于测量小型工件。
按回转轴法设计的圆度测量工具称为圆度仪。
(2)三点法:常将被测工件置于V形块中进行测量(图2)。
测量时,使被测工件在V形块中回转一周,从测微仪(见比较仪)读出最大示值和最小示值,两示值差之半即为被测工件外圆的圆度误差。
此法适用于测量具有奇数棱边形状误差的外圆或内圆,常用2α角为90°、120°或72°、108°的两块V形块分别测量。
(3)两点法:常用千分尺、比较仪等测量,以被测圆某一截面上各直径间最大差值之半作为此截面的圆度误差。
此法适于测量具有偶数棱边形状误差的外圆或内圆。
(4)投影法:常在投影仪上测量,常在投影仪上测量,将被测圆的轮廓影像与绘制在投影屏上的两极限同心圆(图3)比较,从而得到被测件的圆度误差。
此法适用于测量具有刃口形边缘的小型工件。
(5)坐标法:一般在带有电子计算机的三坐标测量机上测量。
按预先选择的直角坐标系统测量出被测圆上若干点的坐标值x、y,通过电子计算机按所选择的圆度误差评定方法计算出被测圆的圆度误差。
圆度误差评定就是将双绞线导线横截面的实际轮廓与理想圆比较的过程。
圆度误差评定方法:①最小区域法:以包容被测圆轮廓的半径差为最小的两同心圆的半径差作为圆度误差。
②最小二乘圆法:以被测圆轮廓上相应各点至圆周距离的平方和为最小的圆的圆心为圆心,所作包容被测圆轮廓的两同心圆的半径差即为圆度误差。
③最小外接圆法:只适用于外圆。
以包容被测圆轮廓且半径为最小的外接圆圆心为圆心,所作包容被测圆轮廓的两同心圆半径差即为圆度误差。
确定圆度误差的方法两点三点法
故该零件合格
检测一无心磨磨削的零件 棱数为未知的奇数 且
给定的圆度公差 为
测
量方法选用
或
测得值 为
测量方法
测得值
圆度误差值的计算
由表 可查得非对称安置组合测量反映系数 当
时
或
的平均反映系数为
由
式可得该零件的圆度误差
与上例类似 就此例而言
如只需对零件进行合格与否的判断 则可直接用下式进行评定 零件合格 零件不合格
被测零件的棱数已知 直接在表 表 中选用反映系数 较大的测量装置 将被测零件置于 测量装置中匀速旋转一周 读取指示器的测得值 用相应的反映系数按下式计算出实际圆度误差值
式中
实际圆度误差值
测得值 即指示器最大读数差值
反映系数
被测零件的棱数未知 一次测量不能正确得出零件的圆度误差 应采用两点法和三点法进行组
外
孔类内表面测量的固定支承中心距
内
式中 如图
被测零件直径 球 或圆柱 支承的直径 固定测量支承夹角 所示
图
附录 两点 三点法应用示例
参考件
检测一棱数为 的圆柱孔 圆度公差 为
测量方法采用
测得值 为
圆度误差值的计算
由表 可直接查得反映系数 当
时
顶式测量的反映系数为
由
式可得该圆柱孔的圆度误差
如只需判断零件是否在给定的公差带范围内 而不必求出具体的圆度误差值时 则可直接 利用测得值 由下式进行评定
术语及定义 圆度误差的测量平面 过测头与工件接触点的一个假想平面 用两点 三点法测量时 假想平
面必须通过固定测量支承
注 测量圆度误差时 零件的被测截面为垂直于其轴线的假想平面 该平面应与测量平面重合
圆度误差的测量和评定(一)(精)

圆度误差的测量和评定(一)摘要:本文介绍、分析和比较了圆度误差的多种测量、评定方法,指出提高测量精度的关键技术是误差分离,评定误差的关键技术是由计算机完成测得数据由测量中心至评定中心的基准转换。
结合教学工作实践,给出了测量实例分析和探讨了一种计算机辅助误差评定的方法。
关键词:圆度误差关键技术基准转换1 引言圆度误差是指在回转体同一径向截面(即垂直于轴线的截面)内,被测实际圆对其理想圆的变动量,用被测实际轮廓对理想圆圆心的最大半径差表示。
测量和评定圆度误差有多种方法,以适应不同的测量对象和不同的精度要求。
本文拟结合教学工作实践,对圆度误差的测量和评定作相关探讨和分析。
2 圆度误差的测量2.1常用测量方法2.1.1 半径测量法用圆度仪测量圆度误差是一种常用的测量法。
图1是圆度仪的两种工作原理示意图。
a图转台式,测量头(带触头的传感器)静止,工件随工作台回转;b图转轴式,测量时工件不动,安装在主轴上的测量头随主轴回转。
仪器按两种方式输出结果:图形记录式或参数直接显示式。
在没有圆度仪或测量精度要求不高的情况下,可采用光学分度头(见图2)。
测量时,各测点位置由分度头等分转角决定,利用测微计得出各测点半径差,然后按比例绘制放大了的实际轮廓,再用某种评定方法求得结果。
当被检零件的批量大时,可用专用标准环测量(见图3)。
测量基准和评定基准均为标准环内径圆——相当于被测实际轮廓的最小外接圆,它与零件形成间隙接近于零的配合。
此外,也可在工具显微镜上用分度盘和灵敏杠杆测量,其原理与用光学分度头测量基本相同。
2.1.2 三点测量法对于圆度误差的一种特殊情况——等径多弧形的棱圆度(特别是奇数棱圆度),可用鞍形架、V形块、三脚内径规等装置进行近似测量(分别见图4a、b、c),这种方法因在两个固定支承和一个在测量方向上移动的测头之间进行,故称为三点测量。
2.1.3 二点测量法该法是在被测零件直径上对置的一个固定支承和一个可在测量方向上移动的测头之间所进行的测量。
3点法圆度误差分离技术的新算法

摘要 :通过对 3点法 圆度误差 分 离技术 的分析 和基 于被测 圆轮廓 几何 特征 不 变 并具有 周 期性
的特 点, 出 了一种 不 需要傅 立 叶变换 、 提 可直接 求解被 测 圆轮廓 圆度误 差 的新算 法—— 矩 阵算 法。
LEIXin q n , LIYa 1 a - ig n ,ZHOU n— i L i h n ,X Ya we I — u 2 UE Y - n js uj 2 u
,
( .col f cai l nt met n ief g i nUn es yo eh o g ,X ’n7 0 4 ,S an i hn ; 1 Sho o hnc s u na E gne n ,X ’ i r t f cnl y ia 10 8 hax,C ia Me aI r l i a v i T o
b a so he smulto y me n ft i a i n. Ke y wor s:i f r t r c s i g t e niu d n o ma i p o e sn e h q e;t e - i tme h d;ma rx;e r r s p a in;r u — on hr e p n t o o ti ro a to e r o nd
并在 3点法 分 离出 的回转误差 运 动进行 分析和 研 究 的基 础 上, 导 出分 离被 测 圆轮 廓 最小 二 乘 圆 推 心 的偏 心运 动和 回转 轴纯 回转误 差运 动 的数 学公 式, 并通 过仿 真验证 了所提 出方 法 的正确性 。 关键 词 :信 息处 理技术 ; 3点法 ;矩 阵 ; 差分 离 ;圆度 ;偏 心运 动 误
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
口 0 =r 0 ( ) ( +a) ( )o + 0 cs
Y 0s  ̄ { )i n
(1 2
图 1 三点 法 圈 2 两点 法 3 匹 洼
G 0 =r 0 ( ) l +a+ + O es + Y ) n + ) ( ) f ) f s f ) ( 1 o 0i n 3
对 ( ) 进行 D T 得 5式 F, S n = ( ) 1 ( ) n 旷(. 7 J
个 传感 器 D 就变 Z了日 法
B 0 =r0 ( ) ( +a + 0cs ) ( )o  ̄+1 日 【n l ¨ 1 C ) ( +a+口 + ( 【s + f =r0 0 ) 圳 =( 0
:
:
【 摘要】 论述 了圆度误差分离的三点法厦其演化形式一二点击和 四点法的基拳原理 , 并对它 : : 各
: :
.
自特点 和测 量精 度进行 了分析 、 讨论 。指 出应针 对具体 情 况选择 适 当的 圆度 误差 分 离方 法。 关 键词 : 差分离 ; 度测 量 ; 误 圆 三点 法 ; 二点 法 ; 四点 法 ; 精度分 析
2 2 四点法 ( 3 . 图 )
在三点法的基础上 , 再增加 四个传感器的输出方程如下 (1 5
(1 6 Leabharlann ^ ) ( ) f J f =r 0 + 0 0 f3 ll
圆周均布 的采样点数 将{ ) 离散化 , 4式 得 S^ f =r f r )+ f P + r +p q ) f )
术手 段 之 一,三 十 多 年来 .国 内外 学 者 不 断地 对 此 加 以研 究 和
. 图 ) 应用。其 中三点法圆度误差分离技术是最早应用 、也是 目前最 2 1 两 点 法 ( 2 在三 法 中 . 安装 角 =r 2 即 P= . , . A0 取 " 、 r / 4 口= 2一 为成熟 的误差分离方法 。后来发展 的二点法 、四点 法实质上可
维普资讯
一
5 4
《 械 设 计与 毹 造 》 A 2 0 N Nahnr Ds n & M n fc r 机 02 o2 cie ei y g a uat e u
文章 编 号 :0 1—3 9 0 2 0 0 5 0 10 9 7l 0 )2— 0 4 1 2
i点洼就演化成了二点近似法 . 如图1 所示 , 三个传感器 A B、 、 c分别安装在工件圆周的不 忽略不计 。这样,
取工件轮廓曲线的最小二乘心 0 为极心, 极角 0 =
旺工件圆
度误差 为 , 日 , f J 主轴回转误差在 X、 y方向上的分量分别为 l 0 0 和 Y 0。于是各传感器的输 出 f J 口 ) c 鲫分别为: () 、( 和 ( 0
1l ll
式中
s ( + /j i ) n n
=s c s 廖 s 称组台信号。 iei n /n (
g=L 2r N/  ̄}
记 =(1/N ^ 2r )
l = ,, 0 1 … 一1 )
『2 l1
P q为 整 数 , P=l 2r 、 且 N/ 1)
由 ()() 4 、5 两式 可 得 两 法 误差 分离 近 似方 群 为
S( =_ 0 +r 0 — ) 【 l f + A
离散形式为 : ( =r +, + / ) ( 1 l 2一¨ 由式 () 7可以得到近似后的圆度误差的频域表示 ;
R( ) sf ) ( n = / n R J
/ f = 1 , / 以看作是 三点法 的演化 。对 三点法及 其演化 形式加 以分析讨 即 =N 4—1采 样 间 隔 A 27 l 当 Ⅳ较 大时 , 很 小 时 口 A目 此 ≈百 2加 权 系数 曲 摸 分 别为 ,. 论 ,研究它们之 间的联系和各 自特点 .以期能够为选择圆度误
圆度误差分 离的三点法及其演化形式与精度分析
韩 正 铜 洪 迈 生
( 中国矿业 大学 , 徐州 2 10 ) ( 海交通 大学 , 上海 2 0 3 208 上 0 0 0 J
● … Lc● t … … … … … … … … … … ● … … 。… … … … … … … … … … … … … … … … … ¨. … ● ● … … ● ● ● ● ● ● ● ●
对 ( 1 3 式分别乘 以不等权系数 1 1 一r ) 、 和 , 然后相加 消 去 r 和 ( ) 0 得到三点法 圆度误差分离 的基本方程 J
5 0 A{ + B( + c 0 {) ) ) ( ) =r ( + r 0+ ) 0+ +口 ( +^ ( 1 f1 4
+ f snf口 + i
f4 ll
式 中 ( 弥为权函数 , )
差分离方法提供一些参考性的帮助。
l l s ( ) s C = i a+ / i 3 n n  ̄0
l l s sn l j na I 8
l 三点法误差分离原理
同位置 ( 安装角分别为 、 , )三传感器 的轴线 交于坐标原点 0 。
这 意味着传感器 口的输 出在组台信号 中占的比重很小 ,I 一以 _
文献标 识码 : B
: … 一 … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … ,. , … … … … … … … … … …
中 图分 类号 : H1 3 T 2
误 分 技 E ) 成 精 测 和 偿 工 重 技 2 三点法的演化形式 差 离 术(T已 为 密 量 补 加 的 要 S
