19.2特殊的平行四边形同步测试题

合集下载

第一章特殊平行四边形检测题

第一早《特殊平仃四边形》检测题一、选择题（每小题3分，共27分）1.从菱形的钝角顶点向对角的两条边作垂线，垂足恰好是该边的中点，贝U 菱形的内角中钝角的度数是（2.顺次连接一个四边形的各边中点，得到了一个矩形，则下列四边形中满足条件的是: ①平行四边形：②菱形;③矩形；④对角线互相垂直的四边形.（）3.已知一矩形的两边长分别为10 cm 和15 cm,其中一个内角的平分线分长边为两部分, 这两部分的长为（）则图中阴影部分的面积为（7.矩形、菱形、正方形都具有的性质是（A.每一条对角线平分一组对角B.对角线相等 8.如图，将一个长为iO 口口，宽为S cm 的矩形纸片先按照从左向右对折，再按照从下向上的方向对折两次后，沿所得矩形两邻边中点的连线（虚线）剪下（如图（ 1））,再打开，得到如图（2）所示的小菱形的面积为（ B. 20 C 宦 C. 4" cni" A.150 ° B. 135C. 120 °D. 100 ° A.①③B.②③C.③④D.②④A.6 cm 和 9 cmB. 5 cm 和 10 cmC. 4 cm 和 11 cmD. 7 cm 和 8 cm 4.如图，在矩形A 肚D 中，匚几 G H 分别为边AS. DA. CD •,班的中点.若45 = 2=4 , A.3 C.6 5.如图，在菱形磁D 中，= = 3，则对角线」〔等于（） A.20 B.15 C.10 D.56.若正方形的对角线长为2 cm ，则这个正方形的面积为（B.2 口口卫C.住 cm-D.C. 对角线互相平分D. 对角线互相垂直 D. 30 cini"C CDD.8第5题图9.如图是一张矩形纸片A5CD = IDcm ,若将纸片沿折叠，使必落在血上，点C的对应点为点F ,若却£ =临n 口，则CD =、填空题（每小题4分，共32 分）10.已知菱形的边长为6, —个内角为60°则菱形的较短对角线的长是11•如图，在菱形ABCD 中，/ 60°点E , F 分别从点B , D 同时以同样的速度沿边 BC , DC 向点C 运动.给出以下四个结论:①肛=AF ;② /闊F = /CF£;③ 当点E , F 分别为边BC , DC 的中点时，△ AEF 是等边三角形;④ 当点E , F 分别为边BC , DC 的中点时，△ AEF 的面积最大.上述正确结论的序号有13.如图，矩形屈™的两条对角线交于点。

特殊的平行四边形试题及参考答案

第一章特殊平行四边形检测题一、选择题（每小题3分，共30分）1.下列四边形中，对角线一定不相等的是（D ）A.正方形B.矩形C.等腰梯形D.直角梯形3.顺次连接一个四边形的各边中点，得到了一个矩形，则下列四边形中满足条件的是（D ） ①平行四边形;②菱形;③等腰梯形;④对角线互相垂直的四边形.A.①③B.②③C.③④D.②④4.已知一矩形的两边长分别为10 cm 和15 cm ，其中一个内角的平分线分长边为两部分，这两部分的长为（B ）A.6 cm 和9 cmB.5 cm 和10 cmC.4 cm 和11 cmD.7 cm 和8 cm5.如图，在矩形中，分别为边的中点.若，，则图中阴影部分的面积为（B ）A .3B .4C .6D.86.如图，在菱形中，，∠，则对角线等于（D ）A .20B .15C .10D .57.若正方形的对角线长为2 cm ，则这个正方形的面积为（B ）A.4B .2C .D .8.矩形、菱形、正方形都具有的性质是（ C ）A .每一条对角线平分一组对角B .对角线相等C .对角线互相平分D .对角线互相垂直A. B . C . D .（1）（2）一、填空题（每小题3分，共24分）11.已知菱形的边长为6，一个内角为60°，则菱形的较短对角线的长是___6______.13.如图，四边形ABCD 是正方形，延长AB 到点E ，使，则∠BCE 的度数是22.5°.14.如图，矩形的两条对角线交于点，过点作的垂线，分别交，于点，，连接，已知△的周长为24 cm ，则矩形的周长是48cm.15.已知，在四边形ABCD 中，90A B C ∠=∠=∠=︒，若添加一个条件即可判定该四边形是正方形，那么这个条件可以是____________. 16.已知菱形的周长为，一条对角线长为，则这个菱形的面积为____96_____.17.如图，在矩形ABCD 中，对角线与相交于点O ，且，则BD 的长为____4____cm ，BC 的长为_______cm.三、解答题（共66分）19.（8分）如图，在△ABC 中，AB =AC ，AD 是△ABC 外角的平分线，已知∠BAC =∠ACD .（1）求证：△ABC ≌△CDA ；（2）若∠B =60°，求证：四边形ABCD 是菱形.证明：（1）∵AB =AC ，∴∠B =∠ACB ，∴∠FAC =∠B +∠ACB =2∠BCA .第5题图第6题图∵AD平分∠FAC，∴∠FAC=2∠CAD，∴∠CAD=∠ACB.在△ABC和△CDA中，∠BAC＝∠DCA，AC＝AC，∠DAC＝∠ACB，∴△ABC≌△CDA.（2）∵∠FAC=2∠ACB，∠FAC=2∠DAC，∴∠DAC=∠ACB，∴AD∥BC.∵∠BAC=∠ACD，∴AB∥CD，∴四边形ABCD是平行四边形.∵∠B=60°，AB=AC，∴△ABC是等边三角形，∴AB=BC，∴平行四边形ABCD是菱形.20.（8分）如图，在□ABCD中，E为BC边上的一点，连接AE、BD且AE=AB.（1）求证：∠ABE=∠EAD；（2）若∠AEB=2∠ADB，求证：四边形ABCD是菱形.证明：（1）在□ABCD中，AD∥BC，∴∠AEB=∠EAD.∵AE=AB，∴∠ABE=∠AEB，∴∠ABE=∠EAD.（2）∵AD∥BC，∴∠ADB=∠DBE.∵∠ABE=∠AEB，∠AEB=2∠ADB，∴∠ABE=2∠ADB，∴∠ABD=∠ABE-∠DBE=2∠ADB-∠ADB=∠ADB，∴AB=AD.又∵四边形ABCD是平行四边形，∴四边形ABCD是菱形.22.（8分）如图，正方形ABCD的边长为3，E，F分别是AB，BC边上的点，且∠EDF=45°.将△DAE 绕点D逆时针旋转90°，得到△DCM.（1）求证：EF=FM；（2）当AE=1时，求EF的长.（1）证明：∵△DAE逆时针旋转90°得到△DCM，∴∠FCM=∠FCD+∠DCM=180°，∴F，C，M三点共线，DE=DM，∠EDM=90°，∴∠EDF+∠FDM=90°.∵∠EDF=45°，∴∠FDM=∠EDF=45°.在△DEF和△DMF中，DE=DM，∠EDF=∠MDF，DF=DF，∴△DEF≌△DMF（SAS），∴EF=MF.（2）解：设EF=MF=x，∵AE=CM=1，且BC=3，∴BM=BC+CM=3+1=4，∴BF=BM－MF=BM－EF=4－x.∵EB=AB－AE=3－1=2，在Rt△EBF中，由勾股定理得EB2+BF2=EF2，即22+（4－x）2=x2，解得：x=，即EF=.23.（8分）如图，在矩形中，相交于点，平分，交于点.若，求∠的度数.解：因为平分，所以.又知，所以因为，所以△为等边三角形，所以因为，所以△为等腰直角三角形，所以．所以，，所以=75°24.（8分）如图所示，在矩形ABCD中，E，F分别是边AB，CD上的点，AE＝CF，连接EF，BF，EF与对角线AC交于点O，且BE＝BF，∠BEF＝2∠BAC.（1）求证：OE＝OF；（2）若BC＝23，求AB的长.25.(8分)已知：如图，在四边形中，∥，平分∠，，为的中点.试说明：互相垂直平分.解：如图，连接∵AB⊥AC，∴∠BAC=90°.因为在Rt△中，是的中点，所以是R t△的斜边BC上的中线，所以，所以．因为平分，所以，所以所以∥.又AD∥BC，所以四边形是平行四边形．又，所以平行四边形是菱形，所以互相垂直平分．。

(人教版)八年级数学下册19.2特殊的平行四边形含答案

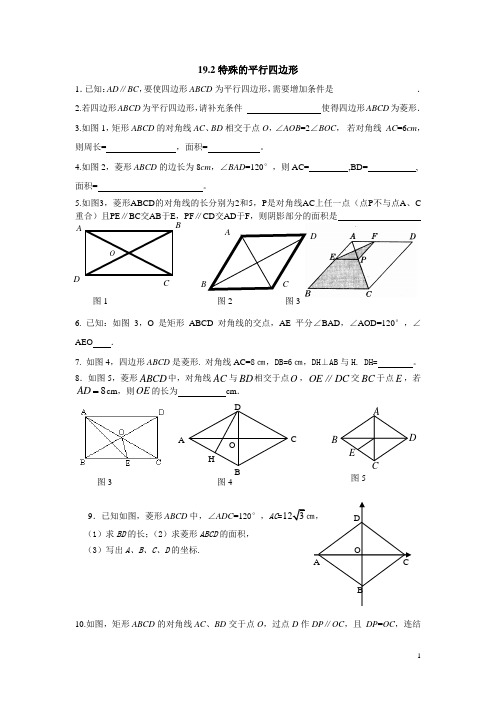
19.2特殊的平行四边形1．已知：AD ∥BC ，要使四边形ABCD 为平行四边形，需要增加条件是___________________． 2.若四边形ABCD 为平行四边形，请补充条件使得四边形ABCD 为菱形． 3.如图1，矩形ABCD 的对角线AC 、BD 相交于点O ，∠AOB =2∠BOC ，若对角线 AC =6cm ，则周长= ，面积= 。

4.如图2，菱形ABCD 的边长为8cm ，∠BAD =120°，则AC= ,BD= , 面积= 。

5.如图3，菱形ABCD 的对角线的长分别为2和5，P 是对角线AC 上任一点（点P 不与点A 、C重合）且PE ∥BC 交AB 于E ，PF ∥CD 交AD 于F ，则阴影部分的面积是图1 图2 图36. 已知：如图3，O 是矩形ABCD 对角线的交点，AE 平分∠BAD ，∠AOD=120°，∠AEO ．7. 如图4，四边形ABCD 是菱形. 对角线AC=8㎝，DB=6㎝，DH ⊥AB 与H. DH= 。

8．如图5，菱形ABCD 中，对角线AC 与BD 相交于点O ，OE DC ∥交BC 于点E ，若8AD cm ，则OE 的长为 cm ．图3 图49．已知如图，菱形ABCD 中，∠ADC =120°，AC =123㎝，（1）求BD 的长；（2）求菱形ABCD 的面积，（3）写出A 、B 、C 、D 的坐标.10.如图，矩形ABCD 的对角线AC 、BD 交于点O ，过点D 作DP ∥OC ，且 DP =OC ，连结B A DCOA BCDABDCOH图5ABDCEABCODCP ，试判断四边形CODP 的形状．并证明。

如果题目中的矩形变为菱形(图一)，结论应变为什么？如果题目中的矩形变为正方形(图二)，结论又应变为什么？10.以△ABC 的边AB 、AC 为边作等边△ABD 和等边△ ACE ，四边形ADFE 是平行四边形．① 当∠BAC 等于时，四边形ADFE 是矩形；② 当∠BAC 等于时，平行四边形ADFE 不存在；③ 当△ABC 分别满足什么条件时，平行四边形ADFE 是菱形、正方形．11.如图1：正方形ABCD 的对角线AC 、BD 相交于点O ，E 是AC 上的一点，连接EB ，过点A 作AM ⊥BE ，垂足M ，AM 交BD 于点F ． ①求证OE =OF ；②如图2所示，若点E 在AC 的延长线上，AM ⊥EB 的延长线于点M ，交DB 的延长线于AODPB CPCDOBA图二B CAEF DA BD C OP 图一点F ，其他条件都不变，则结论“OE=OF”还成立吗？如果成立，请给出证明；如果不成立，请说明理由ABC D O F EM图1ABC DFEM O图2。

数学八年级下人教新课标19.2特殊的平行四边形同步测试题测试题

数学：19.2特殊的平行四边形同步测试题（人教新课标八年级下）一、填空题（每题3分，共30分）1.用一把刻度尺来判定一个零件是矩形的方法是.2．如果边长分别为4cm和5cm的矩形与一个正方形的面积相等，那么这个正方形的边长为______cm．3．（08贵阳市）如图，正方形ABCD的边长为4cm，则图中阴影部分的面积为 cm2．4．如图1，DE∥BC，DF∥AC，EF∥AB，图中共有_______个平行四边形．5若四边形ABCD是平行四边形，请补充条件(写一个即可)，使四边形ABCD是菱形．6．，在平行四边形ABCD中，已知对角线AC和BD相交于点O，△ABO的周长为17，AB＝6，那么对角线AC＋BD＝⒎以正方形ABCD的边BC 为边做等边△BCE，则∠AED的度数为.8．延长正方形ABCD的边AB到E，使BE＝AC，则∠E＝°9．已知菱形ABCD的边长为6，∠A＝60°，如果点P是菱形内一点，且PB＝PD ＝2那么AP的长为．10．在平面直角坐标系中，点A、B、C的坐标分别是A(－2，5)，B(－3，－1)，C(1，－1)，在第一象限内找一点D，使四边形ABCD是平行四边形，那么点D的坐标是．二、选择题（每题3分，共30分）11．如图4在平行四边形ABCD中，∠B=110°，延长AD至F，延长CD至E，连结EF，则∠E＋∠F＝( )A ．110°B ．30°C ．50°D ．70°12．菱形具有而矩形不具有的性质是 ( ) A ．对角相等 B ．四边相等 C ．对角线互相平分 D ．四角相等13．平行四边形ABCD 中，对角线AC 、BD 交于点O ，点E 是BC 的中点．若OE=3 cm ，则AB 的长为 ( ) A ．3 cm B ．6 cm C ．9 cm D ．12 cm14．已知：如图，在矩形ABCD 中，E 、F 、G 、H 分别为边 AB 、BC 、CD 、DA 的中点．若AB ＝2，AD ＝4，则图中阴影部分的面积为 ( ) A ．8 B ．6 C ．4 D ．315．将两块能完全重合的两张等腰直角三角形纸片拼成下列图形：①平行四边形（不包括菱形、矩形、正方形）②矩形③正方形④等边三角形⑤等腰直角三角形 ( ) A ．①③⑤ B ．②③⑤ C ．①②③ D ．①③④⑤16．如图是一块电脑主板的示意图，每一转角处都是直角，数据如图所示(单位：mm)，则该主板的周长是 ( )A ．88 mmB ．96 mmC ．80 mmD ．84 mm（6）E A DC B H G17、（08甘肃省白银市）如图，把矩形ABCD 沿EF对折后使两部分重合，若150∠=，则AEF ∠=（）A ．110°B ．115°C ．120°D ．130°18、（08哈尔滨市）某商店出售下列四种形状的地砖：①正三角形；②正方形；③正五边形；④正六边形。

北师大版数学九年级上册《特殊的平行四边形》单元测试卷(含答案)

《特殊的平行四边形》单元测试卷一．选择题（每小题3分，满分36分）1．下列说法正确的是（）A．有两边和一角分别相等的两个三角形全等B．有一组对边平行，且对角线相等的四边形是矩形C．如果一个角的补角等于它本身，那么这个角等于45°D．点到直线的距离就是该点到该直线的垂线段的长度2．下列说法中不正确的是（）A．四边相等的四边形是菱形B．对角线垂直的平行四边形是菱形C．菱形的对角线互相垂直且相等D．菱形的邻边相等3．如图，菱形ABCD周长为20，对角线AC、BD相交于点O，E是CD的中点，则OE的长是（）A．2.5B．3C．4D．54．如图，在正方形ABCD的外侧，作等边△ABE，则∠BED为（）A．15°B．35°C．45°D．55°5．如图，在矩形ABCD中，AB＝6，BC＝8，过对角线交点O作EF⊥AC交AD于点E，交BC 于点F，则DE的长是（）A．1B．C．2D．6．如图，正方形ABCD中，点E、F分别在边CD，AD上，BE与CF交于点G．若BC＝4，DE ＝AF＝1，则GF的长为（）A．B．C．D．7．一个菱形的边长为6，面积为28，则该菱形的两条对角线的长度之和为（）A．8B．12C．16D．328．把边长分别为1和2的两个正方形按如图的方式放置．则图中阴影部分的面积为（）A．B．C．D．9．如图，在平面直角坐标系中，四边形OABC为菱形，O（0，0），A（4，0），∠AOC＝60°，则对角线交点E的坐标为（）A．（2，）B．（，2）C．（，3）D．（3，）10．如图，在矩形ABCD中，AD＝6，对角线AC与BD交于点O，AE⊥BD，垂足为点E，且AE 平分∠BAO，则AB的长为（）A．3B．4C．D．11．如图，在菱形ABCD中，AB＝5，对角线AC与BD相交于点O，且AC：BD＝3：4，AE⊥CD 于点E，则AE的长是（）A．4B．C．5D．12．如图，在正方形ABCD中，点E，F分别在BC，CD上，AE＝AF，AC与EF相交于点G．下列结论：①AC垂直平分EF；②BE+DF＝EF；③当∠DAF＝15°时，△AEF为等边三角形；④当∠EAF＝60°时，S△ABE ＝S△CEF．其中正确的是（）A．①③B．②④C．①③④D．②③④二．填空题（每小题3分，满分12分）13．如图，矩形ABCD中，AC、BD交于点O，M、N分别为BC、OC的中点．若MN＝4，则AC 的长为．14．如图，已知菱形ABCD的对角线AC，BD交于点O，E为BC的中点，若OE＝3，则菱形的周长为．15．如图，E，F是正方形ABCD的对角线AC上的两点，AC＝8，AE＝CF＝2，则四边形BEDF 的周长是．16．如图，矩形OABC的顶点A，C分别在坐标轴上，B（8，7），D（5，0），点P是边AB或边BC上的一点，连接OP，DP，当△ODP为等腰三角形时，点P的坐标为．三．解答题（17题—20题，每题7分，21题—23题，每题8分，满分52分）17．如图，四边形ABCD中，对角线AC、BD相交于点O，AO＝OC，BO＝OD，且∠AOB＝2∠OAD．（1）求证：四边形ABCD是矩形；（2）若∠AOB：∠ODC＝4：3，求∠ADO的度数．18．如图，在矩形ABCD中，E，F分别是BC，AD边上的点，且AE＝CF．（1）求证：△ABE≌△CDF；（2）当AC⊥EF时，四边形AECF是菱形吗？请说明理由．19．如图，在矩形ABCD中，AB＝3，BC＝4．M、N在对角线AC上，且AM＝CN，E、F分别是AD、BC的中点．（1）求证：△ABM≌△CDN；（2）点G是对角线AC上的点，∠EGF＝90°，求AG的长．20．如图，矩形ABCD中，AB＝8，AD＝6，点O是对角线BD的中点，过点O的直线分别交AB、CD边于点E、F．（1）求证：四边形DEBF是平行四边形；（2）当DE＝DF时，求EF的长．21．如图，已知正方形ABCD的边长为1，正方形CEFG的面积为S1，点E在DC边上，点G在BC的延长线上，设以线段AD和DE为邻边的矩形的面积为S2，且S1＝S2．（1）求线段CE的长；（2）若点H为BC边的中点，连接HD，求证：HD＝HG．22．如图，矩形EFGH的顶点E，G分别在菱形ABCD的边AD，BC上，顶点F，H在菱形ABCD 的对角线BD上．（1）求证：BG＝DE；（2）若E为AD中点，FH＝2，求菱形ABCD的周长．23．如图，在正方形ABCD中，点E是BC的中点，连接DE，过点A作AG⊥ED交DE于点F，交CD于点G．（1）证明：△ADG≌△DCE；（2）连接BF，证明：AB＝FB．参考答案一．选择题（共12小题）1．下列说法正确的是（）A．有两边和一角分别相等的两个三角形全等B．有一组对边平行，且对角线相等的四边形是矩形C．如果一个角的补角等于它本身，那么这个角等于45°D．点到直线的距离就是该点到该直线的垂线段的长度【解答】解：A．有两边和一角分别相等的两个三角形全等；不正确；B．有一组对边平行，且对角线相等的四边形是矩形；不正确；C．如果一个角的补角等于它本身，那么这个角等于45°；不正确；D．点到直线的距离就是该点到该直线的垂线段的长度；正确；故选：D．2．下列说法中不正确的是（）A．四边相等的四边形是菱形B．对角线垂直的平行四边形是菱形C．菱形的对角线互相垂直且相等D．菱形的邻边相等【解答】解：A．四边相等的四边形是菱形；正确；B．对角线垂直的平行四边形是菱形；正确；C．菱形的对角线互相垂直且相等；不正确；D．菱形的邻边相等；正确；故选：C．3．如图，菱形ABCD周长为20，对角线AC、BD相交于点O，E是CD的中点，则OE的长是（）A．2.5B．3C．4D．5【解答】解：∵四边形ABCD为菱形，∴CD＝BC＝＝5，且O为BD的中点，∵E为CD的中点，∴OE为△BCD的中位线，∴OE＝CB＝2.5，故选：A．4．如图，在正方形ABCD的外侧，作等边△ABE，则∠BED为（）A．15°B．35°C．45°D．55°【解答】解：在正方形ABCD中，AB＝AD，∠BAD＝90°，在等边△ABE中，AB＝AE，∠BAE＝∠AEB＝60°，在△AD E中，AD＝AE，∠DAE＝∠BAD+∠BAE＝90°+60°＝150°，所以，∠AED＝（180°﹣150°）＝15°，所以∠BED＝∠AEB﹣∠AED＝60°﹣15°＝45°．故选：C．5．如图，在矩形ABCD中，AB＝6，BC＝8，过对角线交点O作EF⊥AC交AD于点E，交BC 于点F，则DE的长是（）A．1B．C．2D．【解答】解：连接CE，如图所示：∵四边形ABCD是矩形，∴∠ADC＝90°，CD＝AB＝6，AD＝BC＝8，OA＝OC，∵EF⊥AC，∴AE＝CE，设DE＝x，则CE＝AE＝8﹣x，在Rt△CDE中，由勾股定理得：x2+62＝（8﹣x）2，解得：x＝，即DE＝；故选：B．6．如图，正方形ABCD中，点E、F分别在边CD，AD上，BE与CF交于点G．若BC＝4，DE ＝AF＝1，则GF的长为（）A．B．C．D．【解答】解：正方形ABCD中，∵BC＝4，∴BC＝CD＝AD＝4，∠BCE＝∠CDF＝90°，∵AF＝DE＝1，∴DF＝CE＝3，∴BE＝CF＝5，在△BCE和△CDF中，，∴△BCE≌△CDF（SAS），∴∠CBE＝∠DCF，∵∠CBE+∠CEB＝∠ECG+∠CEB＝90°＝∠CGE，cos∠CBE＝cos∠ECG＝，∴，CG＝，∴GF＝CF﹣CG＝5﹣＝，故选：A．7．一个菱形的边长为6，面积为28，则该菱形的两条对角线的长度之和为（）A．8B．12C．16D．32【解答】解：如图所示：∵四边形ABCD是菱形，∴AO＝CO＝AC，DO＝BO＝BD，AC⊥BD，∵面积为28，∴AC•BD＝2OD•AO＝28①∵菱形的边长为6，∴OD2+OA2＝36②，由①②两式可得：（OD+AO）2＝OD2+OA2+2OD•AO＝36+28＝64．∴OD+AO＝8，∴2（OD+AO）＝16，即该菱形的两条对角线的长度之和为16．故选：C．8．把边长分别为1和2的两个正方形按如图的方式放置．则图中阴影部分的面积为（）A．B．C．D．【解答】解：如图，设BC＝x，则CE＝1﹣x易证△ABC∽△FEC∴＝＝＝解得x＝＝××1＝∴阴影部分面积为：S△ABC故选：A．9．如图，在平面直角坐标系中，四边形OABC为菱形，O（0，0），A（4，0），∠AOC＝60°，则对角线交点E的坐标为（）A．（2，）B．（，2）C．（，3）D．（3，）【解答】解：过点E作EF⊥x轴于点F，∵四边形OABC为菱形，∠AOC＝60°，∴＝30°，∠FAE＝60°，∵A（4，0），∴OA＝4，∴＝2，∴，EF＝＝＝，∴OF＝AO﹣AF＝4﹣1＝3，∴．故选：D．10．如图，在矩形ABCD中，AD＝6，对角线AC与BD交于点O，AE⊥BD，垂足为点E，且AE 平分∠BAO，则AB的长为（）A．3B．4C．D．【解答】解：∵四边形ABCD是矩形∴AO＝CO＝BO＝DO，∵AE平分∠BAO∴∠B AE＝∠EAO，且AE＝AE，∠AEB＝∠AEO，∴△ABE≌△AOE（ASA）∴AO＝AB，且AO＝OB∴AO＝AB＝BO＝DO，∴BD＝2AB，∵AD2+AB2＝BD2，∴36+AB2＝4AB2，∴AB＝2故选：C．11．如图，在菱形ABCD中，AB＝5，对角线AC与BD相交于点O，且AC：BD＝3：4，AE⊥CD于点E，则AE的长是（）A．4B．C．5D．【解答】解：∵四边形ABCD是菱形，∴AO＝AC，OB＝BD，AC⊥BD，∵AC：BD＝3：4，∴AO：OB＝3：4，设AO＝3x，OB＝4x，则AB＝5x，∵AB＝5，∴5x＝5，x＝1，∴AC＝6，BD＝8，S菱形ABCD＝，∴，AE＝，故选：B．12．如图，在正方形ABCD中，点E，F分别在BC，CD上，AE＝AF，AC与EF相交于点G．下列结论：①AC垂直平分EF；②BE+DF＝EF；③当∠DAF＝15°时，△AEF为等边三角形；④当∠EAF＝60°时，S△ABE ＝S△CEF．其中正确的是（）A．①③B．②④C．①③④D．②③④【解答】解：①四边形ABCD是正方形，∴AB═AD，∠B＝∠D＝90°．在Rt△ABE和Rt△ADF中，，∴Rt△ABE≌Rt△ADF（HL），∴BE＝DF∵BC＝CD，∴BC﹣BE＝CD﹣DF，即CE＝CF，∵AE ＝AF ，∴AC 垂直平分EF ．（故①正确）．②设BC ＝a ，CE ＝y ，∴BE +DF ＝2（a ﹣y ）EF ＝，∴BE +DF 与EF 关系不确定，只有当y ＝（）a 时成立，（故②错误）．③当∠DAF ＝15°时，∵Rt△ABE ≌Rt△ADF ，∴∠DAF ＝∠BAE ＝15°，∴∠EAF ＝90°﹣2×15°＝60°，又∵AE ＝AF∴△AEF 为等边三角形．（故③正确）．④当∠EAF ＝60°时，设EC ＝x ，BE ＝y ，由勾股定理就可以得出：∴x 2＝2y （x +y ）∵S △CEF ＝x 2，S △ABE ＝，∴S △ABE ＝S △CEF ．（故④正确）．综上所述，正确的有①③④，故选：C ．二．填空题（共4小题）13．如图，矩形ABCD 中，AC 、BD 交于点O ，M 、N 分别为BC 、OC 的中点．若MN ＝4，则AC 的长为16．【解答】解：∵M 、N 分别为BC 、OC 的中点，∴BO ＝2MN ＝8．∵四边形ABCD 是矩形，∴AC＝BD＝2BO＝16．故答案为16．14．如图，已知菱形ABCD的对角线AC，BD交于点O，E为BC的中点，若OE＝3，则菱形的周长为24．【解答】解：∵四边形ABCD是菱形，∴AB＝BC＝CD＝AD，BO＝DO，∵点E是BC的中点，∴OE是△BCD的中位线，∴CD＝2OE＝2×3＝6，∴菱形ABCD的周长＝4×6＝24；故答案为：24．15．如图，E，F是正方形ABCD的对角线AC上的两点，AC＝8，AE＝CF＝2，则四边形BEDF的周长是8．【解答】解：如图，连接BD交AC于点O，∵四边形ABCD为正方形，∴BD⊥AC，OD＝OB＝OA＝OC，∵AE＝CF＝2，∴OA﹣AE＝OC﹣CF，即OE＝OF，∴四边形BEDF为平行四边形，且BD⊥EF，∴四边形BEDF为菱形，∴DE＝DF＝BE＝BF，∵AC＝BD＝8，OE＝OF＝＝2，由勾股定理得：DE＝＝＝2，∴四边形BEDF的周长＝4DE＝4×＝8，故答案为：8．16．如图，矩形OABC的顶点A，C分别在坐标轴上，B（8，7），D（5，0），点P是边AB或边BC上的一点，连接OP，DP，当△ODP为等腰三角形时，点P的坐标为（8，4）或（，7）．【解答】解：∵四边形OABC是矩形，B（8，7），∴OA＝BC＝8，OC＝AB＝7，∵D（5，0），∴OD＝5，∵点P是边AB或边BC上的一点，∴当点P在AB边时，OD＝DP＝5，∵AD＝3，∴PA＝＝4，∴P（8，4）．当点P在边BC上时，只有PO＝PD，此时P（，7）．综上所述，满足条件的点P坐标为（8，4）或（，7）．故答案为（8，4）或（，7）．三．解答题（共7小题）17．如图，四边形ABCD中，对角线AC、BD相交于点O，AO＝OC，BO＝OD，且∠AOB＝2∠OAD．（1）求证：四边形ABCD是矩形；（2）若∠AOB：∠ODC＝4：3，求∠ADO的度数．【解答】（1）证明：∵AO＝OC，BO＝OD，∴四边形ABCD是平行四边形，∵∠AOB＝∠DAO+∠ADO＝2∠OAD，∴∠DAO＝∠ADO，∴AO＝DO，∴AC＝BD，∴四边形ABCD是矩形；（2）解：∵四边形ABCD是矩形，∴AB∥CD，∴∠ABO＝∠CDO，∵∠AOB：∠ODC＝4：3，∴∠AOB：∠ABO＝4：3，∴∠BAO：∠AOB：∠ABO＝3：4：3，∴∠ABO＝54°，∵∠BAD＝90°，∴∠ADO＝90°﹣54°＝36°．18．如图，在矩形ABCD中，E，F分别是BC，AD边上的点，且AE＝CF．（1）求证：△ABE≌△CDF；（2）当AC⊥EF时，四边形AECF是菱形吗？请说明理由．【解答】（1）证明：∵四边形ABCD是矩形，∴∠B＝∠D＝90°，AB＝CD，AD＝BC，AD∥BC，在Rt△ABE和Rt△CDF中，，∴Rt△ABE≌Rt△CDF（HL）；（2）解：当AC⊥EF时，四边形AECF是菱形，理由如下：∵△ABE≌△CDF，∴BE＝DF，∵BC＝AD，∴CE＝AF，∵CE∥AF，∴四边形AECF是平行四边形，又∵AC⊥EF，∴四边形AECF是菱形．19．如图，在矩形ABCD中，AB＝3，BC＝4．M、N在对角线AC上，且AM＝CN，E、F分别是AD、BC的中点．（1）求证：△ABM≌△CDN；（2）点G是对角线AC上的点，∠EGF＝90°，求AG的长．【解答】（1）证明∵四边形ABCD是矩形，∴AB∥CD，∴∠MAB＝∠NCD．在△ABM和△CDN中，，∴△ABM≌△CDN（SAS）；（2）解：如图，连接EF，交AC于点O．在△AEO和△CFO中，，∴△AEO≌△CFO（AAS），∴EO＝FO，AO＝CO，∴O为EF、AC中点．∵∠EGF＝90°，OG＝EF＝，∴AG＝OA﹣OG＝1或AG＝OA+OG＝4，∴AG的长为1或4．20．如图，矩形ABCD中，AB＝8，AD＝6，点O是对角线BD的中点，过点O的直线分别交AB、CD边于点E、F．（1）求证：四边形DEBF是平行四边形；（2）当DE＝DF时，求EF的长．【解答】（1）证明：∵四边形ABCD是矩形，∴AB∥CD，∴∠DFO＝∠BEO，又因为∠DOF＝∠BOE，OD＝OB，∴△DOF≌△BOE（ASA），∴DF＝BE，又因为DF∥BE，∴四边形BEDF是平行四边形；（2）解：∵DE＝DF，四边形BEDF是平行四边形∴四边形BEDF是菱形，∴DE＝BE，EF⊥BD，OE＝OF，设AE＝x，则DE＝BE＝8﹣x在Rt△ADE中，根据勾股定理，有AE2+AD2＝DE2∴x2+62＝（8﹣x）2，解之得：x＝，∴DE＝8﹣＝，在Rt△ABD中，根据勾股定理，有AB2+AD2＝BD2∴BD＝，∴OD＝BD＝5，在Rt△DOE中，根据勾股定理，有DE2﹣OD2＝OE2，∴OE＝，∴EF＝2OE＝．21．如图，已知正方形ABCD的边长为1，正方形CEFG的面积为S1，点E在DC边上，点G在BC的延长线上，设以线段AD和DE为邻边的矩形的面积为S2，且S1＝S2．（1）求线段CE的长；（2）若点H为BC边的中点，连接HD，求证：HD＝HG．【解答】解：（1）设正方形CEFG的边长为a，∵正方形ABCD的边长为1，∴DE＝1﹣a，∵S1＝S2，∴a2＝1×（1﹣a），解得，（舍去），，即线段CE的长是；（2）证明：∵点H为BC边的中点，BC＝1，∴CH＝0.5，∴DH＝＝，∵CH＝0.5，CG＝，∴HG＝，∴HD＝HG．22．如图，矩形EFGH的顶点E，G分别在菱形ABCD的边AD，BC上，顶点F，H在菱形ABCD 的对角线BD上．（1）求证：BG＝DE；（2）若E为AD中点，FH＝2，求菱形ABCD的周长．【解答】解：（1）∵四边形EFGH是矩形，∴EH＝FG，EH∥FG，∴∠GFH＝∠EHF，∵∠BFG＝180°﹣∠GFH，∠DHE＝180°﹣∠EHF，∴∠BFG＝∠DHE，∵四边形ABCD是菱形，∴AD∥BC，∴∠GBF＝∠EDH，∴△BGF≌△DEH（AAS），∴BG＝DE；（2）连接EG，∵四边形ABCD是菱形，∴AD＝BC，AD∥BC，∵E为AD中点，∴AE＝ED，∵BG＝DE，∴AE＝BG，AE∥BG，∴四边形ABGE是平行四边形，∴AB＝EG，∵EG＝FH＝2，∴AB＝2，∴菱形ABCD的周长＝8．23．如图，在正方形ABCD中，点E是BC的中点，连接DE，过点A作AG⊥ED交DE于点F，交CD于点G．（1）证明：△ADG≌△DCE；（2）连接BF，证明：AB＝FB．【解答】解：（1）∵四边形ABCD是正方形，∴∠ADG＝∠C＝90°，AD＝DC，又∵AG⊥DE，∴∠DAG+∠ADF＝90°＝∠CDE+∠ADF，∴∠DAG＝∠CDE，∴△ADG≌△DCE（ASA）；（2）如图所示，延长DE交AB的延长线于H，∵E是BC的中点，∴BE＝CE，又∵∠C＝∠HBE＝90°，∠DEC＝∠HEB，∴△DCE≌△HBE（ASA），∴BH＝DC＝AB，即B是AH的中点，又∵∠AFH＝90°，∴Rt△AFH中，BF＝AH＝AB．。

特殊平行四边形测试题

特殊平行四边形测试题特殊平行四边形是指在平行四边形的基础上，具备某种特定性质的四边形。

它们在几何学中具有一定的研究价值和实际应用。

本文将介绍几道特殊平行四边形的测试题，并详细解答每道题目。

一、题目一已知平行四边形ABCD中，角A的度数是60°，角B的度数是120°，连结BD并延长交线段AC于点E。

请判断并证明四边形AEBD是否为一个特殊平行四边形。

解答：首先，连接AE。

由于平行四边形ABCD的对角线互相平分，所以有∠BED=∠BAC=60°。

然后，观察四边形AEBD。

由于∠BAD=∠BDA=180°-60°-120°=60°，而∠BED=60°，所以∠BAD=∠BED，即两对角相等。

最后，观察四边形AEBD的边长。

根据平行四边形性质，AB∥CD，AE∥BD，因此四边形AEBD为平行四边形。

综上所述，四边形AEBD满足特殊平行四边形的性质，即AEBD为一个特殊平行四边形。

二、题目二在平行四边形ABCD中，连结AC并延长交线段BD于点E，若∠BAC=50°，∠ACB=30°，请判断并证明四边形AEBD是否为一个特殊平行四边形。

解答：首先，连接AE。

由平行四边形的性质可知，∠BAD=∠BDA=180°-∠BAC-∠ACB=180°-50°-30°=100°。

然后，观察四边形AEBD。

由于∠BAC=50°，而∠BED=∠BAC=50°，因此∠BAC=∠BED，即两对角相等。

最后，观察四边形AEBD的边长。

根据平行四边形性质，AB∥CD，AE∥BD，因此四边形AEBD为平行四边形。

综上所述，四边形AEBD满足特殊平行四边形的性质，即AEBD为一个特殊平行四边形。

三、题目三在平行四边形ABCD中，连结AC并延长交线段BD于点E，若∠AEB=110°，请判断并证明四边形AEBD是否为一个特殊平行四边形。

特殊平行四边形测试卷

特殊平行四边形测试卷一、选择题1、已知四边形ABCD ，以下有四个条件．（1）AB CD AB CD =∥，（2）AB AD AB BC ==，（3）A B C D ∠=∠∠=∠，（4）AB CD AD BC ∥，∥ 能判四边形ABCD 是平行四边形的有（）Ａ．1个Ｂ．2个Ｃ．3个Ｄ．4个 2、菱形具有而一般平行四边形不具有的性质是（）A. 对角相等B. 对边相等C. 对角线互相垂直D. 对角线相等 3、菱形的周长为100cm ，一条对角线长为14cm ，它的面积是（）A. 168cm 2B. 336cm 2C. 672cm 2D. 84cm 24、如图，矩形纸片ABCD 中，AB ＝6 cm ，BC ＝8 cm ，现将其沿AE 对折，使得点B 落在边AD 上的点B 1处，折痕与边BC 交于点E ，则CE 的长为( )A ．6 cmB ．4 cmC ．2 cmD ．1 cm 5、如图，菱形纸片ABCD 中，∠A ＝60°，折叠菱形纸片ABCD ，使点C 落在DP (P 为AB 中点)所在的直线上，得到经过点D 的折痕DE ，则∠DEC 的大小为( )A ．78°B ．75°C ．60°D ．45°6、若 ABCD 中，AB=10，BC=14,E 、F 分别为边BC 、AD 上的点，若四边形AECF 为正方形，则AE 的长为（）A. 7B. 4或10C. 5或9D.6或87、如图，在矩形ABCD 中，AB=3，AD=4，P 是AD 上的动点，PE ⊥AC 于E ，PF ⊥BD 于F ，则PE+PF 的值为（）A.2B.25 C.5 D.512（第4题）（第5题）（第7题）8、菱形的周长为20,两邻角的比为2∶1，则一组对边的距离为（） A.32B.332C.3 3D.5329、如图，四边形ABCD 是正方形，延长BC 至点E ，使CE ＝CA ，连结AE 交CD•_P _O _F _E _D _C _B _A于点F ，•则∠AFC 的度数是（）．（A ）150° （B ）125° （C ）135° （D ）112．5°10、如图，在菱形ABCD 中，∠B ＝60°，点E ，F 分别从点B ，D 同时以同样的速度沿边BC ，DC 向点C 运动.给出以下四个结论：① AE=AF ;② EF ∥BD ; ③ 当点E ，F 分别为边BC ，DC 的中点时，△AEF 是等边三角形；④ 当点E ，F 分别为边BC ，DC 的中点时，EF=3BE.上述结论正确的有（） A.1个 B.2个 C.3个 D.4个（第9题）（第10题）二．填空题 11、菱形的两条对角线分别是6 cm ，8 cm ，则菱形的边长为_____，面积为______． 12、如图所示，将直角△ABC 绕AC 的中点O 顺时针旋转180°得到△CDA ，添加一个条件_________，使四边形ABCD 为正方形．13、如图，已知点P 是正方形ABCD 对角线BD 上一点，且BP ＝BC ，则∠ACP 的度数是__ _度14、已知矩形ABCD ，AB ＝3 cm ，AD ＝4 cm ，过对角线BD 的中点O 作BD 的垂直平分线EF ，分别交AD ，BC 于点E ，F ，则AE 的长为__ _cm.（第12题）（第13题）（第14题）15、如图，菱形ABCD 的边长为4，过点A ，C 作对角线AC 的垂线，分别交CB 和AD 的延长线于点E ，F ，AE ＝3，则四边形AECF 的周长为__．16、如图，四边形ABCD 是正方形，△CDE 是等边三角形，则∠AED＝______，∠AEB＝______．17、如图，点O 是矩形ABCD 的中心，E 是AB 上的点，沿CE 折叠后，点B 恰好与点O 重合，若BC =3，则折痕CE 的长为。

特殊平行四边形检测试卷

第一章特殊平行四边形检测试卷一、选择题1. 不能判定四边形ABCD 为平行四边形的题设是（）（A ）AB 平行且等于CD 。

（B ）∠A=∠C ，∠B=∠D 。

（C ）AB=AD ，BC=CD 。

（D ）AB=CD ，AD=BC 。

2.矩形、菱形、正方形都具有的性质是 ( ) A.每一条对角线平分一组对角 B.对角线相等 C.对角线互相平分 D.对角线互相垂直3. 如图，在平行四边形ABCD 中，对角线AC 、BD 相交于点O ，若BD 、AC 的和为cm 18，CD ：DA=2：3，△AOB 的周长为cm 13,那么BC 的长是（） A. cm 6 B. cm 9 C. cm 3 D. cm 124.在直角三角形ABC 中，∠ACB =︒90，∠B =︒60，AC =cm 3，则AB 边上的中线长为（） A. cm 1 B. cm 2 C. cm5.1 D. cm 3 5. 下列说法错误的是（）A.一组对边平行且一组对角相等的四边形是平行四边形.B.每组邻边都相等的四边形是菱形.C.对角线互相垂直的平行四边形是正方形.D.四个角都相等的四边形是矩形. 6.下列命题中，真命题是（）A ．两条对角线垂直的四边形是菱形B ．对角线垂直且相等的四边形是正方形C ．两条对角线相等的四边形是矩形D ．两条对角线相等的平行四边形是矩形 7．将两块能完全重合的两张等腰直角三角形纸片拼成下列图形：①平行四边形（不包括菱形、矩形、正方形）②矩形③正方形④等边三角形⑤等腰直角三角形 ( )A ．①③⑤B ．②③⑤C ．①②③D ．①③④⑤8.如图,已知菱形ABCD 与△ABE,其中D 在BE 上.若AB=17,BD=16,AE=25,则DE 的长度为 ( )A.8B.9C.11D.129. 如图在矩形ABCD 中,AB=10,BC=5,点E,F 分别在AB,CD 上,将矩形ABCD 沿EF 折叠,使点A,D 分别落在矩形ABCD 外部的点A 1,D 1处,则阴影部分图形的周长为 ( ) A.15B.20C.25D.3010．如图，菱形ABCD 中，对角线AC 、BD 相交于点O ，H 为AD 边中点，菱形ABCD 的周长为28，则OH 的长等于（）A. 3.5B. 4C. 7D. 1411．给出以下三个命题：①对角线相等的四边形是矩形；②对角线互相垂直的四边形是菱形；③对角线互相垂直的矩形是正方形；④菱形对角线的平方和等于边长平方的4倍，其中真命题的是（）A ．③B ．①②C ．②③D ．③④ 12.如图,正方形ABCD 中,AB=3,点E 在边CD 上,且CD=3DE.将△ADE 沿AE 对折至△AFE,延长EF 交边BC 于点G,连接AG,CF.下列结论: ①点G 是BC 的中点; ②FG=FC; ③∠GAE =︒45. 其中正确的是 ( )A.①②B.①③C.②③D.①②③ABCDO二、填空题：13.①等边三角形②菱形③平行四边形④矩形（5）正方形五个图形中,既是轴对称图形又是中心对称图形的是 (填写序号).14. 在Rt⊿ABC中，∠ACB =90°，∠A =30°，AC =32，则AB边上的中线为，高为15.菱形ABCD的边长为8cm，∠BAD=120°，则AC= ,BD= ,面积= 。

19.2.1特殊的平行四边形

19.2特殊的平行四边形19.2.1矩形1.矩形具有而平行四边形不具有的性质是（）A.对边相等B.对角相等C.对角互补D.对角线平分2.直角三角形中，两直角边长分别为12和5，则斜边中线长是（） A.26 B.13 C.8.5 D.6.53.矩形ABCD 对角线AC 、BD 交于点O ，AB=5,12,cm BC cm =则△ABO 的周长为等于 .4. 如图所示，四边形ABCD 为矩形纸片．把纸片ABCD 折叠，使点B 恰好落在CD 边的中点E 处，折痕为AF ．若CD ＝6，则AF 等于（） A.34 B.33 C.24D.８5. 如图所示，矩形ABCD 的对角线AC 和BD 相交于点O ，过点O 的直线分别交AD 和BC 于点E 、F ，23AB BC ==，，则图中阴影部分的面积为．6.已知矩形的周长为40cm ，被两条对角线分成的相邻两个三角形的周长的差为8cm ，则较大的边长为 .7. 如图，矩形ABCD 中，AC 与BD 交于O 点，BE AC ⊥于E ，CF BD ⊥于F 。

求证BE=CF 。

8. 如图所示，E 为□ABCD 外，AE ⊥CE,BE ⊥DE ，求证：□ABCD 为矩形9.已知矩形ABCD 和点P ，当点P 在图1中的位置时，则有结论：S △PBC =S △PAC +S △PCD 理由：过点P 作EF 垂直BC ，分别交AD 、BC 于E 、F 两点．∵ S △PBC +S △PAD =12BC ·PF+12AD ·PE=12BC （PF+PE ）=12BC ·EF=12S 矩形ABCDA BCDEF第4题图C又∵ S △PAC +S △PCD +S △PAD =12S 矩形ABCD ∴ S △PBC +S △PAD = S △PAC +S △PCD +S △PAD ．∴S △PB C =S △PA C +S △P CD ．请你参考上述信息，当点P 分别在图2、图3中的位置时，S △PB C 、S △PAC 、S PCD 又有怎样的数量关系?请写出你对上述两种情况的猜想，并选择其中一种情况的猜想给予证明．10. 如图所示，△ABC 中，点O 是AC 边上一个动点，过点O 作直线MN ∥BC ，设MN 交∠BCA 的平分线于E ，交∠BCA 的外角平分线于点F .(1)求证：EO =FO(2)当点O 运动到何处时，四边形AECF 是矩形？并证明你的结论.图2。

【数学八年级下册】人教版数学八年级下册《特殊的平行四边形》同步练习

∵AC＝BC， ∴DF＝CF＝CE＝DE， ∴四边形 DECF 是菱形． 14．
s或 s或
s或
s．
15．．
16．．
三．解答题（共 6 小题） 17．解：（1）∵∠ACB＝90°，D 是 AB 中点，
∴CD＝ AB，同理：ED＝ AB， ∴CD＝ED；
（2）∵CD＝ED，F 是 CE 中点， ∴DF⊥CE， ∵CD＝ AB，AB＝10， ∴CD＝5，
动点，过点 D 分别作 DE⊥AB 于点 E，DF⊥AC 于点 F，点 G 为四边形 DEAF 对角线交
点，则线段 GF 的最小值为
．
16．如图，在矩形 ABCD 中，AB＝8，BC＝6，点 P 为边 AB 上任意一点，过点 P 作 PE⊥
AC，PF⊥BD，垂足分别为 E、F，则 PE+PF＝
．
三．题（共 6 小题） 17．已知：如图，在△ABC 和△ABE 中，∠ACB＝∠AEB＝90°，D 是 AB 中点，联结 DC、
A．
B．
C．
D．
10．如图，正方形 ABCD 中，DE＝2AE＝4，F 是 BE 的中点，点 H 在 CD 上，∠EFH＝45 °，则 FH 的长度为（）
A．
B．5
C．
D．2
二．填空题（共 6 小题） 11．如图，已知直角三角形 ABC 中，∠ABC 为直角，AB＝12，BC＝16，三角形 ACD 为等
特殊的平行四边形
一．选择题（共 10 小题）
1．下列说法：①对角线互相垂直的四边形是菱形；②矩形的对角线垂直且互相平分；③对
角线相等的四边形是矩形；④对角线相等的菱形是正方形；⑤邻边相等的矩形是正方
形．其中正确的是（）

特殊平行四边形练习题

特殊的平行四边形1. 平行四边形、矩形、菱形、正方形的性质：2. 识别方法小结：(1) 识别平行四边形的方法：①两组对边分别平行的四边形是平行四边形；②两组对边分别相等的四边形是平行四边形；③两组对角分别相等的四边形是平行四边形；④对角线互相平分的四边形是平行四边形；⑤一组对边平行且相等的四边形是平行四边形。

(2) 识别矩形的方法：①有一个角是直角的平行四边形是矩形；②对角线相等的平行四边形是矩形；③有三个角是直角的四边形是矩形；④对角线相等且互相平分的四边形是矩形。

(3) 识别菱形的方法：①有一组邻边相等的平行四边形是菱形；②对角线互相垂直的平行四边形是菱形；③四边都相等的四边形是菱形；④对角线互相垂直平分的四边形是菱形。

(4) 识别正方形的方法：①有一组邻边相等且有一个角是直角的平行四边形是正方形；②对角线互相垂直且相等的平行四边形是正方形；③有一组邻边相等的矩形是正方形；④对角线互相垂直的矩形是正方形；⑤有一个角是直角的菱形是正方形；⑥对角线相等的菱形是正方形；⑦对角线互相垂直平分且相等的四边形是正方形。

小结：把以上识别方法的编号分别填入下图中的每一条带方向的线上：（如平行四边形的第一种识别方法的编号为(1) ①，其他方法类似）一、基础达标训练：（A组）1.填空：（1）两条对角线的四边形是平行四边形；（2）两条对角线的四边形是矩形；（3）两条对角线的四边形是菱形；（4）两条对角线的四边形是正方形；（5）两条对角线的平行四边形是矩形；（6）两条对角线的平行四边形是菱形；（7）两条对角线的平行四边形是正方形；（8）两条对角线的矩形是正方形；（9）两条对角线的菱形是正方形。

2.已知□ABCD的周长为42cm，AB：AD = 2∶5，则AB＋AD=________3.已知矩形ABCD的一条对角线AC = 24，则另一条对角线BD = .4.矩形的两条对角线一夹角为60°，一条对角线与较短边的和为21cm，则对角线的长为.5.菱形的两条对角线长为7和16，则菱形的面积为.6.正方形的边长是5cm时，它的周长是，面积是.7.正方形的一条对角线长为8，则正方形的面积为.8.中点四边形：(1) 顺次连接四边形各边中点所得的四边形是.(2) 顺次连接平行四边形各边中点所得的四边形是.(3) 顺次连接矩形各边中点所得的四边形是.(4) 顺次连接菱形各边中点所得的四边形是.(5) 顺次连接正方形各边中点所得的四边形是.9.(2006年黑龙江省)如图，E、F分别是正方形ABCD的边CD、AD上的点，且CE=DF ，AE 、BF 相交于点D ，下列结论①AE=BF ； ②AE ⊥BF ；③ AO=OE ； ④S △AOB =S 四边形DEOF 中，错误的有( ) A ．1个 B ．2个 C ．3个 D ．4个10. (2006年黑龙江省) 如图，在矩形ABCD 中，EF ∥AB ，GH ∥BC ， 11. EF 、GH 的交点P 在BD 上，图中面积相等的四边形有( )A ．3对B ．4对C ．5对D ．6对12. (2006年海南省)如图，在菱形ABCD 中，E 、F 、G 、H 分别是菱形四边的中点，连结EG 与FH 交于点O ，则图中的菱形共有( ) A ．4个 B ．5个 C ．6个 D ．7个13. (2006年云南省昆明市)己知：如图，菱形ABCD 中，∠B=600，AB ＝4，则以AC 为边长的正方形ACEF 的周长为 .14. (2006年宁夏回族自治区)菱形的周长为20cm ，一条对角线长为8cm ，则菱形的面积为 2cm ．15. 矩形ABCD 的对角线AC 、BD 相交于点O ，∠1＝2∠2，若AC ＝1.8cm ，试求AB 的长。

平行四边形与特殊平行四边形测试题与答案

平行四边形与特殊平行四边形测试题一、填空题（每小题3分，共30分）1、如图，正方形ABCD 的对角线AC ，BD 相交于点O ，那么图中共有______个等腰直角三角形。

A. 2B. 5C. 6D. 82、如下图,在矩形ABCD 中,两条对角线相交于点O,∠AOD=120∘, AB=2.5,则这个矩形对角线的长是( ) A. 2.5 B. 5 C. 6 D. 7.53、下列说法正确的是（）(A)对角线互相垂直的四边形是正方形 (B)有一角为直角的菱形是正方形(C)“菱形的对角线互相垂直”的逆命题是真命题 (D)如果一个四边形是轴对称图形，而且有两条互相垂直的对称轴，那么这个四边形一定是菱形 4、下列说法错误的是（）(A)直角三角形斜边上的中线等于斜边的一半 B ．300角所对的直角边等于斜边的一半 (C) 三角形的中位线平行于第三边，且等于第三边的一半 (D)有一个角为直角的四边形是矩形5、菱形的周长是200cm.一条对角线长60cm ，另一条对角线的长度与面积分别是（） (A)80cm 2400cm 2 (B)80cm 1200cm 2 (C)40cm 2400cm 2 (D)40cm 1200cm 26、菱形具有而平行四边形不具有的性质是( )A .内角和是360° B. 对角相等；C. 对边平行且相等； D. 对角线互相垂直.7、如图,先将一张长方形的纸沿虚线对折,再对折,然后按图中虚线剪下,将剪下的纸展开,一定可以得到一个( )A. 菱形B. 矩形C. 正方形D. 平行四边形8、如图,在ABCD 中,E 为AD 的中点,△DEF 的面积为1,则△BCF的面积为( )A.4B.3C.2D.19、已知正方形的对角线长为b ，正方形的面积和周长分别是（） (A).2323b(B)2222bb (C ) 3232bb (D) 21222bb10、如图，在矩形ABCD 中，AB=3，AD=4，P 是AD 上不与A 和D 重合的一个动点，过点P 分别作AC 和BD 的垂线，垂足为E ，F. PE+PF 的值为( ) A.2B125C.2.1D.5二、填空题（每小题4分，共28分） 11、对角线长为2cm 的正方形，边长是______.12、在矩形ABCD 中，两条对角线AC 、BD 相交于点O ，若4AB OB ==，则AD = ；13、依次连接菱形的各边中点，得到的四边形是___________14、一个正方体的表面积是2384cm ，则这个正方体的棱长为________15、边长为5cm 的菱形，一条对角线长是6cm ，则菱形的面积是 cm 2． 16、矩形的两条对角线的一个交角为60 o，两条对角线的长度的和为8cm ，则这个矩形的一条较短边为 cm.17、如图，菱形ABCD 的对角线相交于点O ，过点D 作DE ∥AC ，且DE=AC ，连接CE 、OE ，连接AE ，交OD 于点F ．若AB=2，∠ABC=60°，则AE 的长为___________. 三、解答题（18-20题各6分，21-23题各8分，24-25题各10分，共62分） 18.已知矩形ABCD（1）作对角线AC 的垂直平分线交AD 点E ，交BC 于点F （尺规作图，不写作法，保留作图痕迹）（2）连接AF 、CE ，直接判断四边形AFCE 的形状。

特殊平行四边形单元测试题(含答案) (3)

第一章：特殊的平行四边形单元测试卷（典型题汇总）一、单项选择题（本大题共有15小题，每小题3分，共45分）1、如图，四边形为平行四边形，延长到，使，连接，，，添加一个条件，不能使四边形成为矩形的是（）A.B.C.D.2、如果要证明平行四边形为正方形，那么我们需要在四边形是平行四边形的基础上，进一步证明（）．A. 与互相垂直平分B. 且C. 且D. 且3、过矩形的四个顶点作对角线、的平行线分別交于、、、四点，则四边形是（ ).A. 平行四边形B. 矩形C. 菱形D. 正方形4、能判别一个四边形是正方形的条件是（）.A. 一组邻边相等且对角线互相平分.B. 对角线互相垂直平分且相等.C. —组对边平行，一组对角相等.D. 对角线相等，对边平行且相等.5、设、表示两个集合，我们规定“”表示与的公共部分，并称之为与的交集．例如：若正数，整数，则正整数．若矩形，菱形，则所对应的集合是（）A. 正方形B. 菱形C. 矩形D. 平行四边形6、如图，在矩形中，，，将矩形沿折叠，则重叠部分的面积为（）A.B.C.D.7、如图，正方形的边长为，在各边上顺次截取，则四边形的面积是（）A.B.C.D.8、如图，在中，，，，为边上一动点，于，于，为的中点，则的最小值为（）A.B.C.D.9、下列命题中，真命题是（）A. 两条对角线互相平分的四边形是平行四边形B. 两条对角线互相垂直且相等的四边形是正方形C. 两条对角线互相垂直的四边形是菱形D. 两条对角线相等的四边形是矩形10、如图，已知四边形的四边都相等，等边的顶点、分别在、上，且，则（）A.B.C.D.11、如图，在平行四边形中，用直尺和圆规作的平分线交于点，若，，则的长为（）A.B.C.D.12、如图，分别以直角的斜边，直角边为边向外作等边和等边，为的中点，与交于点，与交于点，，．给出如下结论：①；②四边形为菱形；③；④；其中正确结论的是（）A. ①②③B. ①②④C. ①③④D. ②③④13、如图，在四边形中，、、、分别是、、、的中点，要使四边形是菱形，则四边形只需要满足一个条件，是（）A. 四边形是梯形B. 四边形是菱形C. 对角线D.14、如图，在菱形中，，分别在，上，且，与交于点，连接．若，则的度数为（）A.B.C.D.15、如图，已知号、号两个正方形的面积和为，号、号两个正方形的面积和为，则这个正方形的面积和为（）A.B.C.D.二、填空题（本大题共有5小题，每小题5分，共25分）16、如图，在菱形中，对角线、交于点，为边的中点，若菱形的周长为，则的长为．17、如图，将矩形沿折叠，若,则为.18、1.正方形的定义有一组邻边且一个角是的平行四边形叫做正方形。

2020—2021年最新湘教版八年级数学下册《特殊的平行四边形》同步检测题及参考答案.docx

湘教版2017—2018学年八年级数学下学期2.5—2.7“特殊的平行四边形”同步检测与解析一．选择题（共10小题）1．如图，在矩形ABCD中（AD＞AB），点E是BC上一点，且DE=DA，AF⊥DE，垂足为点F，在下列结论中，不一定正确的是（）A．△AFD≌△DCE B．AF=1AD C．AB=AF D．BE=AD﹣DF22．如图，矩形ABCD的顶点A、C分别在直线a、b上，且a∥b，∠1=60°，则∠2的度数为（）A．30°B．45°C．60°D．75°3．下列关于矩形的说法中正确的是（）A．对角线相等的四边形是矩形B．矩形的对角线相等且互相平分C．对角线互相平分的四边形是矩形D．矩形的对角线互相垂直且平分4．如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，D是AB上一动点，过点D作DE⊥AC于点E，DF⊥BC于点F，连接EF，则线段EF的最小值是（）A．5 B．4.8 C．4.6 D．4.45．菱形具有而一般平行四边形不具有的性质是（）A．对边相等B．对角相等C．对角线互相平分D．对角线互相垂直6．如图，四边形ABCD是菱形，AC=8，DB=6，DH⊥AB于H，则DH等于（）A．245B．125C．5 D．47．如图，四边形ABCD的四边相等，且面积为120cm2，对角线AC=24cm，则四边形ABCD的周长为（）A．52cm B．40cm C．39cm D．26cm8．如图，在平行四边形ABCD中，BC=2AB，CE⊥AB于E，F为AD 的中点，若∠AEF=54°，则∠B=（）A．54°B．60°C．66°D．72°9．△ABC中，∠C=90°，点O为△ABC三条角平分线的交点，OD⊥BC于D，OE⊥AC于E，OF⊥AB于F，且AB=10cm，BC=8cm，AC=6cm，则点O到三边AB、AC、BC的距离为（）A．2cm，2cm，2cm B．3cm，3cm，3cm C．4cm，4cm，4cm D．2cm，3cm，5cm10．小明在学习了正方形之后，给同桌小文出了错题，从下列四个条件：①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD中选两个作为补充条件，使▱ABCD为正方形（如图所示），现有如下四种选法，你认为其中错误的是（）A．①②B．①③C．②③D．②④二．填空题（共8小题）11．如图．两条等宽的长方形纸条倾斜的重叠着，已知长方形纸条宽为3cm，∠ABC=60°，则四边形ABCD的面积为cm2．12．如图，四边形ABCD是轴对称图形，且直线AC是对称轴，AB∥CD，则下列结论：①AC⊥BD；②AD∥BC；③四边形ABCD是菱形；④△ABD≌△CDB．其中正确的是（只填写序号）13．如图，矩形ABCD中，AB=20cm，BC=4cm，点P从A 开始沿折线A﹣B﹣C﹣D以4cm/s的速度运动，点Q从C开始沿CD边以1cm/s的速度移动，如果点P、Q分别从A、C同时出发，当其中一点到达D时，另一点也随之停止运动，设运动时间为t（s），当t= 时，四边形APQD也为矩形．14．如图，△ABC中，∠B=90°，AB=8，BC=6，点D是AC上的任意一点，过点D作DE⊥AB于点E，DF⊥BC于点F，连接EF，则EF 的最小值是．15．如图，以边长为1的正方形的四边中点为顶点作四边形，再以所得四边形四边中点为顶点作四边形，…依次作下去，图中所作的第三个四边形的周长为；所作的第n个四边形的周长为．16．如图，在正方形ABCD中，对角线AC与BD相交于点O，E为BC上一点，CE=5，F为DE的中点．若△CEF的周长为18，则OF的长为．17．如图，正方形ABCD中，点E、F分别为AB、CD上的点，且AB，点O为线段EF的中点，过点O作直线与正方形的一AE=CF=13组对边分别交于P、Q两点，并且满足PQ=EF，则这样的直线PQ（不同于EF）有条．18．如图，在△ABC中，∠ABC=90°，BD为AC边的中线，过点C 作CE⊥BD于点E，过点A作BD的平行线，交CE的延长线于点F，在AF的延长线上截取FG=BD，连接BG、DF．若AB=12，BC=5，则四边形BDFG的周长为．三．解答题（共5小题）19．如图所示，四边形ABCD中，∠ADC=∠ABC=90°，AD=CD，DP⊥AB于点P，若四边形ABCD的面积是36，求DP的长．20．如图，已知点E，F分别是▱ABCD的边BC，AD上的中点，且∠BAC=90°．（1）求证：四边形AECF是菱形；（2）若∠B=30°，BC=10，求菱形AECF面积．21．阅读下面材料：在数学课上，老师请同学思考如下问题：如图1，我们把一个四边形ABCD的四边中点E，F，G，H依次连接起来得到的四边形EFGH是平行四边形吗？小敏在思考问题是，有如下思路：连接AC．结合小敏的思路作答（1）若只改变图1中四边形ABCD的形状（如图2），则四边形EFGH 还是平行四边形吗？说明理由；参考小敏思考问题方法解决一下问题：（2）如图2，在（1）的条件下，若连接AC，BD．①当AC与BD满足什么条件时，四边形EFGH是菱形，写出结论并证明；②当AC与BD满足什么条件时，四边形EFGH是矩形，直接写出结论．22．如图，在四边形ABCD中，已知AD∥BC，AB⊥BC，点E，F在边AB上，且∠AED=45°，∠BFC=60°，AE=2，EF=2﹣3，FC=23．（1）BC= ．（2）求点D到BC的距离．（3）求DC的长．23．在边长为1的正方形ABCD中，点E是射线BC上一动点，AE 与BD相交于点M，AE或其延长线与DC或其延长线相交于点F，G 是EF的中点，连结CG．（1）如图1，当点E在BC边上时．求证：①△ABM≌△CBM；②CG ⊥CM．（2）如图2，当点E在BC的延长线上时，（1）中的结论②是否成立？请写出结论，不用证明．（3）试问当点E运动到什么位置时，△MCE是等腰三角形？请说明理由．“特殊的平行四边形”同步检测解析一．选择题（共10小题）1．（2016•荆门）如图，在矩形ABCD中（AD＞AB），点E是BC上一点，且DE=DA，AF⊥DE，垂足为点F，在下列结论中，不一定正确的是（）A．△AFD≌△DCE B．AF=1AD C．AB=AF D．BE=AD﹣DF2【分析】先根据已知条件判定△AFD≌△DCE（AAS），再根据矩形的对边相等，以及全等三角形的对应边相等进行判断即可．【解答】解：（A）由矩形ABCD，AF⊥DE可得∠C=∠AFD=90°，AD ∥BC，∴∠ADF=∠DEC．又∵DE=AD，∴△AFD≌△DCE（AAS），故（A）正确；（B）∵∠ADF不一定等于30°，∴直角三角形ADF中，AF不一定等于AD的一半，故（B）错误；（C）由△AFD≌△DCE，可得AF=CD，由矩形ABCD，可得AB=CD，∴AB=AF，故（C）正确；（D）由△AFD≌△DCE，可得CE=DF，由矩形ABCD，可得BC=AD，又∵BE=BC﹣EC，∴BE=AD﹣DF，故（D）正确；故选B．【点评】本题主要考查了矩形和全等三角形，解决问题的关键是掌握矩形的性质：矩形的四个角都是直角，矩形的对边相等．解题时注意：在直角三角形中，若有一个锐角等于30°，则这个锐角所对的直角边等于斜边的一半．2．（2016•海南）如图，矩形ABCD的顶点A、C分别在直线a、b 上，且a∥b，∠1=60°，则∠2的度数为（）A．30°B．45°C．60°D．75°【分析】首先过点D作DE∥a，由∠1=60°，可求得∠3的度数，易得∠ADC=∠2+∠3，继而求得答案．【解答】解：过点D作DE∥a，∵四边形ABCD是矩形，∴∠BAD=∠ADC=90°，∴∠3=90°﹣∠1=90°﹣60°=30°，∵a∥b，∴DE∥a∥b，∴∠4=∠3=30°，∠2=∠5，∴∠2=90°﹣30°=60°．故选C．【点评】此题考查了矩形的性质以及平行线的性质．注意准确作出辅助线是解此题的关键．3．（2016•攀枝花）下列关于矩形的说法中正确的是（）A．对角线相等的四边形是矩形B．矩形的对角线相等且互相平分C．对角线互相平分的四边形是矩形D．矩形的对角线互相垂直且平分【分析】根据矩形的性质和判定定理逐个判断即可．【解答】解：A、对角线相等的平行四边形才是矩形，故本选项错误；B、矩形的对角线相等且互相平分，故本选项正确；C、对角线互相平分的四边形是平行四边形，不一定是矩形，故本选项错误；D、矩形的对角线互相平分且相等，不一定垂直，故本选项错误；故选B．【点评】本题考查了矩形的性质和判定的应用，能熟记矩形的性质和判定定理是解此题的关键．4．如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，D是AB上一动点，过点D作DE⊥AC于点E，DF⊥BC于点F，连接EF，则线段EF的最小值是（）A．5 B．4.8 C．4.6 D．4.4【分析】连接CD，利用勾股定理列式求出AB，判断出四边形CFDE 是矩形，根据矩形的对角线相等可得EF=CD，再根据垂线段最短可得CD⊥AB时，线段EF的值最小，然后根据三角形的面积公式列出方程求解即可．【解答】解：如图，连接CD．∵∠ACB=90°，AC=6，BC=8，∴AB==10，∵PE⊥AC，PF⊥BC，∠C=90°，∴四边形CFDE是矩形，∴EF=CD，由垂线段最短可得CD⊥AB时，线段EF的值最小，此时，S△ABC=12BC•AC=12AB•CD，即12×8×6=12×10•CD，解得CD=4.8，∴EF=4.8．故选B．【点评】本题考查了矩形的判定与性质，垂线段最短的性质，勾股定理，判断出CD⊥AB时，线段EF的值最小是解题的关键，难点在于利用三角形的面积列出方程．5．（2016•莆田）菱形具有而一般平行四边形不具有的性质是（）A．对边相等B．对角相等C．对角线互相平分D．对角线互相垂直【分析】由菱形的性质可得：菱形的对角线互相平分且垂直；而平行四边形的对角线互相平分；则可求得答案．【解答】解：∵菱形具有的性质：对边相等，对角相等，对角线互相平分，对角线互相垂直；平行四边形具有的性质：对边相等，对角相等，对角线互相平分；∴菱形具有而一般平行四边形不具有的性质是：对角线互相垂直．故选D．【点评】此题考查了菱形的性质以及平行四边形的性质．注意菱形的对角线互相平分且垂直．6．（2016•枣庄）如图，四边形ABCD是菱形，AC=8，DB=6，DH ⊥AB于H，则DH等于（）A．245B．125C．5 D．4【分析】根据菱形性质求出AO=4，OB=3，∠AOB=90°，根据勾股定理求出AB，再根据菱形的面积公式求出即可．【解答】解：∵四边形ABCD是菱形，∴AO=OC，BO=OD，AC⊥BD，∵AC=8，DB=6，∴AO=4，OB=3，∠AOB=90°，由勾股定理得：AB==5，∵S 菱形ABCD=，∴DH=245，故选A．【点评】本题考查了勾股定理和菱形的性质的应用，能根据菱形的性质得出S 菱形ABCD=是解此题的关键．7．（2016•雅安）如图，四边形ABCD的四边相等，且面积为120cm2，对角线AC=24cm，则四边形ABCD的周长为（）A．52cm B．40cm C．39cm D．26cm【分析】可定四边形ABCD为菱形，连接AC、BD相交于点O，则可求得BD的长，在Rt△AOB中，利用勾股定理可求得AB的长，从而可求得四边形ABCD的周长．【解答】解：如图，连接AC、BD相交于点O，∵四边形ABCD的四边相等，∴四边形ABCD为菱形，AC•BD，∴AC⊥BD，S四边形ABCD=12×24BD=120，解得BD=10cm，∴12∴OA=12cm，OB=5cm，在Rt△AOB中，由勾股定理可得AB==13（cm），∴四边形ABCD的周长=4×13=52（cm），故选A．【点评】本题主要考查菱形的判定和性质，掌握菱形的面积分式是解题的关键，注意勾股定理的应用．8．如图，在平行四边形ABCD中，BC=2AB，CE⊥AB于E，F为AD 的中点，若∠AEF=54°，则∠B=（）A．54°B．60°C．66°D．72°【分析】过F作AB、CD的平行线FG，由于F是AD的中点，那么G 是BC的中点，即Rt△BCE斜边上的中点，由此可得BC=2EG=2FG，即△GEF、△BEG都是等腰三角形，因此求∠B的度数，只需求得∠BEG 的度数即可；易知四边形ABGF是平行四边形，得∠EFG=∠AEF，由此可求得∠FEG的度数，即可得到∠AEG的度数，根据邻补角的定义可得∠BEG的值，由此得解．【解答】解：过F作FG∥AB∥CD，交BC于G；则四边形ABGF是平行四边形，所以AF=BG，即G是BC的中点；连接EG，在Rt△BEC中，EG是斜边上的中线，BC；则BG=GE=FG=12∵AE∥FG，∴∠EFG=∠AEF=∠FEG=54°，∴∠AEG=∠AEF+∠FEG=108°，∴∠B=∠BEG=180°﹣108°=72°．故选D．【点评】此题主要考查了平行四边形的性质、直角三角形的性质以及等腰三角形的判定和性质，正确地构造出与所求相关的等腰三角形是解决问题的关键．9．△ABC中，∠C=90°，点O为△ABC三条角平分线的交点，OD⊥BC于D，OE⊥AC于E，OF⊥AB于F，且AB=10cm，BC=8cm，AC=6cm，则点O到三边AB、AC、BC的距离为（）A．2cm，2cm，2cm B．3cm，3cm，3cm C．4cm，4cm，4cm D．2cm，3cm，5cm【分析】连接OA，OB，OC，利用角的平分线上的点到角的两边的距离相等可知△BDO≌△BFO，△CDO≌△CEO，△AEO≌△AFO，∴BD=BF，CD=CE，AE=AF，又因为点O到三边AB、AC、BC的距离是CD，∴AB=8﹣CD+6﹣CD=10，解得CD=2，所以点O到三边AB、AC、BC的距离为2．【解答】解：连接OA，OB，OC，则△BDO≌△BFO，△CDO≌△CEO，△AEO≌△AFO，∴BD=BF，CD=CE，AE=AF，又∵∠C=90，OD⊥BC于D，OE⊥AC于E，且O为△ABC三条角平分线的交点∴四边形OECD是正方形，则点O到三边AB、AC、BC的距离=CD，∴AB=8﹣CD+6﹣CD=﹣2CD+14，又根据勾股定理可得：AB=10，即﹣2CD+14=10∴CD=2，即点O到三边AB、AC、BC的距离为2cm．故选A【点评】本题主要考查垂直平分线上的点到线段两段的距离相等的性质和边的和差关系．10．小明在学习了正方形之后，给同桌小文出了错题，从下列四个条件：①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD中选两个作为补充条件，使▱ABCD为正方形（如图所示），现有如下四种选法，你认为其中错误的是（）A．①②B．①③C．②③D．②④【分析】利用矩形、菱形、正方形之间的关系与区别，结合正方形的判定方法分别判断得出即可．【解答】解：A、∵四边形ABCD是平行四边形，当①AB=BC时，平行四边形ABCD是菱形，当②∠ABC=90°时，菱形ABCD是正方形，故此选项正确，不合题意；B、∵四边形ABCD是平行四边形，∴当②∠ABC=90°时，平行四边形ABCD是矩形，当AC=BD时，这是矩形的性质，无法得出四边形ABCD是正方形，故此选项错误，符合题意；C、∵四边形ABCD是平行四边形，当①AB=BC时，平行四边形ABCD是菱形，当③AC=BD时，菱形ABCD是正方形，故此选项正确，不合题意；D、∵四边形ABCD是平行四边形，∴当②∠ABC=90°时，平行四边形ABCD是矩形，当④AC⊥BD时，矩形ABCD是正方形，故此选项正确，不合题意．故选：C．【点评】此题主要考查了正方形的判定以及矩形、菱形的判定方法，正确掌握正方形的判定方法是解题关键．二．填空题（共8小题）11．如图．两条等宽的长方形纸条倾斜的重叠着，已知长方形纸条宽为3cm，∠ABC=60°，则四边形ABCD的面积为63cm2．【分析】首先作AE⊥BC于E，AF⊥CD于F，易证得四边形ABCD 是菱形，再由勾股定理求得BC的长，即可求得答案．【解答】解：∵AD∥BC，AB∥CD，∴四边形ABCD是平行四边形，作AE⊥BC于E，AF⊥CD于F，∵∠ABC=60°，∴∠ADF=60°，∵纸条等宽，∴AE=AF，在△ABE和△ADF中，∴△ABE≌△ADF，∴AB=AD，∵AD=BC∴AB=BC，∴该四边形是菱形，∵AE=3cm，∴BE=3，∴BC=2BE=23，∴四边形ABCD的面积=3×23=63cm2．故答案为：63．【点评】此题考查了菱形的判定与性质以及全等三角形的判定与性质．注意准确作出辅助线是解此题的关键．12．（2016•海南）如图，四边形ABCD是轴对称图形，且直线AC是对称轴，AB∥CD，则下列结论：①AC⊥BD；②AD∥BC；③四边形ABCD是菱形；④△ABD≌△CDB．其中正确的是①②③④（只填写序号）【分析】根据轴对称图形的性质，结合菱形的判定方法以及全等三角形的判定方法分析得出答案．【解答】解：因为l是四边形ABCD的对称轴，AB∥CD，则AD=AB，∠1=∠2，∠1=∠4，则∠2=∠4，∴AD=DC，同理可得：AB=AD=BC=DC，所以四边形ABCD是菱形．根据菱形的性质，可以得出以下结论：所以①AC⊥BD，正确；②AD∥BC，正确；③四边形ABCD是菱形，正确；④在△ABD和△CDB中∵∴△ABD≌△CDB（SSS），正确．故答案为：①②③④．【点评】此题考查了轴对称以及菱形的判断与菱形的性质，注意：对称轴垂直平分对应点的连线，对应角相等，对应边相等．13．如图，矩形ABCD中，AB=20cm，BC=4cm，点P从A 开始沿折线A﹣B﹣C﹣D以4cm/s的速度运动，点Q从C开始沿CD边以1cm/s的速度移动，如果点P、Q分别从A、C同时出发，当其中一点到达D时，另一点也随之停止运动，设运动时间为t（s），当t= 4 时，四边形APQD也为矩形．【分析】四边形APQD为矩形，也就是AP=DQ，分别用含t的代数式表示，解即可．【解答】解：根据题意，当AP=DQ时，四边形APQD为矩形．此时，4t=20﹣t，解得t=4（s）．故答案是：4．【点评】本题考查了矩形的判定与性质．此题利用了矩形的对边相等的性质进行解题的．14．如图，△ABC中，∠B=90°，AB=8，BC=6，点D是AC上的任意一点，过点D作DE⊥AB于点E，DF⊥BC于点F，连接EF，则EF 的最小值是 4.8 ．【分析】连接BD，根据矩形的性质可知：EF=BD，当BD最小时，则EF最小，根据垂线段最短可知当EF⊥BD时，则EF最小，再根据三角形的面积为定值即可求出EF的长．【解答】解：∵Rt△ABC中，∠B=90°，AB=8，BC=6，∴AC=10，连接BD，∵DE⊥AB，DF⊥BC，∴四边形EBFD是矩形，∴EF=BD，当BD最小时，则EF最小，根据垂线段最短可知当BD⊥AC时，则BD最小，∴EF=BD==4.8，故答案为：4.8．【点评】本题考查了勾股定理的运用、矩形的判定和性质以及直角三角形的面积的不同求法，题目难度不大，设计很新颖，解题的关键是求DE的最小值转化为其相等线段BD的最小值．15．如图，以边长为1的正方形的四边中点为顶点作四边形，再以所得四边形四边中点为顶点作四边形，…依次作下去，图中所作的第三）个四边形的周长为2；所作的第n个四边形的周长为4（22n．【分析】根据正方形的性质以及三角形中位线的定律，求出第二个，第三个的周长，从而发现规律，即可求出第n个四边形的周长．【解答】解：根据三角形中位线定理得，第一个四边形的边长为=，周长为22，第二个四边形的周长为=4，第三个四边形的周长是：4（2）3=2，2）n，第n个四边形的周长为4（22故答案为2，4（2）n．2【点评】本题考查了正方形的性质以及三角形中位线的定律，以及正方形的周长的求法，根据已知得出规律是解题关键．16．（2016•青岛）如图，在正方形ABCD中，对角线AC与BD相交于点O，E为BC上一点，CE=5，F为DE的中点．若△CEF的周长为．18，则OF的长为72【分析】先根据直角三角形的性质求出DE的长，再由勾股定理得出CD的长，进而可得出BE的长，由三角形中位线定理即可得出结论．【解答】解：∵CE=5，△CEF的周长为18，∴CF+EF=18﹣5=13．∵F为DE的中点，∴DF=EF．∵∠BCD=90°，∴CF=12DE，∴EF=CF=12DE=6.5，∴DE=2EF=13，∴CD===12．∵四边形ABCD是正方形，∴BC=CD=12，O为BD的中点，∴OF是△BDE的中位线，∴OF=12（BC﹣CE）=12（12﹣5）=72．故答案为：72．【点评】本题考查的是正方形的性质，涉及到直角三角形的性质、三角形中位线定理等知识，难度适中．17．（2016•南平）如图，正方形ABCD中，点E、F分别为AB、CDAB，点O为线段EF的中点，过点O作直线与上的点，且AE=CF=13正方形的一组对边分别交于P、Q两点，并且满足PQ=EF，则这样的直线PQ（不同于EF）有 3 条．【分析】能画3条：①与EF互相垂直且垂足为O，构建直角三角形，可以证明两直角三角形全等得EF=PQ；AD，连接PO延长得到PQ；②在AD上截取AP=13AB，连接QO并延长得到PQ．③同理在AB了截取BQ=13【解答】解：这样的直线PQ（不同于EF）有3条，①如图1，过O作PQ⊥EF，交AD于P，BC于Q，则PQ=EF；②如图2，以点A为圆心，以AE为半径画弧，交AD于P，连接PO 并延长交BC于Q，则PQ=EF；③如图3，以B为圆心，以AE为半径画弧，交AB于Q，连接QO并延长交DC于点P，则PQ=EF．【点评】本题考查了正方形的性质和全等三角形的性质与判定，本题虽然是做一条线段与EF相等，实际上是做好两件事：①画线段PQ，②能证明这两条线段相等，这比证明更为复杂，因此首先要构建直角三角形全等，找到与EF相等的边长的位置，本题的线段不止一条，容易丢解，要思考周全．18．如图，在△ABC中，∠ABC=90°，BD为AC边的中线，过点C 作CE⊥BD于点E，过点A作BD的平行线，交CE的延长线于点F，在AF的延长线上截取FG=BD，连接BG、DF．若AB=12，BC=5，则四边形BDFG的周长为26 ．【分析】首先可判断四边形BGFD是平行四边形，再由直角三角形斜边中线等于斜边一半，可得BD=FD，则可判断四边形BGFD是菱形，根据勾股定理求出AC，求出BD，即可得出答案．【解答】解：∵AG∥BD，BD=FG，∴四边形BGFD是平行四边形，∵CF⊥BD，∴CF⊥AG，又∵点D是AC中点，∴BD=DF=12AC，∴四边形BGFD是菱形，∴BG=GF=DF=BD，∵在△ABC中，∠ABC=90°，AB=12，BC=5，由勾股定理得：AC=13，∵BD为△ACB的中线，∴BD=12AC=132，∴BG=GF=DF=BD=132，故四边形BDFG的周长=4GF=26．故答案为：26．【点评】本题考查了菱形的判定与性质、勾股定理及直角三角形的斜边中线的性质，解答本题的关键是判断出四边形BGFD是菱形．三．解答题（共5小题）19．如图所示，四边形ABCD中，∠ADC=∠ABC=90°，AD=CD，DP⊥AB于点P，若四边形ABCD的面积是36，求DP的长．【分析】作DE⊥BC，交BC延长线于E，如图，则四边形BEDP为矩形，再利用等角的余角相等得到∠ADP=∠CDE，则可利用“AAS”证明△ADP≌△CDE，得到DP=DE，S△ADP=S△CDE，所以四边形BEDP为正方形，S四边形ABCD=S矩形BEDP，根据正方形的面积公式得到DP2=36，易得DP=6．【解答】解：作DE⊥BC，交BC延长线于E，如图，∵DP⊥AB，ABC=90°，∴四边形BEDP为矩形，∴∠PDE=90°，即∠CDE+∠PDC=90°，∵∠ADC=90°，即∠ADP+∠PDC=90°，∴∠ADP=∠CDE，在△ADP和△CDE中，，∴△ADP≌△CDE，∴DP=DE，S△ADP=S△CDE，∴四边形BEDP为正方形，S四边形ABCD=S矩形BEDP，∴DP2=36，∴DP=6．【点评】本题考查了全等三角形的判定与性质：全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．也考查了正方形的性质和勾股定理．本题的关键的作辅助线构造两个全等的三角形．20．如图，已知点E，F分别是▱ABCD的边BC，AD上的中点，且∠BAC=90°．（1）求证：四边形AECF是菱形；（2）若∠B=30°，BC=10，求菱形AECF面积．【分析】（1）由平行四边形的性质得出AD=BC，由直角三角形斜边上的中线性质得出AE=12BC=CE，AF=12AD=CF，得出AE=CE=AF=CF，即可得出结论；（2）连接EF交AC于点O，解直角三角形求出AC、AB，由三角形中位线定理求出OE，得出EF，菱形AECF的面积=12AC•EF，即可得出结果．【解答】（1）证明：∵四边形ABCD是平行四边形，∴AD=BC，在Rt△ABC中，∠BAC=90°，点E是BC边的中点，∴AE=12BC=CE，同理，AF=12AD=CF，∴AE=CE=AF=CF，∴四边形AECF是菱形；（2）解：连接EF交AC于点O，如图所示：在Rt△ABC中，∠BAC=90°，∠B=30°，BC=10，∴AC=12BC=5，AB=3AC=53，∵四边形AECF是菱形，∴AC⊥EF，OA=OC，∴OE是△ABC的中位线，∴OE=12AB=，∴EF=53，∴菱形AECF的面积=12AC•EF=12×5×53=．【点评】本题考查了平行四边形的性质、菱形的判定与性质、直角三角形斜边上的中线性质、三角形中位线定理、菱形的面积公式；熟练掌握菱形的判定与性质，并能进行推理论证与计算是解决问题的关键．21．（2016•兰州）阅读下面材料：在数学课上，老师请同学思考如下问题：如图1，我们把一个四边形ABCD的四边中点E，F，G，H依次连接起来得到的四边形EFGH是平行四边形吗？小敏在思考问题是，有如下思路：连接AC．结合小敏的思路作答（1）若只改变图1中四边形ABCD的形状（如图2），则四边形EFGH 还是平行四边形吗？说明理由；参考小敏思考问题方法解决一下问题：（2）如图2，在（1）的条件下，若连接AC，BD．①当AC与BD满足什么条件时，四边形EFGH是菱形，写出结论并证明；②当AC与BD满足什么条件时，四边形EFGH是矩形，直接写出结论．【分析】（1）如图2，连接AC，根据三角形中位线的性质得到EF∥AC，然后根据平行四边形判定定理即可得到结论；AC，EF=12BD，（2）①由（1）知，四边形EFGH是平行四边形，且FG=12HG=1AC，于是得到当AC=BD时，FG=HG，即可得到结论；2②根据平行线的性质得到GH⊥BD，GH⊥GF，于是得到∠HGF=90°，根据矩形的判定定理即可得到结论．【解答】解：（1）是平行四边形，证明：如图2，连接AC，∵E是AB的中点，F是BC的中点，∴EF∥AC，EF=12AC，同理HG∥AC，HG=12AC，综上可得：EF∥HG，EF=HG，故四边形EFGH是平行四边形；（2）①AC=BD．理由如下：由（1）知，四边形EFGH是平行四边形，且FG=12BD，HG=12AC，∴当AC=BD时，FG=HG，∴平行四边形EFGH是菱形，②当AC⊥BD时，四边形EFGH为矩形；理由如下：同（2）得：四边形EFGH是平行四边形，∵AC⊥BD，GH∥AC，∴GH⊥BD，∵GF∥BD，∴GH⊥GF，∴∠HGF=90°，∴四边形EFGH为矩形．【点评】此题主要考查了中点四边形，关键是掌握三角形中位线定理，三角形的中位线平行于第三边且等于第三边的一半．22．如图，在四边形ABCD中，已知AD∥BC，AB⊥BC，点E，F在边AB上，且∠AED=45°，∠BFC=60°，AE=2，EF=2﹣3，FC=23．（1）BC= 3 ．（2）求点D到BC的距离．（3）求DC的长．【分析】（1）由AB⊥BC，FC=23，∠BFC=60°，直接利用三角函数的知识求解即可求得答案；（2）首先过点D作DG⊥BC于点G，由AD∥BC，AB⊥BC，可得DG=AB，继而求得答案；（3）首先可得四边形ABGD是平行四边形，即可求得CG的长，然后由勾股定理求得答案．【解答】解：（1）∵AB⊥BC，∴∠B=90°，∵FC=23，∠BFC=60°，=3；∴BC=FC•sin60°=23×32故答案为：3；（2）过点D作DG⊥BC于点G，∵AD∥BC，AB⊥BC，∴DG=AB，DA⊥AB，∵FC=23，∠BFC=60°，∴BF=FC•cos60°=3，∴DC=AB=AE+EF+BF=2+2﹣3+3=4；（3）∵DA⊥AB，∠AED=45°，∴AD=AE=2，∵DG⊥BC，AB⊥BC，∴DG∥AB，∵AD∥BC，∴四边形ABGD是平行四边形，∴BG=AD=2，∴CG=BC﹣BG=3﹣2=1，∴在Rt△DCG中，CD==17．【点评】此题考查了矩形的判定与性质、勾股定理以及三角函数等知识．注意证得四边形ABGD是平行四边形是解此题的关键．23．在边长为1的正方形ABCD中，点E是射线BC上一动点，AE 与BD相交于点M，AE或其延长线与DC或其延长线相交于点F，G 是EF的中点，连结CG．（1）如图1，当点E在BC边上时．求证：①△ABM≌△CBM；②CG ⊥CM．（2）如图2，当点E在BC的延长线上时，（1）中的结论②是否成立？请写出结论，不用证明．（3）试问当点E运动到什么位置时，△MCE是等腰三角形？请说明理由．【分析】（1）①由正方形的性质得出AB=BC，∠ABM=∠CBM，由SAS证明△ABM≌△CBM即可．②由全等三角形的性质得出∠BAM=∠BCM，由直角三角形斜边上的中线性质得出GC=GF，证出∠GCF=∠F，由平行线的性质得出∠BAM=∠F，因此∠BCM=∠GCF，得出∠BCM+∠GCE=∠GCF+∠GCE=90°，即可得出结论；（2）同（1），即可得出结论；（3）①当点E在BC边上时，由∠MEC＞90°，要使△MCE是等腰三角形，必须EM=EC，得出∠EMC=∠ECM，由三角形的外角性质得出∠AEB=2∠BCM=2∠BAE，由直角三角形的性质得出∠BAE=30°，得出BE=33AB=33；②当点E在BC的延长线上时，同①知BE=3；即可得出结论．【解答】（1）证明：①∵四边形ABCD是正方形，∴AB=BC，∠ABM=∠CBM，在△ABM和△CBM中，，∴△ABM≌△CBM（SAS）．②∵△ABM≌△CBM∴∠BAM=∠BCM，又∵∠ECF=90°，G是EF的中点，∴GC=12EF=GF，∴∠GCF=∠GFC，又∵AB∥DF，∴∠BAM=∠GFC，∴∠BCM=∠GCF，∴∠BCM+∠GCE=∠GCF+∠GCE=90°，∴GC⊥CM；（2）解：成立；理由如下：∵四边形ABCD是正方形，∴AB=BC，∠ABM=∠CBM，在△ABM和△CBM中，，∴△ABM≌△CBM（SAS）∴∠BAM=∠BCM，又∵∠ECF=90°，G是EF的中点，∴GC=GF，∴∠GCF=∠GFC，又∵AB∥DF，∴∠BAM=∠GFC，∴∠BCM=∠GCF，∴∠GCF+∠MCF=∠BCM+MCFE=90°，∴GC⊥CM；（3）解：分两种情况：①当点E在BC边上时，∵∠MEC＞90°，要使△MCE是等腰三角形，必须EM=EC，∴∠EMC=∠ECM，∴∠AEB=2∠BCM=2∠BAE，∴2∠BAE+∠BAE=90°，∴∠BAE=30°，∴BE=33AB=33；②当点E在BC的延长线上时，同①知BE=3．综上①②，当BE=33戓BE=3时，△MCE是等腰三角形．【点评】本题是四边形综合题目，考查了正方形的性质、全等三角形的判定与性质、直角三角形斜边上的中线性质、等腰三角形的性质、直角三角形的性质、含30°角的直角三角形的性质等知识；本题综合性强，有一定难度，证明三角形全等是解决问题的关键．。

特殊平行四边形练习题(答案已做)

特殊平行四边形练习题(答案已做) 特殊平行四边形专题练一、基础知识点复：一）矩形：1、矩形的定义：有四个直角的平行四边形叫矩形。

2、矩形的性质：①.矩形的四个角都是直角；矩形的对角线相等。

②.矩形既是对称图形，又是图形，它有一条对称轴。

3、矩形的判定：①.有四个直角的四边形是矩形。

②.对角线相等的平行四边形是矩形。

③.对角线互相垂直的四边形是矩形。

4、练：①矩形ABCD的两条对角线相交于O，∠AOD=120°，AB=4cm，则矩形对角线AC长为4cm。

②.四边形ABCD的对角线AC，BD相交于点O，能判断它为矩形的题设是（）D．AO=CO，BO=DO，AC⊥BD③.四边形ABCD中，AD//BC，则四边形ABCD是平行四边形，又对角线AC，BD交于点O，若∠1=∠2，则四边形ABCD是矩形。

二）菱形：1、菱形的定义：有一组对边相等的平行四边形叫菱形。

2、菱形的性质：①.菱形的四条边相等；菱形的对角线相等，且每条对角线平分另一条对角线。

②.菱形既是对称图形，又是图形，它有一条对称轴。

3、菱形的判定：①.四个边都相等的四边形是菱形。

②.对角线相等的平行四边形是菱形。

③.对角线互相垂直的四边形是菱形。

4、菱形的面积与两对角线的关系是：面积等于两条对角线的乘积除以2.5、练：①．如图，BD是菱形ABCD的一条对角线，若∠ABD=65°，则∠A=115°。

②．一个菱形的两条对角线分别是6cm，8cm，则这个菱形的周长等于16cm，面积=24cm²。

三、正方形正方形是一种特殊的矩形，它的四边相等且四个角都是直角。

对角线相等且垂直平分。

正方形是一种对称图形，有4条对称轴。

判定一个四边形是正方形，首先需要判定它是矩形，然后再判定它是菱形。

练：1.如果正方形的面积为4，则它的边长为2，对角线长为2√2.2.已知正方形的对角线长为4，则它的边长为2，面积为4.3.在△ABC中，如果AB=AC，点D，E，F分别是边AB，BC，AC的中点，连接DE，EF，要使四边形ADEF是正方形，还需增加条件：∠BAC=90°。