2015人教版高一数学必修二第二章点、直线、平面之间的位置关系作业题及答案解析第2章 2.2.2
高中数学必修2第二章点、直线、平面之间的位置关系测试题+答案

第二章直线与平面得位置关系测试题一、选择题1、设,为两个不同得平面,l,m为两条不同得直线,且l,m,有如下得两个命题:①若∥,则l∥m;②若l⊥m,则⊥、那么( )、A、①就就是真命题,②就就是假命题ﻩB、①就就是假命题,②就就是真命题C、①②都就就是真命题ﻩﻩD、①②都就就是假命题2、如图,ABCD-A1B1C1D1为正方体,下面结论错误..得就就是()、A、BD∥平面CB1D1B、AC1⊥BDC、AC1⊥平面CB1D1D、异面直线AD与CB1角为60°(第2题)3、关于直线m,n 与平面,,有下列四个命题:①m ∥,n ∥且∥,则m∥n;ﻩﻩ②m ⊥,n ⊥且⊥,则m⊥n;③m ⊥,n ∥且∥,则m⊥n; ④m ∥,n ⊥且⊥,则m∥n、其中真命题得序号就就是( )、A、①②ﻩB、③④ﻩﻩC、①④ﻩﻩﻩD、②③4、给出下列四个命题:①垂直于同一直线得两条直线互相平行②垂直于同一平面得两个平面互相平行③若直线l1,l2与同一平面所成得角相等,则l1,l2互相平行④若直线l1,l2就就是异面直线,则与l1,l2都相交得两条直线就就是异面直线其中假.命题得个数就就是( )、A、1ﻩﻩﻩB、2ﻩﻩﻩﻩC、3 ﻩﻩD、45、下列命题中正确得个数就就是( )、①若直线l 上有无数个点不在平面内,则l∥②若直线l与平面平行,则l与平面内得任意一条直线都平行③如果两条平行直线中得一条直线与一个平面平行,那么另一条直线也与这个平面平行④若直线l与平面平行,则l与平面内得任意一条直线都没有公共点A、0个ﻩB、1个ﻩﻩC、2个ﻩﻩﻩD、3个6、两直线l1与l2异面,过l1作平面与l2平行,这样得平面( )、A、不存在ﻩB、有唯一得一个ﻩC、有无数个ﻩﻩﻩD、只有两个7、把正方形ABCD沿对角线AC折起,当以A,B,C,D四点为顶点得三棱锥体积最大时,直线BD与平面ABC所成得角得大小为( )、A、90°ﻩB、60°ﻩC、45°ﻩﻩD、30°8、下列说法中不正确得....就就是( )、A、空间中,一组对边平行且相等得四边形一定就就是平行四边形B、同一平面得两条垂线一定共面C、过直线上一点可以作无数条直线与这条直线垂直,且这些直线都在同一个平面内D、过一条直线有且只有一个平面与已知平面垂直9、给出以下四个命题:①如果一条直线与一个平面平行,经过这条直线得一个平面与这个平面相交,那么这条直线与交线平行②如果一条直线与一个平面内得两条相交直线都垂直,那么这条直线垂直于这个平面③如果两条直线都平行于一个平面,那么这两条直线互相平行④如果一个平面经过另一个平面得一条垂线,那么些两个平面互相垂直其中真命题得个数就就是( )、A、4B、3 ﻩC、2 ﻩD、110、异面直线a,b所成得角60°,直线a⊥c,则直线b与c所成得角得范围为( )、A 、[30°,90°]B 、[60°,90°] ﻩC 、[30°,60°]D、[30°,120°] 二、填空题11、已知三棱锥P -ABC 得三条侧棱PA ,PB ,PC 两两相互垂直,且三个侧面得面积分别为S 1,S 2,S 3,则这个三棱锥得体积为 、12、P就就是△A BC 所在平面外一点,过P 作P O⊥平面,垂足就就是O ,连PA ,PB ,P C、(1)若P A=PB =PC ,则O 为△AB C 得 心; (2)PA ⊥PB ,PA ⊥P C,PC ⊥PB,则O就就是△AB C 得 心;(3)若点P 到三边AB ,B C,CA 得距离相等,则O 就就是△AB C 得 心;(4)若PA =PB =PC ,∠C =90º,则O 就就是AB边得 点; (5)若PA =PB =PC ,AB =AC ,则点O在△ABC 得 线上、 13、如图,在正三角形ABC 中,D ,E,F 分别为各边得中点,G ,H ,I ,J 分别为AF ,A D,BE ,DE 得中点,将△A BC 沿DE ,EF,DF 折成三棱锥以后,GH 与IJ 所成角得度数为 、14、直线l与平面所成角为30°,l ∩=A ,直线m ∈,则m 与l所成角得取值范围 就就是 、15、棱长为1得正四面体内有一点P,由点P 向各面引垂线,垂线段长度分别为d1,d 2,d 3,d 4,则d 1+d2+d 3+d 4得值为 、16、直二面角-l -得棱上有一点A ,在平面,内各有一条射线AB ,AC与l成45°,AB ,AC,则∠BA C= 、三、解答题17、在四面体A BCD 中,△ABC 与△DBC 都就就是边长为4得正三角形、J(第13题)(1)求证:BC ⊥AD ;(2)若点D 到平面AB C得距离等于3,求二面角A-BC -D 得正弦值;(3)设二面角A-BC -D 得大小为,猜想为何值时,四面体A -B CD 得体积最大、(不要求证明)18、 如图,在长方体ABC D—A 1B1C 1D 1中,AB =2,BB 1=BC =1,E 为D 1C 1得中点,连结E D,EC,E B与DB 、(1)求证:平面EDB ⊥平面EB C; (2)求二面角E -DB -C 得正切值、19*、如图,在底面就就是直角梯形得四棱锥S-ABCD 中,A D∥B C,∠ABC =90°, SA ⊥面A BCD ,S A=A B=BC =1,AD =、(1)求四棱锥S—ABCD 得体积;(2)求面SCD 与面S BA 所成得二面角得正切值、 (提示:延长 BA ,CD 相交于点 E ,则直线 SE 就就是 所求二面角得棱、)ﻩﻩﻩ ﻩ ﻩ(第19题)20*、斜三棱柱得一个侧面得面积为10,这个侧面与它所对棱得距离等于6,求这个棱柱得体积、(提示:在 AA 1 上取一点 P ,过 P 作棱柱得截面,使 AA1 垂直于这个截面、)ﻩ ﻩﻩﻩ ﻩﻩﻩ (第20题)ﻬ第二章 点、直线、平面之间得位置关系参考答案一、选择题(第18题)(第17题)1、D解析:命题②有反例,如图中平面∩平面=直线n,l,m,且l∥n,m⊥n,则m⊥l,显然平面不垂直平面,(第1题)故②就就是假命题;命题①显然也就就是假命题,2、D解析:异面直线AD与CB1角为45°、3、D解析:在①、④得条件下,m,n得位置关系不确定、4、D解析:利用特殊图形正方体我们不难发现①②③④均不正确,故选择答案D、5、B解析:学会用长方体模型分析问题,A1A有无数点在平面ABCD外,但AA1与平面ABCD相交,①不正确;A1B1∥平面ABCD,显然A1B1不平行于BD,②不正确;A1B1∥AB,A1B1∥平面ABCD,但AB平面ABCD内,③不正确;l与平面α平行,则l与无公共点,l与平面内得所有直线都没有公共点,④正确,应选B、(第5题)6、B解析:设平面过l1,且l2∥,则l1上一定点P与l2确定一平面,与得交线l3∥l2,且l3 过点P、又过点P与l2平行得直线只有一条,即l3有唯一性,所以经过l1与l3得平面就就是唯一得,即过l1且平行于l2得平面就就是唯一得、7、C解析:当三棱锥D-ABC体积最大时,平面DAC⊥ABC,取AC得中点O,则△DBO就就是等腰直角三角形,即∠DBO=45°、8、D解析:A、一组对边平行就决定了共面;B、同一平面得两条垂线互相平行,因而共面;C、这些直线都在同一个平面内即直线得垂面;D、把书本得书脊垂直放在桌上就明确了、9、B解析:因为①②④正确,故选B、10、A解析:异面直线,所成得角为60°,直线⊥,过空间任一点P,作直线a’∥a,b’∥b, c’∥c、若a’,b’,c’共面则b’与c’成30°角,否则’与’所成得角得范围为(30°,90°],所以直线b与c所成角得范围为[30°,90°] 、二、填空题11、、解析:设三条侧棱长为a,b,c、则ab=S1,bc=S2,ca=S3三式相乘:∴ a2 b2 c2=S1S2S3,∴ abc=2、∵ 三侧棱两两垂直,∴ V=abc·=、12、外,垂,内,中,BC边得垂直平分、解析:(1)由三角形全等可证得O为△ABC 得外心;(2)由直线与平面垂直得判定定理可证得,O 为△ABC 得垂心;(3)由直线与平面垂直得判定定理可证得,O为△ABC 得内心;(4)由三角形全等可证得,O 为AB 边得中点;(5)由(1)知,O 在BC边得垂直平分线上,或说O 在∠BAC得平分线上、13、60°、解析:将△ABC沿DE,EF,DF折成三棱锥以后,GH与IJ所成角得度数为60°、14、[30°,90°]、解析:直线l与平面所成得30°得角为m与l 所成角得最小值,当m在内适当旋转就可以得到l⊥m,即m与l所成角得得最大值为90°、15、、解析:作等积变换:×(d1+d2+d3+d4)=·h,而h=、16、60°或120°、解析:不妨固定AB,则AC有两种可能、三、解答题17、证明:(1)取BC中点O,连结AO,DO、∵△ABC,△BCD都就就是边长为4得正三角形,∴AO⊥BC,DO⊥BC,且AO∩DO=O,∴BC⊥平面AOD、又AD平面AOD,∴BC⊥AD、(第17题)解:(2)由(1)知∠AOD为二面角A-BC-D得平面角,设∠AOD=,则过点D作DE⊥AD,垂足为E、∵BC⊥平面ADO,且BC平面ABC,∴平面ADO⊥平面ABC、又平面ADO∩平面ABC=AO,∴DE⊥平面ABC、∴线段DE得长为点D到平面ABC得距离,即DE=3、又DO=BD=2,在Rt△DEO中,sin==,故二面角A-BC-D得正弦值为、(3)当=90°时,四面体ABCD得体积最大、18、证明:(1)在长方体ABCD-A1B1C1D1中,AB=2,BB1=BC=1,E为D1C1得中点、∴△DD1E为等腰直角三角形,∠D1ED=45°、同理∠C1EC=45°、∴,即DE⊥EC、在长方体ABCD-中,BC⊥平面,又DE平面,∴BC⊥DE、又,∴DE⊥平面EBC、∵平面DEB过DE,∴平面DEB⊥平面EBC、(2)解:如图,过E在平面中作EO⊥DC于O、在长方体ABCD-中,∵面ABCD⊥面,∴EO⊥面ABCD、过O在平面DBC中作OF⊥DB于F,连结EF,∴EF⊥BD、∠EFO为二面角E-DB-C得平面角、利用平面几何知识可得OF=, (第18题)又OE=1,所以,tan EFO=、19*、解:(1)直角梯形ABCD得面积就就是M底面==,∴四棱锥S—ABCD得体积就就是V=·SA·M底面=×1×=、(2)如图,延长BA,CD相交于点E,连结SE,则SE就就是所求二面角得棱、∵AD∥BC,BC=2AD,∴EA=AB=SA,∴SE⊥SB∵SA⊥面ABCD,得面SEB⊥面EBC,EB就就是交线、又BC⊥EB,∴BC⊥面SEB,故SB就就是SC在面SEB上得射影,∴CS⊥SE,∠BSC就就是所求二面角得平面角、∵SB==,BC=1,BC⊥SB,∴tan∠BSC=, ﻩﻩﻩﻩ(第19题)即所求二面角得正切值为、20*、解:如图,设斜三棱柱ABC—A1B1C1得侧面BB1C1C得面积为10,A1A与面BB1C1C得距离为6,在AA1上取一点P作截面PQR,使AA1⊥截面PQR,AA1∥CC1,∴截面PQR⊥侧面BB1C1C,过P作PO⊥QR于O,则PO⊥侧面BB1C1C,且PO=6、∴V斜=S△PQR·AA1=·QR·PO·AA1ﻩﻩﻩ=·PO·QR·BB1=×10×6=30、(第20题)。
人教版高中数学必修二第二章《点、直线、平面之间的位置关系》(内含答案解析)

人教版高中数学必修二第二章《点、直线、平面之前的位置关系》(内含答案解析)一、选择题1.直线a∥平面α,α内有n条直线交于一点,那么这n条直线中与直线a平行的()A.至少有一条B.至多有一条C.有且只有一条D.没有【解析】过a和平面内n条直线的交点只有一个平面β,所以平面α与平面β只有一条交线,且与直线a平行,这条交线可能不是这n条直线中的一条也可能是.故选B.【答案】B2.设a,b是两条直线,α,β是两个平面,若a∥α,a⊂β,α∩β=b,则α内与b相交的直线与a的位置关系是()A.平行 B.相交C.异面 D.平行或异面【解析】条件即为线面平行的性质定理,所以a∥b,又a与α无公共点,故选C.【答案】C3.下列命题中不正确的是()A.两个平面α∥β,一条直线a平行于平面α,则a一定平行于平面βB.平面α∥平面β,则α内的任意一条直线都平行于平面βC.一个三角形有两条边所在的直线平行于一个平面,那么三角形所在平面与这个平面平行D.分别在两个平行平面内的两条直线只能是平行直线或者是异面直线【解析】选项A中直线a可能与β平行,也可能在β内,故选项A不正确;三角形两边必相交,这两条相交直线平行于一个平面,那么三角形所在的平面与这个平面平行,所以选项C正确;依据平面与平面平行的性质定理可知,选项B,D也正确,故选A.【答案】A4.如图2221,四棱锥P ABCD中,M,N分别为AC,PC上的点,且MN∥平面P AD,则()图2221A.MN∥PDB.MN∥P AC.MN∥ADD.以上均有可能【解析】∵MN∥平面P AD,MN⊂平面P AC,平面P AD∩平面P AC=P A,∴MN∥P A.【答案】B5.设平面α∥平面β,A∈α,B∈β,C是AB的中点,当点A、B分别在平面α,β内运动时,动点C()A.不共面B.当且仅当点A、B分别在两条直线上移动时才共面C.当且仅当点A、B分别在两条给定的异面直线上移动时才共面D.无论点A,B如何移动都共面【解析】无论点A、B如何移动,其中点C到α、β的距离始终相等,故点C在到α、β距离相等且与两平面都平行的平面上.【答案】D二、填空题6.下列四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是________(写出所有符合要求的图形序号).图229【解析】①设MP中点为O,连接NO.易得AB∥NO,又AB⊄平面MNP,所以AB∥平面MNP.②若下底面中心为O,易知NO∥AB,NO⊄平面MNP,所以AB与平面MNP不平行.③易知AB∥MP,所以AB∥平面MNP.④易知存在一直线MC∥AB,且MC⊄平面MNP,所以AB与平面MNP不平行.【答案】①③7.在如图2210所示的几何体中,三个侧面AA1B1B,BB1C1C,CC1A1A都是平行四边形,则平面ABC与平面A1B1C1平行吗?______(填“是”或“否”).图2210【解析】因为侧面AA1B1B是平行四边形,所以AB∥A1B1,因为AB⊄平面A1B1C1,A1B1⊂平面A1B1C1,所以AB∥平面A1B1C1,同理可证:BC∥平面A1B1C1.又因为AB∩BC=B,AB⊂平面ABC,BC⊂平面ABC,所以平面ABC∥平面A1B1C1.【答案】是三、解答题8.如图2123,长方体ABCDA1B1C1D1中,E,F分别为棱AA1,CC1的中点.(1)求证:D1E∥BF;(2)求证:∠B1BF=∠D1EA1.图2123【证明】(1)取BB1的中点M,连接EM,C1M.在矩形ABB1A1中,易得EM═∥A1B1,∵A1B1═∥C1D1,∴EM═∥C1D1,∴四边形EMC1D1为平行四边形,∴D1E∥C1M.在矩形BCC1B1中,易得MB═∥C1F,∴BF═∥C1M.∴D1E∥BF.(2)∵ED1∥BF,BM∥EA1,又∠B1BF与∠D1EA1的对应边方向相同,∴∠B1BF=∠D1EA1.9.如图2124,正方体ABCDEFGH中,O为侧面ADHE的中心,求:(1)BE与CG所成的角;(2)FO与BD所成的角.图2124【解】(1)如图,因为CG∥BF,所以∠EBF(或其补角)为异面直线BE与CG所成的角,又△BEF中,∠EBF=45°,所以BE与CG所成的角为45°.(2)连接FH,因为HD═∥EA,EA═∥FB,所以HD═∥FB,所以四边形HFBD为平行四边形,所以HF∥BD,所以∠HFO(或其补角)为异面直线FO与BD所成的角.连接HA、AF,易得FH=HA=AF,所以△AFH为等边三角形,又依题意知O为AH的中点,所以∠HFO=30°,即FO与BD所成的角是30°.10.如图2125是正方体的平面展开图,在这个正方体中,图2125①BM与ED平行;②CN与BE是异面直线;③CN与BM成60°角;④DM与BN是异面直线.以上四个命题中,正确命题的序号是()A.①②③B.②④C.③④ D.②③④【解析】由题意画出正方体的图形如图:显然①②不正确;③CN与BM成60°角,即∠ANC=60°,正确;④正确.【答案】C11.在四面体ABCD中,E、F分别是AB、CD的中点.若BD、AC所成的角为60°,且BD=AC=1.求EF的长度.【解】如图,取BC中点O,连接OE、OF,∵OE∥AC,OF∥BD,∴OE与OF所成的锐角(或直角)即为AC与BD所成的角,而AC、BD所成的角为60°.∴∠EOF=60°或∠EOF=120°.当∠EOF=60°时,EF=OE=OF=21.当∠EOF=120°时,取EF的中点M,连接OM,则OM⊥EF,EF=2EM=2×43=23.。
【优质文档】必修二第二章点、直线、平面之间的位置关系全章练习题(含答案)

§2.1 空间点、直线、平面之间的位置关系
2.1.1 平 面
一、基础过关
1.下列命题: ①书桌面是平面;
②有一个平面的长是 50m,宽是 20m;
③平面是绝对的平、无厚度,可以无限延展的抽象数学概念.
其中正确命题的个数为
()
A.1 个
B.2 个
C. 3 个
D.0 个
2.下列图形中,不一定是平面图形的是 A .三角形
B.菱形
()
C .梯形
D .四边相等的四边形
3.空间中,可以确定一个平面的条件是
()
A .两条直线
B .一点和一条直线
C .一个三角形
D .三个点
4.已知平面 α与平面 β、 γ都相交,则这三个平面可能的交线有
()
A . 1 条或 2 条
B. 2 条或 3 条
即点 S 在交线上, 由于 AB>CD ,则分别延长 AC 和 BD 交于点 E,如图所示. ∵E∈ AC, AC? 平面 SAC, ∴E∈ 平面 SAC. 同理,可证 E∈ 平面 SBD. ∴ 点 E 在平面 SBD 和平面 SAC 的交线上,连接 SE,直线 SE 是平面 SBD 和平面 SAC 的 交线. 8. 证明 ∵ l 1? β, l2? β, l1D ∥ l 2, ∴ l 1、 l 2 交于一点,记交点为 P. ∵ P∈ l 1? α, P∈ l2? γ, ∴P∈ α∩ γ= l3, ∴ l 1, l 2, l3 交于一点. 9. C 10.C 11.③ 12.证明 因为 AB∥ CD,所以 AB,CD 确定平面 AC,AD∩ α= H,因为 H ∈ 平面 AC,H ∈α, 由公理 3 可知, H 必在平面 AC 与平面 α的交线上.同理 F、G、E 都在平面 AC 与平面 α 的交线上,因此 E, F , G, H 必在同一直线上. 13. 证明 (1)∵ C1、 O、 M ∈平面 BDC1, 又 C1、 O、 M ∈ 平面 A1ACC1,由公理 3 知,点 C1、 O、 M 在平面 BDC 1 与平面 A1ACC1 的交线上, ∴ C1、 O、 M 三点共线. (2) ∵ E, F 分别是 AB, A1A 的中点, ∴ EF∥ A1B.∵ A1B∥CD 1, ∴ EF∥ CD 1. ∴ E、 C、 D1、 F 四点共面.
【三维设计】人教版高中数学必修2练习:第二章 点、直线、平面之间的位置关系(含答案解析)

2.1空间点、直线、平面之间的位置关系2.1.1平面平面[导入新知]1.平面的概念几何里所说的“平面”,是从课桌面、黑板面、海面这样的一些物体中抽象出来的.几何里的平面是无限延展的.2.平面的画法(1)水平放置的平面通常画成一个平行四边形,它的锐角通常画成45°,且横边长等于其邻边长的2倍.如图①所示.(2)如果一个平面被另一个平面遮挡住,为了增强它的立体感,把被遮挡部分用虚线画出来.如图②所示.3.平面的表示法图①的平面可表示为平面α、平面ABCD、平面AC或平面BD.[化解疑难]几何中的平面有以下几个特点(1)平面是平的.(2)平面是没有厚度的.(3)平面是无限延展而没有边界的.平面的基本性质[导入新知]平面的基本性质从集合角度理解点、线、面之间的关系(1)直线可以看成无数个点组成的集合,故点与直线的关系是元素与集合的关系,用“∈”或“∉”表示.(2)平面也可以看成点集,故点与平面的关系也是元素与集合的关系,用“∈”或“∉”表示.(3)直线和平面都是点集,它们之间的关系可看成集合与集合的关系,故用“⊂”或“⊄”表示.文字语言、图形语言、符号语言的相互转化[例1] 如右图所示,根据图形用符号表示下列点、直线、平面之间的关系.(1)点P 与直线AB . (2)点C 与直线AB . (3)点M 与平面AC . (4)点A 1与平面AC . (5)直线AB 与直线BC . (6)直线AB 与平面AC . (7)平面A 1B 与平面AC .[解](1)点P∈直线AB;(2)点C∉直线AB;(3)点M∈平面AC;(4)点A1∉平面AC;(5)直线AB∩直线BC=点B;(6)直线AB⊂平面AC;(7)平面A1B∩平面AC=直线AB.[类题通法]三种语言的转换方法(1)用文字语言、符号语言表示一个图形时,首先仔细观察图形有几个平面、几条直线且相互之间的位置关系如何,试着用文字语言表示,再用符号语言表示.(2)根据符号语言或文字语言画相应的图形时,要注意实线和虚线的区别.[活学活用]根据下列符号表示的语句,说明点、线、面之间的位置关系,并画出相应的图形:(1)A∈α,B∉α;(2)l⊂α,m∩α=A,A∉l;(3)P∈l,P∉α,Q∈l,Q∈α.解:(1)点A在平面α内,点B不在平面α内,如图①所示;(2)直线l在平面α内,直线m与平面α相交于点A,且点A不在直线l上,如图②所示;(3)直线l经过平面α外一点P和平面α内一点Q,如图③所示.点、线共面问题[例2]证明两两相交且不共点的3条直线在同一平面内.[解]已知:如图所示,l1∩l2=A,l2∩l3=B,l1∩l3=C.求证:直线l1,l2,l3在同一平面内.法一:(纳入平面法)∵l1∩l2=A,∴l1和l2确定一个平面α.∵l2∩l3=B,∴B∈l2.又∵l2⊂α,∴B∈α.同理可证C∈α.又∵B∈l3,C∈l3,∴l3⊂α.∴直线l1,l2,l3在同一平面内.法二:(辅助平面法)∵l1∩l2=A,∴l1,l2确定一个平面α.∵l2∩l3=B,∴l2,l3确定一个平面β.∵A∈l2,l2⊂α,∴A∈α.∵A∈l2,l2⊂β,∴A∈β.同理可证B∈α,B∈β,C∈α,C∈β.∴不共线的三个点A,B,C既在平面α内,又在平面β内.∴平面α和β重合,即直线l1,l2,l3在同一平面内.[类题通法]证明点、线共面问题的理论依据是公理1和公理2,常用方法有以下几种(1)先由部分点、线确定一个面,再证其余的点、线都在这个平面内,即用“纳入法”.(2)先由其中一部分点、线确定一个平面α,其余点、线确定另一个平面β,再证平面α与β重合,即用“同一法”.(3)假设不共面,结合题设推出矛盾,用“反证法”.[活学活用]下列说法正确的是()①任意3点确定一个平面;②圆上的3点确定一个平面;③任意4点确定一个平面;④两条平行线确定一个平面.A.①②B.②③C.②④D.③④答案:C共线问题[例3]已知△ABC在平面α外,其三边所在的直线满足AB∩α=P,BC∩α=Q,AC∩α=R,如右图所示.求证:P,Q,R 3点共线.[证明]法一:∵AB∩α=P,∴P∈AB,P∈平面α.又∵AB⊂平面ABC,∴P∈平面ABC.∴由公理3可知,点P在平面ABC与平面α的交线上,同理可证Q,R也在平面ABC 与平面α的交线上.∴P,Q,R 3点共线.法二:∵AP∩AR=A,∴直线AP与直线AR确定平面APR.又∵AB∩α=P,AC∩α=R,∴平面APR∩平面α=PR.∵B∈平面APR,C∈平面APR,∴BC⊂平面APR.∵Q∈BC,∴Q∈平面APR,又Q∈α,∴Q∈PR,∴P,Q,R三点共线.[类题通法]点共线:证明多点共线通常利用公理3,即两相交平面交线的唯一性,通过证明点分别在两个平面内,证明点在相交平面的交线上,也可选择其中两点确定一条直线,然后证明其他点也在其上.[活学活用]如右图所示,在正方体ABCD-A1B1C1D1中,设线段A1C与平面ABC1D1交于点Q,求证:B,Q,D1 3点共线.证明:如图所示,连接A1B,CD1.显然B∈平面A1BCD1,D1∈平面A1BCD1.∴BD1⊂平面A1BCD1.同理BD1⊂平面ABC1D1.∴平面ABC1D1∩平面A1BCD1=BD1.∵A1C∩平面ABC1D1=Q,∴Q∈平面ABC1D1.又∵A1C⊂平面A1BCD1,∴Q∈平面A1BCD1.∴Q∈BD1,即B,Q,D1三点共线.2.证明三线共点问题[典例](12分)如下图所示,在四面体ABCD中,E,G分别为BC,AB的中点,F在CD上,H在AD上,且有DF∶FC=DH∶HA=2∶3.求证:EF,GH,BD交于一点.[解题流程][活学活用]如右图所示,在空间四边形各边AD ,AB ,BC ,CD 上分别取E ,F ,G ,H 四点,如果EF ,GH 交于一点P ,求证:点P 在直线BD 上.证明:∵EF ∩GH =P ,∴P ∈EF 且P ∈GH .又∵EF ⊂平面ABD ,GH ⊂平面CBD ,∴P ∈平面ABD ,且P ∈平面CBD ,又P ∈平面ABD ∩平面CBD ,平面ABD ∩平面CBD =BD ,由公理3可得P ∈BD .∴点P 在直线BD 上.一、选择题1.用符号表示“点A 在直线l 上,l 在平面α外”,正确的是( )A.A∈l,l∉αB.A∈l,l⊄αC.A⊂l,l⊄αD.A⊂l,l∉α答案:B2.下列说法正确的是()A.三点可以确定一个平面B.一条直线和一个点可以确定一个平面C.四边形是平面图形D.两条相交直线可以确定一个平面答案:D3.空间两两相交的3条直线,可以确定的平面数是()A.1 B.2C.3 D.1或3答案:D4.下列推断中,错误的是()A.A∈l,A∈α,B∈l,B∈α⇒l⊂αB.A∈α,A∈β,B∈α,B∈β⇒α∩β=ABC.l⊄α,A∈l⇒A∉αD.A,B,C∈α,A,B,C∈β,且A,B,C不共线⇒α,β重合答案:C5.在空间四边形ABCD的边AB,BC,CD,DA上分别取E,F,G,H四点,如果EF 与HG交于点M,那么()A.M一定在直线AC上B.M一定在直线BD上C.M可能在直线AC上,也可能在直线BD上D.M既不在直线AC上,也不在直线BD上答案:A二、填空题6.线段AB在平面α内,则直线AB与平面α的位置关系是________.答案:直线AB⊂平面α7.把下列符号叙述所对应的图形的字母编号填在题后横线上.(1)A∉α,a⊂α________.(2)α∩β=a,P∉α且P∉β________.(3)a⊄α,a∩α=A________.(4)α∩β=a,α∩γ=c,β∩γ=b,a∩b∩c=O________.答案:(1)C(2)D(3)A(4)B8.平面α∩平面β=l,点A,B∈α,点C∈平面β且C∉l,AB∩l=R,设过点A,B,C 3点的平面为平面γ,则β∩γ=________.答案:CR三、解答题9.求证:如果两两平行的3条直线都与另一条直线相交,那么这4条直线共面.解:已知:a∥b∥c,l∩a=A,l∩b=B,l∩c=C.求证:直线a,b,c和l共面.证明:如图所示,因为a∥b,由公理2可知直线a与b确定一个平面,设为α.因为l∩a=A,l∩b=B,所以A∈a,B∈b,则A∈α,B∈α.又因为A∈l,B∈l,所以由公理1可知l⊂α.因为b∥c,所以由公理2可知直线b与c确定一个平面β,同理可知l⊂β.因为平面α和平面β都包含着直线b与l,且l∩b=B,而由公理2的推论2知,经过两条相交直线,有且只有一个平面,所以平面α与平面β重合,所以直线a,b,c和l共面.10.已知正方体ABCD -A1B1C1D1中,E,F分别为D1C1,C1B1的中点,AC∩BD=P,A1C1∩EF=Q.求证:(1)D,B,F,E 4点共面;(2)若A1C交平面DBFE于R点,则P,Q,R 3点共线.证明:如图.(1)连接B1D1,∵EF是△D1B1C1的中位线,∴EF∥B1D1.在正方体AC1中,B1D1∥BD,∴EF∥BD.∴EF,BD确定一个平面,即D,B,F,E四点共面.(2)正方体AC1中,设平面A1ACC1确定的平面为α,又设平面BDEF为β. ∵Q∈A1C1,∴Q∈α.又Q∈EF,∴Q∈β.则Q是α与β的公共点,同理P是α与β的公共点,∴α∩β=PQ.又A1C∩β=R,∴R∈A1C.∴R∈α,且R∈β,则R∈PQ.故P,Q,R 3点共线.2.1.2空间中直线与直线之间的位置关系空间两直线的位置关系[导入新知]1.异面直线(1)定义:不同在任何一个平面内的两条直线.(2)异面直线的画法:2.空间两条直线的位置关系[化解疑难]1.对于异面直线的定义的理解异面直线是不同在任何一个平面内的两条直线.注意异面直线定义中“任何”两字,它指空间中的所有平面,因此异面直线也可以理解为:在空间中找不到一个平面,使其同时经过a ,b 两条直线.例如,如右图所示的长方体中,棱AB 和B 1C 1所在的直线既不平行又不相交,找不到一个平面同时经过这两条棱所在的直线,故AB 与B 1C 1是异面直线.2.空间两条直线的位置关系(1)若从有无公共点的角度来看,可分为两类:直线⎩⎨⎧有且仅有一个公共点——相交直线无公共点——⎩⎪⎨⎪⎧平行直线异面直线(2)若从是否共面的角度看,也可分两类:直线⎩⎨⎧共面直线⎩⎪⎨⎪⎧相交直线平行直线不共面直线:异面直线平行公理及等角定理 [导入新知]1.平行公理(公理4)(1)文字表述:平行于同一条直线的两条直线互相平行.这一性质叫做空间平行线的传递性.(2)符号表述:⎭⎪⎬⎪⎫a ∥b b ∥c ⇒a ∥c . 2.等角定理空间中如果两个角的两边分别对应平行,那么这两个角相等或互补. 3.异面直线所成的角(1)定义:已知两条异面直线a ,b ,经过空间任一点O 作直线a ′∥a ,b ′∥b ,我们把a ′与b ′所成的锐角(或直角)叫做异面直线a 与b 所成的角(或夹角).(2)异面直线所成的角θ的取值范围:0°<θ≤90°.(3)当θ=90°时,a与b互相垂直,记作a⊥b.[化解疑难]对平行公理与等角定理的理解公理4表明了平行的传递性,它可以作为判断两直线平行的依据,同时也给出了空间两直线平行的一种证明方法.等角定理是由平面图形推广到空间图形而得到的,它是公理4的直接应用,并且当这两个角的两边方向分别相同时,它们相等,否则它们互补.两直线位置关系的判定[例1]如右图所示,正方体ABCD-A1B1C1D1中,判断下列直线的位置关系:(1)直线A1B与直线D1C的位置关系是________;(2)直线A1B与直线B1C的位置关系是________;(3)直线D1D与直线D1C的位置关系是________;(4)直线AB与直线B1C的位置关系是________.[答案](1)平行(2)异面(3)相交(4)异面[类题通法]1.判定两条直线平行或相交的方法判定两条直线平行或相交可用平面几何的方法去判断,而两条直线平行也可以用公理4判断.2.判定两条直线是异面直线的方法(1)定义法:由定义判断两直线不可能在同一平面内.(2)重要结论:连接平面内一点与平面外一点的直线,和这个平面内不经过此点的直线是异面直线.用符号语言可表示为A∉α,B∈α,l⊂α,B∉l⇒AB与l是异面直线(如右图).[活学活用]如右图所示,正方体ABCD-A1B1C1D1中,M,N分别是A1B1,B1C1的中点.问:(1)AM和CN是否是异面直线?说明理由.(2)D1B和CC1是否是异面直线?说明理由.解:(1)不是异面直线.理由:∵M,N分别是A1B1,B1C1的中点,∴MN∥A1C1.又A1A D1D,而D1D C1C,∴A1A C1C.∴四边形A1ACC1为平行四边形.∴A1C1∥AC,得到MN∥AC.∴A,M,N,C在同一个平面内,故AM和CN不是异面直线.(2)是异面直线.证明如下:假设D1B与CC1在同一个平面D1CC1内,则B∈平面CC1D1,C∈平面CC1D1,∴BC⊂平面CC1D1.而BC⊥平面CC1D1,BC⊄平面CC1D1,∴假设不成立,故D1B与CC1是异面直线.平行公理及等角定理的应用[例2]如右图所示,在正方体ABCD-A1B1C1D1中,M,M1分别是棱AD和A1D1的中点.(1)求证:四边形BB1M1M为平行四边形;(2)求证:∠BMC=∠B1M1C1.[证明](1)在正方形ADD1A1中,M,M1分别为AD,A1D1的中点,∴MM1AA1.又∵AA1BB1,∴MM1∥BB1,且MM1=BB1,∴四边形BB1M1M为平行四边形.(2)由(1)知四边形BB1M1M为平行四边形,∴B1M1∥BM.同理可得四边形CC1M1M为平行四边形,∴C1M1∥CM.由平面几何知识可知,∠BMC和∠B1M1C1都是锐角.∴∠BMC=∠B1M1C1.[类题通法]1.证明两条直线平行的方法:(1)平行线定义.(2)三角形中位线定理、平行四边形性质等.(3)公理4.2.空间中,如果两个角的两边分别对应平行,那么这两个角相等或互补,当两个角的两边方向都相同时或都相反时,两个角相等,否则两个角互补.因此,在证明两个角相等时,只说明两个角的两边分别对应平行是不够的.[活学活用]已知正方体ABCD-A1B1C1D1中,E,F分别是AA1,CC1的中点.求证:BF ED1.证明:如图所示,取BB1的中点G,连接GC1,GE.∵F 为CC 1的中点, ∴BG C 1F .∴四边形BGC 1F 为平行四边形. ∴BF GC 1.又∵EG A 1B 1,A 1B 1C 1D 1,∴EG D 1C 1,∴四边形EGC 1D 1为平行四边形,∴ED 1GC 1,∴BF ED 1.两异面直线所成的角[例3] 如右图所示,已知长方体ABCD -A 1B 1C 1D 1中,A 1A =AB ,E ,F 分别是BD 1和AD 的中点,求异面直线CD 1,EF 所成的角的大小.[解] 取CD 1的中点G ,连接EG ,DG ,∵E 是BD 1的中点,∴EG ∥BC ,EG =12BC .∵F 是AD 的中点,且AD ∥BC ,AD =BC ,∴DF ∥BC ,DF =12BC ,∴EG ∥DF ,EG =DF ,∴四边形EFDG 是平行四边形, ∴EF ∥DG ,∴∠DGD 1(或其补角)是异面直线CD 1与EF 所成的角.又∵A 1A =AB ,∴四边形ABB 1A 1,四边形CDD 1C 1都是正方形,且G 为CD 1的中点,∴DG ⊥CD 1, ∴∠D 1GD =90°,∴异面直线CD1,EF所成的角为90°.[类题通法]求两异面直线所成的角的三个步骤(1)作:根据所成角的定义,用平移法作出异面直线所成的角.(2)证:证明作出的角就是要求的角.(3)计算:求角的值,常利用解三角形得出.可用“一作二证三计算”来概括.同时注意异面直线所成角θ的取值范围是0°<θ≤90°. [活学活用]已知ABCD-A1B1C1D1是正方体,求异面直线A1C1与B1C所成的角的大小.解:如右图所示,连接A1D和C1D.∵B1C∥A1D,∴∠DA1C1即为异面直线A1C1与B1C所成的角.∵A1D,A1C1,C1D为正方体各面上的对角线,∴A1D=A1C1=C1D,∴△A1C1D为等边三角形.即∠C1A1D=60°.∴异面直线A1C1与B1C所成的角为60°.2.探究空间中四边形的形状问题[典例]在空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.求证:四边形EFGH是平行四边形.[证明] 如右图所示,连接BD .因为EH 是△ABD 的中位线,所以EH ∥BD , 且EH =12BD .同理,FG ∥BD ,且FG =12BD .因此EH ∥FG . 又EH =FG ,所以四边形EFGH 为平行四边形. [多维探究] 1.矩形的判断本例中若加上条件“AC ⊥BD ”,则四边形EFGH 是什么形状? 证明:由例题可知EH ∥BD ,同理EF ∥AC , 又BD ⊥AC ,因此EH ⊥EF , 所以四边形EFGH 为矩形. 2.菱形的判断本例中,若加上条件“AC =BD ”,则四边形EFGH 是什么形状? 证明:由例题知EH ∥BD ,且EH =12BD ,同理EF ∥AC ,且EF =12AC .又AC =BD ,所以EH =EF .又四边形EFGH 为平行四边形, 所以四边形EFGH 为菱形. 3.正方形的判断本例中,若加上条件“AC ⊥BD ,且AC =BD ”,则四边形EFGH 是什么形状? 证明:由探究1与2可知, 四边形EFGH 为正方形. 4.梯形的判断若本例中,E ,H 分别是AB ,AD 中点,F ,G 分别是BC ,CD 上的点,且CF ∶FB =CG ∶GD =1∶2,则四边形EFGH 是什么形状?证明:由题意可知EH 是△ABD 的中位线,则EH ∥BD 且EH =12BD .又∵CF FB =CG GD =12,∴FG ∥BD ,FG BD =FC BC =13,∴FG =13BD ,∴FG ∥EH 且FG ≠EH , ∴四边形EFGH 是梯形. [方法感悟]根据三角形的中位线、公理4证明两条直线平行是常用的方法.公理4表明了平行线的传递性,它可以作为判断两条直线平行的依据,同时也给出空间两直线平行的一种证明方法.一、选择题1.若a ,b ,c 是空间3条直线,a ∥b ,a 与c 相交,则b 与c 的位置关系是( ) A .异面 B .相交 C .平行 D .异面或相交答案:D2.如右图所示,在三棱锥S -MNP 中,E ,F ,G ,H 分别是棱SN ,SP ,MN ,MP 的中点,则EF 与HG 的位置关系是( )A .平行B .相交C .异面D .平行或异面答案:A3.如下图所示是一个正方体的平面展开图,则在正方体中,AB 与CD 的位置关系为( )A .相交B .平行C .异面而且垂直D .异面但不垂直答案:D 4.下列命题:①如果一个角的两边与另一个角的两边分别平行,那么这两个角相等;②如果两条相交直线和另两条直线分别平行,那么这两组直线所成的锐角(或直角)相等;③如果一个角的两边和另一个角的两边分别垂直,那么这两个角相等或互补; ④如果两条直线同时平行于第三条直线,那么这两条直线互相平行. 其中正确的结论有( ) A .1个 B .2个 C .3个 D .4个答案:B5.若P 是两条异面直线l ,m 外的任意一点,则( ) A .过点P 有且仅有一条直线与l ,m 都平行 B .过点P 有且仅有一条直线与l ,m 都垂直 C .过点P 有且仅有一条直线与l ,m 都相交 D .过点P 有且仅有一条直线与l ,m 都异面 答案:B 二、填空题6.直线a ,b ⊂平面α,且a ,b 成的角为40°,经过α外一点A 与a ,b 都成30°角的直线有且只有________条.答案:27.已知正方体ABCD -A 1B 1C 1D 1中,E 为C 1D 1的中点,则异面直线AE 与A 1B 1所成的角的余弦值为________.答案:138.如下图所示,点P ,Q ,R ,S 分别在正方体的4条棱上,且是所在棱的中点,则直线PQ 与RS 是异面直线的一个图是________.答案:③ 三、解答题9.如右图所示,E ,F 分别是长方体A 1B 1C 1D 1-ABCD 的棱A 1A ,C 1C 的中点.求证:四边形B 1EDF 是平行四边形. 证明:设Q 是DD 1的中点,连接EQ ,QC 1.∵E 是AA 1的中点, ∴EQ A 1D 1.又在矩形A 1B 1C 1D 1中,A 1D 1B 1C 1,∴EQ B 1C 1(平行公理). ∴四边形EQC 1B 1为平行四边形.∴B 1E C 1Q . 又∵Q ,F 是DD 1,C 1C 两边的中点,∴QD C 1F . ∴四边形QDFC 1为平行四边形. ∴C 1Q DF .又∵B 1E C 1Q ,∴B 1E DF . ∴四边形B 1EDF 为平行四边形.10.已知三棱锥A -BCD 中,AB =CD ,且直线AB 与CD 成60°角,点M ,N 分别是BC ,AD 的中点,求直线AB 和MN 所成的角.解:如图,取AC 的中点P ,连接PM ,PN ,因为点M ,N 分别是BC ,AD 的中点,所以PM ∥AB ,且PM =12AB ;PN ∥CD ,且PN =12CD ,所以∠MPN(或其补角)为AB与CD所成的角.所以∠PMN(或其补角)为AB与MN所成的角.因为直线AB与CD成60°角,所以∠MPN=60°或∠MPN=120°.又因为AB=CD,所以PM=PN,①若∠MPN=60°,则△PMN是等边三角形,所以∠PMN=60°,即AB与MN所成的角为60°.②若∠MPN=120°,则易知△PMN是等腰三角形.所以∠PMN=30°,即AB与MN所成的角为30°.综上可知:AB与MN所成角为60°或30°.2.1.3 & 2.1.4空间中直线与平面之间的位置关系、平面与平面之间的位置关系空间中直线与平面的位置关系[导入新知]直线与平面的位置关系1.利用公共点的个数也可以理解直线与平面的位置关系.(1)当直线与平面无公共点时,直线与平面平行.(2)当直线与平面有一个公共点时,直线与平面相交.(3)当直线与平面有两个公共点时,它们就有无数个公共点,这时直线在平面内.2.直线在平面外包括两种情形:a∥α与a∩α=A.空间中平面与平面的位置关系 [导入新知]两个平面的位置关系[1.判断面面位置关系时,要利用好长方体(或正方体)这一模型.2.画两个互相平行的平面时,要注意使表示平面的两个平行四边形的对应边平行.直线与平面的位置关系 [例1] 下列说法:①若直线a 在平面α外,则a ∥α;②若直线a ∥b ,直线b ⊂α,则a ∥α;③若直线a ∥b ,b ⊂α,那么直线a 就平行于平面α内的无数条直线.其中说法正确的个数为( ) A .0 B .1 C .2 D .3[答案] B [类题通法]空间中直线与平面只有三种位置关系:直线在平面内、直线与平面相交、直线与平面平行.在判断直线与平面的位置关系时,这三种情形都要考虑到,避免疏忽或遗漏.另外,我们可以借助空间几何图形,把要判断关系的直线、平面放在某些具体的空间图形中,以便于正确作出判断,避免凭空臆断.[活学活用]下列说法中,正确的个数是( )①如果两条平行直线中的一条和一个平面相交,那么另一条直线也和这个平面相交;②一条直线和另一条直线平行,它就和经过另一条直线的任何平面都平行;③经过两条异面直线中的一条直线,有一个平面与另一条直线平行;④两条相交直线,其中一条与一个平面平行,则另一条一定与这个平面平行.A.0 B.1C.2 D.3答案:C平面与平面的位置关系[例2](1)平面α内有无数条直线与平面β平行,问:α∥β是否正确?为什么?(2)平面α内的所有直线与平面β都平行,问:α∥β是否正确?为什么?[解](1)不正确.如图所示,设α∩β=l,则在平面α内与l平行的直线可以有无数条:a1,a2,…,a n,…,它们是一组平行线,这时a1,a2,…,a n,…与平面β都平行(因为a1,a2,…,a n,…与平面β无交点),但此时α与β不平行,α∩β=l.(2)正确.平面α内所有直线与平面β平行,则平面α与平面β无交点,符合平面与平面平行的定义.[类题通法]两个平面的位置关系同平面内两条直线的位置关系类似,可以从有无公共点区分:如果两个平面有一个公共点,那么由公理3可知,这两个平面相交于过这个点的一条直线;如果两个平面没有公共点,那么就说这两个平面互相平行.这样我们可以得出两个平面的位置关系:①平行——没有公共点;②相交——有且只有一条公共直线.若平面α与β平行,记作α∥β;若平面α与β相交,且交线为l,记作α∩β=l.[活学活用]1.在底面为正六边形的六棱柱中,互相平行的面视为一组,则共有________组互相平行的面,与其中一个侧面相交的面共有________个.答案:4 62.如图所示,平面ABC与三棱柱ABC-A1B1C1的其他面之间有什么位置关系?解:∵平面ABC与平面A1B1C1无公共点,∴平面ABC与平面A1B1C1平行.∵平面ABC与平面ABB1A1有公共直线AB,∴平面ABC与平面ABB1A1相交.同理可得平面ABC与平面ACC1A1及平面BCC1B1均相交.3.有关截面图形的形状问题[典例](12分)在正方体ABCD-A1B1C1D1中,点Q是棱DD1上的动点,判断过A,Q,B1三点的截面图形的形状.[解题流程][规范解答]由点Q在线段DD1上移动,当点Q与点D1重合时,截面图形为等边三角形AB1D1,如图①所示.(4分)当点Q与点D重合时,截面图形为矩形AB1C1D,如图②所示.(8分)当点Q不与点D,D1重合时,截面图形为等腰梯形AQRB1,如图③所示.(12分)[活学活用]如图所示,G是正方体ABCD-A1B1C1D1的棱DD1延长线上的一点,E,F是棱AB,BC 的中点.试分别画出过下列各点、直线的平面与正方体表面的交线.(1)过点G及AC;(2)过3点E,F,D1.解:(1)画法:连接GA交A1D1于点M,连接GC交C1D1于点N;连接MN,AC,则MA,CN,MN,AC为所求平面与正方体表面的交线.如图①所示.(2)画法:连接EF交DC的延长线于点P,交DA的延长线于点Q;连接D1P交CC1于点M,连接D1Q交AA1于点N;连接MF,NE,则D1M,MF,FE,EN,ND1为所求平面与正方体表面的交线.如图②所示.一、选择题1.如果在两个平面内分别有一条直线,这两条直线互相平行,那么两个平面的位置关系一定是()A.平行B.相交C.平行或相交D.不能确定答案:C2.如果一条直线与两个平行平面中的一个平行,那么这条直线与另一个平面的位置关系为()A.平行B.相交C.直线在平面内D.平行或直线在平面内答案:D3.若直线l不平行于平面α,且l⊄α,则()A.α内的所有直线与l异面B.α内不存在与l平行的直线C.α内存在唯一的直线与l平行D.α内的直线与l都相交答案:B4.已知直线m,n和平面α,m∥n,m∥α,过m的平面β与α相交于直线a,则n与a的位置关系是()A.平行B.相交C.异面D.以上均有可能答案:A5.给出下列几个说法:①过一点有且只有一条直线与已知直线平行;②过一点有且只有一条直线与已知直线垂直;③过平面外一点有且只有一条直线与该平面平行;④过平面外一点有且只有一个平面与该平面平行.其中正确说法的个数为()A.0 B.1C.2 D.3答案:B二、填空题6.下列命题:①两个平面有无数个公共点,则这两个平面重合;②若l,m是异面直线,l∥α,m∥β,则α∥β.其中错误命题的序号为________.答案:①②7.与空间四边形ABCD 4个顶点距离相等的平面共有________个.答案:78.下列命题正确的有________(填序号).①若直线与平面有两个公共点,则直线在平面内;②若直线l上有无数个点不在平面α内,则l∥α;③若直线l与平面α相交,则l与平面α内的任意直线都是异面直线;④如果两条异面直线中的一条与一个平面平行,则另一条直线一定与该平面相交;⑤若直线l与平面α平行,则l与平面α内的直线平行或异面;⑥若平面α∥平面β,直线a⊂α,直线b⊂β,则直线a∥b.答案:①⑤三、解答题9.如右图所示,在正方体ABCD -A1B1C1D1中M,N分别是A1B1和BB1的中点,则下列直线与平面的位置关系是什么?(1)AM所在的直线与平面ABCD的位置关系;(2)CN所在的直线与平面ABCD的位置关系;(3)AM所在的直线与平面CDD1C1的位置关系;(4)CN所在的直线与平面CDD1C1的位置关系.解:(1)AM所在的直线与平面ABCD相交;(2)CN所在的直线与平面ABCD相交;(3)AM所在的直线与平面CDD1C1平行;(4)CN所在的直线与平面CDD1C1相交.10.已知平面α∩β=l,点A∈α,点B∈α,点C∈β,且A∉l,B∉l,直线AB与l不平行,那么平面ABC与平面β的交线与l有什么关系?证明你的结论.解:平面ABC与β的交线与l相交.证明:∵AB与l不平行,且AB⊂α,l⊂α,∴AB与l一定相交,设AB∩l=P,则P∈AB,P∈l.又∵AB⊂平面ABC,l⊂β,∴P∈平面ABC,P∈β.∴点P是平面ABC与β的一个公共点,而点C也是平面ABC与β的一个公共点,且P,C是不同的两点,∴直线PC就是平面ABC与β的交线.即平面ABC∩β=PC,而PC∩l=P,∴平面ABC与β的交线与l相交.2.2直线、平面平行的判定及其性质2.2.1 & 2.2.2直线与平面平行的判定、平面与平面平行的判定直线与平面平行的判定[导入新知][1.用该定理判断直线a和平面α平行时,必须同时具备3个条件:(1)直线a在平面α外,即a⊄α.(2)直线b在平面α内,即b⊂α.(3)两直线a,b平行,即a∥b.2.该定理的作用:证明线面平行.3.应用时,只需在平面内找到一条直线与已知直线平行即可.平面与平面平行的判定 [导入新知]1.平面与平面平行的判定定理中的平行于一个平面内的“两条相交直线”是必不可少的.2.面面平行的判定定理充分体现了等价转化思想,即把面面平行转化为线面平行.直线与平面平行的判定[例1] 如右图所示,已知公共边为AB 的两个全等的矩形ABCD 和矩形ABEF 不在同一平面内,P ,Q 分别是对角线AE ,BD 上的点,且AP =DQ .求证:PQ ∥平面CBE .[证明] 作PM ∥AB 交BE 于点M ,作QN ∥AB 交BC 于点N ,连接MN ,如图,则PM ∥QN ,PM AB =EP EA ,QN CD =BQBD .∵EA =BD ,AP =DQ ,∴EP =BQ . 又AB =CD ,∴PM QN ,∴四边形PMNQ 是平行四边形,∴PQ ∥MN .又PQ⊄平面CBE,MN⊂平面CBE,∴PQ∥平面CBE.[类题通法]利用直线和平面平行的判定定理证明线面平行的关键是在平面内找一条直线与已知直线平行,常利用平行四边形、三角形中位线定理、平行公理等.[活学活用]如下图所示,已知A1B1C1-ABC是三棱柱,D是AC的中点.求证:AB1∥平面DBC1.证明:∵A1B1C1-ABC是三棱柱,∴四边形B1BCC1是平行四边形,∴连接B1C交BC1于点E,则B1E=EC.连接DE,在△AB1C中,∵AD=DC,∴DE∥AB1.又AB1⊄平面DBC1,DE⊂平面DBC1,∴AB1∥平面DBC1.面面平行的判定[例2]如下图所示,在正方体ABCD -A1B1C1D1中,M,E,F,N分别是A1B1,B1C1,C1D1,D1A1的中点.求证:(1)E,F,B,D四点共面;(2)平面MAN∥平面EFDB.[证明](1)连接B1D1.∵E,F分别是边B1C1,C1D1的中点,∴EF∥B1D1.而BD∥B1D1,∴BD∥EF.∴E,F,B,D四点共面.(2)易知MN∥B1D1,B1D1∥BD,∴MN∥BD.又∵MN⊄平面EFDB,BD⊂平面EFDB,∴MN∥平面EFDB.连接MF.∵M,F分别是A1B1,C1D1的中点,∴MF∥A1D1,MF=A1D1.∴MF∥AD,MF=AD.∴四边形ADFM是平行四边形,∴AM∥DF.又AM⊄平面BDFE,DF⊂平面BDFE,∴AM∥平面BDFE.又∵AM∩MN=M,∴平面MAN∥平面EFDB.[类题通法]两个平面平行的判定定理是确定面面平行的重要方法.解答问题时一定要寻求好判定定理所需要的条件,特别是相交的条件,即与已知平面平行的两条直线必须相交,才能确定面面平行.[活学活用]。
高中数学必修2第二章点、线、面的位置关系知识点+习题+答案

D B A α 相交直线:同一平面内,有且只有一个公共点; ] ]; a 来表 a a 线线平行 A ·α C ·B · A · α P· αLβ 共面直线p线面平行 面面平行 作用:可以由平面与平面平行得出直线与直线平行叫做垂足。
叫做垂足。
的垂线,则这两个ba第 3 页 共 3 页aa b a b //,a a a ÞþýüË^^1、性质定理:垂直于同一个平面的两条直线平行。
符号表示:符号表示:b a b a //,Þ^^a a 2、性质定理:一条直线与一个平行垂直,那么过这条直线的平面也与此平面垂直 符号表示:b a b a ^ÞÌ^a a ,2.3.4平面与平面垂直的性质1、性质定理:、性质定理: 两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直。
符号表示:b b a a b a ^Þïþïýü=^Ì^a l l a a ,2、性质定理:垂直于同一平面的直线和平面平行。
符号表示:符号表示:符号表示:一、异面直线所成的角一、异面直线所成的角1.已知两条异面直线,a b ,经过空间任意一点O 作直线//,//a a b b ¢¢, 我们把a ¢与b ¢所成的锐角(或直角)叫异面直线,a b 所成的角。
所成的角。
2.角的取值范围:090q <£°;垂直时,异面直线当b a ,900=q二、直线与平面所成的角二、直线与平面所成的角1. 定义:平面的一条斜线和它在平面上的射影所成的锐角,叫这条斜线和这个平面所成的角2.角的取值范围:°°££900q 。
三、两个半平面所成的角即二面角:三、两个半平面所成的角即二面角: 1、从一条直线出发的两个半平面所组成的图形叫做二面角。
人教版高中数学必修二第二章《点、直线、平面之间位置关系》(内含解析)

人教版高中数学必修二第二章《点、直线、平面之前的位置关系》(内含解析)一、选择题1.△ABC所在的平面为α,直线l⊥AB,l⊥AC,直线m⊥BC,m⊥AC,则直线l,m的位置关系是()A.相交 B.异面C.平行 D.不确定【解析】因为l⊥AB,l⊥AC且AB∩AC=A,所以l⊥平面ABC.同理可证m⊥平面ABC,所以l∥m,故选C.【答案】C2.设m,n是两条不同的直线,α,β是两个不同的平面.下列命题中正确的是()A.若α⊥β,m⊂α,n⊂β,则m⊥nB.若α∥β,m⊂α,n⊂β,则m∥nC.若m⊥n,m⊂α,n⊂β,则α⊥βD.若m⊥α,m∥n,n∥β,则α⊥β【解析】A中,m,n可能为平行、垂直、异面直线;B中,m,n可能为异面直线;C中,m应与β中两条相交直线垂直时结论才成立.【答案】D3.已知平面α、β和直线m、l,则下列命题中正确的是()A.若α⊥β,α∩β=m,l⊥m,则l⊥βB.若α∩β=m,l⊂α,l⊥m,则l⊥βC.若α⊥β,l⊂α,则l⊥βD.若α⊥β,α∩β=m,l⊂α,l⊥m,则l⊥β【解析】选项A缺少了条件l⊂α;选项B缺少了条件α⊥β;选项C缺少了条件α∩β=m,l⊥m;选项D具备了面面垂直的性质定理的全部条件.故选D.【答案】D4.如图2342,P A⊥矩形ABCD,下列结论中不正确的是()图2342A.PD⊥BD B.PD⊥CDC.PB⊥BC D.P A⊥BD【解析】若PD⊥BD,则BD⊥平面P AD,又BA⊥平面P AD,则过平面外一点有两条直线与平面垂直,不成立,故A不正确;因为P A⊥矩形ABCD,所以P A⊥CD,AD⊥CD,所以CD⊥平面P AD,所以PD⊥CD,同理可证PB⊥BC.因为P A⊥矩形ABCD,所以由直线与平面垂直的性质得P A⊥BD.故选A.【答案】A5.如图2343所示,三棱锥P ABC的底面在平面α内,且AC⊥PC,平面P AC⊥平面PBC,点P,A,B是定点,则动点C的轨迹是()图2343A.一条线段B.一条直线C.一个圆D.一个圆,但要去掉两个点【解析】∵平面P AC⊥平面PBC,AC⊥PC,平面P AC∩平面PBC=PC,AC⊂平面P AC,∴AC⊥平面PBC.又∵BC⊂平面PBC,∴AC⊥BC.∴∠ACB=90°.∴动点C的轨迹是以AB为直径的圆,除去A和B两点.【答案】D二、填空题6.如图239,平面α∩β=CD,EA⊥α,垂足为A,EB⊥β,垂足为B,则CD与AB的位置关系是________.图239【解析】∵EA⊥α,CD⊂α,根据直线和平面垂直的定义,则有CD⊥EA.同样,∵EB⊥β,CD⊂β,则有EB⊥CD.又EA∩EB=E,∴CD⊥平面AEB.又∵AB⊂平面AEB,∴CD⊥AB.【答案】CD⊥AB7.如图2310所示,P A ⊥平面ABC ,在△ABC 中,BC ⊥AC ,则图中直角三角形的个数有________.图2310【解析】 BC ⊂平面ABC PA ⊥平面ABC ⇒PA ∩AC =A AC ⊥BC ⇒BC ⊥平面P AC ⇒BC ⊥PC ,∴直角三角形有△P AB 、△P AC 、△ABC 、△PBC .【答案】 4三、解答题8.如图2311,四边形ABCD 为矩形,AD ⊥平面ABE ,F 为CE 上的点,且BF ⊥平面ACE .求证:AE ⊥BE .图2311【证明】 ∵AD ⊥平面ABE ,AD ∥BC ,∴BC ⊥平面ABE .又AE ⊂平面ABE ,∴AE ⊥BC .∵BF ⊥平面ACE ,AE ⊂平面ACE ,∴AE ⊥BF .又∵BF ⊂平面BCE ,BC ⊂平面BCE ,BF ∩BC =B , ∴AE ⊥平面BCE .又BE ⊂平面BCE ,∴AE ⊥BE .9.如图2312所示,三棱锥ASBC 中,∠BSC =90°,∠ASB =∠ASC=60°,SA=SB=SC.求直线AS与平面SBC所成的角.图2312【解】因为∠ASB=∠ASC=60°,SA=SB=SC,所以△ASB与△SAC都是等边三角形.因此AB=AC.如图所示,取BC的中点D,连接AD,SD,则AD⊥BC.设SA=a,则在Rt△SBC中,BC=a,CD=SD=22a.在Rt△ADC中,AD==22a.则AD2+SD2=SA2,所以AD⊥SD.又BC∩SD=D,所以AD⊥平面SBC.因此∠ASD即为直线AS与平面SBC所成的角.在Rt△ASD中,SD=AD=22a,所以∠ASD=45°,即直线AS与平面SBC所成的角为45°.10.(2015·淮安高二检测)如图2313,四棱锥SABCD的底面ABCD 为正方形,SD⊥底面ABCD,则下列结论中正确的有________个.图2313①AC⊥SB;②AB∥平面SCD;③SA与平面ABCD所成的角是∠SAD;④AB与SC所成的角等于DC与SC所成的角.【解析】因为SD⊥底面ABCD,所以AC⊥SD.因为ABCD是正方形,所以AC⊥BD.又BD∩SD=D,所以AC⊥平面SBD,所以AC⊥SB,故①正确.因为AB∥CD,AB⊄平面SCD,CD⊂平面SCD,所以AB∥平面SCD,故②正确.因为AD是SA在平面ABCD内的射影,所以SA与平面ABCD所成的角是∠SAD.故③正确.因为AB∥CD,所以AB与SC所成的角等于DC与SC所成的角,故④正确.【答案】411.如图2314,AB为⊙O的直径,P A垂直于⊙O所在的平面,M为圆周上任意一点,AN⊥PM,N为垂足.(1)求证:AN⊥平面PBM;(2)若AQ⊥PB,垂足为Q,求证:NQ⊥PB.图2314【证明】(1)∵AB为⊙O的直径,∴AM⊥BM.又P A⊥平面ABM,∴P A⊥BM.又∵P A∩AM=A,∴BM⊥平面P AM.又AN⊂平面P AM,∴BM⊥AN.又AN⊥PM,且BM∩PM=M,∴AN⊥平面PBM.(2)由(1)知AN⊥平面PBM,PB⊂平面PBM,∴AN⊥PB.又∵AQ⊥PB,AN∩AQ=A,∴PB⊥平面ANQ.又NQ⊂平面ANQ,∴PB⊥NQ.。
高中数学必修二2.1空间点、直线、平面之间的位置关系课堂练习及详细答案解析

2.1 空间点、直线、平面之间的位置关系2.1.1 平面知识梳理1 平面含义:平面是无限延展的2 三个公理:(1)公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内符号表示为【公理 1 作用】判断直线是否在平面内.(2)公理2:过不在一条直线上的三点,有且只有一个平面。
符号表示为:A、B、C三点不共线=> 有且只有一个平面α,使A∈α、B∈α、C∈α。
公理 2 作】确定一个平面的依据。
3)公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线。
符号表示为:P∈α∩β => α∩β =L,且P∈L【公理3作用】判定两个平面是否相交的依据知能训练一.选择题1.已知m,n 分别是两条不重合的直线,a,①若m⊥α,n∥b,且α⊥β,则m∥n;③若m∥α,n∥b,且α∥β,则m⊥n;其中真命题的序号是()2.在下列命题中,不是公理的是()A.平行于同一个平面的两个平面平行B.过不在同一直线上的三个点,有且只有一个平面C.如果一条直线上的两点在同一个平面内,那么这条直线上所有点都在此平面内D.如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线3.l1,l 2,l 3是空间三条不同的直线,则下列命题正确的是()A.1 ⊥ l 2,l 2 ⊥ l 3?l 1 ∥ l 3B.1 ⊥ l 2,l 2 ∥l3?l 1⊥ l 3C.1∥ l 2∥l 3? l1,l 2 ,l 3 共面D.l1,l2,l3共点? l1,l2,l 3共面A.①②B.③④C.①④D.②③b 分别垂直于两不重合平面②若m∥a,n∥ b,且α④若m⊥α,n ⊥b,且4.下面四个说法中,正确的个数为()(1)如果两个平面有三个公共点,那么这两个平面重合(2)两条直线可以确定一个平面(3)若M∈α,M∈β,α∩β =l ,则M∈l(4)空间中,相交于同一点的三直线在同一平面内.A. 1 B. 2 C. 3 D. 4 5.已知空间三条直线l 、m、n.若l 与m异面,且l 与n 异面,则()A.m 与n 异面B.m与n 相交C.m 与n 平行D.m与n 异面、相交、平行均有可能6.若m、n 为两条不重合的直线,α、β 为两个不重合的平面,则下列命题中的真命题是()A.若m、n 都平行于平面α,则m、n 一定不是相交直线B.若m、n 都垂直于平面α,则m、n 一定是平行直线C.已知α、β互相垂直,m、n 互相垂直,若m⊥α,n ⊥βD.m、n 在平面α内的射影互相垂直,则m、n 互相垂直7.已知平面α,β,γ,直线m,l ,点A,有下面四个命题,其中正确的命题是()A.若l ? α,m∩α =A,则l 与m 必为异面直线B .若l ∥α,l ∥m,则m∥αC .若l ? α,m?β,l ∥β,m∥α,则α∥βD .若α⊥γ,γ∩α=m,γ∩β =l ,l⊥m,则l ⊥α8.已知α,β 为互不重合的平面,m,n 为互不重合的直线,给出下列四个命题:①若m⊥α,n⊥α,则m∥n;②若m? α,n? α,m∥β,n∥β,,则α∥β;③若α⊥β,α∩β =m,n? α,n⊥m,则n⊥β;④若m⊥α,α⊥β,m∥ n,则n∥β.其中所有正确命题的序号是()A.①③B.②④C.①④D.③④二.填空题9.(文)平面上三条直线x+2y-1=0 ,x+1=0,x+ky=0 ,如果这三条直线将平面划分为六部分,则实数k 的所有取值为.(将你认为所有正确的序号都填上)①0 ② 1/2 ③1 ④2 ⑤ 3.10.空间中有7 个点,其中有 3 个点在同一直线上,此外再无任何三点共线,由这7个点最多可确定个平面.三.解答题1.如图,在四边形ABCD中,已知AB∥ CD,直线AB,BC,AD,DC分别与平面α相交于点E,G,H,F.求证:E,F,G,H四点必定共线.2.四面体ABCD中,E、G分别为BC、AB的中点,F 在CD上,H在AD上,且有DF:FC=2:3.DH:HA=2 :3.(1)证明:点G、E、F、H四点共面;(2)证明:EF、GH、BD交于一点.2.1.2 空间中直线与直线之间的位置关系1 空间的两条直线有如下三种关系:相交直线:同一平面内,有且只有一个公共点;共面直线平行直线:同一平面内,没有公共点;异面直线:不同在任何一个平面内,没有公共点。
【优质文档】人教版高中数学必修二点、直线、平面间的位置关系教材配套习题(附答案可下载)
14. 本题考查学生的推理论证能力 .
第4页 共5页
证明:因为 SA SB SC a ,又 ASC ASB 60 o , A
所以, ASB 与 ASC 是等边三角形, AB AC a .
取 BC 的中点 H ,连接 AH ,所以, AH BC . 在 Rt BSC 中, BS CS a ,所以 SH BC , BC
其中真命题的个数是
个.
三、解答题
12.(1)用符号语言表示语句: “直线 l 经过平面 内一定点 P ,但 l 在 外”,并画出图形 .
第2页 共5页
(2)把下面的符号语言改写成文字语言的形式,并画出图形 . 若直线 a 平面 , A , A a , A 直线 b , a / /b ,则 b .
13. 如图,在长方体 ABCD A' B 'C ' D ' 中,指出 B 'C 、 D 'B 所在直线与各个面所在平面之间的关
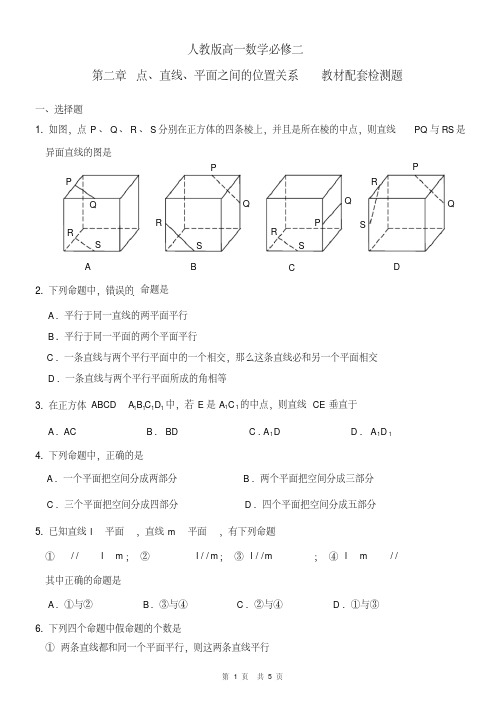
人教版高一数学必修二 第二章 点、直线、平面之间的位置关系 教材配套检测题
一、选择题 1. 如图,点 P 、 Q 、 R 、 S 分别在正方体的四条棱上,并且是所在棱的中点,则直线
PQ 与 RS 是
异面直线的图是
P Q
R S
P
P
R
Q
QQΒιβλιοθήκη R SPS
R
S
A
B
C
D
2. 下列命题中,错.误.的.命题是
A . 平行于同一直线的两平面平行
1. C . 考查:① 异面直线的概念; ② 识图能力,空间想象能力 .
2. A . 考查:平面与平面位置关系的判定与性质问题 . 注重空间想象能力的培养 .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.2.2 平面与平面平行的判定
【课时目标】 1.理解平面与平面平行的判定定理的含义.2.能运用平面与平面平行的判定定理,证明一些空间面面平行的简单问题.
1.平面α与平面β平行是指两平面________公共点.若α∥β,直线a ⊂α,则a 与β
的位置关系为________.
2.下面的命题在“________”处缺少一个条件,补上这个条件,使其构成真命题(M ,n 为直线,α,β为平面),则此条件应为________.
⎭
⎪⎬⎪⎫m
⊂αn ⊂αm ∥βn ∥β ⇒α∥β 一、选择题
1.经过平面α外的两个点作该平面的平行平面,可以作出( )
A .0个
B .1个
C .0个或1个
D .1个或2个
2.α和β是两个不重合的平面,在下列条件中,可判定α∥β的是( )
A .α内有无数条直线平行于β
B .α内不共线三点到β的距离相等
C .l 、M 是平面α内的直线,且l ∥α,M ∥β
D .l 、M 是异面直线且l ∥α,M ∥α,l ∥β,M ∥β
3.给出下列结论,正确的有( )
①平行于同一条直线的两个平面平行;
②平行于同一平面的两个平面平行;
③过平面外两点,不能作一个平面与已知平面平行;
④若a ,b 为异面直线,则过a 与b 平行的平面只有一个.
A .1个
B .2个
C .3个
D .4个
4.若不在同一直线上的三点A 、B 、C 到平面α的距离相等,且AD /∈α,则( )
A .α∥平面ABC
B .△AB
C 中至少有一边平行于α
C .△ABC 中至多有两边平行于
α
D .△ABC 中只可能有一边与α相交
5.正方体EFGH —E 1F 1G 1H 1中,下列四对截面中,彼此平行的一对截面是( )
A .平面E 1FG 1与平面EGH 1
B.平面FHG1与平面F1H1G
C.平面F1H1H与平面FHE1
D.平面E1HG1与平面EH1G
6.两个平面平行的条件是()
A.一个平面内一条直线平行于另一个平面
B.一个平面内两条直线平行于另一个平面
C.一个平面内的任意一条直线平行于另一个平面
D.两个平面都平行于同一条直线
二、填空题
7.已知直线a、b,平面α、β,且a∥b,a∥α,α∥β,则直线b与平面β的位置关系为______.
8.有下列几个命题:
①平面α内有无数个点到平面β的距离相等,则α∥β;
②α∩γ=a,α∩β=b,且a∥b(α,β,γ分别表示平面,a,b表示直线),则γ∥β;
③平面α内一个三角形三边分别平行于平面β内的一个三角形的三条边,则α∥β;
④平面α内的一个平行四边形的两边与平面β内的一个平行四边形的两边对应平行,
则α∥β.其中正确的有________.(填序号)
9.如图所示,在正方体ABCD—A1B1C1D1中,E、F、G、H分别是棱CC1、C1D1、D1D、CD的中点,N是BC的中点,点M在四边形EFGH及其内部运动,则M满足________时,有MN∥平面B1BDD1.
三、解答题
10.如图所示,在正方体ABCD-A1B1C1D1中,S是B1D1的中点,E、F、G分别是BC、DC和SC的中点.求证:平面EFG∥平面BDD1B1.
11.如图所示,B为△ACD所在平面外一点,M,N,G分别为△ABC,△ABD,△BCD 的重心.
(1)求证:平面MNG∥平面ACD;
(2)求S△MNG∶S△ADC.
能力提升
12.三棱柱ABC-A1B1C1,D是BC上一点,且A1B∥平面AC1D,D1是B1C1的中点.求证:平面A1BD1∥平面AC1D.
13.如图所示,在正方体ABCD—A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,问:当点Q在什么位置时,平面D1BQ∥平面P AO?
判定或证明面面平行的方法
(1)面面平行的定义;
(2)面面平行的判定定理:如果一个平面内有两条相交直线平行于另一个平面,那么这两个平面平行;
(3)两个平面同时平行于第三个平面,那么这两个平面平行.
2.2.2 平面与平面平行的判定 答案
知识梳理
1.无 a ∥β 2.M ,n 相交
作业设计
1.C 2.D 3.B 4.B 5.A 6.C 7.b ∥β或b ⊂β
8.③
解析 ①不正确,当两平面相交时,在一个平面两侧分别有无数点满足条件;②不正确,当平面β与γ相交时也可满足条件;③正确,满足平面平行的判定定理;④不正确,当两平面相交时,也可满足条件.
9.M ∈线段FH
解析 ∵HN ∥BD ,HF ∥DD 1,
HN ∩HF =H ,BD ∩DD 1=D ,
∴平面NHF ∥平面B 1BDD 1,
故线段FH 上任意点M 与N 连接,
有MN ∥平面B 1BDD 1.
10.
证明 如图所示,连接SB ,SD ,
∵F 、G 分别是DC 、SC 的中点,
∴FG ∥SD .
又∵SD ⊂平面BDD 1B 1,FG ⊄平面BDD 1B 1,
∴直线FG ∥平面BDD 1B 1.
同理可证EG ∥平面BDD 1B 1,
又∵EG ⊂平面EFG ,
FG ⊂平面EFG ,
EG ∩FG =G ,
∴平面EFG ∥平面BDD 1B 1.
11.(1)证明 (1)连接BM ,BN ,BG 并延长分别交AC ,AD ,CD 于P ,F ,H .
∵M ,N ,G 分别为△ABC ,△ABD ,△BCD 的重心,
则有BM MP =BN NF =BG GH
=2, 且P ,H ,F 分别为AC ,CD ,AD 的中点.
连接PF ,FH ,PH ,有MN ∥PF .
又PF ⊂平面ACD ,MN ⊄平面ACD ,
∴MN ∥平面ACD .
同理MG ∥平面ACD ,MG ∩MN =M ,
∴平面MNG ∥平面ACD .
(2)解 由(1)可知MG PH =BG BH =23
, ∴MG =23
PH . 又PH =12AD ,∴MG =13
AD . 同理NG =13AC ,MN =13
CD . ∴△MNG ∽△ACD ,其相似比为1∶3.
∴S △MNG ∶S △ACD =1∶9.
12.
证明 连接A 1C 交AC 1于点E ,
∵四边形A 1ACC 1是平行四边形,
∴E 是A 1C 的中点,连接ED ,
∵A 1B ∥平面AC 1D ,ED ⊂平面AC 1D ,
∴A 1B 与ED 没有交点,
又∵ED ⊂平面A 1BC ,A 1B ⊂平面A 1BC ,
∴ED ∥A 1B .
∵E 是A 1C 的中点,∴D 是BC 的中点.
又∵D 1是B 1C 1的中点,
∴BD 1∥C 1D ,A 1D 1∥AD ,
∴BD 1∥平面AC 1D ,A 1D 1∥平面AC 1D .
又A 1D 1∩BD 1=D 1,∴平面A 1BD 1∥平面AC 1D .
13.解 当Q 为CC 1的中点时,
平面D 1BQ ∥平面PAO .
∵Q 为CC 1的中点,P 为DD 1的中点,
∴QB ∥PA .
∵P 、O 为DD 1、DB 的中点,∴D 1B ∥PO .
又PO ∩PA =P ,D 1B ∩QB =B ,
D 1B ∥平面PAO ,QB ∥平面PAO ,
∴平面D 1BQ ∥平面PAO .。
