第13章 轴
机械设计基础第13章 齿轮传动习题解答

的接触强度弱?(2)哪个齿轮的弯曲强度弱?为什么?
解:(1)接触强度
相互啮合的一对齿轮,起接触应力相等,即σH1=σH2. 由题意可知,[σH]1=600MPa>[σH2]=500MPa, 因此,大齿轮的接触强度弱。
(2)弯曲强度 相互啮合的一对齿轮,其弯曲强度的大小主要取决于的
YFaYSa
的比值。
[σ F ]
可见,
YFa1YSa1 2.81.55 0.024
[σ F ]1
179
因此,大齿轮的弯曲强度弱。
YFa2YSa2 2.4 1.67 0.028
[σ F ]2
144
YFa1YSa1 YFa2YSa2
[σF]1 [σF]2
13.6受力分析题:图示为圆锥-圆柱齿轮传动装置。轮1为主动轮, 转向如图所示,轮3、4为斜齿圆柱齿轮。 (1)轮3、4的螺旋方向应如何选择,才能使轴Ⅱ上两齿轮的轴向力相 反? (2)画出齿轮2、3所受各分力的方向。
, F2 YFa 2YSa 2
}
40 42 20 70.98 245552Nmm
T2
F1 340 78.34 YFa1YSa1 2.8 1.55
F 2 280 70.98 YFa2YSa2 2.28 1.75
T1
n1 n2
245552 3 736657Nmm
2 1.85
2)计算接触强度允许的输出转矩 H
13.1有一对齿轮传动,m=6mm,z1=20,z2=80,b=40mm.为了 缩小中心距,要改用m=4mm的一对齿轮来代替它。设载
荷系数K,齿数z1、z2及材料不变。试问为了保持原有接 触强度,应取多大的齿宽b?
(附接触强度计算公式:)
H ZHZE
2019秋人教版八年级数学上册教案:第13章4课题:画轴对称图形

1.教学重点
-理解并掌握轴对称图形的定义、性质及在实际图形中的应用;
-学会寻找图形的对称轴,并运用对称轴画轴对称图形;
-了解轴对称图形在实际生活中的应用,培养学生的数学应用意识。
举例:通过讲解和示例,使学生明确轴对称图形的定义,如矩形、正方形、圆等,并掌握其性质,如对角线互相平分、对应角相等、对应边相等等。强调在实际图形中,如何快速找到对称轴,如通过观察图形的特征,寻找中心点或中心线。
二、核心素养目标
1.让学生掌握轴对称图形的基本概念,培养空间观念和几何直观;
2.培养学生观察、分析、解决问题的能力,提高逻辑思维和推理能力;
3.培养学生动手操作和创新能力,学会运用轴对称知识解决实际问题;
4.增强学生团队协作意识,提高沟通与交流能力,培养合作精神;
5.激发学生学习兴趣,培养数学美感,提高审美素养。
2019秋人教版八年级数学上册教案:第13章4课题:画轴对称图形
一、教学内容ห้องสมุดไป่ตู้
2019秋人教版八年级数学上册第13章《轴对称》第4节:课题——画轴对称图形。本节内容主要包括:
1.轴对称图形的定义及性质;
2.如何在实际图形中找到对称轴;
3.利用对称轴画轴对称图形的方法与步骤;
4.轴对称图形在实际生活中的应用。
3.重点难点解析:在讲授过程中,我会特别强调轴对称的定义和如何在实际图形中找到对称轴这两个重点。对于难点部分,如复杂图形的对称轴寻找,我会通过举例和比较来帮助大家理解。
(三)实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与轴对称图形相关的实际问题,如如何设计一个轴对称的图案。
c.设计具有挑战性的问题和任务,让学生在解决实际问题的过程中,运用轴对称知识,提高学生的应用能力;
机械基础 课件 第十三章-带传动
解:(1)传递的圆周力
Fe v P 1000
1000 P 1000 15 Fe 1000N v 15
(2)紧边、松边拉力
170 F1 F1 f 1 1 2.97 rad 2.437 e 180 F2 F2 F F F 1000 1 2 e 解得F 1694 N, F 694 N
设小、大带轮的直径为d1、 d2 ,带长为Ld。 则包角 2
d 2 d1 180 57.3 a 式中“”适用大轮包角2, “”适用小轮包角1 。
d 2 d1 sin 代入 2a
带长Ld: Ld 2AB BC AD
2a cos
弹性滑动 ——是指正常工作时的微量滑动现象,由 拉力差(即带的紧边与松边拉力不等)引 起了带的不同弹性变形量,使得带的速度 低于主动轮的速度,高于从动轮的速度, 带沿着轮面产生滑动。这在带的工作中是 不可避免。
弹性滑动引起的不良后果: ● 使从动轮的圆周速度低于主动轮 ,即 v2 < v1; ● 产生摩擦功率损失,降低了传动效率 ; ● 引起带的磨损,并使带温度升高 ; 打滑引起的不良后果: 打滑将造成带的严重磨损,带的运动处于不稳定状 态,致使传动失效。
第十三章 带传动
§13-1 带传动概述 §13-2 带传动的受力分析
§13-3 带传动的计算 §13-4 V带轮的结构 §13-5 带传动的张紧装置 补充:链传动
挠性传动——
通过中间挠性件传递运动和动力的传动机构; 由主动轮、从动轮和中间挠性件所组成; 包括:带传动、链传动和绳传动。
挠性传动的工作原理——
越大,传动比的变化越大。一般V带传动的滑动率在1%2%内, 一般计算不予考虑。
第13章 工序间加工余量
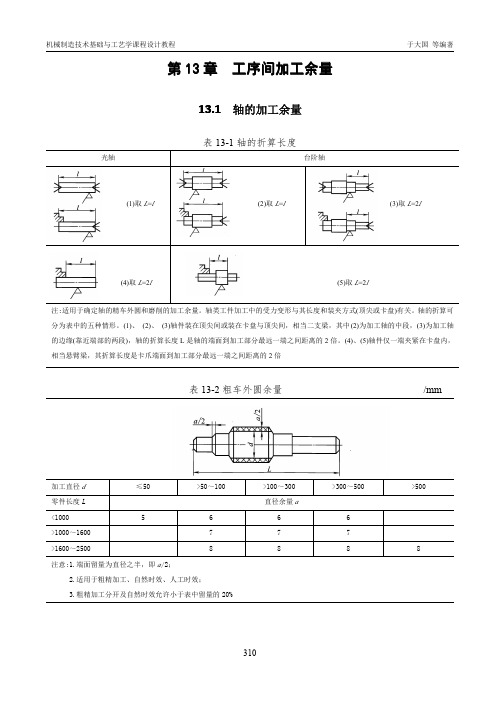
2.表中的公差系指尺寸 L 的公差,当原公差大于该公差时,尺寸公差为原公差值;
3.加工套类零件时余量值可适当增加
13.2 孔、槽的加工余量
表 13-10 精车(铣、刨)槽余量
于大国 等编著 1.2 1.4 1.5 1.7 -0.8
/mm
>500 0.6 0.6 0.6 0.7 0.7 0.8 -0.5
/mm
加工 孔的 直径
钻 第一次 第二次
直径
用车刀 扩孔钻
镗以后
粗铰
精铰 H7 或 H8、H9
加工 孔的 直径
直径
钻 用车刀 扩孔
第一次 第二次 镗以后 钻
粗铰
精铰 H7 或 H8,
H9
3
2.9
-
-
-
-
3
24 22.0
-
23.8 23.8 23.94 24
4
3.9
-
-
-
-
4
25 23.0
-
24.8 24.8 24.94 25
0.3
0.3
0.4
0.5
0.6
>120~260
0.4
0.4
0.5
0.5
0.6
>260~500
0.5
0.5
0.5
0.6
0.7
>500
0.6
0.6
0.6
0.7
0.8
长度公差
-0.12
-0.17
-0.23
-0.3
-0.4
注: 1.加工有台阶的轴时,每个台阶的加工余量应根据该台阶直径 d 及零件的全长 L 分别选用;
≤100
0.2 0.3 0.2 0.3 0.2 0.3 0.2 0.3 0.3 0.3 0.3 0.3 0.3 0.4
第13章思考题解

《大学物理学》(下册)思考题解第13章13-1 一电子以速度v 射入磁感强度为B的均匀磁场中,电子沿什么方向射入受到的磁场力最大?沿什么方向射入不受磁场力作用?答:当v 与B 的方向垂直射入时受到的磁场力最大,当v 与B的方向平行射入时不受磁场力作用。
13-2 为什么不把作用于运动电荷的磁力方向定义为磁感强度的方向? 答:运动电荷受到的磁力方向随电荷速度方向不同而变化;磁感强度是描述磁场的固有性质,它不可能随不同的外来电荷变化。
13-3 试列举电流元Idl 激发磁场d B 与电荷元dq 激发电场d E的异同。
答:电流元Idl 激发磁场24rIdl e d B r μπ⨯=,电荷元dq 激发电场2014r dq d E e r πε= 。
其中r为从电流元Idl 或电荷元dq 到场点的位矢。
磁场d B 和电场d E 都与距离r 的平方成反比,这是它们的相同点。
但是d E 的方向沿径向r e,d B 的方向垂直于由Idl和r e构成的平面,这是它们的不同之处。
13-4 在球面上铅直和水平的两个圆中通以相等的电流,电流流向如图所示。
问球心O 处磁感强度的方向是怎样的?答:取坐标,设圆环1处在XOY 平面内,X 轴向右,Y轴指向纸面内,圆环1的电流在XOY 平面内顺时针方向。
另一圆环2处在XOZ 平面内,Z 轴向上,圆环2电流在XOZ平面内顺时针方向。
圆环1的电流在球心O 处产生的磁感强度是012I B k Rμ=-;圆环2的电流在球心O 处产生的磁感强度是022I B j Rμ=;球心O 处总的磁感强度是012()2I B B B j k Rμ=+=-+,它的数值是02IB R=。
方向如图(在YOZ 平面内看)。
13-5 平面内有一个流过电流I 的圆形回路,问平面内各点磁感强度的方向是否相同?回路所包围的面积的磁场是否均匀?答:平面内各点磁感强度的方向与回路中电流方向成右旋关系;回路所包围面积的磁场不均匀。
机械设计基础(第13章)

25
V带型号:
(1) 分类 普通V带:Y、Z、A、B、C、D、E 窄V带 : SPZ、SPA、SPB、SPC
(2) 当带弯曲时→中性层带长不变→节面 带楔角φ变化(减小) →带轮轮槽角φ 0<40°
26
表13-1 普通V带的截面尺寸(GB11544-89)
型号 ZA B C D E F
b
顶宽b
10 13 17 22 32 38 50
bd
节宽 bd
8.5 11 14 19 27 32 42
高度 h
6 8 10.5 13.5 19 23.5 30
楔角φ
40 ˚
φ
每米质量q(kq/m) 0.06 0.01 0.17 0.30 0.62 0.90 1.52
在V带轮上,与所配用V带的节面宽度相对 应的带轮直径称为基准直径d。
1 F2 n1
F2 n2 2
Ff
F1 工作状态 F1
9
2. 紧松边力的大小
分析: 设带在工作前后带的总长不变,
∵紧边由F0 →F1→拉力增加,带增长 松边由F0 →F2→拉力减少,带缩短
∵总长不变→∴带增长量=带缩短量 ∴F1-F0=F0-F2 ; F1+F2=2F0 (13-4)
3.摩擦力的方向:
→Kα↓
当L>特定条件→绕转次数N↓→传动功率↑→KL >1
当L<特定条件→绕转次数N↑→传动功率↓→KL < 1
当i4.>单1根→Vd2↑带→功σb率2 ↓增→量承△载P力0 ↑→表传(动1功3-率4)↑P.204 → △P0 >0
单根V带的许用功率[P0]
[P0]= (P0+△P0) KαKL (13-14)
但vmin≥5 m/S (P=Fv/1000)
人教版 八年级上册 数学第13--14章 期末复习题(含答案)

人教版八年级上册第13章轴对称章末综合训练一、选择题1. 以下列各组数据为边长,可以构成等腰三角形的是()A.1,1,2 B.1,1,3C.2,2,1 D.2,2,52. 如图,△ABC是等边三角形,D是AC的中点,DE⊥BC于点E,CE=3,则AB的长为()A.11 B.12 C.13 D.143. 在△ABC中,与∠A相邻的外角是110°,要使△ABC为等腰三角形,则∠B 的度数是()A.70°B.55°C.70°或55°D.70°或55°或40°4. 如果点(m-1,-1)与点(5,-1)关于y轴对称,那么m的值为()A.4 B.-4 C.5 D.-55. 如图直线a∥b∥c,等边三角形ABC的顶点B,C分别在直线b和c上,边BC与直线c所夹的锐角为20°,则∠α的度数为()A.20°B.40°C.60°D.80°6. 若点A(2m,2-m)和点B(3+n,n)关于y轴对称,则m,n的值分别为()A.1,-1 B.5 3,13C.-5,7 D.-13,-737. 如图,△ABC中,AB=AC,AD是∠BAC的平分线,已知AB=5,AD=3,则BC的长为()A. 5B. 6C. 8D. 108. 如图,在△ABC中,AC=BC,∠A=40°,观察图中尺规作图的痕迹,可知∠BCG的度数为()A.40°B.45°C.50°D.60°9. 在平面直角坐标系中,已知在y轴与直线x=3之间有一点M(a,3).如果该点关于直线x=3的对称点N的坐标为(5,3),那么a的值为()A.4B.3C.2D.110. 如图,在五边形ABCDE中,AB=AC=AD=AE,且AB∥ED,∠EAB=120°,则∠BCD的度数为()A.150°B.160°C.130°D.60°二、填空题11. 如图,AD是△ABC的边BC上的高,由下列条件中的某一个就能推出△ABC 是等腰三角形的是________.(把所有正确答案的序号都填写在横线上)①∠BAD=∠ACD ②∠BAD=∠CAD③AB+BD=AC+CD ④AB-BD=AC-CD12. 如图,△ABO是关于y轴对称的轴对称图形,点A的坐标为(-2,3),则点B的坐标为________.13. 如图,等腰三角形ABC的底边BC的长为6,面积是24,腰AC的垂直平分线EF分别交AC,AB边于点E,F.若D为BC边的中点,M为线段EF上一动点,则△CDM周长的最小值为________.14. 一个等腰三角形的一边长是2,一个外角是120°,则它的周长是________.15. 定义:等腰三角形的顶角与其一个底角的度数的比值k称为这个等腰三角形的“特征值”.若等腰三角形ABC中,∠A=80°,则它的特征值k=________.16. 如图,点E在等边三角形ABC的边BC上,BE=6,射线CD⊥BC于点C,P是射线CD上一动点,F是线段AB上一动点,当EP+PF的值最小时,BF=7,则AC的长为________.三、解答题17. 如图,已知△ABC中,D为BC边上一点,且AB=AC=BD,AD=CD,求∠BAC的度数.18. 如图,在△ABC中,AB=BD,根据图中的数据,求∠BAC的度数.19. 如图,在等边三角形ABC中,D为AC上一点,E为AB延长线上一点,DE ⊥AC交BC于点F,且DF=EF.(1)求证:CD=BE;(2)若AB=12,求BF的长.20. 如图,在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.(1)如果△ABC三个顶点的坐标分别是A(-2,0),B(-1,0),C(-1,2),△ABC关于y轴对称的图形是△A1B1C1,△A1B1C1关于直线l对称的图形是△A2B2C2,请直接写出△A2B2C2的三个顶点的坐标;(2)如果点P的坐标是(-a,0),其中a>0,点P关于y轴的对称点是P1,点P1关于直线l的对称点是P2,求PP2的长.21. 如图①所示,A,B两地在一条河的两岸,现要在河岸上造一座桥MN,桥造在何处才能使从A地到B地的路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直)[思考1]如图②,如果A,B两地之间有两条平行的河流,我们要建的桥都是与河岸垂直的,我们应该如何找到这个最短的路径呢?[思考2]如图③,如果A,B两地之间有三条平行的河流呢?[拓展]如图④,如果在上述其他条件不变的情况下,两条河并不是平行的,又该如何建桥呢?请将你的思考在下面准备好的图形中表示出来,保留作图痕迹,将行走的路线用实线画出来.链接听P30例2归纳总结人教版八年级上册第13章轴对称章末综合训练-答案一、选择题1. 【答案】 C2. 【答案】B∴∠CDE=30°.∴CD=2CE=6.∵D是AC的中点,∴AC=2CD=12.∴AB=AC=12.3. 【答案】D 当∠B =55°时,可得∠C =55°,∠B =∠C ,△ABC 为等腰三角形;当∠B =40°时,可得∠C =70°=∠A ,△ABC 为等腰三角形.4. 【答案】B5. 【答案】D∵△ABC 是等边三角形,∴∠ACB =60°.∴∠α=∠ACE =∠ACB +∠BCE =60°+20°=80°.6. 【答案】C7. 【答案】C8. 【答案】C∵AC =BC ,∴CG 平分∠ACB ,∠A =∠B =40°.∵∠ACB =180°-∠A -∠B =100°, ∴∠BCG =12∠ACB =50°.9. 【答案】D又∵点M (a ,3)到直线x=3的距离为3-a ,∴3-a=2.∴a=1.10. 【答案】A∴∠E =180°-∠EAB =180°-120°=60°.又∵AD =AE ,∴△ADE 是等边三角形.∴∠EAD =60°.∴∠BAD =∠EAB -∠EAD =120°-60°=60°.∵AB =AC =AD ,∴∠B =∠ACB ,∠ACD =∠ADC.在四边形ABCD 中,∠BCD =∠B +∠ADC =12(360°-∠BAD)=12×(360°-60°)=150°. 故选A.二、填空题12. 【答案】(2,3)13. 【答案】11 ∵△ABC 是等腰三角形,D 是BC 边的中点, ∴AD ⊥BC.∴S △ABC =12BC·AD =12×6×AD =24,解得AD =8.∵EF 是线段AC 的垂直平分线,∴点A 关于直线EF 的对称点为点C ,MA =MC. ∴MC +DM =MA +DM≥AD. ∴AD 的长为MC +DM 的最小值.∴△CDM 周长的最小值=(MC +DM)+CD =AD +12BC =8+12×6=8+3=11.14. 【答案】615. 【答案】85或14 ∴特征值k=80°50°=85.②当∠A 为底角时,顶角的度数为180°-80°-80°=20°, ∴特征值k =20°80°=14. 综上所述,特征值k 为85或14.16. 【答案】10如图,作点E 关于直线CD 的对称点G ,过点G 作GF ⊥AB 于点F ,交CD 于点P ,则此时EP +PF 的值最小.∵∠B =60°,∠BFG =90°,∴∠G =30°. ∵BF =7,∴BG =2BF =14.∴EG =8. ∴CE =CG =4.∴AC =BC =10.三、解答题17. 【答案】解:∵AD =CD ,∴设∠DAC =∠C =x°. ∵AB =AC =BD ,∴∠BAD =∠BDA =∠DAC +∠C =2x°, ∠B =∠C =x°.∴∠BAC =3x°.∵∠B +∠BAC +∠C =180°,∴5x =180, 解得x =36.∴∠BAC =3x°=108°.18. 【答案】解:∵∠ADB =30°+40°=70°,AB =BD , ∴∠BAD =∠ADB =70°.∴∠BAC =∠BAD +∠CAD =100°.19. 【答案】解:(1)证明:如图,过点D 作DM ∥AB ,交CF 于点M ,则∠MDF =∠E.∵△ABC 是等边三角形, ∴∠CAB =∠CBA =∠C =60°. ∵DM ∥AB ,∴∠CDM =∠CAB =60°,∠CMD =∠CBA =60°. ∴△CDM 是等边三角形. ∴CM =CD =DM.在△DMF 和△EBF 中,⎩⎨⎧∠MDF =∠E ,DF =EF ,∠DFM =∠EFB ,∴△DMF≌△EBF(ASA).∴DM=BE. ∴CD=BE.(2)∵ED⊥AC,∠CAB=∠CBA=60°,∴∠E=∠FDM=30°.∴∠BFE=∠DFM=30°.∴BE=BF,DM=MF.∵△DMF≌△EBF,∴MF=BF.∴CM=MF=BF.又∵BC=AB=12,∴BF=13BC=4.20. 【答案】解:(1)△A2B2C2的三个顶点的坐标分别是A2(4,0),B2(5,0),C2(5,2).(2)如图①,若0<a≤3,∵点P与点P1关于y轴对称,P(-a,0),∴P1(a,0).又∵点P1与点P2关于直线x=3对称,设P2(x,0),可得=3,即x=6-a.∴P2(6-a,0),则PP2=6-a-(-a)=6-a+a=6.如图②,若a>3,∵点P与点P1关于y轴对称,P(-a,0),∴P1(a,0).又∵点P1与点P2关于直线x=3对称,设P2(m,0),可得=3,即m=6-a.∴P2(6-a,0),则PP2=6-a-(-a)=6-a+a=6.综上,PP2的长为6.21. 【答案】如图①所示,MN即为所求.[思考1] 如图②所示,折线AMNEFB即为所求.[思考2] 如图③所示,折线AMNGHFEB即为所求.[拓展] 如图④所示,折线AMNEFB即为所求.人教版 八年级上册 第14章 整式的乘法与因式分解 章末综合训练一、选择题1. 化简(x 3)2,结果正确的是() A .-x 6 B .x 6C .x 5D .-x 52. 计算(x -1)2的结果是() A .x 2-x +1 B .x 2-2x +1 C .x 2-1D .2x -23. 计算(2x +1)(2x -1)的结果为( )A .4x 2-1B .2x 2-1C .4x -1D .4x 2+14. 若3×9m ×27m =321,则m 的值是( )A .3B .4C .5D .65. 下列各式中,能用完全平方公式计算的是()A .(x -y )(x +y )B .(x -y )(x -y )C .(x -y )(-x -y )D .-(x +y )(x -y )6. 下列各式中,计算正确的是()A .()222p q p q -=- B .()22222a b a ab b +=++ C .()2242121a a a +=++ D .()2222s t s st t --=-+7. 化简(-2x -3)(3-2x )的结果是( ) A .4x 2-9B .9-4x 2C .-4x 2-9D .4x 2-6x +98. 若(x +a )2=x 2+bx +25,则( )A .a =3,b =6B .a =5,b =5或a =-5,b =-10C .a =5,b =10D .a =-5,b =-10或a =5,b =109. 若n 为正整数,则(2n +1)2-(2n -1)2的值( )A .一定能被6整除B .一定能被8整除C .一定能被10整除D .一定能被12整除10. 若a ,b ,c 是三角形三边的长,则代数式2222a b c ab +--的值( ).A.大于零B.小于零 C 大于或等于零D .小于或等于零二、填空题11. 观察下列从左到右的变形:⑴()()3322623a b a b ab -=-; ⑵()ma mb c m a b c -+=-+⑶()22261266x xy y x y ++=+;⑷()()22323294a b a b a b +-=- 其中是因式分解的有 (填括号)12. 若x -y =6,xy =7,则x 2+y 2的值等于________.13. 如果(x +my )(x -my )=x 2-9y 2,那么m =________.14. 填空:()()22552516a a a b +-=-15. 课本上,公式(a -b )2=a 2-2ab +b 2是由公式(a +b )2=a 2+2ab +b 2推导得出的.已知(a +b )4=a 4+4a 3b +6a 2b 2+4ab 3+b 4,则(a -b )4=________________.16. 分解因式:432234232a a b a b ab b ++++=_______.三、解答题17. 计算:(41)(41)a a ---+18. 分解因式:44()()a x a x +--19. 分解因式:42231x x -+;20. 分解因式:222332154810ac cx ax c +--21. 分解因式:2222(3)2(3)(3)(3)x x x x -+--+-;人教版 八年级上册 第14章 整式的乘法与因式分解 章末综合训练-答案一、选择题1. 【答案】B2. 【答案】B3. 【答案】A4. 【答案】B5. 【答案】B6. 【答案】C7. 【答案】A8. 【答案】D 所以x 2+2ax +a 2=x 2+bx +25.所以⎩⎨⎧2a =b ,a 2=25,解得⎩⎨⎧a =5,b =10或⎩⎨⎧a =-5,b =-10.9. 【答案】B10. 【答案】B 【解析】222222222(2)()()()a b c ab a ab b c a b c a b c a b c +--=-+-=--=-+--又因为a ,b ,c 是三角形三边的长,所以a c b +>,a b c <+即0a b c -+>,0a b c --<,()()0a b c a b c -+--<,22220a b c ab +--<二、填空题11. 【答案】其中⑴是单项式变形,⑷是多项式的乘法运算,⑵中并没有写成几个整式的乘积的形式,只有⑶是因式分解12. 【答案】50 所以x 2+y 2=(x -y)2+2xy =62+2×7=50.13. 【答案】±314. 【答案】()()2254542516a b a b a b +-=-【解析】()()2254542516a b a b a b +-=-15. 【答案】a 4-4a 3b +6a 2b 2-4ab 3+b 4所以(a -b)4=[a +(-b)]4=a 4+4a 3(-b)+6a 2(-b)2+4a(-b)3+(-b)4=a 4-4a 3b +6a 2b 2-4ab 3+b 4.16. 【答案】222()a b ab ++【解析】4322342222222222232()2()()a a b a b ab b a b ab a b a b a b ab ++++=++++=++三、解答题17. 【答案】222(41)(41)(4)1161a a a a ---+=--=-【解析】222(41)(41)(4)1161a a a a ---+=--=-18. 【答案】228()ax a x +【解析】442222()()()()()()a x a x a x a x a x a x ⎡⎤⎡⎤+--=+--++-⎣⎦⎣⎦[][]22()()()()()()a x a x a x a x a x a x ⎡⎤=+--++-++-⎣⎦222222(22)8()x a a x ax a x =⋅⋅+=+19. 【答案】22(15)(15)x x x x +++-【解析】42422222222312125(1)(5)(15)(15)x x x x x x x x x x x -+=++-=+-=+++-20. 【答案】22(23)(165)c x a c --【解析】222323223215481032101548ac cx ax c ac c cx ax +--=-+- 22222(165)3(516)(23)(165)c a c x c a c x a c =-+-=--21. 【答案】22x x-+(2)(3)【解析】22222222 -+--+-=+-=-+;(3)2(3)(3)(3)(6)(2)(3)x x x x x x x x。
理论力学第13章动量矩定理

mi
rC x′
C
y′ y
mi vi mvC
LC ri mi vi
x
LO rC mvC LC
LO rC mvC LC
dLO d (e) (rC mvC LC ) r i Fi dt dt
r i rC ri
drC dLC d (e) i Fi ( e ) mvC rC mvC r C Fi r dt dt dt
v R
应用动量矩定理
O
FOx
mg
M
(e)
WR
dLO (e ) M dt
WR 2 a W 2 (JO R ) g
P
v
JO W dv ( R) WR R g dt
W
z
例 题3
z
求:此时系统的角速度 解:取系统为研究对象
M
A
(e ) z
0
A
B
a l
a
B
Lz 恒量
l
由质心坐标公式,有
z
vi z′ ri r′ i rC x′
C
mi
y′ y
O
mi ri mrC 0
x
LC ri mi vir
§13-6 刚体的平面运动微分方程
LC J C
由质心运动定理和相对于质 心的动量矩定理,有:
y
Fn
y′
D
F2 F1
maC Fi ( e ) d (e) J C J C M C ( Fi ) dt
用于质点系的外力对质心的主矩 ,这就是质点系相对于质心(平移
系)的动量矩定理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第13章 轴
13.1 轴的功用和类型
轴是机器中的重要零件之一,用来支持旋转的机械零件。
根据承受载荷的不同,轴可分为转轴、传动轴和心轴三种。转轴既传递转矩又承受弯矩,
如齿轮减速器中的轴;传动轴只传递转矩而不承受弯矩或弯矩很小。如汽车的传动轴;心轴只
承受弯矩而不传递转矩,如铁路车辆的轴、自行车的前轴。
按轴线的形状轴还可分为:直轴(下面4个图)、曲轴和挠性钢丝轴。曲轴常用于往复式
机械中。挠性钢丝轴是由几层紧贴在一起的钢丝层构成的,可以把转矩和旋转运动灵活地传到
任何位置,常用于振捣器等设备中。本章只研究直轴。
轴的设计,主要是根据工作要求并考虑制造工艺等因素,选用合适的材料,进行结构设计,
经过强度和刚度计算,定出轴的结构形状和尺寸,必要时还要考虑振动稳定性。
13.2 轴的常用材料
轴的材料常采用碳素钢和合金钢。
碳素钢承 35、45、50等优质碳素结构钢因具有较高的综合力学性能,应用较多,其中
以45号钢用得最为广泛。为了改善其力学性能,应进行正火或调质处理。不重要或受力较小
的轴,可采用Q235、Q275等碳素结构钢。
合金钢 合金钢具有较高的力学性能,但价格较贵,多用于有特殊要求的轴。例如:采
用滑动轴承的高速轴,常用20Cr、20CrMnTi等低碳合金结构钢,经渗碳淬火后可提高轴颈耐
磨性;汽轮发电机转子轴在高温、高速和重载条件下工作,必须具有良好的高温力学性能,常
采用40CrNi、38CrMoAlA等合金结构钢。值得注意的是:钢材的种类和热处理对其弹性模量
的影响甚小,因此,如欲采用合金钢或通过热处理来提高轴的刚度并无实效。此外,合金钢对
应力集中的敏感性较高,因此设计合金钢轴时,更应从结构上避免或减小应力集中,并减小其
表面粗糙度。
轴的毛坯一般用圆钢或锻件,有时也可采用铸钢或球墨铸铁。例如,用球墨铸铁制造曲轴、
凸轮轴,具有成本低廉、吸振性较好、对应力集中的敏感性较低、强度较好等优点。
下表13-1列出几种轴的常用材料及其主要力学性能。
13.3 轴的结构设计与强度计算
13.3.1 轴的结构设计
轴的结构设计就是使轴的各部分具有合理的形状和尺寸。其主要要求是:1)轴应便于加
工。轴上零件要易于装拆(制造安装要求);2)轴和轴上零件要有准确的工作位置(定位);3)
各零件要牢固而可靠地相对固定(固定);4)改善受力状况,减小应力集中。
下面逐项讨论这些要求,并结合下图所示的单级齿轮减速器的高速轴加以说明。
一、制造安装要求
为便于轴上零件的装拆,常将轴做成阶梯形。对于一般剖分式箱体中的轴,它的直径从
轴端逐渐向中间增大。如上图所示,可依次将齿轮、套筒、左端滚动轴承、轴承盖和带轮从轴
的左端装拆,另一滚动轴承从右端装拆。为使轴上零件易于安装,轴端及各轴段的端部应有倒
角。
轴上磨削的轴段,应有砂轮越程槽(上图中③与③的交界处);车制螺纹的轴段,应有退
刀槽。
在满足使用要求的情况下,轴的形状和尺寸应力求简单,以便于加工。
二、轴上零件的定位
阶梯轴上截面变化处叫做轴肩,起轴向定位作用。在上图中,④、⑤间的轴肩使齿轮在
轴上定位;①、②间的轴肩使带轮定位;③、⑤间的轴肩使右端滚动轴承定位。
有些零件依靠套简定位,如上图中的左端滚动轴承。
三、轴上零件的固定
轴上零件的轴向固定,常采用轴肩、套筒、螺母或轴端挡圈(又称压板)等形式。在上
图中,齿轮能实现轴向双向固定。齿轮受轴向力时,向右是通过④、⑤间的轴肩,并由③、③
间的轴肩顶在滚动轴承内圈上;向左则通过套筒顶在滚动轴承内圈上。无法采用套筒或套筒太
长时,可采用圆螺母加以固定(下左图)。带轮的轴向固定是靠①、②间的轴肩以及轴端挡圈。
下右图所示是轴端档圈的一种型式。
采用套简、螺母、轴端挡圈作轴向固定时,应把装零件的轴段长度做得比零件轮我短2~
3mm,以确保套筒、螺母或轴端挡圈能靠紧零件端面。
为了保证轴上零件紧靠定位面(轴肩),轴肩的圆角半径r必须小于相配零件的倒角C
1
或圆角半径R,轴肩高h必须大于C1或R(下图)。
轴向力较小时,零件在轴上的固定可采用弹性挡圈(下左图)或紧定螺钉(下右图)。
轴上零件的周向固定,大多采用键、花键或过盈配合等联接形式。采用键联接时,为加
工方便,各轴段的键槽应设计在同一加工直线上,并应尽可能采用同一规格的键槽截面尺寸(下
图)。
四、改善轴的受力状况,减小应力集中
合理布置轴上的零件可以改善轴的受力状况。例如,上图所示为起重机卷筒的两种布置
方案,图a的结构中,大齿轮和卷筒联成一体,转矩经大齿轮直接传给卷筒,故卷筒轴只受弯
矩而不传递扭矩,在起重同样载荷W时,轴的直径可小于图b的结构。再如,当动力从两轮
输出时,为了减小轴上载荷,应将输入轮布置在中间,如下图a所示,这时轴的最大转矩为
T1;而在图b的布置中,轴的最大转矩为T1十T2。
改善轴的受力状况的另一重要方面就是减小应力集中。合金钢对应力集中比较敏感,尤需
加以注意。
零件截面发生突然变化的地方,都会产生应力集中现象。因此对阶梯轴来说,在截面尺
寸变化处应采用圆角过渡,圆角半径不宜过小,并尽量避免在轴上(特别是应力大的部位)开
横孔、切口或凹槽。必须开横孔时,孔边要倒圆。在重要的结构中,可采用卸载槽B(下图a)、
过渡肩环(下图b)或凹切圆角(图c)增大轴肩圆角半径,以减小局部应力。在轮毂上做出
卸载槽B(图d),也能减小过盈配合处的局部应力。
13.3.2 轴的强度计算
轴的强度计算应根据轴的承载情况,采用相应的计算方法。常见的轴的强度计算方法有以
下两种:
一、按扭转强度计算
这种方法适用于只承受转矩的传动轴的精确计算,也可用于既受弯矩又受扭矩的轴的近似
计算。
对于只传递转矩的圆截面轴,其强度条件为
对于既传递转短又承受弯矩的轴,也可用上式初步估算的直径,设计公式为
常用材料的C值和τ值见下表。
此外,也可采用经验公式来估算轴的直径。例如在一般减速器中,高速输入轴的直径可
按与其相联的电动机轴的直径D估算,d=(0.8~1. 2)D;各级低速轴的轴径可按同级齿轮中
心距 a估算,d=(0.3~0.4)a。
二、按弯扭合成强度计算
下图为一单级圆柱齿轮减速器的设计草图,图中各符号表示有关的长度尺寸。显然,当
零件在草图上布置妥当后,外载荷和支承反力的作用位置即可确定。由此可作轴的受力分析及
绘制弯矩图和转矩图。这时就可按弯扭合成强度计算轴径。
对于一般钢制的轴,可用第三强度理论(即最大切应力理论)求出危险截面的当量应力
σe,其强度条件为
将σb和τ值代入上面的强度条件公式,得:
由于一般转轴的弯曲应力为对称循环变应力,而扭切应力的循环特性往往不同,考虑两
者循环特性不同的影响,对上式中的转矩T乘以折合系数α,即
对于有键槽的截面,应将计算出的轴径加大4%左右。若计算出的轴径大于结构设计初步
估算的轴径,则表明结构图中轴的强度不够,必须修改结构设计;若计算出的轴径小于结构设
计的估算轴径,且相差不很大,一般就以结构设计的轴径为准。
对于一般用途的轴,按上述方法设计计算即可。对于重要的轴,尚须作进一步的强度校
核(如安全系数法),其计算方法可查阅有关参考书。
轴的许用弯曲应力见下表(MPa)。
13.3.3 轴的刚度计算
轴受弯矩作用会产生弯曲变形(上左图),受转矩作用会产生扭转变形(上右图)。如果
轴的刚度不够,就会影响轴的正常工作。例如电机转子轴的挠度过大,会改变转子与定子的间
隙而影响电机的性能。又如机床主轴的刚度不够,将影响加工精度。因此,为了使轴不致因刚
度不够而失效,设计时必须根据轴的工作条件限制其变形量,即
计算轴在弯矩作用下所产生的挠度y和转角θ的方法很多。在材料力学课程中已研究过
两种:l)按挠度曲线的近似微分方程式积分求解;2)变形能法。
轴的许用变形量见下表。
13.3.4 轴的临界转速的概念
由于回转件的结构不对称、材质不均匀、加工有误差等原因,要使回转件的重心精确地
位于几何轴线上,几乎是不可能的。实际上,重心与几何轴线间一般总有一微小的偏心距,因
而回转时产生离心力,使轴受到周期性载荷的干扰。
若轴所受的外力频率与轴的自振频率一致时,运转便不稳定而发生显著的振动,这种现
象称为轴的共振。产生共振时轴的转速称为临界转速。如果轴的转速停滞在临界转速附近,轴
的变形将迅速增大,以至达到使轴,甚至整个机器破坏的程度。因此,对于重要的,尤其是高
转速的轴必须计算其临界转速,并使轴的工作转速n避开临界转速nc。
轴的临界转速可以有许多个,最低的一个称为一阶临界转速,其余为二阶、三阶……。
工作转速低于一阶临界转速的轴称为刚性轴;超过一阶临界转速的轴称为挠性轴。
