【7A文】三大模型辅助线
初中数学辅助线专题

初中数学辅助线专题初中数学辅助线专题在初中数学中,辅助线是一个常用的解题技巧。
它可以帮助我们简化问题、寻找规律、搭建思维框架,提高解题效率。
下面将介绍几种常见的辅助线及其运用。
1. 垂直辅助线:垂直辅助线是指与已知线段或角度垂直的辅助线。
通过画垂直辅助线,可以将问题中的图形分解为更简单的部分,从而更容易求解。
例如,在解决正方形内接圆问题时,可以通过画一条从正方形的一个顶点到内接圆心的垂直辅助线,将问题转化为求直角三角形的斜边长。
2. 平行辅助线:平行辅助线是指与已知线段或角度平行的辅助线。
通过画平行辅助线,可以将问题中的图形分割为更容易处理的几何图形,为解题提供方便。
例如,在解决平行四边形面积问题时,可以通过画一条平行于底边的辅助线,将问题转化为求两个三角形的面积。
3. 对称辅助线:对称辅助线是指通过已知图形中心的辅助线。
通过画对称辅助线,可以将问题中的图形分割为相等的部分,并且可以利用对称性质解题。
例如,在解决正多边形内角和问题时,可以通过画一条从正多边形中心到顶点的辅助线,将问题转化为求正多边形的内角和与外角和。
4. 中位线:中位线是指连接一个三角形的一个顶点和对边中点的线段。
中位线具有许多特殊性质,例如三角形三条中位线交于一点,该点被称为三角形的重心。
通过画中位线,可以将问题中的三角形分割为更简单的几何图形,进而解决问题。
除了以上介绍的辅助线,还有许多其他类型的辅助线可以应用于解决不同类型的数学问题。
当我们遇到一个复杂的几何问题时,可以尝试使用辅助线来简化问题,找到解题的突破口。
通过熟练掌握辅助线的使用技巧,并灵活运用,我们可以更加高效地解决数学问题。
圆中的重要模型之辅助线模型(八大类)(学生版)

圆中的重要模型之辅助线模型(八大类)在平面几何中,与圆有关的许多题目需要添加辅助线来解决。
百思不得其解的题目,添上合适的辅助线,问题就会迎刃而解,思路畅通,从而有效地培养学生的创造性思维。
添加辅助线的方法有很多,本专题通过分析探索归纳八类圆中常见的辅助线的作法。
模型1、遇弦连半径(构造等腰三角形)【模型解读】已知AB 是⊙O 的一条弦,连接OA ,OB ,则∠A =∠B .在圆的相关题目中,不要忽略隐含的已知条件。
当我们要解决有关角度、长度问题时,通常可以连接半径构造等腰三角形,利用等腰三角形的性质、勾股定理及圆中的相关定理,还可连接圆周上一点和弦的两个端点,根据圆周角的性质可得相等的圆周角,解决角度或长度的计算问题1(2022·山东聊城·统考中考真题)如图,AB ,CD 是⊙O 的弦,延长AB ,CD 相交于点P .已知∠P =30°,∠AOC =80°,则BD 的度数是()A.30°B.25°C.20°D.10°2(2023•南召县中考模拟)如图,⊙O 的直径AB 与弦CD 的延长线交于点E ,若DE =OB ,∠AOC =84°,则∠E 等于()A.42°B.28°C.21°D.20°3(2023·江苏沭阳初三月考)如图,已知点C 是⊙O 的直径AB 上的一点,过点C 作弦DE ,使CD =CO .若AD 的度数为35°,则BE 的度数是.4(2023年山东省淄博市中考数学真题)如图,△ABC是⊙O的内接三角形,AB=AC,∠BAC=120°,D 是BC边上一点,连接AD并延长交⊙O于点E.若AD=2,DE=3,则⊙O的半径为()A.10B.310 C.210 D.3102模型2、遇弦作弦心距(解决有关弦长的问题)【模型解读】已知AB是⊙O的一条弦,过点OE⊥AB,则AE=BE,OE2+AE2=OA2。
第二讲三大模型辅助线
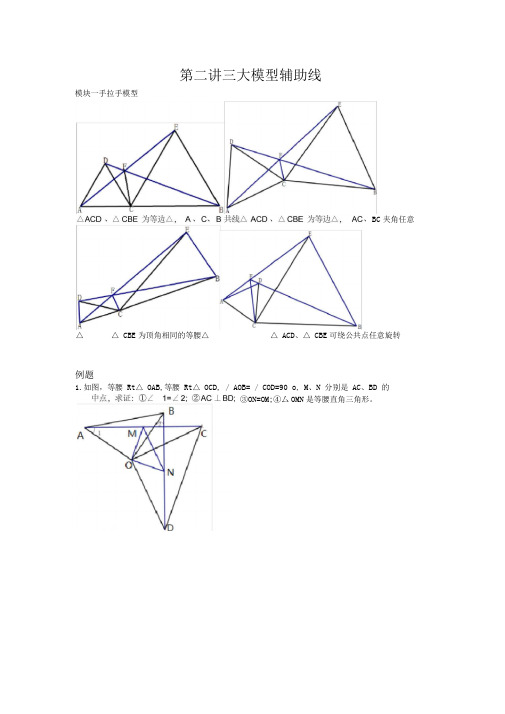
第二讲三大模型辅助线例题1.如图,等腰 Rt △ OAB,等腰 Rt △ OCD, / AOB= / COD=90 o , M 、N 分别是 AC 、BD 的③ON=OM;④厶OMN是等腰直角三角形。
模块一手拉手模型△ CBE 为顶角相同的等腰△ △ ACD 、△ CBE 可绕公共点任意旋转△ACDBC 夹角任意2.如图1,图2,图3,在^ ABC 中,分别以AB 、AC 为边,向外作正三角形, 正方形,正五边形, CD 相交于0。
1,求证:△ ABE ADC ; 1,/ B0C=;如图 2,/ B0C=;如图 3,/ B0C=; 4,已知AB 、AD 是以AB 为边向△ ABC 外所作正n 边形的一组邻边; AC 、AE 是以 的延长线相交于点 0。
如图4,/ B0C= BE 、 如图 如图 如图 AC 为边向外所作正 n 边形的一组邻边, (用含n 的式子表示)BE 、CD 4证明你的猜想。
,并根据图 DOGCEHB圈4B '角度到△ ADE 的位置,设BC 与DE 交于M将^ ABC 绕A 点顺时针方向旋转 3.如图,4.如图,△ ABC 中,/ ACB=90o, / CAD=30 o,AC=BC=AD,CE 丄CD,且CE=CD,连接BD、② BE=BC;③AD丄BE;④CD=1.BD模块二夹半角模型(旋转构造全等三角形)正方形 ABCD 中,/ EAF=45o,则 DF + BE=EF ;正方形 ABCD 中,/ EAF=45 0,则 DF — BE=EF已知:/ B +/ D=180o,AB=AD, / EAF= a ,/ BAD=2 a,贝U: BE + DF=EF(含勾股定理)已知:/ A=60 0, / BDC=120 o, / MDN=60 o,DB=DC或 CN — BM=MNF5.如图,已知正方形ABCD中,/ EAF=45o, (1)求证:BE+DF=EF, (2)若连接BD 交AE 于M ,交AF 于N,求证:BM2+DN 2=MN 2.6.如图,在直角坐标系中,A (4,0)、B (0,4)、D (0,1),若E(x , 4),EB 丄OB于7.在四边形 ABCD 中,AC=AB,DC=DB, / CAB=60o,/ CDB=120o,E 是 AC 上一 点,F 是AB 延长线上一点,且 CE=BF.在图1中,求证:DE=DF;在图1中,若G 在AB 上且/ EDG=60o ,试猜想CE 、EG 、BG 之间 的数量关系并证明;运用(1) (2)解答中所积累的经验和知识,完成下题:如图 2,在四边形 ABCD 中,/ ABC=90o,/ CAB= / CAD=30o,E 在 AB 上,DE8.已知如图,五边形 ABCDE 中,AB=AE,BC+DE=CD, /ABC+ /AED=180o.求证: (1)AD 平分/ CDE ,(2)/ BAE=2 / CAD 。
中考数学10大类辅助线

中考数学10大类辅助线
中考数学中,常见的辅助线有以下10大类:
1.垂直辅助线:通过一个点和另一直线的垂直线,常用于求两条
直线的垂直关系、求直角三角形等问题。
2.平行辅助线:通过一点和一条直线,与已知的另一直线平行,
常用于求两条直线的平行关系、求平行四边形等问题。
3.中垂线:将一个线段的中点与另一点相连的线段,用于求线段
的中点、判断三角形的等腰性质等问题。
4.角平分线:将一个角分成两个相等的角的线段,通常用于求角
的平分线、求角的刻度等问题。
5.对称辅助线:通过一个点,找到与已知点关于某一直线对称的点,用于求对称点的位置、对称图形等问题。
6.高线:将一个顶点到对立边的垂线段,常用于求三角形的高度、找到垂心等问题。
7.过定点画圆:通过一个已知点和一个已知的半径,画出以该点为圆心的圆,常用于求圆的位置关系、圆与线的交点等问题。
8.过三点画圆:通过给定的三个点,画出以这三点为圆上三个点的圆,用于求圆与三角形的关系等问题。
9.共轭辅助线:通过两个点,在给定条件下找到与已知直线共轭的直线,常用于求一对共轭角、共轭点等问题。
10.谁是谁的辅助线:在解题过程中,发现和已知量之间存在特定的几何关系时,可以将某个量作为另一个量的辅助线,通过推导或等式的变形求解。
以上是中考数学中常用的10大类辅助线。
通过合理地运用这些辅助线,可以帮助我们更好地解决各种几何问题,提高解题的效率和准确性。
初中数学全等三角形中的基本模型及常用辅助线

03
常用辅助线方法
中线法
中线倍长法
通过延长中线至等长,构造全等 三角形,常用于证明线段相等或 角相等。
中线性质应用
利用中线将三角形面积平分,或 将三角形划分为两个面积相等的 小三角形。
角平分线法
角平分线性质
角平分线上的点到角两边的距离相等 ,利用此性质可以构造全等三角形。
角平分线与平行线组合
通过作角平分线的平行线,构造相似 三角形,进而证明线段成比例或求线 段长度。
填空题答题技巧
准确理解题意
01
认真阅读题目,明确题目所考察的知识点和要求。
灵活运用知识
02
根据题目所给的条件和要求,灵活运用所学的知识点进行解答
。
注意答案的完整性和准确性
03
在填写答案时,要注意答案的完整性和准确性,避免漏填或错
填。
解答题答题思路展示
分析题意
认真阅读题目,理解题意,明确题目所考 察的知识点和要求。
基本模型与常用辅助 线
掌握在解决全等问题 时常用的辅助线作法 ,如倍长中线、截长 补短等。
熟悉几种常见的全等 三角形基本模型,如 角平分线模型、中线 模型等。
课堂检测题目设置及评价
题目设置
设置涵盖全等三角形定义、性质、判定方法以及基本模型和常用辅助线 的题目。
题目难度适中,既考查学生对基础知识的掌握,又考查其灵活运用能力 。
对应角相等
全等三角形的对应角相等。
周长相等
全等三角形的周长相等。
面积相等
全等三角形的面积相等。
典型例题解析
例1
解析
已知△ABC和△DEF中,AB = DE,BC = EF ,∠B = ∠E,求证:△ABC ≌ △DEF。
“史上最全”初中几何学习资料:模型辅助线中考高分必备宝典

“史上最全”初中几何学习资料:模型辅助线中考高分必备宝
典
在初中数学中,几何的重要性不言自明,作为和代数并列为初中数学两大知识点的几何,常常因为图形变化多端,方法多种多样而被称为数学中的变形金刚。
学生刚接触平面几何的学习,或许都会遇到这样或那样的困惑,特别是对平面几何中所使用的一些方法感到不适应。
为了减轻同学们学习几何的难度,小编特意熬夜整理了初中几何的全部必考模型和辅助线添加方法大全。
【推荐】初中几何辅助线大全(52页)

作辅助线的方法一:中点、中位线,延线,平行线。
如遇条件中有中点,中线、中位线等,那么过中点,延长中线或中位线作辅助线,使延长的某一段等于中线或中位线;另一种辅助线是过中点作已知边或线段的平行线,以达到应用某个定理或造成全等的目的。
二:垂线、分角线,翻转全等连。
如遇条件中,有垂线或角的平分线,可以把图形按轴对称的方法,并借助其他条件,而旋转180度,得到全等形,,这时辅助线的做法就会应运而生。
其对称轴往往是垂线或角的平分线。
三:边边若相等,旋转做实验。
如遇条件中有多边形的两边相等或两角相等,有时边角互相配合,然后把图形旋转一定的角度,就可以得到全等形,这时辅助线的做法仍会应运而生。
其对称中心,因题而异,有时没有中心。
故可分“有心”和“无心”旋转两种。
四:造角、平、相似,和、差、积、商见。
如遇条件中有多边形的两边相等或两角相等,欲证线段或角的和差积商,往往与相似形有关。
在制造两个三角形相似时,一般地,有两种方法:第一,造一个辅助角等于已知角;第二,是把三角形中的某一线段进行平移。
故作歌诀:“造角、平、相似,和差积商见。
”托列米定理和梅叶劳定理的证明辅助线分别是造角和平移的代表)五:两圆若相交,连心公共弦。
如果条件中出现两圆相交,那么辅助线往往是连心线或公共弦。
六:两圆相切、离,连心,公切线。
如条件中出现两圆相切(外切,内切),或相离(内含、外离),那么,辅助线往往是连心线或内外公切线。
七:切线连直径,直角与半圆。
如果条件中出现圆的切线,那么辅助线是过切点的直径或半径使出现直角;相反,条件中是圆的直径,半径,那么辅助线是过直径(或半径)端点的切线。
即切线与直径互为辅助线。
如果条件中有直角三角形,那么作辅助线往往是斜边为直径作辅助圆,或半圆;相反,条件中有半圆,那么在直径上找圆周角——直角为辅助线。
即直角与半圆互为辅助线。
八:弧、弦、弦心距;平行、等距、弦。
如遇弧,则弧上的弦是辅助线;如遇弦,则弦心距为辅助线。
初中几何中常用的辅助线方法的资料

初中几何是学生学习几何知识的基础阶段,掌握正确的辅助线技巧对于解决几何问题至关重要。
下面是一份关于初中几何中常用的辅助线方法的资料,希望能帮助到您。
一、基本概念辅助线:在解决几何问题时,为了更好地展现图形的性质或构建所需的条件,临时添加的线段称为辅助线。
辅助线不改变原图形的基本结构,但能帮助我们发现解题的关键线索。
二、常用辅助线方法1. 过顶点作垂线●应用场景:证明直角、等腰三角形的性质,求解高、距离等问题。
●示例:证明一个三角形是直角三角形时,可以尝试从一个顶点向对边作垂线,利用勾股定理。
2. 连接中点●应用场景:证明线段倍长、中位线性质、平行四边形和梯形的构造。
●示例:证明两条线段相等时,连接它们的中点,利用中位线定理。
3. 平行线构造●应用场景:形成相似三角形、构造平行四边形、证明角度关系。
●示例:为证明两个角相等,可以在其中一个角的一边上作一条平行于另一角所在直线的辅助线,从而构成一对内错角或同位角。
4. 过顶点作平行线●应用场景:构造全等三角形、证明角平分线性质。
●示例:证明两角相等时,可以从一个角的顶点出发作一条平行于另一个角一边的线,这样可以构造出一组等角的三角形。
5. 延长线段●应用场景:寻找共线点、证明交比不变、构造平行线。
●示例:当需要证明四点共线时,延长某些线段,利用交叉线段的比值相等来证明。
6. 作角平分线或垂直平分线●应用场景:证明等腰三角形、等边三角形性质,解决与圆相关的几何问题。
●示例:证明一个点在三角形某边的垂直平分线上,可以过该点作这条边的垂线,利用垂直平分线的性质。
三、技巧总结1.观察图形特征:首先分析图形的已知条件和所求目标,根据图形的特殊形状或已知条件选择合适的辅助线方法。
2.尝试多种方案:有时候,一种辅助线方法可能不足以解决问题,需要尝试几种不同的方法。
3.灵活运用定理:熟练掌握各种几何定理,并能灵活应用到辅助线的构造中。
4.练习与总结:多做练习,每次解题后总结辅助线的使用经验,逐步提高解题效率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二讲三大模型辅助线
模块一手拉手模型
△ACD、△CBE为等边△,A、C、B共线△ACD、△CBE为等边△,AC、BC夹角任意
△ACD、△CBE为顶角相同的等腰△△ACD、△CBE可绕公共点任意旋转
例题
1.如图,等腰Rt△OAB,等腰Rt△OCD,∠AOB=∠COD=90º,M、N分别是AC、BD的中
点,求证:①∠1=∠2;②AC⊥BD;③ON=OM;④△OMN是等腰直角三角形。
2.如图1,图2,图3,在△ABC中,分别以AB、AC为边,向外作正三角形,正方形,正五边形,BE、CD相交于O。
如图1,求证:△ABE≌△ADC;
如图1,∠BOC=;如图2,∠BOC=;如图3,∠BOC=;
如图4,已知AB、AD是以AB为边向△ABC外所作正n边形的一组邻边;AC、AE是以AC为边向外所作正n边形的一组邻边,BE、CD的延长线相交于点O。
如图4,∠BOC=(用含n的式子表示),并根据图4证明你的猜想。
3.如图,将△ABC 绕A 点顺时针方向旋转 角度到△ADE 的位置,设BC 与DE 交于M 点,连接AM,求∠AMD 的度数。
4.如图,△ABC 中,∠ACB=90º,∠CAD=30º,AC=BC=AD,CE ⊥CD,且CE=CD ,连接BD 、 DE 、BE,
求证:
①∠ECA=165º;
②BE=BC;
③AD ⊥BE; ④
BD
CD =1.
模块二夹半角模型(旋转构造全等三角形)
正方形ABCD中,∠EAF=45º,则DF+BE=EF ;正方形ABCD中,∠EAF=45º,则DF-BE=EF
已知:∠A=60º,∠BDC=120º,∠MDN=60º,DB=DC
则:CN+BM=MN或CN-BM=MN
已知:∠B+∠D=180º,AB=AD,∠EAF=α,∠BAD=2α,则:BE+DF=EF
(含勾股定理)
5.如图,已知正方形ABCD中,∠EAF=45º,(1)求证:BE+DF=EF,(2)若连接BD交AE于M,交AF于N,求证:BM²+DN²=MN².
6.如图,在直角坐标系中,A(4,0)、B(0,4)、D(0,1),若E(G,4),EB⊥OB于
B,且满足∠EAD=45º,试求线段EB的长度。
7.在四边形ABCD中,AC=AB,DC=DB,∠CAB=60º,∠CDB=120º,E是AC上一点,F是AB延长线上一点,且CE=BF.
(1)在图1中,求证:DE=DF;
(2)在图1中,若G在AB上且∠EDG=60º,试猜想CE、EG、BG之间的数量关系并证明;
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图2,在四边形ABCD中,∠ABC=90º,∠CAB=∠CAD=30º,E在AB上,DE ⊥AB,且∠DCE=60º,若AE=3,则BE的长为()。
8.已知如图,五边形ABCDE中,AB=AE,BC+DE=CD,∠ABC+∠AED=180º.求证:(1)AD平分∠CDE,(2)∠BAE=2∠CAD。
模块三三垂直模型
已知:直线m经过等腰Rt⊿ABC的直角顶点A,过两锐角顶点作m的垂线段
则:△ABE≌△CAF
B、C、D、F四点共线,Rt⊿ABC≌Rt⊿DEF;AB⊥DE。
9.如图,△ABE和△ACD为等腰直角三角形,AM⊥BC于M,MA交ED于N,求证:EN=DN.
10.已知:AD∥BC,∠ABC=∠CDE=90º,CD=DE,AD=2,BC=3,求S△EAD。
11.如图,已知P(2,2),BC⊥AP.求证:(1)求OM+OC
的值;⑵求OB-OA的值。
12.已知等腰Rt△ABC,∠BAC=90º,AD=CF,AE⊥BD,BD、EF交于点G,
求证:△DFG为等腰三角形。
13.如图,等腰Rt △ABC 中,∠B=90º,点P 在BC 上,以AP 为腰在△ABC 外侧作等腰Rt △APQ,连PQ 交AB 于N ,连CQ 交AB 于M.P 在边BC 上。
⑴若CP=2BP ,求BM CP 的值。
⑵若CQ 平分∠ACB ,求BM
CP 的值。
14.已知:Rt △ABC,BC=a,AC=b,AB=c,正方形ABDE 、BCHI 、ACGF,⑴求六边形DEFGHI 的面积;⑵探索EF 、GH 、DI 能否构成三角形的三边?若能,请求出该三角形的面积与△ABC 面积的关系;若不能,请说明理由。
