中考数学专题复习-常用辅助线截长补短
截长补短法

全等三∴角∠形之C巧+短添∠法辅助D=线1—8—0截°长补
例题 如图,AC∥BD,EA、EB分别
平分∠CAB和∠DBA,点E在CD上,
补短法 F求证:AB=AC+BD。 E D 补短法:一般有两种方式—— 一种是 将某短线段延长,使延长的一部分等
C A
于另一条已知的较短的长度,另一种
是线延将段长某。短AC线至段直F,接延使长C至F等=于BD较或长的使AF=
B
全等三角形之巧添辅助线——截长补 短法
例题 如图,AC∥BD,EA、EB分别
平分∠CAB和∠DBA,点E在CD上,
补短法 F求证:AB=AC+BD。
E
D
(1)延长AC至F,使CF=BD,连
C A
接EF 要证
再证△AEF≌△AE
√(2)△延C长EFA≌C至△FD,EB使,AF=AB,连接EF
B 可得到△AEF≌△AEB,再证△CEF≌
练习如:图,△ABC中,∠CAB=∠CBA=45°,
CA=CB,点E为BC的中点,CN⊥AE交AB于N。 (1)求证:∠1=∠2 (2)求证:AE=CN+EN (请用多种方法证
B 明)F 补短法:过点B作BF⊥BC交CN的延长线于点
N E
1
C 2A
可证得△CBF≌△ACE,从而得到AE= 再证△BEN≌△BFN,可得EN=FN.
[串点成面·握全局]
一、近代交通业发展的原因、特点及影响 1.原因 (1)先进的中国人为救国救民,积极兴办近代交通业,促 进中国社会发展。 (2)列强侵华的需要。为扩大在华利益,加强控制、镇压 中国人民的反抗,控制和操纵中国交通建设。 (3)工业革命的成果传入中国,为近代交通业的发展提供 了物质条件。
全等三角形辅助线系列之三---截长补短类辅助线作法大全

全等三角形辅助线系列之三---截长补短类辅助线作法大全-CAL-FENGHAI.-(YICAI)-Company One1全等三角形辅助线系列之三 与截长补短有关的辅助线作法大全一、截长补短法构造全等三角形截长补短法,是初中数学几何题中一种辅助线的添加方法,也是把几何题化难为易的一种思想.所谓“截长”,就是将三者中最长的那条线段一分为二,使其中的一条线段等于已知的两条较短线段中的一条,然后证明其中的另一段与已知的另一条线段相等;所谓“补短”,就是将一个已知的较短的线段延长至与另一个已知的较短的长度相等,然后求出延长后的线段与最长的已知线段的关系.有的是采取截长补短后,使之构成某种特定的三角形进行求解.截长补短法作辅助线,适合于证明线段的和、差、倍、分等类的题目.典型例题精讲【例1】 如图,在ABC ∆中,60BAC ∠=︒,AD 是BAC ∠的平分线,且AC AB BD =+,求ABC ∠的度数.【解析】法一:如图所示,延长AB 至E 使BE BD =,连接ED 、EC .由AC AB BD =+知AE AC =,而60BAC ∠=︒,则AEC ∆为等边三角形.注意到EAD CAD ∠=∠,AD AD =,AE AC =, 故AED ACD ∆∆≌.从而有DE DC =,DEC DCE ∠=∠,故2BED BDE DCE DEC DEC ∠=∠=∠+∠=∠.所以20DEC DCE ∠=∠=︒,602080ABC BEC BCE ∠=∠+∠=︒+︒=︒. 法二:在AC 上取点E ,使得AE AB =,则由题意可知CE BD =. 在ABD ∆和AED ∆中,AB AE =,BAD EAD ∠=∠,AD AD =, 则ABD AED ∆∆≌,从而BD DE =, 进而有DE CE =,ECD EDC ∠=∠, AED ECD EDC ∠=∠+∠=2ECD ∠. 注意到ABD AED ∠=∠,则:1318012022ABC ACB ABC ABC ABC BAC ∠+∠=∠+∠=∠=︒-∠=︒,故80ABC ∠=︒.【答案】见解析.【例2】 已知ABC ∆中,60A ∠=︒,BD 、CE 分别平分ABC ∠和.ACB ∠,BD 、CE 交于点O ,试判断BE 、CD 、BC 的数量关系,并加以证明.【解析】BE CD BC +=,理由是:在BC 上截取BF BE =,连结OF , 利用SAS 证得BEO ∆≌BFO ∆,∴12∠=∠,∵60A ∠=︒,∴1901202BOC A ∠=︒+∠=︒,∴120DOE ∠=︒,∴180A DOE ∠+∠=︒,∴180AEO ADO ∠+∠=︒, ∴13180∠+∠=︒,∵24180∠+∠=︒,∴12∠=∠,∴34∠=∠, 利用AAS 证得CDO ∆≌CFO ∆,∴CD CF =, ∴BC BF CF BE CD =+=+.【答案】见解析.【例3】 如图,已知在△ABC 内,60BAC ∠=︒,40C ∠=︒,P 、Q 分别在BC 、CA 上,并且AP 、BQ 分别是∠BAC 、∠ABC 的角平分线,求证:BQ AQ AB BP +=+.DOECB A4321FDOE CB A【解析】延长AB 至D ,使BD BP =,连DP .在等腰△BPD 中,可得40BDP ∠=︒, 从而40BDP ACP ∠=︒=∠,△ADP ≌△ACP (ASA ),故AD AC =又40QBC QCB ∠=︒=∠,故 BQ QC =,BD BP =. 从而BQ AQ AB BP +=+.【答案】见解析.【例4】 如图,在四边形ABCD 中,BC BA >,AD CD =,BD 平分∠ABC ,求证:180A C ∠+∠=︒.【解析】延长BA 至F ,使BF BC =,连FD△BDF ≌△BDC (SAS ), 故DFB DCB ∠=∠,FD DC =又AD CD =,故在等腰△BFD 中,DFB DAF ∠=∠ 故有180BAD BCD ∠+∠=︒【答案】见解析.【例5】 点M ,N 在等边三角形ABC 的AB 边上运动,BD DC =,120BDC ∠=︒,60MDN ∠=︒,求证:MN MB NC =+.QPCBACDB A【解析】延长NC 至E ,使得CE MB =∵ BDC ∆是等腰三角形,且120BDC ∠=︒,∴30DBC DCB ∠=∠=︒ ∵ ABC ∆是等边三角形. ∴60ABC ACB BAC ∠=∠=∠=︒∴90MBD ABC DBC ACB DCB DCN DCE ∠=∠+∠=∠+∠=∠=∠=︒ 在DBM ∆和DCE ∆中,BD DC =,MB CE =, ∴ DBM DCE ∆∆≌. ∴DE DM =, 12∠=∠.又∵ 160NDC ∠+∠=︒,∴ 2+60NDC END ∠∠=∠=︒. 在MDN ∆与EDN ∆中,ND ND =,60MDN EDN ∠=∠=︒,DE DM = ∴ MND END ∆∆≌∴ MN EN NC MB ==+【答案】见解析.【例6】 如图在△ABC 中,AB AC >,12∠=∠,P 为AD 上任意一点,求证:AB AC PB PC ->-.【解析】延长AC 至F ,使AF AB =,连PD△ABP ≌△AFP (SAS ) 故BP PF =由三角形性质知1BMNM CBA21EABCDMN< PB PC PF PC CF AF AC AB AC -=-=-=-【答案】见解析.【例7】 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上.求证:BC AB DC =+.【解析】在BC 上截取BF AB =,连接EF∵BE 平分∠ABC ,∴ABE FBE ∠=∠又∵BE BE =,∴△ABE ≌△FBE (SAS ),∴A BFE ∠=∠.∵AB 180A D ∠+∠=︒180BFE CFE ∠+∠=︒D CFE ∠=∠DCE FCE ∠=∠CE CE =CD CF=BC BF CF AB CD =+=+M ABCD AB MN DM ⊥ABC ∠N MD MNDM MN =AD 上截取AG AM =,∴DG MB =,∴45AGM =︒∠∴135DGM MBN ==︒∠∠,∴ADM NMB =∠∠, ∴DGM MBN ∆∆≌,∴DM MN =.【答案】见解析.【例8】 已知:如图,ABCD 是正方形,FAD FAE ∠=∠,求证:BE DF AE +=.DEC BAN CDE B M A NCDEB M A FE DCBAM F EDCB A【解析】延长CB 至M ,使得BM DF =,连接AM .∵AB AD =,AD CD ⊥,AB BM ⊥,BM DF = ∴ABM ADF ∆∆≌∴AFD AMB ∠=∠,DAF BAM ∠=∠ ∵AB CD ∥∴AFD BAF EAF BAE BAE BAM EAM ∠=∠=∠+∠=∠+∠=∠ ∴AMB EAM ∠=∠,AE EM BE BM BE DF ==+=+【答案】见解析.【例9】 如图所示,已知正方形ABCD 中,M 为CD 的中点,E 为MC 上一点,且2BAE DAM ∠=∠.求证:AE BC CE =+.【解析】分析证明一条线段等于两条线段和的基本方法有两种:(1)通过添辅助线“构造”一条线段使其为求证中的两条线段之和,再证所构造的线段与求证中那一条线段相等.(2)通过添辅助线先在求证中长线段上截取与线段中的某一段相等的线段,再证明截剩的部分与线段中的另一段相等.我们用(1)法来证明.【答案】延长AB 到F ,使BF CE =,则由正方形性质知AF AB BF BC CE =+=+下面我们利用全等三角形来证明AE AF =.为此,连接EF 交边BC 于G .由于对顶角BGF CGE ∠=∠,所以()Rt ΔBGF CGE AAS ∆≌,从而12BG GC BC FG EG ===,,BG DM =于是()Rt ΔRt ΔABG ADM SAS ≌,所以12BAG DAM BAE EAG ∠=∠=∠=∠,AG 是EAF ∠的平分线【例10】 五边形ABCDE 中,AB AE =,BC DE CD +=,180ABC AED ∠+∠=︒,求证:AD 平分∠CDE .M EDCBAF【解析】延长DE 至F ,使得EF BC =,连接AC .∵180ABC AED ∠+∠=︒,180AEF AED ∠+∠=︒,∴ABC AEF ∠=∠ ∵AB AE =,BC EF =,∴△ABC ≌△AEF . ∴EF BC =,AC AF =∵BC DE CD +=,∴CD DE EF DF =+= ∴△ADC ≌△ADF ,∴ADC ADF ∠=∠ 即AD 平分∠CDE .【答案】见解析.【例11】 若P 为ABC ∆所在平面上一点,且120APB BPC CPA ∠=∠=∠=︒,则点P 叫做ABC ∆的费马点.(1)若点P 为锐角ABC ∆的费马点,且60ABC ∠=︒,34PA PC ==,,则PB 的值为_____;(2)如图,在锐角ABC ∆外侧作等边ACB ∆′,连结BB ′. 求证:BB ′过ABC ∆的费马点P ,且BB PA PB PC =++′.【解析】(1)(2)证明:在BB ′上取点P ,使120BPC ∠=︒, 连结AP ,再在PB ′上截取PE PC =,连结CE .∵120BPC ∠=︒,∴60EPC ∠=︒,∴PCE ∆为正三角形, ∴PC CE =,60PCE ∠=︒,120CEB ∠=︒′, ∵ACB ∆′为正三角形,∴AC B C =′,60ACB ∠=︒′, ∴60PCA ACE ACE ECB ∠+∠=∠+∠=︒′,∴PCA ECB ∠=∠′, ∴ACP B CE ∆∆≌′,∴120APC B CE ∠=∠=︒′,PA EB =′, ∴120APB APC BPC ∠=∠=∠=︒,CEDB AABDEFC B'CBA∴P为ABC∆的费马点,P∴BB′过ABC∆的费马点,且BB EB PB PE PA PB PC′′.=++=++【答案】见解析.AB'EPB课后复习【作业1】已知,AD 平分∠BAC ,AC AB BD =+,求证:2B C ∠=∠.【解析】延长AB 至点E ,使AE AC =,连接DE∵AD 平分∠BAC ,∴EAD CAD ∠=∠ ∵AE AC =,AD AD =,∴△AED ≌△ACD (SAS ),∴E C ∠=∠ ∵AC AB BD =+,∴AE AB BD =+∵AE AB BE =+,∴BD BE =,∴BDE E ∠=∠ ∵ABC E BDE ∠=∠+∠,∴2ABC E ∠=∠,∴2ABC C ∠=∠.【答案】见解析.【作业2】如图,△ABC 中,2AB AC =,AD 平分∠BAC ,且AD BD =,求证:CD ⊥AC .【解析】在AB 上取中点F ,连接FD .则△ADB 是等腰三角形,F 是底AB 的中点,由三线合一知 DF ⊥AB ,故90AFD ∠=︒ △ADF ≌△ADC (SAS )90ACD AFD ∠=∠=︒,即:CD ⊥AC【答案】见解析.DCBAECBADCDBA【作业3】如图所示,ABC ∆是边长为1的正三角形,BDC ∆是顶角为120︒的等腰三角形,以D 为顶点作一个60︒的MDN ∠,点M 、N 分别在AB 、AC 上,求AMN ∆的周长.【解析】如图所示,延长AC 到E 使CE BM =.在BDM ∆与CDE ∆中,因为BD CD =,90MBD ECD ∠=∠=︒,BM CE =, 所以BDM CDE ∆∆≌,故MD ED =.因为120BDC ∠=︒,60MDN ∠=,所以60BDM NDC ∠+∠=︒. 又因为BDM CDE ∠=∠,所以60MDN EDN ∠=∠=︒. 在MND ∆与END ∆中,DN DN =,60MDN EDN ∠=∠=︒,DM DE =, 所以MND END ∆∆≌,则NE MN =,所以AMN ∆的周长为2.【答案】见解析.【作业4】已知:AC 平分∠BAD ,CE ⊥AB ,180B D ∠+∠=︒,求证:AE AD BE =+.【解析】在AE 上取F ,使EF EB =,连接CF∵CE ⊥ABE D CBA∴90∠=∠=︒CEB CEF∵EB EF=,CE CE=,∴△CEB≌△CEF∴B CFE∠=∠∵180+,180∠+∠=︒CFE CFA∠∠=︒B D∴D CFA∠=∠∵AC平分∠BAD∴DAC FAC∠=∠∵AC AC=∴△ADC≌△AFC(SAS)∴AD AF=∴AE AF FE AD BE=+=+【答案】见解析.。
几何辅助线之截长补短 总结+例题

截长补短专题知识导航“截长补短”是几何证明题中十分重要的方法,通常用来证明几条线段的数量关系,即若题目条件或结论中含有“c b a =+”的条件,需要添加辅助线时可以考虑“截长补短”的方法。
截长法:在较长的线段上截取一条线段等于较短线段,再设法证明较长线段的剩余线段等于另外的较短线段。
补短法:①延长较短线段中的一条,使延长出来的线段等于另外的较短线段,然后证明两线段之和等于较长线段。
即延长a ,得到b ,证:c b a =+。
②延长较短线段中的一条,使延长后的线段等于较长线段,然后证明延长出来的部分等于另一条较短线段。
即延长a ,得到c ,证:a c b -=。
【核心考点1】角平分线相关截长补短1. 如图,BP 平分ABC ∠,D 为BP 上一点,E ,F 分别在BA ,BC 上,且满足DE DF =,若140BED ∠=︒,则BFD ∠的度数是( )A .40︒B .50︒C .60︒D .70︒【分析】作DG AB ⊥于G ,DH BC ⊥于H ,根据角平分线的性质得到DH DG =,证明Rt DEG Rt DFH ∆≅∆,得到DEG DFH ∠=∠,根据互为邻补角的性质得到答案.【解答】解:作DG AB ⊥于G ,DH BC ⊥于H ,D 是ABC ∠平分线上一点,DG AB ⊥,DH BC ⊥, DH DG ∴=,在Rt DEG ∆和Rt DFH ∆中, DG DHDE DF=⎧⎨=⎩, ()Rt DEG Rt DFH HL ∴∆≅∆,DEG DFH ∴∠=∠,又180DEG BED ∠+∠=︒, 180BFD BED ∴∠+∠=︒,BFD ∴∠的度数18014040=︒-︒=︒,故选:A .2. 已知,如图,ABC ∆中,2C B ∠=∠,12∠=∠,求证:AB AC CD =+.【分析】在AB 上截取AE AC =,由“SAS ”可证ADE ADC ∆≅∆,可证DE DC =,C AED ∠=∠,可证B BDE ∠=∠,可得BE DE DC ==,即结论可得. 【解答】证明:如图,在AB 上截取AE AC =,AE AC =,12∠=∠,AD AD =()ADE ADC SAS ∴∆≅∆DE DC ∴=,C AED ∠=∠, 2C B ∠=∠,AED B BDE ∠=∠+∠,B BDE ∴∠=∠ BE DE DC ∴==,AB AE BE =+, AB AC DC ∴=+。
完整版)截长补短类辅助线作法

完整版)截长补短类辅助线作法截长补短类辅助线作法是解决三条线段之间数量关系问题的常用方法。
其中,“截长”是将最长的线段一分为二,使其中一条等于已知的较短线段之一,然后证明另一段与已知另一条线段的数量关系;“补短”是将一条较短的线段延长至与另一条较短的线段相等,然后证明延长后的线段与最长的线段的数量关系。
需要注意的是,截长补短类辅助线作法一般用于三条线段之间的数量关系问题,特别是当线段前的系数不是1时,可能会涉及到含特殊角的直角三角形。
在构造辅助线时,需要结合题目条件选择适当的方法,并不是所有题目都适用于截长和补短方法。
下面是一些例题的精讲:1.在图中,以D为顶点作一个边长为a的正三角形,连接AD、BD、CD,点E、F分别在AB、AC上,且AE=EF=FB,求△XXX的周长。
2.已知△ABC中,DP⊥BC,证明BD平分∠ABC,BC上有动点P;DP平分∠BDC时,求BD、CD、CP三者的数量关系。
3.已知△ABC中,D、E、F分别平分∠A、∠B、∠C,交于点P,试判断AD:DB、BE:EC、CF:FA的数量关系,并加以证明。
4.在△ABC中,AD是角平分线,点F、E分别在AC、AB上,且AF=DE,证明BF=CE。
5.在图中,以D为顶点作一个边长为a的正三角形,连接AD、BD、CD,点E、F分别在AB、AC上,且AE=EF=FB,求△XXX的周长。
6.已知正方形ABCD中,M为CD的中点,E为MC上一点,且∠AED=45°,证明AE=BD。
7.五边形ABCDE中,AD平分∠CDE,证明XXX。
8.在△ABC中,D是三角形外一点,且∠ACD=∠BCD,AB与CD交于点E,证明XXX。
9.如图1所示,AB、CD平行,AE、DE分别平分∠A、∠D,并交于点E。
过点E的直线分别交AM、DN于B、C。
1)当点B、C分别位于点AD的同侧时,猜想AD、AB、CD之间的存在的数量关系。
2)试证明你的猜想。
中考专题中线倍长法和截长补短
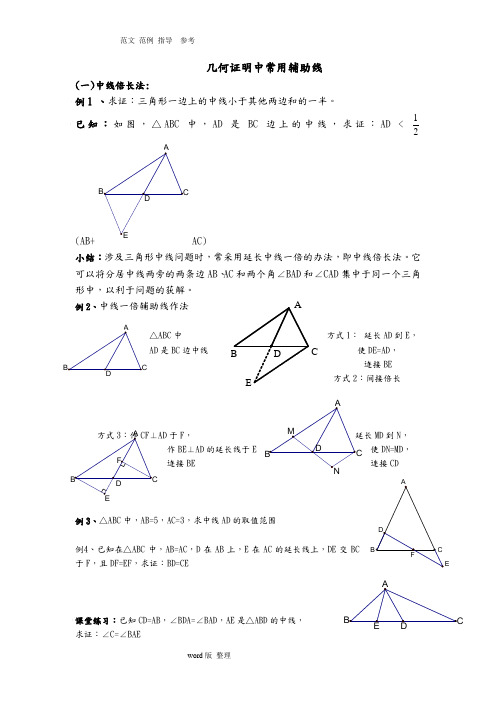
几何证明中常用辅助线 (一)中线倍长法:例1 、求证:三角形一边上的中线小于其他两边和的一半。
已知:如图,△ABC 中,AD 是BC 边上的中线,求证:AD ﹤21 (AB+AC)小结:涉及三角形中线问题时,常采用延长中线一倍的办法,即中线倍长法。
它可以将分居中线两旁的两条边AB 、AC 和两个角∠BAD 和∠CAD 集中于同一个三角形中,以利于问题的获解。
例2、中线一倍辅助线作法△ABC 中方式1: 延长AD 到E , AD 是BC 边中线使DE=AD , 连接BE方式2:间接倍长AD 于F ,MD 到N , 作BE ⊥AD 的延长线于使DN=MD , 连接连接CD例3、△ABC 中,AB=5,AC=3,求中线AD的取值范围例4、已知在△ABC 中,AB=AC ,D 在AB 上,E 在AC 的延长线上,DE 交BC 于F ,且DF=EF ,求证:BD=CE课堂练习:已知CD=AB ,∠BDA=∠BAD ,AE 是△ABD 的中线, 求证:∠C=∠BAEC作业:1、在四边形ABCD 中,AB ∥DC ,E 为BC 边的中点,∠BAE=∠EAF ,AF 与DC 的延长线相交于点F 。
试探究线段AB 与AF 、CF 之间的数量关系,并证明你的结论2、已知:如图,∆ABC 中,∠C=90︒,CM ⊥AB 于M ,AT 平分∠BAC 交CM 于D ,交BC 于T ,过D 作DE//AB 交BC 于E ,求证:CT=BE.3:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF(二)截长补短法教八年级上册课本中,在全等三角形部分介绍了角的平分线的性质,这一性质在许多问题里都有着广泛的应用.而“截长补短法”又是解决这一类问题的一种特殊方法,在无法进行直接证明的情形下,利用此种方法常可使思路豁然开朗.请看几例. 例1.已知,如图1-1,在四边形ABCD 中,BC >AB ,AD =DC ,BD平分∠ABC .求证:∠BAD +∠BCD =180°.分析:因为平角等于180°,因而应考虑把两个不在一起的通过全等转化成为平角,图中缺少全等的三角形,因而解题的关键在于构造直角三角形,可通过“截长补短法”来实现.证明:过点D 作DE 垂直BA 的延长线于点E ,作DF ⊥BC 于点F ,如图1-2∵BD 平分∠ABC ,∴DE =DF , 在Rt △ADE 与Rt △CDF 中,⎩⎨⎧==CD AD DFDE ∴Rt △ADE ≌Rt △CDF (HL ),∴∠DAE =∠DCF .DABCM TEABCD图1-1FEDCBA图1-2又∠BAD +∠DAE =180°,∴∠BAD +∠DCF =180°, 即∠BAD +∠BCD =180°.例2. 如图2-1,AD ∥BC ,点E 在线段AB 上,∠ADE =∠CDE ,∠DCE =∠ECB .求证:CD =AD +BC .分析:结论是CD =AD +BC ,可考虑用“截长补短法”中的“截长”,即在CD 上截取CF =CB ,只要再证DF =DA 即可,这就转化为证明两线段相等的问题,从而达到简化问题的目的. 证明:在CD 上截取CF =BC ,如图2-2在△FCE 与△BCE 中,⎪⎩⎪⎨⎧=∠=∠=CE CE BCE FCE CB CF ∴△FCE ≌△BCE (SAS ),∴∠2=∠1.又∵AD ∥BC ,∴∠ADC +∠BCD =180°,∴∠DCE +∠CDE =90°, ∴∠2+∠3=90°,∠1+∠4=90°,∴∠3=∠4. 在△FDE 与△ADE 中,⎪⎩⎪⎨⎧∠=∠=∠=∠43DEDE ADE FDE ∴△FDE ≌△ADE (ASA ),∴DF =DA , ∵CD =DF +CF ,∴CD =AD +BC .例3. 已知,如图3-1,∠1=∠2,P 为BN 上一点,且PD ⊥BC 于点D ,AB +BC =2BD .求证:∠BAP +∠BCP =180°.分析:与例1相类似,证两个角的和是180°,可把它们移到一起,让它们是邻补角,即证明∠BCP =∠EAP ,因而此题适用“补短”进行全等三角形的构造. 证明:过点P 作PE 垂直BA 的延长线于点E ,如图3-2∵∠1=∠2,且PD ⊥BC ,∴PE =PD , 在Rt △BPE 与Rt △BPD 中,⎩⎨⎧==BPBP PDPE ∴Rt △BPE ≌Rt △BPD (HL ),∴BE =BD .∵AB +BC =2BD ,∴AB +BD +DC =BD +BE ,∴AB +DC =BE 即DC =BE -AB =AE .在Rt △APE 与Rt △CPD 中,⎪⎩⎪⎨⎧=∠=∠=DC AE PDC PEA PD PE ∴Rt △APE ≌Rt △CPD (SAS),∴∠PAE =∠PCD 又∵∠BAP +∠PAE =180°,∴∠BAP +∠BCP =180°例4. 已知:如图4-1,在△ABC 中,∠C =2∠B ,∠1=∠2.ADB CEF1234图2-2ABCDP12N图3-1P12NABCD E 图3-2A 12求证:AB =AC +CD .分析:从结论分析,“截长”或“补短”都可实现问题的转化,即延长AC 至E 使CE =CD ,或在AB 上截取AF =AC . 证明:方法一(补短法)延长AC 到E ,使DC =CE ,则∠CDE =∠CED ,如图4-2 ∴∠ACB =2∠E ,∵∠ACB =2∠B ,∴∠B =∠E , 在△ABD 与△AED 中,⎪⎩⎪⎨⎧=∠=∠∠=∠AD AD E B 21 ∴△ABD ≌△AED (AAS ),∴AB =AE . 又AE =AC+CE =AC +DC ,∴AB =AC +DC . 方法二(截长法)在AB 上截取AF =AC ,如图4-3 在△AFD 与△ACD 中,⎪⎩⎪⎨⎧=∠=∠=AD AD AC AF 21 ∴△AFD ≌△ACD (SAS ),∴DF =DC ,∠AFD =∠ACD . 又∵∠ACB =2∠B ,∴∠FDB =∠B ,∴FD =FB . ∵AB =AF +FB =AC +FD ,∴AB =AC +CD .上述两种方法在实际应用中,时常是互为补充,但应结合具体题目恰当选择合适思路进行分析。
中考数学第四章 三角形 重难 微专项3 全等三角形中常用的辅助线技巧

= ,
在△ACD和△AED中,ቐ ∠1 = ∠2,
= ,
∴△ACD≌△AED,
∴∠AED=∠C=90°,CD=ED.
重难·微专项3 全等三角形中常用的辅助线技巧
例题
又AC=BC,∴∠B=45°,∴∠EDB=∠B=45°,
∴DE=BE,∴CD=BE.
∴∠DBE=60°,
1
∴BD= BE,
2
∴TF=2BD,即BF-AB=2BD.
重难·微专项3 全等三角形中常用的辅助线技巧
突破点2 旋转
运用旋转的全等变换,可以把分散的条件集中到一个三角形中.
模型1
绕定点旋转60°,构造全等三角形
如图,△ABC为等边三角形,点P在△ABC内,将△ABP绕点A逆时针旋转
明剩下的线段等于另一条短线段.
补短法:延长短线段,使其延长部分等于另一条短线段,然后证明延长
后的线段等于长线段(或延长短线段,使延长后的线段等于长线段,然
后证明延长部分等于另一条短线段).
重难·微专项3 全等三角形中常用的辅助线技巧
例题
例1
如图,在Rt△ABC中,∠C=90°,BC=AC,AD平分∠BAC交BC于点D.
60°,得到△ACP',则△ABP≌△ACP',且△APP'为等边三角形.
重难·微专项3 全等三角形中常用的辅助线技巧
例题
例2
如图,在四边形ABCD中,AB=BC,∠ABC=60°,∠ADC=30°,则线段
AD,CD和BD之间的数量关系为 AD2+CD2=BD2 .
重难·微专项3 全等三角形中常用的辅助线技巧
∵BA=BT,∠ABT=60°,
中考数学复习指导:证明全等时常见的五种辅助线

证明全等时常见的五种辅助线在证明三角形全等时有时需添加辅助线,对学习几何证明不久的学生而言往往是难点.下面介绍证明全等时常见的五种辅助线,供同学们学习时参考.一、截长补短一般地,当所证结论为线段的和、差关系,且这两条线段不在同一直线上时,通常可以考虑用截长补短的办法:或在长线段上截取一部分使之与短线段相等;或将短线段延长使其与长线段相等.例1.如图1,在△ABC中,∠ABC=60°,AD、CE分别平分∠BAC、∠ACB.求证:AC=AE+CD.分析:要证AC=AE+CD,AE、CD不在同一直线上.故在AC上截取AF=AE,则只要证明CF=CD.证明:在AC上截取AF=AE,连接OF.∵AD、CE分别平分∠BAC、∠ACB,∠ABC=60°∴∠1+∠2=60°,∴∠4=∠6=∠1+∠2=60°.显然,△AEO≌△AFO,∴∠5=∠4=60°,∴∠7=180°-(∠4+∠5)=60°在△DOC与△FOC中,∠6=∠7=60°,∠2=∠3,OC=OC∴△DOC≌△FOC,CF=CD∴AC=AF+CF=AE+CD.二、中线倍长三角形问题中涉及中线(中点)时,将三角形中线延长一倍,构造全等三角形是常用的解题思路.例2.已知三角形的两边长分别为7和5,那么第三边上中线长x的取值范围是().分析:要求第三边上中线的取值范围,只有将将中线与两个已知边转移到同一个三角形中,然后利用三角形的三边关系才能进行分析和判断.解:如图2所示,设AB=7,AC=5,BC上中线AD=x.延长AD至E,使DE = AD=x.∵AD是BC边上的中线,∴BD=CD∠ADC=∠EDB(对顶角)∴△ADC≌△EDB∴BE=AC=5∵在△ABE中AB-BE<AE<AB+BE即7-5<2x<7+5 ∴1<x<6三、作平行线当三角形问题中有相等的角或等腰等条件时,可通过作平行线将相等的角转换到某一个三角形中得到另外的等腰三角形或相等的角,从而为证明全等提供条件.例3.如图3,在等腰△ABC中,AB=AC,在AB上截取BD,在AC延长线上截取CE,且使CE=BD.连接DE交BC于F.求证:DF=EF.分析:要证DF=EF,必须借助三角形全等.而现有图形中没有全等三角形.由等腰三角形条件,可知∠B=∠ACB,作DH∥AE,可得∠DHB=∠ACB.则△DBH为等腰三角形.证明:作DH∥AE交BC于H.∴∠DHB=∠ACB,∵AB=AC,∴∠B=∠ACB∴∠DHB=∠B,DH=BD∵CE=BD∴DH= CE又DH∥AE,∠HDF=∠E∠DFH=∠EFC(对顶角)∴△DFH≌△EFC(AAS)∴DF=EF四、补全图形在一些求证三角形问题中,延长某两条线段(边)相交,构成一个封闭的图形,可找到更多的相等关系,有助于问题的解决.例4.如图4,在△ABC中,AC=BC,∠B=90°,BD为∠ABC的平分线.若A点到直线BD的距离AD为a,求BE的长.分析:题设中只有一条已知线段AD,且为直角边,而要求的BE为斜边.要找到它们之间的关系,需设法构造其他的全等三角形.证明:延长AD、BC相交于F.由BD为∠ABC的平分线,BD⊥AF.易证△ADB≌△FDB∴FD= AD=a AF=2a∠F=∠BAD又∠BAD+∠ABD=90°,∠F+∠FAC=90°∴∠ABD=∠FAC∵BD为∠ABC的平分线∴∠ABD=∠CBE∴∠FAC=∠CBE,而∠ECB=∠ACF=90°,AC=BC∴△ACF≌△BCE(ASA)∴BE=AF=2a五、利用角的平分线对称构造全等角的平分线是角的对称轴,在证明全等过程中不仅提供了两个相等的角,还有一条公共边,利用角的平分线在角的两边上截取相等的线段,或向两边作垂线,对称构造出全等三角形是常用的证明方法.例5.如图5,在四边形ABCD中,已知BD平分∠ABC,∠A+∠C=180°.证明:AD=CD.分析:由角的平分线条件,在BC上截取BE=BA,可构造△ABD≌△EBD,从而AD=DE.则只要证明DE=CD.证明:在BC上截取BE=BA,连接DE.由BD平分∠ABC,易证△ABD≌△EBD∴AD=DE∠A=∠BED又∠A+∠C=180°,∠BED+∠DEC=180°∴∠DEC=∠C,∴DE=CD∴AD=CD。
第12讲 辅助线专题(3)-截长补短
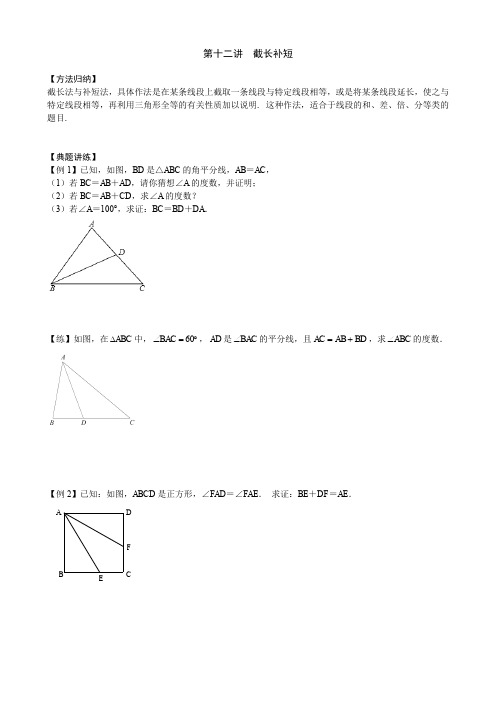
【例 2】已知:如图,ABCD 是正方形,∠FAD=∠FAE. 求证:BE+DF=AE.
A
D
F
B
E
C
【练】如图所示.已知正方形 ABCD 中,M 为 CD 的中点,E 为 MC 上一点,且∠BAE=2∠DAM.求证: AE=BC+CE.
第十二讲 截长补短
【方法归纳】 截长法与补短法,具体作法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,使之与 特定线段相等,再利用三角形全等的有关性质加以说明. 这种作法,适合于线段的和、差、倍、分等类的 题目.
【典题讲练】 【例 1】已知,如图,BD 是△ABC 的角平分线,AB=AC, (1)若 BC=AB+AD,请你猜想∠A 的度数,并证明; (2)若 BC=AB+CD,求∠A 的度数? (3)若∠A=100°,求证:BC=BD+DA.
7、(思考题)如图,△ ABC 中,AB=AC,AB⊥AC,D 为 AC 的中点,过点 A 作 AE⊥BD 于点 E,AE 的延 长线交 BC 于点 F,连接 DF,求证:(1)∠ADB=∠CDF;(2)BD=AF+FD.
A
D E
B
F
C
【家庭作业】 1、如图,在 △ABC 中, AD BC 于点 D , B 2C .求证: AB BD CD .
A
C
DB
2、已知,在 ABC 中,AB AC ,BD 平分 ABC 且交 AC 于点 D .若 BAC 108 ,求证:BC AB CD .
3、五边形 ABCDE 中,AB=AE,BC+DE=CD,∠ABC+∠AED=180°,求证:AD 平分∠CDE.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.截长补短1.已知ACB ∆,B ACB ∠=∠,D ,E 分别是AB 及AC 延长线上的一点,且BD CE =,连接DE 交底BC 于G ,求证GD GE =.答案:见解析 解析: 解法1:过E 作EF AB ∥,交BC 的延长线于F ,则=B F ∠∠ ∵3=4∠∠,3=B ∠∠,4B ∴∠=∠ ∴4=F ∠∠,∴CE =CF , 在GEF ∆与GDB ∆中,12DB CE EF B F ∠=∠⎧⎪==⎨⎪∠=∠⎩∴GFE GBD ∆∆≌AAS ()GED C BA1243FK C GE D BA∴G DG =E 解法2:过D 点作DK AC ∥交BC 于K , 过D 点作DF BC ∥交AC 于F , ∴四边形DKCF 是平行四边形, ∴DK =FC ,1ACB ∠=∠, ∵B ACB ∠=∠,∴1B ∠=∠, ∴DB =DK =CE =CF , ∴C 是EF 中点,又∵BC DF ∥, ∴G 是DE 中点,∴DG =EG2.如图所示,在ABC △中,100A ∠=︒,40ABC ∠=︒,BD 是ABC ∠的平分线,延长BD 至E ,使DE AD =.求证:BC AB CE =+答案:见解析1F KCGED BAEDCA解析:在BC 上取一点F ,使得BFBA =,连接DF ,∵BD 是ABC ∠的平分线,∴ABD FBD ∠=∠, 在ADB △与FDB △中,ABD FB BF BA BD BD D =⎧=∠=∠⎪⎨⎪⎩∴ADB FDB △≌△(SAS), ∴DFAD =,又∵DA DE =, ∴DF DE =∵100A ∠=︒,AB AC = ∴40ABC ∠=︒∵BD 是ABC ∠的平分线, ∴20ABD ∠=︒∴60ADB FDB ∠=∠=︒, ∵60CDE ADB ∠=∠=︒, ∴60FDC EDC ∠=∠=︒, 在DCF △与DCE △中,F EDCAFDC ED CD CD C =∠=∠⎪⎨⎪⎩, ∴DCF DCE △≌△(SAS), ∴FC EC =∴BC BF FC AB EC =+=+3.如图,在ABC △中,2B C ∠=∠,BAC ∠的平分线AD 交BC 与D .求证:AB BD AC +=.答案:见解析 解析:在AC 上取一点E ,使得AB AE =连结DE .AD 平分BAC ∠,∴BAD EAD =∠∠,在ABD △和AED △中DC B AEDC B ABAD EAD ∠=∠, AD AD =∴ABD AED △≌△SAS (), ∴BD ED =,B AED ∠=∠又∵2AED EDC C B C ∠=∠+∠=∠=∠EDC C ∴∠=∠,ED EC =,BD EC =∴,AC AE EC AB BD ∴=+=+∴AB BD AC +=.方法二:在AB 的延长线上取一点E使得AC AE =,连结DE . 在AED △和ACD △中,AC AE =EAD CAD ∠=∠,AD AD =,∴AED ACD △≌△,∴C E ∠=∠, 又∵22ABC E BDE C BDE ∠=∠+∠=∠=∠ ∴E BDE ∠=∠∴BE BD =, ∴AB BD AE AC +== ∴AB BD AC +=.ABCDE4.如图所示,在ABC △中,AD BC ⊥于点D ,2B C ∠=∠.求证:AB BD CD +=.答案:见解析 解析:如图,在CD 上截取DE DB =,连接AE . ∵AD BC ⊥,DE DB =, ∴AE AB =,于是B AEB ∠=∠,又∵AEB C CAE ∠=∠+∠,2B C ∠=∠, ∴CAE C ∠=∠, 于是AE EC =,故AB BD AE ED EC ED CD +=+=+=.5.如图,正方形ABCD 的边长为1,点F 在线段CD 上运动,AE 平分BAF ∠交BC 边于点E .求证:AFDF BE =+.C D BAABD E C答案:见解析 解析:证明:如图,延长CB 至点G ,使得BG DF =,连结AG . ∵ABCD 是正方形, ∴在ADF ∆和ABG ∆中,AD AB =90ADF ABG ∠=∠=°, DF BG =.∴Rt Rt (SAS)ADF ABG ∆∆≌, ∴AF AG =,DAF BAG ∠=∠. 又∵AE 是BAF ∠的平分线. ∴EAFBAE ∠=∠,∴DAF EAF BAG BAE ∠+∠=∠+∠. 即EAD GAE ∠=∠.∵AD BC ∥,∴GEA EAD ∠=∠, ∴GEA GAE ∠=∠,∴AG GE =.FEDC BAGFE DCBA即AG BG BE =+. ∴AF BG BE =+, ∴AF DF BE =+.6.如图,在正方形ABCD 中,F 是CD 的中点,E 是BC 边上的一点,且AF 平分DAE ∠,求证:AE EC CD =+答案:见解析 解析:解一:作FH AE H ⊥于∵AF 平分DAE ∠,90D ∠=︒,FH AE ⊥,∴DAFEAF ∠=∠,FH FD =,在Rt AHF △与Rt ADF △中, ∵AF 为公共边,FH FD =FE DCB AHFEDCBA∴R AFH AFD t Rt ∆∆≌HL (). ∴AHAD =,HF DF =.∵DF FC HF ==,FE 为公共边,90C FHE ∠=∠=︒, ∴()EFH EFC HL ∆∆≌ ∴HE CE =.∵AE AH HE =+,AG AD CD ==,HE CE =, ∴AE EC CD =+.解二:延长AF BC ,交于点G∵F 是CD 的中点,∴DF FC =, ∵在正方形ABCD 中,AD BC ∥, ∴90D FCG ∠=∠=︒,G FAD ∠=∠, ∴ADF CFG ∆∆≌AAS (), ∴CG AD CD ==,G FAD ∠=∠, ∵DAFEAF ∠=∠∴G EAF ∠=∠ ∴AE EG =∴AE EC CG EC CD =+=+.GFE DC B A7.如图所示.已知正方形ABCD 中,M 为CD 的中点,E 为MC 上一点, 且2BAE DAM ∠=∠.求证:AE BC CE =+.答案:见解析 解析: 证明:如图,延长AB 到F ,使BF CE =,连接EF 与BC 相交于点N , 在BFN △和CEN △中,90FBN C BNF CNE BF CE ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩, ∴BFN CEN AAS △≌△(), ∴12BN CN BC ==,EN FN =, 又∵M 是CD 的中点,∴12DM CD =, M EDCBA在正方形ABCD 中,AB BC CD ==,90D ABC ∠=∠=︒, ∴BNDM =,()ABN ADM SAS ≅△△,∴BAN DAM ∠=∠, ∵2BAE DAM ∠=∠, ∴BAN EAN ∠=∠,∴AN 既是AEF △的角平分线也是中线, ∴AE AF =,∵AFAB BF =+,∴AE BC CE =+.8.在ABC △中,AD 平分BAC ∠,AB BD AC +=.求:B C ∠∠的值.答案:见解析 解析:如图,在AC 上截取AE AB =,连接DE .CD B AECD B A∵AD 平分BAC ∠, ∴BAD EAD ∠=∠, 在ABD △与ADE △中,AB AE BAD EAD AD AD =⎧⎪∠=∠⎨⎪=⎩, ∴ABD AED SAS △≌△(), ∴B AED ∠=∠,DE BD =, 而AB BD AC AE CE +==+, ∴DE CE =, ∴EDC C ∠=∠,而AED C EDC ∠=∠+∠, ∴C B C ∠=∠-∠,∴12C B ∠=∠, ∴:2:1B C ∠∠=.9.如图,ABC ∆中,120BAC ∠=︒,AD BC ⊥于D ,且AB BD CD +=,则C ∠的大小是_____________.AB CD答案:见解析 解析:如图,在DC 上取DE DB =,连接AE , ∵AD BC ⊥,∴90ADB ADC ∠=∠=︒, 在ABD ∆与AED ∆中,90DE DB ADB ADC AD AD =⎧⎪∠=∠=︒⎨⎪=⎩ABD AED ∆∆≌()SAS .AB AE CE ==,AEB B ∠=∠, AB BD CD +=,AE DE CD +=∴,又EC DE CD +=,AE EC =∴,C EAC ∠=∠∴,AEC C EAC ∠=∠+∠∴, 2B AEB C ∠=∠=∠,1801802120BAC B C C C ∠=︒-∠-∠=︒-∠-∠=︒∴,得20C ∠=︒.10.如图,AC 平分BAD ∠,CE AB ⊥,且180B D ∠+∠=︒,求证:AE AD BE =+.EAB CD答案:见解析 解析: 解法一过C 作AD 的垂线交AD 延长线于F ,CE AB ⊥,90F BEC ∠=∠=︒∴,又AC 平分BAD ∠,EC FC =∴,在Rt EAC △与Rt FAC △中,EC FC =,AC AC =, Rt EAC Rt FAC △≌△()HL ,AE AF =∴,∵180B ADC ∠+∠=︒,180FDC ADC ∠+∠=︒, ∴FDC B ∠=∠, 在BCE △与DCF △中,E DCBAFE DCBAEC FC =,90F BEC ∠=∠=︒, FDC B ∠=∠,BCE DCF ≌△△ BE DF =∴,∴AE AD DF AD BE =+=+11.正方形ABCD 中,E 为上的一点,F 为CD 上的一点,BE DF EF +=,求EAF ∠的度数.答案:见解析 解析:延长EB 使得BG DF = ,连接AG , 在ABG △ 和ADF △ 中,FED CBA GFED CBA由90AB AD ABG ADF BG DF =⎧⎪∠=∠=︒⎨⎪=⎩, 可得ABG ADF SAS △≌△(), DAF BAG ∴∠=∠ ,AF AG = ,又EF DF BE EB BG EG =+=+= ,AE AE = ,在AEG △ 和AEF △ 中,AE AE GE FE AG AF =⎧⎪=⎨⎪=⎩, AEG AEF SSS ∴△≌△(), EAG EAF ∴∠=∠,90DAF EAF BAE ∠+∠+∠=︒ 90EAG EAF ∴∠+∠=︒, 45EAF ∴∠=︒ .12.如图,在ABC △中,60B ∠=︒,AD CE 、分别是BAC ∠、BCA ∠的平分线,AD CE 、相交于点F ,请你判断并写出FE 与FD 之间的数量关系;请说明理由.答案:见解析 解析:FE FD =.理由如下:如图1,在AC 上截取AG AE =,连接FG ,∵AD 是BAC ∠的平分线, ∴12∠=∠,在AEF △和AGF △中,12AG AE AF AF =⎧⎪∠=∠⎨⎪=⎩, ∴AEF AGF SAS △≌△(), ∴AFE AFG ∠=∠,FE FG =, ∵60B ∠=︒,∴18060120BAC ACB ∠+∠=︒-︒=︒, ∵AD 、CE 分别是BAC ∠、BCA ∠的平分线,∴122BAC ∠=∠,132ACB ∠=∠, ∴11231206022BAC ACB ∠+∠=∠+∠=⨯︒=︒(), ∴60AFE CFD AFG ∠=∠=∠=︒.∴180180606060CFG AFG CFD ∠=︒-∠-∠=︒-︒-︒=︒, ∴CFG CFD ∠=∠, ∵CE 是BCA ∠的平分线, ∴34∠=∠,在CFG △和CFD △中,34CFG CFD FC FC∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴CFG CFD ASA △≌△(), ∴FG FD =, ∴FE FD =;13.如图,在四边形ABCD 中,AC 平分DAB ∠,若AB AD >,DC BC =. 求证:180B D ∠+∠=︒.答案:见解析 解析:证明:如图,在AB 上截取AD AF =,连接FC . ∵AC 平分DAB ∠, ∴12∠=∠,在ADC △与AFC △中,12AD AF AC AC =⎧⎪∠=∠⎨⎪=⎩, ∴ADC AFC SAS △≌△(), ∴4D ∠=∠,CD CF =.又∵DC BC =, ∴FC BC =, ∴3B ∠=∠,∴34180B D ∠+∠=∠+∠=︒,即180B D ∠+∠=︒.14.已知:如图1,在边长为5的正方形ABCD 中,点E F 、分别是BC DC 、边上的点,且AE EF ⊥,2BE =. (1)求:EC CF 的值;(2)延长EF 交正方形外角平分线CP 于点P (图2),试判断AE 与EP 的大小关系,并说明理由.答案:见解析 解析: (1)∵AE EF ⊥, ∴2390∠+∠=︒, ∵四边形ABCD 为正方形, ∴90B C ∠=∠=︒,∴1390∠+∠=︒,12∠=∠, ∴ABE ECF △∽△, ∴::5:2EC CF AB BE ==;(2)在AB 上取一点M ,使BM BE =,连接ME .∴AM CE =. ∴45BME ∠=︒, ∴135AME ∠=︒. ∵CP 是外角平分线, ∴45DCP ∠=︒, ∴135ECP ∠=︒. ∴AME ECP ∠=∠.∵90AEB BAE ∠+∠=︒,90AEB CEF ∠+∠=︒, ∴BAE CEF ∠=∠.∴AME PCE ASA △≌△(). ∴AE EP =.15.如图,已知正方形ABCD 中,E F 、分别是BC 、CD 上的点,且AF 平分DAE ∠.求证:AE DF BE =+.答案:见解析解析:证明:延长CB 到G ,使BG DF =,连接AG (如图)∵AD AB =,90D ABG ∠=∠=︒,∴ADF ABG SAS △≌△(), ∴5G ∠=∠,13∠=∠,∵12∠=∠,∴23∠=∠,∴2434∠+∠=∠+∠,即FAB EAG ∠=∠,∵CD AB ∥,∴5FAB EAG ∠=∠=∠,∴EAG G ∠=∠,∴AE EB BG EB DF =+=+.16.如图正方形ABCD 中,点E 、F 分别在BC 、CD 上,且45EAF ∠=︒. 求证:BE DF EF +=;答案:见解析解析:(1)证明:延长EB 至H ,使BH DF =,连接AH ,∵在正方形ABCD 中,∴ADF ABH ∠=∠,ADF ABH ∠=∠,在ADF △和ABH △中,∵AD AB ADF ABH DF HB =⎧⎪∠=∠⎨⎪=⎩,∴ADF ABH SAS △≌△(), ∴BAH DAF ∠=∠,AF AH =,∴90FAH ∠=︒,∴45EAF EAH ∠=∠=︒,在FAE △和HAE △中,∵FAE EAH AE AE ⎪∠=∠⎨⎪=⎩,∴FAE HAE SAS △≌△(), ∴EF HE BE HB ==+,∴EF BE DF =+,17.如图,在四边形ABCD 中,AB AD =,180B D ∠+∠=︒,E 、F 分别是边BC ,CD 上的点,且12EAF BAD ∠=∠,求证:EF BE FD =+.答案:见解析解析:证明:将ADF △顺时针旋转得到ABG △,使得AD 与AB 重合,则ADF ABG △≌△,∴FAG BAD ∠=∠,AF AG =,DF GB =, ∵12EAF BAD ∠=∠, ∴EAF EAG ∠=∠,在EAG △和EAF △中,EAF EAG AE AE ⎪∠=∠⎨⎪=⎩,∴EAG EAF SAS △≌△()∴GE EF =,∵GE GB BE DF BE =+=+,∴EF BE FD =+.18.如图,在四边形ABCD 中,AC 平分BAD ∠,过C 作CE AB ⊥于E ,并且1()2AE AB AD =+,求ABC ADC ∠+∠的度数.答案:见解析解析:过C 作CF 垂直AD 于F ,∵AC 平分BAD ∠,∴FAC EAC ∠=∠,∵CE AB ⊥,CF AD ⊥,∴90DFC CEA ∠=∠=︒,∴AFC AEC AAS △≌△(), ∴AF AE =,CF CE =,∵1()2AE AB AD =+, ∴2AE AB AD =+,又∵AD AF DF =-,AB AE BE =+,AF AE =, ∴2AE AE BE AE DF =++-,∴BE DF =,∵90DFC CEB ∠=∠=︒,CF CE =,∴CDF CEB SAS △≌△(), ∴ABC CDF ∠=∠,∵180ADC CDF ∠+∠=︒,∴180ABC ADC ∠+∠=︒.19.已知凸四边形ABCD 中,180ABC ADC ∠+∠=︒,AC 平分BAD ∠,过C 作AB 的垂线交AB 于E ,求证:12AE AB AD =+().答案:见解析解析:证明:过C作CM AD⊥于M,CE AB⊥,∴90M CEB∠=∠=︒,180ABC ADC∠+∠=︒,180MDC ADC∠+∠=︒,∴B MDC∠=∠,AC平分BAD∠,CM AD⊥,CE AB⊥,∴CM CE=,MAC EAC∠=∠,在MAC△和EAC△中,90MAC EACM AECAC AC∠=∠⎧⎪∠=∠=︒⎨⎪=⎩,MAC EAC AAS∴△≌△(),AM AE∴=,90M BEC∠=∠=︒,∴在Rt DMC△和Rt BEC△中CD BCCM CE=⎧⎨=⎩,Rt DMC Rt BEC HL∴△≌△(),BE DM∴=,∴22 AB AD AE BE AD AE DM AD AM AE +=++=++==,即12AE AB AD =+().20.已知如图,在四边形ABCD 中,AC 平分BAD ∠,CE AB ⊥于E ,且12AE AB AD =+(),求证:B ∠与D ∠互补.答案:见解析解析:证明:在AB 上截取AF AD =,连接CF , AC 平分BAD ∠,BAC CAD ∴∠=∠,又AC AC =,ACF ACD SAS ∴△≌△(), AF AD AFC D ∴=∠=∠,,12AE AB AD =+(), EF BE ∴=,又CE AB ⊥,BC FC ∴=,CFB B ∴∠=∠,180B D CFB AFC ∴∠+=∠+∠=︒,即B ∠与D ∠互补.21.如图,已知四边形ABCD 中,AC 平分BAD ∠,CE AB ⊥于点E ,且12AE AB AD =+().如果120D ∠=︒,则B ∠等于 .答案:60︒解析:解:如图,在AB 上截取AF AD =,连接CF ,AC 平分BAD ∠,AC 为公共边,AFC ADC ∴△≌△,ADC AFC ∴∠=∠,12AE AB AD =+(),AF AD =, 12AF EF AF BF AF ∴+=++(), ∴12EF BF =, EF BE ∴=,CE AB ⊥,ABC BFC ∴∠=∠,180ADC ABC ∴∠+∠=︒,120D ∠=︒,60B ∴∠=︒.故答案为:60︒.22.如图,四边形ABCD 中,AC 平分BAD ∠,CE AB ⊥于E ,2AD AB AE +=.求证:180B ADC ∠+∠=︒.答案:见解析解析:证明:过C 作CF 垂直AD 于F , AC 平分BAD ∠,FAC EAC ∴∠=∠,CE AB ⊥,CF AD ⊥,90DFC CEB ∴∠=∠=︒,AFC AEC ∴△≌△,AF AE ∴=,CF CE =,2AE AB AD =+,又AD AF DF =-,AB AE BE =+,AF AE =,2AE AE BE AE DF ∴=++-,BE DF ∴=,90DFC CEB ∠=∠=︒,CF CE =,CDF CEB ∴△≌△,ABC CDF ∴∠=∠,180ADC CDF ∠+∠=︒,180B ADC ∴∠+∠=︒.23.如图所示,ABC ∆是边长为1的正三角形,BDC ∆是顶角为120的等腰三角形,以D 为顶点作一个60的MDN ∠,点M 、N 分别在AB 、AC 上,求AMN ∆的周长.答案:见解析 解析:如图所示,延长AC 到E 使CE BM =. 在BDM ∆与CDE ∆中,∵BD CD =,90MBD ECD ∠=∠=︒,BM CE =, ∴BDM CDE ∆∆≌, 故MD ED =.∵120BDC ∠=︒,60MDN ∠=︒, ∴60BDM NDC ∠+∠=︒. 又∵BDM CDE ∠=∠, ∴60MDN EDN ∠=∠=. 在MND ∆与END ∆中,NM EDC BADN DN =,60MDN EDN ∠=∠=︒,DM DE =,∵MND END ∆∆≌, 则NE MN =,∴AMN ∆的周长AM AN MN AM AN NE =++=++AM AN NC CE =+++ AM AN NC BM =+++ AB AC =+2=.24.如图,在ABC △中,AB BD AC +=,ABC ∠的平分线AD 交BC 与D .求证:2B C ∠=∠.答案:见解析 解析:在AC 上取一点E ,使得AB AE =,连结DE .在△ABD 和AED △中,AB AE =,BAD EAD ∠=∠,DC B AEDC B AAD AD =.∴ABD AED △≌△, ∴BD ED =,B AED ∠=∠ 又∵AB BD AC +=, ∴EC BD ED ==2AED EDC C C B ∠=∠+∠=∠=∠.25.如图,ABC △中,AB AC =,108A ∠=︒,BD 平分ABC ∠交AC 于D 点.求证:BC AC CD =+.答案:见解析 解析:在BC 上截取E 点使BE BA =,连结DE .∵BD 平分ABC ∠,∴ABD EBD ∠=∠. 在ABD △与EBD △中∵AB EB =,ABD EBD ∠=∠,BD BD =, ∴ABD EBD △≌△,∴A DEB ∠=∠,AB CDE DCB A∵108A ∠=︒,∴108DEB ∠=︒, ∴72DEC ∠=︒.∵AB AC =,且108BAC ∠=︒, ∴36ABC C ∠=∠=︒.∴13618542ADB C ABC ∠=∠+∠=︒+︒=︒, ∴72CDE ∠=︒, ∴CDE DEC ∠=∠, ∴CD CE =, ∵BC BE EC =+, ∴BC AC CD =+.26.如图,ABC △中,A ∠的平分线交BC 于D ,AB AC CD =+,40B ∠=︒,那么C ∠的大小是__________.答案:80︒ 解析:在AB 上取点E ,使得AE AC =,连接DE .D CB A∵AE AC =,BAD CAD ∠=∠,AD AD =,∴ACD AED △≌△, ∴C AED ∠=∠,CD CE =, ∵AB AC CD =+,AE AC =, ∴CD BE DE ==, ∴40EBD EDB ∠=∠=︒,80AED B BDE =+=︒∠∠∠,80C AED ∠=∠=︒.26.如图,在ABC △中,90BAC ∠=︒,2B C ∠=∠,D 点在BC 上,AD 平分BAC ∠,若1AB =,则BD 的长为____________.答案:见解析 解析:在BC 上截取AE AB =,连接DE ,ED CB AD CB A∵AE AB =,BAD CAD ∠=∠,AD AD =,∴ABD AED △≌△∴BD DE =,ABD AED ∠=∠,AB AE =,∵90BAC ∠=︒,2B C ∠=∠, ∴60B ∠=︒,30C ∠=︒, ∴30DEC C ∠=︒=∠, ∴DE CE =,∴1BD AC AB =-=.27.已知:在ABC △中,AB CD BD =-,AD BC ⊥,求证:2B C ∠=∠.答案:见解析解析:延长DB 到点E ,使BE AB =,如图2,ED CB AD CBA∴E EAB ∠=∠, ∵AB CD BD =-, ∴ED CD =,在AED △和ACD △中,AD BC ⊥,ED CD =,AD AD =,∴AED ACD △≌△, ∴E C ∠=∠, ∴2B C ∠=∠.28.已知等腰,,的平分线交于,则.答案:见解析解析:如图,延长BD 到E ,使DE AD =,在BC 上截取BF BA =.图2EAB CD ABC ∆100A ∠=︒ABC ∠AC D BD AD BC +=DCB A∵12∠=∠,BD 为公共边,∴BAD BFD △≌△,AD FD =,ADB FDB ∠=∠,∵1111(180100)20222ABC ∠=∠=⨯︒-︒=︒, ∴180(1)180(10020)60ADB A ∠=︒-∠+∠=︒-︒+︒=︒. ∴60FDB ∠=︒,故60FDC ∠=︒,60EDC ∠=︒. ∵DF DE =,∴DFC DEC △≌△, ∴E DFC ∠=∠,34∠=∠.∵2206080DFC FDB ∠=∠+∠=︒+︒=︒, ∴80E ∠=︒.∵440∠=︒,∴340∠=︒, 故3480ECB ∠=∠+∠=︒. ∴ECB E ∠=∠,故BC BE =. ∵BE BD DE =+, ∴BC BD AD =+.BADC21FE43。
