§2.8用算子符号表示微分方程
信号与系统第二章第一讲

则相应于1的k阶重根,有k项:
( A1t k 1 A2t k 2 Ak 1t Ak )e1t ( Ai t k i )e1t
i 1
k
例2-3
信 号 与 系 统
求如下所示的微分方程的齐次解。
Hale Waihona Puke d3 d2 d r (t ) 7 2 r (t ) 16 r (t ) 12r (t ) e(t ) 3 dt dt dt
等式两端各对应幂次的系数应相等,于是有:
信 号 与 系 统
特解为: 联立解得:
3B1 1 4 B1 3B2 2 2 B 2 B 3 B 0 2 3 1
统
线性时不变系统
线性的常系数微分方程
按照元件的约束特性及 系统结构的约束特性
也即:
具体系统物理模型
常系数微分方程建立
(1)元件端口的电压与电流约束关系
iR (t ) R
信 号 与 系 统
vR (t )
C
vR (t ) iR (t ) R
dvC (t ) iC (t ) C dt
vR (t ) Ri R (t )
与
时域经典法就是直接求解系统微分方程的方法。这种方 系 法的优点是直观,物理概念清楚,缺点是求解过程冗繁,应 用上也有局限性。所以在20世纪50年代以前,人们普遍喜欢 统 采用变换域分析方法(例如拉普拉斯变换法),而较少采用时 域经典法。20世纪50年代以后,由于δ(t)函数及计算机的普 遍应用,时域卷积法得到了迅速发展,且不断成熟和完善, 已成为系统分析的重要方法之一。时域分析法是各种变换域 分析法的基础。
信 号 与 系 统
is (t )
微分方程的算子算法【精选】

(1) P(D)( f1( x) f2 ( x)) P(D) f1(x) P(D) f2 (x)
(2) [P1(D) p2 (D)] f ( x) P1(D) f ( x) p2 (D) f ( x)
(3) P(D) P1(D)P2 (D),则
P(D) f (x) P1(D)[P2 (D) f (x)] P2 (D)[P1(D) f (x)]
10
常系数线性微分方程的算子解法
1
9.算子 P ( D)的基本性质及运算法则
(1)
1 (
P(D)
f1( x)
f2 ( x))
1 P(D)
f1( x)
1 P(D)
f2 ( x)
(2) P(D) P1(D)P2 (D),则
1 f ( x) 1 [ 1 f ( x)] 1 [ 1 f ( x)]
, D2
d2 dx 2
,L
, Dn
DDn1
dn dx n
P(D) Dn p1Dn1
P(D) y 0
3
常系数线性微分方程的算子解法
2.解的结构
线性算子 P(D)( y1 y2 ) P(D) y1 P(D) y2 定理1 方程(1)的通解为:y y(x) y *(x) ,其中y(x)
cos x
cos x P(2 )
(P(2 )
0)
12
常系数线性微分方程的算子解法
1
10.算子 P ( D) 的运算公式
(4)
1 [exv( x)] ex 1 v( x)
P(D)
P( D)
(5) 设fk ( x) b0 b1x L bk xk , P(0) pn 0,则
§2.8 用算子符号表示微分方程

当求系统的零状态响应时,则要解r(t)=H(p)e(t)的非齐次方 当求系统的零状态响应时,则要解r )=H 程。 由上述可以看出:在时域分析中, 由上述可以看出:在时域分析中,算子符号形式提供了简 单易行的辅助分析手段,但本质上与经典法分析系统相同, 单易行的辅助分析手段,但本质上与经典法分析系统相同,而形 式上又与后述的拉普拉斯变换分析相似。 式上又与后述的拉普拉斯变换分析相似。 返回
e(t)
-
i(t) 1
1H
i(t) 2
1
i(t) 3
1F
用算子符号建立微分方程(续2) 用算子符号建立微分方程(
di di di 3 1 − 2 − 3 =0 dt dt dt di di − 1 + 2 + i 2 − i 3 = e( t ) dt dt − di 1 − i + di 3 + i + t i dt = 0 2 3 ∫− ∞ 3 dt dt
− p p + 3
−1
e ( t ) 0
( 2 p 2 + 10 p + 3 )i 2 = pe ( t )
d 2 i2 即: 2 2 + 10 di 2 + 3i 2 = d e ( t ) dt dt dt
1H 1H
+
例2-8-2:如图所示电路,激 如图所示电路, 励电压为e ),请用算子符号列 励电压为e(t),请用算子符号列 写求电流i 的微分方程。 写求电流i1(t)的微分方程。 解:列出3个网孔的回路方程 列出3
( C 0 p n + C 1 p n −1 + L + C n − 1 p + C n )r ( t ) = ( E 0 p m + E 1 p m −1 + L + E m −1 p + E m )e ( t ) D ( p ) = C 0 p n + C 1 p n −1 + L + C n −1 p + C n N ( p ) = E 0 p m + E 1 p m −1 + L + E m −1 p + E m
信号与系统王明泉版本~第二章习题解答
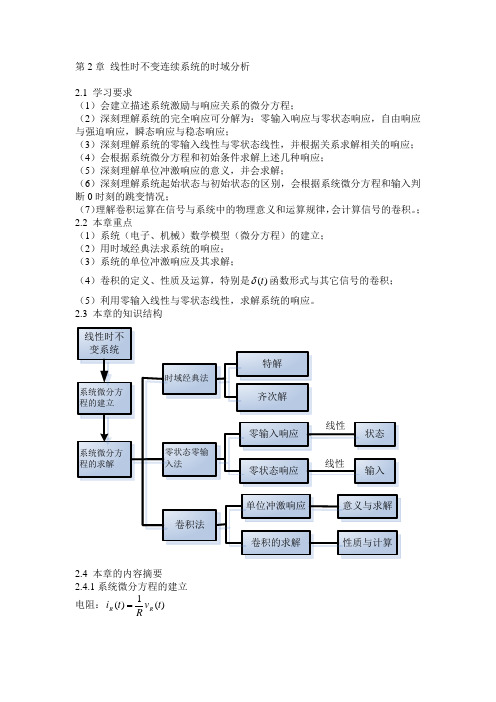
第2章 线性时不变连续系统的时域分析2.1 学习要求(1)会建立描述系统激励与响应关系的微分方程;(2)深刻理解系统的完全响应可分解为:零输入响应与零状态响应,自由响应与强迫响应,瞬态响应与稳态响应;(3)深刻理解系统的零输入线性与零状态线性,并根据关系求解相关的响应; (4)会根据系统微分方程和初始条件求解上述几种响应; (5)深刻理解单位冲激响应的意义,并会求解;(6)深刻理解系统起始状态与初始状态的区别,会根据系统微分方程和输入判断0时刻的跳变情况; (7)理解卷积运算在信号与系统中的物理意义和运算规律,会计算信号的卷积。
; 2.2 本章重点(1)系统(电子、机械)数学模型(微分方程)的建立; (2)用时域经典法求系统的响应; (3)系统的单位冲激响应及其求解;(4)卷积的定义、性质及运算,特别是()t δ函数形式与其它信号的卷积; (5)利用零输入线性与零状态线性,求解系统的响应。
2.3 本章的知识结构2.4 本章的内容摘要2.4.1系统微分方程的建立电阻:)(1)(t v Rt i R R =电感:dtt di L t v L L )()(= )(d )(1)(0t i v Lt i L tL L +=⎰∞-ττ 电容:dtt dv C t i C C )()(= ⎰+=tt L C C t i i Ct v 0)(d )(1)(0ττ 2.4.2 系统微分方程的求解 齐次解和特解。
齐次解为满足齐次方程t n t t h e c e c e c t y 32121)(λλλ+⋅⋅⋅++=当特征根有重根时,如1λ有k 重根,则响应于1λ的重根部分将有k 项,形如t k t k t k t k h e c te c e t c e t c t y 111112211)(λλλλ++⋅⋅⋅++=--- 当特征根有一对单复根,即bi a +=2,1λ,则微分方程的齐次解bt e c bt e c t y at at h sin cos )(21+= 当特征根有一对m 重复根,即共有m 重ib a ±=2,1λ的复根,则微分方程的齐次解bt e t c bt te c bt c t y at m m at h cos cos cos )(121-+⋅⋅⋅++= bt e t d bt te d bt e d at m m at at sin sin sin 121-+⋅⋅⋅+++ 特解的函数形式与激励函数的形式有关。
微分方程引入介绍微分方程的概念和基本符号表示法

导数描述了函数值随自变量变化而变化的速率,即函数在某一点处的切线斜率。
导数符号
函数$y = f(x)$的微分用$df$或$Delta y$表示。
微分描述了函数值在某一小区间内的变化量,即函数的局部变化率。微分与导数密切相关,微分是导数乘以自变量的微分。
微分符号
微分的定义
一阶常系数线性微分方程求解方法
1. 首先求出对应的齐次方程$y' + p(x)y = 0$的通解$y_h$。
2. 然后利用常数变易法或待定系数法求出非齐次方程的一个特解$y_p$。
3. 最后将齐次方程的通解和非齐次方程的一个特解相加,得到非齐次方程的通解$y = y_h + y_p$。
02
01
04
03
初值问题是微分方程的一类重要问题,它要求在给定的初始条件下求解微分方程。对于一阶常系数线性微分方程,初值问题的求解步骤如下
CATALOGUE
04
1
2
3
对于一阶常系数线性齐次方程$y' + p(x)y = 0$,其求解步骤如下
1. 写出方程的特征方程$r + p(x) = 0$,解得特征根$r = -p(x)$。
2. 根据特征根,得到方程的通解形式为$y = Ce^{-p(x)x}$,其中C为任意常数。
1
对于一阶常系数线性非齐次方程$y' + p(x)y = q(x)$,其求解步骤如下
边值问题是微分方程的一类重要问题,它要求求解满足一定边界条件的微分方程的解。常见的边值问题包括两点边值问题、多点边值问题等。
求解边值问题的基本步骤如下
1. 根据问题的实际背景,建立微分方程及相应的边界条件。
微分方程的公式

微分方程的基本公式和应用微分方程是数学中一个重要且广泛应用的分支,它在物理、工程、经济和其他科学领域中都有着广泛的应用。
在微分方程中,我们经常会遇到一些基本公式,这些公式不仅在理论上有着非常重要的意义,同时在实际应用中也有着广泛的价值。
一、一阶常微分方程的基本公式一阶常微分方程的一般形式为:y' = f(x,y),其中 y' 表示 y关于 x 的导数,f(x,y) 是一个已知的函数。
1. 可分离变量的一阶常微分方程如果一阶常微分方程可以写成下面的形式:dy/dx = g(x)h(y)其中 g(x) 和 h(y) 都是已知函数,则这个方程可以通过分离变量的方法来求解。
2. 齐次一阶常微分方程如果一阶常微分方程可以写成下面的形式:dy/dx = F(y/x)其中 F(z) 是关于 z 的已知函数,则这个方程可以通过齐次化的方法来解决。
3. 一阶线性常微分方程如果一阶常微分方程可以写成下面的形式:dy/dx + P(x)y = Q(x)其中 P(x) 和 Q(x) 都是关于 x 的已知函数,则这个方程可以通过积分因子的方法来解决。
4. 其他一阶常微分方程还有一些一阶常微分方程没有特殊的形式,这些方程可以通过变量代换、替换或其他方法来求解。
二、高阶常微分方程的基本公式除了一阶常微分方程,还有二阶甚至更高阶的微分方程需要求解。
1. 二阶常微分方程的基本公式二阶常微分方程的一般形式为:y'' + p(x)y' + q(x)y = f(x),其中 y'' 表示 y 对 x 的二阶导数。
2. 高阶常微分方程的基本公式高阶常微分方程的一般形式为:y^(n) + p1(x)y^(n-1) + ... + pn(x)y = f(x),其中 y^(k) 表示 y 对 x 的第 k 阶导数。
三、微分方程的应用微分方程不仅在理论上有着非常重要的意义,同时在实际应用中也有着广泛的价值,主要体现在以下几个方面:1. 物理问题的模拟微分方程可以用来模拟物理问题,如弹性碰撞问题、自由落体问题等。
微分方程

du 2 x e x dx
du x e dx
2x
du x e dx
2x
du x e dx du x e dx 1 1 2x 2x u x e d 2 x xde 2 2
2x
2x
1 2x 1 2x 1 2x 1 2x xe e dx xe e c 2 2 2 4 1 2x 1 2x 2 x y ( xe e c)e 2 4 ce
2 x
1 1 x 2 4
dy 2 y x 的通解 p( x) 2 例7 求 dx
微分方程 第一节 第二节 微分方程的基本概念 一阶微分方程
第一节
微分方程的基本概念
1. 微分方程的定义:含有自变量 x,
x 的未知函数 y,
y
的任意阶导数(或微分)的方程称为微分方程。
例如:
d y x y dx n ( x) ( y) C 2 d y dy dy 2 2 y sin x dx dx dx
2 x
e
由初始条件得 特解为
2 x
e
3 x
2 x
c 1
y e e
2 x
第二节 定义: 含有 x, y和 其一般形式为
一阶微分方程
y的方程 叫做 一阶微分方程。 dy x F ( y, y, x) 0 例如 dx y y f ( x)
的方程叫做特
三种一阶微分方程的解法 一、特殊类型的一阶微分方程 一阶微分方程中不含有 殊类型的一阶微分方程。
y 1 y 1 ln ln c 通解为 c 2 2 1 x 1 x
2
2
由初始条件得 c 2 特解为 2 x y 1
积的性质2.10 用算子符号表示微分方程

§2.8 卷积的性质(一)移不变性质123f f f *=如果 , 那么10230()()f t t f f t t -*=-,20130()()f t t f f t t -*=-, 2112312()()()f t t f t t f t t t -*-=--证明:123()()()f t f t f t *=, 也就是123[()()]()f f t d f t τττ∞-∞⨯-=⎰102102()[()()]f t t f f t f t d τττ∞-∞-*=-⨯-⎰………………………(1式) 设0t ατ=-,代入(1式)积分中,可得10212030()[()()]()f t t f f f t t d f t t ααα∞-∞-*=⨯--=-⎰84214性质的应用参考教材第页-题(二)卷积代数12211.commutative law f f f f *=* 12312132.[]distributive law f f f f f f f *+=*+* 1231233.[][]associative law f f f f f f **=**(三)卷积的微分和积分1.两函数相卷积后的导数等于两函数之一的导数与另一函数相卷积.(证明见p65-67)121221[]df df d f f f f dt dt dt*=*=* 2.两函数相卷积后的积分等于两函数之一的积分与另一函数相卷积.121212[]*()[()]*tt tf f dt f f d f d f ττττ-∞-∞-∞*==⎰⎰⎰ 21112222()()t t t df d f f f f d f d dt dt ττττ-∞-∞-∞*=*=*⎰⎰⎰ 12:()f f s t *=若则有()()()12()()()m n m n f t f t s t +*=,m n 和取正整数时表示求导,为负整数时表示积分。
