习题答案(第六版)
财务会计习题集(第六版)参考答案

第一章总论一、单选题1.c2.A3.B4.D5.A6.B7.A8.C9.A10.C 二、多项选择题1.ABC2.CDE3.ABC4.ABC5.ACD6.ABCDE7.ABCDE 8.ABCD9.BCD10.ABCDE三、判断改错题1.√2.×3.√4.×5.√ 6.× 7.×8.√ 9.× 10.√四、填空题1.2.资产负债表利润表3.基本准则具体准则准则指南4.自公历一月一日起至十二月三十一日止5.人民币6.具体准则统驭和指导作用7.资产负债所有者权益收入费用利润8.法律行政法规第二章货币资金和结算业务一、单项选择题1.D2.C3.C4.B5.D6.C7.D 8.A 9.A 10.B 11.C二、多项选择题1.CDE2. ABCD3.ABCDE4.ABCE5.ABD6.BE7.AB8.CDE9.CD 10.BD三、判断改错题1. ×2.√3.×4.×5.×6.×7.×8.√9.× 10. √ 11.× 12.× 13. √ 14. 15.× 16.×四、填空题1.库存现金银行存款其他货币资金2.坐支现金3.库存现金日记账银行存款日记账4.银行进账单银行进账单回单5.库存现金非库存现金6.不准出租、出借账户不准签发空头支票和远期支票不准套取银行信用7.恪守信用、履约付款谁的钱进谁的账、由谁支配银行不垫款8.现金支票转账支票普通支票定额银行本票不定额银行本票9.一个月10.商业承兑汇票银行承兑汇票11.10 000元 3天 10天12.银行存款日记账对账单13.1 000 5 000 10 000 50 000五、业务核算题习题一1. 借:其他应收款—王红 1 000贷:银行存款 1 0002. 借:库存现金 45 000贷:银行存款 45 000 3. 借:应付职工薪酬 45 000贷:库存现金 45 000 4. 借:管理费用—办公费 320贷:银行存款 3205. 借:银行存款 11 700贷:主营业务收入 10 000应交税费—应交增值税(销) 1 7006. 借:管理费用—差旅费 850库存现金 150贷:其他应收款—王红 1 000 7. 借:管理费用—邮电费 250贷:银行存款 2508. 借:银行存款 417贷:财务费用—利息 417现金、银行存款日记账登记略习题二1. 借:预付账款—围城公司 50 000贷:银行存款 50 000 2. 借:其他应收款—业务科 1 000贷:银行存款 1 0003. 借:银行存款 44 640贷:应收账款—长江公司 44 6404. 借:材料采购—江城公司 22 000应交税费—应交增值税(进) 3740贷:应付票据—银行承况汇票 25 7405. 借:销售费用—广告费 20 000贷:银行存款 20 0006. 借:应收账款—光华工厂 23 200贷:其他业务收入 19 500应交税费—应交增值税(销) 3 315银行存款 3857. 借:其他应收款—周明 700贷:银行存款 7008. 借:银行存款 6 054.75贷:主营业务收入 5 175.00 应交税费—应交增值税(销) 879.759. 借:其他货币资金—银行汇票 54 000贷:银行存款 54 00010. 借:应收账款—幸福商场 10 000贷:应收票据—商业承兑汇票 10 00011. 借:材料采购—围城公司 9 100应交税费—应交增值税(进) 1487.50贷:银行存款 10587.50 借:原材料—甲材料 5 500--乙材料 4 000贷: 材料采购—围城公司 9 500借: 材料采购—围城公司 400贷:材料成本差异—原材料 40012. 借:银行存款 18 400贷:应收账款—黄河公司 18 400习题三本单位银行存款调节后余额=380 547+ 10 000-0=390 547银行对账单调节后余额=390 797 +0-250=390 547习题四银行存款调节后余额=898 509.33+361.20-125.75=898 744.78银行对账单调节后余额=886 053.11+12 578.25+150.36+86.4-123.34 =898 744.78第三章、应收及预付款项一、单项选择题1.C2.D3.A4.D5.B6.C7.D8.A二、多项选择题1.ABDE2.BC3.ABCDE4.CE5.AC6.ABCD7.BCDE8.BD三、判断改错题1.×2.×3.×4.√5.√6.√7.√8.×9.√ 10.√四、填空题1.实际发生额2.总价(全价) 财务费用3.应收账款主营业务收入银行存款应收账款5.管理费用坏账准备坏账准备应收账款6.坏账准备资产类备抵调整7.应收款项余额的一定比例进行8.银行存款应收票据9.财务费用10.其他应收款11.资产类供货单位企业尚未结转的预付款项企业尚未补付的款项五.业务核算题习题一1.借:应收账款—某商场 11 700贷:主营业务收入—A产品 10 000 应交税费—应交增值税(销) 1 700 2.借:银行存款 11 700贷:应收账款—某商场 11 7003.借:应收账款—外地甲企业 117 200贷:主营业务收入—B产品 10 000应交税费—应交增值税(销) 17 000银行存款 2004.借:应收票据—商业承兑汇票(外地甲企业) 117 200贷:应收账款—外地甲企业 117 200 5.(1)借:应收账款—外地某商店 3 000贷:坏账准备 3 000 借:银行存款 3 000贷: 应收账款—外地某商店 3 000(2)借:坏账准备 5 000贷:应收账款—红旗商场 5 000(3)应提坏账准备=300万×5‰=15 000应补提坏账准备=15000-10000=5 000借:管理费用—坏账损失 5 000贷:坏账准备 5 0006.(1)借:管理费用—坏账损失 3 000贷:应收账款—某单位 3 000(2)借: 应收账款—某单位 2 000贷: 管理费用—坏账损失 2 000借:银行存款 2 000贷: 应收账款—某单位 2 000习题二1.借:应收票据—商业承兑汇票(甲企业) 46 800贷:主营业务收入—A产品 40 000 应交税费—应交增值税(销) 6 8002.借:应收账款—甲企业 46 800贷: 应收票据—商业承兑汇票(甲企业) 46 8003. 借:银行存款 46 800贷: 应收账款—甲企业 46 8004.贴现利息=50000×5‰×3=750贴现所得额=50000-750=49 250借:银行存款 49 250财务费用—利息 750贷: 应收票据—商业承兑汇票 50 000习题三1.借:预付账款—红星工厂 10 000贷:银行存款 10 0002.借:原材料—甲材料 1 8000应交税费—应交增值税(进) 3 060贷: 预付账款—红星工厂 10 000银行存款 11 0603.借:其他应收款—代垫水电费 1 000贷:银行存款 1 0004.借:应收利息 600贷:财务费用—利息 6005.借:银行存款 1 750贷:应收利息 1 100财务费用—利息 6506.(1)借:其他应收款—总务科 1 000贷:银行存款 1000(2)借:管理费用—其他费用 400贷:库存现金 4007.借:其他应收款—王明 1 000贷:银行存款 1 0008.借:管理费用—差旅费 1 200贷: 其他应收款—王明 1 000 库存现金 200第四章金融资产参考答案一、单项选择题1.A 2.D 3.A 4.B 5.C 6.C 7.C二、多项选择题1. ABCD.2.ABCD 3.ABCD 4.ACD.5.AC 6.ABC三、判断改错题1.×2.√3.√4.×5.×6.√7.√8.×四、填空题1.以公允价值计量且其变动计入当期损益的金融资产.持有至到期投资.贷款和应收账款、可供出售金融资产。
同济大学第六版高等数学上下册课后习题答案5-2

同济大学第六版高等数学上下册课后习题答案5-2 1. 试求函数⎰=xtdt y 0sin 当x =0及4π=x 时的导数. 解 x tdt dx d y x sin sin 0=='⎰, 当x =0时, y '=sin0=0; 当4π=x 时, 224sin =='πy . 2. 求由参数表示式⎰=t udu x 0sin , ⎰=tudu y 0cos 所给定的函数y 对x 的导数.解 x '(t )=sin t , y '(t )=cos t , t t x t y dx dy cos )()(=''=. 3. 求由⎰⎰=+x y ttdt dt e 000cos 所决定的隐函数y 对x 的导数dxdy . 解 方程两对x 求导得0cos =+'x y e y ,于是 ye x dx dy cos-=. 4. 当x 为何值时, 函数⎰-=x t dt te x I 02)(有极值? 解 2)(x xe x I -=', 令I '(x )=0, 得x =0. 因为当x <0时, I '(x )<0; 当x >0时, I '(x )>0,所以x =0是函数I (x )的极小值点.5. 计算下列各导数:(1)⎰+2021x dt t dx d ; (2)⎰+32411x x dt tdx d ; (3)⎰x xdt t dx d cos sin 2)cos(π. 解 (1)dxdu dt t du d u x dt t dx d u x ⋅+=+⎰⎰02202112令 421221x x x u +=⋅+=.(2)⎰⎰⎰+++=+323204044111111x x x x dt tdx d dt t dx d dt t dx d ⎰⎰+++-=3204041111x x dt t dx d dt t dx d )()(11)()(11343242'⋅++'⋅+-=x x x x 12281312xx x x +++-=. (3)⎰⎰⎰+-=x x x x dt t dx d dt t dx d dt t dx d cos 02sin 02cos sin 2)cos()cos()cos(πππ ))(cos cos cos())(sin sin cos(22'+'-=x x x x ππ)cos cos(sin )sin cos(cos 22x x x x ππ⋅-⋅-=)sin cos(sin )sin cos(cos 22x x x x πππ-⋅-⋅-=)sin cos(sin )sin cos(cos 22x x x x ππ⋅+⋅-=)sin cos()cos (sin 2x x x π-=.6. 计算下列各定积分:(1)⎰+-adx x x 02)13(; 解 a a a x x x dx x x a a+-=+-=+-⎰230230221|)21()13(. (2)⎰+2142)1(dx xx ; 解 852)11(31)22(31|)3131()1(333321332142=---=-=+---⎰x x dx x x . (3)⎰+94)1(dx x x ; 解 94223942194|)2132()()1(x x dx x x dx x x +=+=+⎰⎰ 6145)421432()921932(223223=+-+=. (4)⎰+33121x dx ; 解 66331arctan 3arctan arctan 13313312πππ=-=-==+⎰x x dx . (5)⎰--212121x dx ; 解 3)6(6)21arcsin(21arcsin arcsin 1212121212πππ=--=--==---⎰x x dx .(6)⎰+a x a dx 3022; 解 a a a a xa x a dx aa 30arctan 13arctan 1arctan 1303022π=-==+⎰. (7)⎰-1024x dx ; 解 60arcsin 21arcsin 2arcsin 410102π=-==-⎰x x dx . (8)dx x x x ⎰-+++012241133; 解 013012201224|)arctan ()113(1133---+=++=+++⎰⎰x x dx x x dx x x x 41)1arctan()1(3π+=----=. (9)⎰---+211e x dx ; 解 1ln 1ln ||1|ln 12121-=-=+=+------⎰e x x dx e e . (10)⎰402tan πθθd ; 解 4144tan )(tan )1(sec tan 40402402πππθθθθθθπππ-=-=-=-=⎰⎰d d . (11)dx x ⎰π20|sin |; 解 ⎰⎰⎰-=ππππ2020sin sin |sin |xdx xdx dx x πππ20cos cos x x +-==-cos π +cos0+cos2π-cos π=4.(12)⎰20)(dx x f , 其中⎪⎩⎪⎨⎧>≤+=1 211 1)(2x x x x x f . 解 38|)61(|)21(21)1()(2131022121020=++=++=⎰⎰⎰x x x dx x dx x dx x f . 7. 设k 为正整数. 试证下列各题: (1)⎰-=ππ0cos kxdx ; (2)⎰-=ππ0sin kxdx ; (3)⎰-=πππkxdx 2cos ; (4)⎰-=πππkxdx 2sin . 证明 (1)⎰--=-=--==ππππππ000)(sin 1sin 1|sin 1cos k k k k kx k kxdx . (2))(cos 1cos 1cos 1sin ππππππ-+-=-=--⎰k k k k x k k kxdx 0cos 1cos 1=+-=ππk kk k . (3)πππππππππ=+=+=+=---⎰⎰22|)2sin 21(21)2cos 1(21cos 2kx k x dx kx kxdx . (4)πππππππππ=+=-=-=---⎰⎰22|)2sin 21(21)2cos 1(21sin 2kx k x dx kx kxdx . 8. 设k 及l 为正整数, 且k ≠l . 试证下列各题:(1)⎰-=ππ0sin cos lxdx kx ; (2)⎰-=ππ0cos cos lxdx kx ;(3)⎰-=ππ0sin sin lxdx kx . 证明 (1)⎰⎰----+=ππππdx x l k x l k lxdx kx ])sin()[sin(21sin cos 0])cos()(21[])cos()(21[=----++-=--ππππx l k l k x l k l k . (2)⎰⎰---++=ππππdx x l k x l k lxdx kx ])cos()[cos(21cos cos 0])sin()(21[])sin()(21[=--+++=--ππππx l k l k x l k l k . (3)⎰⎰----+-=ππππdx x l k x l k lxdx kx ])cos()[cos(21sin sin . 0])sin()(21[])sin()(21[=--+++-=--ππππx l k l k x l k l k . 9. 求下列极限:(1)x dt t x x ⎰→020cos lim;(2)⎰⎰→x t x t x dt te dt e 0220022)(lim .解 (1)11cos lim cos lim 20020==→→⎰x x dt t x x x . (2)22222200002200)(2lim )(lim x xt x t x xt x t x xe dt e dt e dtte dt e '⋅=⎰⎰⎰⎰→→ 22222002002lim 2lim x x t x x x xt x xe dt e xe edt e ⎰⎰→→=⋅=2212lim 22lim 2020222=+=+=→→x e x e e x x x x x . 10. 设⎩⎨⎧∈∈=]2 ,1[ ]1 ,0[ )(2x x x x x f . 求⎰=x dt t f x 0)()(ϕ在[0, 2]上的表达式, 并讨论ϕ(x )在(0, 2)内的连续性.解 当0≤x ≤1时, 302031)()(x dt t dt t f x xx ===⎰⎰ϕ; 当1<x ≤2时, 6121212131)()(2211020-=-+=+==⎰⎰⎰x x tdt dt t dt t f x xx ϕ. 因此 ⎪⎩⎪⎨⎧≤<-≤≤=21 612110 31)(23x x x x x ϕ. 因为31)1(=ϕ, 3131lim )(lim 30101==-→-→x x x x ϕ, 316121)6121(lim )(lim 20101=-=-=+→+→x x x x ϕ, 所以ϕ(x )在x =1处连续, 从而在(0, 2)内连续.11. 设⎪⎩⎪⎨⎧><≤≤=ππx x x x x f 或0 00 sin 21)(. 求⎰=x dt t f x 0)()(ϕ在(-∞, +∞)内的表达式.解 当x <0时,00)()(00===⎰⎰xx dt dt t f x ϕ; 当0≤x ≤π时,21cos 21|cos 21sin 21)()(000+-=-===⎰⎰x t tdt dt t f x x xx ϕ; 当x >π时,πππϕ000|cos 210sin 21)()(t dt tdt dt t f x x x -=+==⎰⎰⎰ 10cos 21cos 21=+-=π. 因此 ⎪⎩⎪⎨⎧≥≤≤-<=ππϕx x x x x 10 )cos 1(210 0)(. 12. 设f (x )在[a , b ]上连续, 在(a , b )内可导且f '(x )≤0,⎰-=x adt t f a x x F )(1)(. 证明在(a , b )内有F '(x )≤0.证明 根据积分中值定理, 存在ξ∈[a , x ], 使))(()(a x f dt t f x a -=⎰ξ. 于是有)(1)()(1)(2x f ax dt t f a x x F x a -+--='⎰ ))(()(1)(12a x f a x x f a x ----=ξ )]()([1ξf x f ax --=. 由 f '(x )≤0可知f (x )在[a , b ]上是单调减少的, 而a ≤ξ≤x , 所以f (x )-f (ξ)≤0. 又在(a , b )内, x -a >0, 所以在(a , b )内 0)]()([1)(≤--='ξf x f ax x F .。
高等数学(第六版)课后习题(完整版)及答案

高等数学课后答案习题1-11. 设A =(-∞, -5)⋃(5, +∞), B =[-10, 3), 写出A ⋃B , A ⋂B , A \B 及A \(A \B )的表达式. 解 A ⋃B =(-∞, 3)⋃(5, +∞), A ⋂B =[-10, -5), A \B =(-∞, -10)⋃(5, +∞), A \(A \B )=[-10, -5).2. 设A 、B 是任意两个集合, 证明对偶律: (A ⋂B )C =A C ⋃B C . 证明 因为x ∈(A ⋂B )C ⇔x ∉A ⋂B ⇔ x ∉A 或x ∉B ⇔ x ∈A C 或x ∈B C ⇔ x ∈A C ⋃B C , 所以 (A ⋂B )C =A C ⋃B C .3. 设映射f : X →Y , A ⊂X , B ⊂X . 证明 (1)f (A ⋃B )=f (A )⋃f (B ); (2)f (A ⋂B )⊂f (A )⋂f (B ). 证明 因为y ∈f (A ⋃B )⇔∃x ∈A ⋃B , 使f (x )=y⇔(因为x ∈A 或x ∈B ) y ∈f (A )或y ∈f (B ) ⇔ y ∈f (A )⋃f (B ), 所以 f (A ⋃B )=f (A )⋃f (B ). (2)因为y ∈f (A ⋂B )⇒∃x ∈A ⋂B , 使f (x )=y ⇔(因为x ∈A 且x ∈B ) y ∈f (A )且y ∈f (B )⇒ y ∈ f (A )⋂f (B ), 所以 f (A ⋂B )⊂f (A )⋂f (B ).4. 设映射f : X →Y , 若存在一个映射g : Y →X , 使X I f g = , Y I g f = , 其中I X 、I Y 分别是X 、Y 上的恒等映射, 即对于每一个x ∈X , 有I X x =x ; 对于每一个y ∈Y , 有I Y y =y . 证明: f 是双射, 且g 是f 的逆映射: g =f -1.证明 因为对于任意的y ∈Y , 有x =g (y )∈X , 且f (x )=f [g (y )]=I y y =y , 即Y 中任意元素都是X 中某元素的像, 所以f 为X 到Y 的满射.又因为对于任意的x 1≠x 2, 必有f (x 1)≠f (x 2), 否则若f (x 1)=f (x 2)⇒g [ f (x 1)]=g [f (x 2)] ⇒ x 1=x 2.因此f 既是单射, 又是满射, 即f 是双射.对于映射g : Y →X , 因为对每个y ∈Y , 有g (y )=x ∈X , 且满足f (x )=f [g (y )]=I y y =y , 按逆映射的定义, g 是f 的逆映射.5. 设映射f : X →Y , A ⊂X . 证明: (1)f -1(f (A ))⊃A ;(2)当f 是单射时, 有f -1(f (A ))=A .证明 (1)因为x ∈A ⇒ f (x )=y ∈f (A ) ⇒ f -1(y )=x ∈f -1(f (A )), 所以 f -1(f (A ))⊃A . (2)由(1)知f -1(f (A ))⊃A .另一方面, 对于任意的x ∈f -1(f (A ))⇒存在y ∈f (A ), 使f -1(y )=x ⇒f (x )=y . 因为y ∈f (A )且f 是单射, 所以x ∈A . 这就证明了f -1(f (A ))⊂A . 因此f -1(f (A ))=A .6. 求下列函数的自然定义域: (1)23+=x y ;解 由3x +2≥0得32->x . 函数的定义域为) ,32[∞+-.(2)211xy -=;解 由1-x 2≠0得x ≠±1. 函数的定义域为(-∞, -1)⋃(-1, 1)⋃(1, +∞). (3)211x xy --=;解 由x ≠0且1-x 2≥0得函数的定义域D =[-1, 0)⋃(0, 1]. (4)241x y -=; 解 由4-x 2>0得 |x |<2. 函数的定义域为(-2, 2). (5)x y sin =;解 由x ≥0得函数的定义D =[0, +∞). (6) y =tan(x +1);解 由21π≠+x (k =0, ±1, ±2, ⋅ ⋅ ⋅)得函数的定义域为 12-+≠ππk x (k =0, ±1, ±2, ⋅ ⋅ ⋅).(7) y =arcsin(x -3);解 由|x -3|≤1得函数的定义域D =[2, 4]. (8)xx y 1arctan 3+-=;解 由3-x ≥0且x ≠0得函数的定义域D =(-∞, 0)⋃(0, 3).(9) y =ln(x +1);解 由x +1>0得函数的定义域D =(-1, +∞). (10)xe y 1=.解 由x ≠0得函数的定义域D =(-∞, 0)⋃(0, +∞). 7. 下列各题中, 函数f (x )和g (x )是否相同?为什么? (1)f (x )=lg x 2, g (x )=2lg x ; (2) f (x )=x , g (x )=2x ;(3)334)(x x x f -=,31)(-=x x x g . (4)f (x )=1, g (x )=sec 2x -tan 2x . 解 (1)不同. 因为定义域不同.(2)不同. 因为对应法则不同, x <0时, g (x )=-x . (3)相同. 因为定义域、对应法则均相相同. (4)不同. 因为定义域不同.8. 设⎪⎩⎪⎨⎧≥<=3||03|| |sin |)(ππϕx x x x , 求)6(πϕ, )4(πϕ, )4(πϕ-, ϕ(-2), 并作出函数y =ϕ(x )的图形.解 21|6sin |)6(==ππϕ, 22|4sin |)4(==ππϕ, 22|)4sin(|)4(=-=-ππϕ, 0)2(=-ϕ. 9. 试证下列函数在指定区间内的单调性: (1)x x y -=1, (-∞, 1);(2)y =x +ln x , (0, +∞).证明 (1)对于任意的x 1, x 2∈(-∞, 1), 有1-x 1>0, 1-x 2>0. 因为当x 1<x 2时, 0)1)(1(112121221121<---=---=-x x x x x x x x y y , 所以函数x x y -=1在区间(-∞, 1)内是单调增加的.(2)对于任意的x 1, x 2∈(0, +∞), 当x 1<x 2时, 有0l n )()l n ()l n (2121221121<+-=+-+=-x xx x x x x x y y ,所以函数y =x +ln x 在区间(0, +∞)内是单调增加的.10. 设 f (x )为定义在(-l , l )内的奇函数, 若f (x )在(0, l )内单调增加, 证明f (x )在(-l , 0)内也单调增加.证明 对于∀x 1, x 2∈(-l , 0)且x 1<x 2, 有-x 1, -x 2∈(0, l )且-x 1>-x 2. 因为f (x )在(0, l )内单调增加且为奇函数, 所以f (-x 2)<f (-x 1), -f (x 2)<-f (x 1), f (x 2)>f (x 1),这就证明了对于∀x 1, x 2∈(-l , 0), 有f (x 1)< f (x 2), 所以f (x )在(-l , 0)内也单调增加. 11. 设下面所考虑的函数都是定义在对称区间(-l , l )上的, 证明: (1)两个偶函数的和是偶函数, 两个奇函数的和是奇函数;(2)两个偶函数的乘积是偶函数, 两个奇函数的乘积是偶函数, 偶函数与奇函数的乘积是奇函数.证明 (1)设F (x )=f (x )+g (x ). 如果f (x )和g (x )都是偶函数, 则 F (-x )=f (-x )+g (-x )=f (x )+g (x )=F (x ), 所以F (x )为偶函数, 即两个偶函数的和是偶函数. 如果f (x )和g (x )都是奇函数, 则F (-x )=f (-x )+g (-x )=-f (x )-g (x )=-F (x ), 所以F (x )为奇函数, 即两个奇函数的和是奇函数. (2)设F (x )=f (x )⋅g (x ). 如果f (x )和g (x )都是偶函数, 则 F (-x )=f (-x )⋅g (-x )=f (x )⋅g (x )=F (x ), 所以F (x )为偶函数, 即两个偶函数的积是偶函数. 如果f (x )和g (x )都是奇函数, 则F (-x )=f (-x )⋅g (-x )=[-f (x )][-g (x )]=f (x )⋅g (x )=F (x ), 所以F (x )为偶函数, 即两个奇函数的积是偶函数. 如果f (x )是偶函数, 而g (x )是奇函数, 则F (-x )=f (-x )⋅g (-x )=f (x )[-g (x )]=-f (x )⋅g (x )=-F (x ), 所以F (x )为奇函数, 即偶函数与奇函数的积是奇函数.12. 下列函数中哪些是偶函数, 哪些是奇函数, 哪些既非奇函数又非偶函数? (1)y =x 2(1-x 2); (2)y =3x 2-x 3;(3)2211x xy +-=;(4)y =x (x -1)(x +1);(5)y =sin x -cos x +1;(6)2x x aa y -+=.解 (1)因为f (-x )=(-x )2[1-(-x )2]=x 2(1-x 2)=f (x ), 所以f (x )是偶函数. (2)由f (-x )=3(-x )2-(-x )3=3x 2+x 3可见f (x )既非奇函数又非偶函数.(3)因为())(111)(1)(2222x f x x x x x f =+-=-+--=-, 所以f (x )是偶函数. (4)因为f (-x )=(-x )(-x -1)(-x +1)=-x (x +1)(x -1)=-f (x ), 所以f (x )是奇函数. (5)由f (-x )=sin(-x )-cos(-x )+1=-sin x -cos x +1可见f (x )既非奇函数又非偶函数. (6)因为)(22)()()(x f a a a ax f x x x x =+=+=-----, 所以f (x )是偶函数.13. 下列各函数中哪些是周期函数?对于周期函数, 指出其周期: (1)y =cos(x -2);解 是周期函数, 周期为l =2π. (2)y =cos 4x ;解 是周期函数, 周期为2π=l .(3)y =1+sin πx ;解 是周期函数, 周期为l =2. (4)y =x cos x ; 解 不是周期函数. (5)y =sin 2x .解 是周期函数, 周期为l =π. 14. 求下列函数的反函数: (1)31+=x y ;解 由31+=x y 得x =y 3-1, 所以31+=x y 的反函数为y =x 3-1. (2)xx y +-=11;解 由x x y +-=11得y yx +-=11, 所以x x y +-=11的反函数为xx y +-=11.(3)dcx b ax y ++=(ad -bc ≠0);解 由d cx b ax y ++=得a cy bdy x -+-=, 所以d cx b ax y ++=的反函数为acx b dx y -+-=.(4) y =2sin3x ;解 由y =2sin 3x 得2arcsin 31yx =, 所以y =2sin3x 的反函数为2arcsin 31x y =.(5) y =1+ln(x +2);解 由y =1+ln(x +2)得x =e y -1-2, 所以y =1+ln(x +2)的反函数为y =e x -1-2.(6)122+=x xy .解 由122+=x x y 得y y x -=1log 2, 所以122+=x x y 的反函数为xx y -=1log 2. 15. 设函数f (x )在数集X 上有定义, 试证: 函数f (x )在X 上有界的充分必要条件是它在X 上既有上界又有下界.证明 先证必要性. 设函数f (x )在X 上有界, 则存在正数M , 使|f (x )|≤M , 即-M ≤f (x )≤M . 这就证明了f (x )在X 上有下界-M 和上界M .再证充分性. 设函数f (x )在X 上有下界K 1和上界K 2, 即K 1≤f (x )≤ K 2 . 取M =max{|K 1|, |K 2|}, 则 -M ≤ K 1≤f (x )≤ K 2≤M ,即 |f (x )|≤M .这就证明了f (x )在X 上有界.16. 在下列各题中, 求由所给函数复合而成的函数, 并求这函数分别对应于给定自变量值x 1和x 2的函数值:(1) y =u 2, u =sin x , 61π=x , 32π=x ; 解 y =sin 2x , 41)21(6sin 221===πy ,43)23(3sin 222===πy .(2) y =sin u , u =2x , 81π=x ,42π=x ;解 y =sin2x , 224sin )82sin(1==⋅=ππy ,12sin )42sin(2==⋅=ππy . (3)u y =, u =1+x 2, x 1=1, x 2= 2;解 21x y +=, 21121=+=y , 52122=+=y . (4) y =e u , u =x 2, x 1 =0, x 2=1;解 2x e y =, 1201==e y , e e y ==212.(5) y =u 2 , u =e x , x 1=1, x 2=-1. 解 y =e 2x , y 1=e 2⋅1=e 2, y 2=e 2⋅(-1)=e -2.17. 设f (x )的定义域D =[0, 1], 求下列各函数的定义域: (1) f (x 2);解 由0≤x 2≤1得|x |≤1, 所以函数f (x 2)的定义域为[-1, 1]. (2) f (sin x );解 由0≤sin x ≤1得2n π≤x ≤(2n +1)π (n =0, ±1, ±2⋅ ⋅ ⋅), 所以函数f (sin x )的定义域为 [2n π, (2n +1)π] (n =0, ±1, ±2⋅ ⋅ ⋅) . (3) f (x +a )(a >0);解 由0≤x +a ≤1得-a ≤x ≤1-a , 所以函数f (x +a )的定义域为[-a , 1-a ]. (4) f (x +a )+f (x -a )(a >0).解 由0≤x +a ≤1且0≤x -a ≤1得: 当210≤<a 时, a ≤x ≤1-a ; 当21>a 时, 无解. 因此当210≤<a 时函数的定义域为[a , 1-a ], 当21>a 时函数无意义.18. 设⎪⎩⎪⎨⎧>-=<=1||11||01||1)(x x x x f , g (x )=e x , 求f [g (x )]和g [f (x )], 并作出这两个函数的图形. 解 ⎪⎩⎪⎨⎧>-=<=1|| 11|| 01|| 1)]([x x x e e e x g f , 即⎪⎩⎪⎨⎧>-=<=0 10 001)]([x x x x g f .⎪⎩⎪⎨⎧>=<==-1|| 1|| e 1|| )]([101)(x e x x e e x f g x f , 即⎪⎩⎪⎨⎧>=<=-1|| 1|| 11|| )]([1x e x x e x f g . 19. 已知水渠的横断面为等腰梯形, 斜角ϕ=40︒(图1-37). 当过水断面ABCD 的面积为定值S 0时, 求湿周L (L =AB +BC +CD )与水深h 之间的函数关系式, 并指明其定义域.图1-37解 40sin hDC AB ==, 又从)]40cot 2([21Sh BC BC h =⋅++ 得h hS BC ⋅-=40cot 0, 所以h h S L 40sin 40cos 20-+=. 自变量h 的取值范围应由不等式组h >0,040cot 0>⋅-h hS确定, 定义域为40cot 00S h <<.20. 收敛音机每台售价为90元, 成本为60元. 厂方为鼓励销售商大量采购, 决定凡是订购量超过100台以上的, 每多订购1台, 售价就降低1分, 但最低价为每台75元.(1)将每台的实际售价p 表示为订购量x 的函数; (2)将厂方所获的利润P 表示成订购量x 的函数; (3)某一商行订购了1000台, 厂方可获利润多少? 解 (1)当0≤x ≤100时, p =90.令0.01(x 0-100)=90-75, 得x 0=1600. 因此当x ≥1600时, p =75. 当100<x <1600时,p =90-(x -100)⨯0.01=91-0. 01x . 综合上述结果得到⎪⎩⎪⎨⎧≥<<-≤≤=1600 75160010001.091100090x x x x p . (2)⎪⎩⎪⎨⎧≥<<-≤≤=-=1600 15160010001.0311000 30)60(2x x x x x x x x p P . (3) P =31⨯1000-0.01⨯10002=21000(元).习题1-21. 观察一般项x n 如下的数列{x n }的变化趋势, 写出它们的极限: (1)nn x 21=; 解 当n →∞时, nn x 21=→0, 021lim =∞→n n . (2)nx n n 1)1(-=;解 当n →∞时, n x n n 1)1(-=→0, 01)1(lim =-∞→nn n .(3)212nx n +=; 解 当n →∞时, 212n x n +=→2, 2)12(lim 2=+∞→n n . (4)11+-=n n x n ;解 当n →∞时, 12111+-=+-=n n n x n →0, 111lim =+-∞→n n n .(5) x n =n (-1)n .解 当n →∞时, x n =n (-1)n 没有极限.2. 设数列{x n }的一般项nn x n 2cos π=. 问n n x ∞→lim =? 求出N , 使当n >N 时, x n与其极限之差的绝对值小于正数ε , 当ε =0.001时, 求出数N .解 0lim =∞→n n x .n n n x n 1|2c o s||0|≤=-π. ∀ε >0, 要使|x n -0|<ε , 只要ε<n 1, 也就是ε1>n . 取]1[ε=N , 则∀n >N , 有|x n -0|<ε .当ε =0.001时, ]1[ε=N =1000.3. 根据数列极限的定义证明:(1)01lim 2=∞→n n ;分析 要使ε<=-221|01|n n , 只须ε12>n , 即ε1>n . 证明 因为∀ε>0, ∃]1[ε=N , 当n >N 时, 有ε<-|01|2n , 所以01lim2=∞→n n .(2)231213lim =++∞→n n n ;分析 要使ε<<+=-++n n n n 41)12(21|231213|, 只须ε<n41, 即ε41>n .证明 因为∀ε>0, ∃]41[ε=N , 当n >N 时, 有ε<-++|231213|n n , 所以231213lim =++∞→n n n .(3)1lim 22=+∞→na n n ; 分析 要使ε<<++=-+=-+na n a n n a n n a n n a n 22222222)(|1|, 只须ε2a n >. 证明 因为∀ε>0, ∃][2εa N =, 当∀n >N 时, 有ε<-+|1|22n a n , 所以1lim 22=+∞→na n n .(4)19 999.0lim =⋅⋅⋅∞→个n n . 分析 要使|0.99 ⋅ ⋅ ⋅ 9-1|ε<=-1101n , 只须1101-n <ε , 即ε1lg 1+>n . 证明 因为∀ε>0, ∃]1lg 1[ε+=N , 当∀n >N 时, 有|0.99 ⋅ ⋅ ⋅ 9-1|<ε , 所以19 999.0lim =⋅⋅⋅∞→个n n . 4. a u n n =∞→lim , 证明||||lim a u n n =∞→. 并举例说明: 如果数列{|x n |}有极限, 但数列{x n }未必有极限.证明 因为a u n n =∞→lim , 所以∀ε>0, ∃N ∈N , 当n >N 时, 有ε<-||a u n , 从而||u n |-|a ||≤|u n -a |<ε .这就证明了||||lim a u n n =∞→.数列{|x n |}有极限, 但数列{x n }未必有极限. 例如1|)1(|lim =-∞→n n , 但n n )1(lim -∞→不存在.5. 设数列{x n }有界, 又0lim =∞→n n y , 证明: 0lim =∞→n n n y x .证明 因为数列{x n }有界, 所以存在M , 使∀n ∈Z , 有|x n |≤M .又0lim =∞→n n y , 所以∀ε>0, ∃N ∈N , 当n >N 时, 有M y n ε<||. 从而当n >N 时, 有εε=⋅<≤=-M M y M y x y x n n n n n |||||0|,所以0lim =∞→n n n y x .6. 对于数列{x n }, 若x 2k -1→a (k →∞), x 2k →a (k →∞),证明: x n →a (n →∞).证明 因为x 2k -1→a (k →∞), x 2k →a (k →∞), 所以∀ε>0, ∃K 1, 当2k -1>2K 1-1时, 有| x 2k -1-a |<ε ; ∃K 2, 当2k >2K 2时, 有|x 2k -a |<ε .取N =max{2K 1-1, 2K 2}, 只要n >N , 就有|x n -a |<ε . 因此x n →a (n →∞). 习题1-31. 根据函数极限的定义证明: (1)8)13(lim 3=-→x x ;分析 因为|(3x -1)-8|=|3x -9|=3|x -3|,所以要使|(3x -1)-8|<ε , 只须ε31|3|<-x .证明 因为∀ε>0, ∃εδ31=, 当0<|x -3|<δ时, 有|(3x -1)-8|<ε , 所以8)13(lim 3=-→x x .(2)12)25(lim 2=+→x x ;分析 因为|(5x +2)-12|=|5x -10|=5|x -2|, 所以要使|(5x +2)-12|<ε , 只须ε51|2|<-x .证明 因为∀ε >0, ∃εδ51=, 当0<|x -2|<δ时, 有 |(5x +2)-12|<ε , 所以12)25(lim 2=+→x x .(3)424lim 22-=+--→x x x ; 分析 因为|)2(||2|244)4(2422--=+=+++=--+-x x x x x x x ,所以要使ε<--+-)4(242x x , 只须ε<--|)2(|x . 证明 因为∀ε >0, ∃εδ=, 当0<|x -(-2)|<δ时, 有ε<--+-)4(242x x , 所以424lim 22-=+--→x x x .(4)21241lim 321=+--→x x x . 分析 因为|)21(|2|221|212413--=--=-+-x x x x ,所以要使ε<-+-212413x x , 只须ε21|)21(|<--x . 证明 因为∀ε >0, ∃εδ21=, 当δ<--<|)21(|0x 时, 有ε<-+-212413x x , 所以21241lim 321=+--→x x x . 2. 根据函数极限的定义证明:(1)2121lim 33=+∞→x xx ; 分析 因为333333||21212121x x x x x x =-+=-+, 所以要使ε<-+212133x x , 只须ε<3||21x , 即321||ε>x . 证明 因为∀ε >0, ∃321ε=X , 当|x |>X 时, 有 ε<-+212133x x , 所以2121lim 33=+∞→x xx . (2)0sin lim =+∞→xx x .分析 因为x xx x x 1|s i n |0s i n≤=-.所以要使ε<-0sin xx , 只须ε<x1, 即21ε>x . 证明 因为∀ε>0, ∃21ε=X , 当x >X 时, 有ε<-0s i n xx , 所以0sin lim =+∞→xx x .3. 当x →2时, y =x 2→4. 问δ等于多少, 使当|x -2|<δ时, |y -4|<0.001? 解 由于当x →2时, |x -2|→0, 故可设|x -2|<1, 即1<x <3. 要使|x 2-4|=|x +2||x -2|<5|x -2|<0.001, 只要0002.05001.0|2|=<-x .取δ=0.0002, 则当0<|x -2|<δ时, 就有|x 2-4|<0. 001.4. 当x →∞时, 13122→+-=x x y , 问X 等于多少, 使当|x |>X 时, |y -1|<0.01?解 要使01.034131222<+=-+-x x x , 只要397301.04||=->x , 故397=X . 5. 证明函数f (x )=|x |当x →0时极限为零. 证明 因为|f (x )-0|=||x |-0|=|x |=|x -0|, 所以要使|f (x )-0|<ε, 只须|x |<ε.因为对∀ε>0, ∃δ=ε, 使当0<|x -0|<δ, 时有 |f (x )-0|=||x |-0|<ε, 所以0||lim 0=→x x .6. 求,)(x x x f = xx x ||)(=ϕ当x →0时的左﹑右极限, 并说明它们在x →0时的极限是否存在.证明 因为11lim lim )(lim 000===---→→→x x x x x x f , 11lim lim )(lim 000===+++→→→x x x x x x f ,)(lim )(lim 0x f x f x x +→→=-,所以极限)(lim 0x f x →存在.因为1lim ||lim )(lim 000-=-==---→→→xx x x x x x x ϕ,1lim||lim )(lim 000===+++→→→x x x x x x x x ϕ, )(lim )(lim 0x x x x ϕϕ+→→≠-,所以极限)(lim 0x x ϕ→不存在.7. 证明: 若x →+∞及x →-∞时, 函数f (x )的极限都存在且都等于A , 则A x f x =∞→)(lim .证明 因为A x f x =-∞→)(lim , A x f x =+∞→)(lim , 所以∀ε>0,∃X 1>0, 使当x <-X 1时, 有|f (x )-A |<ε ; ∃X 2>0, 使当x >X 2时, 有|f (x )-A |<ε .取X =max{X 1, X 2}, 则当|x |>X 时, 有|f (x )-A |<ε , 即A x f x =∞→)(lim .8. 根据极限的定义证明: 函数f (x )当x →x 0 时极限存在的充分必要条件是左极限、右极限各自存在并且相等.证明 先证明必要性. 设f (x )→A (x →x 0), 则∀ε>0, ∃δ>0, 使当0<|x -x 0|<δ 时, 有 |f (x )-A |<ε .因此当x 0-δ<x <x 0和x 0<x <x 0+δ 时都有 |f (x )-A |<ε .这说明f (x )当x →x 0时左右极限都存在并且都等于A . 再证明充分性. 设f (x 0-0)=f (x 0+0)=A , 则∀ε>0, ∃δ1>0, 使当x 0-δ1<x <x 0时, 有| f (x )-A <ε ; ∃δ2>0, 使当x 0<x <x 0+δ2时, 有| f (x )-A |<ε .取δ=min{δ1, δ2}, 则当0<|x -x 0|<δ 时, 有x 0-δ1<x <x 0及x 0<x <x 0+δ2 , 从而有 | f (x )-A |<ε , 即f (x )→A (x →x 0).9. 试给出x →∞时函数极限的局部有界性的定理, 并加以证明.解 x →∞时函数极限的局部有界性的定理: 如果f (x )当x →∞时的极限存在, 则存在X >0及M >0, 使当|x |>X 时, |f (x )|<M .证明 设f (x )→A (x →∞), 则对于ε =1, ∃X >0, 当|x |>X 时, 有|f (x )-A |<ε =1. 所以 |f (x )|=|f (x )-A +A |≤|f (x )-A |+|A |<1+|A |.这就是说存在X >0及M >0, 使当|x |>X 时, |f (x )|<M , 其中M =1+|A |. 习题1-41. 两个无穷小的商是否一定是无穷小?举例说明之. 解 不一定.例如, 当x →0时, α(x )=2x , β(x )=3x 都是无穷小, 但32)()(lim 0=→x x x βα, )()(x x βα不是无穷小.2. 根据定义证明:(1)392+-=x xy 当x →3时为无穷小;(2)xx y 1sin =当x →0时为无穷小.证明 (1)当x ≠3时|3|39||2-=+-=x x x y . 因为∀ε>0, ∃δ=ε , 当0<|x -3|<δ时, 有εδ=<-=+-=|3|39||2x x x y ,所以当x →3时392+-=x xy 为无穷小.(2)当x ≠0时|0||1sin |||||-≤=x xx y . 因为∀ε>0, ∃δ=ε , 当0<|x -0|<δ时, 有εδ=<-≤=|0||1sin |||||x xx y ,所以当x →0时xx y 1sin =为无穷小.3. 根据定义证明: 函数x x y 21+=为当x →0时的无穷大. 问x 应满足什么条件, 能使|y |>104?证明 分析2||11221||-≥+=+=x x x x y , 要使|y |>M , 只须M x >-2||1, 即21||+<M x .证明 因为∀M >0, ∃21+=M δ, 使当0<|x -0|<δ时, 有M x x >+21,所以当x →0时, 函数xx y 21+=是无穷大.取M =104, 则21014+=δ. 当2101|0|04+<-<x 时, |y |>104. 4. 求下列极限并说明理由:(1)xx x 12lim +∞→;(2)xxx --→11lim 20.解 (1)因为xx x 1212+=+, 而当x →∞ 时x 1是无穷小, 所以212lim =+∞→x x x .(2)因为x x x +=--1112(x ≠1), 而当x →0时x 为无穷小, 所以111lim 20=--→x x x .5. 根据函数极限或无穷大定义, 填写下表:f (x )→Af (x )→∞f (x )→+∞f (x )→-∞x→x 0 ∀ε>0, ∃δ>0, 使 当0<|x -x 0|<δ时,有恒|f (x )-A |<ε.x →x 0+x →x 0-x →∞∀ε>0, ∃X >0, 使当|x |>X 时,有恒|f (x )|>M .x →+∞x →-∞解 f (x )→A f (x )→∞ f (x )→+∞ f (x )→-∞ x →x 0∀ε>0, ∃δ>0, 使当0<|x -x 0|<δ∀M >0, ∃δ>0, 使当∀M >0, ∃δ>0, 使当∀M >0, ∃δ>0, 使当时, 有恒|f (x )-A |<ε.0<|x -x 0|<δ时, 有恒|f (x )|>M .0<|x -x 0|<δ时, 有恒f (x )>M .0<|x -x 0|<δ时, 有恒f (x )<-M .x→x 0+ ∀ε>0, ∃δ>0,使当0<x -x 0<δ时, 有恒|f (x )-A |<ε.∀M >0,∃δ>0, 使当0<x -x 0<δ时, 有恒|f (x )|>M .∀M >0, ∃δ>0, 使当0<x -x 0<δ时, 有恒f (x )>M .∀M >0, ∃δ>0, 使当0<x -x 0<δ时, 有恒f (x )<-M .x →x 0- ∀ε>0, ∃δ>0,使当0<x 0-x <δ时, 有恒|f (x )-A |<ε.∀M >0,∃δ>0, 使当0<x 0-x <δ时, 有恒|f (x )|>M .∀M >0, ∃δ>0, 使当0<x 0-x <δ时, 有恒f (x )>M .∀M >0, ∃δ>0, 使当0<x 0-x <δ时, 有恒f (x )<-M .x →∞∀ε>0, ∃X >0, 使当|x |>X 时, 有恒|f (x )-A |<ε.∀ε>0, ∃X >0, 使当|x |>X 时, 有恒|f (x )|>M .∀ε>0, ∃X >0, 使当|x |>X 时, 有恒f (x )>M .∀ε>0, ∃X >0, 使当|x |>X 时, 有恒f (x )<-M .x →+∞∀ε>0, ∃X >0, 使当x >X 时, 有恒|f (x )-A |<ε.∀ε>0, ∃X >0, 使当x >X 时, 有恒|f (x )|>M .∀ε>0, ∃X >0, 使当x >X 时, 有恒f (x )>M .∀ε>0, ∃X >0, 使当x >X 时, 有恒f (x )<-M .x →-∞∀ε>0, ∃X >0,使当x <-X 时, 有恒|f (x )-A |<ε.∀ε>0, ∃X >0,使当x <-X 时, 有恒|f (x )|>M .∀ε>0, ∃X >0,使当x <-X 时, 有恒f (x )>M .∀ε>0, ∃X >0,使当x <-X 时, 有恒f (x )<-M .6. 函数y =x cos x 在(-∞, +∞)内是否有界?这个函数是否为当x →+∞ 时的无穷大?为什么?解 函数y =x cos x 在(-∞, +∞)内无界.这是因为∀M >0, 在(-∞, +∞)内总能找到这样的x , 使得|y (x )|>M . 例如y (2k π)=2k π cos2k π=2k π (k =0, 1, 2, ⋅ ⋅ ⋅),当k 充分大时, 就有| y (2k π)|>M .当x →+∞ 时, 函数y =x cos x 不是无穷大.这是因为∀M >0, 找不到这样一个时刻N , 使对一切大于N 的x , 都有|y (x )|>M . 例如0)22cos()22()22(=++=+ππππππk k k y (k =0, 1, 2, ⋅ ⋅ ⋅),对任何大的N , 当k 充分大时, 总有N k x >+=22ππ, 但|y (x )|=0<M .7. 证明: 函数xx y 1sin 1=在区间(0, 1]上无界, 但这函数不是当x →0+时的无穷大.证明 函数x x y 1sin 1=在区间(0, 1]上无界. 这是因为∀M >0, 在(0, 1]中总可以找到点x k , 使y (x k )>M . 例如当221ππ+=k x k (k =0, 1, 2, ⋅ ⋅ ⋅)时, 有22)(ππ+=k x y k ,当k 充分大时, y (x k )>M .当x →0+ 时, 函数xx y 1sin 1=不是无穷大. 这是因为∀M >0, 对所有的δ>0, 总可以找到这样的点x k , 使0<x k <δ, 但y (x k )<M . 例如可取πk x k 21=(k =0, 1, 2, ⋅ ⋅ ⋅),当k 充分大时, x k <δ, 但y (x k )=2k πsin2k π=0<M . 习题1-51. 计算下列极限:(1)35lim22-+→x x x ;解 9325235lim222-=-+=-+→x x x . (2)13lim 223+-→x x x ; 解 01)3(3)3(13lim 22223=+-=+-→x x x . (3)112lim 221-+-→x x x x ;解 02011lim )1)(1()1(lim 112lim 121221==+-=+--=-+-→→→x x x x x x x x x x x . (4)xx xx x x 2324lim 2230++-→;解 2123124lim 2324lim 202230=++-=++-→→x x x x x x x x x x .(5)hx h x h 220)(lim -+→;解 x h x hx h hx x h x h x h h h 2)2(lim 2lim )(lim 02220220=+=-++=-+→→→. (6))112(lim 2x x x +-∞→;解 21lim 1lim2)112(lim 22=+-=+-∞→∞→∞→x x x x x x x . (7)121lim 22---∞→x x x x ;解 2111211lim 121lim 2222=---=---∞→∞→xx x x x x x x . (8)13lim 242--+∞→x x xx x ;解 013lim 242=--+∞→x x x x x (分子次数低于分母次数, 极限为零). 或 012111lim 13lim 4232242=--+=--+∞→∞→xx x x x x x x x x . (9)4586lim 224+-+-→x x x x x ; 解 32142412lim )4)(1()4)(2(lim 4586lim 44224=--=--=----=+-+-→→→x x x x x x x x x x x x x .(10))12)(11(lim 2x x x -+∞→;解 221)12(lim )11(lim )12)(11(lim 22=⨯=-⋅+=-+∞→∞→∞→x x x x x x x . (11))21 41211(lim nn +⋅⋅⋅+++∞→;解 2211)21(1lim )21 41211(lim 1=--=+⋅⋅⋅++++∞→∞→n n n n . (12)2)1( 321limn n n -+⋅⋅⋅+++∞→;解 211lim 212)1(lim )1( 321lim 22=-=-=-+⋅⋅⋅+++∞→∞→∞→n n n n n n n n n n .(13)35)3)(2)(1(limnn n n n +++∞→; 解 515)3)(2)(1(lim3=+++∞→n n n n n (分子与分母的次数相同, 极限为 最高次项系数之比).或 51)31)(21)(11(lim 515)3)(2)(1(lim3=+++=+++∞→∞→n n n n n n n n n . (14))1311(lim 31xx x ---→;解 )1)(1()2)(1(lim )1)(1(31lim )1311(lim 2122131x x x x x x x x x x x x x x x ++-+--=++--++=---→→→ 112l i m 21-=+++-=→x x x x .2. 计算下列极限:(1)2232)2(2lim -+→x x x x ;解 因为01602)2(lim 2322==+-→x x x x , 所以∞=-+→2232)2(2lim x x x x . (2)12lim 2+∞→x xx ;解 ∞=+∞→12lim2x x x (因为分子次数高于分母次数). (3))12(lim 3+-∞→x x x .解 ∞=+-∞→)12(lim 3x x x (因为分子次数高于分母次数).3. 计算下列极限:(1)xx x 1sin lim 20→;解 01sin lim 20=→xx x (当x →0时, x 2是无穷小, 而x 1sin 是有界变量).(2)xx x arctan lim ∞→.解 0arctan 1lim arctan lim =⋅=∞→∞→x x x x x x (当x →∞时, x 1是无穷小,而arctan x 是有界变量). 4. 证明本节定理3中的(2).习题1-51. 计算下列极限:(1)35lim22-+→x x x ;解 9325235lim222-=-+=-+→x x x . (2)13lim 223+-→x x x ; 解 01)3(3)3(13lim 22223=+-=+-→x x x . (3)112lim 221-+-→x x x x ;解 02011lim )1)(1()1(lim 112lim 121221==+-=+--=-+-→→→x x x x x x x x x x x . (4)xx xx x x 2324lim 2230++-→;解 2123124lim 2324lim 202230=++-=++-→→x x x x x x x x x x . (5)hx h x h 220)(lim -+→;解 x h x hx h hx x h x h x h h h 2)2(lim 2lim )(lim 02220220=+=-++=-+→→→. (6))112(lim 2xx x +-∞→; 解 21lim 1lim2)112(lim 22=+-=+-∞→∞→∞→x x x x x x x . (7)121lim 22---∞→x x x x ;解 2111211lim 121lim 2222=---=---∞→∞→xx x x x x x x . (8)13lim 242--+∞→x x xx x ;解 013lim 242=--+∞→x x x x x (分子次数低于分母次数, 极限为零).或 012111lim 13lim 4232242=--+=--+∞→∞→xx x x x x x x x x .(9)4586lim 224+-+-→x x x x x ; 解 32142412lim )4)(1()4)(2(lim 4586lim 44224=--=--=----=+-+-→→→x x x x x x x x x x x x x .(10))12)(11(lim 2x x x -+∞→;解 221)12(lim )11(lim )12)(11(lim 22=⨯=-⋅+=-+∞→∞→∞→x x x x x x x . (11))21 41211(lim n n +⋅⋅⋅+++∞→; 解 2211)21(1lim )21 41211(lim 1=--=+⋅⋅⋅++++∞→∞→n n n n .(12)2)1( 321limn n n -+⋅⋅⋅+++∞→;解 211lim 212)1(lim )1( 321lim 22=-=-=-+⋅⋅⋅+++∞→∞→∞→n n n n n n n n n n . (13)35)3)(2)(1(lim n n n n n +++∞→;解 515)3)(2)(1(lim 3=+++∞→nn n n n (分子与分母的次数相同, 极限为 最高次项系数之比).或 51)31)(21)(11(lim 515)3)(2)(1(lim3=+++=+++∞→∞→n n n n n n n n n .(14))1311(lim 31xx x ---→;解 )1)(1()2)(1(lim )1)(1(31lim )1311(lim 2122131x x x x x x x x x x x x x x x ++-+--=++--++=---→→→ 112l i m 21-=+++-=→x x x x . 2. 计算下列极限:(1)2232)2(2lim -+→x x x x ; 解 因为01602)2(lim 2322==+-→x x x x , 所以∞=-+→2232)2(2limx x x x .(2)12lim 2+∞→x x x ;解 ∞=+∞→12lim2x x x (因为分子次数高于分母次数). (3))12(lim 3+-∞→x x x .解 ∞=+-∞→)12(lim 3x x x (因为分子次数高于分母次数).3. 计算下列极限:(1)xx x 1sin lim 20→;解 01sin lim 20=→xx x (当x →0时, x 2是无穷小, 而x 1sin 是有界变量).(2)xx x arctan lim ∞→.解 0arctan 1lim arctan lim =⋅=∞→∞→x x x x x x (当x →∞时, x 1是无穷小,而arctan x 是有界变量). 4. 证明本节定理3中的(2).习题 1-71. 当x →0时, 2x -x 2 与x 2-x 3相比, 哪一个是高阶无穷小?解 因为02lim 2lim202320=--=--→→xx x x x x x x x , 所以当x →0时, x 2-x 3是高阶无穷小, 即x 2-x 3=o (2x -x 2).2. 当x →1时, 无穷小1-x 和(1)1-x 3, (2))1(212x -是否同阶?是否等价?解 (1)因为3)1(lim 1)1)(1(lim 11lim212131=++=-++-=--→→→x x x x x x x x x x x , 所以当x →1时, 1-x 和1-x 3是同阶的无穷小, 但不是等价无穷小.(2)因为1)1(lim 211)1(21lim 121=+=--→→x x x x x , 所以当x →1时, 1-x 和)1(212x -是同阶的无穷小, 而且是等价无穷小.3. 证明: 当x →0时, 有: (1) arctan x ~x ;(2)2~1sec 2xx -.证明 (1)因为1tan limarctan lim 00==→→y yxx y x (提示: 令y =arctan x , 则当x →0时, y →0), 所以当x →0时, arctan x ~x .(2)因为1)22sin 2(lim 22sin 2lim cos cos 1lim 2211sec lim 202202020===-=-→→→→x xx x x x x xx x x x x , 所以当x →0时, 2~1s e c2x x -. 4. 利用等价无穷小的性质, 求下列极限: (1)xx x 23tan lim 0→;(2)mn x x x )(sin )sin(lim 0→(n , m 为正整数);(3)x x x x 30sin sin tan lim -→; (4))1sin 1)(11(tan sin lim320-+-+-→x x x x x . 解 (1)2323lim 23tan lim 00==→→x x x x x x .(2)⎪⎩⎪⎨⎧<∞>===→→mn m n m n x x x x mn x m n x 0 1lim )(sin )sin(lim00. (3)21cos 21lim sin cos cos 1lim sin )1cos 1(sin lim sin sin tan lim 220203030==-=-=-→→→→x x x x x x xx x x x x x x x x . (4)因为32221)2(2~2s i n t a n 2)1(c o s t a n t a n s i n x x x x x x x x x -=⋅--=-=-(x →0),23232223231~11)1(11x x x x x ++++=-+(x →0), x x x x x ~s i n ~1s i n 1s i n 1s i n1++=-+(x →0),所以 33121l i m )1s i n 1)(11(tan sin lim 230320-=⋅-=-+-+-→→xx x x x x x x x .5. 证明无穷小的等价关系具有下列性质: (1) α ~α (自反性);(2) 若α ~β, 则β~α(对称性); (3)若α ~β, β~γ, 则α~γ(传递性). 证明 (1)1lim =αα, 所以α ~α ;(2) 若α ~β, 则1lim =βα, 从而1lim =αβ. 因此β~α ;(3) 若α ~β, β~γ, 1lim lim lim =⋅=βαγβγα. 因此α~γ.习题1-81. 研究下列函数的连续性, 并画出函数的图形:(1)⎩⎨⎧≤<-≤≤=21 210 )(2x x x x x f ;解 已知多项式函数是连续函数, 所以函数f (x )在[0, 1)和(1, 2]内是连续的. 在x =1处, 因为f (1)=1, 并且1lim )(lim 211==--→→x x f x x , 1)2(lim )(lim 11=-=++→→x x f x x . 所以1)(lim 1=→x f x , 从而函数f (x )在x =1处是连续的.综上所述,函数f (x )在[0, 2]上是连续函数.(2)⎩⎨⎧>≤≤-=1|| 111 )(x x x x f .解 只需考察函数在x =-1和x =1处的连续性. 在x =-1处, 因为f (-1)=-1, 并且)1(11l i m )(l i m 11-≠==---→-→f x f x x , )1(1lim )(lim 11-=-==++-→-→f x x f x x ,所以函数在x =-1处间断, 但右连续.在x =1处, 因为f (1)=1, 并且1l i m )(l i m 11==--→→x x f x x =f (1), 11lim )(lim 11==++→→x x x f =f (1), 所以函数在x =1处连续.综合上述讨论, 函数在(-∞, -1)和(-1, +∞)内连续, 在x =-1处间断, 但右连续. 2. 下列函数在指出的点处间断, 说明这些间断点属于哪一类, 如果是可去间断点, 则补充或改变函数的定义使它连续:(1)23122+--=x x xy , x =1, x =2;解 )1)(2()1)(1(23122---+=+--=x x x x x x x y . 因为函数在x =2和x =1处无定义, 所以x =2和x =1是函数的间断点.因为∞=+--=→→231lim lim 2222x x xy x x , 所以x =2是函数的第二类间断点;因为2)2()1(limlim 11-=-+=→→x x y x x , 所以x =1是函数的第一类间断点, 并且是可去间断点. 在x =1处, 令y =-2, 则函数在x =1处成为连续的.(2)x x y tan =, x =k , 2ππ+=k x (k =0, ±1, ±2, ⋅ ⋅ ⋅);解 函数在点x =k π(k ∈Z)和2ππ+=k x (k ∈Z)处无定义, 因而这些点都是函数的间断点.因∞=→x x k x tan lim π(k ≠0), 故x =k π(k ≠0)是第二类间断点;因为1tan lim 0=→x x x ,0tan lim2=+→x x k x ππ(k ∈Z), 所以x =0和2ππ+=k x (k ∈Z) 是第一类间断点且是可去间断点.令y |x =0=1, 则函数在x =0处成为连续的;令2 ππ+=k x 时, y =0, 则函数在2ππ+=k x 处成为连续的.(3)xy 1cos 2=, x =0;解 因为函数x y 1cos 2=在x =0处无定义, 所以x =0是函数xy 1cos 2=的间断点. 又因为xx 1cos lim 20→不存在, 所以x =0是函数的第二类间断点. (4)⎩⎨⎧>-≤-=1311x x x x y , x =1.解 因为0)1(lim )(lim 11=-=--→→x x f x x 2)3(lim )(lim 11=-=++→→x x f x x , 所以x =1是函数的第一类不可去间断点.3. 讨论函数x x x x f nnn 2211lim)(+-=∞→的连续性, 若有间断点, 判别其类型. 解 ⎪⎩⎪⎨⎧<=>-=+-=∞→1|| 1|| 01|| 11lim )(22x x x x x x x x x f nn n . 在分段点x =-1处, 因为1)(lim )(lim 11=-=---→-→x x f x x , 1lim )(lim 11-==++-→-→x x f x x , 所以x =-1为函数的第一类不可去间断点.在分段点x =1处, 因为1lim )(lim 11==--→→x x f x x , 1)(lim )(lim 11-=-=++→→x x f x x , 所以x =1为函数的第一类不可去间断点.4. 证明: 若函数f (x )在点x 0连续且f (x 0)≠0, 则存在x 0的某一邻域U (x 0), 当x ∈U (x 0)时, f (x )≠0.证明 不妨设f (x 0)>0. 因为f (x )在x 0连续, 所以0)()(lim 00>=→x f x f x x , 由极限的局部保号性定理, 存在x 0的某一去心邻域)(0x U , 使当x ∈)(0x U时f (x )>0, 从而当x ∈U (x 0)时, f (x )>0. 这就是说, 则存在x 0的某一邻域U (x 0), 当x ∈U (x 0)时, f (x )≠0.5. 试分别举出具有以下性质的函数f (x )的例子:(1)x =0, ±1, ±2, 21±, ⋅ ⋅ ⋅, ±n , n1±, ⋅ ⋅ ⋅是f (x )的所有间断点, 且它们都是无穷间断点; 解 函数x x x f ππcsc )csc()(+=在点x =0, ±1, ±2, 21±, ⋅ ⋅ ⋅, ±n , n 1±, ⋅ ⋅ ⋅处是间断的且这些点是函数的无穷间断点.(2)f (x )在R 上处处不连续, 但|f (x )|在R 上处处连续;解 函数⎩⎨⎧∉∈-=Q Qx x x f 1 1)(在R 上处处不连续, 但|f (x )|=1在R 上处处连续.(3)f (x )在R 上处处有定义, 但仅在一点连续.解 函数⎩⎨⎧∉-∈=Q Q x x x x x f)(在R 上处处有定义, 它只在x =0处连续.习题1-91. 求函数633)(223-+--+=x x x x x x f 的连续区间, 并求极限)(lim 0x f x →, )(lim 3x f x -→及)(lim 2x f x →.解 )2)(3()1)(1)(3(633)(223-++-+=-+--+=x x x x x x x x x x x f , 函数在(-∞, +∞)内除点x =2和x =-3外是连续的, 所以函数f (x )的连续区间为(-∞, -3)、(-3, 2)、(2, +∞).在函数的连续点x =0处, 21)0()(lim 0==→f x f x . 在函数的间断点x =2和x =-3处, ∞=-++-+=→→)2)(3()1)(1)(3(lim)(lim 22x x x x x x f x x , 582)1)(1(lim)(lim 33-=-+-=-→-→x x x x f x x . 2. 设函数f (x )与g (x )在点x 0连续, 证明函数 ϕ(x )=max{f (x ), g (x )}, ψ(x )=min{f (x ), g (x )} 在点x 0也连续.证明 已知)()(lim 00x f x f x x =→, )()(lim 00x g x g x x =→.可以验证] |)()(|)()([21)(x g x f x g x f x -++=ϕ,] |)()(|)()([21)(x g x f x g x f x --+=ψ.因此 ] |)()(|)()([21)(00000x g x f x g x f x -++=ϕ,] |)()(|)()([21)(00000x g x f x g x f x --+=ψ.因为] |)()(|)()([21lim )(lim 00x g x f x g x f x x x x x -++=→→ϕ] |)(lim )(lim |)(lim )(lim [210000x g x f x g x f x x x x x x x x →→→→-++=] |)()(|)()([210000x g x f x g x f -++==ϕ(x 0),所以ϕ(x )在点x 0也连续.同理可证明ψ(x )在点x 0也连续.3. 求下列极限: (1)52lim 20+-→x x x ;。
习题答案(第六版)

兰州交通大学《通信原理》精品课程第一章绪论本章主要内容:(1)通信系统的模型与基本概念(2)通信技术的现状与发展(3)信息的度量(4)通信系统的主要性能指标本章重点:1.通信系统的一般模型与数字通信系统模型2.离散信源的信息量、熵的计算3.数字通信系统的主要性能指标:码元传输速率与信息传输速率以及它们的关系、误码率与误信率本章练习题:1-1.已知英文字母e出现的概率为,x出现的概念为,试求e和x的信息量。
查看参考答案o1-2.某信源符号集由A,B,C,D和E组成,设每一符号独立出现,其出现概率分别为14,18,1 8,316和516。
试求该信息源符号的平均信息量。
查看参考答案o1-3.设有4个符号,其中前3个符号的出现概率分别为14,18,18,且各符号的出现是相对独立的。
试计算该符号集的平均信息量。
查看参考答案o1-4.一个由字母A 、B 、C 、D 组成的字,对于传输的每一个字母用二进制脉冲编码,00代替A ,01代替B ,10代替C ,11代替D ,每个脉冲宽度为5ms .(1)不同的字母是等可能出现时,试计算传输的平均信息速率; (2)若每个字母出现的可能性分别为103,41,41,51====D C B A P P P P试计算传输的平均信息速率。
查看参考答案o1-5.国际摩尔斯电码用“点”和“划”的序列发送英文字母,“划”用持续3单位的电流脉冲表示,“点”用持续1个单位的电流脉冲表示;且“划”出现的概率是“点”出现概率的13。
(1)计算“点”和“划”的信息量; (2)计算“点”和“划”的平均信息量。
查看参考答案o1-6.设一信息源的输出由128个不同的符号组成,其中16个出现的概率为132,其余112个出现概率为1224。
信息源每秒发出1000个符号,且每个符号彼此独立。
试计算该信息源的平均信息速率。
查看参考答案o1-7.设一数字传输系统传送二进制码元的速率为2400B,试求该系统的信息速率;若该系统改为传送16进制信号码元,码元速率不变,则这时的系统信息速率为多少(设各码元独立等概率出现)查看参考答案o1-8.若题1―2中信息源以1000B速率传送信息。
语文习题册第六版 下册 参考答案

语文习题册(第六版下册) 参考答案第一单元1 雨中登泰山一、基础知识1、C2、C3、A4.A5.(1)不就是就就是(2)不但还(3)只有才(4)不管都6.李健吾登泰山而小天下会当凌绝顶二、课文理解1.B2.D三、语段精读(一)1、B2、B3、D4.C5、D6.白纱比喻水气花纹比喻水流(二)1、本小题选项设计有误,正确答案为(4)(5)(1)(2)(6)(3)。
也可让学生将C 选项中的(1)(5)顺序颠倒,这样就可选C。
2.B3、A14.C四、拓展训练1.(1)× (2)×(3)√2.这些事物可以形容日出时色彩的浓郁、变幻与奇丽,把光的色彩表现得更加强烈而鲜明,更能引起美的想象。
3、用这些动物来比喻,显示了一种极其活跃,而又变幻莫测的日出动态过程,更好地描写了日出时候景色的奇丽。
2 故都的秋一、基础知识1、B2、(1)冷落、寂寞(2)着,穿(衣) (3)抑止(4)古时指到了暮年仍不得志的知识分子(5)长久3、C4、(1)排比(2)比喻(3)拟人(4)反问5、(1)创造社沉沦(2)秋尽江南草木凋(3)欧阳修秋声赋二、课文理解1、秋晨静观秋槐落蕊秋蝉残鸣雨后话凉秋枣奇树(意思答对即可)。
2.这样写,就把自己对于秋的感受提高到一个理性的高度,抒发对于北国之秋的特殊情感。
这段文字的中心句:“足见有感觉的动物,有情趣的人类,对于秋,总就是一样的能特别引起深沉,幽远、严厉、萧索的感触来的。
”3、C三、语段精读(一)1.B2.A3.C4、C25、C(二)1、B2.A3.C4.C(三)1.南国之秋“色彩不浓,回味不永”。
2、对比手法。
3.排比句“廿四桥的明月,钱塘江的秋潮,普陀山的凉雾,荔枝湾的残荷”,从多个角度说明南方之秋“色彩不浓,回味不永”;排比句“正像就是黄酒之与白干,稀饭之与馍馍,鲈鱼之与大蟹,黄犬之与骆驼”,酣畅淋漓地对南国之秋与北国之秋进行对比描写。
比喻句“南国之秋,……比起北国的秋来,正像就是黄酒之与白干,稀饭之与馍馍,鲈鱼之与大蟹,黄犬之与骆驼”,表现了南方之秋秋味的平淡、稀薄、柔软与范围的狭小,北国之秋秋味的浓烈、厚实、刚强与范围的广大。
机械制图习题集答案(第六版)大连理工大学高等教育出版社

3-4-4 3-4-5 3-5-1 3-5-2 3-5-3 3-5-4 3-5-5 3-5-6 3-6-1
3-6-2 3-10-1 3-6-3 3-10-2 3-7-1 3-10-3 3-7-2 3-10-4 3-7-3 3-10-5 3-8-1 3-10-6 3-8-2 3-11-1 3-9-1 3-11-2 3-9-2 3-12-1
2021/6/25
5-3-2 5-3-3 5-3-4 5-4-1 5-4-2 5-4-3 5-4-4 5-5-1 5-5-2
5-6-1 5-6-2 5-7-1 5-7-2 5-7-3 5-7-4 5-8-1 5-8-2 5-8-3
5-8-4 5-8-5 5-8-6 5-9 5-10 5-11 5-12 5-13-1 5-13-2
1-6-2
1-4-2-4
1-5-1-1
1-3-1-1.在指定位置,仿照示例画出直线、圆、斜线
2021/6/25
1-3-1-2.在指定位置,仿照示例画出直线、圆、斜线。
2021/6/25
1-3-1-3.在指定位置,仿照示例画出直线、圆、斜线。
2021/6/25
1-3-2-1.用作图法作圆的内接正五边形。
中点
2021/6/25
1-3-2-2.用作图法作圆的内接正六边形。
R
2021/6/25
1-3-3-1.在指定位置, 用同心圆法画椭圆(长轴60 mm、短轴 40
mm)。
2021/6/25
1-3-3-2.在指定位置, 用四心法画椭圆。
2021/6/25
1-3-4.参照图形给出的尺寸,用 1 : 1的比例在右边位置画出 图形
5-13-3 5-13-4 5-14-1 5-14-2 5-14-3 5-14-4 5-15-1 5-15-2 5-16-1
同济大学第六版高等数学上下册课后习题答案5-1

同济大学第六版高等数学上下册课后习题答案5-11. 利用定积分定义计算由抛物线y =x 2+1, 两直线x =a 、x =b (b >a )及横轴所围成的图形的面积.解 第一步: 在区间[a , b ]内插入n -1个分点i nab a x i -+=(i =1, 2, ⋅ ⋅ ⋅, n -1), 把区间[a , b ]分成n 个长度相等的小区间, 各个小区间的长度为: nab x i -=∆(i =1, 2, ⋅ ⋅ ⋅, n ). 第二步: 在第i 个小区间[x i -1, x i ] (i =1, 2, ⋅ ⋅ ⋅, n )上取右端点i nab a x i i -+==ξ, 作和 nab i n a b a x f S ni i i ni n -⋅+-+=∆=∑∑==]1)[()(211ξ ∑=+-+-+-=n i i na b i n a b a a n a b 12222]1)()(2[]6)12)(1()(2)1()(2[)(222n n n n na b n n n a b a na n a b +++⋅-++⋅-+-= ]16)12)(1()()1)(()[(222+++-++-+-=nn n a b n n a b a a a b . 第三步: 令λ=max{∆x 1, ∆x 2, ⋅ ⋅ ⋅ , ∆x n }nab -=, 取极限得所求面积 ∑⎰=→∆==ni i i ba x f dx x f S 10)(lim )(ξλ]16)12)(1()()1)(()[(lim 222+++-++-+-=∞→nn n a b n n a b a a a b n a b a b a b a b a a a b -+-=+-+-+-=)(31]1)(31)()[(3322.2. 利用定积分定义计算下列积分:(1)xdx ba ⎰(a <b ); (2)dx e x ⎰10.解 (1)取分点为i n a b a x i -+=(i =1, 2, ⋅ ⋅ ⋅, n -1), 则nab x i -=∆(i =1, 2, ⋅ ⋅ ⋅, n ). 在第i 个小区间上取右端点i nab a x i i -+==ξ (i =1, 2, ⋅ ⋅ ⋅, n ). 于是∑∑⎰=∞→=∞→-⋅-+=∆=ni n n i i i n ba nab i n a b a x xdx 11)(lim lim ξ )(21]2)1()()([lim )(22222a b n n n a b a b a a b n -=+-+--=∞→. (2)取分点为n i x i =(i =1, 2, ⋅ ⋅ ⋅, n -1), 则nx i 1=∆(i =1, 2, ⋅ ⋅ ⋅, n ). 在第i 个小区间上取右端点nix i i ==ξ (i =1, 2, ⋅ ⋅ ⋅, n ). 于是) (1lim 1lim 21110n n n n n n i n i n xe e e nn e dx e +⋅⋅⋅++==∞→=∞→∑⎰1)1(]1[lim1])(1[1lim 11111-=--=--⋅=∞→∞→e e n e e e e e nnn n nn n n n .3. 利用定积分的几何意义 说明下列等式: (1)1210=⎰xdx ; (2)41102π=-⎰dx x ;(3)⎰-=ππ0sin xdx ;(4)⎰⎰=-2022cos 2cos πππxdx xdx .解 (1)⎰102xdx 表示由直线y =2x 、x 轴及直线x =1所围成的面积, 显然面积为1.(2)⎰-1021dx x 表示由曲线21x y -=、x 轴及y 轴所围成的四分之一圆的面积, 即圆x 2+y 2=1的面积的41:41411212ππ=⋅⋅=-⎰dx x . (3)由于y =sin x 为奇函数, 在关于原点的对称区间[-π, π]上与x 轴所夹的面积的代数和为零, 即⎰-=ππ0sin xdx .(4)⎰-22cos ππxdx 表示由曲线y =cos x 与x 轴上]2,2[ππ-一段所围成的图形的面积. 因为cos x为偶函数, 所以此图形关于y 轴对称. 因此图形面积的一半为⎰20cos πxdx , 即⎰⎰=-2022cos 2cos πππxdx xdx .4. 水利工程中要计算拦水闸门所受的水压力, 已知闸门上水的压强p (单位面积上的压力大小)是水深h 的函数, 且有p =9⋅8h (kN/m 2). 若闸门高H =3m , 宽L =2m , 求水面与闸门顶相齐时闸门所受的水压力P .解 建立坐标系如图. 用分点i nHx i =(i =1, 2, ⋅ ⋅ ⋅, n -1)将区间[0, H ]分为n 分个小区间, 各小区间的长为nHx i =∆(i =1, 2, ⋅ ⋅ ⋅, n ). 在第i 个小区间[x i -1, x i ]上, 闸门相应部分所受的水压力近似为 ∆P i =9.8x i l ⋅∆x i . 闸门所受的水压力为22118.42)1(lim 8.9lim 8.98.9lim H L nn n H L n Hi n H L x L x P n ni n ni i i n ⋅=+⋅=⋅=∆⋅⋅=∞→=∞→=∞→∑∑.将L =2, H =3代入上式得P =88.2(千牛).5. 证明定积分性质: (1)⎰⎰=ba ba dx x f k dx x kf )()(; (2)ab dx dx ba ba -==⋅⎰⎰1.证明 (1)⎰∑∑⎰=∆=∆==→=→ba ni i i ni i i ba dx x f k x f k x kf dx x kf )()(lim )(lim )(1010ξξλλ.(2)a b a b x x dx ni i ni i ba -=-=∆=∆⋅=⋅→=→=→∑∑⎰)(lim lim 1lim 101010λλλ.6. 估计下列各积分的值: (1)⎰+412)1(dx x ; (2)⎰+ππ4542)sin 1(dx x ;(3)⎰331arctan xdx x ;(4)⎰-022dx e xx.解 (1)因为当1≤x ≤4时, 2≤x 2+1≤17, 所以 )14(17)1()14(2412-⋅≤+≤-⋅⎰dx x , 即 51)1(6412≤+≤⎰dx x . (2)因为当ππ454≤≤x 时, 1≤1+sin 2x ≤2, 所以 )445(2)sin 1()445(14542ππππππ-⋅≤+≤-⋅⎰dx x ,即 ππππ2)sin1(4542≤+≤⎰dx x .(3)先求函数f (x )=x arctan x 在区间]3 ,31[上的最大值M 与最小值m .21arctan )(x x x x f ++='. 因为当331≤≤x 时, f '(x )>0, 所以函数f (x )=x arctan x 在区间]3 ,31[上单调增加. 于是3631arctan31)31(π===f m , 33arctan 3)3(π===f M .因此)313(3arctan )313(36331-≤≤-⎰ππxdx x ,即32arctan 9331ππ≤≤⎰xdx x . (4)先求函数xx e x f -=2)(在区间[0, 2]上的最大值M 与最小值m .)12()(2-='-x e x f xx , 驻点为21=x .比较f (0)=1, f (2)=e 2,41)21(-=e f ,得41-=e m , M =e 2. 于是)02()02(220412-⋅≤≤-⎰--e dx e e xx,即 41022222---≤≤-⎰e dx dx e e xx .7. 设f (x )及g (x )在[a , b ]上连续, 证明:(1)若在[a , b ]上 f (x )≥0, 且0)(=⎰ba dx x f , 则在[a ,b ]上f (x )≡0; (2)若在[a , b ]上, f (x )≥0, 且f (x )≢0, 则0)(>⎰ba dx x f ;(3)若在[a , b ]上, f (x )≤g (x ), 且⎰⎰=b a ba dx x g dx x f )()(, 则在[ab ]上f (x )≡g (x ).证明 (1)假如f (x )≢0, 则必有f (x )>0. 根据f (x )在[a , b ]上的连续性, 在[a , b ]上存在一点x 0, 使f (x 0)>0, 且f (x 0)为f (x )在[a , b ]上的最大值.再由连续性, 存在[c , d ]⊂[a , b ], 且x 0∈[c , d ], 使当x ∈[c , d ]时, 2)()(0x f x f >. 于是0)(2)()()()()()(0>-≥≥++=⎰⎰⎰⎰⎰c d x f dx x f dx x f dx x f dx x f dx x f dc bd d c c a b a . 这与条件0)(=⎰ba dx x f 相矛盾. 因此在[a ,b ]上f (x )≡0.(2)证法一 因为f (x )在[a , b ]上连续, 所以在[a , b ]上存在一点x 0, 使f (x 0)>0, 且f (x 0)为f (x )在[a , b ]上的最大值.再由连续性, 存在[c , d ]⊂[a , b ], 且x 0∈[c , d ], 使当x ∈[c , d ]时, 2)()(0x f x f >. 于是⎰⎰>-≥≥badcc d x f dx x f dx x f 0)(2)()()(0. 证法二 因为f (x )≥0, 所以0)(≥⎰ba dx x f . 假如0)(>⎰ba dx x f 不成立. 则只有0)(=⎰ba dx x f , 根据结论(1), f (x )≡0, 矛盾. 因此0)(>⎰ba dx x f . (3)令F (x )=g (x )-f (x ), 则在[a ,b ]上F (x )≥0且0)()()]()([)(=-=-=⎰⎰⎰⎰ba b a b a b a dx x f dx x g dx x f x g dx x F ,由结论(1), 在[a , b ]上F (x )≡0, 即f (x )≡g (x ).4. 根据定积分的性质及第7题的结论, 说明下列积分哪一个的值较大: (1)⎰102dx x 还是⎰103dx x ?(2)⎰212dx x 还是⎰213dx x ? (3)⎰21ln xdx 还是⎰212)(ln dx x ? (4)⎰10xdx 还是⎰+10)1ln(dx x ? (5)⎰10dx e x 还是⎰+10)1(dx x ?解 (1)因为当0≤x ≤1时, x 2≥x 3, 所以⎰⎰≥103102dx x dx x . 又当0<x <1时, x 2>x 3, 所以⎰⎰>103102dx x dx x . (2)因为当1≤x ≤2时, x 2≤x 3, 所以⎰⎰≤213212dx x dx x . 又因为当1<x ≤2时, x 2<x 3, 所以⎰⎰<213212dx x dx x .(3)因为当1≤x ≤2时, 0≤ln x <1, ln x ≥(ln x )2, 所以⎰⎰≥21221)(ln ln dx x xdx . 又因为当1<x ≤2时, 0<ln x <1, ln x >(ln x )2, 所以⎰⎰>21221)(ln ln dx x xdx . (4)因为当0≤x ≤1时, x ≥ln(1+x ), 所以⎰⎰+≥1010)1ln(dx x xdx . 又因为当0<x ≤1时, x >ln(1+x ), 所以⎰⎰+>1010)1ln(dx x xdx .(5)设f (x )=e x -1-x , 则当0≤x ≤1时f '(x ) =e x -1>0, f (x )=e x -1-x 是单调增加的. 因此当0≤x ≤1时, f (x )≥f (0)=0, 即e x ≥1+x , 所以⎰⎰+≥1010)1(dx x dx e x . 又因为当0<x ≤1时, e x >1+x , 所以⎰⎰+>1010)1(dx x dx e x .。
机械制图习题集(第6版)参考答案全解
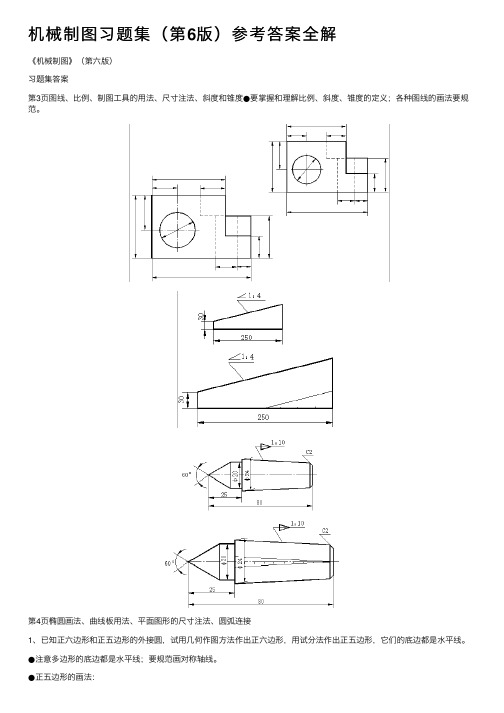
机械制图习题集(第6版)参考答案全解《机械制图》(第六版)习题集答案第3页图线、⽐例、制图⼯具的⽤法、尺⼨注法、斜度和锥度●要掌握和理解⽐例、斜度、锥度的定义;各种图线的画法要规范。
第4页椭圆画法、曲线板⽤法、平⾯图形的尺⼨注法、圆弧连接1、已知正六边形和正五边形的外接圆,试⽤⼏何作图⽅法作出正六边形,⽤试分法作出正五边形,它们的底边都是⽔平线。
●注意多边形的底边都是⽔平线;要规范画对称轴线。
●正五边形的画法:①求作⽔平半径ON的中点M;②以M为圆⼼,MA为半径作弧,交⽔平中⼼线于H。
③AH为五边形的边长,等分圆周得顶点B、C、D、E④连接五个顶点即为所求正五边形。
2、⽤四⼼圆法画椭圆(已知椭圆长、短轴分别为70mm、45mm)。
●参教P23四⼼圆法画椭圆的⽅法做题。
注意椭圆的对称轴线要规范画。
3~4、在平⾯图形上按1:1度量后,标注尺⼨(取整数)。
5、参照左下⽅所⽰图形的尺⼨,按1:1在指定位置处画全图形。
第6页点的投影1、按⽴体图作诸点的两⾯投影。
●根据点的两⾯投影的投影规律做题。
2、已知点A在V⾯之前36,点B在H⾯之上,点D在H⾯上,点E在投影轴上,补全诸的两⾯投影。
●根据点的两⾯投影的投影规律、空间点的直⾓坐标与其三个投影的关系及两点的相对位置做题。
3、按⽴体图作诸点的两⾯投影。
●根据点的三⾯投影的投影规律做题。
4、作出诸点的三⾯投影:点A(25,15,20);点B距离投影⾯W、V、H分别为20、10、15;点C在A之左,A之前15,A之上12;点D在A之下8,与投影⾯V、H等距离,与投影⾯W的距离是与H⾯距离的3.5倍。
●根据点的投影规律、空间点的直⾓坐标与其三个投影的关系及两点的相对位置做题。
各点坐标为:A(25,15,20)B(20,10,15)C(35,30,32)D(42,12,12)5、按照⽴体图作诸点的三⾯投影,并表明可见性。
●根据点的三⾯投影的投影规律做题,利⽤坐标差进⾏可见性的判断。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
兰州交通大学《通信原理》精品课程/txyl09/index.htm第一章绪论本章主要内容:(1)通信系统的模型与基本概念(2)通信技术的现状与发展(3)信息的度量(4)通信系统的主要性能指标本章重点:1.通信系统的一般模型与数字通信系统模型2.离散信源的信息量、熵的计算3.数字通信系统的主要性能指标:码元传输速率与信息传输速率以及它们的关系、误码率与误信率本章练习题:1-1.已知英文字母e出现的概率为0.105,x出现的概念为0.002,试求e和x的信息量。
•查看参考答案o1-2.某信源符号集由A,B,C,D和E组成,设每一符号独立出现,其出现概率分别为14,18,1 8,316和516。
试求该信息源符号的平均信息量。
•查看参考答案o1-3.设有4个符号,其中前3个符号的出现概率分别为14,18,18,且各符号的出现是相对独立的。
试计算该符号集的平均信息量。
•查看参考答案o1-4.一个由字母A 、B 、C 、D 组成的字,对于传输的每一个字母用二进制脉冲编码,00代替A ,01代替B ,10代替C ,11代替D ,每个脉冲宽度为5ms .(1)不同的字母是等可能出现时,试计算传输的平均信息速率;(2)若每个字母出现的可能性分别为 103,41,41,51====D C B A P P P P试计算传输的平均信息速率。
• 查看参考答案o1-5.国际摩尔斯电码用“点”和“划”的序列发送英文字母,“划”用持续3单位的电流脉冲表示,“点”用持续1个单位的电流脉冲表示;且“划”出现的概率是“点”出现概率的13。
(1)计算“点”和“划”的信息量;(2)计算“点”和“划”的平均信息量。
• 查看参考答案o1-6.设一信息源的输出由128个不同的符号组成,其中16个出现的概率为132,其余112个出现概率为1224。
信息源每秒发出1000个符号,且每个符号彼此独立。
试计算该信息源的平均信息速率。
• 查看参考答案o1-7.设一数字传输系统传送二进制码元的速率为2400B ,试求该系统的信息速率;若该系统改为传送16进制信号码元,码元速率不变,则这时的系统信息速率为多少(设各码元独立等概率出现)?• 查看参考答案o1-8.若题1―2中信息源以1000B 速率传送信息。
(1)试计算传送1h 的信息量;(2)试计算传送1h 可能达到的最大信息量。
• 查看参考答案 o1-9.如果二进制独立等概信号的码元宽度为ms 5.0,求B R 和b R ;若改为四进制信号,码元宽度不变,求传码率B R 和独立等概率时的传信率b R 。
• 查看参考答案o1-10.已知某四进制数字传输系统的传信率为2400/b s ,接收端在0.5h 内共收到216个错误码元,试计算该系统的误码率e P 。
o第二章 确知信号本章主要内容:(1)信号和系统的分类(2)能量信号和功率信号时域及频域分析本章重点:1.确知信号的频谱、频谱密度、能量谱密度和功率谱密度2.确知信号的自相关函数和互相关函数本章练习题:2-1 试证明图2-1中周期性信号的频谱为()s t =04(1)cos(21)21nn n t n ππ∞=-++∑•查看参考答案o2-2 设一个信号可以表示成=+ts t tπθ()2cos(2)-∞<<∞试问它是功率信号还是能量信号,并求出其功率谱密度或能量谱密度。
•查看参考答案o2-3 设有一信号如下:⎪⎩⎪⎨⎧<≥-=000)exp(2)(t t t t x试问它是功率信号还是能量信号,并求出其功率谱密度或能量谱密度。
• 查看参考答案o2-4 试问下列函数中哪一些满足谱密度的性质:(1)2()2cos f f δπ+(2) ()a f a δ+-(3)2exp()a f - • 查看参考答案o2-5试求出()cos s t A t ω=的自相关函数,并从其自相关函数求出其功率。
• 查看参考答案o2-6 设信号()s t的傅里叶变换为()sin/S f f fππ=,试求此信号的自相关函数()sRτ。
•查看参考答案o2-7已知一信号()s t 的自相关函数为 ()2k s k e R ττ-=k =常数 (1) 试求其功率谱密度()sf P 和功率P 试画出()s R τ和()s f P 的曲线。
• 查看参考答案o2-8 已知一信号()s t 的自相关函数是以2为周期的周期性函数: ()1R ττ=- 11τ-≤<试求()s t 的功率谱密度()s f P 并画出其曲线。
• 查看参考答案o2-9 已知一信号的双边带功率谱密度为 42101010()0s f kHz f kHz f P -⎧-<<+=⎨⎩其他试求其平均功率。
• 查看参考答案第三章 随机过程本章主要内容:(1)随机过程(2)平稳随机过程(3)高斯随机过程(4)平稳随机过程通过线性系统(5)窄带随机过程(6)正弦波加窄带随机过程(7)高斯白噪声和带限高斯白噪声本章重点:1.随机过程的基本概念,统计特性和数字特征2.平稳随机过程的定义、自相关函数和功率谱密度的性质3.高斯过程的特性4.窄带随机过程的特性5.高斯白噪声的特性本章练习题:3-1.设X 是1,0==σa 的高斯随机变量,试确定随机变量d cX Y +=的概率密度函数)(y f ,其中d c ,均为常数。
• 查看参考答案o3-2.设一个随机过程)(t ξ可表示成 )2cos(2)(θπξ+=t t式中,θ是一个离散随机变量,且21)0(==θP 21)2(==πθP 试求)1(ξE 及)1,0(ξR 。
• 查看参考答案o3-3.设随机过程tXtXtY21sincos)(ωω-=,若1X与2X是彼此独立且均值为0、方差为2σ的高斯随机变量,试求:(1))]([tYE、)]([2tYE(2))(tY的一维分布密度函数)(yf;(3)),(21ttR和),(21ttB。
•查看参考答案ooo3-4.已知)(t X 和)(t Y 是统计独立的平稳随机过程,且它们的均值分别为x a 和y a ,自相关函数分别为)(τx R 和)(τy R 。
(1)试求乘积)()()(t Y t X t Z *=的自相关函数。
(2)试求之和)()()(t Y t X t Z +=的自相关函数。
• 查看参考答案o3-5.已知随机过程)cos()()(θω+=t t m t Z c ,其中,)(t m 是广义平稳过程,且其自相关函数为 )(τm R =⎪⎩⎪⎨⎧-+011ττ 其它1001<≤<<-ττ 随机变量θ在(0,2π)上服从均匀分布,它与)(t m 彼此统计独立。
(1) 证明)(t z 是广义平稳的;(2) 试画出自相关函数)(τz R 的波形;(3) 试求功率谱密度)(f R z 及功率S 。
• 查看参考答案oo3-6.已知噪声)(t n 的自相关函数为)(τn R =τk e k -2 (k 为常数)(1)试求其功率谱密度)(f P n 及功率N ; (2)试画出)(τn R 及)(f P n 的图形。
• 查看参考答案o3-7.一个均值为a ,自相关函数为)(τX R 的平稳随机过程)(t X 通过一个线性系统后的输出过程为)()()(T t X t X t Y -+= (T 为延迟时间)(1)试画出该线性系统的框图;(2)试求)(t Y 的自相关函数和功率谱密度。
• 查看参考答案o3-8. 一个中心频率为c f 、带宽为B 的理想带通滤波器如图3-4所示。
假设输入是均值为零、功率谱密度为20n 的高斯白噪声,试求: )(f H O c f -c f B B图3-4(1)滤波器输出噪声的自相关函数;(2)滤波器输出噪声的平均功率;(3)输出噪声的一维概率密度函数。
• 查看参考答案o3-9. 一个RC 低通滤波器如图3-5所示,假设输入是均值为零、功率谱密度为20n 的高斯白噪声,试求:(1)输出噪声的功率谱密度和自相关函数;(2)输出噪声的一维概率密度函数。
RC图3-5• 查看参考答案on的高斯白噪3-10. 一个LR低通滤波器如图3-6所示,假设输入是均值为零、功率谱密度为2声,试求:(1)输出噪声的自相关函数;(2)输出噪声的方差。
图3-6•查看参考答案o3-11.设有一个随机二进制矩形脉冲波形,它的每个脉冲的持续时间为b T ,脉冲幅度取1±的概率相等。
现假设任一间隔b T 内波形取值与任何别的间隔内取值统计无关,且具有宽平稳性,试证:(1)自相关函数)(τξR =⎪⎩⎪⎨⎧-0/1b T τ bb T T >≤ττ (2)功率谱密度 2)]([)(b b fT Sa T P πωξ= 3-12. 图3-7为单个输入、两个输出的线性滤波器,若输入过程)(t η是平稳的,求)(1t ξ与)(2t ξ的互功率密度的表达式。
)(1t h )(2t h )(t η(1t ξ)(2t ξ 图3-7• 查看参考答案o3-13.设平稳过程)(t X 的功率谱密度为)(ωx P ,其自相关函数为)(τx R 。
试求功率谱密度为)]()([2100ωωωω-++x x P P 所对应的过程的自相关函数(其中,0ω为正常数)。
3-14.)(t X 是功率谱密度为)(f P x 的平稳随机过程,该过程通过图3-8所示的系统。
图3-8(1)输出过程)(t Y 是否平稳?(2)求)(t Y 的功率谱密度。
• 查看参考答案o3-15. 设)(t X 是平稳随机过程,其自相关函数在(-1,1)上为)1()(ττ-=x R ,是周期为2的周期性函数。
试求)(t X 的功率谱密度)(ωx P ,并用图形表示。
• 查看参考答案o3-16.设)()(21t x t x 与为零值且互不相关的平稳随机过程,经过线性时不变系统,其输出分别为)()(21t z t z 与,试证明)()(21t z t z 与也是互不相关的。
• 查看参考答案o第四章 信 道本章主要内容:(1)信道分类(2)无线信道和有线信道(3)信道的数学模型(4)信道特性对传输的影响(5)信道中的噪声(6)信道容量本章重点:1.调制信道模型及编码信道模型的特性2.恒参信道的传输特性及其对信号的影响3.随参信道的传输媒质的三个特点及多径传播对信号的影响本章练习题:4-1.设一条无线链路采用视距传播方式通信,其收发天线的架设高度都等于40m,若不考虑大气折射率的影响,试求其最远通信距离。
•查看参考答案o4-2.设一条天波无线电信道,用高度等于400km的2F层电离层反射电磁波,地球的等效半径等于(6370×4/3)km,收发天线均架设在地平面,试计算其通信距离大约可以达到多少千米?•查看参考答案o4-3.若有一平流层平台距离地面20km,试按上题给定的条件计算其题覆盖地面的半径等于多少千米。
