材料力学试题1
材料力学习题及答案
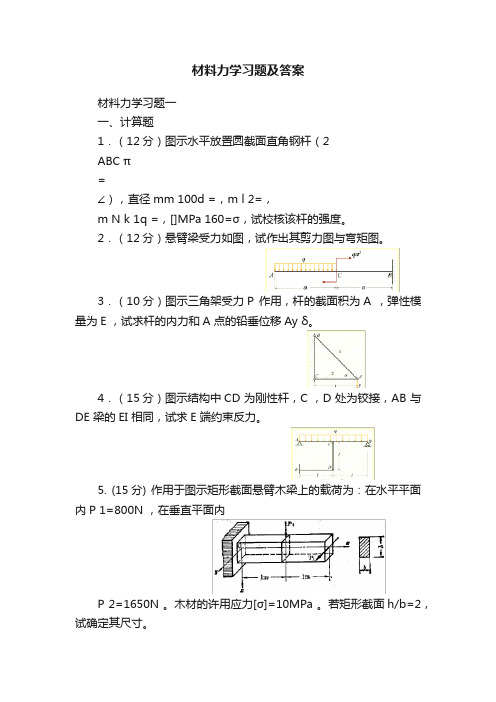
材料力学习题及答案材料力学习题一一、计算题1.(12分)图示水平放置圆截面直角钢杆(2ABC π=∠),直径mm 100d =,m l 2=,m N k 1q =,[]MPa 160=σ,试校核该杆的强度。
2.(12分)悬臂梁受力如图,试作出其剪力图与弯矩图。
3.(10分)图示三角架受力P 作用,杆的截面积为A ,弹性模量为E ,试求杆的内力和A 点的铅垂位移Ay δ。
4.(15分)图示结构中CD 为刚性杆,C ,D 处为铰接,AB 与DE 梁的EI 相同,试求E 端约束反力。
5. (15分) 作用于图示矩形截面悬臂木梁上的载荷为:在水平平面内P 1=800N ,在垂直平面内P 2=1650N 。
木材的许用应力[σ]=10MPa 。
若矩形截面h/b=2,试确定其尺寸。
三.填空题(23分)1.(4分)设单元体的主应力为321σσσ、、,则单元体只有体积改变而无形状改变的条件是__________;单元体只有形状改变而无体积改变的条件是__________________________。
2.(6分)杆件的基本变形一般有______、________、_________、________四种;而应变只有________、________两种。
3.(6分)影响实际构件持久极限的因素通常有_________、_________、_________,它们分别用__________、_____________、______________来加以修正。
4.(5分)平面弯曲的定义为______________________________________。
5.(2分)低碳钢圆截面试件受扭时,沿____________截面破坏;铸铁圆截面试件受扭时,沿____________面破坏。
四、选择题(共2题,9分)2.(5分)图示四根压杆的材料与横截面均相同,试判断哪一根最容易失稳。
答案:()材料力学习题二二、选择题:(每小题3分,共24分)1、危险截面是______所在的截面。
材料力学I期末考试题及答案

材料力学I期末考试题及答案一、选择题(每题2分,共20分)1. 材料力学中,下列哪一项不是基本假设?A. 均匀性假设B. 连续性假设C. 各向同性假设D. 各向异性假设答案:D2. 在拉伸试验中,材料的屈服强度是指:A. 弹性极限B. 屈服极限C. 强度极限D. 断裂强度答案:B3. 影响材料弹性模量的因素不包括:A. 材料种类B. 温度C. 材料的几何形状D. 加载速度答案:C4. 梁的弯曲应力公式为:A. σ = My/IB. σ = Mx/IC. σ = VQ/ID. σ = Vx/I答案:A5. 材料力学中,下列哪一项不是应力状态的描述?A. 正应力B. 剪应力C. 应力集中D. 应力梯度答案:D6. 材料的疲劳破坏通常发生在:A. 最大应力处B. 最小应力处C. 应力集中处D. 应力均匀处答案:C7. 根据材料力学理论,下列哪一项不是材料的强度理论?A. 最大正应力理论B. 最大剪应力理论C. 最大应变理论D. 能量理论答案:D8. 梁的弯曲变形公式为:A. v = (Mx/EI)(1 - x^2/L^2)B. v = (Mx/EI)(1 - x^3/L^3)C. v = (Mx/EI)(1 - x/L)D. v = (Mx/EI)(1 - x^2/L^3)答案:B9. 材料的塑性变形是指:A. 弹性变形B. 永久变形C. 可逆变形D. 弹性和塑性变形的总和答案:B10. 在拉伸试验中,材料的弹性模量可以通过下列哪一项来确定?A. 弹性阶段的斜率B. 屈服阶段的斜率C. 断裂阶段的斜率D. 塑性变形阶段的斜率答案:A二、填空题(每题2分,共20分)1. 材料力学中,__________是指材料在外力作用下发生形变,但当外力移除后,形变能够完全恢复的性质。
答案:弹性2. 当材料受到拉伸时,其内部产生的__________应力称为正应力。
答案:垂直3. 材料力学中,__________是指材料在外力作用下发生形变,但当外力移除后,形变不能完全恢复的性质。
材料力学试题1及答案[精选五篇]
![材料力学试题1及答案[精选五篇]](https://img.taocdn.com/s3/m/95be31c8c9d376eeaeaad1f34693daef5ef71390.png)
材料力学试题1及答案[精选五篇]第一篇:材料力学试题1及答案材料力学卷1一、结构构件应该具有足够的、和。
(本题3分)二、低碳钢拉伸破坏经历了四个典型阶段:阶段、阶段、阶段和阶段。
衡量材料强度的指标是、。
(本题6分)三、在其他条件不变的前提下,压杆的柔度越大,则临界应力越、临界力越;材料的临界柔度只与有关。
(本题3分)四、两圆截面杆直径关系为:D2=3D1,I则Z2分)=IZ1;WZ2=WZ1I; P2=IP1;WP2=WP1;(本题8五、已知构件上危险点的应力状态,计算第一强度理论相当应力;第二强度理论相当应力;第三强度理论相当应力;第四强度理论相当应力。
泊松比μ=0.3。
(本题15分)六、等截面直杆受力如图,已知杆的横截面积为A=400mm,P=20kN。
试作直杆的轴力图;计算杆内的最大正应力;材料的弹性模量E=200Gpa,计算杆的轴向总变形。
(本题15分)2七、矩形截面梁,截面高宽比h=2b,l=4米,均布载荷q=30kN/m 许用应力的剪力图、弯矩图2、设计梁的截面(本题20分)。
[σ]=100MPa,1、画梁八、一圆木柱高l=6米,直径D=200mm,两端铰支,承受轴向载荷F=50kN,校核柱子的稳定性。
已知木材的许用应力[σ]=10MPa,折减系数与柔度的关系为:ϕ=3000λ2。
(本题15分)九、用能量法计算结构B点的转角和竖向位移,EI已知。
(本题15分)答案:一、结构构件应该具有足够的强度、刚度和稳定性。
(本题3分)二、低碳钢拉伸破坏经历了四个典型阶段:弹性阶段、屈服阶段、强化阶段和颈缩阶段。
衡量材料强度的指标是屈服极限、强度极限。
(本题6分)三、在其他条件不变的前提下,压杆的柔度越大,则临界应力越小、临界力越小;材料的临界柔度只与材料有关。
(本题3分)四、两圆截面杆直径关系为:D2=3D1,; I则Z2=81IZ1WZ2=27WZ1;IP2=81IP1;WP2=27WP1;(本题8分)五、解:三、(15分)解:主应力第一强度理论相当应力第二强度理论相当应力第三强度理论相当应力σ1=52.4MPaσ2=7.64MPaσ3=0MPaσr1=σ1=52.4MPaσr2=σ1-μ(σ2+σ3)=50.2MPa σr3=σ1-σ3=52.4MPa1(σ1-σ2)2+(σ2-σ3)2+(σ3-σ1)2=49MPa2 第四强度理论相当应力六、解:轴力图如图所示(三段共6分,每一段2分)σr4=[]σ=由:NANmax2P2⨯20⨯1000===100MPaAA400(3分)得:(6分)Nl10000⨯1000∆l=∑=+0=0.125mm(伸长)EA200⨯1000⨯400(5分)σmax=七、解:画梁的受力图(2分)∑M=0⇒Y⨯4-q⨯2⨯5=0 ⇒Y=0⇒Y+Y-q⨯2=0⇒Y由∑由ABABYB=75kN(2分)A=-15kN(2分)梁的剪力图、弯矩图如图所示(4分)最大剪力为:Fs=60kN 最大弯矩为:M=60kNm(2分)Mσ=WZbh22b3WZ==63(2分)(2分)σmax=M3M33⨯60000000<[σ]⇒b≥3==96.55mmWZ2[σ]2⨯100(2分)=96.55mmh=193.1mm!(2分)所以梁截面尺寸为:b八、解:圆截面的惯性半径和柔度为:i=μl1⨯6000Dλ===120=50mmi504(5分)(5分)30003000ϕ=2==0.2082λ120由公式(5分)P50⨯103σ===1.59MPa2<[σst]=ϕ[σ]=0.208⨯10=2.08MPa(5分)A3.14⨯100柱子满足稳定性要求。
(完整版)材料力学试卷及答案,推荐文档
C
2m
G 3N AB
G1
N AC 2
55.766 kN
B
G2 3N AB 529.591kN
4m
A G
[G] {G1, G2}min 55.766kN
三、图示变截面杆由两种材料制成。AE 段为铜质,EC 段为钢质。钢的许用应力 钢 160MPa ,铜的许用应力
为 铜 120MPa 。AB 段横截面面积是 BC 段横截面面积的两倍, AAB 1000mm2 。外力作用线沿杆轴线方向,
P 60kN 。试对此杆进行强度校核。又若已知 E钢 210GPa , E铜 100GPa 。试计算杆的纵向变形和 AB 截面
的相对位移。
N AD 2P
N DE N EB P
N BC P
铜杆 max 120 MPa 压应力 钢杆 max 120 MPa
l AC 0.94 mm
100mm
4F A
C
l
l
60mm
F
D
B
l
100mm
1
六、单元体应力如图所示,试计算主应力,并求第四强度理论的相当应力。(10 分)
y=100MPa x=100MPa x=100MPa
七、图示矩形截面柱承受压力 F1=100kN 和 F2=45kN 的作用,F2 与轴线的偏心距 e=200mm。b=180mm, h=300mm。求max 和min。(15 分)
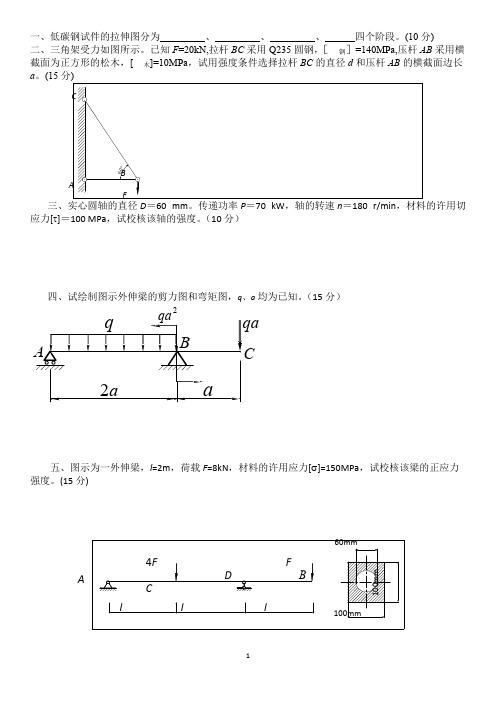
根 10 号槽钢组成,横截面面积为 2548mm 2 。材料都是 A3 钢,许用应力 120MPa 。不计两杆的自重,求允
许的最大起吊重量 G。
N AC
G sin
G N AC 2
N BC
N AC cos
材料力学试卷及答案7套
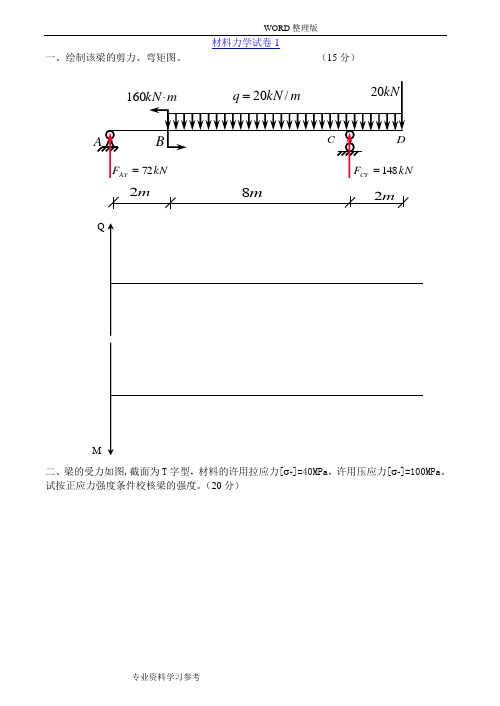
材料力学试卷1一、绘制该梁的剪力、弯矩图。
(15分)二、梁的受力如图,截面为T 字型,材料的许用拉应力[σ+]=40MPa ,许用压应力[σ-]=100MPa 。
试按正应力强度条件校核梁的强度。
(20分)m8m 2m2M三、求图示单元体的主应力及其方位,画出主单元体和应力圆。
(15分)四、图示偏心受压柱,已知截面为矩形,荷载的作用位置在A 点,试计算截面上的最大压应力并标出其在截面上的位置,画出截面核心的形状。
(15分) 30170302002m3m1m30五、结构用低碳钢A 3制成,A 端固定,B 、C 为球型铰支,求:允许荷载[P]。
已知:E=205GPa ,σs =275MPa ,σcr =338-1.12λ,,λp =90,λs =50,强度安全系数n=2,稳定安全系数n st =3,AB 梁为N 016工字钢,I z =1130cm 4,W z =141cm 3,BC 杆为圆形截面,直径d=60mm 。
(20分)六、结构如图所示。
已知各杆的EI 相同,不考虑剪力和轴力的影响,试求:D 截面的线位移和角位移。
(15分)材料力学2一、回答下列各题(共4题,每题4分,共16分)1、已知低碳钢拉伸试件,标距mm l 1000=,直径mm d 10=,拉断后标距的长度变为mm l 1251=,断口处的直径为mm d 0.61=,试计算其延伸率和断面收缩率。
2、试画出图示截面弯曲中心的位置。
aa3、梁弯曲剪应力的计算公式zzQS =τ,若要计算图示矩形截面A 点的剪应力,试计算z S 。
4、试定性画出图示截面截面核心的形状(不用计算)。
4/h矩形 圆形 矩形截面中间 挖掉圆形圆形截面中间 挖掉正方形二、绘制该梁的剪力、弯矩图。
(15分) 三、图示木梁的右端由钢拉杆支承。
已知梁的横截面为边长等于0.20m 的正方形,q=4OKN/m,弹性模量E 1=10GPa ;钢拉杆的横截面面积A 2=250mm 2,弹性模量E 2=210GPa 。
材料力学试题及答案

材料力学试题及答案一、选择题(每题2分,共20分)1. 材料力学中,下列哪一项不是基本力学性质?A. 弹性B. 塑性C. 硬度D. 韧性2. 材料在拉伸过程中,当应力达到屈服点后,材料将:A. 断裂B. 产生永久变形C. 恢复原状D. 保持不变3. 材料的弹性模量是指:A. 材料的密度B. 材料的硬度C. 材料的抗拉强度D. 材料在弹性范围内应力与应变的比值4. 根据材料力学的胡克定律,下列说法正确的是:A. 应力与应变成正比B. 应力与应变成反比C. 应力与应变无关D. 应力与应变成线性关系5. 材料的疲劳寿命是指:A. 材料的总寿命B. 材料在循环加载下达到破坏的周期数C. 材料的断裂寿命D. 材料的磨损寿命6. 材料的屈服强度是指:A. 材料在弹性范围内的最大应力B. 材料在塑性变形开始时的应力C. 材料的抗拉强度D. 材料的极限强度7. 材料的断裂韧性是指:A. 材料的硬度B. 材料的抗拉强度C. 材料抵抗裂纹扩展的能力D. 材料的屈服强度8. 材料力学中的泊松比是指:A. 材料的弹性模量B. 材料的屈服强度C. 材料在拉伸时横向应变与纵向应变的比值D. 材料的断裂韧性9. 在材料力学中,下列哪一项是衡量材料脆性程度的指标?A. 弹性模量B. 屈服强度C. 断裂韧性D. 泊松比10. 材料在受力过程中,当应力超过其极限强度时,将:A. 发生弹性变形B. 发生塑性变形C. 发生断裂D. 恢复原状答案1. C2. B3. D4. A5. B6. B7. C8. C9. C10. C试题二、简答题(每题10分,共30分)1. 简述材料力学中材料的三种基本力学性质。
2. 解释什么是材料的疲劳现象,并简述其对工程结构的影响。
3. 描述材料在拉伸过程中的四个主要阶段。
答案1. 材料的三种基本力学性质包括弹性、塑性和韧性。
弹性指的是材料在受到外力作用时发生变形,当外力移除后能够恢复原状的性质。
塑性是指材料在达到一定应力水平后,即使外力移除也无法完全恢复原状的性质。
材料力学I期末考试题及答案
材料力学I期末考试题及答案一、选择题(每题2分,共20分)1. 材料力学中,下列哪个参数不是描述材料弹性性质的?A. 弹性模量B. 屈服强度C. 泊松比D. 剪切模量答案:B2. 在拉伸试验中,材料的屈服点是指:A. 应力达到最大值时对应的应变B. 应力达到最大值时对应的应力C. 材料开始发生塑性变形的应力D. 材料发生断裂的应力答案:C3. 根据胡克定律,下列哪个说法是正确的?A. 应力与应变成正比B. 应力与应变成反比C. 应力与应变成二次方关系D. 应力与应变成对数关系答案:A4. 在材料力学中,下列哪个参数是用来描述材料的韧性的?A. 弹性模量B. 屈服强度C. 硬度D. 冲击韧性答案:D5. 材料力学中,下列哪个参数是用来描述材料的塑性变形能力的?A. 弹性模量B. 屈服强度C. 硬度D. 延伸率答案:D6. 根据材料力学的基本原理,下列哪个说法是错误的?A. 应力是单位面积上的力B. 应变是单位长度的变化量C. 应力和应变都是标量D. 应力和应变之间存在线性关系答案:C7. 在材料力学中,下列哪个参数是用来描述材料的硬度的?A. 弹性模量B. 屈服强度C. 布氏硬度D. 冲击韧性答案:C8. 材料力学中,下列哪个参数是用来描述材料的疲劳强度的?A. 弹性模量B. 屈服强度C. 疲劳极限D. 冲击韧性答案:C9. 在材料力学中,下列哪个参数是用来描述材料的抗拉强度的?A. 弹性模量B. 屈服强度C. 抗拉强度D. 冲击韧性答案:C10. 材料力学中,下列哪个参数是用来描述材料的压缩强度的?A. 弹性模量B. 屈服强度C. 压缩强度D. 冲击韧性答案:C二、填空题(每题2分,共20分)1. 材料力学中,应力的定义是单位面积上的_______。
答案:力2. 材料力学中,应变的定义是单位长度上的_______。
答案:长度变化3. 材料力学中,弹性模量是描述材料_______性质的物理量。
答案:弹性4. 材料力学中,泊松比是描述材料在受到_______作用时,横向应变与纵向应变的比值。
材料力学试题1
轴向拉压1. 等截面直杆CD 位于两块夹板之间,如图示。
杆件与夹板间的摩擦力与杆件自重保持平衡。
设杆CD 两(A)q =(B) (C) (D)2. (A) (C)3. 在A 和(A) 0;(B) 30;(C) 45;(D) 60。
4. 1和杆2求载荷F (A) 2][A σ(C) A ][σ5. (A) (C)6. (A) (B) 减小杆(C) 三杆的横截面面积一起加大; (D) 增大α角。
7. 图示超静定结构中,梁AB 伸长和杆2种答案中的哪一种? (A) βαsin 2sin 21l l ∆=∆; (B) βαcos 2cos 21l l ∆=∆;(C) αβsin 2sin 21l l ∆=∆; (D) αβcos 2cos 21l l ∆=∆。
8. 图示结构,AC 为刚性杆,杆1以下四种情况,问哪一种正确? (A) 两杆轴力均减小; (B) 两杆轴力均增大;(C) 杆1轴力减小,杆2轴力增大; (D) 杆1轴力增大,杆2轴力减小。
9. 结构由于温度变化,那么:(A) (B) (C) (D)10. 图示受力结构中,假设杆1和杆移=AyΔ ,水平位移Ax Δ11. 一轴向拉杆,横截面为b a ⨯(a ﹥短边的比值为 。
另一轴向拉杆,横截面是长半轴和短半轴分别为12. 一长为l ,横截面面积为A 的最大应力=max σ ,杆的总伸长13. 图示杆1和杆2设两杆温度都下降T ∆,.应力之间的关系是1σ ____2σ。
〔填入符号<,=,>〕题1-13答案:1. D2. D3. C4. B5. B6. B7. C8. C9. B10.EAFlEA Fl 3;11. b a ;椭圆形 12.Egl gl 22ρρ,13. >,=14. 试证明受轴向拉伸的圆截面杆,其横截面沿圆周方向的线应变s ε等于直径的相对改变量d ε。
证:()d s πππεε=∆=-∆+=dd d d d d 证毕。
15. 如下图,一实心圆杆1在其外外表紧套空心圆管2。
材料力学试题及答案全
材料力学试题一、填空题(共15分)1、 (5分)一般钢材的弹性模量E = 210 GPa ;吕材的弹性模量E = 70 GPa2、 (10分)图示实心圆锥杆受扭转外力偶作用,材料的剪切弹性模量为G ,该杆的man τ1、(5(A )各向同性材料;(B )各向异性材料; (C 正确答案是 A 。
2、(5分)边长为d 杆(1)是等截面,杆(2荷系数d k 和杆内最大动荷应力d σ论:(A )()(,)()(1max 21d d d k k σ<<(B )()(,)()(1max 21d d d k k σ><(C )()(,)()(1max 21d d d k k σ<>(D )1max 21()(,)()(d d d k k σ>>正确答案是 A 。
三、计算题(共75分) 1、(25应力相等,求:(1)直径比21/d d ; (2)扭转角比AB φ解:AC 轴的内力图:(105);(10355M Nm M BC AB ⨯=⨯= 由最大剪应力相等:8434.05/3/16/1050016/10300321323313max==⨯=⨯==d d d d W M n n ππτ 由;594.0)(23232;41221242411=••=•=⇒∴⋅=d M M M d G d G a M GI l M n n n n BC AB P n ππφφφ(2)2、(3、(15分)有一厚度为6mm 的钢板在板面的两个垂直方向受拉,拉应力分别为150Mpa 和55Mpa ,材料的E=2.1×105Mpa ,υ =0.25。
求钢板厚度的减小值。
解:钢板厚度的减小值应为横向应变所产生,该板受力后的应力状态为二向应力状态,由广义胡克定律知,其Z 向应变为:0244.010)55150(101.225.0)(69-=⨯+⨯-=+-=y x z E σσνε则 mm t Z Z 146.0-=⨯=∆ε(本资料素材和资料部分来自网络,仅供参考。
材料力学试题及答案
材料力学试题及答案一、选择题(每题5分,共25分)1. 下列哪个选项是材料力学的基本假设之一?A. 材料是各向同性的B. 材料是各向异性的C. 材料是均匀的D. 材料是线弹性的答案:A2. 在材料力学中,下列哪个公式表示杆件的正应力?A. σ = F/AB. τ = F/AC. σ = F/LD. τ = F/L答案:A3. 当材料受到轴向拉伸时,下列哪个选项是正确的?A. 拉伸变形越大,材料的强度越高B. 拉伸变形越小,材料的强度越高C. 拉伸变形与材料的强度无关D. 拉伸变形与材料的强度成正比答案:B4. 下列哪种材料在拉伸过程中容易发生断裂?A. 钢材B. 铸铁C. 铝合金D. 塑料答案:B5. 下列哪个选项表示材料的泊松比?A. μ = E/GB. μ = G/EC. μ = σ/εD. μ = ε/σ答案:C二、填空题(每题10分,共30分)6. 材料力学研究的是材料在______作用下的力学性能。
答案:外力7. 材料的强度分为______强度和______强度。
答案:屈服强度、断裂强度8. 材料在受到轴向拉伸时,横截面上的正应力公式为______。
答案:σ = F/A三、计算题(每题25分,共50分)9. 一根直径为10mm的圆钢杆,受到轴向拉伸力F=20kN 的作用,求杆件横截面上的正应力。
解:已知:d = 10mm,F = 20kNA = π(d/2)^2 = π(10/2)^2 = 78.5mm^2σ = F/A = 20kN / 78.5mm^2 = 255.8N/mm^2答案:杆件横截面上的正应力为255.8N/mm^2。
10. 一根长度为1m的杆件,受到轴向拉伸力F=10kN的作用,已知材料的弹性模量E=200GPa,泊松比μ=0.3,求杆件的伸长量。
解:已知:L = 1m,F = 10kN,E = 200GPa,μ = 0.3ε = F/(EA) = 10kN / (200GPa × π(10mm)^2) =0.025δ = εL = 0.025 × 1000mm = 25mm答案:杆件的伸长量为25mm。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
轴向拉压1. 等截面直杆CD位于两块夹板之间,如图示。
杆件与夹板间的摩擦力与杆件自重保持平衡。
设杆CD(B)(C)2.(C)3.B(B)(C)4.杆1同)(C)5.的?(C)6.措施?(A)加大杆3的横截面面积;(B) 减小杆3的横截面面积;(C)三杆的横截面面积一起加大;(D) 增大α角。
7.的伸长和杆2l∆(A) sin1l∆(B) cos1l∆(C) sin1l∆(D) cos18.(A)(B)(C) 杆1(D) 杆19.(A)(B)(C)(D)10.Δ,水平位移=Ay11.12. 一长为l引起的最大应力13. 图示杆1和杆2的材料和长度都相同,但横截面面积1A >2A 。
若两杆温度都下降T ∆,则两杆轴力之间的关系是N1F N2F ,正应力之间的关系是1σ ____2σ。
(填入符号<,=,>)题1-13答案:1. D2. D3. C4. B5. B6. B7. C8. C9. B10.EAFlEA Fl 3; 11. ba;椭圆形 12. E gl gl 22ρρ,13. >,=14. 试证明受轴向拉伸的圆截面杆,其横截面沿圆周方向的线应变s ε等于直径的相对改变量d ε。
证:()d s πππεε=∆=-∆+=ddd d d d 证毕。
15. 如图所示,一实心圆杆1在其外表面紧套空心圆管2。
设杆的拉压刚度分别为11A E 和22A E 。
此组合杆承受轴向拉力F ,试求其长度的改变量。
(假设圆杆和圆管之间不发生相对滑动)解: 由平衡条件 FF F =+2N 1N (1)变形协调条件222N 111N A E l F A E l F = (2)由(1)(2)得 2211111N A E A E FlA E l F l+==∆16. 设有一实心钢管,在其外表面紧套一铜管。
材料的弹性模量和线膨胀系数分别为1E ,2E 和1l α,2l α,且2l α>1l α。
两管的横截面面积均为A 。
如果两者紧套的程度不会发生相互滑动,试证明当组合管升温T ∆后,其长度改变为()12211E T l E E ll l ∆+=∆αα证:由平衡条件 2N 1N F F = (1)变形协调条件2211l l l l ∆-∆=∆+∆T T222N 2111N 1A E lF T l A E l F T l l l -∆=+∆αα (2)由(1)(2)得()2121121N E E AE TEF l l +∆-=αα钢)α≤[][]21tan ==στα胶缝截面与横截面的夹角 57.26=α20. 图示防水闸门用一排支杆支撑(图中只画出1根),各杆直径为mm 150=d的圆木,许用应力[]MPa 10=σ,设闸门受的水压力与水深成正比,水的质量密度ρ=33m kg 100.1⨯,若不考虑支杆的稳定问题,试求支杆间的最大距离。
(取2s m 10=g)解:设支杆间的最大距离为x ,闸门底部A 处水压力的集度为40q ,闸门AB 的受力如图∑=0AM ,αcos 413210F q =⨯⨯ N F F =≤[]2π41d σ53cos =α,m kN 3030x gx q ==ρ得:m 42.9=x21. 图示结构中AC 为刚性梁,BD 为斜撑杆,载荷F 可沿梁AC 水平移动。
试问:为使斜杆的重量最小,斜撑杆与梁之间的夹角θ应取何值?解:载荷F 移至C 处时,杆BD 的受力最大,如图。
θcos h Fl F BD=A ≥[][]σθσcos h FlF BD=杆BD 的体积[]θσθ2sin 2sin Flh AV ==当12sin =θ时,V 最小即重量最轻,故 454π==θ22. 图示结构,BC 为刚性梁,杆1和杆2的横截面面积均为A许用应力分别为[]1σ和[]2σ,且[][]212σσ=。
载荷F 可沿梁其移动范围为0≤x ≤l 。
试求:(1) 从强度方面考虑,当x 为何值时,许用载荷[]F 为最大,其最大值F 为多少?(2) 该结构的许用载荷[]F 多大?解:(1) 杆BC 受力如图1N F =[]A 1σ,2N F =[]A 2σ[][]A A F F F 12N21N max 233σσ==+=3l x =(2) F 在C 处时最不利 2N F F=≤[]A 2σ4N2所以结构的许用载荷 [][]A F 2σ=23. 图示结构,杆1和杆2的横截面面积为A ,材料的弹性模量为E ,其拉伸许用应力为[]+σ,压缩许用应力为[]-σ,且[][]+-=σσ2,载荷F 可以在刚性梁BCD 上移动,若不考虑杆的失稳,试求: (1) 结构的许用载荷[]F 。
(2) 当x 为何值时(0<x <l 2为多少?解:(1) F 在B ∑=0DM,1N -F l F 1N 21F F =≤[]A -σ21∑=0CM ,2N F F =≤[]A +σ 结构的许用载荷[][]A F +=σ(2) F 在CD 间能取得许用载荷最大值,梁受力如图(2)∑=0yF,02N 1N =-+F F F∑=0BM,022N 1N =-+Fx l F l Fx l l F F -=21N ,lx l F F -=2NF ≤[]xl Al --2σ,F ≤[]lx Al --σl x x l -=-121,23lx =[][]+-==σσA A F 42max24. 在图示结构中,杆BC 和杆BD 的材料相同,且受拉和受压时的许用应力相等,已知载荷F ,杆BC 长l ,许用应力[]σ。
为使结构的用料最省,试求夹角α的合理值。
(1)N2(2)[][]σασαααcot cos sin cos 21lF Fl l A l A V +=+=),(00d d ααα==V0sin 1cos sin cos sin 020*******=--ααααα, 即0cos sin cos 2sin 02020202=-αααα 2tan 0=α当 74.540=α时,V 最小,结构用料最省。
25. 如图所示,外径为D ,壁厚为δ,长为l 的均质圆管,由弹性模量E ,泊松比ν的材料制成。
若在管端的环形横截面上有集度为q 的均布力作用,试求受力前后圆管的长度,厚度和外径的改变量。
解:长度的改变量ElqE l l l ===∆σε 厚度的改变量 Eqδννεδδεδ-=-='=∆外径的改变量 EqD D D D ννεε-=-='=∆26. 正方形截面拉杆,边长为cm 22,弹性模量GPa 200=E ,泊松比3.0=ν。
当杆受到轴向拉力作用后,横截面对角线缩短了mm 012.0,试求该杆的轴向拉力F 的大小。
解:对角线上的线应变3000.040012.0-=-='ε则杆的纵向线应变001.0='-=νεε杆的拉力kN 160==EA F ε27. 图示圆锥形杆的长度为l ,材料的弹性模量为E ,质量密度为ρ,试求自重引起的杆的伸长量。
解:x 处的轴向内力 ()()()x x A g x gV x F ⋅==31N ρρ杆的伸长量()()()()⎰⎰⋅==∆l lx x EA x x gA x EA x x F l 0 0 N d 3d ρ⎰==l Egl E x gx 0 263d ρρ28. 设图示直杆材料为低碳钢,弹性模量GPa 200=E ,杆的横截面面积为2cm 5=A ,杆长m 1=l ,加轴向拉力kN 150=F,测得伸长l=1mm 4=∆l 。
试求卸载后杆的残余变形。
解:卸载后随之消失的弹性变形mm 5.1e ==∆EAFll 残余变形为mm 5.2e p=∆-∆=∆l l l29. 图示等直杆,已知载荷F ,BC 段长l ,横截面面积A ,弹性模量E ,质量密度ρ,考虑自重影响。
试求截面B 的位移。
解:由整体平衡得gAl F C ρ34=BC 段轴力()⎪⎭⎫⎝⎛-=l x gA x F 34Nρ截面B 的位移())(65d 34d 2 0 0 N ↓-=⎪⎭⎫ ⎝⎛-==∆=⎰⎰Egl x EA l x gA EA xx F l Δl lBC B ρρ30. 已知图示结构中三杆的拉压刚度均为EA ,设杆AB 为刚体,载荷F ,杆AB 长l 。
试求点C 的铅垂位移和水平位移。
解:杆AB 受力如图0N2=F , 2N3N1FF F ==EAFll l Δy 231=∆=∆= 因为杆AB不变形。
又沿45由A 移至A '。
所以 EAFlΔΔy x 2== 31. 电子秤的传感器是一个空心圆筒,承受轴向拉伸或压缩。
已知圆筒外径mm 80=D ,壁厚mm 9=δ,材料的弹性模量GPa 210=E 。
在称某重物时,测得筒壁的轴向应变610476-⨯-=ε,试问该物重多少?解:圆筒横截面上的正应力E AFεσ==()22π41d D E EA F -⋅==εεmm 622=-=δD d 该物重 kN 67.200=FN3'xΔ32. 图示受力结构,AB 为刚性杆,CD 为钢制斜拉杆。
已知杆CD 的横截面面积2mm 100=A ,弹性模量GPa 200=E。
载荷kN 51=F ,kN 102=F ,试求:(1)杆CD 的伸长量l ∆; (2)点B 的垂直位移B ∆。
解:杆AB 受力如图∑=0AM,022212N=--F F F ()kN 2202212N =+=F F F mm 2N ==∆EAlF l mm 66.5222=∆==l ΔΔC B33. 如图示,直径mm 16=d的钢制圆杆AB处铰接。
当D 处受水平力F 作用时,测得杆AB 已知钢材拉伸时的弹性模量GPa 210=E 。
试求:(1)力F 的大小; (2)点D 的水平位移。
解:折杆BCD 受力如图 (1)∑=0CM,025.1N =⨯-⨯F FkN 5.2825.125.1N===A E F F ε (2)mm 1.8m 8001.0===∆l lε5.12l ΔDx ∆= mm 4.25.12==l ΔDx ε34. 如图示等直杆AB 在水平面内绕A 设杆件的横截面面积为A ,质量密度为ρ。
则截______________N =C F 。
答:⎪⎭⎫ ⎝⎛-22x l x A ωρ1B35. 如图示,两端固定的等直杆AB ,已知沿轴向均匀分布的载荷集度为q ,杆长为l ,拉压刚度为EA ,试证明任意一截面的位移()EAx l qx x 2-=δ,最大的位移EAql82max =δ。
证:由平衡条件得 0=-+ql F F B A()EAqlEA l F EA x qx F EA x F l A l A l2d d 20 0 N -=-==∆⎰⎰由变形协调条件0=∆l ,得2ql F A =,()EAx l qx EA qx EA qlx EA qx EA x F x EA qx F A xA x 2222d 22 0 -=-=-=-=⎰δ 令0='xδ,02=-qx ql即当2lx =时,杆的位移最大,EAql EA l l l q 82222max =⎪⎭⎫⎝⎛-=δ 证毕。
