八年级数学上册三角形复习课件
合集下载
人教部初二八年级数学上册 复习三角形全等的判定 名师教学PPT课件
千里之行 始于足下
谢谢！
个条件
，使得△ABE≌△ACD.
思路
隐含条件∠A为公共角
已
找夹边（ASA）
知
两
角
找对边（AAS）
一题多解唤醒学生思维力
原题：如图，AB=CD, BF⊥AC,DE⊥AC,AE=CF.求证：BF=DE.
● 【变式1】如图，AB=CD, BF⊥AC,DE⊥AC,AE=CF.求 证：BD平分EF.
● 【变式2】如图，AB=CD, BF⊥AC,DE⊥AC,AE=CF.想想：BD 平分EF吗?
你还能编写出变式4,，变式5吗？如果能，请编写并解答。
典例分析：
例1、如图所示，已知AC=AD，请你添加一个条
件
，使得△ABC≌△ABD.
思路
隐含条件AB=AB
找另一边 (SSS) 已 知 两 边 找夹角 (SAS)
变式1：如图，已知∠C=∠D，请你添加一个
条件
，使得△ABC≌△ABD.
思路
隐含条件AB=AB
三角形全等的判定
复习课
复习导纲
问题：
如图,已知AB=AD，CB=CD,△ABC 和△ABD全等吗？为什么？（课 本第43页 第1题）
变式1：如图，已知AB=AD，请你添加一个条件 变式2：如图，已知∠B=∠D，请你添加一个条件
，使得△ABC≌△ADC。 ，使得△ABC≌△ADC.
变式3：已知∠CAB=∠CAD，请你添加一个条件 ，使得△ABC≌△ADC
小试牛刀
1.如图，已知AB=AD，AC=AE，∠1=∠2， 求证：BE=DC
A
12
CE
B
D
请同学们 注意书写 格式哦！
小试牛刀
八年级数学上册 第1章 全等三角形章末复习课件
则( )
D
A．△ABD≌△AFE B．△AFE≌△ADC
C．△AFE≌△DFC D．△ABC≌△ADE
第十四页，共三十二页。
3. 如图，点B在AE上，且∠CAB＝∠DAB，若要使△ABC≌△ABD，可补充的条件(tiáojiàn)
是 AC＝AD ．(写出一个即可)
4.如图，把一长一短两根细木棍的一端用螺钉铰合在一起，使长木棍的另一端与射线BC的端点B重
第三页，共三十二页。
讲练结合
1、下列(xiàliè)四个图形中，全等的图形是（ C ）
A．①和② B．①和③ C．②和③ D．③和④
2、下面(xià mian)是5个全等的正六边形 A、B、C、D、E ，请你仔细观察 A、B、C、D 四个
图案，其中与 E 图案完全相同的是(
).
C
第四页，共三十二页。
角,EF=2.1 cm ,EH=1.1 cm ，HN=3.3 cm .
(1)写出其他(qítā)对应边及对应角； (2)求线段NM及线段HG的长度.
解： (1)∵△EFG≌△NMH,∴最长边FG和MH是对应(duìyìng)边， 其他对应边是EF和NM、EG和NH；对应角是∠E和∠N、 ∠EGF和∠NHM. (2)由(1)知NM=EF=2.1 cm ,GE=HN=3.3 cm ,
5.尺规作图
作一个角等于(děngyú)已知角
知道△ABC 的六个元素中的某三个元素，根据确定三角形的条件，以下四种情 况可作出△ABC： ① 已知三边；
② 已知两边(liǎngbiān)及其夹角； ③ 已知两角及其夹边；
④ 已知两角和其中一角的对边.
2021/12/13
第二十九页，共三十二页。
布置作业
沪科版数学八年级上册1全等三角形判定复习课件
求证：CD=AB＋BD A
B
D
C
课堂练习
5.如图：在四边形ABCD中，点E在边CD上，连接AE、BE并延长AE交BC
的延长线于点F，给出下列5个关系式：：①AD∥BC，②，DE=EC③
∠1=∠2，④∠3=∠4，⑤AD+BC=AB。将其中三个关系式作为已知，
另外两个作为结论，构成正确的命题。请用序号写出两个正确的命
• 变式1：以上条件不变，将△ABC绕点C顺时
针旋转10度，以上的结论还成立吗？
A
E
B D
C
例3变式2
• 例4.已知，△ABC和△ECD都是等边三角形，且 点B，C，D在一条直线上求证：BE=AD
• 变式：以上条件不变，将△ABC绕点C顺时针旋
转60度，以上的结论还成立吗？
E
A
D C
例3变式3
• 例5.已知，△ABC和△ECD都是等边三
角形，当△ABC绕点C顺时针旋转ɑ时，
连接BE，DA；结论BE=AD还成立吗？
若成立请加以证明。
E
A
E
A
B
B
D
C
D C
例3变式4
引申：例6.已知，△ABC和△ECD都是等边三角形，且点
B交，于CN，，D试在判一定条△直Ｃ线Ｍ上Ｎ，的AC形与状BE相交于M，CE与EAD相
解：△ＣＭＮ是等边三角形
A
M
课堂练习
3.已知点A，E，F，C在同一条直线上，且AE＝CF，过
E F两点分别作DE⊥AC，BF⊥AC，且AB＝CD，（
１）求证：BD平分 EF（2）若将△DEC的边EC沿AC方
向移动，变化为2时，其余条件不变，上述结论是否成立
，说明理由
B
D
C
课堂练习
5.如图：在四边形ABCD中，点E在边CD上，连接AE、BE并延长AE交BC
的延长线于点F，给出下列5个关系式：：①AD∥BC，②，DE=EC③
∠1=∠2，④∠3=∠4，⑤AD+BC=AB。将其中三个关系式作为已知，
另外两个作为结论，构成正确的命题。请用序号写出两个正确的命
• 变式1：以上条件不变，将△ABC绕点C顺时
针旋转10度，以上的结论还成立吗？
A
E
B D
C
例3变式2
• 例4.已知，△ABC和△ECD都是等边三角形，且 点B，C，D在一条直线上求证：BE=AD
• 变式：以上条件不变，将△ABC绕点C顺时针旋
转60度，以上的结论还成立吗？
E
A
D C
例3变式3
• 例5.已知，△ABC和△ECD都是等边三
角形，当△ABC绕点C顺时针旋转ɑ时，
连接BE，DA；结论BE=AD还成立吗？
若成立请加以证明。
E
A
E
A
B
B
D
C
D C
例3变式4
引申：例6.已知，△ABC和△ECD都是等边三角形，且点
B交，于CN，，D试在判一定条△直Ｃ线Ｍ上Ｎ，的AC形与状BE相交于M，CE与EAD相
解：△ＣＭＮ是等边三角形
A
M
课堂练习
3.已知点A，E，F，C在同一条直线上，且AE＝CF，过
E F两点分别作DE⊥AC，BF⊥AC，且AB＝CD，（
１）求证：BD平分 EF（2）若将△DEC的边EC沿AC方
向移动，变化为2时，其余条件不变，上述结论是否成立
，说明理由
沪科版数学八年级上册14.1全等三角形课件(共19张PPT)
如图，按同一底版印制的两枚邮票，它们的形状相同、大小一样。
全等形定义：能够完全重合的两个图形，叫做全等形.
全等形性质：如果两个图形全等，它们的形状相同，大小相等.
1.与下左图所示图形全等的是 ．
①、④
2.下列说法：①用一张底片冲洗出来的2张1寸相片是全等的； ②所有正三角形是全等形； ③面积相等的图形一定是全等形．其中正确的是 ．
两个三角形全等是通过什么方法验证的？
平移
解：对应边是：__________________________________
对应角是：__________________________________
AC与DF，AB与DE，BC与EF
∠A与∠D，∠B与∠E，∠C与∠F
A
C
B
如图△AOC≌△BOD
1.对应边是：________________________
2.∠AOC的对应角是________
∠A的对应角是________
OC与OD，AC与BD
∠BOD
∠B
O
D
小结：有对顶角的，对顶角也是对应角.
想一想： 有什么办法判断两个三角形全等？用数学式子表示两个三角形全等,并指出对应角、对应边.
旋转
A
B
C
D
A
A
B
B
D
C
如图△ABD≌△ABC
大角对大角，小角对小角
公共角一定是对应角
对顶角一定是对应角
同学们再见！
授课老师：
时间：2024年9月1日
第十四章 全等三角形
14.1 全等三角形
学习目标
学习重难点
重点
难点
1.了解全等形，明确全等三角形的概念.2.掌握全等三角形的性质，识别全等三角形的对应边和对应角.
全等形定义：能够完全重合的两个图形，叫做全等形.
全等形性质：如果两个图形全等，它们的形状相同，大小相等.
1.与下左图所示图形全等的是 ．
①、④
2.下列说法：①用一张底片冲洗出来的2张1寸相片是全等的； ②所有正三角形是全等形； ③面积相等的图形一定是全等形．其中正确的是 ．
两个三角形全等是通过什么方法验证的？
平移
解：对应边是：__________________________________
对应角是：__________________________________
AC与DF，AB与DE，BC与EF
∠A与∠D，∠B与∠E，∠C与∠F
A
C
B
如图△AOC≌△BOD
1.对应边是：________________________
2.∠AOC的对应角是________
∠A的对应角是________
OC与OD，AC与BD
∠BOD
∠B
O
D
小结：有对顶角的，对顶角也是对应角.
想一想： 有什么办法判断两个三角形全等？用数学式子表示两个三角形全等,并指出对应角、对应边.
旋转
A
B
C
D
A
A
B
B
D
C
如图△ABD≌△ABC
大角对大角，小角对小角
公共角一定是对应角
对顶角一定是对应角
同学们再见！
授课老师：
时间：2024年9月1日
第十四章 全等三角形
14.1 全等三角形
学习目标
学习重难点
重点
难点
1.了解全等形，明确全等三角形的概念.2.掌握全等三角形的性质，识别全等三角形的对应边和对应角.
第十一章 三角形复习整理 (第1课时 知识要点)数学八年级上册同步教学课件(人教版)
解：延长BC交OD于点M，如图所示．
∵多边形的外角和为360°，
∴∠OBC＋∠MCD＋∠CDM
＝360°－225°＝135°.
M
∵∠BOD＋∠OBC＋∠MCD＋∠CDM＝180°，
∴∠BOD＝45°.
针对练习
1.已知等腰三角形的一边长为4，另一边长为8，则这个等腰三角形的周长
为 (C ) A.16
B.20或16
C.20
D.12
2.若(a-1)2+|b-2|=0,则以a,b为边长的等腰三角形的周长为 5 .
考点二 三角形中的重要线段 例3. 如图，D是△ABC的边BC上任意一点，E、F分别是线段AD、CE的中
∠1=∠2=（180°－108°）÷2=36° ∠3=∠4=∠1=∠2=36°， ∴ ∠CAD=∠BAE－∠1－∠3=108°－36°－36°=36°．
课堂练习
1．长度分别为2，3，3，4的四根细木棒首尾相连，围成一个三角形(木
棒允许连接，但不允许折断)，得到的三角形的最长边为( B )
A．4
B．5
知识四 三 角 形 的 高 、 中 线 与 角 平 分 线
2.三角形的中线： ① 两个三角形的面积相等； ② 两个三角形的周长的差等于这两个三角形另两边的差. ③ 三条中线相交于一点（重心）
3.三角形的角平分线 A
B
D
∵ ∠ ABD= ∠ CBD
∴ AD是△ABC的角平分线
B
D
C
A EC
知识五 三 角 形 的 内 角 和 与 外 角 的 性 质
1.三角形的内角和： ① 三角形三个内角的和等于180°. ② 直角三角形的两个锐角互余．
A A
B
C
人教版初中八年级上册数学-期末复习 第12章全等三角形 课件(共48张PPT)
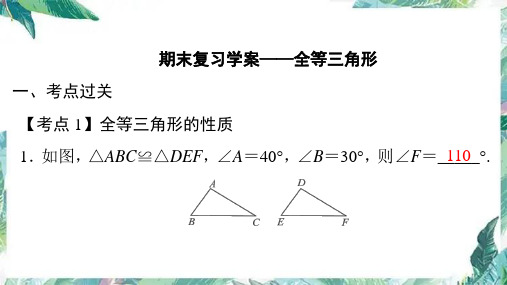
的依据是_H__L_.
第3题
4．如图，AO＝BO，下列条件不能判定△AOD≌△BOC 的是( B )
A．OC＝OD C． ∠A＝∠B
第4题 B．AD＝BC D．∠C＝∠D
【考点 3】角平分线的性质和判定 5．如图，在△ABC 中，∠C＝90°，AD 平分∠BAC，AB＝6，CD
＝2，则点 D 到 AB 的距离是_2_，△ABD 的面积是_6_.
用 HL 证 Rt△ABC≌Rt△DEC. 得 ∠A＝∠D， 从而 AB∥DE.
10．如图，在△ABC 和△DEF 中，下面有四个条件，请你在其中 选 3 个作为题设，余下的 1 个作为结论，写一个真命题，并加 以证明. ① AB＝DE；②AC＝DF；③∠ABC＝∠DEF；④BE ＝CF.
题设：①③④；结论：② 证明提示：BC＝BE＋EC＝CF＋EC＝EF. 用 SAS 证明△ABC≌△DEF，从而 AC＝DF.
证明：(1)如图，连接 AF， ∵Rt△ABC≌Rt△ADE，∴AC＝AE，BC＝DE， ∵∠ACB＝∠AEF＝90°，AF＝AF， ∴Rt△ACF≌Rt△AEF， ∴CF＝EF.∴BF＋EF＝BF＋CF＝BC， ∴BF＋EF＝DE；
(2)如图，DE＝BF－EF，理由是： 连接 AF，∵Rt△ABC≌Rt△ADE， ∴AC＝AE，BC＝DE， ∵∠E＝∠ACF＝90°，AF＝AF， ∴Rt△ACF≌Rt△AEF，∴CF＝EF， ∴DE＝BC＝BF－FC＝BF－EF，即 DE＝BF－EF.
24．已知 Rt△ABC≌Rt△ADE，其中∠ACB＝∠AED＝90°. (1)将这两个三角形按图①方式摆放，使点 E 落在 AB 上，DE 的延长线交 BC 于点 F.求证：BE＋EF＝DE； (2)改变△ADE 的位置，使 DE 交 BC 的延长线于点 F(如图②)， 写出此时 BF、EF 与 DE 之间的等量关系，并说明理由．
第3题
4．如图，AO＝BO，下列条件不能判定△AOD≌△BOC 的是( B )
A．OC＝OD C． ∠A＝∠B
第4题 B．AD＝BC D．∠C＝∠D
【考点 3】角平分线的性质和判定 5．如图，在△ABC 中，∠C＝90°，AD 平分∠BAC，AB＝6，CD
＝2，则点 D 到 AB 的距离是_2_，△ABD 的面积是_6_.
用 HL 证 Rt△ABC≌Rt△DEC. 得 ∠A＝∠D， 从而 AB∥DE.
10．如图，在△ABC 和△DEF 中，下面有四个条件，请你在其中 选 3 个作为题设，余下的 1 个作为结论，写一个真命题，并加 以证明. ① AB＝DE；②AC＝DF；③∠ABC＝∠DEF；④BE ＝CF.
题设：①③④；结论：② 证明提示：BC＝BE＋EC＝CF＋EC＝EF. 用 SAS 证明△ABC≌△DEF，从而 AC＝DF.
证明：(1)如图，连接 AF， ∵Rt△ABC≌Rt△ADE，∴AC＝AE，BC＝DE， ∵∠ACB＝∠AEF＝90°，AF＝AF， ∴Rt△ACF≌Rt△AEF， ∴CF＝EF.∴BF＋EF＝BF＋CF＝BC， ∴BF＋EF＝DE；
(2)如图，DE＝BF－EF，理由是： 连接 AF，∵Rt△ABC≌Rt△ADE， ∴AC＝AE，BC＝DE， ∵∠E＝∠ACF＝90°，AF＝AF， ∴Rt△ACF≌Rt△AEF，∴CF＝EF， ∴DE＝BC＝BF－FC＝BF－EF，即 DE＝BF－EF.
24．已知 Rt△ABC≌Rt△ADE，其中∠ACB＝∠AED＝90°. (1)将这两个三角形按图①方式摆放，使点 E 落在 AB 上，DE 的延长线交 BC 于点 F.求证：BE＋EF＝DE； (2)改变△ADE 的位置，使 DE 交 BC 的延长线于点 F(如图②)， 写出此时 BF、EF 与 DE 之间的等量关系，并说明理由．
湘教版八年级上册数学 2.1.1三角形的边 复习课后习题练习课件
(3)你能说明上述结论为什么成立吗？ 解：延长BP交AC于点D. 在△ABD中，AB＋AD>BP＋PD①， 在△PDC中，PD＋DC>PC②. ①＋②，得AB＋AD＋PD＋DC>BP＋PD＋PC， 即AB＋AC>PB＋PC.
14．小明和小红在一本数学资料书上看到这样一道竞 赛题：“已知△ABC的三边长分别为a，b，c，且 |b＋c－2a|＋(b＋c－5)2＝0，求b的取值范围．”
5．【2019•台州】下列长度的三条线段，能组成三角形的 是( B ) A．3，4，8 B．5，6，10 C．5，5，11 D．5，6，11
6．【中考•金华】若长度分别为a，3，5的三条线段能组 成一个三角形，则a的值可以是( C ) A．1 B．2 C．3 D．8
7．【中考•自贡】已知三角形的两边长分别为1和4，第三 边长为整数，则该三角形的周长为( C ) A．7 B．8 C．9 D．10
(3)小明和小红一起去问数学老师，老师说：“根据你们 二人的求解，利用书上三角形的三边满足的关系，即 可求出答案．”你知道答案吗？请写出过程．
解：由三角形的三边关系， 得当 5－b≥52，即 b≤52时，b＋52＞5－b， 所以54＜b≤52； 当 5－b＜52，即 b＞52时，5－b＋52＞b，所以52＜b＜145； 所以 b 的取值范围为54＜b＜145.
12．某木材市场上木棒规格与价格如下表：
规格
1m 2m 3m 4m 5m 6m
价格(元/根) 10 15 20 25 30 35
小明的爷爷要做一个三角形的支架养鱼用，现有两根 长度为3 m和5 m的木棒，还需要到该木材市场上购买 一根．
(1)有几种规格的木棒可供小明的爷爷选择？ 解：设第三根木棒长x m，由三角形的三边关系可得 5－3＜x＜5＋3，即2＜x＜8.故规格为3 m，4 m，5 m， 6 m的四种木棒可供小明的爷爷选择．
人教版数学八年级上册第十一章 三角形说课课件(共33张PPT)
4.说教法学法
➢说学法
学生的学习应当是一个生动活泼的、主动的和 富有个性的过程。所以利用学生的好奇心设疑， 组织活泼互动、有效的教学活动，鼓励学生积极 参与，在学生在经历观察、实验、猜测、推理、 验证等活动过程中，体会了数学学习方法，体验 到了自主探索和合作交流快乐，更好更准确的理 解和掌握了本节课的内容。
第十一章 《三角形》说课
第十一章 《三角形》说课
接下来我将从以下六个方面展开我的说课
说课标
说教材
说学情
说教学 设计
说教学 评价
说教法 学法
说课标
1.说课标
➢ 初二学段的课程标准
经历探索物体与图形基本性质、变换、位置关系的 过程，掌握三角形、多边形以及轴对称等的基本性质， 掌握基本的识图、作图等技能；体会证明的必要性、掌 握基本的推理技能；在探索图形的性质、图形的变换以 及平面图形与空间几何体的相互转换等活动过程中，初 步建立空间观念，发展几何直觉。
5.说教学设计
重难点突破二：探究多边形的内角和公式
追问1:这里连接对角线起到什么作用？
将四边形分割成两个三角形， 进而将四边形的内角和问题转化为 两个三角形所有内角和的问题。
5.说教学设计
重难点突破二：探究多边形的内角和公式
追问2:类比前面的过程，你能探索出五边形的内角 和吗？六边形呢？
基于以上分析，学生不 难想到将五边形、六边形分 别分割成三个、四个三角形， 从而得到它们的内角和 。
l
通过添加与边BC
BA C
平行的辅助线l，利用
平行线的性质和平角
的定义即可证明结论．
B
C
重难点突破一：探究并证明三角形内角和定理
追问3 结合下图，你能写出已知、求证和证明吗？ 已知：△ABC．求证：∠A +∠B + ∠C = 180°．