新疆2019-2020第二学期七年级数学期末测试题
2019-2020学年度上学期七年级数学形成性测试题(十)(共12套)
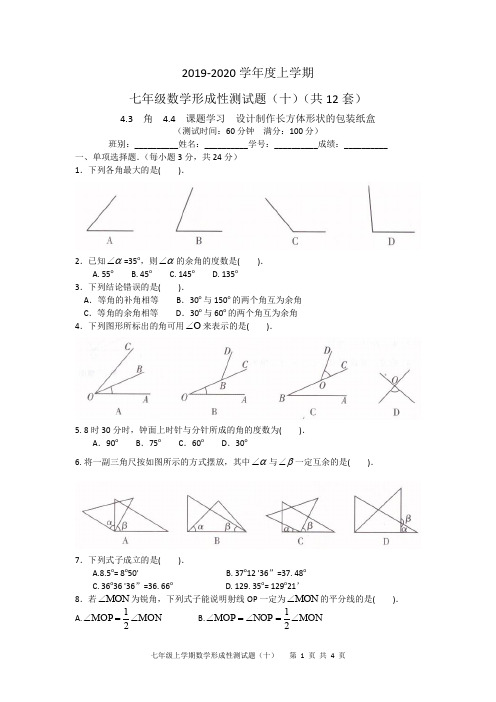
2019-2020学年度上学期七年级数学形成性测试题(十)(共12套)4.3 角 4.4 课题学习 设计制作长方体形状的包装纸盒(测试时间:60分钟 满分:100分)班别:__________姓名:__________学号:__________成绩:__________一、单项选择题.(每小题3分,共24分) 1.下列各角最大的是( ).2.已知α∠=35o ,则α∠的余角的度数是( ). A. 55o B. 45o C. 145o D. 135o3.下列结论错误的是( ).A .等角的补角相等B .30o 与150o 的两个角互为余角C .等角的余角相等D .30o 与60o 的两个角互为余角 4.下列图形所标出的角可用O ∠来表示的是( ).5. 8时30分时,钟面上时针与分针所成的角的度数为( ). A .90o B .75o C .60o D .30o6. 将一副三角尺按如图所示的方式摆放,其中α∠与β∠一定互余的是( ).7.下列式子成立的是( ).A.8.5o = 8o 50'B. 37o 12 '36”=37. 48oC. 36o 36 '36”=36. 66oD. 129. 35o = 129o 21’8.若MON ∠为锐角,下列式子能说明射线OP 一定为MON ∠的平分线的是( ). A.MON MOP ∠=∠21 B.MON NOP MOP ∠=∠=∠21C.NOP MOP ∠=∠D.NOP MOP MON ∠+∠=∠ 二、填空题.(每小题4分,共24分)9.若A ∠=43o ,则A ∠的补角的度数是_________。
10.计算:48o 39’+67o 41’=______________.11.已知o18021=∠+∠,o18032=∠+∠,根据____________,得31∠=∠. 12.如图,把一张长方形纸片折叠后,量得oAOB 110=∠,,则=∠OC B ,_______o13.如图,在灯塔D 处观测到轮船A 位于北偏西54O 方向上,轮船曰位于南偏东15O 方向上,则∠AOB 的度数为_____________。
新疆乌鲁木齐市第八中学2019-2020学年第二学期七年级(下)期末考试数学试卷 解析版

2019-2020学年新疆乌鲁木齐八中七年级(下)期末数学试卷一.选择题(共8小题)1.下列各点中,在第三象限的点是()A.(﹣1,﹣4)B.(1,﹣4)C.(﹣1,4)D.(1,4)2.若a<b,则下列不等式中正确的是()A.a﹣5<b﹣5B.a﹣b>0C.D.﹣3a<﹣3b 3.如图,DE∥BC,BE平分∠ABC,若∠1=70°,则∠CBE的度数为()A.20°B.35°C.55°D.70°4.下列调查中,适宜采用全面调查方式的是()A.调查市场上矿泉水的质量情况B.了解全国中学生的身高情况C.调查某批次电视机的使用寿命D.调查乘坐动车的旅客是否携带了违禁物品5.在下列各数:3.1415926,,0.2,,,,中,无理数的个数是()A.2B.3C.4D.56.不等式4﹣3x≥2x﹣6的非负整数解有()A.1个B.2个C.3个D.4个7.某车间有60名工人生产太阳镜,1名工人每天可生产镜片200片或镜架50个.应如何分配工人生产镜片和镜架,才能使产品配套?设安排x名工人生产镜片,y名工人生产镜架,则可列方程组()A.B.C.D.8.某大型超市从生产基地购进一批水果,运输过程中质量损失10%,假设不计超市其它费用,如果超市要想至少获得20%的利润,那么这种水果的售价在进价的基础上应至少提高()A.40%B.33.4%C.33.3%D.30%二.填空题(共6小题)9.“x的2倍与3的差不小于1”用不等式表示为:.10.在平面直角坐标系中,点A(x﹣1,2﹣x)关于y轴对称的对称点在第一象限,则实数x的取值范围是.11.如图,计划把水从河中引到水池A中,先过点A作AB⊥CD,垂足为点B,然后沿AB 开渠,能使所开的渠道最短,这样设计的依据是.12.四个形状、大小相同的长方形,如图,拼成一个大的长方形,如果大长方形的周长为28厘米,那么,每块小长方形的面积是平方厘米.13.小明统计了他家今年5月份打电话的次数及通话时间,并列出了频数分布表:通话时间x/min0<x≤55<x≤1010<x≤1515<x≤20频数(通话次数)201695则通话时间超过15min的频率为.14.规定用符号[x]表示一个实数的整数部分,例如[3.69]=3.[]=1,按此规定,[﹣1]=.三.解答题(共9小题)15.计算:(﹣1)3++(﹣1)0﹣.16.解方程组.17.解不等式组:.18.按要求完成下列证明如图,AB∥CD,CB∥DE,求证:∠B+∠D=180°.证明:∵AB∥CD,∴∠B=().∵CB∥DE,∴∠C+=180°().∴∠B+∠D=180°.19.在图中,A(﹣1,4)、B(﹣4,﹣1)、C(1,1),将△ABC向右平移5个单位长度,再向上平移3个单位长度.请回答下列问题.(1)平移后的三个顶点坐标分别为:A1,B1,C1;(2)画出平移后△A1B1C;(3)求△ABC的面积.20.如图,已知直线AB和CD相交于点O,∠COE=90°,OF平分∠AOE.(1)写出∠BOE的余角;(2)若∠COF的度数为29°,求∠BOE的度数.21.体育委员统计了全班同学60秒跳绳的次数,并列出下面的频数分布表:次数60≤x<8080≤x<100100≤x<120频数1225次数120≤x<140140≤x<160160≤x<180频数1552(1)全班有多少学生?(2)组距是多少?组数是多少?(3)跳绳次数x在100≤x<140范围的学生占全班学生的百分之几?(4)画出适当的统计图表示上面的信息.(5)你怎样评价这个班的跳绳成绩?22.张翔从学校出发骑自行车去县城,中途因道路施工步行一段距离,1.5h后到达县城.他骑车的平均速度是15km/h,步行的平均速度是5km/h,路程长20km,他骑车与步行各用多少时间?23.为提高饮水质量,越来越多的居民选购家用净水器.一商场抓住商机,从厂家购进了A、B两种型号家用净水器共160台,A型号家用净水器进价是150元/台,B型号家用净水器进价是350元/台,购进两种型号的家用净水器共用去36000元.(1)求A、B两种型号家用净水器各购进了多少台;(2)为使每台B型号家用净水器的毛利润是A型号的2倍,且保证售完这160台家用净水器的毛利润不低于11000元,求每台A型号家用净水器的售价至少是多少元.(注:毛利润=售价﹣进价)参考答案与试题解析一.选择题(共8小题)1.下列各点中,在第三象限的点是()A.(﹣1,﹣4)B.(1,﹣4)C.(﹣1,4)D.(1,4)【分析】根据平面直角坐标系中各个象限的点的坐标的符号特点即可解答.【解答】解:∵第三象限的点的坐标特点是横纵坐标均小于0,∴结合四个选项中只有A(﹣1,﹣4 )符合条件.故选:A.2.若a<b,则下列不等式中正确的是()A.a﹣5<b﹣5B.a﹣b>0C.D.﹣3a<﹣3b 【分析】根据不等式的性质,逐项判断即可.【解答】解:∵a<b,∴a﹣5<b﹣5,∴选项A符合题意;∵a<b,∴a﹣b<0,∴选项B不符合题意;∵a<b,∴a<b,∴选项C不符合题意;∵a<b,∴﹣3a>﹣3b,∴选项D不符合题意.故选:A.3.如图,DE∥BC,BE平分∠ABC,若∠1=70°,则∠CBE的度数为()A.20°B.35°C.55°D.70°【分析】根据平行线的性质可得∠1=∠ABC=70°,再根据角平分线的定义可得答案.【解答】解:∵DE∥BC,∴∠1=∠ABC=70°,∵BE平分∠ABC,∴∠CBE=∠ABC=35°,故选:B.4.下列调查中,适宜采用全面调查方式的是()A.调查市场上矿泉水的质量情况B.了解全国中学生的身高情况C.调查某批次电视机的使用寿命D.调查乘坐动车的旅客是否携带了违禁物品【分析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果较近似.【解答】解:A、数量较大,不易全面调查,适合抽查,故本选项错误;B、数量较大,不易全面调查,适合抽查,故本选项错误;C、数量较大,不易全面调查,适合抽查,故本选项错误;D、事关重大,必须进行全面调查,故本选项正确.故选:D.5.在下列各数:3.1415926,,0.2,,,,中,无理数的个数是()A.2B.3C.4D.5【分析】根据无理数的定义即可判定求解.【解答】解:在下列各数:3.1415926,,0.2,,,,中,根据无理数的定义可得,无理数有,两个.故选:A.6.不等式4﹣3x≥2x﹣6的非负整数解有()A.1个B.2个C.3个D.4个【分析】首先利用不等式的基本性质解不等式,再从不等式的解集中找出适合条件的正整数即可.【解答】解:移项,得﹣3x﹣2x≥﹣6﹣4,合并同类项,得:﹣5x≥﹣10,系数化成1得:x≤2.则非负整数解是:0、1和2共3个.故选:C.7.某车间有60名工人生产太阳镜,1名工人每天可生产镜片200片或镜架50个.应如何分配工人生产镜片和镜架,才能使产品配套?设安排x名工人生产镜片,y名工人生产镜架,则可列方程组()A.B.C.D.【分析】等量关系为:生产镜片工人数量+生产镜架工人数量=60,镜片数量=2×镜架数量,把相关数值代入即可求解.【解答】解:设安排x名工人生产镜片,y名工人生产镜架,由题意,得.故选:C.8.某大型超市从生产基地购进一批水果,运输过程中质量损失10%,假设不计超市其它费用,如果超市要想至少获得20%的利润,那么这种水果的售价在进价的基础上应至少提高()A.40%B.33.4%C.33.3%D.30%【分析】缺少质量和进价,应设购进这种水果a千克,进价为y元/千克,这种水果的售价在进价的基础上应提高x,则售价为(1+x)y元/千克,根据题意得:购进这批水果用去ay元,但在售出时,只剩下(1﹣10%)a千克,售货款为(1﹣10%)a×(1+x)y元,根据公式×100%=利润率可列出不等式,解不等式即可.【解答】解:设购进这种水果a千克,进价为y元/千克,这种水果的售价在进价的基础上应提高x,则售价为(1+x)y元/千克,由题意得:×100%≥20%,解得:x≥≈33.4%,经检验,x≥是原不等式的解.∵超市要想至少获得20%的利润,∴这种水果的售价在进价的基础上应至少提高33.4%.故选:B.二.填空题(共6小题)9.“x的2倍与3的差不小于1”用不等式表示为:2x﹣3≥1.【分析】首先表示x的2倍与3的差为2x﹣3,再表示不小于1可得不等式.【解答】解:由题意得:2x﹣3≥1.故答案为:2x﹣3≥1.10.在平面直角坐标系中,点A(x﹣1,2﹣x)关于y轴对称的对称点在第一象限,则实数x的取值范围是x<1.【分析】首先根据关于y轴对称的对称点所在象限可确定点A在第二象限,再根据第二象限内点的坐标符号可得不等式组,再解不等式组即可.【解答】解:∵点A(x﹣1,2﹣x)关于y轴对称的对称点在第一象限,∴点A(x﹣1,2﹣x)在第二象限,∴,解得:x<1,故答案为:x<1.11.如图,计划把水从河中引到水池A中,先过点A作AB⊥CD,垂足为点B,然后沿AB 开渠,能使所开的渠道最短,这样设计的依据是垂线段最短.【分析】根据垂线段的性质,可得答案.【解答】解:先过点A作AB⊥CD,垂足为点B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是垂线段最短;故答案为:垂线段最短.12.四个形状、大小相同的长方形,如图,拼成一个大的长方形,如果大长方形的周长为28厘米,那么,每块小长方形的面积是12平方厘米.【分析】设每块小长方形的长为xcm,宽为ycm,则由图形可得长是宽的3倍,再结合周长为28厘米,可列出二元一次方程组,解出长和宽,然后相乘即可得每个小长方形的面积.【解答】解:设每块小长方形的长为xcm,宽为ycm,由题意得:解得∴每块小长方形的面积是:6×2=12(cm2)故答案为:12.13.小明统计了他家今年5月份打电话的次数及通话时间,并列出了频数分布表:通话时间x/min0<x≤55<x≤1010<x≤1515<x≤20频数(通话次数)201695则通话时间超过15min的频率为0.1.【分析】根据频率的计算公式:频率=计算即可.【解答】解:通话时间超过15min的频率为:=0.1,故答案为:0.1.14.规定用符号[x]表示一个实数的整数部分,例如[3.69]=3.[]=1,按此规定,[﹣1]=2.【分析】先求出(﹣1)的范围,再根据范围求出即可.【解答】解:∵9<13<16,∴3<<4,∴2<﹣1<3,∴[﹣1]=2.故答案是:2.三.解答题(共9小题)15.计算:(﹣1)3++(﹣1)0﹣.【分析】先根据数的乘方法则与开方法则、0指数幂的运算法则计算出各数,再根据实数混合运算的法则进行计算即可.【解答】解:原式=﹣1+2+1﹣=.16.解方程组.【分析】方程组利用加减消元法求出解即可.【解答】解:,②﹣①得:x=6,将x=6代入①得:y=4,则方程组的解为.17.解不等式组:.【分析】本题可根据不等式组分别求出x的取值,然后画出数轴,数轴上相交的点的集合就是该不等式的解集.若没有交集,则不等式无解.【解答】解:不等式组可以转化为:,在坐标轴上表示为:∴不等式组的解集为x<﹣7.18.按要求完成下列证明如图,AB∥CD,CB∥DE,求证:∠B+∠D=180°.证明:∵AB∥CD,∴∠B=∠C(两直线平行,内错角相等).∵CB∥DE,∴∠C+∠D=180°(两直线平行,同旁内角互补).∴∠B+∠D=180°.【分析】直接利用平行线的性质分别得出各角之间的关系,进而得出答案.【解答】证明:∵AB∥CD,∴∠B=∠C(两直线平行,内错角相等),∵CB∥DE,∴∠C+∠D=180°(两直线平行,同旁内角互补),∴∠B+∠D=180°.故答案为:∠C,两直线平行,内错角相等;∠D;两直线平行,同旁内角互补.19.在图中,A(﹣1,4)、B(﹣4,﹣1)、C(1,1),将△ABC向右平移5个单位长度,再向上平移3个单位长度.请回答下列问题.(1)平移后的三个顶点坐标分别为:A1(4,7),B1(1,2),C1(6,4);(2)画出平移后△A1B1C;(3)求△ABC的面积.【分析】(1)根据横坐标右移加,左移减,纵坐标上移加,下移减即可得出三个顶点的坐标;(2)根据网格结构分别找到三个顶点的位置,再顺次连接即可得出答案;(3)将△ABC补全为矩形,然后利用作差法求解即可.【解答】解:(1)∵A(﹣1,4)、B(﹣4,﹣1)、C(1,1),将△ABC向右平移5个单位长度,再向上平移3个单位长度,∴A1坐标为(4,7),点B1坐标为(1,2),C1坐标为(6,4);故答案为:(4,7),(1,2),(6,4);(2)所画图形如下:(3)如图,S△ABC=S矩形EBGF﹣S△ABE﹣S△GBC﹣S△AFC=5×55×35×22×3=255﹣3=;20.如图,已知直线AB和CD相交于点O,∠COE=90°,OF平分∠AOE.(1)写出∠BOE的余角;(2)若∠COF的度数为29°,求∠BOE的度数.【分析】(1)根据对顶角相等和余角的定义解答即可;(2)首先根据∠COF=29°,∠COE=90°,求出∠EOF的度数,再根据角平分线的概念求得∠AOE,再利用邻补角的关系求得∠BOE的度数.【解答】解:(1)∵直线AB和CD相交于点O,∠COE=90°,∴∠BOD=∠AOC,∠DOE=90°,∴∠BOE+∠BOD=90°,∴∠BOE+∠AOC=90°,∴∠BOE的余角是∠BOD和∠AOC;(2)∵∠COF=29°,∠COE=90°,∴∠EOF=90°﹣29°=61°,又OF平分∠AOE,∴∠AOE=122°,∵∠BOE+∠AOE=180°,∴∠BOE=180°﹣∠AOE=58°.21.体育委员统计了全班同学60秒跳绳的次数,并列出下面的频数分布表:次数60≤x<8080≤x<100100≤x<120频数1225次数120≤x<140140≤x<160160≤x<180频数1552(1)全班有多少学生?(2)组距是多少?组数是多少?(3)跳绳次数x在100≤x<140范围的学生占全班学生的百分之几?(4)画出适当的统计图表示上面的信息.(5)你怎样评价这个班的跳绳成绩?【分析】(1)依据频数分布表的数据进行计算即可;(2)依据频数分布表的数据进行判断即可;(3)依据频数分布表的数据进行计算即可;(4)依据频数分布表的数据,画出频数分布直方图即可;(5)依据数据的分布特征进行判断即可.【解答】解:(1)全班学生人数为:1+2+25+15+5+2=50(人);(2)组距是20,组数是6;(3)跳绳次数x在100≤x<140范围的学生占全班学生的百分比为×100%=80%;(4)如图所示:(5)这个班的跳绳成绩,大多数同学在100≤x<140范围内,极少数同学在60≤x<100和160≤x<180范围内.22.张翔从学校出发骑自行车去县城,中途因道路施工步行一段距离,1.5h后到达县城.他骑车的平均速度是15km/h,步行的平均速度是5km/h,路程长20km,他骑车与步行各用多少时间?【分析】首先设他骑车用了x小时,根据骑车时间+步行时间=1.5小时表示出步行时间,再由骑车路程+步行路程=20千米,根据等量关系列出方程,解方程即可.【解答】解:设他骑车所用时间为x小时,则他步行的时间为:(1.5﹣x)小时,根据题意,得:15x+5(1.5﹣x)=20,解得:x=1.25,则他步行时间为:1.5﹣1.25=0.25(小时).答:他骑车用了1.25小时,步行用了0.25小时.23.为提高饮水质量,越来越多的居民选购家用净水器.一商场抓住商机,从厂家购进了A、B两种型号家用净水器共160台,A型号家用净水器进价是150元/台,B型号家用净水器进价是350元/台,购进两种型号的家用净水器共用去36000元.(1)求A、B两种型号家用净水器各购进了多少台;(2)为使每台B型号家用净水器的毛利润是A型号的2倍,且保证售完这160台家用净水器的毛利润不低于11000元,求每台A型号家用净水器的售价至少是多少元.(注:毛利润=售价﹣进价)【分析】(1)设A种型号家用净水器购进了x台,B种型号家用净水器购进了y台,根据“购进了A、B两种型号家用净水器共160台,购进两种型号的家用净水器共用去36000元.”列出方程组解答即可;(2)设每台A型号家用净水器的毛利润是a元,则每台B型号家用净水器的毛利润是2a元,根据保证售完这160台家用净水器的毛利润不低于11000元,列出不等式解答即可.【解答】解:(1)设A种型号家用净水器购进了x台,B种型号家用净水器购进了y台,由题意得,解得.答:A种型号家用净水器购进了100台,B种型号家用净水器购进了60台.(2)设每台A型号家用净水器的毛利润是a元,则每台B型号家用净水器的毛利润是2a元,由题意得100a+60×2a≥11000,解得a≥50,150+50=200(元).答:每台A型号家用净水器的售价至少是200元.。
2019-2020年七年级下学期第二次月考数学试题含答案解析

P 2P 1POCB AD 11题2019-2020年七年级下学期第二次月考数学试题含答案解析6.若不等式组⎩⎨⎧<≥b x ax 无解,则有( )A 、a b >B 、a b <C 、a b =D 、b ≤a 7.已知a>b>c>0,则以a 、b 、c 为三边组成三角形的条件是( ) A.b+c>a B.a+c>b C.a+b>c D.以上都不对 8.下列正多边形的组合中,能够铺满地面不留缝隙的是( ) A.正八边形和正三角形 B.正五边形和正八边形 C.正六边形和正三角形 D.正六边形和正五边形9.如果三角形的一个外角小于与它相邻的内角,那么这个三角形一定是( ) A.锐角三角形 B.直角三角形 C.钝角三角形 D.任意三角形10.现用甲.乙两种运输车将46吨抗旱物资运往灾区,甲种运输车载重5吨,乙种运输车载重4吨,安排车辆不超过10辆,则甲种运输车至少应安排( ) A.4辆 B.5辆 C.6辆 D.7辆 11.已知,如图,点P 关于OA 、OB 的对称点分别是P 1,P 2, 分别交OA 、OB 于C,D,P 1P 2=6cm,则△PCD 的周长为( ) A.3cm B.6cm C.12cm D.无法确定二、填空题(每题3分,7题共21分)12.把方程2x-3y+5=0写成用含有y 的代数式表示x 的形式为__________________;13.已知方程组{2x+y=7x+2y=8,则x -y = ,x +y = 。
14.一个两位数,两个数位上的数字一个是另一个的2倍,若把此两位数的两个数字对调,所得新数比原数大27,则此两位数是 .15..若不等式()327m x -<的解集为13x >-,则m 的值为 .16.、过m 边形的顶点能作7条对角线,n 边形没有对角线,k 边形有k 条对角线,则 (m-k )n =___.17.一个多边形的每一个外角都等于36°,则该多边形的内角和等于 .18.一个多边形的每一个内角都相等,并且它的一个外角与一个内角之比为2:3,则这个多边形是 边形. 三、作图题题目 一 二 三 四 总分 得分19.(6分)如图,直线a ⊥b,请你设计两个不同的轴对称图形,使a 、b 都是它的对称轴.abba20.(3分)将上图中的小船向左平移5格,画出平移后的小船.21.(3分)如图,A 、B 、C 三点表示三个镇的地理位置,随着乡镇工业的发展需要, 现三镇联合建造一所变电站,要求变电站到三镇的距离相等 ,请画出变电站的位置(用P 点表示),并简单说明理由.四、解答题22.解方程(组)(每题6分,共12分) (1)142312-+=-y y (2)5615.2320.4x y x y +=⎧⎨-=-⎩23.(6分)解不等式组⎪⎩⎪⎨⎧≤--<+2123932x x ,并把解集在数轴上表示出来24.(8分)已知正多边形的内角和与其外角和的和为900°,求边数及每个内角的度数CBA13题25.(8分)如图,在⊿ABC中,∠B=75º,∠C=45º,AD是高,AE是∠BAC的平分线,求∠DAE的度数.26.(8分)《一千零一夜》中有这样一段文字:有一群鸽子,其中一部分在树上欢歌,另一部分在地上觅食,树上的一只鸽子对地上觅食的鸽子说:“若从你们中飞上来一只,则树下的鸽子就是整个鸽群的三分之一,若从树上飞下去一只,则树上、树下的鸽子就一样多了。
2019-2020学年度第一学期期末考试七年级数学试题参考答案

2019—2020学年度第一学期期末考试七年级数学试题参考答案说明:解答题各小题只给出了一种解法及评分标准.其他解法,只要步骤合理,解答正确,均应给出相应的分数.一、选择题:每小题3分,满分30分题号 1 2 3 4 5 6 7 8 9 10答案 B D C B A B A C D C二、填空题:本题共5小题,每题3分,共15分11.1;12.36;13.-6;14.250;15.8m+12.三、解答题:本题共7小题,共55分.要写出必要的文字说明或演算步骤.16.(本小题6分)(每正确画出一个图形得2分,共6分)17.(本小题6分)解:(1)(1)A-2B=(3a2-5ab)-2(a2-2ab)1分=3a2-5ab-2a2+4ab 2分=a2-ab. 3分(2)∵|3a +1|+(2-3b )2=0,∴3a +1=0,2-3b =0,解得a =13-,b =23. 4分 ∴A -2B =a 2-ab . =2112333⎛⎫⎛⎫---⨯ ⎪ ⎪⎝⎭⎝⎭ 5分 =121993+=. 6分 18.(本小题7分)(1)画图:如图所示. 4分(每正确画出一条射线得2分)(2)解:由题意知:∠MOG =110°,∠MOA =40°, 5分∴∠AOG=∠MOG -∠MOA =110°-40°=70° 射线OG 表示的方向是北偏东70°. 7分19.(本小题8分)解:(1)设甲、乙两车合作还需要x 天运完垃圾,根据题意,得31151530x x ++= 2分解得:x =8 3分答:甲、乙两车合作还需要8天运完垃圾.4分 (2)设乙车每天租金为y 元,则甲车每天租金为(y +100)元,根据题意,得 (3+8)(y +100)+8y =3950 6分解得:y =150 7分150+100=250答:甲车每天租金为250元,乙车每天租金为150元. 8分20.(本小题8分)解:(1)∵OB 平分∠AOC ,∴∠BOC =21∠COA =21×30°=15°. 1分同理:∠DOC =21∠EOC =21×90°=45°. 2分∴∠BOD =∠BOC +∠DOC =15°+45°=60°. 3分(2)∵OB 平分∠AOC ,∴∠COA =2∠BOC =2α. 4分同理:∠EOC =2∠DOC =2β. 5分∴∠AOE =∠COA +∠EOC =2α+2β. 6分(3)∠AOE =2∠BOD . 8分21.(本小题9分)(1)答:第①步错误,原因是去括号时,2这项没有乘以3;2分第④步错误,原因是应该用8除以2,小马用2除以8了. 4分【原因只要叙述合理即可得分】(2)解:7531164y y ---=,去分母得:12-2(7-5y )=3(3y -1). 6分去括号得:12-14+10y =9y -3. 7分移项得:10y -9y =-3-12+14. 8分合并同类项,得:y =-1. 9分22.(本小题11分)解:(1)EF =2020-(-2020)=4040. 2分(2)①当点P 是线段AB 的中点时,则PA =PB .所以x -(-2)=3-x .解得:x =0.5. 4分②当点A 是线段PB 的中点时,则PA =AB .所以(-2)-x =3-(-2).解得:x =-7. 6分③当点B 是线段P A 的中点时,则PB =AB .所以x -3=3-(-2).解得:x =8. 8分(3)答:在点A 左侧存在一点Q ,使点Q 到点A ,B 的距离和为19. 9分解:设点Q 表示的数是y .因为QA +QB =19,所以(-2)-y +3-y =19. 10分解得:y=-9.所以点Q表示的数是-9.11分。
人教版2019-2020学年第一学期七年级数学期末模拟试题(B卷)(解析版)

人教版2019-2020学年第一学期七年级期末模拟试题(B卷)数学试卷考试时间:100分钟满分:120分姓名:__________ 班级:__________考号:__________注意事项:1、填写试题的答案请用黑色签字笔填写;2、班级、姓名、考号字迹务必填写工整.一、选择题(共10题;共30分)1.下列各数中,绝对值最小的数是()A.0B.1C.-3D.2.下列各图形中,不是正方体表面展开图的是( )A. B. C. D.3.如图,数轴A、B上两点分别对应实数a、b,则下列结论正确的是()A.a+b>0B.ab >0C.a-b>0D.<4.下列说法正确的是()A.不是单项式B.单项式的系数是1C.﹣7ad的次数是2D.3x﹣2y不是多项式5.方程的解是().A. B. C. D.6.将方程去分母,下面变形正确的是( )A. B. C. D.7.某种品牌的彩电降价30%以后,每台售价为元,则该品牌彩电每台原价应为()A.0.7a元B.0.3a元C.元D.元8.如图,点B在点A的方位是()A.南偏东B.北偏西C.西偏北D.东偏南9.多项式合并同类项后不含xy项,则k的值是()A. B. C. D.010.分数, , , , , , , , ,…将这列数排成如图形式,那么第8行第7个数是()A. B. C. D.二、填空题(共8题;共32分)11.如图,是用火柴棍摆出的一系列三角形图案,按这种方式摆下去,摆第5个图形时,需要的火柴棍为___________根.12.p在数轴上的位置如图所示,化简:=___________.13.如图是我市某连续7天的最高气温与最低气温的变化图,根据图中信息可知,这7天中最大的日温差是__________℃.14.计算:=___________.15.已知关于x的一元一次方程a(x-3)=2x-3a的解是x=3,则a=___________.16.若2x|m|-1 =5是一元一次方程,则m的值为____________.17.多项式是___________次__________项式.18.单项式的次数是_________________.三、解答题(一)(共3题;共20分)19.(8分)解方程:(1)(2)20.(6分)有理数a、b、c在数轴上的位置如图,化简:|a+b|-|b-1|-|a-c|-|1-c|.21.(6分)已知如图,点O在直线AB上,射线OC平分∠DOB.若∠COB=35°,求∠AOD的度数.22.(6分)如图A在数轴上所对应的数为-2.(1)点B在点A右边距A点4个单位长度,求点B所对应的数;(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点B以每秒2个单位长度沿数轴向右运动,当点A运动到-6所在的点处时,求A,B两点间距离.23.(7分)老师在黑板上书写了一个正确的演算过程,随后用一张纸挡住了一个二次三项式,形式如下:+3(x﹣1)=x2﹣5x+1(1)求所挡的二次三项式;(2)若x=﹣1,求所挡的二次三项式的值.24.(7分)某开发商进行商铺促销,广告上写着如下条款:投资者购买商铺后,必须由开发商代为租赁5年,5年期满后由开发商以比原商铺标价高20%的价格进行回购,投资者可在以下两种购铺方案中做出选择:方案一:投资者按商铺标价一次性付清铺款,每年可以获得的租金为商铺标价的10%.方案二:投资者按商铺标价的八五折一次性付清铺款,2年后每年可以获得的租金为商铺标价的10%,但要缴纳租金的10%作为管理费用.(1)请问:投资者选择哪种购铺方案,5年后所获得的投资收益率更高?为什么?(注:投资收益率=×100%)(2)对同一标价的商铺,甲选择了购铺方案一,乙选择了购铺方案二,那么5年后两人获得的收益将相差5万元.问:甲、乙两人各投资了多少万元?25.(9分)如图,在平面内有A、B、C三点,(1)画直线AC,线段BC,射线AB;(2)在(1)的条件下,在线段BC上任取一点D(不同于B、C),连接线段AD;(3)在(1)(2)的条件下,数数看,此时图中线段共有________条。
2019--2020第二学期期末考试七年级数学试题(附答案)

54 678 !"!,4 $$%($%!))
!!p@q# %!$*%#"$!0#! Ó×p§VØYÙb!
七年级数学试卷 98 第(页共-页
54 678 !#!,4
!!rs;<. k&()* )* ÚzxY1¨./-() L/ Û(* L0'(4(*+'.4 )!+Ü'(*. D#!
货 物种类
货厢型号 装货量
甲 乙
A
35x 吨 15x 吨
B
25(50-x)吨 35(50-x)吨
解:设用 A 型货厢 x 节,则用 B 型货厢(50-x)节,由题意,得 35x 25(50 x) 1530 15x 35(50 x) 1150
解得 28≤x≤30. 因为 x 为整数,所以 x 只能取 28,29,30.
所以∠CED=∠AEF=55°,
七年级数学参考答案,第 1页,共 3 页
所以∠ACD=180°-∠CED-∠D =180°-55°-42=83°.
22. (7 分)∠3 两直线平行,同位角相等 已知 等量代换 DG 内错角相等,两直线平行。 两直线平行,同旁内角互补。
23.(9 分)
分组 600≤ x <800 800≤ x <1000 1000≤ x <1200 1200≤ x <1400 1400≤ x <1600 1600≤ x <1800
七年级数学试卷 98 第,页共-页
54 678 !+!##4
!!>WXµ±®FYZ[#*("\GYZ[##*"\]^1?ZUÝ_Z[X`ab ?ZUic() \YÑCDZd*"e!;<FYZ[(*\#GYZ[#*\ifg1 e( hZdFYZ[!*\#GYZ[(*\ifg1e) hZdij²Ü]^ () \Y ZdDe®klYXmO: lßàCËn.O:
北师大版七年级数学下册2019-2020年度第二学期期末模拟测试卷一(含答案)

北师大版七年级数学下册2019-2020 年度第二学期期末模拟测试卷一一、选择题(共10 小题,每小题 3 分,计30 分,每小题只有一个选项是符合要求的)1.下列计算正确的是()A.3a2﹣4a2=a2 B.a2•a3=a6 C.a10÷a5=a2 D.(a2)3=a62.下列算式能用平方差公式计算的是()A.(2a+b)(2b﹣a)B.C.(3x﹣y)(﹣3x+y)D.(﹣m﹣n)(﹣m+n)3.将一张矩形的纸对折,然后用笔尖在上面扎出“B”,再把它铺平,你可见到()A.B.C.D.4.将一质地均匀的正方体骰子掷一次,观察向上一面的点数,与点数3 相差2 的概率是()A.B.C.D.5.已知三角形三边分别为2,a﹣1,4,那么a 的取值范围是()A.1<a<5 B.2<a<6 C.3<a<7 D.4<a<66.星期天,小王去朋友家借书,下图是他离家的距离y(千米)与时间x(分钟)的函数图象,根据图象信息,下列说法正确的是()A.小王去时的速度大于回家的速度B.小王在朋友家停留了 10 分钟C.小王去时所花的时间少于回家所花的时间D.小王去时走上坡路,回家时走下坡路7.三角形的三条高线的交点在三角形的一个顶点上,则此三角形是()A.直角三角形B.锐角三角形C.钝角三角形D.等腰三角形8.已知实数a、b 满足a+b=2,ab=,则a﹣b=()A.1 B.﹣ C.±1 D.±9.如图:∠A+∠B+∠C+∠D+∠E+∠F 等于()A.180°B.360°C.540°D.720°10.如图,在△ABC 中,点D、E、F 分别是BC、AD、EC 的中点,若△ABC 的面积是16,则△BEF 的面积为()A.4 B.6 C.8 D.10二、填空题(共 4 小题,每小题 3 分,计12 分)11.上海合作组织青岛峰会期间,为推进“一带一路”建设,中国决定在上海合作组织银行联合体框架内,设立300 亿元人民币等值专项贷款,将300 亿元用科学记数法表示为元.12.∠1 与∠2 有一条边在同一直线上,且另一边互相平行,∠1=60°,则∠2=.13.如图,点P 关于OA、OB 的对称点分别为C、D,连接CD,交OA 于M,交OB 于N,若PMN 的周长=8 厘米,则CD 为厘米.14.如图,已知∠BAC=∠DAE=90°,AB=AD,要使△ABC≌△ADE,还需要添加的条件是(只需添加一个条件即可)三、解答题(共9 小题,计78 分解答应写出过程)15.(12分)计算(1)106÷10﹣2×100(2)(a+b﹣3)(a﹣b+3)(3)103×97(利用公式计算)(4)(﹣3a2b)2(2ab2)÷(﹣9a4b2)16.(6分)已知:如图,∠A=∠F,∠C=∠D.求证:BD∥CE.17.(6分)先化简,再求值:[(x+2y)2﹣(3x+y)(3x﹣y)﹣5y2]÷(2x),其中x=﹣,y=1.18.(6分)如图,在正方形网格中,△ABC 是格点三角形,画出△ABC 关于直线l对称的△A1B1C1.19.(9分)将分别标有数字 1,2,3 的三张卡片洗匀后,背面朝上放在桌面上.请完成下列各题.(1)随机抽取1 张,求抽到奇数的概率.(2)随机抽取一张作为十位上的数字(不放回),再抽取一张作为个位上的数字,能组成哪些两位数?(3)在(2)的条件下,试求组成的两位数是偶数的概率.20.(8分)如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.(1)求证:△ABC≌△DEF;(2)若∠A=55°,∠B=88°,求∠F 的度数.21.(9分)如图,直线 AB 与 CD 相交于点 O,∠AOM=90°.(1)如图1,若射线OC 平分∠AOM,求∠AOD 的度数;(2)如图2,若∠BOC=4∠NOB,且射线OM 平分∠NOC,求∠MON 的度数.22.(10分)已知一个等腰三角形的两个内角分别为(2x﹣2)°和(3x﹣5)°,求这个等腰三角形各内角的度数.23.(12 分)如图 1,在△ABC 中,∠BAC=90°,AB=AC,过点 A 作直线 DE,且满足BD⊥DE 于点 D,CE⊥DE 于点 E,当 B,C 在直线 DE 的同侧时,(1)求证:DE=BD+CE.(2)如果上面条件不变,当B,C 在直线DE 的异侧时,如图2,问BD、DE、CE 之间的数量关系如何?写出结论并证明.(3)如果上面条件不变,当B,C 在直线DE 的异侧时,如图3,问BD、DE、CE 之间的数量关系如何?写出结论并证明.参考答案一、选择题1.D.2.D.3.C.4.B.5.C.6.B.7.A.8.C.9.B.10.A.二、填空题(共4 小题,每小题3 分,计12 分)11.3×1010.12.60°或120°.13.8.14.AE=AC.三、解答题(共9 小题,计78 分解答应写出过程)15.解:(1)原式=106+2+0=108;(2)原式=a2﹣(b﹣3)2=a2﹣b2+6b﹣9;(3)原式=(100+3)×(100﹣3)=1002﹣32=10000﹣9=9991;(4)原式=(9a4b2)•(2ab2)÷(﹣9a4b2)=﹣2ab2.16.证明:∵∠A=∠F,∴AC∥DF,∴∠C=∠FEC,∵∠C=∠D,∴∠D=∠FEC,∴BD∥CE.17.解:原式=(x2+4xy+4y2﹣9x2+y2﹣5y2)÷2x=(﹣8x2+4xy)÷2x=﹣4x+2y,当x=﹣、y=1 时,原式=﹣4×(﹣)+2×1=2+2=4.18.解:如图,△A1B1C1 即为所求.19.解:(1)在这三张卡片中,奇数有:P(抽到奇数)=;(2)可能的结果有:(1,2)、(1,3)、(2,1)、(2,3)、(3,1)、(3,2);(3)由(2)得组成的两位数是偶数的概率==.20.证明:(1)∵AC=AD+DC,DF=DC+CF,且AD=CF∴AC=DF在△ABC 和△DEF 中,∴△ABC≌△DEF(SSS)(2)由(1)可知,∠F=∠ACB∵∠A=55°,∠B=88°∴∠ACB=180°﹣(∠A+∠B)=180°﹣(55°+88°)=37°∴∠F=∠ACB=37°21.解(1)∵∠AOM=90°,OC 平分∠AOM,∴∠AOC=∠AOM=×90°=45°,∵∠AOC+∠AOD=180°,∴∠AOD=180°﹣∠AOC=180°﹣45°=135°,即∠AOD 的度数为135°;(2)∵∠BOC=4∠NOB∴设∠NOB=x°,∠BOC=4x°,∴∠CON=∠COB﹣∠BON=4x°﹣x°=3x°,∵OM 平分∠CON,∴∠COM=∠MON=∠CON=x°,∵∠BOM=x+x=90°,∴x=36°,∴∠MON=x°=×36°=54°,即∠MON 的度数为54°.22.解:①当(2x﹣2)°和(3x﹣5)°是两个底角时,2x﹣2=3x﹣5,x=3,∴三个内角分别是4°,4°,172°;②当2x﹣2 是顶角时,2x﹣2+2(3x﹣5)=180°,解得x=24,∴三个内角分别是46°,67°,67°;③当3x﹣5 是顶角时,3x﹣5+2(2x﹣2)=180°,解得x=27,∴三个内角分别是76°,52°,52°23.(1)证明:如图1,∵BD⊥DE,CE⊥DE,∴∠D=∠E=90°,∵∠BAC=90°,∴∠BAD+∠CAE=90°.∵∠BAD+∠ABD=90°,∴∠CAE=∠ABD.在△ADB 和△CEA 中,,∴△ADB≌△CEA(AAS),∴BD=AE,AD=CE,∵DE=AD+AE,∴DE=CE+BD;(2)解:BD=DE+CE,理由:如图2,∵BD⊥DE,CE⊥DE,∴∠ADB=∠CEA=90°.∴∠BAD+∠ABD=90°.∵∠BAD+∠EAC=90°∴∠ABD=∠EAC.在△ADB 和△CEA 中,,∴△ADB≌△CEA(AAS),∴BD=AE,AD=CE.∵AE=AD+ED,∴BD=DE+CE.(3)解:DE=CE﹣BD,理由是:如图3,同理易证得:△ABD≌△CAE(AAS),∴BD=AE,AD=CE,∵DE=AD﹣AE,∴DE=CE﹣BD.。
2020苏科版数学七年级下册《期末考试卷》(附答案)

2019-2020学年度第二学期期末测试苏科版七年级数学试题学校________ 班级________ 姓名________ 成绩________一、选择题(本大题共有6小题,每小题3分,共18分)1. ﹣3的相反数是( ) A. 13- B. 13 C. 3- D. 32.如图,过△ABC 的顶点A ,作BC 边上的高,以下作法正确的是( )A.B. C. D. 3.下列多项式相乘,可以用平方差公式直接计算的是( )A. (x +5y )(x -5y )B. (-x +y )(y -x )C. (x +3y )(2x -3y )D. (3x -2y )(2y -3x ) 4.下列图形中,由12∠=∠,能得到AB CD ∥的是( )A. B. C. D. 5.有一根长的金属棒,欲将其截成x 根7mm 长的小段和y 根长的小段,剩余部分作废料处理,若使废料最少,则正整数应分别为( )A.B. C. D. 6.给出下列4个命题:①垂线段最短;②互补的两个角中一定是一个为锐角,另一个为钝角;③同旁内角相等,两直线平行;④同旁内角的两个角的平分线互相垂直.其中真命题的个数为( )A. 1B. 2C. 3D. 4二、填空题(本大题共有10小题,每小题3分,共30分)7.生物学家发现了一种病毒长度约为0.00000432毫米,数据0.00000432用科学记数法表示为____________.8.命题“如果a >b ,那么ac >bc ”逆命题是_____.9.若x 2_4x +m 是一个完全平方式,则m=_____.10.一个多边形的内角和是720°,这个多边形的边数是__.11.若a m =3,a n =2,则a m +n =_______;12.关于x 的不等式组24337x x x+>⎧⎨<+⎩的解集是____. 13.若a 2-3b =4,则2a 2-6b +2019=_____.14.如图,AB ∥CD ,则∠1+∠3—∠2的度数等于 __________.15.某经销商销售一批电话手表,第一个月以550元/块的价格售出60块,第二个月起降价,以500元/块的价格将这批电话手表全部售出,销售总额超过了5.5万元,这批电话手表至少有_____块.16.一副直角三角尺如图①叠放,现将45°的三角尺ADE 固定不动,将含30°的三角尺ABC 绕顶点A 顺时针转动,要求两块三角尺的一组边互相平行.如图②,当∠BAD=15°时,有一组边BC ∥DE ,请再写出两个符合要求的∠BAD (0°<∠BAD <180°)的度数_________.三、解答题(本大题共有10小题,共102分.解答时应写出必要的步骤)17.计算:(1)-4+28-(-18)+(-24); (2)0221(2)()|35|2π-+--+-18.解方程:(1)x +2 =7-4x ; (2)123123x x +--= 19.(1)计算:(-3a 3)2·2a 3-4a 12÷a 3;(2)先化简,再求值:(a +b )2-2a (a -b )+(a +2b )(a -2b ),其中a =-1,b =4.20.因式分解:(1)216x -; (2)22242x xy y -+.21.解不等式2151132x x -+-≤,把它的解集在数轴上表示出来,并求出这个不等式的负整数解.22.如图,在8×8的正方形网格中,每个小正方形的边长都为1个单位长度,△ABC的顶点都在正方形网格的格点上.(1)将△ABC经平移后得到△A′B′C′,点A的对应点是点A′.画出平移后所得的△A′B′C′;(2)连接AA′、CC′,则四边形AA′C′C的面积为.23.(1)把下面的证明补充完整:如图,已知直线EF分别交直线AB、CD于点M、N,AB∥CD,MG平分∠EMB,NH平分∠END.求证:MG∥NH证明:∵AB∥CD(已知)∴∠EMB=∠END()∵MG平分∠EMB,NH平分∠END(已知),∴∠EMG=12∠EMB,∠ENH=12∠END(),∴(等量代换)∴MG∥NH().(2)你在第(1)小题的证明过程中,应用了哪两个互逆的真命题?请直接写出这一对互逆的真命题.24.有A、B两种型号台灯,若购买2台A型台灯和6台B型台灯共需610元.若购买6台A型台灯和2台B 型台灯共需470元.(1)求A、B两种型号台灯每台分别多少元?(2)采购员小红想采购A、B两种型号台灯共30台,且总费用不超过2200元,则最多能采购B型台灯多少台?25.已知:如图,AB平分∠CBD,∠DBC=60°,∠C=∠D.(1)若AC⊥BC,求∠BAE的度数;(2)请探究∠DAE与∠C的数量关系,写出你的探究结论,并加以证明;(3)如图,过点D作DG∥BC交CE于点F,当∠EFG=2∠DAE时,求∠BAD的度数.26.有一个边长为m+3的正方形,先将这个正方形两邻边长分别增加1和减少1,得到的长方形①的面积为S1.(1)试探究该正方形的面积S与S1的差是否是一个常数,如果是,求出这个常数;如果不是,说明理由;(2)再将这个正方形两邻边长分别增加4和减少2,得到的长方形②的面积为S2.①试比较S1,S2的大小;②当m为正整数时,若某个图形的面积介于S1,S2之间(不包括S1,S2)且面积为整数,这样的整数值有且只有16个,求m的值.答案与解析一、选择题(本大题共有6小题,每小题3分,共18分)1. ﹣3的相反数是()A.13- B.13C. 3-D. 3【答案】D【解析】【分析】相反数的定义是:如果两个数只有符号不同,我们称其中一个数为另一个数的相反数,特别地,0的相反数还是0.【详解】根据相反数的定义可得:-3的相反数是3.故选D.【点睛】本题考查相反数,题目简单,熟记定义是关键.2.如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是()A. B. C. D.【答案】A【解析】【分析】经过一个顶点作对边所在的直线的垂线段,叫做三角形的高,根据概念即可得出.【详解】根据定义可得A是作BC边上的高,C是作AB边上的高,D是作AC边上的高.故选A.考点:三角形高线的作法3.下列多项式相乘,可以用平方差公式直接计算的是()A. (x+5y)(x-5y)B. (-x+y)(y-x)C. (x+3y)(2x-3y)D. (3x-2y)(2y-3x)【答案】A【解析】【分析】根据平方差公式的特点进行判断即可.【详解】A. (x +5y )(x -5y )能用平方差公式进行计算,故本选项正确;B. (-x +y )(y -x )=-(x -y )(y -x )不能用平方差公式进行计算,故本选项错误;C. (x +3y )(2x -3y )不能用平方差公式进行计算,故本选项错误;D. (3x -2y )(2y -3x )不能用平方差公式进行计算,故本选项错误;故选A.【点睛】本题考查平方差公式,解题的关键是熟练掌握平方差公式.4.下列图形中,由12∠=∠,能得到AB CD ∥的是( ) A. B. C. D.【答案】B【解析】【分析】根据平行线的判定对各选项进行逐一分析即可.【详解】A.∵∠1=∠2是同旁内角,∴不能判断∠1=∠2,故本选项错误;B.作∠3如下图,∵∠1=∠3,∴∠1=∠2,则AB CD ∥,故本选项正确;C. ∠1=∠2可得AC BD P 不能得到AB CD ∥,故本选项错误;D. ∠1=∠2不能得到AB CD ∥,故本选项错误.故选B.【点睛】本题考查平行线的判定,解题的关键是掌握平行线的判定方法.5.有一根长的金属棒,欲将其截成x 根7mm 长的小段和y 根长的小段,剩余部分作废料处理,若使废料最少,则正整数应分别为( ) A.B. C. D. 【答案】B【解析】根据题意得:7x+9y≤40,则∵40-9y≥0且y是非负整数,∴y的值可以是:0或1或2或3或4.当x的值最大时,废料最少,因而当y=0时,x≤40/7 ,则x=5,此时,所剩的废料是:40-5×7=5mm;当y=1时,x≤31/7 ,则x=4,此时,所剩的废料是:40-1×9-4×7=3mm;当y=2时,x≤22/7 ,则x=3,此时,所剩的废料是:40-2×9-3×7=1mm;当y=3时,x≤13/7 ,则x=1,此时,所剩的废料是:40-3×9-7=6mm;当y=4时,x≤4/7 ,则x=0,此时,所剩的废料是:40-4×9=4mm.则最小的是:x=3,y=2.故选B.6.给出下列4个命题:①垂线段最短;②互补的两个角中一定是一个为锐角,另一个为钝角;③同旁内角相等,两直线平行;④同旁内角的两个角的平分线互相垂直.其中真命题的个数为()A. 1B. 2C. 3D. 4【答案】A【解析】【分析】①根据垂线段的性质即可判断,②如果两个都是直角则可判断,③根据平行线的判定定理可判断,④因为没说明两直线平行,所以不能得出.【详解】①应该是连接直线为一点与直线上的所有线段,垂线段最短,所以错误;②如果两个都是直角则可判断“互补的两个角中一定是一个为锐角,另一个为钝角”错误;③根据平行线的判定定理可判断同旁内角相等,两直线平行正确;④因为没说明两直线平行,所以不能得出,故错误.故选A【点睛】本题考查垂线段的性质、平行线的判定,解题的关键是掌握垂线段的性质、平行线的判定.二、填空题(本大题共有10小题,每小题3分,共30分)7.生物学家发现了一种病毒的长度约为0.00000432毫米,数据0.00000432用科学记数法表示为____________.【答案】4.32×10-6;【解析】分析:绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10n - ,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定. 本题解析:将0.00000432用科学记数法表示为4.32×610- .故答案为4.32×610-.点睛:本题考查了用科学计数法表示较小的数,一般形式为10n a -⨯ ,其中110a ≤< ,n 为由原数左边起第一个不为零的数字前面的0的个数决定.8.命题“如果a >b ,那么ac >bc ”的逆命题是_____.【答案】如果ac >bc ,那么a >b【解析】【分析】逆命题就是题设和结论互换.【详解】“如果a >b ,那么ac >bc ”的逆命题是若“ac >bc ,则a >b.【点睛】本题考查逆命题,解题的关键是知道逆命题就是题设和结论互换.9.若x 2_4x +m 是一个完全平方式,则m=_____.【答案】4.【解析】【分析】根据完全平方公式的定义即可解答.【详解】因为x 2_4x +m 是一个完全平方式,所以x 2_4x +m =(x _m )22=,则m=4.【点睛】本题考查完全平方公式的定义,解题的关键是掌握完全平方公式的定义.10.一个多边形的内角和是720°,这个多边形的边数是__.【答案】6【解析】分析】根据内角和定理180°•(n ﹣2)即可求得.【详解】解:∵多边形的内角和公式为(n ﹣2)•180°,∴(n ﹣2)×180°=720°,解得n=6,∴这个多边形的边数是6.故答案为6.【点睛】此题考查多边形内角与外角,解题关键在于掌握计算公式.11.若a m=3,a n=2,则a m+n=_______;【答案】6【解析】【分析】先根据同底数幂的乘法法则把代数式化为已知的形式,再把已知代入求解即可.【详解】∵a m•a n=a m+n,∴a m+n=a m•a n=3×2=6.【点睛】解答此题的关键是熟知同底数幂的乘法法则,同底数幂相乘,底数不变,指数相加,即a m•a n=a m+n.12.关于x的不等式组24337xx x+>⎧⎨<+⎩的解集是____.【答案】17 22x-<<.【解析】【分析】先分别解得不等式组的两个不等式,再进行求解,即可得到解集.【详解】因为24337xx x+>⎧⎨<+⎩,则1272xx⎧>-⎪⎪⎨⎪<⎪⎩,则可得解集是1722x-<<.【点睛】本题考查不等式组的求解,解题的关键是掌握不等式组的求解的方法.13.若a2-3b=4,则2a2-6b +2019=_____.【答案】2027【解析】【分析】将a2-3b=4代入原式=2(a2-3b)+2019,计算可得.【详解】当a2−3b=4时,原式=2(a2−3b)+2019=2×4+2019=2027,故答案为2027. 【点睛】本题考查有理数的加减运算,解题的关键是掌握整体代入法.14.如图,AB∥CD,则∠1+∠3—∠2的度数等于__________.【答案】180°【解析】∵AB∥CD,∴∠1=∠EFD,∵∠2+∠EFC=∠3,∠EFD=180°-∠EFC,∴∠1+∠3—∠2=180°15.某经销商销售一批电话手表,第一个月以550元/块的价格售出60块,第二个月起降价,以500元/块的价格将这批电话手表全部售出,销售总额超过了5.5万元,这批电话手表至少有_____块.【答案】105【解析】设这批手表有x块,550×60+500(x−60)>55000,解得x>104.故这批电话手表至少有105块,故答案为105.16.一副直角三角尺如图①叠放,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动,要求两块三角尺的一组边互相平行.如图②,当∠BAD=15°时,有一组边BC∥DE,请再写出两个符合要求的∠BAD(0°<∠BAD<180°)的度数_________.【答案】45°,60,105°,135°【解析】【分析】分情况讨论AB∥DE的情况,即可得到答案.【详解】(1)∵∠BAD=45°,∠BAC=90°,∴∠CAF=45°,∴∠D=∠CAF=45°,∴DE∥AC;(2)如图所示,当∠BAD=60°时,∴∠B=∠BAD=60°,∴BC∥AD;(3)当∠BAD=105°时,如图,即∠BAD=∠BAE+∠EAD=105°,∴∠BAE=∠BAD-∠EAD=105°-45°=60°,∴∠BAE=∠B=60°,∴BC∥AE;(4)当∠BAD=135°时,如图,则∠EAB=∠BAD-∠EAD=135°-45°=90°.∴∠EAB=∠E=90°,∴AB∥DE.【点睛】本题考查平行线的判定,解题的关键是分情况讨论.三、解答题(本大题共有10小题,共102分.解答时应写出必要的步骤)17.计算:(1)-4+28-(-18)+(-24); (2)0221(2)()|35|2π-+--+- 【答案】(1)18;(2)3.【解析】【分析】(1)根据有理数的加减运算法则,先去括号,再进行运算,即可得到答案;(2)根据指数幂和绝对值的运算法则,即可得到答案.【详解】(1)先去括号,则原式=-4+281824+-=241824+-=18;(2)根据指数幂和绝对值的性质可得原式=1442+-+=3.【点睛】本题考查有理数的加减运算、指数幂和绝对值的运算,解题的关键是熟练掌握有理数的加减运算、指数幂和绝对值的运算.18.解方程:(1)x +2 =7-4x ; (2)123123x x +--= 【答案】(1)x =1;(2)79x =. 【解析】【分析】(1)先移项,再系数化1,即可得到答案; (2)先去分母,再去括号、移项、合并同类项,系数化为1,即可得到答案. 【详解】(1)解:移项得:472x x +=-,合并同类项得:55=x ;解得:x =1; (2)解:去分母得:()3(1)6223x x +-=-,去括号、移项、合并同类项得:97x =,解得:79x =. 【点睛】本题考查解一元一次方程,解题的关键是掌握一元一次方程基本求解步骤. 19.(1)计算:(-3a 3)2·2a 3-4a 12÷a 3;(2)先化简,再求值:(a +b )2-2a (a -b )+(a +2b )(a -2b ),其中a =-1,b =4.【答案】(1)14a 9;(2)-64.【解析】【分析】 (1)根据指数幂和同底数幂的乘除运算,即可得到答案;(2)根据完全平方公式和多项式乘以多项式的性质,进行计算即可得到答案.【详解】(1)根据指数幂和同底数幂的乘除运算,则原式=639924a a a •-=14a 9;(2)解:根据完全平方公式和多项式乘以多项式的性质,则原式=222222224a ab b a ab a b ++-++-=234b ab -+;当a =-1,b =4时,原式=31616-⨯-=-64.【点睛】本题考查指数幂、同底数幂的乘除运算、完全平方公式和多项式乘以多项式的性质,解题的关键是熟练掌握指数幂、同底数幂的乘除运算、完全平方公式和多项式乘以多项式的性质.20.因式分解:(1)216x -; (2)22242x xy y -+.【答案】(1)()()44x x +-;(2)()22x y - 【解析】【分析】根据平方差公式即可得到答案.【详解】(1)根据平方差公式,则原式=()()44x x +-;(2)解:原式=()2222x xy y -+,根据平方差公式,则22242x xy y -+=()22x y -. 【点睛】本题考查平方差公式,解题的关键是掌握平方差公式.21.解不等式2151132x x -+-≤,把它的解集在数轴上表示出来,并求出这个不等式的负整数解. 【答案】1x ≥-;解集在数轴上表示见解析;负整数解为-1.【解析】【分析】先去分母,再去括号,移项,合并同类项,把化系数为1即可求出x 的取值范围,再在数轴上表示出不等式的解集,找出符合条件的x 的非负整数解即可.【详解】去分母得: 2(21)3(51)6x x --+≤,去括号、移项、合并同类项得:1111x -≤,解得:1x ≥-;解集在数轴上表示如下:,所以负整数解为-1.【点睛】本题考查解一元一次不等式和解集在数轴上表示,解题的关键是掌握解一元一次不等式的基本步骤.22.如图,在8×8的正方形网格中,每个小正方形的边长都为1个单位长度,△ABC的顶点都在正方形网格的格点上.(1)将△ABC经平移后得到△A′B′C′,点A的对应点是点A′.画出平移后所得的△A′B′C′;(2)连接AA′、CC′,则四边形AA′C′C的面积为.【答案】(1)见解析;(2)6.【解析】【分析】(1)直接利用平移的性质得出对应点位置进而得出答案;(2)直接利用三角形面积求法进而得出答案.【详解】解:(1)如图所示:△A′B′C′,即为所求;(2)四边形AA′C′C的面积为:2×12×6=6.故答案为6.【点睛】此题主要考查了平移变换以及三角形面积求法,正确得出对应点位置是解题关键.23.(1)把下面的证明补充完整:如图,已知直线EF分别交直线AB、CD于点M、N,AB∥CD,MG平分∠EMB,NH平分∠END.求证:MG∥NH证明:∵AB∥CD(已知)∴∠EMB=∠END()∵MG平分∠EMB,NH平分∠END(已知),∴∠EMG=12∠EMB,∠ENH=12∠END(),∴(等量代换)∴MG∥NH().(2)你在第(1)小题的证明过程中,应用了哪两个互逆的真命题?请直接写出这一对互逆的真命题.【答案】(1)见解析;(2)两直线平行,同位角相等;同位角相等,两直线平行.【解析】【分析】(1)先利用平行线的性质得∠EMB=∠END,再根据角平分线的定义得到∠EMG=12∠EMB,∠ENH=12∠END,则∠EMG=∠ENH,然后根据平行线的判定方法可得到MG∥NH.(2)由(1)可以得到答案.【详解】证明:∵AB∥CD(已知)∴∠EMB=∠END(两直线平行,同位角相等)∵MG平分∠EMB,NH平分∠END(已知)∴∠EMG=12∠EMB,∠ENH=12∠END(角平分线定义),∴∠EMG=∠ENH(等量代换)∴MG∥NH(同位角相等,两直线平行).(2)两直线平行,同位角相等;同位角相等,两直线平行【点睛】本题考查平行线的判定和性质,解题的关键是掌握平行线的判定方法和性质.24.有A、B两种型号台灯,若购买2台A型台灯和6台B型台灯共需610元.若购买6台A型台灯和2台B 型台灯共需470元.(1)求A、B两种型号台灯每台分别多少元?(2)采购员小红想采购A、B两种型号台灯共30台,且总费用不超过2200元,则最多能采购B型台灯多少台?【答案】(1)A、B两种型号台灯每台分别50、85元;(2)最多能采购B型台灯20台.【解析】【分析】(1)设A 、B 两种型号台灯每台分别x 、y 元,由题意列方程,再解答即可得到答案;(2)设能采购B 型台灯a 台,由题意得到一元一次不等式,即可得到答案.【详解】(1)解:设A 、B 两种型号台灯每台分别x 、y 元,依题意可得:2661062470x y x y +=⎧⎨+=⎩, 解得:5085x y =⎧⎨=⎩, 答:A 、B 两种型号台灯每台分别50、85元.(2)解:设能采购B 型台灯a 台,依题意可得:50(30)852200a a -+≤,解得:20a ≤.答:最多能采购B 型台灯20台.【点睛】本题考查二元一次方程组和一元一次不等式,解题的关键是掌握二元一次方程组和一元一次不等式的应用.25.已知:如图,AB 平分∠CBD ,∠DBC =60°,∠C =∠D .(1)若AC ⊥BC ,求∠BAE 的度数;(2)请探究∠DAE 与∠C 的数量关系,写出你的探究结论,并加以证明;(3)如图,过点D 作DG ∥BC 交CE 于点F ,当∠EFG =2∠DAE 时,求∠BAD 的度数.【答案】(1)∠BAE ==120°;(2)结论:∠DAE =2∠C —120°.证明见解析;(3)∠BAD =66°.【解析】【分析】(1)根据角平分线的性质得到∠CBD =60°,由于∠BAE 是△ABC 的外角,则可以得到答案. (2)根据三角形内角和性质和四边形内角和,进行计算即可得到答案.(3)根据对顶角的性质可得∠EFG =∠DF A ,根据平行线的性质得2∠DAE +∠C =180°,再根据角平分线的性质即可得到答案.【详解】解:∵AC ⊥BC∴∠BCA =90°,∵AB 平分∠CBD ,∴∠ABC=12∠CBD, ∠CBD=60°,∴∠ABC=30°,∵∠BAE是△ABC的外角,∴∠BAE=∠BCA+∠ABC=120°.结论:∠DAE=2∠C—120°.证明:∵∠DAE+∠DAC=180°,∴∠DAC =180°—∠DAE,∵∠DAC+∠DBC+∠C+∠D =360°,∴180—∠DAE+∠DBC+∠C+∠D =360°,∵∠DBC=60°,∠C=∠D,∴2∠C—∠DAE=120°,∴∠DAE=2∠C—120°.解:∵∠EFG和∠DF A是对顶角,∴∠EFG=∠DF A,∵∠EFG=2∠DAE,∴∠DF A=2∠DAE,∵DG∥BC,∴∠DF A+∠C=180°,∴2∠DAE +∠C=180°,∵∠DAE=2∠C—120°,∴∠DAE=48°,∴∠DAC =132°,∵AB平分∠CBD,∴∠DBA=∠CBA,∵∠C=∠D,∴∠BAD=∠BAC,∴∠BAD=12∠DAC=66°【点睛】本题考查角平分线的性质、平行线的性质和三角形内角和性质,解题的关键是熟练掌握角平分线的性质、平行线的性质和三角形内角和性质.26.有一个边长为m+3的正方形,先将这个正方形两邻边长分别增加1和减少1,得到的长方形①的面积为S 1.(1)试探究该正方形的面积S 与S 1的差是否是一个常数,如果是,求出这个常数;如果不是,说明理由; (2)再将这个正方形两邻边长分别增加4和减少2,得到的长方形②的面积为S 2. ①试比较S 1,S 2的大小;②当m 为正整数时,若某个图形的面积介于S 1,S 2之间(不包括S 1,S 2)且面积为整数,这样的整数值有且只有16个,求m 的值.【答案】(1)解:S 与S 1的差是是一个常数,S 与S 1的差是1;(2)①当-2m +1﹥0,即-1﹤m ﹤12时,1s ﹥2s ;当-2m +1﹤0,即m ﹥12时,1s ﹤2s ;当-2m +1= 0,即m =12时,1s = 2s ;②m = 9. 【解析】【分析】 (1)根据完全平方公式和多项式乘以多项式,计算即可得到答案. (2)①先计算S 1,S 2,则有1221s s m -=-+,再分情况讨论,即可得到答案. ②根据题意列不等式16<21m -≤17,即可得到答案.【详解】(1)解:S 与S 1的差是是一个常数,∵()22369s m m m =+=++,()()()()2131314268s m m m m m m =+++-=++=++ ∴()()22169681s s m m m m -=++-++=,∴S 与S 1的差是1. (2)∵()()()()2131314268s m m m m m m =+++-=++=++ ()()()()2234327187s m m m m m m =+++-=++=++∴()()2212688721s s m m m m m -=++-++=-+,∴当-2m +1﹥0,即-1﹤m ﹤12时,1s ﹥2s ; 当-2m +1﹤0,即m ﹥12时,1s ﹤2s ;当-2m +1= 0,即m =12时,1s = 2s ; ②由①得,S 1﹣S 2=-2m +1,∴12s s 21m -=-+,∵m 为正整数,∴2121m m -+=-,∵一个图形的面积介于S 1,S 2之间(不包括S 1,S 2)且面积为整数,整数值有且只有16个,∴16<21m -≤17,∴172<m ≤9,∵m 为正整数,∴m = 9.【点睛】本题考查完全平方公式和不等式,解题的关键是熟练掌握完全平方公式和不等式.。
