《图形的旋转》复习课导学案
第1课时图形的旋转变换(导学案)

本单元的主要内容有旋转及平移和旋转在拼图中的应用。
1.使学生进一步认识图形的轴对称,探索图形成轴对称的特征和性质,能在方格纸上画出一个图形的轴对称图形。
2.进一步认识图形的旋转,探索图形旋转的特征和性质,能在方格纸上把简单图形旋转90°。
3.初步学会运用对称、平移和旋转的方法在方格纸上设计图案,进一步增强空间观念。
4.让学生在上述活动中,欣赏图形变换所创造出的美,进一步感受对称、平移和旋转在生活中的应用,体会数学的价值。
〔1〕图形的旋转变换〔1课时〕〔2〕方格纸上图形的旋转变换〔1课时〕〔3〕利用平移、旋转设计图案〔1课时〕单元重点知识归纳与易错警示〔1课时〕本单元的教学结合学生熟悉的生活情境,让学生通过亲自动手、亲自体验和独立思考来开展学生的空间想象力和思维能力。
这样让学生真正地、充分地进行活动和探究。
第1课时图形的旋转变换课。
〔5分钟〕戏〞图。
图1 图2提问:图1让你玩,你准备怎样操作?图2呢?3.列举生活中常见到的类似现象。
4.引导学生观察并描述这些物体在运动的过程中有什么共同特征。
5.导入课题:这节课我们来一起学习图形的旋转变换。
〔板书课题〕顺时针旋转90°放在右下角。
图2把上面的图形逆时针旋转90°放在左下角。
〔用手势示范一下顺时针和逆时针〕3.学生列举:风车转动、开关水龙头。
4.小组讨论后选代表汇报:它们都是绕着一个点或轴转动的。
5.明确本节课的学习内容。
〔2〕电梯的升降运动。
〔〕〔3〕方向盘的运动。
〔〕〔4〕开教室的门。
〔〕答案:〔1〕√〔2〕×〔3〕√〔4〕√2.观察并填空。
〔1〕指针从“12〞绕点O顺时针旋转°到“1〞。
〔2〕指针从“1〞绕点O顺时针旋转60°到“〞。
〔3〕指针从“〞绕点O顺时针旋转60°到“11〞。
答案:〔1〕30 〔2〕3〔3〕93.填空题。
从1:00到4:00时针顺时针旋转了〔〕°。
图形的旋转(一)导学案

学习重点:通过生活事例,认识图形的旋转,探索图形旋转的特征和性质。
学习难点:通过动手操作,能在方格纸上画出简单几何组合图形旋转90°后的图形。
探究案
探究1:什么是顺时针方向?什么是逆时针方向?
探究2:图形旋转必须知道那些条件?
探究3:怎样进行简单图形的旋转?
陈炉镇雷家坡小学2014-2015学年度第二学期六年级数学导学案主备:组长:编号:009班级:六年级姓名:
课题:图形的旋转(一)1课时
学习目标:
知识与技能:
通过生活事例,认识图形的旋转,探索图形旋转的特征和性质。
ห้องสมุดไป่ตู้过程与方法:
通过动手操作,能在方格纸上画出简单几何组合图形旋转90°后的图形。
情感态度价值观:
探究4:在我们日常生活中,你在哪看见过旋转现象?说说他是怎样旋转的?
我的疑问
纠错
我的收获
课后反思
训练案
九年级数学: 23.1.2《图形的旋转》导学案

八级下册数学科导学案主备人:审核组长:一、学习目标:1.知识与技能理解对应点到旋转中心的距离相等;理解对应点与旋转中心所连线段的夹角等于旋转角;理解旋转前、后的图形全等.掌握以上三个图形的旋转的基本性质的运用.先复习旋转及其旋转中心、旋转角和旋转的对应点概念,接着用操作几何、实验探究图形的旋转的基本性质.2.过程与方法(1)让学生感受生活中的几何,•通过不同的情景设计归纳出图形旋转的有关概念,并用这些概念来解决一些问题.(2)•通过复习图形旋转的有关概念从中归纳出“对应点到旋转中心的距离相等,对应点与旋转中心所连线段的夹角等于旋转角,旋转前后的图形全等”等重要性质,并运用它解决一些实际问题.(3)经历复习图形的旋转的有关概念和性质,分析不同的旋转中心,•不同的旋转角,出现不同的效果并对各种情况进行分类.3.情感、态度与价值观让学生经历观察、操作等过程,了解图形旋转的概念,从事图形旋转基本性质的探索活动,进一步发展空间观察,培养运动几何的观点,增强审美意识.让学生通过独立思考,自主探究和合作交流进一步体会旋转的数学内涵,获得知识,体验成功,享受学习乐趣.让学生从事应用所学的知识进行图案设计的活动,享受成功的喜悦,激发学二、学习重难点:1.图形的旋转的基本性质及其应用.2.运用操作实验几何得出图形的旋转的三条基本性质.三、预习感知1.在图形旋转中,下列说法错误的是()A.图形上各点的旋转角度相同;B.旋转不改变图形的大小、形状;C.由旋转得到的图形也一定可以由平移得到;D.对应点到旋转中心的距离相等3.通过观察第57页图形的旋转,你能发现图形的旋转哪些基本性质吗?归纳:①旋转前、后的图形______;②对应点到__________________________;③每一对对应点与_________所连线段的夹角等于_______;④图形的旋转是由________和________决定。
四、合作探究1.旋转的性质①对应点到旋转中心的距离相等。
小学五年级数学下册《图形的旋转》导学案

小学五年级数学下册《图形的旋转》导学案学习目标:1.认识图形的旋转,探索图形旋转的特征和性质,能在方格纸上把筒单图形旋转90度。
2.学生初步学会应用对称,平移和旋转的方法在方格纸杀个设计图案。
3.观察,想象,分析和推理等过程,独立探究,增强空间观念。
学习重点:掌握轴对称图形、特征。
新知识一、激趣定标(1)自学P5――6的例3和例4(2)在日常生活中大家还见过哪些轴对称图形呢?(3)课文第3页的六幅图。
画出这些轴对称图形的对称轴。
(4)我还能提出什么问题?怎么解答?二、自学互动(适时点拨)1.课文第5页例题3的钟面。
(1)观察,描述旋转现象(2)根据旋转现象,想想看,要想把一个旋转现象描述清楚,应该从哪些方面去说明?2、课文第5页例题例3的风车。
(1)从图1到图2,风车发生了怎样的变化呢?你是怎样判断风车旋转的角度的?(2)风车旋转后,每个三角形的位置都发生了变化,那什么没有发生变化?(3)如果将风车在图2的基础上,继续绕点O逆时针旋转180°,那么黄色的三角形应该转到什么位置?这条线段应该转到什么位置?3、课文第5页例4.(1)自己尝试画一画。
(2)作品展示,交流画法。
4、我的收获三、达标检测一、认真思考,准能填好。
1.变换图形的位置可以有()、()等方法;按比例放大或缩小图形可以改变图形的()而不改变它的()2.圆是轴对称图形,它有()条对称轴。
在我们学习认识过的平面图形中,是轴对称图形的还有()。
3.将一个三角形按2:1的比放大后,面积是原来的()倍。
4.一个30。
的角,将它的一条边旋转()。
可得到一个直角。
5.长方形有()条对称轴;正方形有()条对称轴;圆有()条对称轴。
二、仔细推敲,准确判断。
1.线段也是轴对称图形。
()2.将一个平行四边形木框拉成一个长方形后、周长不变,面积不变。
()3.把一个图按1:3的比缩小后,周长会比原来缩小3倍,面积会比原来缩小6倍。
()三、反复权衡,慎重选择。
六年级下册数学教案-《图形的旋转》导学案 北师大版

《图形的旋转》导学案一、教学目标1. 知识与技能:使学生能够在方格纸上画出一个图形的旋转图形,能够根据旋转后的图形确定旋转中心和旋转角,并理解对应点与旋转中心所连线段的夹角就是旋转角。
2. 过程与方法:通过观察、操作、想象,培养学生的观察能力、操作能力和空间想象力。
3. 情感态度和价值观:激发学生探索图形变化的兴趣,体会数学在生活中的应用。
二、教学重点使学生理解图形旋转的特征,学会在方格纸上画出一个图形旋转90°后的图形。
三、教学难点如何确定旋转中心及旋转角。
四、教学过程1. 导入通过生活中的旋转现象,如钟表的指针、开锁等,引导学生发现旋转的普遍性和趣味性,从而引出课题——《图形的旋转》。
2. 新课讲授(1)初步感知旋转出示一些简单的图形,如线段、角、三角形等,让学生观察这些图形旋转后的样子,引导学生发现旋转的特征:大小不变,形状不变,方向改变。
(2)探究旋转三要素让学生动手操作,尝试将一个图形旋转一定的角度,并引导学生发现旋转的三要素:旋转中心、旋转方向、旋转角度。
重点强调旋转中心是旋转的点,旋转方向可以是顺时针或逆时针,旋转角度是旋转的大小。
(3)学习在方格纸上画出一个图形旋转90°后的图形以正方形为例,引导学生学习如何在方格纸上画出一个图形旋转90°后的图形。
步骤如下:a. 找到旋转中心,通常是对角线的交点。
b. 以旋转中心为中心,画一个半径等于对应点到旋转中心的距离的圆。
c. 将对应点沿圆弧旋转90°,得到新的对应点。
d. 连接新的对应点,得到旋转后的图形。
3. 巩固练习让学生独立完成一些图形的旋转练习,加深对旋转的理解和掌握。
4. 课堂小结通过提问方式,让学生回顾本节课所学内容,总结旋转的特征和画法。
五、作业布置1. 完成课后练习题。
2. 观察生活中还有哪些旋转现象,并尝试用今天所学的知识进行解释。
六、板书设计图形的旋转一、旋转的特征:大小不变、形状不变、方向改变二、旋转的三要素:旋转中心、旋转方向、旋转角度三、在方格纸上画出一个图形旋转90°后的图形的方法四、生活中的旋转现象通过本节课的学习,我们了解了图形旋转的特征和画法,希望大家能够灵活运用所学知识,解决实际问题。
《图形的旋转》复习课导学案

《图形的旋转》复习课导学案学习目标:1、掌握旋转的特征,理解旋转的基本性质。
2、理解中心对称、中心对称图形的定义,了解它们的联系。
3、掌握关于原点对称的点的坐标特点。
学习重点:旋转的性质、中心对称、中心对称图形、坐标系中关于x 轴、y 轴、原点对称的点的特征。
教学难点:和旋转有关的综合题目的分析过程。
一、课前热身2、 如图,∠AOB =90°,∠B =30°,△AOB ’可以看作是由△AOB 绕点O 顺时针旋转α角度得到的,若点A ’在AB 上,则旋转角α的大小可以是 ( )A .30°B .45°C .60°D .90°3、如图所示,在方格纸上建立的平面直角坐标系中,将△ABO 绕点O 按顺时针方向旋转90°,得A B O ''△ ,则点A '的坐标为 ( ). A .(3,1) B .(3,2) C .(2,3) D .(1,3)4、、下列图形中,既是轴对称图形,又是中心对称图形的是( )A .等腰梯形B .平行四边形C .正三角形D .矩形5、单词NAME 的四个字母中,是中心对称图形的是 ( )A .NB .A C.M D .E6、某校计划修建一座既是中心对称图形又是轴对称图形的花坛,从学生中征集到的设计方案有等腰三角形、正三角形、等腰梯形、菱形等四种方案,你认为符合条件的是( )A .等腰三角形B .正三角形C .等腰梯形D .菱形7.如图,E 、F 分别是正方形ABCD 的边BC 、CD 上的点,BE=CF ,连接AE 、BF ,将△ABE 绕正方形的中心按逆时针方向转到△BCF ,旋转角为α(0°<α<180°),则∠α= . 二、知识点归纳 1.旋转的定义:把一个平面图形绕平面内 转动 就叫做图形的旋转. 旋转的三要素:旋转 ;旋转 ;旋转旋转的基本性质:(1)对应点到 的距离相等。
九年级数学科旋转复习课导学案
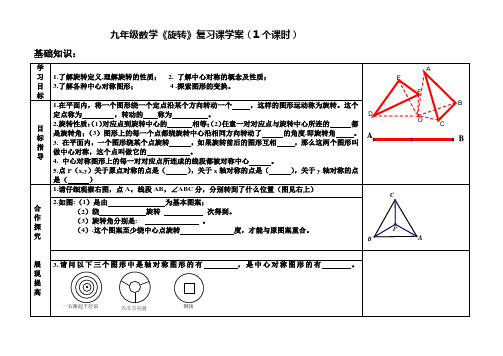
九年级数学《旋转》复习课学案(1个课时)基础知识:①②③典型例题:例1、如图,在正方形ABCD 中,E 是CB 延长线上一点,△ABE 经过旋转后得到△ADF,请按图回答:(1)旋转中心是哪一点? (2)旋转角是多少度? (3)∠EAF 等于多少度? (4)经过旋转,点B 与点E 分别移动到什么位置? (5)若点G 是线段BE 的中点,经过旋转后,点G 移到了什么位置?请在图形上作出.(6)连结EF,请判断△AEF 的形状,并说明理由. (7)试判断四边形ABCD 与AFCE 面积的大小关系,说明理由。
例2、如图,ABC ∆是等腰直角三角形,BC 是斜边,将ABP ∆绕点A 逆时针旋转后,能与ACD ∆重合,如果AP=3,求PD 的长。
B例3如图,点P 是正方形ABCD 内一点,且PA=1,PB=2,PC=3,试求APB ∠的度数。
例4如图,在等腰ABC ∆中,AB=AC, ABC α∠=,在四边形BDEC 中,DB=DE, 2BDE α∠=,M 为CE 中点,连结AM,DM.(1)在图中画出DEM ∆关于点M 成中心对称的图形; (2)求证:AM DM ⊥ ; (3)当α= ,AM=DM..B C牛刀小试:1、一个平行四边形绕着它对角线的交点旋转90○能够与它本身重合,则该四边形是 ( )A.矩形B.菱形C.正方形D.无法确定 2、如图,ΔABC 和ΔADE 均为正三角形,则图中可看作是旋转关系的三角形是 ( ) A. ΔABC 和ΔADE B. ΔABC 和ΔABD C. ΔABD 和ΔACE D. ΔACE 和ΔADE3、钟表的秒针匀速旋转一周需要60秒.20秒内,秒针旋转的角度是 ;分针经过15 分后,分针转过的角度是 ; 分针从数字12出发,转过150○,则它指的数字是 ;4、如图,ABC △中(23)A -,,(31)B -,,(12)C -,. (1)将ABC △向右平移4个单位长度,画出平移后的111A B C △; (2)画出ABC △关于x 轴对称的222A B C △;(3)将ABC △绕原点O 旋转180 ,画出旋转后的333A B C △;(4)在111A B C △,222A B C △,333A B C △中,△______与△______成轴对称,对称轴是______;△______与△______成中心对称,对称中心的坐标是______。
《图形的旋转(1)》导学案

《图形的旋转(1)》导学案一、学习目标1、知道旋转的定义以及相关概念2、能记住旋转的基本性质3、利用性质解决相关问题 二、重点:1. 旋转的定义以及相关概念2.旋转的基本性质难点:利用性质解决相关问题 (一).自学教材P56并填空:把一个平面图形___着平面内某一点O_____一个角度,就叫做图形的旋转,点O 叫做_________,转动的角叫做________。
所以,旋转的决定因素....是_________和_________。
(二).自学检测:1.钟表的分针匀速旋转一周需要60分.(1)指出它的旋转中心;(2)经过20分,分针旋转了_________度。
2.如图,类似于钟表的指针,将△OAB ,它绕O 点按顺时针方向旋转得到△OEF ,在这个旋转过程中:(1)旋转中心是______旋转角是__________(2)经过旋转,点A 、B 分别转到______________ 3.如图:∆ABC 是等边三角形,D 是BC 上一点,∆ABD 经过旋转后到达∆ACE 的位置。
(1)旋转中心是_______(2)旋转了_______度.(3)如果M 是AB 的中点,那么经过上述旋转后,点M 转到了________________。
(三)自学教材P57探究,总结归纳旋转的性质。
①_______________________________________________________ ②__________________________________________________________ ③_____________________________________________________________ (四)旋转性质的应用1、已知△ABC 是直角三角形,∠ACB=90°,AB=5㎝,BC=3厘米,△ABC 绕点C 逆时针方向旋转90°后得到△DEC ,则∠D=______,∠B=______,DE=_______㎝, EC=______㎝,AE=_______㎝,DE 与AB 的位置关系为_________________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《图形的旋转》复习课导学案
学习目标:1、掌握旋转的特征,理解旋转的基本性质。
2、理解中心对称、中心对称图形的定义,了解它们的联系。
3、掌握关于原点对称的点的坐标特点。
学习重点:旋转的性质、中心对称、中心对称图形、坐标系中关于x 轴、y 轴、原点对称的点的特征。
教学难点:和旋转有关的综合题目的分析过程。
一、课前热身
2、 如图,∠AOB =90°,∠B =30°,△AOB ’可以看作是由△AOB 绕点O 顺时针旋转α角度得到的,若点A ’在AB 上,则旋转角α的大小可以是 ( )
A .30°
B .45°
C .60°
D .90°
3、如图所示,在方格纸上建立的平面直角坐标系中,将△ABO 绕点O 按顺时针方向旋转90°,得
A B O ''△ ,则点A '的坐标为 ( ). A .(3,1) B .(3,2) C .(2,3) D .(1,3)
4、、下列图形中,既是轴对称图形,又是中心对称图形的是( )
A .等腰梯形
B .平行四边形
C .正三角形
D .矩形
5、单词NAME 的四个字母中,是中心对称图形的是 ( )
A .N
B .A C.M D .E
6、某校计划修建一座既是中心对称图形又是轴对称图形的花坛,从学生中征集到的设计方案有等腰三角形、正三角形、等腰梯形、菱形等四种方案,你认为符合条件的是( )
A .等腰三角形
B .正三角形
C .等腰梯形
D .菱形
7.如图,E 、F 分别是正方形ABCD 的边BC 、CD 上的点,
BE=CF ,连接AE 、BF ,将△ABE 绕正方形的中心按逆时针方向转到
△BCF ,旋转角为α(0°<α<180°),则∠α= .
二、知识点归纳
1.旋转的定义:把一个平面图形绕平面内 转动 就叫做图形
的旋转. 旋转的三要素:旋转 ;旋转 ;旋转
旋转的基本性质:(1)对应点到 的距离相等。
(2)每一组对应点与旋转中心所连线段的夹角相等都等于 。
(3)旋转前后的两个图形是 。
3、点(x ,y )关于x 轴对称后是( , ) 点( , )关于y 轴对称后是(-x ,y )
点(x ,y )关于原点对称后是( , )
三、例题讲析
例1、(1)点(2,-3)关于x 轴对称后为( , ),关于y 轴对称后为( , ),关于原点对称后为( , )。
(2)已知点P (2x ,2y +4)与点Q (2
x +1,-4y )关于原点对称,求x+y 的值。
例2、已知正方形ABCD 和正方形AEFG 有一个公共点A ,点G 、E 分别在线段AD 、AB (1)如图1,连结DF 、BF ,若将正方形AEFG 绕点A 按顺时针方向旋转,判断命题:“在旋转的过程中线段DF 与BF 的长始终相等。
”是否正确,若正确请证明,若不正确请举反例说明;
(2)若将正方形AEFG 绕点A 按顺时针方向旋转,连结DG ,在旋转的过程中,你能否找到一条线段的长与线段DG 的长始终相等。
并以图2为例说明理由。
例 3. 如图,已知ABC △的三个顶点的坐标分别为(23)A -,、(60)B -,、(10)C -,.
(1)请直接写出点A 关于原点对称的点的坐标;
(2)将ABC △绕坐标原点O 逆时针旋转90°.画出图形,直接写出点B 的对应点的坐标;
四、针对性练习
1、在平面直角坐标系中,点(23)P -,关于原点对称点P '的坐标是
2、如图,已知点O 是正三角形ABC 三条高的交点,现将△AOB 绕点O 至少 要旋
转几度后与△BOC 重合。
( )
A. 60°
B. 120°
C. 240°
D. 360°
3、如图,在△ABC 中,∠BAC=1200,以BC 为边向形外作等边三角形△BCD ,
把△ABD 绕着点D 按顺时针方向旋转600后得到△ECD (点A 、C 、E 三点共
线),若AB=3,AC=2,求∠BAD 的度数与AD 的长.
第23章图形的旋转复习课课后补偿作业
姓名: 1、点A 的坐标为(2,0),把点A 绕着坐标原点顺时针旋转︒135到点B ,那么B 点的坐标是
2、直线y=x-3上有一点p (m-5,2m ),p 关于原点对称的点p '的坐标是
3、如图,在△ABC 中,∠ACB =90º,∠ABC =30º,AC =1.现在将△ABC 绕点C 逆时针旋转至△A ′B ′C ,使得点A ′恰好落在AB 上,连接BB ′,则BB ′的长度为 .
4、 如图,正方形ABCD 与正三角形AEF 的顶点A 重合,将△AEF 绕顶点A 旋转,在旋转过程中,当BE=DF 时,∠BAE 的大小可以是 .
C
B D
A
E O B C A
3题图 4题图 5题图 6题图
5、如图,在△ABC中,∠C=30º.将△ABC绕点A顺时针旋转60º得△ADE,AE与BC交于点F,则∠ABF=º.
6、点P是正方形ABCD边AB上一点(不与A、B重合),连接PD并将线段PD绕点P顺时针旋转90°,得线段PE,连接BE,则∠C BE等于.
7、下列图形中,既是轴对称图形,又是中心对称图形的是
( )
A、(1)(2)(3)(4)
B、(1)(2)(3)
C、(1)(3)
D、(3)
小组评价教师评价。
