matlab相关图形实现代码
Matlab绘图代码
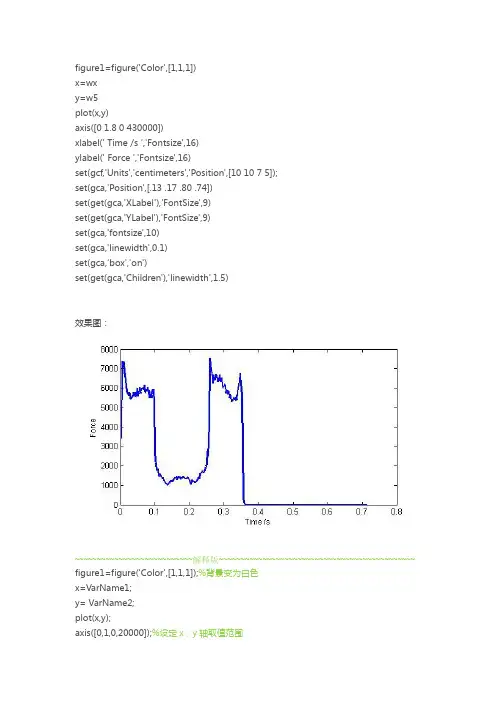
figure1=figure('Color',[1,1,1])x=wxy=w5plot(x,y)axis([01.80430000])xlabel('Time /s','Fontsize',16)ylabel('Force','Fontsize',16)set(gcf,'Units','centimeters','Position',[10 10 7 5]);set(gca,'Position',[.13 .17 .80 .74])set(get(gca,'XLabel'),'FontSize',9)set(get(gca,'YLabel'),'FontSize',9)set(gca,'fontsize',10)set(gca,'linewidth',0.1)set(gca,'box','on')set(get(gca,'Children'),'linewidth',1.5)效果图:~~~~~~~~~~~~~~~~~~~~~~~~~~~解释版~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ figure1=figure('Color',[1,1,1]);%背景变为白色x=VarName1;y=VarName2;plot(x,y);axis([0,1,0,20000]);%设定x,y轴取值范围xlabel('Plastic stress','Fontsize',16);%X轴标签ylabel('Yeild stress /MPa','Fontsize',16);%Y轴标签%title(‘DP980应力应变曲线’,’Fontsize’,16);%标题%text(x,y, 'String');%在指定位置添加文本说明set(gcf,'Units','centimeters','Position',[10 10 7 5]);%设置图片大小为7cm×5cm%get hanlde to current axis返回当前图形的当前坐标轴的句柄,%(the first element is the relative distance of the axes to the left edge of the figure,... %the second the vertical distance from the bottom, and then the width and height; set(gca,'Position',[.13 .17 .80 .74]);%设置xy轴在图片中占的比例set(get(gca,'XLabel'),'FontSize',9);%图上文字为9 point或小5号set(get(gca,'YLabel'),'FontSize',9);%set(get(gca,'TITLE'),'FontSize',9);set(gca,'fontsize',9);set(gca,'linewidth',0.5); %坐标线粗0.5磅set(gca,'box','off');%Controls the box around the plotting areaset(get(gca,'Children'),'linewidth',1.5);%设置图中线宽1.5磅%set(gca,'color','r');%背景变为红色set(gcf,'Position',[100 100 260 220]);%这句是设置绘图的大小,不需要到word里再调整大小。
4阶锁相环matlab

4阶锁相环matlab4阶锁相环是一种广泛应用于通信系统和控制系统中的控制算法,其主要用于抑制信号的相位偏移和频率误差。
本文将以回答关于4阶锁相环在Matlab中的应用为主题,一步一步地介绍相关知识和实例。
第一步:了解锁相环的基本原理要学习和应用4阶锁相环,首先需要了解锁相环的基本原理。
锁相环是一种控制系统,它通过比较输入信号和参考信号的相位差异,并根据差异调整输出信号的相位和频率,使其与参考信号同步。
在一个理想的锁相环中,输出信号的相位和频率将与参考信号完全一致。
第二步:了解4阶锁相环的结构4阶锁相环是一种具有更高精度和更快响应速度的锁相环。
它由相位解调器、低通滤波器、环路滤波器和控制电压产生器等组成。
相位解调器用于将输入信号分解为正弦和余弦分量,低通滤波器用于提取正弦分量,环路滤波器用于对正弦分量进行进一步处理,而控制电压产生器则根据环路滤波器的输出产生对输出信号的调整。
第三步:编写Matlab代码实现4阶锁相环在Matlab中实现4阶锁相环可以通过调用DSP System Toolbox 中的相位锁定环模块来完成。
以下是一个简单的示例代码:matlab设置相关参数omega_n = 2*pi*1e4; 自然频率zeta = 0.707; 阻尼系数Kp = 1; 比例增益Ki = 1; 积分增益创建4阶锁相环loop = dspPLL('PhaseDetectorGain', Kp, ...'LoopBandwidth', omega_n, ...'DampingFactor', zeta, ...'LoopFilterGain', Ki);生成输入信号fs = 1e6; 采样率t = 0:1/fs:1;fin = 1000; 输入信号频率inputSignal = cos(2*pi*fin*t);执行锁相环[outputSignal, controlVoltage] = loop(inputSignal);绘制输出信号和调整电压figure;subplot(2,1,1);plot(t, inputSignal, 'b', t, outputSignal, 'r');xlabel('Time (s)');ylabel('Amplitude');legend('Input Signal', 'Output Signal');subplot(2,1,2);plot(t, controlVoltage, 'g');xlabel('Time (s)');ylabel('Control Voltage');legend('Control Voltage');通过上述代码,可以生成一个包含输入信号、输出信号和调整电压的图形,并显示相应的波形。
matlab colorbar的代码

标题:深入探讨 MATLAB colorbar 的代码实现与应用在 MATLAB 中,colorbar 是一种用于显示图形颜色对应数值的重要功能。
它可以帮助我们更直观地理解图形中不同颜色所代表的数据大小,提高数据可视化的效果。
在本文中,我将详细介绍 MATLAB 中colorbar 的代码实现与应用,并结合实际案例进行深入探讨,以便更好地理解和应用这一功能。
一、colorbar 的基本介绍在 MATLAB 中,colorbar 函数可以在当前图形中添加一个颜色刻度条,用于显示图中颜色的对应数值。
它通常用于在绘制颜色图时显示颜色与数值之间的关系,使图形更具可读性。
1. 使用方法要在 MATLAB 中使用 colorbar 函数,可以简单地在绘图后调用该函数即可。
例如:```matlabsurf(peaks);colorbar;```这段代码将在 peaks 图形上添加一个 colorbar。
2. 参数设置colorbar 函数还可以接受一系列参数,用于设置颜色刻度条的位置、标签、刻度等。
可以使用 'location' 参数设置 colorbar 位置,'FontSize' 参数设置字体大小,'Ticks' 参数设置刻度等。
具体的参数设置可以根据实际需求进行灵活调整。
二、实例分析接下来,我们将结合一个实例来详细介绍colorbar 的代码实现与应用。
假设我们有一个 10x10 的矩阵数据 data,我们希望使用 imagesc 函数将其可视化,并添加 colorbar 来显示颜色与数值之间的对应关系。
代码如下:```matlabdata = rand(10,10);imagesc(data);colorbar;```在这段代码中,我们首先生成一个随机矩阵 data,然后使用 imagesc 函数将其可视化。
最后使用 colorbar 函数添加颜色刻度条,用于显示颜色与数值之间的对应关系。
MATLAB绘图函数代码及图形

')
case 2,result = M1-M2; case 3,result = M1*M2; case 4,result = M1/M2; end disp('The result is :'); disp(result); end %End function 第三题 矩阵的操作 function y=f3 while(1) disp('--------------------------------------'); disp('1 - 转置'); disp('2 - 求秩'); disp('3 - 求逆'); disp('4 - 行列式'); disp('0 -Exit'); ch = input('Choose an item to continue:'); if( ch == 0) return; end M = input('Enter the Matrix:'); switch(ch) case 1,result = M'; case 2,result = rank(M); case 3,result = inv(M); case 4,result = det(M); end disp('The transform result is :'); disp(result); end %End function end end end 第四题 向量的判定 function y=f4(vec_1,vec_2,dem_1) vec_1=input(' 第一个向量:') vec_2=input(' 第二个向量:') Sel_2=input(' 选择: 1 -判断两向量是否共线 2 -判断三向量是否共面') if Sel_2==1 A=[vec_1;vec_2] if rank(A)==1 disp(' 两向量共线!') else disp(' 两向量不共线!') end else if Sel_2==2
matlab图形操作

matlab图形操作本⽂对matlab中利⽤图形句柄对图⽚属性进⾏设置的操作进⾏简单的总结说明:(1)对图窗和坐标轴属性进⾏整体设置可以通过gcf和gca语句获取当前图窗句柄和坐标轴句柄,通过该句柄可以对图窗和坐标轴的各项属性进⾏操作。
图窗和坐标轴分别包含如下属性:% 图窗属性... ...Children: [1×1 Axes] Color: [0.9400 0.9400 0.9400]Colormap: [256×3 double] CurrentAxes: [1×1 Axes]... ...InnerPosition: [680 558 560 420] PaperUnits: 'centimeters'OuterPosition: [672 550 576 514] Position: [680 558 560 420]Units: 'pixels'% 坐标轴属性... ...Box: 'on' BoxStyle: 'back'Children: [1×1 Line] Color: [1 1 1]FontAngle: 'normal' FontName: 'Helvetica'FontSize: 10 FontSizeMode: 'auto'FontSmoothing: 'on' FontUnits: 'points'FontWeight: 'normal' GridColor: [0.1500 0.1500 0.1500]GridLineStyle: '-' Legend: [0×0 GraphicsPlaceholder]LineWidth: 0.5000 OuterPosition: [0 0 1 1]Parent: [1×1 Figure] Position: [0.1300 0.1100 0.7750 0.8150]Title: [1×1 Text] TitleFontWeight: 'normal'Units: 'normalized' UserData: []View: [0 90] Visible: 'on'... ...XAxis: [1×1 NumericRuler] XAxisLocation: 'bottom'XColor: [0.1500 0.1500 0.1500] XColorMode: 'auto'XDir: 'normal' XGrid: 'off'XLabel: [1×1 Text] XLim: [0 100]XScale: 'linear' XTick: [0 10 20 30 40 50 60 70 80 90 100]XTickLabel: {11×1 cell} XTickLabelRotation: 0YAxis: [1×1 NumericRuler] YColor: [0.1500 0.1500 0.1500]YGrid: 'off' YLabel: [1×1 Text]YLim: [0 100] YScale: 'linear'YTick: [0 10 20 30 40 50 60 70 80 90 100] YTickLabel: {11×1 cell}YTickLabelRotation: 0 ZLabel: [1×1 Text]ZLim: [-1 1] ZScale: 'linear'ZTick: [-1 0 1] ZTickLabel: ''ZTickLabelRotation: 0... ...上⾯仅仅是展⽰了图窗和坐标轴部分重要且常⽤的属性,它们的全部属性可通过查matlab的帮助⽂档或直接在matlab的命令⾏上输⼊gcf、gca或通过如下图所⽰的属性窗⼝进⾏查询和设置。
利用Matlab绘制各类特殊图形的实例代码

利⽤Matlab绘制各类特殊图形的实例代码Matlab绘图介绍强⼤的绘图功能是Matlab的特点之⼀,Matlab提供了⼀系列的绘图函数,⽤户不需要过多的考虑绘图的细节,只需要给出⼀些基本参数就能得到所需图形,这类函数称为⾼层绘图函数。
此外,Matlab还提供了直接对图形句柄进⾏操作的低层绘图操作。
这类操作将图形的每个图形元素(如坐标轴、曲线、⽂字等)看做⼀个独⽴的对象,系统给每个对象分配⼀个句柄,可以通过句柄对该图形元素进⾏操作,⽽不影响其他部分。
Matlab绘制特殊图形1. 绘制极坐标图说明:使⽤polarplot函数绘制极坐标图,每组数据表⽰⼀条闭合曲线,共有20条曲线构成20条封闭同⼼曲线。
t = linspace(0,2*pi,500);y = 1+0.3*sin(20*t)+0.1*sin(30*t)+0.1*sin(40*t);polarplot(t,y,t,1.1*y,t,1.2*y,t,1.3*y,t,1.4*y,t,1.5*y,t,1.6*y,t,1.7*y,t,1.8*y,t,1.9*y,...t,2.0*y,t,2.1*y,t,2.2*y,t,2.3*y,t,2.4*y,t,2.5*y,t,2.6*y,t,2.7*y,t,2.8*y,t,2.9*y,'linewidth',1.5);2. 单条曲线绘制分段函数(反⽐例函数y=1/x)说明:反⽐例函数在x接近于0时,趋近于奇异(1/0 趋近于⽆穷⼤),使⽤nan⾮数对图形进⾏镂空,可以实现⼀条曲线绘制y=1/x的整个定义域。
x = linspace(-3,3,500);f = @(x) 1./x;y = f(x);for ii = 1:length(x)if abs(x(ii))<0.03x(ii) = nan;y(ii) = nan;endendplot(x,y)legend('y=1/x')3. 正⽅体内绘制随机分布的颜⾊⽚图说明:使⽤plot3绘制正⽅体12条边,使⽤fill3函数绘制颜⾊⽚,颜⾊⽚位置和填充颜⾊随机⽣成。
matlab加工自由曲面程序代码
一、引言Matlab是一种高级技术计算语言和交互环境,被广泛用于工程、科学和数学领域的计算与模拟。
在Matlab中,加工自由曲面是一项常见的任务,例如创建和修改三维曲面模型。
本文将介绍如何使用Matlab 编写程序代码来加工自由曲面,以实现对曲面的精确控制和调整。
二、准备工作在编写程序代码之前,首先需要明确自由曲面的定义和参数化方法。
自由曲面通常由参数方程或控制点构成,对于不同的曲面类型,需要选择合适的参数化方法。
还需要了解Matlab中与曲面加工相关的函数和工具,以便在编写程序时能够调用这些资源。
三、编写程序代码1. 定义自由曲面在Matlab中,可以使用符号变量和代数表达式定义自由曲面的参数方程。
对于二次曲面,可以使用二次多项式表示其参数方程。
具体代码如下:syms u vx = a*u^2 + b*v^2 + c*u*v + d*u + e*v + f;y = g*u^2 + h*v^2 + i*u*v + j*u + k*v + l;z = m*u^2 + n*v^2 + o*u*v + p*u + q*v + r;其中a-r为曲面的系数,u和v为曲面的参数。
2. 控制曲面形状通过调整曲面的参数和系数,可以控制曲面的形状。
可以通过改变系数a-r的值来实现对曲面的放大缩小、旋转、偏移等操作。
具体代码如下:a = 1;b = 1;c = 0;d = 0;e = 0;f = 0;g = 1; h = 1; i = 0; j = 0; k = 0; l = 0;m = 1; n = 1; o = 0; p = 0; q = 0; r = 0;这里以简单的二次曲面为例,通过调整系数的数值来控制曲面的形状。
3. 曲面绘制和可视化在定义和控制曲面之后,可以使用Matlab中的绘图函数将曲面绘制出来。
可以使用surf函数创建曲面图形,并通过设置图形属性来进行可视化调整。
具体代码如下:[u, v] = meshgrid(-2:0.1:2);x = a*u.^2 + b*v.^2 + c*u.*v + d*u + e*v + f;y = g*u.^2 + h*v.^2 + i*u.*v + j*u + k*v + l;z = m*u.^2 + n*v.^2 + o*u.*v + p*u + q*v + r;surf(x, y, z);四、应用实例在实际应用中,自由曲面加工可以用于创建各种复杂的曲面模型。
matlab画圆锥双曲线函数代码
一、概述在数学和工程领域中,圆锥双曲线是一种重要的曲线类型。
它在描述椭圆、双曲线等曲线时具有广泛的应用价值。
而Matlab作为一种强大的数学软件工具,可以方便地绘制各种函数曲线,包括圆锥双曲线。
本文旨在介绍如何使用Matlab的函数代码绘制圆锥双曲线,并提供一些示例代码和图形演示。
二、绘制圆锥双曲线函数代码1. 定义圆锥双曲线的参数圆锥双曲线的一般方程为:(x^2 / a^2) - (y^2 / b^2) = 1其中a和b分别为圆锥双曲线在x轴和y轴上的半轴长度。
在Matlab 中,我们可以先定义这两个参数值,例如:a = 3;b = 2;2. 生成圆锥双曲线的点集接下来,我们需要生成圆锥双曲线上的一系列点集,以便后续绘制曲线。
可以利用参数方程来生成点集,例如:t = -3:0.01:3;x = a*cosh(t);y = b*sinh(t);这里利用双曲函数cosh和sinh来生成点集,t为参数,-3到3之间适当取值,可以使得生成的点集具有较好的曲线效果。
3. 绘制圆锥双曲线利用Matlab的绘图函数plot来连接生成的点集,实现圆锥双曲线的绘制,例如:plot(x, y);title('Hyperbola'); xlabel('x-axis'); ylabel('y-axis');legend('Hyperbola');这样就可以在Matlab中绘制出指定参数下的圆锥双曲线图形了。
三、示例代码和图形演示为了更直观地展示Matlab绘制圆锥双曲线的过程,以下是一个完整的示例代码和对应的图形演示:```matlab定义圆锥双曲线参数a = 3;b = 2;生成圆锥双曲线的点集t = -3:0.01:3;x = a*cosh(t);y = b*sinh(t);绘制圆锥双曲线plot(x, y);title('Hyperbola'); xlabel('x-axis'); ylabel('y-axis');legend('Hyperbola');```运行上述示例代码后,可以得到如下图形演示:【插入圆锥双曲线图形】四、总结本文介绍了如何使用Matlab的函数代码绘制圆锥双曲线,并提供了具体的示例代码和图形演示。
MatLab图形绘制功能口令及代码
第二讲MatLab图形绘制功能一、二维平面图形基本绘图函数hold on 命令用于在已画好的图形上添加新的图形plot是绘制一维曲线的基本函数,但在使用此函数之前,我们需先定义曲线上每一点的x及y座标。
下例可画出一条正弦曲线:x=0:0.001:10; % 0到10的1000个点的x座标y=sin(x); % 对应的y座标plot(x,y); % 绘图Y=sin(10*x);plot(x,y,'r:',x,Y,'b') % 同时画两个函数若要改变颜色,在座标对後面加上相关字串即可:x=0:0.01:10;plot(x,sin(x),'r')若要同时改变颜色及图线型态(Line style),也是在坐标对後面加上相关字串即可:plot(x,sin(x),'r*')用axis([xmin,xmax,ymin,ymax])函数来调整图轴的范围axis([0,6,-1.5,1])MATLAB也可对图形加上各种注解与处理:xlabel('x轴'); % x轴注解ylabel('y轴'); % y轴注解title('余弦函数'); % 图形标题legend('y = cos(x)'); % 图形注解gtext('y = cos(x)'); % 图形注解 ,用鼠标定位注解位置grid on; % 显示格线fplot的指令可以用来自动的画一个已定义的函数分布图,而无须产生绘图所须要的一组数据做为变数。
其语法为fplot('fun',[xmin xmax ymin ymax]),其中fun 为一已定义的函数名称,例如sin, cos等等;而xmin, xmax, ymin, ymax则是设定绘图横轴及纵轴的下限及上限。
以下的例子是将一函数 f(x)=sin(x)/x 在-20<x<20,-0.4<y<1.2之间画出:>> fplot('sin(x)./x',[-20 20 -0.4 1.2])【例】画椭圆1232222=+y xa = [0:pi/50:2*pi]';%角度 π20- X = cos(a)*3; %参数方程 Y = sin(a)*2;plot(X,Y);xlabel('x'), ylabel('y'); title('椭圆')图形窗口的分割一般用命令subplot: subplot(2,2,1);subplot(2,3,4);MATLAB还有其他各种二维绘图函数,以适合不同的应用,详见下表。
八叉树算法 matlab代码
八叉树算法简介在计算机图形学和计算机视觉领域,八叉树算法是一种常用的数据结构,用于对三维空间进行分割和索引。
八叉树是一种树形结构,每个节点可以有最多8个子节点,因此得名为八叉树。
它的主要思想是将三维空间递归地划分为八个子立方体,从而实现对三维数据的快速检索和查询。
八叉树的构造八叉树的构造过程是通过递归实现的。
下面是八叉树的构造算法:1.初始化根节点,将整个空间作为根节点的区域。
2.对于每个节点,判断其区域中是否存在点或物体。
3.如果节点的区域中只有一个点或物体,则将该节点标记为叶子节点,并保存相应的点或物体信息。
4.如果节点的区域中有多个点或物体,则将该节点划分为八个子节点,每个子节点负责其父节点区域的1/8子区域。
5.对于每个子节点,重复步骤2-4,直到满足终止条件。
6.构造完整的八叉树后,可以根据需要进行查询和检索。
八叉树的应用八叉树算法在计算机图形学和计算机视觉领域有广泛的应用,以下是几个常见的应用场景:三维场景管理八叉树可以用于对三维场景进行管理和索引。
它可以将复杂的三维场景分割为多个子立方体,每个子立方体都有自己的节点,从而实现对场景中物体的高效检索和渲染。
点云数据处理八叉树也常用于处理点云数据。
点云是由大量点组成的三维数据集,通过八叉树可以对点云进行高效的存储和处理。
八叉树可以将点云数据划分为多个子区域,从而减少不必要的计算和存储开销。
基于体素的渲染八叉树在体素渲染中也有应用。
体素渲染是一种基于体素(三维像素)的渲染方法,八叉树可以对体素数据进行分割和索引,加速体素渲染的计算速度。
碰撞检测八叉树还可以用于碰撞检测。
在计算机游戏中,需要检测物体之间是否发生碰撞,八叉树可以将物体进行精确的划分,通过判断物体所在的子节点是否重叠,可以有效地进行碰撞检测。
八叉树的优缺点八叉树作为一种常用的数据结构,具有以下优点和缺点:优点•高效的数据检索和查询能力,可以减少不必要的计算和存储开销。
•可以对大规模的三维数据进行高效的管理和处理,提高计算效率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
根据数据点绘制饼图和针状图: x=[1 2 3 4 5 6]; >> subplot(2,2,1);pie(x); >> subplot(2,2,2);pie3(x); >> subplot(2,2,3);stem(x); >>subplot(2,2,4);stem3(x);
5%
10%
14%
19%
24%
29%
24%
29%
19%
5%14%
10%0
2
4
6
2
4
6
5
10
01
2
05
10
根据数据点绘制向量场图、羽状图和罗盘图: x=[1 2 3 4 5 6];y=[1 2 3 4 5 6]; u=[1 2 3 4 5 6];v=[1 2 3 4 5 6]; subplot(2,2,1);quiver(x,y,u,v); subplot(2,2,2);quiver(x,y,u,v,'r'); subplot(2,2,3);feather(u,v); subplot(2,2,4);compass(u,v);
024680
246
802468
246
80
5
10
15
2
4
6
5 10
30
210
60240
90270
120
300
150330
180
rand(m,n)产生m ×n 均匀分布的随机矩阵,元素取值在0.0~1.0。
randn 函数:产生标准正态分布的随机数或矩阵的函数。
Y = randn(m,n) 或 Y = randn([m n])返回一个m*n 的随机项矩阵。
> theta=10*rand(1,50); %确定50个随机数theta >> Z=peaks; %确定Z 为峰值函数peaks >> x=0:0.01:2*pi;y=sin(x); %确定正弦函数数据点x.y >> t=randn(1000,1); %确定1000个随机数t
>> subplot(2,2,1);rose(theta); %关于(theta )的玫瑰花图 >> subplot(2,2,2);area(x,y); %关于(x,y)的面积图
>> subplot(2,2,3);contour(Z); %关于Z 的等值线图(未填充) >> subplot(2,2,4);hist(t); %关于t 的柱状图
5 10
30
210
60
240
90270
120300150330
18000246
-1
-0.500.5
110
20
30
40
10
2030
40-4
-2
2
4
100
200
300
[A,C]=bucky;%使用bucky 函数产生一稀疏邻接矩阵 >> t=[1 2 3 4 5 6];%确定向量t
>> x=0:0.7:4*pi;y=x.*exp(sin(x));l=0.1*y; %确定x,y 及误差条长度 >> subplot(2,2,1);gplot(A,C); %关于【A,C 】的拓扑图 >> subplot(2,2,2);stairs(t); %关于t 的阶梯图
>> subplot(2,2,3);errorbar(x,y,l); %关于(x,y )的误差条形图 >> subplot(2,2,4);comet(x,y); %关于(x,y)的彗星图
-1-0.5
0.5
1
-1-0.50
0.5
10
2
4
6
12
3
4
5
6
-5
5
10
15
05
101520250
5
10
051015
20
clf
x=-5:0.1:5; y=-4:0.1:4;
[x,y]=meshgrid(x,y);%生成变量x,y 的网格点(矩阵) z=0.5*(x.^3+y.^2);%生成变量z mesh(x,y,z);%绘制三维网格曲面
colormap(hsv);%设置三维网格曲面色图 brighten(0.60);%加量当前图形
-5
5
-4
-2
2
4
-100-50
50
100
三维图形制作:
x=-5:0.1:5;
y=-5:0.1:5;
[x,y]=meshgrid(x,y);%生成变量x,y的网格点(矩阵)
z=0.5*x.^3+y.^2;
subplot(2,3,1);mesh(x,y,z);%三维网格表面
subplot(2,3,2);surf(x,y,z);%三维曲面
subplot(2,3,3);meshc(x,y,z);%三维网格表面(具有等值线)subplot(2,3,4);surfc(x,y,z);%三维曲面(具有等值线)subplot(2,3,5);meshz(x,y,z);%三维网格表面(具有零平面)。
