双代号网络图中虚工作时间参数计算的探讨(精)
双代号网络图中虚工作时间参数计算的探讨

双 代 号 网络 图 中虚 工 作 时 间参 数 计 算 的探 讨
兰 立Байду номын сангаас华
摘 要: 通过分析研究对把虚工作视 同实工作进 行其时 间参数计算的观点提 出质疑 , 出计算双代号 网络 图各 实工作 时 得
间参数 时不要进行虚 工作 时间参数计算的结论 , 并指 出何时进行虚 工作 时间参数计 算会 对其相 关实工作 时间参数产 生
工作也进行其 时间参数 的计算 E 有 些教材认 为可把虚工 作视 同 ; 实工作也进行其 时间参数 的计算 , 这样 有利于保证 各实工 作 的时 间参数计算结果 的正 确E3; 2 有些参 考文 献则认 为虚工 作 只起 到 ,
表达相关工作正确 的逻辑关 系的作 用 , 不必计算 虚工作 的时间参
E , 、 迟 必 须 开 始 时 间 ( s , 、 迟 必 须 结 束 时 间 )最 L ) 最 有 向箭杆表达计划所要 完成 的各 工作及 其先 后顺 序和相 互关 系 时间 ( ( ,、 L ) 总时差( F一 和 自由时差 ( 丁 , ) F ,6个 。其 中总时差是 指 ) 而构成的 网络状图形 。用有 向箭杆表 示工作 , 箭尾 表示工作 的开
图 2 平行 工 作 的 正 确 表 示 形 式 图 3 平 行 工 作 的 错 误 表 示 形 式
数[ 。到底该 不该 计算 虚工作的时间参数 , 计算 虚工作 的时 间参
数对其他各实工作 的时 问参数 有何 影响 , 时会产 生影 响 , 何 现就 这些 问题作一深入 分析和探讨 。
它等于 始, 箭头表示 工作 的结束 , 头和 箭尾衔 接 的地方 画上 圆圈并 编 各工作 在不影响计划总工期 的情况下所 具有 的机 动时间 , 箭 或 号码 , 用箭 头和箭尾 的号码① 一⑨ 作 为这项 工作 的代号 , 圆圈则 该工作 的最迟必须开始时间减去该工 作的最早 可能开始时 间, 称 为节 如图 1 OE , 所示 。 该 工作 的最迟必须结束时间减去该工 作的最早 可能结束时 间; 自 由时差是 指各 工作在不 影响 紧后工 作最 早可 能开始 时间 的前提 下, 所具有 的机动 时问 , 它等 于其 紧后工 作最 早可能 开始 时间 的 最小值减去该工作最早可能结束 时间E 这里所指 的工作 都是实 ,
3-3-3双代号网络时间参数计算

FFi-j = ETj – ETi – Di-j
1.3.2 节点计算法
50 0
50 10
40 40
TFi-j FFi-j
0 0 20 0 20 0
ETj LTj
00
0 0
00
0 0
节点时间参数的计算
• •
图上计算法 图上计算法的原理和步骤与分析计 算法相同,它是在网络图上直接进行计 算的一种方法。 • 采用图上计算法时,首先确定采用 的时间参数标注形式。
•
• •
第三步:确定计算工期TC 第四步:自下而上计算工作最迟必 须结束时间,以结束时间为依据,减去 工作持续时间即算出最迟必须开始时间, 填于第⑤栏和第⑥栏。 • 第五步:计算工作总时差 • 第六步:计算工作自由时差 • 第七步:标明关键工作和关键线路
1.3.1 工作时间计算法
③ 自由时差与总时差的关系
ESi-j = max(ESh-i +Dh-i )
式中: ESh-i工作 i-j 的紧前工作h-i持续时间。
同一节点所有外向工作最早开始时间相同
1.3.1 工作时间计算法
⑵ 最早完成时间
最早完成时间EFi-j是在各紧前工作全部完成后, 本工作有可能完成的最早时刻。最早完成时间等于 最早开始时间加上本工作的持续时间。
同一节点的所有内向工作最迟完成时间相同
EFi-j= ESi-j + Di-j
1.3.1 工作时间计算法
⑶ 最迟完成时间
是在不影响整个计划按期完成的前提下,本工作最迟必
须完成的时间。最迟完成时间LFi-j 应从终点节点开始,逆着 箭线方向依次逐项计算。
① 终节点的最迟完成时间LFi-j按该网络计划的计划工期确定:
双代号网络图详解

A
C
E
B
D
F
A
C
E
B
D
F
用虚箭线连接逻辑关系
练习
按下列工作的逻辑关系,分别绘制双代号网络图
1、A、B均完成后进行C、D;C完成后进行E;D完成后进行F。
2、A、B均完成后进行C;B、D均完成后进行E;C、E完成后进行F
3、A、B、C均完成后进行D;B、C完成后进行E;D、E完成后进行F。
4、A完成后进行B、C、D;B、C、D完成后进行E;C、D完成后进行F。
无紧后工作的工作,其结束节点的位置号为网络图中各个工作的开始节点位置号的“最大值加1” 编制双代号网络图,并按逻辑关系作些调整,绘制正确的网络图
绘制步骤 根据已知的紧前工作确定出紧后工作。 确定出各工作的开始节点和结束节点位置号。 根据节点位置号和逻辑关系绘出网络图。
二、举例
解:列出关系表
B
A
5、双代号网络图中,严禁出现没有箭头节点或没有箭尾节点的箭线。如图所示。
绘制网络图时,箭线不宜交叉;当交叉不可避免时,可用过桥法或指向法。如图所示。
当双代号网络图的某些节点有多条外向箭线或多条内向箭线时,为使图形简洁,可使用母线法绘制(但应满足一项工作用一条箭线和相应的一对结点表示),如图所示。
练习:
2、已知各工作的逻辑关系见下表,绘制双代号网络图并对节点进行编号。
1、已知各工作的逻辑关系见下表,绘制双代号网络图并对节点进行编号。
工作
A
B
C
D
E
F
G
H
I
J
紧前工作
—
A
B
B
B
C、D
C、E
F、G
双代号网络计划时间参数计算

根据含义,工作总时差应按下式计算:
EFi-j ESi-j Di-j
j i LFi-j LSi-j
8.工作自由时差的计算
工作自由时差是指在不影响其紧后工作最早开始时间的前提下可以
机动的时间,以 表示。这时工作活动的时间范围被限制在本身最早开
始时间与其紧后工作的最早开始时间之间,从这段时间中扣除本身的工
h i j ETh ETj Dh-i k Dj-k
2.网络计划的计算工期 网络计划的计算工期等于其终点节点的最早时间,即 3.网络计划的计划工期 网络计划的计划工期如未规定要求工期,其值等于计算工期,即 4.节点最迟时间的计算
节点的最迟时间是指该节点前各内向工作的最迟完成时刻,以表 示。应由网络图的终点节点开始,逆着箭线的方向依次逐项计算。
22 22 0
12 122
0 14 14 0 14 17 3 16 19 3 14 14 0 15 15 0 19 19 0 22 22 0 ESi-j LSi-j EFi-j LFi-j TFi-j FFi-j 22???
(二)按节点计算法计算时间参数 节点计算法是以节点为讨论对象,先计算节点的最早时间和最迟
(2)其它工作的最迟完成时间等于其紧后工作的最迟完成时间与该
紧后工作的工作历时之差的最小值,即:
当工作与其紧后工作之间无虚工作时:
i j k LFi-j Di-j Dj-k LFj-k
当工作通过虚工作与其紧后工作相连时: 式中, - 工作的紧后工作()的最早{开始?}时间; - 工作的紧后工作()的工作历时。
(三)关键工作与关键线路
根据网络计划的时间参数计算的结果,即可判别关键工作和关键线
路:
没有机动时间的工作,即总时差最小的工作为关键工作。
市政专题15--双代号网络图专题 (2)

束。 (2)节点编号可以不连续,比如有 5 个节点,你可以是 1、2、3、5、6,也可以是 2、3、
5、6、7 等等,但是,编号必须是唯一的,不允许重复。且沿箭头方向,编号顺序 是由小到大的。
(3)节点 起点节点 分类 终点节点 中间节点
每条线路上的波形线数值即为其自由时间,如无波形线,则其自由时差为 0。如 FFA=0,FFB=4。其他同理。 4、总时差: (1)分别计算一项工作其后续各条线路的波形线之和,取其最小值。 (2)该最小值加上本工作的自由时差,即为本工作的总时差。
以 C 工作为例,其后续有两条线路,一条线路的波形线之和为 2,一条为 3, 取小值 2,由于 C 工作的自由时差为 0,则 2+0=2,所以 C 工作的总时差为 2, 即 TFC=2。 5、最迟开始时间: 最早开始时间加上其总时差即为最迟开始时间。 如 C 工作的最迟开始时间,等于 8+2=10,即 LSC=10 6、最迟完成时间: 最早完成时间加上其总时差即为最迟完成时间,也可用最迟开始时间加上该工作的 持续时间求得。仍以 C 工作为例,其最迟完成时间既可以用最迟开始时间 10 加
⑤ 总时差(TFi-j): 一项工作在不影响总工期的前提下,可以利用的机动时间。即在不影响总工期的 前提下,允许拖延的最长时间。例如一项工作的总时差是 5,那么这项工作拖延 1-5 天,都不会影响总工期,超过 5 天总工期才会受到影响。
⑥ 自由时差(FFi-j):
一项工作在不影响其紧后工作最早开始的前提下,可以利用的机动时间。即在不 影响其紧后工作最早开始的前提下,允许拖延的最长时间。例如一项工作的自由 时差是 5,那么这项工作拖延 1-5 天,都不会影响其紧后工作的最早开始,超过 5 天其紧后工作的最早开始时间才会受到影响。 补充:⑦ 时间间隔:
双代号网络图时间参数计算技巧

双代号网络图时间参数计算技巧从左向右累加,多个紧前取大,计算最早开始结束;从右到左累减,多个紧后取小,计算最迟结束开始。
紧后左上-自己右下=自由时差。
上方之差或下方之差是总时差。
计算某工作总时差的简单方法:①找出关键线路,计算总工期;②找出经过该工作的所有线路,求出最长的时间③该工作总时差=总工期-②⏹一、非常有用的要点:⏹任何一个工作总时差≥自由时差⏹自由时差等于各时间间隔的最小值(这点对六时参数的计算非常有用)⏹关键线路上相邻工作的时间间隔为零,且自由时差=总时差⏹关键工作:总时差最小的工作⏹①最迟开始时间—最早开始时间(最小)⏹②最迟完成时间—最早完成时间(最小)⏹一、在网络计划中,计算工期是根据终点节点的最早完成时间的最大值⏹二、双代号网络图六时参数的计算步骤(比书上简单得多)⏹步骤一:⏹1、先计算A上再计算A下⏹2、计算从起始工作往结束工作方向⏹3、起点的A上=0,下一个的A上=前一个的A下,当遇到多指向(如4#点)时要取数值大的A下。
4、A下=A上+D(持续时间)⏹步骤二:⏹1、先计算B下再计算B上⏹2、计算从结束工作往起始工作方向⏹3、结束点B下=T(需要的总时间=结束工作节点中最大的A下)结束点B上=T-D(持续时间)⏹4、B下=前一个的B上(这里的前一个是从终点起算的)⏹4、B下=前一个的B上(这里的前一个是从终点起算的)遇到多指出去的时如1#点,取数值小的B上B上=B下—D(持续时间)⏹步骤三:总时差=B上-A上=B下-A下(如果不相等,你就是算错了)⏹步骤四:自由时差=紧后工作A上(取最小的)-本工作A下双代号时标网络图时间参数计算技巧双代号时标网络计划是以时间坐标为尺度编制的网络计划,以实箭线表示工作,以虚箭线表示虚工作,以波形线表示工作的自由时差。
双代号时标网络图⏹1、关键线路⏹在时标双代号网络图上逆方向看,没有出现波形线的线路为关键线路(包括虚工作)。
⏹如图中①→②→⑥→⑧⏹2、时差计算⏹1)自由时差⏹双代号时标网络图自由时差的计算很简单,就是该工作箭线上波形线的长度。
双代号网络图计算

双代号网络图计算
i--工作开始
j--工作结束
ES--最早开始时间:取i之前的各个工作EF的最大值
EF--最早结束时间:ES+D
(持续时间)
LS--最晚开始时间:LF-D
LF--最晚结束时间:取j之后的各个工作LS的最小值
TF--总时差:ES-LS
-EF
FF--自由时差:ES
(后一项工作)
总时差最小的工作为关键工作,全部由关键工作组成的线路为关键线路,关键线路是总的持续时间最长的线路。
涉及到进度控制问题,即需要调整工期时,赶工费低的工作优先压缩工作时间。
以下内容将有助于理解:
怎样理解虚箭头:
当两项工作(图(a)中A和B)的代号相同时,
使用虚工作加以区分。
由此来理解逻辑关系:
规律是:
正推求ES、EF,取紧前工作中的最大值;反推求LS、LF,取紧后工作中的最小值。
网络图绘制与双代号网络计划时间参数的计算
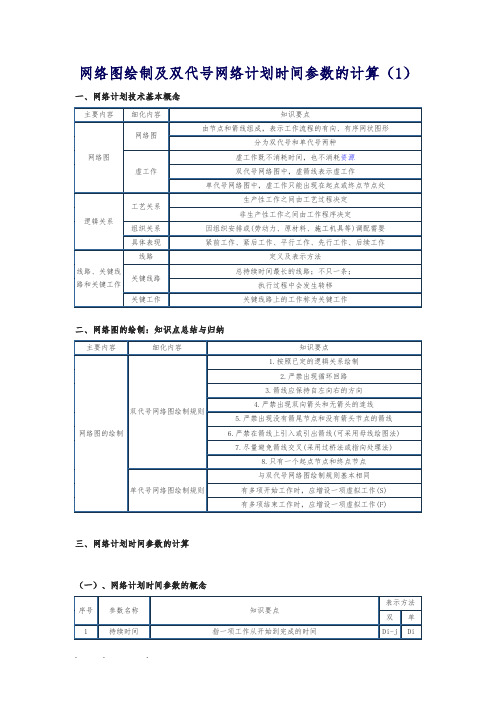
网络图绘制及双代号网络计划时间参数的计算(1)一、网络计划技术基本概念二、网络图的绘制:知识点总结与归纳三、网络计划时间参数的计算(一)、网络计划时间参数的概念(二)、双代号网络计划时间参数的计算双代号网络计划的时间参数既可以按工作计算,也可以按节点计算。
A.按工作计算法所谓按工作计算法,就是以网络计划中的工作为对象,直接计算各项工作的时间参数。
这些时间参数包括:工作的最早开始时间和最早完成时间、工作的最迟开始时间和最迟完成时间、工作的总时差和自由时差。
此外,还应计算网络计划的计算工期。
为了简化计算,网络计划时间参数中的开始时间和完成时间都应以时间单位的终了时刻为标准。
如第3天开始即是指第3天终了(下班)时刻开始,实际上是第4天上班时刻才开始;第5天完成即是指第5天终了(下班)时刻完成。
下面是按工作计算法计算时间参数的过程。
1.计算工作的最早开始时间和最早完成时间工作最早开始时间和最早完成时间的计算应从网络计划的起点节点开始,顺着箭线方向依次进行。
其计算步骤如下:(1)以网络计划起点节点为开始节点的工作,当未规定其最早开始时间时,其最早开始时间为零。
(2)工作的最早完成时间可利用公式(3—3)进行计算:EFi-J=ESi-j+Di—j (3—3)(3)其他工作的最早开始时间应等于其紧前工作最早完成时间的最大值。
(4)网络计划的计算工期应等于以网络计划终点节点为完成节点的工作的最早完成时间的最大值。
2.确定网络计划的计划工期网络计划的计划工期应按公式(3—1)或公式(3—2)确定。
①当已规定了要求工期时,计划工期不应超过要求工期,即:Tp≤Tr (3—1)②当未规定要求工期时,可令计划工期等于计算工期,即:Tp=Tc (3—2)3.计算工作的最迟完成时间和最迟开始时间工作最迟完成时间和最迟开始时间的计算应从网络计划的终点节点开始,逆着箭线方向依次进行。
其计算步骤如下:(1)以网络计划终点节点为完成节点的工作,其最迟完成时间等于网络计划的计划工期。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
・施工技术・文章编号 :100926825(2008 0620159202双代号网络图中虚工作时间参数计算的探讨收稿日期 :2007210229作者简介 :兰立华 (19662 , 男 , 高级工程师 , 江西理工大学应用科学学院 , 江西赣州 341000兰立华摘要 :通过分析研究对把虚工作视同实工作进行其时间参数计算的观点提出质疑 , 得出计算双代号网络图各实工作时间参数时不要进行虚工作时间参数计算的结论 , 并指出何时进行虚工作时间参数计算会对其相关实工作时间参数产生影响。
关键词 :双代号网络 , 虚工作 , 时间参数中图分类号 :TU723文献标识码 :A引言双代号网络图是工程建设的规划、设计 , 特别是施工及其相关工作的计划中应用较为普遍的一种网络计划形式 , 而构成的网络状图形。
始 , , 在绘制双代号网络图时 , 为了使前后各工作的逻辑关系表达正确 , 常常需要引入虚工作。
计算各实工作的时间参数时 , 现有J G J/T 121299工程网络计划技术规程规定必须把虚工作视同实工作也进行其时间参数的计算 [1]; 有些教材认为可把虚工作视同实工作也进行其时间参数的计算 , 这样有利于保证各实工作的时间参数计算结果的正确 [2,3]; 有些参考文献则认为虚工作只起到表达相关工作正确的逻辑关系的作用 , 不必计算虚工作的时间参数 [4]。
到底该不该计算虚工作的时间参数 , 计算虚工作的时间参数对其他各实工作的时间参数有何影响 , 何时会产生影响 , 现就这些问题作一深入分析和探讨。
1工作与虚工作的概念及时间参数 1. 1工作与虚工作的概念工作也称活动 , 是指完成一项任务的过程。
一般情况下 , 工作需要消耗时间和资源 , 有的则仅消耗时间而不消耗资源。
在双代号网络图中 , 有一种既不消耗时间也不消耗资源的工作 , 这就是虚工作 , 它用虚箭杆来表示 [1]。
如图 2所示 , 其中节点②—③工作即为虚工作。
1. 2虚工作的作用1 用于表达平行工作之间的平行关系。
根据双代号网络图的绘制规则 , 不得有两个或两个以上的箭杆从同一节点出发且同时指向同一节点。
表达工作之间的平行关系时 , 可以增加虚工作来表达它们之间的关系。
如表达平行工作 A ,B 时 , 应增加虚工作②—③ (见图 2 。
而图 3的表示方式则是错误的。
2 用于反映一些工作与另一些工作之间的逻辑制约关系。
如表达“ 工作 A ,B 完成后 , 工作 D 才能开始 , 工作 B ,C 完成后 , 工作 E 才能开始” (见图 4 , 如取消虚工作 , 则违反双代号网络图的。
3(ES i 2j 、最早可能结束 EF i 2j 、最迟必须开始时间 (L S i 2j 、最迟必须结束时间 (L F i 2j、总时差 (T F i 2j 和自由时差 (FF i 2j 6个。
其中总时差是指各工作在不影响计划总工期的情况下所具有的机动时间 , 它等于该工作的最迟必须开始时间减去该工作的最早可能开始时间 , 或该工作的最迟必须结束时间减去该工作的最早可能结束时间 ; 自由时差是指各工作在不影响紧后工作最早可能开始时间的前提下 , 所具有的机动时间 , 它等于其紧后工作最早可能开始时间的最小值减去该工作最早可能结束时间 [1], 这里所指的工作都是实工作。
关键工作为网络计划中总时差最小的工作 ; 关键线路为自始至终全部由关键工作组成的线路或线路上总的工作持续时间最长的线路 [2]。
2虚工作时间参数计算对各实工作时间参数的影响 2. 1对虚工作时间参数计算的 3种观点1 现有 J G J/T 121299工程网络计划技术规程规定 :按工作计算法计算时间参数应在确定各项工作的持续时间之后进行。
虚工作必须视同实工作计算 , 其持续时间为零 [1]。
2 为避免在计算工作时间参数时把各工作的逻辑关系搞错 ,从而将各实工作的时间参数算错 , 可以将虚工作视同实工作并进行其时间参数的计算 , 计算时取虚工作的持续时间为零 [2,3]。
3 因虚工作只起到表达各相关实工作之间逻辑关系的作用 ,・951・第 34卷第 6期 2008年 2月山西建筑 SHANXI ARCHITECTUREVol.34No. 6Feb. 2008所以在计算各实工作的时间参数时不必计算虚工作的时间参数 [4]。
2. 2 3种观点对各实工作时间参数的影响根据时间参数的定义 , 因为虚工作的持续时间为零 , 所以把虚工作视同实工作计算其时间参数对其他各实工作的最早可能开始时间、最早可能结束时间、最迟必须开始时间、最迟必须结束时间、总时差 5个时间参数的计算结果没有影响 , 但对某实工作的自由时差计算结果有时会产生影响。
这就是当某实工作的紧后工作只有虚工作且该实工作不是关键线路上的关键工作 , 虚工作的紧后实工作的最早可能开始时间与该实工作的最早可能结束时间不等时 , 则在计算该实工作的自由时差时 , 是否把虚工作视同实工作计算其时间参数对该实工作的自由时差的计算结果有影响 , 不过对其他实工作的自由时差的计算结果没有影响。
除此之外 , 是否把虚工作视同实工作计算其时间参数对该实工作的自由时差的计算结果没有影响。
主要原因有以下几点 :1 当某实工作的紧后工作只有虚工作 , 路上的关键工作 , 该实工作的最早可能结束时间不等时 , 时差时 , 很显然 , , 虚工 , 则该实工作的自由时差为零 ; , 早完成时间不相等 , 则该实工作的自由时差不为零 , 如图 5, 图 6所示。
2 当某实工作的紧后工作只有虚工作且该实工作不是关键线路上的关键工作 , 虚工作的紧后实工作中至少有一个实工作的最早可能开始时间与该实工作的最早可能结束时间相等时 , 是否把虚工作视同实工作计算其时间参数对该实工作的自由时差没有影响 , 该实工作的自由时差为零 , 如图 7所示。
3 当某实工作的紧后工作只有虚工作且该工作是关键线路上的关键工作时 , 则关键线路上的工作自由时差都为零。
4 当某实工作的紧后工作不全为虚工作时 , 因虚工作对各实工作的最早可能开始时间、最早可能结束时间没有影响 , 所以是否把虚工作视同实工作计算其时间参数对各实工作的自由时差的计算结果没有影响。
如图 5, 图 6所示的网络图 , 关键工作①—④和④—⑤ , 关键线路为①—④—⑤ , 如果把虚工作②—③ , ②—④视同实工作时 , B 工作的自由时差为零, 各工作的时间参数计算结果如图 5所示 ; 如果不计算虚工作②—③ , ②—④的时间参数 , 则 B 工作的自由时差为 2, 不为零 , 各工作的时间参数计算结果如图 6所示。
,B 工作的自由时差应为 2。
由此可 , 得出错误结果。
3结语为减少计算量 , 避免误导 , 在计算双代号网络图中各实工作的时间参数时 , 须弄清虚工作表达的各相关实工作之间正确的逻辑关系 , 但不要计算虚工作的时间参数。
当某实工作的紧后工作只有虚工作且该实工作不是关键线路上的关键工作 , 虚工作的紧后实工作的最早可能开始时间与该实工作的最早可能结束时间不等时 , 则不能把虚工作视同实工作计算其时间参数 , 否则会导致该实工作自由时差的计算结果错误 , 给工程建设的规划、设计 , 特别是施工及其相关工作的进度计划安排带来混乱 , 甚至将各工作先后顺序颠倒。
参考文献 :[1]JG J/T 121299, 网络图计算规范 [S].[2]赵志缙 , 应惠清 . 建筑施工 [M ].上海 :同济大学出版社 ,2003. [3]郭正兴 , 李金根 . 建筑施工 [M ].南京 :东南大学出版社 ,2004. [4]田彦华 , 李海霞 . 全国监理工程师执业资格考试复习指导 [M ].天津 :天津大学出版社 ,2002.A Probe into the calcaulation of the timeparameter of dummy activity in the activity 2on 2arrow net workLAN Li 2hu aAbstract :This paper deeply analyze , and doubts about the view that dummy activity is cousiderd as normal activity to conduct the calculation of time parameter. The paper reaches the conclusion that the time parameters of dummy activity should not be included when calculating the time parameters of all the normal activities in activity 2on 2arrow network. It also points out the time when the calculation of the time parameter of dummy activity is conducted ,during which the time parameter of the related activitieswill be affected. K ey w ords :activity 2on 2arrow network , dummy activity , time parameter・061・第 34卷第 6期 2008年 2月山西建筑。
