多重共线性回归分析及其实验报告
实验报告多重共线性
西南科技大学Southwest University of Science and Technology 经济管理学院计量经济学实验报告——多元线性回归的检验专业班级：国贸0903姓名：王鑫学号： 20092438任课教师：龙林成绩：简单线性回归模型的处理实验目的：掌握多元回归参数的估计和检验的处理方法。
实验要求：学会建立模型，估计模型中的未知参数等。
试验用软件：Eviews实验原理：线性回归模型的最小二乘估计、回归系数的估计和检验。
实验内容：1、实验用样本数据：运用Eviews软件，建立1990—2001年中国国内生产总值X和深圳市收入Y的回归模型，做简单线性回归分析，并对回归结果进行检验。
以研究我国国内生产总值对深圳市收入的影响。
年份地方预算内财政收入Y（亿元）国内生产总值(GDP)X（亿元）1990 21.7037 171.6665 1991 27.3291 236.6630 1992 42.9599 317.3194 1993 67.2507 449.2889 1994 74.3992 615.1933 1995 88.0174 795.6950 1996 131.7490 950.0446 1997 144.7709 1130.0133 1998 164.9067 1289.0190 1999 184.7908 1436.0267 2000 225.0212 1665.4652 2001 265.6532 1954.6539经过简单的回归分析后得出表EQ1：Dependent Variable: YMethod: Least SquaresDate: 11/28/11 Time: 18:31Sample: 1990 2001Included observations: 12Variable CoefficientStd. Error t-Statistic Prob.C -3.611151 4.161790 -0.867692 0.4059X 0.134582 0.003867 34.80013 0.0000 R-squared 0.991810 Mean dependent var 119.8793 Adjusted R-squared 0.990991 S.D. dependent var 79.36124S.E. of regression 7.532484 Akaike infocriterion 7.027338Sum squared resid 567.3831 Schwarz criterion 7.108156Log likelihood -40.16403 F-statistic 1211.049Durbin-Watson stat 2.051640 Prob(F-statistic) 0.00000其中拟合优度为：0.991810有很强的线性关系。
实验二__多元线性回归模型和多重共线性范文
实验二__多元线性回归模型和多重共线性范文多元线性回归是一种常用的统计分析方法，用于研究多个自变量与一个因变量之间的关系。
在进行多元线性回归分析时，一个重要的问题是多重共线性。
多重共线性是指多个自变量之间存在高度相关性，这会导致回归模型的不稳定性，参数估计的不准确性，以及对自变量的解释能力下降等问题。
在进行多元线性回归分析之前，首先需要对自变量之间的相关性进行检验。
常用的方法有相关系数、方差膨胀因子（VIF）等。
相关系数用于衡量两个变量之间的线性关系，其值介于-1和1之间，接近于1表示高度正相关，接近于-1表示高度负相关。
VIF用于衡量一个自变量与其他自变量之间的相关性，其值大于1且越接近于1，表示相关性越强。
如果发现多个自变量之间存在高度相关性，即相关系数接近于1或VIF接近于1，就需采取措施来解决多重共线性问题。
一种常用的方法是通过增加样本量来消除多重共线性。
增加样本量可以提高模型的稳定性，减小参数估计的方差。
但是，增加样本量并不能彻底解决多重共线性问题，只能部分缓解。
另一种常用的方法是通过变量选择来解决多重共线性问题。
变量选择可以将高度相关的自变量从模型中剔除，保留与因变量高度相关的自变量。
常用的变量选择方法包括前向选择、逐步回归和岭回归等。
这些方法都是根据一定的准则逐步筛选变量，直到得到最佳模型为止。
在变量选择中，需要注意在变量剔除的过程中，要确保剩余变量之间的相关性尽可能小，以提高模型的稳定性和准确性。
此外，还可以通过变换变量来解决多重共线性问题。
变换变量可以通过对自变量进行平方项、交互项等操作，以减小相关性。
变换变量的方法需要根据实际情况来选择，具体操作可以参考相关的统计学方法教材。
总之，多元线性回归模型在实际应用中经常遇到多重共线性问题。
通过检验自变量之间的相关性，选择合适的变量和适当的变量变换方法，可以有效解决多重共线性问题，提高模型的稳定性和准确性。
在具体的研究中，应根据实际情况选择适合的方法来解决多重共线性问题，以确保回归分析结果的可靠性和有效性。
多重共线性实验报告
【实验名称】：多重共线性的检验方法和处理【实验目的】：掌握多重共线性的原理【实验原理】：综合统计检验法、相关系数矩阵检验法、逐步回归法【实验步骤】：一、创建一个新的工作文件：二、输入样本数据：三、用普通最小二乘法估计模型：由于解释变量个数较多，并且解释变量之间可能存在相关性，为了降低这种相关性以减弱序列相关性对模型的影响，我们先对各个解释变量和被解释变量取对数：即在Eviews软件的命令框执行：genr lnY=log（Y），genr lnX1=log（X1）,genr lnX2=log （X2）……genr lnX5=log（X5）我们设粮食生产函数为：LnY=β0+β1lnX1+β2lnX2+β3lnX3+β4lnX4+β5lnX5+μ用运普通最小二乘法估计：下表给出了采用Eviews软件对表一的数据进行回归分析的统计结果：Dependent Variable: LNYMethod: Least SquaresDate: 12/19/13 Time: 10:05Sample: 1983 2007C -4.173174 1.923624 -2.169434 0.0429LNX1 0.381145 0.050242 7.586182 0.0000 LNX2 1.222289 0.135179 9.042030 0.0000 LNX3 -0.081110 0.015304 -5.300024 0.0000 LNX4 -0.047229 0.044767 -1.054980 0.3047R-squared 0.981597 Mean dependent var 10.70905 Adjusted R-squared 0.976753 S.D. dependent var 0.093396 S.E. of regression 0.014240 Akaike info criterion -5.459968 Sum squared resid 0.003853 Schwarz criterion -5.167438 Log likelihood 74.24960 F-statistic 202.6826 Durbin-Watson stat 1.791427 Prob(F-statistic) 0.000000根据上表估计出的参数，可以得到如下普通最小二乘法估计模型：lnY=‐4.17+0.381lnX1+1.222lnX2‐0.081lnX3‐0.047lnX4‐0.101lnX5四、模型检验：1、数学检验：由于R2为0.9816接近于一，且F=202.68>F0.05（5，9）=2.74，故认为粮食产量和上述解释变量之间的总体线性关系显著；但是就X4,X5来说，其t检验的参数较小，尚不能通过t检验，因此怀疑模型中存在多重共线性。
Eviews多重共线性实验报告
实验三 多重共线性【实验目的】掌握多重共线性问题出现的来源、后果、检验及修正的原理，以及相关的Eviews 操作方法. 【实验内容】以《计量经济学学习指南与练习》补充习题4-18为数据，练习检查和克服模型的多重共线性的操作方法。
【4—18】表4-3列出了被解释变量Y 及解释变量1X ，2X ,3X ,4X 的时间序列观察值。
（1） 用OLS 估计线性回归模型，并采用适当的方法检验多重共线性; （2） 用逐步回归法确定一个较好的回归模型.【实验步骤】（1） 建立线性回归模型并检验多重共线性1、 建立模型利用表4-3数据分别建立Y 关于1X 、2X 、3X 、4X 的散点图（SCAT i X Y ）.可以看到Y 与1X 、2X 、4X 都呈现正的线性相关，与3X 关系不明显。
首先建立一个多元线性回归模型（LS Y C 1X 2X 3X 4X ）.输出结果中，C 、1X 、3X 、4X 的系数都通不过显著性检验。
2、 检验多重共线性进一步选择Covariance Analysis 的Correlation,得到变量之间的偏相关系数矩阵，观察偏相关系数。
可以发现，Y 与1X 、2X 、4X 的相关系数都在0.9以上，但输出结果中,解释变量1X 、4X 的回归系数却无法通过显著性检验。
认为解释变量之间存在多重共线性。
（2） 用逐步回归法克服多重共线性1、 找出最简单的回归形式分别作Y 与1X 、2X 、3X 、4X 间的回归（LS Y C i X ）。
即:（1）1122.0942.0X Y +=∧（1。
64） (11。
7)9383.02=RD.W.=1。
6837(2）2205.0497.5X Y +=∧(17。
9) (7。
63）8640.02=RD.W.=0。
6130(3）3095.0090.17X Y -=∧(2。
14) （-1.19)0450.02=RD.W.=0。
6471（4）4055.0018.2X Y +=∧(2.25) (6。
统计学第五次实验-多重共线性实验报告
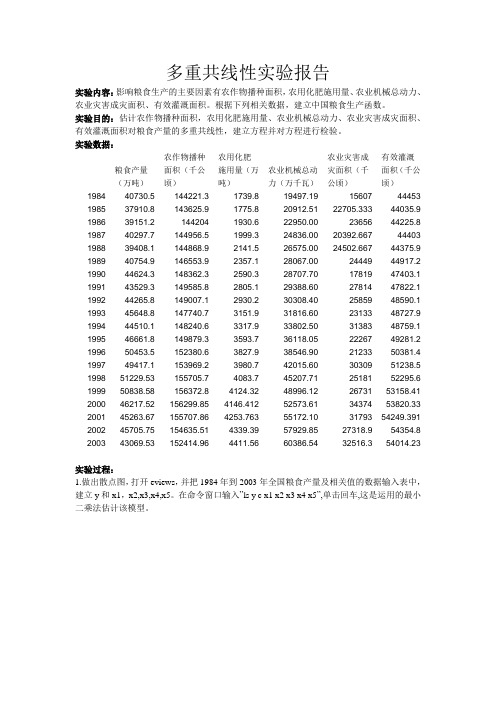
多重共线性实验报告实验内容：影响粮食生产的主要因素有农作物播种面积，农用化肥施用量、农业机械总动力、农业灾害成灾面积、有效灌溉面积。
根据下列相关数据，建立中国粮食生产函数。
实验目的：估计农作物播种面积，农用化肥施用量、农业机械总动力、农业灾害成灾面积、有效灌溉面积对粮食产量的多重共线性，建立方程并对方程进行检验。
实验数据：粮食产量（万吨）农作物播种面积（千公顷）农用化肥施用量（万吨）农业机械总动力（万千瓦）农业灾害成灾面积（千公顷）有效灌溉面积（千公顷）1984 40730.5 144221.3 1739.8 19497.19 15607 44453 1985 37910.8 143625.9 1775.8 20912.51 22705.333 44035.9 1986 39151.2 144204 1930.6 22950.00 23656 44225.8 1987 40297.7 144956.5 1999.3 24836.00 20392.667 44403 1988 39408.1 144868.9 2141.5 26575.00 24502.667 44375.9 1989 40754.9 146553.9 2357.1 28067.00 24449 44917.2 1990 44624.3 148362.3 2590.3 28707.70 17819 47403.1 1991 43529.3 149585.8 2805.1 29388.60 27814 47822.1 1992 44265.8 149007.1 2930.2 30308.40 25859 48590.1 1993 45648.8 147740.7 3151.9 31816.60 23133 48727.9 1994 44510.1 148240.6 3317.9 33802.50 31383 48759.1 1995 46661.8 149879.3 3593.7 36118.05 22267 49281.2 1996 50453.5 152380.6 3827.9 38546.90 21233 50381.4 1997 49417.1 153969.2 3980.7 42015.60 30309 51238.5 1998 51229.53 155705.7 4083.7 45207.71 25181 52295.6 1999 50838.58 156372.8 4124.32 48996.12 26731 53158.41 2000 46217.52 156299.85 4146.412 52573.61 34374 53820.33 2001 45263.67 155707.86 4253.763 55172.10 31793 54249.391 2002 45705.75 154635.51 4339.39 57929.85 27318.9 54354.8 2003 43069.53 152414.96 4411.56 60386.54 32516.3 54014.23实验过程：1.做出散点图，打开eviews，并把1984年到2003年全国粮食产量及相关值的数据输入表中，建立y和x1，x2,x3,x4,x5。
多重共线性案例分析实验报告
《多重共线性案例分析》实验报告表2由此可见，该模型，可决系数很高，F 检验值173.3525,明显显著。
但是当时,不仅、系数的t 检验不显著，而且系数的符号与预期的相反，这表明很可能存在严重的多重共线性。
9954.02=R 9897.02=R 05.0=α776.2)610()(025.02=-=-t k n t α2X 6X 6X②.计算各解释变量的相关系数，选择X2、X3、X4、X5、X6数据，点”view/correlations ”得相关系数矩阵表3由关系数矩阵可以看出：各解释变量相互之间的相关系数较高，证实确实存在严重多重共线性相。
4.消除多重共线性①采用逐步回归的办法，去检验和解决多重共线性问题。
分别作Y 对X2、X3、X4、X5、X6的一元回归 如下图所示变量 X2 X3 X4 X5 X6 参数估计值0.08429.0523 11.6673 34.3324 2014.146 t 统计量8.665913.1598 5.1967 6.4675 8.74870.90370.95580.77150.83940.9054表4 按的大小排序为：X3、X6、X2、X5、X4。
以X3为基础，顺次加入其他变量逐步回归。
首先加入X6回归结果为：t=(2.9086) (0.46214)2R 2R 631784.285850632.7639.4109ˆX X Y t ++-=957152.02=R1995 1375.7 62900 464.0 61.5 115.70 5.97 1996 1638.4 63900 534.1 70.5 118.58 6.49 1997 2112.7 64400 599.8 145.7 122.64 6.60 1998 2391.2 69450 607.0 197.0 127.85 6.64 1999 2831.9 71900 614.8 249.5 135.17 6.74 2000 3175.5 74400 678.6 226.6 140.27 6.87 2001 3522.4 78400 708.3 212.7 169.80 7.01 2002 3878.4 87800 739.7 209.1 176.52 7.19 2003 3442.3 87000 684.9 200.0 180.98 7.30表1：1994年—2003年中国游旅收入及相关数据表2：OLS 回归表3：关系数矩阵变量 X2 X3 X4 X5 X6 参数估计值0.08429.0523 11.6673 34.3324 2014.146 t 统计量8.665913.1598 5.1967 6.4675 8.74870.90370.95580.77150.83940.9054表4：Y 对X2、X3、X4、X5、X6的一元回归六、实验结果及分析1. 在参数估计模型和关系数矩阵中， ，可决系数很高，F 检验值173.3525,明显显著。
Eviews多重共线性实验报告-V1
Eviews多重共线性实验报告-V1本文主要将Eviews多重共线性实验报告进行整理，旨在帮助读者更好地理解和应用多重共线性实验结果。
1. 研究背景多重共线性是指在回归模型中，自变量之间存在高度相关的情况。
这种相关关系会导致模型的不稳定性，降低模型的解释能力和预测能力。
因此，在进行回归分析时，需要对多重共线性进行检测和处理。
2. 数据来源和处理本次实验所使用的数据来自某公司销售数据，共有18个自变量和1个因变量。
在进行回归分析之前，需要对数据进行预处理。
首先，我们通过观察变量间的相关系数矩阵来初步判断是否存在多重共线性。
如果存在高度相关的自变量，可以考虑通过主成分分析等方法来降维，减少变量间的冗余。
本实验中，我们发现变量间的相关性较小，因此没有进行降维操作。
3. 模型建立我们采用逐步回归的方法建立回归模型，并对模型的适配度和稳定性进行评估。
首先，我们使用全模型（包含所有自变量）进行回归分析，并得到如下统计结果：R-squared：0.7767Adj. R-squared：0.7152F-statistic：12.38（显著）通过观察模型的系数，我们发现存在一些变量的系数非常大，而一些变量的系数非常小甚至为0，这也是多重共线性的表现之一。
为了进一步检验模型的稳定性和解释能力，我们采用逐步回归的方法进行变量筛选。
在此过程中，我们设置的入模标准是F统计量显著，出模标准是T统计量显著或P值小于0.05。
最终，我们得到了一个包含4个自变量的最优模型，其统计结果如下：R-squared：0.7224Adj. R-squared：0.6812F-statistic：17.69（显著）通过观察模型的系数，我们发现所有自变量的系数都显著，且大小合理。
这说明通过逐步回归的方法，我们成功地排除了多重共线性的影响，建立了一个具有较好稳定性和解释能力的模型。
4. 结论和建议在本实验中，我们成功地应用了Eviews工具，通过逐步回归的方法检验和处理多重共线性，建立了一个较为稳定和解释能力强的回归模型。
计量经济学多元线性回归多重共线性异方差实验报告
计量经济学实验报告多元线性回归、多重共线性、异方差实验报告一、研究目的和要求：随着经济的发展，人们生活水平的提高，旅游业已经成为中国社会新的经济增长点。
旅游产业是一个关联性很强的综合产业，一次完整的旅游活动包括吃、住、行、游、购、娱六大要素，旅游产业的发展可以直接或者间接推动第三产业、第二产业和第一产业的发展。
尤其是假日旅游，有力刺激了居民消费而拉动内需。
2012年，我国全年国内旅游人数达到亿人次，同比增长%，国内旅游收入万亿元，同比增长%。
旅游业的发展不仅对增加就业和扩大内需起到重要的推动作用，优化产业结构，而且可以增加国家外汇收入，促进国际收支平衡，加强国家、地区间的文化交流。
为了研究影响旅游景区收入增长的主要原因，分析旅游收入增长规律，需要建立计量经济模型。
影响旅游业发展的因素很多，但据分析主要因素可能有国内和国际两个方面，因此在进行旅游景区收入分析模型设定时，引入城镇居民可支配收入和旅游外汇收入为解释变量。
旅游业很大程度上受其产业本身的发展水平和从业人数影响，固定资产和从业人数体现了旅游产业发展规模的内在影响因素，因此引入旅游景区固定资产和旅游业从业人数作为解释变量。
因此选取我国31个省市地区的旅游业相关数据进行定量分析我国旅游业发展的影响因素。
二、模型设定根据以上的分析，建立以下模型Y=β0+β1X1+β2X2+β3X3+β4X4+Ut参数说明：Y ——旅游景区营业收入/万元X1——旅游业从业人员/人X2——旅游景区固定资产/万元X3——旅游外汇收入/万美元X4——城镇居民可支配收入/元收集到的数据如下（见表）：表 2011年全国旅游景区营业收入及相关数据（按地区分）数据来源：1.中国统计年鉴2012，2.中国旅游年鉴2012。
三、参数估计利用做多元线性回归分析步骤如下：1、创建工作文件双击图标，进入其主页。
在主菜单中依次点击“File\New\Workfile”，出现对话框“Workfile Range”。
计量经济学多重共线性实验报告
计量经济学实验报告一、实验目的：1、熟悉和掌握Eviews在多重共线性模型中的应用，如何判断和解决多重共线性问题。
2、加深对课程理论知识的理解和应用。
二、实验问题：农村居民各种不同类型的收入对消费支出影响（2006年）农村居民收入（Y）主要来源于4项：即农业经营收入（X1）、工资性收入（X2）、财产性收入（X3）及转移性收入（X4）。
（1）利用线性模型或双对数模型进行分析。
（2）回归模型中存在多重共线性吗？三、实验数据：由老师提供（本实验报告截取从北京到新疆共31组数据）四、实验步骤：1、建立新的工作文件，输入数据，分别保存为Y（农村居民收入），X1（农业经营收入）、X2（工资性收入）、X3（财产性收入）、及X4（转移性收入）。
2、建立线性模型：Y = a1*X1 + a2*X2 +a3*X3 + a4*X4 + u得到方程：Y = 0.6268809567*X1 + 0.481134931*X2 - 0.255544644*X3 + 2.683018467*X4 + 479.30109493、分析由图中数据可以看出，在最小二乘法下，模型的R平方和F值较大，表明模型中各解释变量对Y的联合线性作用显著；但是X3（财产性收入）的系数是负的，这不符合经济学意义，财产性收入应当与消费支出正相关，故怀疑模型存在多重共线性。
4、检验：计算解释变量之间的简单相关系数：在“quick”菜单中选“group statistics”项中的“correlation”命令。
在出现“serieslist”对话框时，直接输入X1，X2，X3，X4出现如下结果从表中可以看出，解释变量X1、X3、X4之间存在高度线性相关。
4、修正第一步：运用OLS方法逐一求Y对各个解释变量的回归。
（1）Y = 0.8997862236*X1 + 1541.033294t值 15.32947 12.29913prob.值 0.0000 0.0000R2=0.890148 F=234.9925（2）Y = 0.2487123305*X2 + 2505.747921t值 0.527219 2.676297prob.值 0.6021 0.0121R2= 0.009494 F=0.277960（3）Y = 8.049228785*X3 + 1943.170851t值 9.28666 11.56389prob.值 0.0000 0.0000R2=0.748356 F= 86.24206（4）Y = 5.928884198*X4 + 1631.299987t值 9.212266 8.434353prob.值 0.0000 0.0000R2= 0.745314 F=84.86584结合经济意义和统计检验结果分析，在4个一元回归模型中消费支出Y对X1工资性收入线性关系最强，拟合程度较好，与经验相符，因此选（1）为初始的回归模型。
多重共线性回归分析及其实验报告
实验报告实验题目：多重共线性的研究指导老师：学生一：学生二：实验时间：2011年10月多重线性回归分析及其实验报告实验目的：为了更好地了解财政收入构成，需要定量地分析影响财政收入的因素模型设定及其估计：经分析，影响财政收入的主要因素，农业增加值X1，工业增加值X2，建筑业增加值X3，总人口X4，受灾面积X5.为此设定了如下形式的计量经济模型：Y=β1+β2X1+β3X2+β4X3+β5X4+β6X5+u0其中，Y为财政收入（元），X1农业增加值（元），X2为工业增加值(元)，X3为建筑业增加值（元），X4为总人口（万人），X5为受灾面积（千公顷）为估计模型参数，收集1978~2007年财政收入及其影响因素数据，如图：1978~2007年财政收入及其影响因素数据年份财政收入CS/亿元农业增加值NZ/亿元工业增加值GZ/亿元建筑业增加值JZZ/亿元总人口TPOP/万人受灾面积SZM/千公顷1978 1132.3 1027.5 1607 138.2 96259 50790 1979 1146.6 1270.2 1769.7 143.8 97542 39370 1980 1159.9 1371.4 1996.5 195.5 98705 44526 1981 1175.8 1559.5 2048.5 207.1 100072 39790 1982 1212.3 1777.4 2162.3 220.7 101654 33130 1983 1367 1978.5 2375.8 270.6 103008 34710 1984 1642.5 2316.1 2789 316.7 104357 31890 1985 2004.6 2564.3 3448.5 417.9 105851 44365 1986 2122 2788.7 3987.5 525.7 107507 47170 1987 2199.4 3233 4565.9 665.8 109300 42090 1988 2357.6 3865.4 5062 810 111026 50870 1989 2664.5 5062 8087.3 794 112704 46991 1990 2937.4 5342.3 10284.5 859.4 114333 384741991 3149.48 5866.8 14188 1015.1 115823 55472 1992 3483.48 6963.6 19480.5 1415 117171 51333 1993 4348.95 9572.7 19480.4 2266.5 118517 48829 1994 5218.1 12315.7 24950.7 2964.7 119850 55043 1995 6242.2 14015.8 29447.6 3728.8 121121 45821 1996 7407.99 14441.8 32921.4 4387.4 122389 46898 1997 8615.14 14917.6 34018.4 4985.8 123626 53429 1998 9875.95 14944.5 40036 5172.1 124761 59145 1999 11444.08 15871.8 43580.6 5522.3 125786 49981 2000 13395.23 16537 47431.6 5913.7 126743 54688 2001 16386.04 17381.8 54945.5 6465.5 127627 52215 2002 18903.64 21412.7 65210 7490.8 128453 47119 2003 21715.25 22420 76912.6 8694.3 129227 54506 2004 26396.47 21224 87632.4 8967.8 129988 37106 2005 31649.29 22420 89834.5 10133.8 130756 38818 2006 38760.2 24040.9 91310.9 11851.1 131448 41091 2007 51321.45 28095 107367.2 14014.1 132129 48992利用Eviews软件，生成Y、X1、X2、X3、X4、X5等数据，采用这些数据进行OLS回归，结果如下Dependent Variable: YMethod: Least SquaresDate: 10/24/11 Time: 22:49Sample: 1978 2007Included observations: 30Variable Coefficient Std. Error t-Statistic Prob.C -6734.394 11259.37 -0.598115 0.5554X1 -1.678611 0.328371 -5.111937 0.0000X2 0.071078 0.081171 0.875666 0.3899X3 5.699199 0.745591 7.643870 0.0000X4 0.101481 0.114244 0.888277 0.3832X5 -0.010922 0.057578 -0.189691 0.8511R-squared 0.983660 Mean dependent var 10047.83Adjusted R-squared 0.980255 S.D. dependent var 12585.61S.E. of regression 1768.473 Akaike info criterion 17.97048Sum squared resid 75059958 Schwarz criterion 18.25072Log likelihood -263.5572 F-statistic 288.9512Durbin-Watson stat 0.898668 Prob(F-statistic) 0.000000由此可见，该模型R2=0.983660，R2=0.980255可决系数很高，F检验值为288.9512，明显显著。
多重共线性实训报告
一、实训背景多重共线性是指回归模型中存在两个或两个以上的自变量高度相关，导致回归系数估计不准确、显著性检验失效等问题。
为了解决多重共线性问题，我们进行了一次多重共线性实训，通过实际操作，了解和掌握多重共线性的检验方法和解决策略。
二、实训目的1. 理解多重共线性的概念和产生原因；2. 掌握多重共线性的检验方法；3. 学习解决多重共线性的策略；4. 培养实际操作能力和问题解决能力。
三、实训内容1. 数据收集与整理本次实训选用某地区居民消费支出数据作为研究对象，数据包括居民收入、教育支出、医疗支出、娱乐支出等变量。
2. 数据分析（1）多重共线性检验采用方差膨胀因子（VIF）和条件指数（CI）对数据进行多重共线性检验。
VIF值越大，表示多重共线性程度越高；CI值越小，表示多重共线性程度越低。
（2）解决多重共线性策略针对检验出的多重共线性问题，采取以下策略进行解决：1）剔除高度相关的变量：通过VIF和CI筛选出高度相关的变量，并将其剔除。
2）主成分分析（PCA）：将高度相关的变量通过主成分分析转换为低维变量，降低多重共线性。
3）岭回归：在回归模型中引入岭参数，对回归系数进行惩罚，降低多重共线性。
四、实训过程1. 数据导入与预处理首先，将数据导入统计软件（如SPSS、R等），然后进行数据清洗，包括处理缺失值、异常值等。
2. 多重共线性检验（1）计算VIF和CI通过软件中的相关系数矩阵，计算每个变量的VIF和CI值。
（2）筛选出高度相关的变量根据VIF和CI值，筛选出高度相关的变量。
3. 解决多重共线性问题（1）剔除高度相关的变量根据筛选结果，将高度相关的变量从模型中剔除。
（2）主成分分析对剩余变量进行主成分分析，将高度相关的变量转换为低维变量。
（3）岭回归在回归模型中引入岭参数，对回归系数进行惩罚。
4. 结果分析通过上述处理，多重共线性问题得到有效解决。
对比处理前后的回归系数，发现回归系数估计更加准确，显著性检验更加有效。
Eviews多重共线性实验报告(1)
Eviews多重共线性实验报告(1)Eviews多重共线性实验报告1. 实验背景多重共线性是指在回归分析中，自变量之间存在高度相关，导致回归系数的不稳定性和误差方差的增大。
在实践中，多重共线性是经济预测分析的重要问题，如何诊断和处理多重共线性是经济学研究中的重要课题。
2. 实验目的通过Eviews软件进行多重共线性诊断，掌握运用Eviews软件解决多重共线性问题的技巧，提高经济预测和分析的准确度和可靠性。
3. 实验流程（1）收集所需要进行回归分析的数据。
（2）在Eviews中建立回归模型，运行回归分析。
（3）通过Eviews的诊断功能，检验回归模型中自变量之间的线性相关。
（4）运用Eviews的多重共线性处理方法，解决自变量之间的多重共线性问题。
4. 实验结果（1）通过Eviews的诊断功能，我们可以得到多重共线性诊断报告，其中显示了变量之间的相关系数矩阵、方差膨胀因子（VIF）、条件指数（CI）、特征值（eigenvalue）、特征向量（eigenvector）等诊断指标。
通过观察相关系数矩阵和VIF，我们可以发现是否存在高度相关的自变量。
当VIF大于10时，就表明存在多重共线性。
（2）如果诊断报告中存在多重共线性问题，我们可以通过Eviews中的多重共线性处理方法解决。
其中包括删除相关系数较高的变量、采用主成分回归法、采用岭回归等方法，具体方法应根据实际情况来选择。
5. 实验结论通过Eviews的多重共线性诊断和处理，我们可以更加准确地进行回归分析，避免了多重共线性所带来的偏误和不稳定性。
在实际应用中，我们应根据具体情况选择适当的处理方法，以得到更加可靠的预测结果。
实验报告三(多重共线性)
实验三多重共线性一、研究的目的要求一直以来，钢铁一直是衡量一个国家经济实力的一个标志。
近年来，随着经济的不断发展。
我国钢铁产量及供应量也在不断提升。
为了确定影响中国钢铁供应量的主要因素，需要建立计量分析模型，分析影响我国钢铁供应量的主要因素。
二、模型设定为了全面反映影响我国钢铁供应量的主要因素，选取了我国1986-2005年我国钢材供应量的具体数据，选择“钢材供应量（万吨）Y”作为被解释变量，“原油产量（万吨）X2”、“生铁产量（万吨）X3”、“原煤产量（万吨）X4”、“电力产量（亿千瓦小时）X5”、“固定资产投资（亿元）X6”、“国内生产总值（亿元）X7”、和“铁路运输量（万吨）X8”作为解释变量。
收集的数据如下：利用EViews软件，生成Y t、X2、X3、X4、X5、X6、X7、X8等的数据，采用这些对模型进行OLS回归，结果如下图所示：由此可见，该模型R2=0.997857，修正的可决系数为0.996606，可决系数高，F检验值为798.0921，明显显著。
但是当α= 0.05时，t a/2(n-k)=t0.025(20-9)=2.201,不仅X2、X4、X6、X7、X8 的系数t检验不显著，而且X2、X4、X7系数的符号与预期相反，这表明很可能存在严重的多重共线性。
计算各解释变量的相关系数，选择X2、X3、X4、X5、X6、X7、X8的数据，点“view/correlation”得相关系数矩阵，如下图：由相关系数矩阵可以看出，各解释变量相互之间的相关系数较高，证实确实存在严重的多重共线性。
三、修正多重共线性采用逐步回归的办法，去检验和解决多重共线性问题。
分别作Y对X2、X3、X4、X5、X6、X7、X8一元回归，结果如下图所示：其中，X5的方程修正的可决系数最大，以X5为基础，顺次加入其他变量逐步回归。
结果如下图：加入新变量的回归结果经比较，加入X3的方程的修正的可决系数为0.997005，改进最大，而且各参数的t检验显著，选择保留X3，再加入其他新变量逐步回归，结果如下图所示：加入新变量的回归结果经比较，无论加入哪一个变量，修正的可决系数均没有有所提高，反而下降，且新加入的参数的t检验不显著，并为负值不合理。
实验报告6-多重共线性
2014-2015学年第 一 学期实 验 报 告实验课程名称 多重共线性的检验与修正专 业 班 级 金融1204学生 学号 31205382学 生 姓 名 黄聪聪实验指导教师 董美双编号：实验名称多重共线性检验与修正指导老师董美双成绩专业金融班级金融1204 姓名黄聪聪学号 31205382一、实验目的目的：通过实验，理解并掌握多重共线性的原理，熟悉掌握对多元模型的多重共线性问题进行检验和修正的方法与步骤。
要求：熟练掌握检验多重共线性检验的不显著系数法、系数符号判断法、相关系数矩阵法、拟合优度法、Frisch综合分析法；消除多重共线性：可以综合应用各种方法。
验证性部分用教材中的例题7.6的数据，按步骤做。
或者自己收集数据按上面的步骤做一遍，把结果输出到word文档中。
步骤： 1.模型的参数估计（至少有3个解释变量）；2.检验是否存在多重共线性；方法一：不显著系数法；方法二：系数符号法方法三：相关系数矩阵法方法四：Frish综合分析法——逐步回归法3.多重共线性的修正：差分法、取对数法、逐步回归法等。
4.得出修正后的模型。
1.模型的参数估计（至少有3个解释变量）Dependent Variable: BUSTRAVLMethod: Least SquaresDate: 07/26/14 Time: 10:09Sample: 1 40C 2744.680 2641.672 1.038994 0.3064FARE -238.6544 451.7281 -0.528314 0.6008 GASPRICE 522.1132 2658.228 0.196414 0.8455 INC -0.194744 0.064887 -3.001294 0.0051POP 1.711442 0.231364 7.397176 0.0000 DENSITY 0.116415 0.059570 1.954253 0.0592R-squared 0.921026 Mean dependent var 1933.175 Adjusted R-squared 0.906667 S.D. dependent var 2431.757 S.E. of regression 742.9113 Akaike info criterion 16.21666 Sum squared resid 18213267 Schwarz criterion 16.51221 Log likelihood -317.3332 F-statistic 64.14338估计方程为：LANDAREA DENSITYPOPINC GASPRICEFARE SBU16.112.071.119.011.52265.23868.2744ˆ-++-+-=2.检验是否存在多重共线性方法一：不显著系数法Dependent Variable: BUSTRAVLMethod: Least SquaresDate: 07/26/14 Time: 10:09Sample: 1 40C 2744.680 2641.672 1.038994 0.3064FARE -238.6544 451.7281 -0.528314 0.6008GASPRICE 522.1132 2658.228 0.196414 0.8455INC -0.194744 0.064887 -3.001294 0.0051POP 1.711442 0.231364 7.397176 0.0000DENSITY 0.116415 0.059570 1.954253 0.0592LANDAREA -1.155230 1.802638 -0.640855 0.5260R-squared 0.921026 Mean dependent var 1933.175Adjusted R-squared 0.906667 S.D. dependent var 2431.757S.E. of regression 742.9113 Akaike info criterion 16.21666Sum squared resid 18213267 Schwarz criterion 16.51221Log likelihood -317.3332 F-statistic 64.14338Durbin-Watson stat 2.082671 Prob(F-statistic) 0.000000由表格可知，样本整体拟合优度达到92.1%，意味着模型解释变量整理能够解释因变量的92.1%，即说服力相对较强。
多重共线性检验实训报告
一、实训背景在计量经济学和统计分析中，多重共线性是指模型中的多个自变量之间存在高度的相关性。
这种相关性会导致回归系数估计的不稳定，影响模型的预测能力和解释力。
因此，对多重共线性进行检验和修正对于确保模型的准确性和可靠性至关重要。
本实训旨在通过实际操作，学习如何使用SPSS软件进行多重共线性检验，并探讨相应的修正方法。
二、实训目的1. 理解多重共线性的概念及其对模型的影响。
2. 掌握使用SPSS软件进行多重共线性检验的方法。
3. 学习识别多重共线性的存在，并掌握相应的修正方法。
4. 提高对计量经济学模型诊断和修正的实际操作能力。
三、实训内容1. 数据准备本实训使用的数据集为某城市房价与多个影响因素的相关数据，包括房价（被解释变量）和收入、教育水平、交通便利性、周边设施等（解释变量）。
2. SPSS软件操作（1）数据导入首先，将数据集导入SPSS软件。
在SPSS界面中，点击“文件”菜单，选择“打开”，找到数据文件并导入。
（2）多重共线性检验导入数据后，进行以下操作：a. 点击“分析”菜单，选择“回归”，再选择“线性”。
b. 将被解释变量拖入“因变量”框，将解释变量拖入“自变量”框。
c. 点击“统计”菜单，选择“共线性诊断”。
d. 点击“继续”，然后点击“确定”。
（3）结果分析SPSS会自动计算并显示多重共线性的检验结果，主要包括方差膨胀因子（VIF）和容忍度（Tolerance）。
3. 结果分析（1）方差膨胀因子（VIF）VIF用于衡量变量之间相关性的程度。
一般来说，VIF值大于10表示存在多重共线性问题。
本实训中，我们发现收入、教育水平和交通便利性三个变量的VIF值均大于10，说明这三个变量之间存在严重的多重共线性。
（2）容忍度（Tolerance）容忍度是VIF的倒数，用于衡量变量之间独立性的程度。
一般来说，容忍度值小于0.1表示存在多重共线性问题。
本实训中，我们发现收入、教育水平和交通便利性的容忍度值均小于0.1，进一步证实了这三个变量之间存在多重共线性。
多重共线性的检验和解决的实验报告1
多重共线性的检验和解决的实验报告1
实验三报告
⼀、实验⽬的：
1.掌握多重共线性的识别⽅法
2.能针对具体问题提出解决多重共线性问题的措施
⼆、实验步骤：
1 相关系数法检验多重共线性
( 1 )点击Eviews6.reg注册然后点击Eviews6.exe
(2) 在file —new —workfile 在start date 和end date 输⼊1960、1982点击确定
(3) 在proc中找到import输⼊Excel 表并在弹出的对话框中输⼊Y X2 X3 X4
X5 X6 检查数据输⼊是否正确
(4)在Eviews 编辑框中输⼊ls Y C X1 X2 X3 X4 进⾏回归，结果如下t值
检验不符合。
说明解释变量之间很可能存在多重共线性。
2 画图法检验是否存在多重共线性：
在quick 中点击Graph在弹出的对话框中输⼊X1 Y 、X2 Y、X3 Y X4 Y点击确定，分别选择scatter 选择带回归线，分别可以看出各⾃变量与Y之间的线性关系,也说明解释变量之间可能存在多重共线性。
综合以上两种检验说明解释变量之间存在多重共线性。
3多重共线性的补救措施（逐步回归法）:
（1）分别对四个⾃变量进⾏回归，选拟合优度最⼤的X1作为基本⽅程即Y=-12.45554+0.117845X1，采⽤逐步回归法分别对其进⾏回归
通过以上实验得到i i i x x x 321i 1856.38818.11036.05926.127y
+-+-= Y-X1-X2（留，可决系数升⾼，符号正确）-X3（留，可决系数升⾼，符号正确）
-X4（删，可决系数升⾼，X4的系数不显著）。
多重共线性实验报告
多重共线性实验报告多重共线性实验报告导言多重共线性是统计学中一个重要的问题，它指的是自变量之间存在高度相关性，从而导致回归模型的不稳定性和不可靠性。
本实验旨在通过构建多重共线性模型，探讨其对回归分析结果的影响，并提出相应的解决方案。
实验设计本实验采用了一个虚拟数据集，包含了10个自变量和一个因变量。
首先，我们通过计算自变量之间的相关系数矩阵，判断是否存在多重共线性。
然后，我们构建了一个多重共线性模型，并对其进行回归分析。
最后，我们比较了多重共线性模型和无多重共线性模型的结果，以及采取不同解决方案对结果的影响。
多重共线性检验通过计算自变量之间的相关系数矩阵，我们发现其中存在一些高度相关的自变量。
例如，自变量A和自变量B之间的相关系数为0.8，自变量C和自变量D之间的相关系数为0.7。
这些高度相关的自变量可能会导致多重共线性问题。
多重共线性模型为了模拟多重共线性的情况，我们构建了一个多重共线性模型。
该模型包含了自变量A、B、C和D，并假设它们之间存在高度相关性。
我们使用最小二乘法进行回归分析，并得到了模型的回归系数和显著性检验结果。
多重共线性模型的结果通过对多重共线性模型进行回归分析，我们发现自变量A和自变量B的回归系数都显著为0，而自变量C和自变量D的回归系数都显著为1。
这表明多重共线性模型无法准确估计自变量的影响。
此外，模型的显著性检验结果也不可靠，因为多重共线性导致了回归系数的不稳定性。
解决方案一：剔除相关性较高的自变量为了解决多重共线性问题，我们可以考虑剔除相关性较高的自变量。
在本实验中，我们选择剔除自变量B和自变量D，因为它们与其他自变量的相关系数较高。
重新进行回归分析后，我们发现模型的回归系数和显著性检验结果都变得更加稳定和可靠。
解决方案二：主成分分析另一个常用的解决多重共线性问题的方法是主成分分析。
主成分分析可以将原始自变量转换为一组无关的主成分，从而降低自变量之间的相关性。
在本实验中，我们对自变量进行主成分分析，并选择前两个主成分进行回归分析。
多重共线性试验报告
由上表可以看出，解释变量之间相关系数至少为0.824076大于0.8经比较可知，新加入X5的回归模型Y=f(x2,x5)，X5回归系数为负，不符合实际的经济意义且检验不通过；新加入X3的回归模型Y=f(x2,x3)及新加入X4的回归模型Y=f(x2,x4)但X3和X4回归系数的T检验不通过；新加入X2的回归模型Y=f(x2,x1)回归系数T检验通过，而且2R比一元回归模型Y=f(x2) 的2R提高，因此，为最优的二元回归模型，以此为基础，建立三元回归模型：Ls y c x2 x1 x3在X2、X1基础上，加入X3后的回归模型y=f( x2, x1, x3)，2R有所下降，且检验不显著；加入X4或X5后回归模型y =f(x2, x1 ,x4)或y =f( x2, x1, x5)回归系数T检验不显著，甚至X4的回归系数也不符合经济理论分析和经验判断；加入y =f( x2, x1, x5)与加入X4后的回归模型相同，X5回归系数经济意义不合理且相较而言加入X3后的回归模型y=f( x2, x1, x3)其回归系数经济合理，果，以此为基础，建立四元回归模型：经检验X4和X5的回归系数符号为负值，且X1与X5的T检验不显著。
逐步回归估计结果表：X2 X1 X3 X4 X5 2RY=f(x2) 0.8841(62.4859)0.9952Y=f(x2,x1) 0.4872(4.3234) 0.4159(3.5394)0.997047Y=f(x2,x3) 0.8066 0.053765 0.995251White Heteroskedasticity Test:F-statistic 0.900543 Probability 0.489763 Obs*R-squared 3.888230 Probability 0.421344例5．服装需求函数。
根据理论和经验分析，影响居民服装需求Y的主要因素有：可支配收入X、流动资产拥有量K、服装类价格指数P1和总物价指数P0 ，统计资料如下。
实验报告3 多重共线性
E V I E W S操作实验题目：多重共线性实验类型：基本操作实验目的：掌握利用Eviews进行多元线性回归；存在多重共线性的基础上掌握逐步回归法的基本操作；及方差扩大因子的计算方法。
实验内容：（按要求完成下面题目）4.6 理论上认为影响能源消费需求总量的因素主要有经济发展水平、收入水平、产业发展、人民生活水平提高、能源转换技术等因素。
为此，收集了中国能源消费总量Y (万吨标准煤)、国内生产总值(亿元)X1(代表经济发展水平)、国民总收入(亿元)X2(代表收入水平)、工业增加值(亿元)X3、建筑业增加值(亿元)X4、交通运输邮电业增加值(亿元)X5(代表产业发展水平及产业结构)、人均生活电力消费(千瓦小时)X6(代表人民生活水平提高)、能源加工转换效率(%)X7(代表能源转换技术)等在1985-2002年期间的统计要求：(1)建立对数线性多元回归模型(2)如果决定用表中全部变量作为解释变量，你预料会遇到多重共线性的问题吗？为什么？(3)如果有多重共线性，你准备怎样解决这个问题？明确你的假设并说明全部计算。
实验步骤：一、设定模型Y=β0+β1X1+β2X2+β3X3+β4X4+β5X5+β6X6+β7X7+u二、估计参数1、各解释变量的相关系数矩阵：X1 X2 X3 X4 X5 X6 X7X1 1.000000 0.9999780.9996710.9988680.9918430.9934890.722545X2 0.999978 1.000000.9997280.9989480.9912510.992990.725681X3 0.999671 0.9997281.000000.9989830.9909460.9921480.732289X4 0.998868 0.9989480.9989831.000000.9878390.9888740.737354X5 0.991843 0.9912510.9909460.9878391.000000.9988290.682852X6 0.993489 0.99299 0.9921480.9888740.9988291.000000.680992X7 0.722545 0.7256810.7322890.7373540.6828520.6809921.00000可以看出，各解释变量之间的相关系数较高，证明存在多重共线性。
多重共线性实验报告-lucas
多重共线性实验报告-l u c a s-CAL-FENGHAI.-(YICAI)-Company One1《计量经济学》实验报告四图6.4.1 Eviews 输出的回归结果分析：模型R 2=0.970391 0.9518852 R 可决系数很高，F 检验值52.43740，显著。
但当α=5%时，t 统计值=1.7613，X4和X5系数的t 检验不显著，同时X5的系数为负号不符合实际，这表明很可能存在多重共线性。
STEP2：检验计算各解释变量的相关系数，选择X1、X2、X3、X4、X5数据，点击“quick\group statistics\correlation ”的相关系数矩阵，见表6.4.1。
有相关系数矩阵可以看出：各解释变量相关之间的相关系数较高，证实存在严重多重共线性。
表6.4.1 自变量相关系数矩阵STEP3：消除多重共线性采用逐步回归的办法，检验和解决多重共线性问题。
分别作Y 对X1、X2、X3、X4、X5的一元回归，结果如表6.4.2。
Dependent Variable: Y Method: Least Squares Date: 05/12/03 Time: 13:56 Sample: 1974 1987 Included observations: 14Variable Coefficient Std. Error t-Statistic Prob.C -90.92074 19.32929 -4.703781 0.0005 X1 0.316925 0.026081 12.15161 0.0000R-squared 0.924841 Mean dependent var 142.7129 Adjusted R-squared 0.918578 S.D. dependent var 26.09805。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
实验报告
实验题目：多重共线性的研究指导老师：
学生一：
学生二：
实验时间：2011年10月
多重线性回归分析及其实验报告
实验目的：为了更好地了解财政收入构成，需要定量地分析影响财政收入的因素
模型设定及其估计：经分析，影响财政收入的主要因素，农业增加值X1，工业增加值X2，建筑业增加值X3，总人口X4，受灾面积X5.为此设定了如下形式的计量经济模型：
Y=β
1+β
2
X1+β
3
X2+β
4
X3+β
5
X4+β
6
X5+u0
其中，Y为财政收入（元），X1农业增加值（元），X2为工业增加值(元)，X3为建筑业增加值（元），X4为总人口（万人），X5为受灾面积（千公顷）
为估计模型参数，收集1978~2007年财政收入及其影响因素数据，如图：
1978~2007年财政收入及其影响因素数据
年份
财政收入CS/亿
元
农业增加值
NZ/亿元
工业增加值
GZ/亿元
建筑业增加
值JZZ/亿元
总人口
TPOP/万
人
受灾面积
SZM/千公顷1978 1132.3 1027.5 1607 138.2 96259 50790 1979 1146.6 1270.2 1769.7 143.8 97542 39370 1980 1159.9 1371.4 1996.5 195.5 98705 44526 1981 1175.8 1559.5 2048.5 207.1 100072 39790 1982 1212.3 1777.4 2162.3 220.7 101654 33130 1983 1367 1978.5 2375.8 270.6 103008 34710 1984 1642.5 2316.1 2789 316.7 104357 31890 1985 2004.6 2564.3 3448.5 417.9 105851 44365 1986 2122 2788.7 3987.5 525.7 107507 47170 1987 2199.4 3233 4565.9 665.8 109300 42090 1988 2357.6 3865.4 5062 810 111026 50870 1989 2664.5 5062 8087.3 794 112704 46991 1990 2937.4 5342.3 10284.5 859.4 114333 38474
1991 3149.48 5866.8 14188 1015.1 115823 55472 1992 3483.48 6963.6 19480.5 1415 117171 51333 1993 4348.95 9572.7 19480.4 2266.5 118517 48829 1994 5218.1 12315.7 24950.7 2964.7 119850 55043 1995 6242.2 14015.8 29447.6 3728.8 121121 45821 1996 7407.99 14441.8 32921.4 4387.4 122389 46898 1997 8615.14 14917.6 34018.4 4985.8 123626 53429 1998 9875.95 14944.5 40036 5172.1 124761 59145 1999 11444.08 15871.8 43580.6 5522.3 125786 49981 2000 13395.23 16537 47431.6 5913.7 126743 54688 2001 16386.04 17381.8 54945.5 6465.5 127627 52215 2002 18903.64 21412.7 65210 7490.8 128453 47119 2003 21715.25 22420 76912.6 8694.3 129227 54506 2004 26396.47 21224 87632.4 8967.8 129988 37106 2005 31649.29 22420 89834.5 10133.8 130756 38818 2006 38760.2 24040.9 91310.9 11851.1 131448 41091 2007 51321.45 28095 107367.2 14014.1 132129 48992
利用Eviews软件，生成Y、X1、X2、X3、X4、X5等数据，采用这
些数据进行OLS回归，结果如下
Dependent Variable: Y
Method: Least Squares
Date: 10/24/11 Time: 22:49
Sample: 1978 2007
Included observations: 30
Variable Coefficient Std. Error t-Statistic Prob.
C -6734.394 11259.37 -0.598115 0.5554
X1 -1.678611 0.328371 -5.111937 0.0000
X2 0.071078 0.081171 0.875666 0.3899
X3 5.699199 0.745591 7.643870 0.0000
X4 0.101481 0.114244 0.888277 0.3832
X5 -0.010922 0.057578 -0.189691 0.8511
R-squared 0.983660 Mean dependent var 10047.83
Adjusted R-squared 0.980255 S.D. dependent var 12585.61
S.E. of regression 1768.473 Akaike info criterion 17.97048
Sum squared resid 75059958 Schwarz criterion 18.25072
Log likelihood -263.5572 F-statistic 288.9512
Durbin-Watson stat 0.898668 Prob(F-statistic) 0.000000
由此可见，该模型R2=0.983660，R2=0.980255可决系数很高，F检验值为288.9512，明显显著。
但是，当 =0.05时，t a2/(n-k)=t025.0（30-6）=2.064,X2、X4的系数t检验不显著，而且X5的系数的符号与预期相反，这表明很可能存在严重的多从共线性。
相关系数矩阵
变量X1 X2 X3 X4 X5
X1 1.000000 0.969706 0.972734 0.946742 0.297017
X2 0.969706 1.000000 0.991036 0.880790 0.162275
X3 0.972734 0.991036 1.000000 0.875033 0.183445
X4 0.946742 0.880790 0.875033 1.000000 0.398598
X5 0.297017 0.162275 0.183445 0.398598 1.000000 由相关系数矩阵可以看出，各解释变量相互之间的相关系数较高，证实确实存在严重的多重共线性。
修正多重共线性：
采用逐步回归的方法，分别作Y对X1、X2、X3、X4、X5的一元回归：
一元回归估计结果
加入新变量的回归结果（一）
经比较，新加入X1的方程R2=0.98102,改进最大，而且各参数的T检验显著，选择保留X1，在加入其他变量逐步回归，结果如下：
加入新变量的回归结果（二）
在X1，X3基础上加上X2后的方程R 2有所改善，且各参数
的T 检验都显著。
而加入X4时，R 2
有所下降 ，且X4参数的T 检验变得不显著。
加入X5后，R 2
有所下降，X4参数的T 检验变得不显著，甚至X5
参数的符号也变得不合理。
保留X2，再加入其他新变量逐步回归，结果如下：
加入新变量的回归结果（三）
当加入X4，有所下降，参数的T 检验不显著。
加入X5 ，R 2也有
所下降，参数的T 检验不显著，且参数为负值不合理。
说明主要是
X4，X5引起了多重共线性，予以剔除。
最后修正多重共线性影响后的回归结果为：
Y=2957.433+1.457X1+0.082847X2+5.400387X3
T=4.555717 (-8.726769) (1.104935) (8.330814)
R2=0.983121 R2=0.981174 F=504.7988 DW=0.749673
这说明，在其他因素不变的情况下，当农业增加值每增加1元，工业增加值和建筑业增加值分别增加1元时，平均来说，财政收入将分别增加1.457元、0.082847元和5.400387元。