第八章 电路
第八章:集成运放放大电路

+
+ uo uo1 IR e
-
Rc
+ RL u -o2 T2 Rb E
u ic
uo= 0 (理想化)。
_V
Re
+ ui2 -
EE
共模电压放大倍数
Auc 0
8.2.3 具有恒流源的差分放大电路
根据共模抑制比公式: Re K CMR Rb rbe 加大Re,可以提高共模抑 制比。为此可用恒流源T3来 + 代替Re 。 u
8.2 差分放大电路
差分放大电路(Differential Amplifier) 又称差动放大电路,简称差放,是构成 多级直接耦合放大电路的基本单元电路。 它具有温漂小、便于集成等特点,常用 作集成运算放大器的输入级。
8.2.1 直接耦合放大电路的零点漂移现象 1. 零点漂移现象及其产生的原因 直接耦合放大电路在输入信号为零时, 会出现输出端的直流电位缓慢变化的现 象,称为零点漂移,简称零漂。
uo2 T2 Rb -
Au d
u i1 RL - ( Rc // )
u id
2
Rb rbe
2
+ ui2 -
+
ib
+
ic rbe β ib RL uo1
2
差模输入电阻:
+
Rid 2Rb rbe
输出电阻:
ui1 +
Rb
+
RC
-+
Ro 2Rc
(2)加入共模信号
ui1=ui2 =uic, uid=0。 设ui1 ,ui2 uo1 , uo2 。 因ui1 = ui2, uo1 = uo2
第八章 常用电气控制电路图

2.工作原理
当需要电动机停机时,按下停止按钮SB1, 该线路中的电动机在刚刚脱离三相交流电源时 ,由于电动机转子的惯性速度仍然很高,速度 继电器 KS的常开触点仍然处于闭合状态,所 以接触器KM2线圈能够依靠SB1按钮的按下通电 自锁。于是,两相定子绕组获得直流电源,电 动机进入能耗制动。当电动机转子的惯性速度 接近零时,KS常开触点复位,接触器KM2线圈 断电而释放,能耗制动结束。
图是一例转子绕组 串联若干级电阻,以 达到减少启动电流的 目的,在启动后逐级 切除电阻,使电动机 逐步正常运转的启动 按钮操作控制线路。 图中KM1为线路接触 器, KM2、KM3、KM4 为短接电阻启动接触 器。
2.工作原理
合上电源开关QS,按下启动按钮SB2,接触器 KM1得电,主触点闭合,电动机转子串联三组电 阻R1~R3作降压启动,在转速逐步升高电动机 转到一定时候时,逐次按下按钮SB3、SB4、SB5 ,接触器线圈KM2、KM3、KM4依次吸合,其常开 辅助触头KM2、KM3、KM4依次闭合并自锁,将三 组电阻逐一短接,使电动机投入正常运转。 应用范围:本线路适用于手动操作绕线式电 动机串联电阻启动的场合。
十三、速度原则控制的能耗制动控制线路
1.识图指导 图所示为速度原则控 制的能耗制动控制线路。 该线路与时间原则控制的 能耗制动控制线路基本相 同,这里仅是控制电路中 取消了时间继电器KT的线 圈及其触点电路,而在电 动机轴端安装了速度继电 器KS,并且用KS的常开触 点取代了KT延时打开的常 闭触点。
十四、两管整流能耗制动控制线路
图是由两只二极管构成的 电动机能耗制动控制线路图。 1.识图指导 由两只二极管整流的可正 转、反转能耗制动控制线路如 图8-14所示。该控制线路电动 机能正转、反转运行。停机时 ,切断三相交流电源,给定子 绕组通以直流电源,产生制动 转矩,阻止转子旋转。通过二 极管整流提供直流制动电流。
电力电子技术第八章 吸收电路..

第八章 吸收电路 Ls iLs Rs iDf Df uDf + T
Ls Io Cs
+ -
iLs(0)=Irr
Rs
Ud
N2 u0 U d N1
D
uCs(0)=0 Cs
iL
s
Ud 二极管被强制关断 T
Irr
Rs
阴极 阳极
Cs
+ uCs 返 回 上 页 下 页
第八章 吸收电路
假设斩波器工作
在连续电流模式,
第八章 吸收电路
将边界条件
uDf (0 ) I rr Rs 和
2 s
I rr Rs U d I rr R dt Cs Ls Ls 2 d uDf duDf 代入到 Ls Cs RsCs uDf U d 2 dt dt duDf (0 )
Ls I rr t 得:uDf (t ) U d e cosat Cs cos
8.2.3 吸收电路分析
通过变压器耦合
的单相二极管整流
器工作在线性区域。 变压器原边的开关 断开时,二极管开 始导通 。
Ud N1
Rs
Cs
N2
D
+
C0
u0 -
返 回
上 页
下 页
第八章 吸收电路
Rs
Ls iLs
Cs
N2 Ud N1
+ -
D
+ u0
iD
当变压器原边的开关闭合时,漏电感和二极
管中的电流逐渐减小。
始电流为Irr,吸收电路中电容上的初始电压假设为
零。
返 回
上 页
下 页
第八章 吸收电路
图中等效电路Rs=0,此时
第八章 正弦波振荡电路
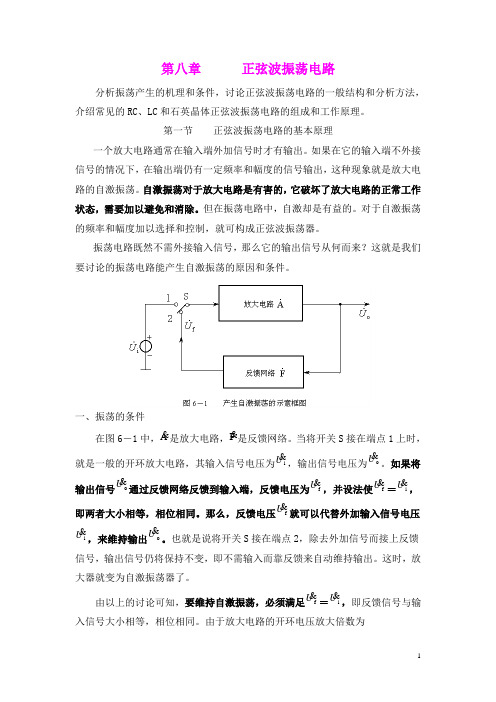
第八章 正弦波振荡电路分析振荡产生的机理和条件,讨论正弦波振荡电路的一般结构和分析方法,介绍常见的RC 、LC 和石英晶体正弦波振荡电路的组成和工作原理。
第一节 正弦波振荡电路的基本原理一个放大电路通常在输入端外加信号时才有输出。
如果在它的输入端不外接信号的情况下,在输出端仍有一定频率和幅度的信号输出,这种现象就是放大电路的自激振荡。
自激振荡对于放大电路是有害的,它破坏了放大电路的正常工作状态,需要加以避免和消除。
但在振荡电路中,自激却是有益的。
对于自激振荡的频率和幅度加以选择和控制,就可构成正弦波振荡器。
振荡电路既然不需外接输入信号,那么它的输出信号从何而来?这就是我们要讨论的振荡电路能产生自激振荡的原因和条件。
一、振荡的条件在图6-1中,A是放大电路,F 是反馈网络。
当将开关S 接在端点1上时,就是一般的开环放大电路,其输入信号电压为i U ,输出信号电压为o U 。
如果将输出信号o U 通过反馈网络反馈到输入端,反馈电压为f U ,并设法使f U=i U ,即两者大小相等,相位相同。
那么,反馈电压f U就可以代替外加输入信号电压i U ,来维持输出o U 。
也就是说将开关S 接在端点2,除去外加信号而接上反馈信号,输出信号仍将保持不变,即不需输入而靠反馈来自动维持输出。
这时,放大器就变为自激振荡器了。
由以上的讨论可知,要维持自激振荡,必须满足f U=i U ,即反馈信号与输入信号大小相等,相位相同。
由于放大电路的开环电压放大倍数为i o A U U = o f F U U =若i f U U =,则F A=o fi oU U U U =1(F A称为环路增益)。
因此,振荡电路维持自激振荡的条件是:F A=1 即F A=1称为幅值平衡条件。
其物理意义为:信号经放大电路和反馈网络构成的闭环回路后,幅值保持不变,既无增加也无衰减。
f a ϕϕ+=2n π(n =0,1,2……)称为相位平衡条件。
波形产生电路与变换电路

通常定义矩形波为高电平的时间T2与周期T之比为占空 比D, 即
D T2 T
第八章 波形产生电路与变换电路
R
RW
RW′
图
VD2
8–5
△
uC
- ∞ Ro
+
占
C
+
uo
空 比
可
调
R3 VDz3
R2
VDz4
±Uz
电 路
D T2 RW' rd1 R T RW rd1 rd2 2R
第八章 波形产生电路与变换电路
8.1.3 锯齿波产生电路
R3
△ △
R2
- ∞ Ro A1 +
uo1
+
VDz3
C VD1
RW′
RW VD2
-∞
A2 + +
uo
R′
VDz4
±Uz
R″
图 8 – 8 锯齿波产生电路
第八章 波形产生电路与变换电路
uo uo1
Uz
R2 R3
U
z
O
R2 R3
Uz
-Uz
T1
T2
第八章 波形产生电路与变换电路
8.1.2 三角波产生电路
R3
R2
C
△ △
- ∞ Ro A1 +
uo1 R
-∞
+ VDz1
A2 + +
uo
R′
±Uz
VDz2
R″
图 8 – 6 三角波产生电路
第八章 波形产生电路与变换电路
1. 工作原理
uo1
+Uz
O
t
-Uz
第8章 非正弦周期电流电路

I0(1) I1(1) I 2(1) 18.57 21.801 5.547 56.31
(20.319 j2.281) 20.446 6.405 A
u(3) =70.7cos(3t 30 )V 单独作用(图c)
70.7 U (3) 2 30 V 50 30 V
第八章 非正弦周期电流电路
非正弦周期电流电路:线性电路在非正弦周期电 源或直流电源与不同频率正弦电源的作用下,达到稳 态时的电路。 本章主要介绍非正弦周期电流电路的一种分析方 法:谐波分析法。
8-1 非正弦周期电流和电压 8-2 非正弦周期信号的傅立叶展开 8-3 非正弦周期量的有效值、平均值 和平均功率 8-4 非正弦周期电流电路的计算
其平均功率为
1 T P pdt T 0
代入 (8 7) 式展开有以下各项
1 T 0 U 0 I 0dt U 0 I 0 T
1 T 0 U mk cos(kt uk ) I mk cos(kt ik )dt U k I k cos( uk ik ) T 1 T 0 U 0 I mk cos(kt ik )dt 0 T 1 T 0 I 0U mk cos(kt uk )dt 0 T 1 T 0 U mk cos(kt uk ) I mn cos(nt in )dt 0 (k n) T
U 0 I 0 U k I k cos k
k 1
(8 8)
式中
I 0、U 0 为直流分量, I k、U k 为 k 次谐波有效值,
k uk ik
第k次谐波电压电流的相位差。
注意
直流与交流分量之间不产生平均功率;不同频率的 正弦分量之间也不产生平均功率。
第八章 交流电路

L
i B
u AB
由于电感元件内存在着自感电动势eL ,它本身就是 一个交流电源,当eL >0时A是这电源的负极,B是 它的正极;当eL<0时,电源的极性也跟着反过来。
18
电感上的电压 电压是指电位降落。电位降落的正 负与选择回路的绕行方向有关。 AC 如选择回路的绕行方向和电流的方 向一致,比如在上图的电路中也取 为顺时针方向,则电感元件上的电 位降落u(t)应指的是
由上式知,电容的功率以电流频率的二倍随时间变 化,瞬时值是时正时负的,这表明电容周期性地从 电源吸取能量又重新回馈回电源。一周期的平均功 率为 1 T 1 T PC 0 PC dt 0 IU C cos 2t dt 0 T T 2 这表明电容在电路中的作用仅是吞吐能量而并不消 耗能量。吞吐功率的最大值为
u( t ) U m cos(t u )
dq 得 i(t ) Qm sin t Qm cos(t ) dt 2
q Qm cos t 电容器上的电压与q成正比 u( t ) C C Qm u 0 i 可知 I m Qm U m 2 C
(3)电容有隔直流、通交流、高频短路的作用,电 感有阻高频、通低频的作用等。
25
(4)相位差在交流电路的元件组合电路中起着突出 的作用。单个元件在功率问题上相位差的作用也是很 重要的。 (5)实际元件严格说来都不是单纯的元件。实际元 件必定具有电阻、电容、电感几方面的综合特性, 可以作为纯元件的适当组合来处理。 。
Pn IU C I Z C
2
15
Pn 称为电容的无功功率。
PC
uC
i
t
16
例题1 一个25微法的电容元件,在20伏、50周电源的 作用下,电路中的电流为多少?将电源的频率改换 为500周,并保持电压不变,电流变为多少? U 2fCU ,当 U = 20 伏, f = 50 周时,代 解 I ZC
电工学第八章 基本放大电路

RL RC//RL
返回
(3)电压放大倍数的计算
•
•
Ui I b rbe
•
•
•
UoIcRL IbRL
式中 RL RC//RL 则放大电路的电压放大倍数
•
Au
U0
•
Ui
R' L rbe
输出端开路时(未接RL)
Au
RC rbe
结 论
❖ Au与β、rbe和并联电阻 有关;
❖负载电阻RL越小,放大倍数越小; ❖ 输入电压与输出电压相位相反。
返回
放大电路可分为静态和动态两种情况来分析。
动态:输入端加上输入信号时,放大电路的工作状态。
❖ 此时,电路中电流和电压值是直流和交流分量叠加。 ❖ iB、iC、iE、uBE和uCE,称为动态值(直流分量和交流 分量的叠加) ❖ 对放大电路的动态分析就是采用放大电路的交流通道, 确定电压放大倍数Au,输入电阻ri,输出电阻ro等。 ❖ 动态分析方法:微变等效电路法和图解法 直流通道——只考虑直流信号的分电路。 交流通道——只考虑交流信号的分电路。
步骤: ❖ 用估算法确定IB; ❖ 由输出特性曲线确定IC和UCE。
由 U CE U CC ICR C 得
IC=0时, UCEUCC
UCE=0时,I C
U CC RC
返回
(1)输入输出特性曲线
如下图所示,(IBQ,UBEQ) 和( ICQ,UCEQ )分别对 应于输入输出特性曲线上的一个点,称为静态工
0.0m 4 A40A
IC IB
3.750.04
1.5mA
U CE U CC ICR C
1 2 1.5 1 0 34 130
6V
返回
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
i , Im , I
§8. 3 相量法基础
两个正弦量的相加
i1 = 2 I1 co ω t +ψ1 ) s(
i2 =
2 I2 co ω t +ψ2 ) s(
角频率: 角频率: ω 有效值: 有效值:
u, i i1 I1
i1 0
ω
i2
i2 I2
i1+i2 →i3 i3 ω I3 ωt
初相位: 初相位: Ψ 1
不能比较相位差
(4) i1(t) = 5cos(100 t − 30 ) π
0
i2(t) = 3cos(100 t −1500 ) π
ϕ = −300 −(−1500 ) = 1200
i2(t) = −3cos(100 t + 30 ) π
0
两个正弦量进行相位比较时应满足同频率、同函数、 两个正弦量进行相位比较时应满足同频率、同函数、同符 且在主值范围比较。 号,且在主值范围比较。
jθ
A= a + jb
A=| A| e =| A| ∠ θ
jθ
A=| A| e
A=| A| e jθ =| A| (cosθ + j sinθ ) = a + jb
3)两种表示法的关系: 两种表示法的关系: 两种表示法的关系
Im b
A |A|
A=a+jb A=|A|ejθ =|A| θ
直角坐标表示 极坐标表示 0 或
R
交流i 交流
R
W = RI T
2
W = ∫ R (t)dt i
2 0
T
电流有效 值定义为
1 T 2 I= ∫0 i (t )dt T
def
有效值也称均方根值 (root-meen-square)
同样,可定义电压有效值: 同样,可定义电压有效值: 正弦电流、 正弦电流、电压的有效值 设 i(t)=Imcos(ω t+Ψ )
•
u(t) = 2Ucos(ω t +θ ) ⇔ U = U θ ∠
( 取实部: 对A(t)取实部: Re[A t)] = 取实部
2Icos(ω t +Ψ )
对于任意一个正弦时间函数都有唯一与其对应的复数函数
i = 2Icos(ω t +Ψ) ↔ A t) = 2Ie (
jψ
j(ω t+ ) Ψ
A(t)还可以写成 还可以写成
A t) = 2Ie ejωt = 2 I ejωt (
第8章
重点: 重点:
相量法
正弦量的表示、相位差; 1. 正弦量的表示、相位差; 2. 正弦量的相量表示 电路定理的相量形式; 3. 电路定理的相量形式;
8.1
1.复数 的表示形式 1.复数A的表示形式 复数 Im b
复数
) A=a+jb (j = −1 为虚数单位
Im b A |A|
A
θ
0 1) a Re 2) 0 a Re
复常数
•
A(t)包含了三要素:I、 Ψ 、ω ,复常数包含了Ι , Ψ 。 包含了三要素: 、 包含了三要素
对应的相量。 称 I = I∠ 为正弦量 i(t) 对应的相量。 Ψ
•
i (t ) = 2 I cos(ω t + φ ) ⇔ I = I ∠φ
相量的模表示正弦量的有效值 相量的幅角表示正弦量的初相位 同样可以建立正弦电压与相量的对应关系: 同样可以建立正弦电压与相量的对应关系:
ω = 2π f = 2π T
单位: 单位: rad/s ,弧度 / 秒 i Im O T 2π π tωt
初相位(initial phase angle)φ (3) 初相位 φ 反映正弦量的计时起点。 反映正弦量的计时起点。
Φ
同一个正弦量,计时起点不同,初相位不同。 同一个正弦量,计时起点不同,初相位不同。
Im = 2I
i(t) = Im cos(ω t +Ψ ) = 2I cos(ω t +Ψ )
同理,可得正弦电压有效值与最大值的关系: 同理,可得正弦电压有效值与最大值的关系:
U=
1 2
Um
或
Um = 2U
若一交流电压有效值为U=220V,则其最大值为Um≈311V; ,则其最大值为 若一交流电压有效值为 ; U=380V, , Um≈537V。 。 ) 工程上说的正弦电压、电流一般指有效值, 注 (1)工程上说的正弦电压、电流一般指有效值,如设 备铭牌额定值、电网的电压等级等 。 但绝缘水平 、 耐压值 备铭牌额定值 、 电网的电压等级等。 但绝缘水平、 指的是最大值。 因此, 指的是最大值 。 因此 , 在考虑电器设备的耐压水平时应按 最大值考虑。 最大值考虑。 (2)测量中,电磁式交流电压、电流表读数均为有效值。 )测量中,电磁式交流电压、电流表读数均为有效值。 (3)区分电压、电流的瞬时值、最大值、有效值的符号。 区分电压、电流的瞬时值、最大值、有效值的符号。
周期性电流、 4. 周期性电流、电压的有效值
周期性电流、电压的瞬时值随时间而变, 周期性电流、电压的瞬时值随时间而变,为了衡量其 大小工程上采用有效值来表示。 大小工程上采用有效值来表示。 周期电流、电压有效值 周期电流、电压有效值(effective value)定义 定义
直流I 直流
物 理 意 义
1 f = T
单位: , 兹 单位:Hz,赫(兹)
周期T 重复变化一次所需的时间。 单位: , 周期 :重复变化一次所需的时间。 单位:s,秒 频率f 每秒重复变化的次数。 频率 :每秒重复变化的次数。
2. 正弦量的三要素
i(t)=Imcos(ω t+ φ)
(1)幅值 振幅、 最大值) (1) 幅值 (amplitude) (振幅、 最大值)Im 反映正弦量变化幅度的大小。 反映正弦量变化幅度的大小。 角频率(angular frequency)ω (2) 角频率 相位变化的速度, 反映正弦量变化快慢。 相位变化的速度, 反映正弦量变化快慢。
都可以看成旋转因子。 故 +j, –j, -1 都可以看成旋转因子。
8.2 正弦量
正弦电流电路 激励和响应均为正弦量的电路称 为正弦电路或交流电路。 为正弦电路或交流电路。 i 波形: 波形: 瞬时值表达式: 瞬时值表达式: T O t
1. 正弦量
i(t)=Imcos(ω t+φ )
Ι
φ/ω
周期T 和频率f 周期 (period)和频率 (frequency) : 和频率
设 u(t)=Umcos(ω t+φu), i(t)=Imcos(ω t+ φ i) 则 相位差 :ϕ = (ω t+ φ u)- (ω t+ φ i)= φ u等于初相位之差
φi
规定: 规定: |ϕ | ≤π (180°)。 °。
• ϕ >0, u超前 ϕ 角,或i 滞后u ϕ 角(u 比i先到达最大值); 超前i 先到达最大值) 超前 先到达最大值 u, i u i O
Ψ2Leabharlann Ψ3因同频的正弦量相加仍得到同频的正弦量,所以, 因同频的正弦量相加仍得到同频的正弦量,所以,只 要确定初相位和有效值(或最大值)就行了。因此, 要确定初相位和有效值(或最大值)就行了。因此,
正弦量
复数
实际是变 换的思想
1正弦量的相量表示 造一个复函数
A t) = 2Ie (
j(ωt +Ψ)
( = 2Icos(ωt + Ψ) + j 2Isin ωt +Ψ)
θ
a Re
| A|= a2 + b2 b = ctg θ ar a 2.复数运算
a =| A| cosθ b =| A| sinθ
Im A2
图解法
(1)加减运算 (1)加减运算——采用代数形式 采用代数形式 加减运算 若 则
A1=a1+jb1, A2=a2+jb2 A1±A2=(a1±a2)+j(b1±b2)
o
= 180.2+ j126.2+ 2.238+ j6.329
= 182.5+ j132.5 = 225.5∠36o
旋转因子: (3) 旋转因子: 复数
Im
A• ejθ
θ A Re
ejθ =cosθ
+jsinθ =1∠θ ∠
0
A• ejθ 相当于 逆时针旋转一个角度θ ,而模不变。 相当于A逆时针旋转一个角度 而模不变。
5∠47 +10∠− 25 = ?
o
5∠47o +10∠− 25o = (3.41+ j3.657) +(9.063− j4.226)
= 12.47 − j0.569 = 12.48∠− 2.61o
例2.
解
(17 + j9) (4+ j6) 220∠35 + =? 20+ j5 19.24∠27.9o ×7.211∠56.3o 原 =180.2+ j126.2 + 式 20.62∠ .04o 14 = 180.2+ j126.2+ 6.728∠70.16o
φ uφ i ϕ 先到达最大值。 • ϕ <0, i 超前 uϕ 角,或u 滞后 i ϕ 角,i 比 u 先到达最大值。 ,
ωt
特殊相位关系: 特殊相位关系:
ϕ =±π (±180o ) ,反相: 反相: ±π ±
u, i u u i 0 u, i u i 0 iω t
ϕ = 0, 同相: 同相:
u, i
0 ϕ= π/2: π/2
ωt
u 超前 i π/2, 不说 u 滞后 i 3π/2; π/2 π ; i 滞后 u π/2, 不说 i 超前 u 3π/2。 π/2 π 。
