五年级下册数学试题——五升六讲义第10讲 约数与倍数(奥数版块) 北师大版【精品】
五年级奥数约数与倍数

理解记忆理论部分-☆星级☆约数和倍数;若整数a能够被b整除,a叫做b的倍数,b就叫做a的约数。
☆公约数:几个数公有的约数,叫做这几个数的公约数;其中最大的一个,叫做这几个数的最大公约数。
☆最大公约数的性质:1、几个数都除以它们的最大公约数,所得的几个商是互质数。
2、几个数的最大公约数都是这几个数的约数。
3、几个数的公约数,都是这几个数的最大公约数的约数。
4、几个数都乘以一个自然数m,所得的积的最大公约数等于这几个数的最大公约数乘以m。
例如:12的约数有1、2、3、4、6、1218的约数有:1、2、3、6、9、18那么12和18的公约数有:1、2、3、6那么12和18最大的公约数是:6记作(12,18)=6☆求最大公约数的基本方法:1、分解质因数法:先分解质因数,然后把相同的因数连乘起来。
2、短除法:先找公有的约数,然后相乘。
3、辗转相除法:每一次都用除数和余数相除,能够整除的那个余数,就是所求的最大公约数。
思维方法巩固训练部分-☆星级■经验规律总结:通过举例观察两个数的最大公约数与它们的和、差、积之间的关系。
1.求(26,78)、(196,165)、(55,84,141)2.两个自然数的和是88,最大公约数是8,求这两个数。
3.两个自然数的积是384,最大公约数是8,求这两个数。
4.已知两数的和是104055,这两个数的最大公约数是6937,求这两个数。
5.若两个数的积是5766,它们的最大公约数是31,求这两个数。
6.有男同学27人,女同学18人,一起去划船(每条船不超过6人),要保证每条船上男女同学都分别相等,应该租几条船?7.把一张长120厘米,宽80厘米的长方形的纸裁成同样大小的正方形(纸无剩余),至少能裁多少张?8.把长132厘米,宽60厘米,厚36厘米的木料,锯成尽可能大的同样的大小的正方体,求锯成的正方体的棱长与锯成的块数。
9.四个互不相同的自然数的积是370,求这四个数及它们的最大公约数。
(北京版)五年级数学下册 因数和倍数 课件

计算并观察下面的除法算式,你发现有哪几种不同的情况。
15÷5= 3 1.5÷5 0.3 =80÷20 4 =6÷5= 1.2
24÷4=6
3.6÷0.9 4 =24÷0.4=60 16÷3 5……1
=
除尽
15÷5=3 1.5÷5=0.3 80÷20=4 6÷5=1.2 24÷4=6 3.6÷0.9=4 24÷0.4=60
北京版五年级数学下册
教学目标
• 使大家进一步理解整除的意义。 • 使同学们掌握整除、因数与倍数的概念,
以及它们之间的相互依存关系,渗透辨 证唯物主义思想。 • 培养大家的抽象概括与观察思考的能力。
哪些是自然数?
5 0 7.1 1 0.2 2
哪些是自然数?
5 0 7.1 1 0.2 2
自然数都是整数.但我们在研究整除、因数和倍数时,所说的数都是指除 0以外的自然数.
32÷8=4 35÷0.7=50
40÷30=1 ……10 51÷17=3
20÷9=2……2 4.8÷1.2=4
4.2÷6=0.7
60÷5=12
如果数a能被数b整除,a就叫做b的倍数, ··
b就叫做a的约数或者因数。
例:15能被5整除,我们就说,15是5的 倍数,5是15的约数或因数。
如果数a能被数b整除,a就叫做b的倍数,
除尽
1.5÷5=0.3 6÷5=1. 32.6÷0.9= 424÷0.4=60
24÷4=6 3.6÷0.9=4 24÷0.4=60 16÷3=5…… 1
整除
15÷5= 3 24÷4= 6 80÷20 4 =
除尽包括整除。能除尽的不一定能整除, 能整除的一定能除尽。
试2:下面各题哪些是整除?哪些是除尽? 哪些都不是?为什么?
北京课改版五年级数学下册第三单元因数和倍数知识点汇总

第三单元因数和倍数一、因数和倍数1.在整数除法中,如果商是整数且没有余数,那么被除数就是除数和商的倍数,除数和商就是被除数的因数。
用字母表示:如果a÷b=c(a、b、c都是不为0的自然数),那么b、c就是a的因数,a就是b、c的倍数,因数和倍数是相互依存的。
2.因数和倍数的关系。
因数和倍数是两个不同但又互相依存的概念,二者不能单独存在,既不能单独说谁是倍数,也不能说单独说谁是因数,应该说谁是谁的倍数,谁是谁的因数。
3.求一个数的因数的方法。
(1)列乘法算式找:把这个数写成两个整数相乘的形式,算式中的每个整数都是这个数的因数。
(2)列除法算式找:用这个数分别除以大于等于1且小于等于它本身的所有整数,所得的商是整数且无余数时,这些除数和商就是这个数的因数。
4.表示一个数的因数的方法:列举法,集合法。
5.一个数的因数的特点:一个数的因数的个数是有限的,其中最小的因数是1,最大的因数是它的本身。
6.找一个数的倍数的方法。
(1)列乘法算式找:用这个数依次与非0自然数相乘,所得的积就是这个数的倍数。
(2)列除法算式找:哪些非0自然数除以这个数的商是整数且没有余数,这些非0自然数就是这个数的倍数。
7.表示一个数的倍数的方法:列举法,集合法。
8. 2的倍数的特征:个位上是0、2、4、6、8的数,都是2的倍数。
9. 5的倍数的特征:个位上是0或5的数,都是5的倍重点提示:在自然数中,0是一个特殊的数。
0乘任何数都等于0,所以0是任何一个非0自然数的倍数,任何非0自然数都是0的因数,因此,在研究因数和倍数时,我们所说的数指的是不包括0的自然数。
知识巧记:因数和倍数,单独不存在,互相来依靠,永远不分开。
重点提示:一个非0自然数既是它本身的倍数,又是它本身的因数。
易错题:判断:在自然数中,最小的奇数是1,最小的偶数是2。
( )。
错解分析:没有注意自然数0,0是最小的偶数。
数。
10.同时是2和5的倍数的特征:个位上是0的数,就同时是2和5的倍数。
五年级下册数学试题-五升六讲义第12讲图形周长(奥数版块)北师大版(含答案)
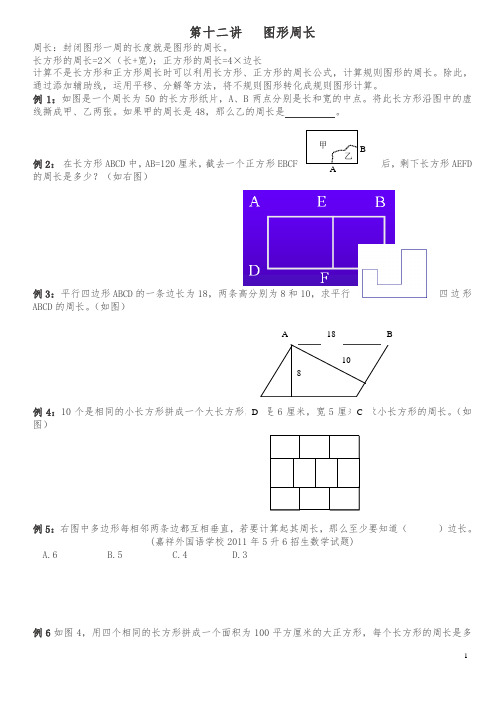
第十二讲 图形周长周长:封闭图形一周的长度就是图形的周长。
长方形的周长=2×(长+宽);正方形的周长=4×边长计算不是长方形和正方形周长时可以利用长方形、正方形的周长公式,计算规则图形的周长。
除此,通过添加辅助线,运用平移、分解等方法,将不规则图形转化成规则图形计算。
例1:如图是一个周长为50的长方形纸片,A 、B 两点分别是长和宽的中点。
将此长方形沿图中的虚线撕成甲、乙两张。
如果甲的周长是48,那么乙的周长是 。
例2: 在长方形ABCD 中,AB=120厘米,截去一个正方形EBCF 后,剩下长方形AEFD 的周长是多少?(如右图)例3:平行四边形ABCD 的一条边长为18,两条高分别为8和10,求平行四边形ABCD 的周长。
(如图)例4:10个是相同的小长方形拼成一个大长方形,长是6厘米,宽5厘米,求小长方形的周长。
(如图)例5:右图中多边形每相邻两条边都互相垂直,若要计算起其周长,那么至少要知道( )边长。
(嘉祥外国语学校2011年5升6招生数学试题)A.6B.5C.4D.3例6如图4,用四个相同的长方形拼成一个面积为100平方厘米的大正方形,每个长方形的周长是多甲 乙 A B BA CD 18 10 8少厘米?例7:如图.阴影部分是一个正方形.求大长方形的周长.巩固练习:1.6年级衔接班招生考试题)把一个边长为a的正方形,分成两个完全相等的长方形,这个两个长方形的周长之和是。
2.将长5厘米、宽2厘米的长方形硬纸片如图一层、二层、三层、……地排下去:(1)排到第5层,一周的长是()厘米。
(2)当周长为280厘米时,一共有()层。
3.求图2的周长4.如图6,在长方形ABCD中,AD=120厘米,截去一个正方形EDCF后,问还剩下长方形AEFB的周长是多少厘米?图45. 如图12 ,10个相同的小长方形拼成一个大长方形,长是6厘米,宽是5厘米,求小长方形的周长6.下图是一个公园的平面图,A 是公园的大门.问小明从A 门进公园,不重复地沿道路走公园一圈,他走了多少米?7.下图是某建设物的设计图,如图所示(单位米)现根据需要在它周围绕电线一圈,试求需电线多少米?8.用15个边长2厘米的小正方形摆成如下图的形状,求图形周长是多少厘米?9.下图是一块小麦地,已知条件如图中所示.这块地的周长是 米.10.下图“十”字的横与竖都长6厘米.问“十”间的周长是 厘米.11.求下图上“凹”形的周长.单位厘米50米 50米 1 3 51 1 1 1 12 33 4 4 360米 240米 A 图6 图1212.下图是由若干个相等的正方形组成的“土山”两个字,已知每个正方形的边长是3厘米,这两个字的周长分别是 、 .13.下图是由三个相同的长方形纸片组成的一个“5”字,已知长方形长4厘米,宽2厘米,“5”字周长是 厘米.14.把边长分别是5厘米、4厘米、3厘米和2厘米的4个正方形按从大到小的顺序排成一行(如图),排成的图形周长是多少厘米?15.将一张边长为12厘米的正方形纸对折,再将对折后的纸沿它的竖直中线(下图虚纸)剪开,得到三个矩形纸片,其中两个较小的矩形的周长之和是多少厘米?16.一个正方形被分成了5个相等的长方形.每个长方形的周长都是40厘米,求正方形的周长是多少厘米?如图所示.17.如图正方形ABCD 的边长为4cm,每边被四等分.求图中所有正方形周长的和.18.如图,长方形ABCD 中有一个正方形EFGH ,且AF=16厘米,HC=13厘米,求长方形ABCD 的周长是多少厘米。
北师大版本 数学五年级下册 倍数和因数

倍数与因数
4×9=36(人)
5×7=35(人)
认一认。
4×9=36
36是4的倍数,36也是9的倍 数,4和9都是36的因数。
5×7=35
35是5的倍数,35也是7的倍 数,5和7都是35的因数。
试一试
根据算式说一说哪个数是哪个数的倍数,哪个 数是哪个数的因数?
25×3=75
20×5=100
75是25和3的倍数 25和3是75的因数
100是20和5的倍数 20和5是100的因数
想想做做
讨论:哪个算式能说出谁是谁的倍数? 谁是谁的因数?
14×2=28 36÷4=9 15+4=19 13-7=6
注意:
我们只在自然数(零除外)范围内 研究倍数和因数。
请说出8和24,8和2谁是谁依存,不能单独存在 系
24
不能说8是倍数,8是因数
你能找出多少个3的倍数?
3 × 1=( 3 )
3 × 2=( 6 )
3 × 3=(
……
9
)
3的倍数有 3,6,9,12,15,18 ……
小蜗牛找倍数(找出3的倍数)。
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
1.
2.根据算式,说一说哪个数是哪个数的倍数,哪 个数是哪个数的因数。
14×6=84
20×7=140
45÷9=5
3.小兔子过河。
把9个珠子放在计数器的十位和 个位上,能拨出哪些数?这些 数与珠子的个数9有什么关系?
本节课我们主要学习了哪些 内容?同学之间互相讨论一 下!
试一试
2的倍数有 2,4,6,8,10,12…… 5的倍数有 5,10,15,20,25……
小学奥数教程:约数与倍数(二)全国通用(含答案)

1. 本讲主要对课本中的:约数、公约数、最大公约数;倍数、公倍数、最小公倍数性质的应用。
2. 本讲核心目标:让孩子对数字的本质结构有一个深入的认识,例如:(1)约数、公约数、最大公约数;倍数、公倍数、最小公倍数的内在关系;(2)整数唯一分解定理:让学生自己初步领悟“任何一个数字都可以表示为...⨯⨯⨯☆☆☆△△△的结构,而且表达形式唯一”一、 约数、公约数与最大公约数概念(1)约数:在正整数范围内约数又叫因数,整数a 能被整数b 整除,a 叫做b 的倍数,b 就叫做a 的约数;(2)公约数:如果一个整数同时是几个整数的约数,称这个整数为它们的“公约数”;(3)最大公约数:公约数中最大的一个就是最大公约数;(4)0被排除在约数与倍数之外1. 求最大公约数的方法①分解质因数法:先分解质因数,然后把相同的因数连乘起来.例如:2313711=⨯⨯,22252237=⨯⨯,所以(231,252)3721=⨯=;②短除法:先找出所有共有的约数,然后相乘.例如:2181239632,所以(12,18)236=⨯=;③辗转相除法:每一次都用除数和余数相除,能够整除的那个余数,就是所求的最大公约数.用辗转相除法求两个数的最大公约数的步骤如下:先用小的一个数除大的一个数,得第一个余数;再用第一个余数除小的一个数,得第二个余数;又用第二个余数除第一个余数,得第三个余数;这样逐次用后一个余数去除前一个余数,直到余数是0为止.那么,最后一个除数就是所求的最大公约数.(如果最后的除数是1,那么原来的两个数是互质的).例如,求600和1515的最大公约数:151********÷=;6003151285÷=;315285130÷=;28530915÷=;301520÷=;所以1515和600的最大公约数是15.2. 最大公约数的性质①几个数都除以它们的最大公约数,所得的几个商是互质数;②几个数的公约数,都是这几个数的最大公约数的约数;③几个数都乘以一个自然数n ,所得的积的最大公约数等于这几个数的最大公约数乘以n .3. 求一组分数的最大公约数先把带分数化成假分数,其他分数不变;求出各个分数的分母的最小公倍数a ;求出各个分数的分子的最大公约数b ;b a即为所求. 4. 约数、公约数最大公约数的关系(1)约数是对一个数说的;(2)公约数是最大公约数的约数,最大公约数是公约数的倍数知识点拨 教学目标5-4-2.约数与倍数(二)二、倍数的概念与最小公倍数(1)倍数:一个整数能够被另一整数整除,这个整数就是另一整数的倍数(2)公倍数:在两个或两个以上的自然数中,如果它们有相同的倍数,那么这些倍数就叫做它们的公倍数(3)最小公倍数:公倍数中最小的那个称为这些正整数的最小公倍数。
5年级奥数讲义(最大公约数最小公倍数)

第五讲最大公因数与最小公倍数 (教师版)例1、437与323的最大公约数是多少?基本概念:1、公约数和最大公约数 几个数公有的约数........,叫做这几个数的公约数..........;其中最大的一个.......,叫做这几个数的最大公约数............。
例如:12的约数有1,2,3,4,6,12;30的约数有1,2,3,5,6,10,15,30。
12和30的公约数有1,2,3,6,其中6是12和30的最大公约数。
一般地我们用(a,b )表示a,b 这两个自然数的最大公约数,如(12,30)=6。
如果(a,b )=1,则a,b 两个数是互质数。
2、公倍数和最小公倍数几个数公有的倍数,叫做这几个数的公倍数;其中最小的一个,叫做这几个数的最小公倍数。
例如:12的倍数有12,24,36,48,60,72,… 18的倍数有18,36,72,90,…12和18的公倍数有:36,72…其中36是12和 18的最小公倍数。
一般地,我们用[a,b]表示自然数,a,b 的最小公倍数,如[12,18]=36。
3、最大公约数与最小公倍数的求法A .最大公约数求两个数的最大公约数一般有以下几种方法 (1)分解质因数法 (2)短除法 (3)辗转相除法 (4)小数缩倍法 (5)公式法前两种方法在数学课本中已经学过,在这里我们主要介绍辗转相除法。
当两个整数不容易看出公约数时(一般是数字比较大),我们可以合用辗转相除法。
B .最小公倍数求几个数的最小公倍数的方法也有以下几种方法: (1)分解质因数法 (2)短除法 (3)大数翻倍法(4)a×b =(a,b )×[a,b]上面的公式表示:两个数的乘积等于这两个数的最大公约数和最小公倍数的乘积。
例2、24871和3468的最小公倍数是多少?练习254216933的最简分数是多少?例3、把一块长90厘米,宽42厘米的长方形铁板剪成边长都是整厘米,面积都相等的小正方形铁板,恰无剩余。
五年级下册数学试题-五升六讲义第4讲分数应用题(奥数板块)北师大版

一、量率对应 解答分数应用题首先应从分率入手找出单位“1”的量,如果单位“1”的量已知则用乘法解,如果单位“1”的量未知,则用除法解。
(1)已读了多少页例1一本书30页,已读了52, (2)还剩下多少页(3)已读的比剩下的少多少页全书的分率:( );已读的分率:( ) 剩下的分率:( );已读比剩下少的分率:( )练习1(1)白花多少朵红花有60朵,白花比红花多61, (2)白花比红花多多少朵(3)两种花一共有多少朵 红花的分率:( );白花的分率:( ); 白花比红花多的分率;( );两种花一共的分率:( )例2一辆汽车4小时行了全程的31,照这样的速度,再行几小时到达练习2:六(1)班,男生比女生少8人,女生比男生多31,全班多少人例3 小红看一本小说,第一天看总页数的121还多19页,第二天看的比总页数的81少17页,还余下93页,这本书共多少页练习3一批木料,先用去总数的52,又用去总数的94,这时用去的比剩下的多21方,这批木料共多少方二、抓不变量:解答较复杂的分数应用题时,我们往往从题目中找出不变量,把不变的量看做单位1,将已知条件进行转化,找出所求数量相当于单位1的几分之几,再列式解答。
例1:晶晶三天看完一本书,第一天看了全书的41,第二天看了的52,第二天比第一天多看了15页。
这本书共有多少页练习1:有一批货物,第一天运了这批货物的41,第二天运的是第一天的53,还剩90吨没有运。
这批货物有多少吨例2:甲数是乙数的32,乙数是丙数的43,甲、乙、丙的和是216。
甲、乙、丙各是多少练习2:甲数是乙数的65,乙数是丙数的43,甲、乙、丙的和是152。
甲、乙、丙各是多少例3:牛的头数比羊的头数多20%,羊的头数比牛的头数少几分之几练习3:甲仓存粮的吨数比乙仓的少25%,乙仓存粮的吨数比甲仓多几分之几例4:某工厂有三个车间,第一车间的人数占总人数的1,第二车间人数是第三车间的43。
已知第一车间比第二车间少40人,三个车间一共多少人练习4:图书角有故事书、科技书、文艺书这三种书,故事书的本书占总数的52,科技书的本书是文艺书的43,文艺书比故事书少20本。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十讲倍数与约数
一、最大公约数
知识点几个数公有的约数叫做这几个数的公约数,其中最大的一个公约数叫做这几个数的最大公约数。
我们可以把自然数a、b的最公约数记作(a、b),如果(a、b)=1,则a和b互质。
求几个数的最大公约数可以用分解质因数和短除法等方法。
一个自然数的约数个数为奇数个时,这个自然数是完全平方数.
求约数个数与所有约数的和的公式
1、求任一整数约数的个数
一个整数的约数的个数是在对其严格分解质因数后,将每个质因数的指数(次数)加1后所得的乘积。
如1400严格分解质因数之后为32
⨯⨯,所以它的约数有(3+1)×(2+1) ×(1+1)=4
257
×3×2=24个。
(包括1和1400本身)
2、求任一整数的所有约数的和
一个整数的所有约数的和是在对其严格分解质因数后,将它的每个质因数依次从1加至这个质因数的最高次幂求和,然后再将这些得到的和相乘,乘积便是这个合数的所有约数的和。
如:33
210002357
=⨯⨯⨯,所以21000所有约数的和为
2323
++++++++=
(1222)(13)(1555)(17)74880
例题1、12和15的公约数有哪些?其中最大的公约数是多少?
练习1、a=3×5×7,b=3×5×13,c=3×5×17,这三个数的最大公约数是多少?
例题2、(1)360的约数一共有多少个。
它所有约数的和是多少?
(2) 在1到100的所有自然数中,约数个数是奇数个的数一共有多少个?
练习2、(1)105有几个约数?它们的和是多少?
(2)1—100中只有三个约数的有哪些,这些数的和是多少?
例题3、一张长方形的纸,长75厘米,宽6分米。
现在要把它裁成一块块正方形,而且正方形边长为整厘米数,有几种裁法?如果要使裁得的正方形面积最大,可以裁多少块?
练习3、用一张长1072毫米、宽469毫米的长方形纸,剪成面积相等的正方形,并且最后没有剩余,这些正方形的边长最长是多少?
例题4、一个长方体木块,长2.7米,宽1.8分米,高1.5分米。
要把它切成大小相等的正方体木块,不许有剩余,正方体的棱长最大是多少分米?
练习4、一个长方体木块的长是45厘米、宽36厘米、高24厘米。
要把它切成大小相等的正方体木块,不许有剩余,求所切正方体木块的棱长最长是多少厘米?
例题5、一个数除200余4,除300余6,除500余10.求这个数最大是多少?
练习5、一个数除425余5,除500少4除300余6,这个数最大是多少?
例题6、一条道路由甲村经过乙村到丙村。
已知甲、乙村相距360米,乙、丙村相距675米。
现在准备在路边裁树,要求相邻两棵树之间距离相等,并在甲、乙两村和乙、丙两村的中点都要种上树,求相邻两棵树之间的距离最多是多少米?
练习6、一条公路由A经B到C。
已知A、B相距300米,B、C相距215米。
现在路边植树,要求相邻两树间的距离相等,并在B点及AB、BC的中点上都要植一棵,那么两树间的距离最多有多少米?
二、最小公倍数
知识点:几个数公有的倍数叫做这几个数的公倍数,其中最小的一个公倍数,叫做这几个数的最小公倍数。
自然数a、b的最小公倍数可以记作[a、b],当(a、b)=1时,[a、b]= a×b。
例题1、12和14的最小公倍数是多少?
练习1、3,5,12的最小公倍数是多少?
例题2、一个数,被3除余1,被4除余2,被7除余5,这样的数中最小一个是多少?
练习2、有一批水果,总数在1000以内,如果每24个装一箱,最后差2个;如果每28个装一箱,最后还是差2个;如果每32个装一箱,最后一箱只有30个。
这批水果共有多少个?
例题3、一块砖长20厘米,宽12厘米,厚6厘米。
要堆成正方体至少需要这样的砖头多少块?
练习3、有200块长6厘米、宽4厘米、高3厘米的长方体木块,要把这些木块堆成一个尽可能大的正方体,这个正方体的体积是多少立方厘米?
例题4、甲每秒跑3米,乙每秒跑4米,丙每秒跑2米,三人沿600米的环形跑道从同一地点同时同方向跑步,经过多少时间三人又同时从出发点出发?
练习4、一环形跑道长240米,甲、乙、丙从同一处同方向骑车而行,甲每秒行8米,乙每秒行6米,丙每秒行5米。
至少经过几分钟,三人再次从原出发点同时出发?
例题5、从学校到少年宫的这段公路上,一共有37根电线杆,原每两根电线杆之间相距50米,现在要改成每两根之间相距60米,除两端两根不需移动外,中途还有多少根不必移动?
练习五、插一排红旗共26面。
原每两面之间的距离是4米,现在改为5米。
如果起点一面不移动,还可以有几面不移动?
例题6、在一根长木棍上用红、黄、蓝三种颜色做标记,分别将木棍平均分成了10等份、12等份和15等份。
如果沿这三种标记把木棍锯断,木棍总共被锯成多少段?
练习六、用红笔在一根木棍上做了三次记号,第一次把木棍分成12等份,第二次把棍分成15等份,第三次把木棍分成20等份,然后沿着这些红记号把木棍锯开,一共锯成多少小段?
三、最大公约数和最小公倍数综合应用
知识点两个数的最大公因数和最小公倍数有着下列关系:
最大公因数×最小公倍数=两数的乘积,即(a,b)×[a,b]=a×b
例题1、两个数的最大公因数是15,最小公倍数是90,求这两个数分别是多少?
练习1、两个自然数的和是52,它们的最大公约数是4,最小公倍数是144,这两个数各是多少?
例题2、两个自然数的积是360,最小公倍数是120,这两个数各是多少?
练习2、已知两个数的最小公倍数是210,它们的积是1260.它们的和是72,求这两个数的差。
例题3、两个自然数的最大公约数是6,最小公倍数是180,这样的数共有几组?
练习三、最小公倍数是120,最大公约数为4的数共有几组?
课后练习:
1、下列判断中,正确的有()个。
A、1
B、2
C、3
D、4
①自然数a除以自然数b,商是4。
那么a是a与b的最小公倍数。
②两个面积相等的三角形,一定能拼成一个平行四边形。
③长方体的每个面一定都是长方形,而不可能有正方形。
④一个数,既是32的倍数,又是32的因数,那么这个数就是32。
⑤在小数点后面添上0或去掉0,小数的大小不变。
2、互质的两个合数,它们的最小公倍数是702,这两个数分别是、。
3、一个数,被10除余7,被7除余4,被4除余1,这样的数中最小一个是。
4、一个自然数,它的最小因数、最大因数、最小倍数之和恰好是2009,这个数是。
5、甲数=5
5⨯
4
⨯。
甲、乙两数的最大公因数是,最小公倍数4⨯
⨯,乙数=4
5
是。
6、某校五年级有学生若干人,若3人一排最后余1人,7人一排余5人,8人一排余6人,五年级至少有人。
7、甲数=2×3×5,乙数=2×2×7,丙数=2×3×7,甲、乙、丙的最大公因数是,最小公倍数。
8,这个分数是。
8、一个分数的分子与分母的和是161,约分后得
15
9、梨和苹果共100只,分给三年级的小朋友,每组分梨6只,苹果8只,梨正好分完,苹果还余2只,那么梨有只,苹果有只。
10、将一个长60分米、宽45分米的长方形铁皮剪割成若干个小正方形铁皮,如果铁皮正好没有剩余,那么至少剪割成个。
11、有连续的三个自然数a、1+
a,它们恰好分别为5、4、3的倍数,这三个自
+
a、2
然数中最小的数至少是.
12、沿湖的环形小路旁边每隔10米栽一颗柳树,每隔12米栽一颗腊梅,但如果位置重叠,就只栽腊梅。
李大爷沿湖散步一圈,发现共有柳树180颗,那么沿湖一周的长度是米。
13、某校五年级一班的同学开展活动。
若每2人分为一组,则敲好多出1人;若每3人分为一组,则恰好多出2人,若每7人分为一组,则恰好多出5人,那么,该班至少有人。
14、深冬的一个早晨,李明和他爸爸踏着积雪,一前一后沿着一个圆形跑道从同一起点朝同一方向跑步锻炼,爸爸每步50厘米,李明每步30厘米,雪地上脚印时有重合,一圈跑下,一共留有1680个脚印,这个跑道一圈的长度是多少米?
15、甲、乙、丙三人绕着400米的跑道跑步,甲每分钟跑50米,乙每分钟跑80米,丙每分钟跑100米,他们三人从同一起点出发,至少再过多少分钟,他们又能同时从同一起点出发?。
