4.4直线和圆的位置关系(1)
直线圆的位置关系1直线与圆的位置关系

返回目录
温故知新
要点探究
典例探究
法二:直线 l 的方程为 y=k(x-4),即 kx-y-4k=0.
圆心 O 到直线 l 的距离 d= | 4k | ,圆 O 的半径 r=2 2 . k2 1
(1)当 d= | 4k | <2 2 ,即-1<k<1 时,直线 l 与圆 O 相交. k2 1
(2)当 d= | 4k | =2 2 ,即 k=±1 时,直线 l 与圆 O 相切. k2 1
返回目录
温故知新
要点探究
典例探究
1.直线与圆有三种位置关系: (1)直线与圆相交,有两个公共点; (2)直线与圆相切,只有一个公共点; (3)直线与圆相离,没有公共点. 2.直线与圆的位置关系的判定方法: (1)代数法:直线与圆的方程联立消去 y(或 x)得到关于 x(或 y)的一元二次方程,此方程的判别式为 Δ,则
温故知新
要点探究
典例探究
返回目录
温故知新
要点探究
典例探究
探究要点一:直线与圆相交 1.直线与圆相交求交点坐标,只需联立两方程求解二元二次方程组即可. 2.直线与圆相交时弦长的求法 (1)求出交点坐标,利用两点间距离公式,求出弦长; (2)利用弦长公式求:
d=|x1-x2| 1 k 2 = (1 k 2 ) (x1 x2 )2 4x1x2
返回目录
温故知新
要点探究
典例探究
变式训练 1-1:已知圆 O:x2+y2=8,过 P(4,0)的直线 l 的斜率 k 在什么范围内取值时,直线 l 与圆 O: (1)相交?(2)相切?(3)相离?
解:法一:设直线 l 的方程为 y=k(x-4),
y k(x 4)
4[1].4_直线和圆的位置关系(1)
![4[1].4_直线和圆的位置关系(1)](https://img.taocdn.com/s3/m/272b487e1711cc7931b71641.png)
独立作业
11
驶向胜利 的彼岸
挑战自我
•
习题4.4
1-2题
•祝你成功!
‹# ›
结束寄语
下课了!
•具有丰富知识和经验的人,比 只须一种知识和经验更容易产 生新的联想和独到的见解。
‹# ›
义务教育课程标准实验教科书数学· 九年级· 上册(泰山版)
九年级数学(上)第四章: 对圆的进一步认识
5.直线和圆的位置关系(1) 切线及切线性质定理
直线与圆的位置关系
• 作一个圆,把直尺边缘看成一条直线.固定圆,平移直尺,
O O
●
●
O
●
相交
相切
相离
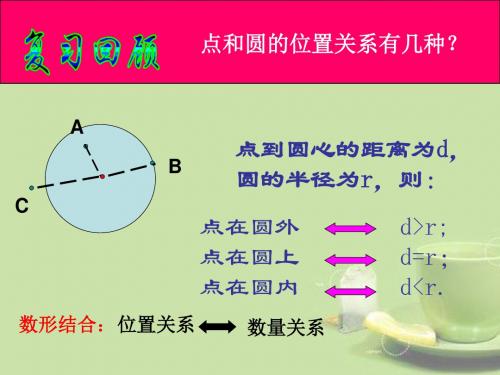
直线和圆有哪几种位置关系? 有三种位置关系: 直线和圆有惟一公共点(即直线和圆相切)时,这条直线 叫做圆的切线,这个惟一的公共点叫做切点.
d ┐ 相切
d ┐ 相离
• 直线和圆相交
d < r;
d = r;
直线和圆相切
直线和圆相离
d > r;
‹# ›
p58 T4-6
8
‹# ›
开启
智慧
驶向胜 利彼岸
‹# ›
例题欣赏
10
• 1.已知Rt△ABC的斜边AB=8cm,直角边AC=4cm. (1)以点C为圆心作圆,当半径为 多长时,AB与⊙C相切?
‹# ›
想一想6ຫໍສະໝຸດ 直线与圆的位置关系量化揭密
• 如图,圆心O到直线l的距离d与⊙O的半径r的大小有什 么关系?
r r
●
●
O ┐d
O
r
●
O
相交
d ┐ 相切
直线和圆的位置关系(1)

直线和圆的位置关系教学目标孟祥丽(一)教学知识点1.理解直线与圆有相交、相切、相离三种位置关系.2.了解切线的概念,探索切线与过切点的直径之间的关系.(二)能力训练1.经历探索直线与圆位置关系的过程,培养学生的探索能力.2.通过观察得出“圆心到直线的距离d和半径r的数量关系”与“直线和圆的位置关系”的对应与等价,从而实现位置关系与数量关系的相互转化.(三)情感与价值观通过探索直线与圆的位置关系的过程,体验数学活动充满着探索与创造,感受数学的严谨性以及数学结论的确定性.在数学学习活动中获得成功的体验,锻炼克服困难的意志,建立自信心.教学重点经历探索直线与圆位置关系的过程.理解直线与圆的三种位置关系.了解切线的概念以及切线的性质.教学难点:经历探索直线与圆的位置关系的过程,归纳总结出直线与圆的三种位置关系.探索圆的切线的性质.教学过程一.新课讲解1.复习点到直线的距离的定义如图,C为直线AB外一点,从C向AB引垂线,D为垂足,则线段CD即为点C到直线AB的距离.2.探索直线与圆的三种位置关系直线和圆有三种位置关系,如下图:它们分别是相交、相切、相离.当直线与圆相切时(即直线和圆有唯一公共点),这条直线叫做圆的切线,当直线与圆有两个公共点时,叫做直线和圆相交.当直线与圆没有公共点时,叫做直线和圆相离.投影片(§3.5.1A)(1)从公共点的个数来判断:直线与圆有两个公共点时,直线与圆相交;直线与圆有唯一公共点时,直线与圆相切;直线与圆没有公共点时,直线与圆相离.(2)从点到直线的距离d与半径r的大小关系来判断:d<r时,直线与圆相交;d=r时,直线与圆相切;d>r时,直线与圆相离.投影片(§3.5.1B)[例1]已知Rt△ABC的斜边AB=8cm,AC=4cm.(1)以点C为圆心作圆,当半径为多长时,AB与⊙C相切?(2)以点C为圆心,分别以2cm和4cm的长为半径作两个圆,这两个圆与AB分别有怎样的位置关系?3.议一议(投影片§3.5.1C)(1)你能举出生活中直线与圆相交、相切、相离的实例吗?(2)上图(1)中的三个图形是轴对称图形吗?如果是,你能画出它们的对称轴吗?(3)如图(2),直线CD与⊙O相切于点A,直径AB与直线CD有怎样的位置关系?说一说你的理由.小结本节课我们学习了那些内容?板书设计1.直线与圆的三种位置关系(1).相交:(2).相切;(3).相离2.直线与圆的位置关系从公共点数来判断:(1)唯一公共点(2)两个公共点(3)没有公共点3.从d与r间的数量关系来判断(1)d>r(2)d=r(3) d<r2.圆的切线的性质:圆的切线垂直于过切点的半径.课后反思。
直线和圆的位置关系(1)
在实际应用中,常采用第二种方法判定。
3、切线的性质:圆的切线垂直于过切点的直 径
拓展 已知⊙A的直径为6,点A的坐标为 (-3,-4),则x轴与⊙A的位置关系是 _相__离__, y轴与⊙A的位置关系是_相__切__。
出它们的对称轴吗?
相
离
B
2、右图,直线CD与⊙O相切于
点A,直径AB与直线CD有怎样的
●
O
位置关系?说说你的理由.
CA D
3、你看得懂小颖和小亮的做法吗?
点拨
B
小颖的理由是:
●O
∵右图是轴对称图形,
AB是对称轴,
C
A
D
∴沿直线AB对折图形时,AC与AD 重合,
∴ ∠BAC=∠BAD=90°.
利用圆的轴对称性
B
∴当∠r=A2=c6m0时°,.d>r,AB与⊙C相离
;因C当此Dr,=当4Ac半Cm径时si长n,dA为<r2,43AsBicn与m6时⊙0,0CAB相与2交⊙3.Cc相m切. .
B
C
1、如图,在Rt△ABC中,∠C=90°,AB=5cm,
A相C切=,3则cm这,个以圆C的为半圆径心是的圆与152AcmB 。
A
2、直线L 和⊙O有公共点,则直线L与⊙O( D ). A、相离;B、相切;C、相交;D、相切或相交。
3.⊙O的半径为3 ,圆心O到直线l的距离为d,若直线l
与⊙O没有公共点,则d为( A):
A.d >3 B.d<3 C.d ≤3 D.d =3
4.判断:若直线和圆相切,则该直线和圆一定有一个公共
直线和圆的位置关系(1)角度问题

归纳:连半径,证垂直,得切线
强调:到圆心的距离等于半径的直线是的切线;
归纳:作垂直,证半径,得切线
2.切线的性质 切线的性质定理: 圆的切线垂直于经过切点的半径;
常用辅助线 圆心与切点的连线
1、切线长: 在经过圆外一点的切线上, 这点和切点之间的线段的长, 叫做这点到圆的切线长。
2、切线长定理:从圆外一点引圆的两条切线, 它们的切线长相等, 圆心和这一点的连线平分这 两条切线的夹角。
公共点情况
相切
•O rd 1 d=r
相离
r O• d 0 d>r
d与r的数量关系
1.切线的判定方法 (1)和圆只有一个公共点的直线是圆的切线; (2)到圆心的距离等于半径的直线是的圆的切线; (3)过半径外端点且和这条半径垂直的直线是圆
的切线.
常用辅助线 强调:过半径外端点且和这条半径垂直的直线是
的外接圆。 (Ⅰ)求证:AC是⊙O的切线。 (Ⅱ)当BD是⊙O的直径时(如图②), 求∠CAD的度数。
3.(2012天津22题)已知⊙O中,AC为直径, MA,MB分别切⊙O于点A,B。 (Ⅰ)如图①,若∠BAC=25°,
求∠AMB的大小。
(Ⅱ)如图②,过点B作BD⊥AC于点E, 交⊙O于点D,若BD=MA,求∠AMB的大小。
1、三角形内切圆的定义:
与三角形各边都相切的圆叫做三角形的内切圆。 三角形的内切圆
O
圆的外切三角形
2、三角形内心的定义:
三角形内切圆的圆心叫做三角形的内心, 内心是三角形三条角平分线的交点,它到三边 的距离相等。
A
E F
O
B
C
D
知识网络
相离d>r 相切d=r
直线与圆的位置关系(一)

直线与圆的位置关系(一)指教:江苏省丹阳市第五中学 林伟民(特级教师)一.教学目标1.依据直线和圆的方程,能熟练求出它们的交点坐标;2.掌握通过利用圆心到直线的距离和圆的半径来判断直线和圆的位置关系;3.掌握通过联立直线和圆方程的方程组的解的个数来研究直线和圆的位置关系;4.会求直线被圆截得的弦长;二.教学重点判断直线和圆的位置关系三.教学难点判断直线和圆的位置关系时设方程要注重斜率的讨论四.教学过程1.直线和圆的位置关系:2.直线和圆的位置关系判断方法: (1)几何法:(考察圆心到直线的距离d 与圆的半径的关系)当 时,直线和圆相交; 当 时,直线和圆相切; 当 时,直线和圆相离. (2)代数法:将直线和圆的方程联立,考察方程组220Ax By C x y Dx Ey F ++=⎧⎨++++=⎩, 消元后:得20axbx c ++=,设其判别式为∆,则:∆ ⇔直线与圆相交;∆ ⇔直线和圆相切; ∆ ⇔直线和圆相离.小结:图 形位置关系 几何特征 公共点个数代数特征3.直线被圆截得的弦长:当直线和圆有两个交点时,设弦长为l ,弦心距为d ,半径为r ,则有l =例1:判断下列各组中直线l 与圆C 的关系:① :10l x y +-= 22:4C x y += ② :4380l x y --= ()22:11C x y ++= ③ :40l x y +-= 22:20C x y x ++=例2:已知直线y x b =+,圆的方程是222x y +=; 当b 为何值时,圆与直线: ① 无公共点?② 有一个公共点? ③ 有两个公共点?例3: 求直线230x y +-=被圆22(2)(1)4x y -++=截得的弦长;变式:① 以点(1,3)为圆心,被直线3470x y --=截得弦长为245的圆方程;② 若直线过点(3,6),且被圆2225x y +=截得弦长为8,求直线方程.探究一:若直线经过的点在圆上或圆内,弦长为8,满足条件的直线有几条?(两条)探究二,若直线过点(3,6),被圆2225x y +=截得的弦长为多少时,满足条件的直线只有一条?(弦长为10,此时直线过圆心,截得的弦正好为直径。
直线和圆的位置关系(1)

16.已知:如图,PA 切⊙O 于 A 点,PO 交⊙O 于 B 点.PA=15cm,PB=9cm. 求⊙O 的半径长.
4
鸡西市第十九中学初四数学组
5
9.已知:如图,△ABC 内接于⊙O,过 A 点作直线 DE,当∠BAE=∠C 时,试确定直线 DE 与⊙O 的位置关系,并证明你的结论.
10.已知:如图,割线 ABC 与⊙O 相交于 B,C 两点,E 是 若∠EDA=∠AMD. 求证:AD 是⊙O 的切线.
的中点,D 是⊙O 上一点,
11.已知:如图,Rt△ABC 中,∠ACB=90°,以 AC 为直径的半圆 O 交 AB 于 F,E 是 BC 的中点.求证:直线 EF 是半圆 O 的切线.
例 2.如图,已知 RtABC 的斜边 AB 8cm , AC 4cm .⑴ 以点 C 为圆心作圆,当半径为 多长时,直线 AB 与⊙C 相切?为什么?⑵ 以点 C 为圆心,分别以 2cm 和 4cm 为半径作 两个圆,这两个圆与直线 AB 分别有怎样的位置关系?
【当堂训练】
1.直线与圆在同一平面上做相对运动时,其位置关系有______种,它们分别是 ____________ 2.直线和圆_________时,叫做直线和圆相交,这条直线叫做____________. 直线和圆_________时,叫做直线和圆相切,这条直线叫做____________. 这个公共点叫做_________. 直线和圆____________时,叫做直线和圆相离. 3.设⊙O 的半径为 r,圆心 O 到直线 l 的距离为 d, _________ 直线 l 和圆 O 相离; _________ 直线 l 和圆 O 相切; _________ 直线 l 和圆 O 相交. 4.圆的切线的性质定理是__________________________________________.
直线与圆的位置关系(1)

《直线与圆的位置关系(1)》教学设计1.学习目标描述(知识与技能、过程与方法、情感态度与价值观)知识与技能:1.利用投影演示探索直线和圆的运动变化过程,经历直线与圆的三种位置关系得产生过程;2.在运动中体验直线与圆的位置关系,并观察理解直线与圆的“公共点的个数”的变化,培养猜想、分析、概括、归纳能力.3.正确判别直线与圆的位置关系,或根据直线与圆的位置关系正确的得出圆心到直线的距离与圆的半径之间的大小关系或直线与圆的公共点的个数.情感态度与价值观:1.通过本节课的学习,深刻体会直线与圆的位置关系在生活中的广泛存在和运用价值,激发学生的学习兴趣,使学生主动参与数学学习活动。
2.在判别直线与圆的位置关系中进一步培养学生观察、分析、归纳、概括等一般能力和审美能力。
2. 学习重难点分析图片电脑演示:海上日出1.观察三幅太阳升起的照片,地平线与太阳的位置关系是怎样的?2.观察三幅太阳落山的照片,地平线与太阳的位置关系是怎样的?你发现这个自然现象反映出直线和圆的位置关系有哪几种?观察图形,归纳出直线和圆的位置关系的定义及相关概画出圆心到直线关系。
学生学生回答后,教师总结并板书:如果⊙O的半径w为r ,圆心O 到直线l的距离为d,,那么:(1)直线l和⊙O相学会用4560H pAB 例1、在Rt△ABC 中,∠C=90°,AC=3cm,BC=4cm,以C 为圆心,r为半径的圆与AB有怎样的位置关系?为什么?(1)r=2cm,(2)r=2.4cm,(3)r=3cm.(此题为课本第36页课内练习第1题的第2小题)分析:因为题中给出了⊙C的半径,所以解题的关键是求圆心到直线的距离,然后与r 比较,确定⊙C与A B的关系.例2、已知Rt△ABC的斜边AB=8cm,直角边AC=4cm. 以点C为圆心作圆,当半径为多长时,AB与⊙C相切?例2:点O为∠ABC平分线例3、(即课本的例2)如图,海中有一个小岛P,该岛四周12海里内暗礁.今有货轮四由西向东航行,开始在A点观测P在北偏东60°处, 行驶10海里后到达B点观测P在北偏东45°处,货轮继续向东航行.你认为货轮继续向东航行途中会有触礁的危险吗?分析:要解决这个问题,首先要把它转化为学生和老师一起解AC DB。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、点和圆的位置关系有几种?
(1)d<r (2)d=r (3)d>r 点在圆内 点在圆上 点 在圆外
2、“大漠孤烟直,长河落日圆” 是唐朝诗人王 维的诗句,它描述了黄昏日落时分塞外特有的景 象。如果我们把太阳看成一个圆,地平线看成一 条直线,那你能根据直线与圆的公共点的个数想象 一下,直线和圆的位置关系有几种?
你发现这个自然现象反映出直线和圆的位置关系有哪几种?
a(地平线)
(3) (2) (1)
观察三幅太阳落山的照片,地平线与太阳的位置关 系是怎样的?
直线和圆的位置关系
O O O
l l l
(1)直线和圆没有公共点时,叫做直线和圆相离. (2)直线和圆有唯一公共点时,叫做直线和圆相切; 这时直线叫做圆的切线. 唯一的公共点叫做切点. (3)直线和圆有两个公共点时,叫做直线和圆相交, 这时直线叫做圆的割线,两个公共点叫做交点。
d = 5cm ; 3)若AB和⊙O相交,则 0cm≤ d < 5cm . 相交 3.直线和圆有2个交点,则直线和圆_________; 相切 直线和圆有1个交点,则直线和圆_________; 相离 直线和圆有没有交点,则直线和圆_________;
例1:在Rt△ABC中∠C= 90°AC=3cm,BC=4cm,以C为圆心,r 为半径的圆与斜边AB所在的直线有怎样的关系?为什么? (1) r=2cm (2) r=2.4cm (3) r=3cm
B
B B D
D
D C A
C
A
C
A
讨论:
在Rt△ABC中,∠C=90°,AC=3cm, BC=4cm,以C为圆心,r为半径作圆。
0cm<r<2.4cm 1、当r满足________________ 时,⊙C与直线AB相离。
B
r=2.4cm 2、当r满足____________ 时,⊙C与直线AB相切。
1、直线与圆相离、相切、相交的定义。切点 Nhomakorabea切线
交点
交点
割线
相离
相切
相交
直线和圆的位置关系是用直线和圆的公共点的个数 来定义的,即直线与圆没有公共点、只有一个公共点、 有两个公共点时分别叫做直线和圆相离、相切、相交。
思考:一条直线和一个圆,如果有公共点能不能多于 两个呢?
是是非非
1、直线与圆最多有两个公共 点 。…………………( √ )
.O
是是非非
2、若C为⊙O上的一点,则过点C的直线与 ⊙O相切。… … … …( × )
.O
.C
是是非非
3 、若A、B是⊙O外两点, 则直线AB 与⊙O相离。… … … … …( × )
.A2
.A1 .A .O
.B2
.B1 .B
是是非非
4、若C为⊙O内一点,则过点C的
直线与⊙O相交。( √ )
B
5
4
D
C
3
A
已知等腰直角三角形的直角边长为2cm,以直角顶点为 圆心,以r为半径画圆,当r在何范围内取值时 (1)所画的圆与斜边所在的直线相交? (2)所画的圆与斜边相交?
作业: P129 A组 1题
希望大家如这朝阳,
越升越高!越开越艳!
5
4
3、当r满足 r>2.4cm ____________时, ⊙C与直线AB相交。
D
C
3
A
想一想?
r=2.4cm 当r满足___________ 或3cm<r≤4cm 时,⊙C与 _____________
线段AB只有一个公共点.
在Rt△ABC中,∠C=90°, AC=3cm,BC=4cm, 以C为圆心,r为半径作圆。
C .
O .
2、用圆心到直线的距离d和圆半径r的数量关系, 来揭示圆和直线的位置关系。
r o d l r o d l
r o d
l
(1)直线l 和⊙O相离 (2)直线l 和⊙O相切 (3)直线l 和⊙O相交
d>r d=r d<r
总结:
判定直线 与圆的位置关系的方法有____种: 两
直线 与圆的公共点 (1)根据定义,由________________
的个数来判断; 圆心到直线的距离d与半径r (2)根据性质,由_________________ 的关系来判断。
在实际应用中,常采用第二种方法判定。
r O d
┐
r O d
┐
O
r
l
d ┐
l
l
直线与圆的位置关系判定方法: 直线和圆的位置关系 公共点个数 圆心到直线距离 d 与半径 r 关系 公共点名称 直线名称 相离 0 d>r 无 无 相切 1 d=r 切点 切线 相交 2 d<r 交点 割线
三、练习与例题
1、已知圆的直径为13cm,设直线和圆心的距离为d : 2 1)若d=4.5cm ,则直线与圆 相交 , 直线与圆有____个公共点. 1 相切 2)若d=6.5cm ,则直线与圆______, 直线与圆有____个公共点. 相离 0 3)若d= 8 cm ,则直线与圆______, 直线与圆有____个公共点. 2、已知⊙O的半径为5cm, 圆心O与直线AB的距离为d, 根据 条件填写d的范围: 1)若AB和⊙O相离, 则 d > 5cm 2)若AB和⊙O相切, 则 ;
