2018九上第9周周末作业答案
九年级上学期英语周末作业(第9周)

九年级上学期英语周末作业(第9周)II.词汇。
( )1. — What did the teacher ask you to do?— To find the correct answers in ten seconds by myself.A. wrongB. cleverC. right() 2. —Will you go to the fair with Linda tomorrow?— Yes. I am certain that I will go there with her.A. sureB. freeC. sorry( )3. — Why do you look so worried?—Because I can’t solve the problem.I’m afraid I can’t pass the exam.A. faceB. deal withC. set off( ) 4. —Did you have a good time at Mary’s birthday party?— Yes. I was happy with everythingthat Mary arranged for us.A. was proud ofB. was pleased withC. was excited about( )5. — What were you doing when I called you last night?— I was filling the bath with water.A. making the bath filled ofB. cleaning the bath withC. making the bath full of( ) 6. Sorry, I took your books to my home by mistakeyesterday.A. in totalB. wronglyC. by accident( ) 7. She is my sister, so I have no reason to doubt her story.A. trustB. feel unsure aboutC. retell( ) 8. — Did the old woman know ____ truth?— Yes, she did. Her son was sent to ______ prison two years ago. It made her so sad.A. a; theB. the; theC. the; /( ) 9. — Is the ring made ______ gold?—Yes, it is. I also have a pendant (坠饰) and it is made of gold _______ the same weight.A. from; ofB. of; atC. of; of( ) 10. — The problem seems _____ to solve.— Yes. The manager seems ______ more people to help him.A. difficult; to callB. difficultly; callingC. difficultly; to call( )11. —_____ that you don’t add water into the pot.— OK. If I do that, the soup in the pot will ________.A. Make sure; run awayB. To be sure; run overC. Make sure; run over( ) 12. --- When will Jenny and T om come back?--- Jenny will be back ______ an hour and Tom will return ______ one o’clock.A. in, inB. after, afterC. in, after( ) 13. — Would you mind my _______ your computer?— _______. But it may not work well.A. to use ; SureB. using ; Go aheadC. using ; I’m afraid not( )14. — Does the man order his son ____the horse in his free time?— Yes. He hopes that his son can take part in the _____ in the coming competition.A. to ride; racingB. ride; boxingC. riding; racing( )15. — Does your sister have long _____hair?—Yes, she looks so beautiful. Andshe always wears a necklace made of _______ .A. golden; goldenB. gold; goldC. golden; goldⅢ. 语法填空。
苏教版九年级上册语文阶段第九周周末作业

九年级语文第九周周末试卷一、积累与运用(30分)(一).给加点字注音或根据拼音写汉字:(4分)怅wǎng()yān( )红nì( ) 烦jie()据精髓.( ) 瑰.( )宝zi sui( ) 拾()级(二)、填空、默写:(18分)1._________________________,是石缝间漏下的滴泉。
2.晓战随金鼓,_______________。
________________,直为斩楼兰。
3.___________________________,春风不度玉门关。
4.这正如地上的路;_____________________,______________,也便成了路。
5.然而我又不愿意他们因为要一气,都如我的辛苦展转而生活,6.关关雎鸠,_______________。
_________________,君子好逑。
7.,正是河豚欲上时。
8 ,死即举大名耳,。
9《关雎》首节写小伙子对理想配偶“求之不得”,只能将美好的愿望寄托在想像中的诗句是,。
”10.《蒹葭》中写意中人行踪的句子有“,。
”11.写出表明物候的两句古诗或谚语:,。
(三).选出对《格列佛游记》表述不准确的一项()(2分)A.格列佛历险的第一个地方是小人国利立浦特。
这是个十二分之一的缩微国度。
小人国的人为了把他这个庞然大物运到京城,动用了五百工匠,制造了一个长七英尺、宽四英尺、有二十个轮子的木架。
B.格列佛历险到大人国布罗卜丁奈格时经历了几件事,如,有一天他在草坪上玩耍,突然下起了一阵冰雹,他被一阵网球似的冰雹打得遍体鳞伤。
C.格列佛历险到日本,他管它叫飞鸟或浮岛。
岛的中心有一个直径大约五十码的陷窟,天文学家就从大圆顶洞进入这个陷窟口,这个陷窟口被称为“天文学家之洞”。
D.格列佛出外航海,当了船长。
他的部下共谋不轨,把他抛弃在不知名的陆地上。
举动理性、观察敏锐的一匹灰色斑马和一匹栗色马把他领进家里,他得到主人的帮助和教导,专心学习马国的语言。
苏科版数学九年级上册第九周周末作业
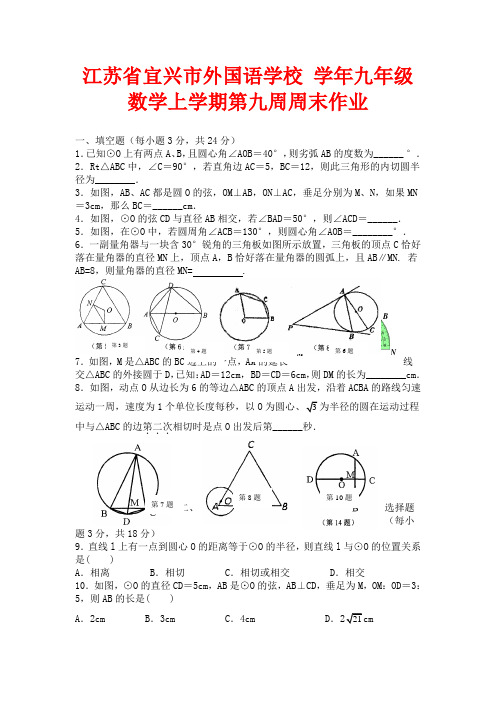
N M C BA 江苏省宜兴市外国语学校 学年九年级数学上学期第九周周末作业一、填空题(每小题3分,共24分)1.已知⊙O 上有两点A 、B ,且圆心角∠AOB =40°,则劣弧AB 的度数为______ °.2.Rt △ABC 中,∠C =90°,若直角边AC =5,BC =12,则此三角形的内切圆半径为________.3.如图,AB 、AC 都是圆O 的弦,OM ⊥AB ,ON ⊥AC ,垂足分别为M 、N ,如果MN =3cm ,那么BC =______cm .4.如图,⊙O 的弦CD 与直径AB 相交,若∠BAD =50°,则∠ACD =______.5.如图,在⊙O 中,若圆周角∠ACB =130°,则圆心角∠AOB =________°.6.一副量角器与一块含30°锐角的三角板如图所示放置,三角板的顶点C 恰好落在量角器的直径MN 上,顶点A ,B 恰好落在量角器的圆弧上,且AB ∥MN. 若AB=8,则量角器的直径MN= .7.如图,M 是△ABC 的BC 边上的一点,AM 的延长线交△ABC 的外接圆于D ,已知:AD =12cm , BD =CD =6cm ,则DM 的长为________cm .8.如图,动点O 从边长为6的等边△ABC 的顶点A 出发,沿着ACBA 的路线匀速运动一周,速度为1个单位长度每秒,以O 为圆心、3为半径的圆在运动过程中与△ABC 的边第二次...相切时是点O 出发后第______秒.二、选择题(每小题3分,共18分)9.直线l 上有一点到圆心O 的距离等于⊙O 的半径,则直线l 与⊙O 的位置关系是( )A .相离B .相切C .相切或相交D .相交10.如图,⊙O 的直径CD =5cm ,AB 是⊙O 的弦,AB ⊥CD ,垂足为M ,OM :OD =3:5,则AB 的长是( )A .2cmB .3cmC .4cmD .221cm第10题第3题第4题 第5题第6题 第7题 第8题11. ⊙O 是等边三角形ABC 的外接圆,⊙O 的半径为2,则等边三角形ABC 的边长为( )A .3B .5C . 23D .2512.10.如图,由等边三角形、正方形、圆组成的轴对称图案等边三角形与三个正方形的面积和的比值为( )A .32B .1C .3D .33213.如图,在平面直角坐标系中,⊙P 的圆心是(2,a)(a>2),半径为2,函数y =x 的图象被OP 所截的弦AB 的长为23,则a 的值是( )A .23B .2+2C .22D .2+314.如图,MN 是半径为1的⊙O 的直径,点A 在⊙O 上,∠AMN =30°,B 为AN 弧的中点,点P 是直径MN 上一个动点,则PA +PB 的最小值为( )A .22B .2C .1D .2三、解答题(共6大题,共58分.解答应写出必要的计算过程、推理步骤或文字说明.)15.(本题满分10分)某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径.下图是水平放置的破裂管道有水部分的截面.(1)作图题:请你用圆规、直尺作出这个输水管道的圆形截面的圆心;(不写作法,保留作图痕迹)(2)若这个输水管道有水部分的水面宽AB =8,水面最深的地方的高度为2,求这个圆形截面的半径.19.如图,四边形ABCD 内接于⊙O ,并且AD 是⊙O 的直径,C 是弧BD 的中点,AB 和DC 的延长线交于⊙O 外一点E.求证:BC=EC.第12题第13题 第14题21、如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在»AD上.(1)求∠E的度数;(2)连接OD、OE,当∠DOE=90°时,AE恰好为⊙O的内接正n边形的一边,求n的值.22、已知:如图,△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.(1)求证:∠DAC=∠DBA;(2)求证:P是线段AF的中点;(3)连接CD,若CD﹦3,BD﹦4,求⊙O的半径和DE的长.23、先阅读材料,再解答问题:小明同学在学习与圆有关的角时了解到:在同圆或等圆中,同弧(或等弧)所对的圆周角相等.如图,点A、B、C、D均为⊙O上的点,则有∠C=∠D.小明还发现,若点E在⊙O外,且与点D在直线AB同侧,则有∠D >∠E.请你参考小明得出的结论,解答下列问题:如图1,在平面直角坐标系xOy中,点A的坐标为(0,7),点B的坐标为(0,3),点C的坐标为(3,0) .①在图1中作出△ABC的外接圆;②若在x轴的正半轴上有一点D,且∠ACB =∠ADB,则点D的坐标为;(2) 如图2,在平面直角坐标系xOy中,点A的坐标为(0,m),点B的坐标为(0,n),其中m>n>0.点P为x轴正半轴上的一个动点,当∠APB此时点P的坐标.24、如图,以点P(﹣1,0)为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=2,将△ABC绕点P旋转180°,得到△MCB.(1)求B、C两点的坐标;(2)请在图中画出线段MB、MC,并判断四边形ACMB 的形状(不必证明),求出点M的坐标;(3)动直线l从与BM重合的位置开始绕点B顺时针旋转,到与BC重合时停止,设直线l与CM交点为E,点Q为BE的中点,过点E作EG⊥BC于G,连接MQ、QG.请问在旋转过程中∠MQG的大小是否变化?若不变,求出∠MQG的度数;若变化,请说明理由.。
周末作业九答案

(4)该实验物体的速度是指物体A从斜面上由静止滚下与物体B即将碰撞时的速度,它是通过(选填“高度”或“质量”)来改变的
(5)实验表明,同一物体A从斜面高处滚下,高度越大,物体B被撞得越远,可得结论
(6)若要研究物体动能与质量的关系,则需不同质量的物体从斜面高度由静止滚下,并观察记录.
(2)转化法:实验中通过小球对木块做功的多少来反映动能的大小;
(3)根据步骤一和步骤二中小球的不同高度来判断其移动距离大小;
【解答】解:
(1)分析步骤一、二,可以发现:采用了同一物体,质量是不变的,从不同高度处滚下,速度是不同的,是想探究动能大小与速度的关系;
(2)小球动能的大小是通过比较木块被推动距离的长短得出的,该实验中物体的动能是指小球撞击滑块时的动能.
(4)比较A、B两球,发现B球陷入沙深度更大,由此 可得出结论:.
(5)小球在下落过程陷入沙面前,将重力势能转化为能,陷入沙中后到小球静止过程中,将机械能转化为能.
四、计算题
14、一辆小汽车在平直公路上匀速行驶,发动机的牵引力为2000N,速度为108km/h.
(1)求小汽车匀速行驶时受到的阻力大小.
(2)求牵引力在10min内所做的功.
(3)若发动机的牵引力用F表示,小汽车的速度用v表示,请推导出牵引力的功率P=Fv.
参考答案
一、选择题
1、D【考点】速度公式及其应用;惯性;动能大小的比较.
【分析】(1)惯性是物体的一种属性,惯性大小只与物体的质量有关;
(2)比较两小车在相等的时间内通过的路程,判断其速度大小;然后根据动能大小的影响因素判断其动能的大小;
三、实验,探究题
10、
11、(1)速度;(2)A; (3)B被撞的距离大小; (4)高度;(5)当物体质量相同时,物体的速度越大,动能越大;(6)相同
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018年九上第9周周末作业(参考答案)(请用红笔订正)一、 选择题: (每小题3分,共30分)11、______4_________ 12、21y x =- 13、_____6__________14、_____8cm____15、_____60π_______16、_____1_______三、解答题:(本大题共9小题,满分102分.解答应写出文字说明、证明过程或演算步骤.)17. (本小题满分9分)解下列方程(1)2(1)4x -= (2)27100x x -+= (3)23620x x -+=(1)1212123,1x x x x -=-=-==-或 (2)122,5x x == (3)12x x ==每小题3分,方法不限。
18. (本小题满分9分)已知0342=+-x x ,求)x 1(21x 2+--)(的值.方法一:212222224301,34112(1)=1-1-21+1=-46=312(1)=3-1-21+3=-4812(1)=-49x x x x x x x x x x x x -+====--+--+∴--+分当时,()()()分当时,()()()分()分方法二2222243043(1)2(1)21224131849x x x x x x x x x x x -+=∴-=-∴--+=-+--=--=--=-4分6分7分分分19. (本小题满分10分)如图,在平面直角坐标系中,△ABC 的三个顶点坐标分别为A (2-,1-)、B (1-,1)、C (0,2-).学校 姓名 班级 考号(1) 点B 关于坐标原点O 对称的点的坐标为__________; (2) 将△ABC 绕点C 顺时针旋转 90,画出旋转后得到的△11A B C ;(3) 求旋转过程中点B 经过的路线长。
(1)(1,-1) 3分 (2)图略 3分(3)1BB l = 4分20.(本小题满分10分)如图,PA 、PB 是圆O 的切线,点A 、 B 分别为两切点,AC 是圆O 的直径,∠ACB =70°,求∠P 的度数。
解:连结AB∵ PA 、PB 是圆O 的切线∴ PA=PB 2分 ∴ ∠PAB=∠PBA 3分 又∵ AC 是圆O 的直径∴ ∠PAB+∠CAB=90°,∠CAB+∠C=90° 7分 ∴ ∠PAB=∠C=70° 8分 ∴ ∠PAB=∠PBA=∠C=70° 9分 ∴ ∠P =40° 10分 21. (本小题满分10分) 解:(1)214133y x x =-+ 3分 (2)只要画出大致图象即可给1分,顶点坐标1(2,)3-答对给1分,对称轴为直线:2x =,答对给1分,直接写成2x =也算对(3)当13x x <>或时,0>y ,全部答对给4分,答对一半给2分22. (本小题满分12分)如图,ABC △中,以AB 为直径的O ⊙交AC 于点D ,DBC BAC ∠=∠.(1)求证:BC 是O ⊙的切线;(2)若O ⊙的半径为2,30BAC ∠=°,求图中阴影部分的面积. (1)证:∵ AB 是圆O 的直径∴ ∠ADB=90° 2分 ∴ ∠A+∠ABD=90° 3分 又∵ DBC BAC ∠=∠∴ ∠DBC+∠ABD=90° 5分 ∴ BC 是O ⊙的切线 6分 (2)解:连结OD ∵ OA=OD ∴ ∠ADO=∠A=30°∴ ∠BOD=60° 8分∴B O D B O D 2=S -S 6021=-22s i n 60360223S ππ⨯⨯⨯⨯⨯=-△阴影扇形 12分 23. (本小题满分12分)某商场将每件进价为80元的某种商品原来按每件100元出售,一天可售出100件.后来经过市场调查,发现这种商品单价每降低1元,其销量可增加10件. (1)求商场经营该商品原来一天可获利润多少元? (2)设后来该商品每件降价x 元,商场每天可获利润y 元.① 若商场经营该商品一天要获利润2210元,则每件商品应降价多少元?② 求y 与x 之间的函数关系式,并根据关系式求出该商品如何定价可使商场所获利润最多?最多为多少?解:(1)原来每天可以获利:100(10080)2000⨯-= 2分 (2)① 设每件商品应降价x 元,则:212(10010x)(20x)2210x 102103,7x x x +⋅-=-+=== 7分②()()21001020101002000y x x x x =+-=-++ 10分当52b x a =-=时,2max 422504ac b y a-== 12分24. (本小题满分14分)已知抛物线2y ax bx c =++的对称轴为直线2x =,且与x 轴交于A 、B两点,与y 轴交于点C ,其中A (1,0),C (0,-3).(1)求抛物线的解析式;(2)若点P 在抛物线上运动(点P 异于点A ),①如图1,当△PBC 的面积与△ABC 的面积相等时,求点P 的坐标; ②如图2,当∠PCB =∠BCA 时,求直线CP 的解析式.解:(1)由题意,得0322a b c c ba⎧⎪++=⎪=-⎨⎪⎪-=⎩,解得43a b c =⎧⎪=⎨⎪=-⎩∴抛物线的解析式为243y x x =-+-. 3分(2)①令2430x x -+-=,解得1213x x ==, ∴B (3, 0) 则直线BC 的解析式为3y x =- 当点P 在x 轴上方时,如图1,过点A 作直线BC 的平行线交抛物线于点P ,∴设直线AP 的解析式为y x n =+,∵直线AP 过点A (1,0),∴直线AP 的解析式为1y x =-,交y 轴于点(01)E -,. 解方程组2143y x y x x =-⎧⎨=-+-⎩,得12121201x x y y ==⎧⎧⎨⎨==⎩⎩, ∴点1(21)P , 5分 当点P 在x 轴下方时,如图1,根据点(01)E -,,可知需把直线BC 向下平移2个单位,此时交抛物线于点23P P 、,得直线23P P 的解析式为5y x =-,解方程组2543y x y x x =-⎧⎨=-+-⎩,得1212x x y y ⎧⎧==⎪⎪⎪⎪⎨⎨⎪⎪=⎪⎪⎩⎩∴233737((2222P P --,,, 7分 综上所述,点P 的坐标为:1(21)P ,,23P P , 8分②过点B 作AB 的垂线,交CP 于点F .如图2,∵(30)(03)B C -,,, ∴OB =OC ,∴∠OCB =∠OBC =45° ∴∠CBF =∠ABC =45°又∵∠PCB =∠BCA ,BC =BC ∴△ACB ≌△FCB∴BF =BA =2,则点F (3,-2)又∵CP 过点F ,点C ∴直线CP 的解析式为133y x =-. 14分25. (本小题满分14分)如图,在平面直角坐标系xOy 中,矩形OABC 的边OA 、OC 分别在y 轴和x 轴的正半轴上,且长分别为m 、4m (m >0),D 为边AB 的中点,一抛物线l 经过点A 、D 及点M (﹣1,﹣1﹣m ).(1)求抛物线l 的解析式(用含m 的式子表示);(2)把△OAD 沿直线OD 折叠后点A 落在点A ′处,连接OA ′并延长与线段BC 的延长线交于点E ,若抛物线l 与线段CE 相交,求实数m 的取值范围;(3)在满足(2)的条件下,求出抛物线l 顶点P 到达最高位置时的坐标.解:(1)设抛物线l 的解析式为2y ax bx c =++,将A (0,m ),D (2m ,m ),M (﹣1,﹣1﹣m )三点的坐标代入,得2c m 4m a 2mb c m a b c 1m =⎧⎪++=⎨⎪-+=--⎩,解得a 1b 2m c m=-⎧⎪=⎨⎪=⎩。
2分 ∴抛物线l 的解析式为2y x 2mx m =-++。
3分 (2)设A ′D 与x 轴交于点M ,过点A ′作A ′N ⊥x 轴于点N , ∵把△OAD 沿直线OD 折叠后点A 落在点A ′处,∴△OAD ≌△OA ′D ,OA =OA ′=m ,AD =A ′D =2m ,∠OAD =∠OA ′D =90°,∠ADO =∠A ′DO 。
∵矩形OABC 中,AD ∥OC ,∴∠ADO =∠DOM 。
∴∠A ′DO =∠DOM 。
∴DM =OM 。
4分 设DM =OM =x ,则A ′M =2m ﹣x , 在Rt △OA ′M 中,∵OA ′2+A ′M 2=OM 2, ∴()222m 2m x x +-=,解得5x m 4=。
∵OA M11S OM A N OA A M 22∆'=⋅'='⋅',∴3m m 34A N m 55m 4⋅'==。
6分∴4ON m 5==。
∴A ′点坐标为(4m 5,3m 5-)。
7分 易求直线OA ′的解析式为3y x 4=-,当x =4m 时,3y 4m 3m 4=-⋅=-,∴E 点坐标为(4m ,3m -)。
当x =4m 时,()222y x 2mx m 4m 2m 4m m 8m m =-++=-+⋅+=-+, 8分 ∴抛物线l 与直线CE 的交点为(4m ,28m m -+)。
∵抛物线l 与线段CE 相交,∴23m 8m m 0-≤-+≤。
∵m >0,∴38m 10-≤-+≤,解得11m 82≤≤。
10分(3)∵()22211y x 2mx m x m m m m 82=-++=--++≤≤,, ∴当x =m 时,y 有最大值2m m +。
11分又∵2211m m m 24⎛⎫+=+- ⎪⎝⎭,∴当11m 82≤≤时,2m m +随m 的增大而增大。
12分 ∴当m =12时,顶点P 到达最高位置,22113m m 224⎛⎫+=+= ⎪⎝⎭。
∴此时抛物线l 顶点P 到达最高位置时的坐标为(12,34)。
14分。
